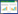文章信息
- 王亮, 安志朋, 史东华
- WANG Liang, AN Zhipeng, SHI Donghua
- 几何精确梁的Hamel场变分积分子
- Hamel's Field Variational Integrator of Geometrically Exact Beam
- 北京大学学报(自然科学版), 2016, 52(4): 692-698
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 692-698
-
文章历史
- 收稿日期: 2015-10-19
- 修回日期: 2016-03-14
- 网络出版日期: 2016-07-12
几何精确梁的动力学广泛存在于大范围运动的力学系统中, 例如, 可应用于柔性机器人[1], 使之可以做大量复杂的变形, 从而完成更多具有挑战性的工作; 也可用于聚合物长链的动力学模拟, 在研究DNA的动力学[2]中发挥重要作用。对于几何精确梁的模型, Reissner[3]首先提出大范围运动的应变梁模型, Antman等[4-5]在此基础上进行完善, 得到经典的Kirchhoff-Love模型。Simo等[6]在上述模型的基础上考虑剪切变形, 使之广泛适用于梁的大位移和大转动的运动情形。
在几何精确梁的数值模拟算法研究方面, 传统方法是直接对运动方程进行离散, 这类方法大都不能保持系统的力学和几何结构, 存在数值耗散问题, 不适用于长时间的运动模拟[7]。Marsden等[8]基于经典力学中Hamilton原理的离散形式, 提出的变分积分子在一定程度上可以克服上述缺陷。Lew等[9]指出, 变分积分子能够较好地保持系统的几何结构, 避免传统离散方法的数值耗散问题。对于几何精确梁, Demoures等[10]提出李群和李代数变分积分子, 得到保持能量和动量的几何算法, 但该算法对空间和时间分别离散, 没有充分利用势能的欧式群不变性进行约化, 实现过程较复杂。Ball等[11]对有限维系统提出Hamel变分积分子, 其框架可统一描述李群及李代数变分积分子, 尤其适用于带对称性的非完整约束力学系统。Shi等[12]将其在场论框架下推广, 得到Hamel场变分积分子。本文将其应用于几何精确梁, 得到一种新的保结构算法。
本文在回顾几何精确梁模型后, 重新推导几何精确梁的Hamel场方程, 进而用Hamel场变分积分子得到几何精确梁的离散运动方程。最后给出实例, 说明该算法能长时间保持能量、动量和几何结构的特点。
1 几何精确梁的动力学 1.1 几何精确梁的Lagrange函数首先回顾几何精确梁的动力学模型[13]。
取定物质标架的一组固定基{E1, E2, E3}, 初始时梁位于(E2, E3)平面上。设梁长为l, 密度为ρ, 截面
因几何精确梁的截面做刚体运动, 其位形由中线的位置函数
| $ \phi = (S + u,w,z):[0,l] \to {{\boldsymbol{\rm{R}}}^3} $ |
和截面的旋转矩阵
| $ \mathit{\Lambda }{\rm{:[0, }}l{\rm{]}} \to {\rm{SO(3)}} $ |
给出。
考虑主丛(E, B, πBE), 其中
| $ {\rm{E = B}} \times {\rm{SE}}(3),\;\;\;{\rm{B}} = \boldsymbol{{\rm{R}}} \times [{\rm{0}},{\rm{l}}], $ |
πBE为丛投影。梁的位形空间为上述丛光滑截面的全体C∞(πBE)。下文为方便起见, 记
| $ g = \left( {\begin{array}{*{20}{c}} \mathit{\Lambda } &\phi \\ 0&1 \end{array}} \right) \in {C^\infty }({\pi _{BE}}), $ |
并不加声明地利用映射
| $ \left( {\begin{array}{*{20}{c}} {\hat \omega }&\gamma \\ 0&0 \end{array}} \right) \leftrightarrow \left( {\begin{array}{*{20}{c}} \omega \\ \gamma \end{array}} \right) $ |
建立同构
| $ \mathfrak{s}\mathfrak{e}(3)\cong {{\boldsymbol{\rm{R}}}^6} $ |
此处
| $ \hat{\omega }:=\left( \begin{matrix} 0 &-{{\omega }^{3}} & {{\omega }^{2}} \\ {{\omega }^{3}} & 0 &-{{\omega }^{1}} \\ -{{\omega }^{2}} & {{\omega }^{1}} & 0 \\ \end{matrix} \right)\in \mathfrak{s}\mathfrak{e}(3)。 $ |
引入对流速度
| $ {{\xi }^{t}}={{g}^{-1}}\dot{g}={{(\omega, \gamma )}^{\text{T}}}, $ | (1) |
以及对流应变变量
| $ {{\xi }^{s}}={{g}^{-1}}g'-{{e}_{2}}={{(\mathit{\Omega}, \ \mathit{\Gamma )}}^{\text{T}}}, $ | (2) |
其中,
几何精确梁适用于大范围运动的一个主要原因在于其Lagrange函数具有欧式群作用不变性, 故可表示为
| $ l({\xi ^t}, {\xi ^s}) = \int_{\;0}^{\;\ell } {\frac{1}{2}\left[{\left\langle {{D_1}{\xi ^t}, {\xi ^t}} \right\rangle-\left\langle {{D_2}{\xi ^s}, {\xi ^s}} \right\rangle } \right]} \;{\rm{d}}S\;, $ |
其中,
| $ {D_1} = {\mathop{\rm diag}\nolimits} (J, M), \;\;{D_2} = {\rm{diag}}({C_1}, {C_2}), $ |
其中
| $ \begin{array}{l} {C_1} = {\mathop{\rm diag}\nolimits} (EI, G{I_2}, EI)\;, \\ {C_2} = {\mathop{\rm diag}\nolimits} (GA, EA, GA)。 \end{array} $ |
J为惯性矩阵
| $ J =-{\int_{\cal A} {\rho \left( {\widehat {{\varsigma ^1}{E_1} + {\varsigma ^3}{E_3}}} \right)} ^2}{\rm{d}}{\varsigma ^1}{\rm{d}}{\varsigma ^3}\;, $ |
据上述Lagrange函数, 可以定义作用泛函为
| $ {\cal L} = \int_{\;{t_1}}^{\;{t_2}} {\int_{\;0}^{\;\ell } {\frac{1}{2}\left[{\left\langle {{D_1}{\xi ^t}, {\xi ^t}} \right\rangle-\left\langle {{D_2}{\xi ^s}, {\xi ^s}} \right\rangle } \right]} \;{\rm{d}}S\;{\rm{d}}t} 。 $ |
此外, 通过计算易得下列变分公式:
| $ \begin{array}{l} {\rm{\delta }}{\xi ^t} = \dot \eta + \left[{{\xi ^t}, \eta } \right]\;, \;\\ {\rm{\delta }}{\xi ^s} = \eta ' + [{\xi ^s} + {e_2}, \eta]。 \end{array} $ |
其中,
①在Hamel场论标架下, 易验证若取一
| $ \left[{\left( {\begin{array}{*{20}{c}} {{\omega _1}}\\ {{\gamma _1}} \end{array}} \right)\;, \;\left( {\begin{array}{*{20}{c}} {{\omega _2}}\\ {{\gamma _2}} \end{array}} \right)} \right] = \left( {\begin{array}{*{20}{c}} {{\omega _1} \times {\omega _2}}\\ {{\omega _1} \times {\gamma _2} -{\omega _2} \times {\gamma _1}} \end{array}} \right)。 $ |
由上述变分公式和Hamilton原理, 容易计算得到梁的Hamel场方程为
| $ \frac{\partial }{{\partial t}}{D_1}{\xi ^t}- \frac{\partial }{{\partial S}}{D_2}{\xi ^s}- {\left[{{\xi ^t}, {D_1}{\xi ^t}} \right]^*} + {\left[{{\xi ^s} + {e_2}, {D_2}{\xi ^s}} \right]^{\rm{*}}} = 0\;, $ | (3) |
边界条件为
| $ {D_2}{\xi ^s}{\left| {_{S = 0} = 0\;,\;{D_2}{\xi ^s}} \right|_{S = \ell }} = 0 , $ | (4) |
其中[·, ·]*为
| $ {\left[{\left( {\begin{array}{*{20}{c}} {{u_1}}\\ {{v_1}} \end{array}} \right)\;, \;\left( {\begin{array}{*{20}{c}} {{u_2}}\\ {{v_2}} \end{array}} \right)} \right]^*} = -\left( {\begin{array}{*{20}{c}} {{u_1} \times {u_2} + {v_1} \times {v_2}}\\ {{u_1} \times {v_2}} \end{array}} \right)。 $ |
从式(1)和(2)求解g需要如下相容性条件:
| $ \frac{\partial }{{\partial t}}{\xi ^s}- \frac{\partial }{{\partial s}}{\xi ^t} = \left[{{\xi ^s} + {e_2}, {\xi ^t}} \right]。 $ |
这可以从式(1)和(2)出发, 直接计算验证。相容性条件是由
求解
设梁的空间节点数为K, 空间步长为Δh, 时间步长为Δt, 时间步数为N。
为方便起见, 以下对于序列{qi, j}, 令
| $ \begin{array}{l} {q_{i + 1/2, j}}: = \frac{1}{2}({q_{i, j}} + {q_{i + 1, j}})\;, \;1 \le j \le K, \\ {q_{i, j + 1/2}}: = \frac{1}{2}({q_{i, j}} + {q_{i, j + 1}})\;, \;0 \le j \le K, \end{array} $ |
其中
| $ {l^d} = {l^d}({\xi ^t}_{i + 1/2, j}, {\xi ^s}_{i, j + 1/2}) = \Delta t\Delta h\;l({\xi ^t}_{i + 1/2, j}, {\xi ^s}_{i, j + 1/2})\;, $ |
相应的作用和为
| $ {s^d} = \sum\limits_{i = 0}^{N-1} {\sum\limits_{j = 1}^K {{l^d}({\xi ^t}_{i + 1/2, j}, {\xi ^s}_{i, j + 1/2})} } 。 $ |
利用离散变分原理易得如下结论:序列
| $ \{ {\xi ^t}_{i + 1/2, j}, {\xi ^s}_{i, j + 1/2}|0 \le i \le N-1, \;\;1 \le j \le K\} $ |
满足离散变分原理①
①对适用于一般Lagrange场论的离散Hamel场方程, 参见文献[12]。
| $ {\rm{\delta }}{s^d} = {\rm{\delta }}\sum\limits_{i = 0}^{N-1} {\sum\limits_{j = 1}^K {{l^d}({\xi ^t}_{i + 1/2, j}, {\xi ^s}_{i, j + 1/2})} } = 0, $ |
其中,
| $ \begin{array}{l} {\rm{\delta }}{\xi ^t}_{i + 1/2, j} = \frac{1}{{\Delta t}}\left( {{\eta _{i + 1, j}}- {\eta _{i, j}}} \right) + \left[{{\xi ^t}_{i + 1/2, j}, {\eta _{i + 1/2, j}}} \right]\;, \\ {\rm{\delta }}{\xi ^s}_{i, j + 1/2} = \frac{1}{{\Delta h}}\left( {{\eta _{i, j + 1}} - {\eta _{i, j}}} \right) + \left[{{\xi ^s}_{i, j + 1/2} + {e_2}, {\eta _{i, j + 1/2}}} \right]\;, \end{array} $ |
当且仅当序列
| $ \begin{array}{l} \frac{1}{{\Delta t}}{D_1}({\xi ^t}_{i + 1/2, j}- {\xi ^t}_{i- 1/2, j})- \frac{1}{{\Delta h}}{D_2}({\xi ^s}_{i, j + 1/2} - {\xi ^s}_{i, j - 1/2}) - \\ \frac{1}{2}{[{\xi ^t}_{i + 1/2, j}, {D_1}{\xi ^t}_{i + 1/2, j}]^*} - \frac{1}{2}{[{\xi ^t}_{i-1/2, j}, {D_1}{\xi ^t}_{i-1/2, j}]^*} + \\ \frac{1}{2}{\left[{{\xi ^s}_{i, j + 1/2} + {e_2}, {D_2}{\xi ^s}_{i, j + 1/2}} \right]^*} + \frac{1}{2}{\left[{{\xi ^s}_{i, j-1/2} + {e_2}, {D_2}{\xi ^s}_{i, j-1/2}} \right]^*}\\ = 0\;, \end{array} $ | (5) |
及以下离散的相容性条件
| $ \begin{array}{l} \frac{1}{{\Delta t}}({\xi ^s}_{i + 1, j + 1/2}- {\xi ^s}_{i, j + 1/2})- \frac{1}{{\Delta h}}({\xi ^t}_{i + 1/2, j + 1}- {\xi ^t}_{i + 1/2, j})\\ = \left[{\frac{1}{2}({\xi ^s}_{i + 1, j + 1/2} + {\xi ^s}_{i, j + 1/2} + 2{e_2}), \frac{1}{2}({\xi ^t}_{i + 1, j + 1} + {\xi ^t}_{i + 1/2, j})} \right], \end{array} $ | (6) |
边界条件为
| $ {D_2}{\xi ^s}_{i, 1/2} = 0, {D_2}{\xi ^s}_{i, K + 1/2} = 0。 $ |
用
| $ \begin{array}{l} {\left[{{\xi ^t}_{i + 1/2, j}\;, \;{D_1}{\xi ^t}_{i + 1/2, j}} \right]^*} = - \left( {\begin{array}{*{20}{c}} {{\omega _{i + 1/2, j}} \times J{\gamma _{i + 1/2, j}}}\\ {{\omega _{i + 1/2, j}} \times M{\gamma _{i + 1/2, j}}} \end{array}} \right), \\ {\left[{{\xi ^s}_{i, j + 1/2}\; + {e_2}, \;{D_2}{\xi ^s}_{i, j + 1/2}} \right]^*}\\ = - \left( {\begin{array}{*{20}{c}} {\Omega {\;_{i, j + 1/2}} \times {C_1}\Omega {\;_{i, j + 1/2}} + ({\Gamma _{i, j + 1/2}} + {E_2}) \times {C_2}{\Gamma _{i, j + 1/2}}}\\ {\Omega {\;_{i, j + 1/2}} \times {C_2}{\Gamma _{i, j + 1/2}}} \end{array}} \right), \\ \left[{\frac{1}{2}\left( {{\xi ^s}_{i + 1, j + 1/2} + {\xi ^s}_{i, j + 1/2} + 2{e_2}} \right)\;, \frac{1}{2}\left( {{\xi ^t}_{i + 1/2, j + 1} + {\xi ^t}_{i + 1/2, j}} \right)} \right]\\ = \frac{1}{4}\left( {\begin{array}{*{20}{c}} {\left( {\Omega {\;_{i + 1, j + 1/2}} + \Omega {\;_{i, j + 1/2}}} \right) \times \left( {{\omega _{i + 1/2, j + 1}} + {\omega _{i + 1/2, j}}} \right)}\\ {\left( {\Omega {\;_{i + 1, j + 1/2}} + \Omega {\;_{i, j + 1/2}}} \right) \times \left( {{\gamma _{i + 1/2, j + 1}} + {\gamma _{i + 1/2, j}}} \right)} \end{array}} \right) -\\ \frac{1}{4}\left( {\begin{array}{*{20}{c}} 0\\ {\left( {{\omega _{i + 1/2, j + 1}} + {\omega _{i + 1/2, j}}} \right) \times \left( {{\Gamma _{i + 1, j + 1/2}} + {\Gamma _{i, j + 1/2}} + 2{E_2}} \right)} \end{array}} \right)。 \end{array} $ |
该离散格式的实现步骤如下:
1)给定i, 输入序列
| $ \{ {\xi ^s}_{i, j + 1/2}|0 \le j \le K\} $ |
和
| $ \{ {\xi ^t}_{i-1/2, j}|1 \le j \le K\}, $ |
并代入离散格式(5)中, 通过修正的牛顿迭代法求解非线性方程组, 更新序列
| $ \{ {\xi ^t}_{i + 1/2, j}|1 \le j \le K\}。 $ |
2)将所得的序列
| $ \{ {\xi ^t}_{i + 1/2, j}|1 \le j \le K\} $ |
和
| $ \{ {\xi ^s}_{i, j + 1/2}|0 \le j \le K\}, $ |
代入离散格式(6)中, 求解线性方程组, 更新序列
| $ \{ {\xi ^s}_{i + 1, j + 1/2}|0 \le j \le K\} 。 $ |
3)重复步骤1和2, 可得到所有节点处的值。
4)根据序列
| $ \{ {\xi ^t}_{i + 1/2, j}|0 \le i \le N-1, \;\;1 \le j \le K\}, $ |
并利用指数映射
| $ \operatorname{Exp}:\mathfrak{s}\mathfrak{e}(3)\to \operatorname{SE}(3) $ |
及公式
| $ {g_{i + 1, j}} = {g_{i, j}}{\mathop{\rm Exp}\nolimits} (\Delta t{\xi ^t}_{i + 1/2, j}), $ | (7) |
迭代可得到
| $ \left\{ {{g_{i + 1, j}}\left| {0 \le i \le N-1, 1 \le j \le K} \right.} \right\}。 $ |
由几何精确梁的离散格式及离散的Noether定理[8]可以验证, 上述算法保持如下定义的离散动量:
| $ {\boldsymbol{J}_{i-1/2}} = \sum\limits_{j = 1}^K {\Delta hAd_{g_{_{i-1/2, j}}^{-1}}^*({D_1}{\xi ^t}_{i - 1/2, j})} = \sum\limits_{j = 1}^K {\Delta h\left( {\begin{array}{*{20}{c}} {{\boldsymbol{a}_{i - 1/2, j}}}\\ {{\boldsymbol{b}_{i - 1/2, j}}} \end{array}} \right)} , $ |
其中,
| $ \begin{array}{l} \boldsymbol{A}d_{{{(\Lambda, \phi )}^{-1}}}^*(u, v) = (\Lambda u + \phi \times \Lambda v, \Lambda v)\;, \\ {\boldsymbol{a}_{i-1/2, j}} = {\Lambda _{i-1/2, j}}J{\omega _{i - 1/2, j}} + {\phi _{i - 1/2, j}} \times {\Lambda _{i - 1/2, j}}M{\gamma _{i - 1/2, j}}\;, \\ {\boldsymbol{b}_{i - 1/2, j}} = {\Lambda _{i - 1/2, j}}M{\gamma _{i - 1/2, j}}, 1 \le i \le N。 \end{array} $ |
考虑初始位置如图 1所示的不受外力的几何精确梁。其参数[15]如下:梁l=2π/3, 横截面是边长为a=0.1的正方形, 密度ρ=1000, 杨氏模量E=107, 泊松比ν=0.35。
|
| 图 1. 梁的初始状态示意图 Figure 1. Schematic of the deformation of beam |
取时间步长为Δt=10-4 s, 空间节点数K=101。根据上述的初始位形, 计算得到初始的对流应变变量为
| $ \begin{array}{l} {\mathit{\Gamma }_1} =-1\;, \;{\mathit{\Gamma }_2} = \;{\mathit{\Gamma }_3} = 0\;, \\ \mathit{\Gamma } {\;_1} = \mathit{\Gamma } {\;_2} = \mathit{\Gamma } {\;_3} = 0\;, \end{array} $ |
且给定梁的初速度为
| $ \begin{array}{l} {\gamma _1} = \sin ({\rm{\pi }}S/\ell )\;, \;{\gamma _2} = 1\;, \;{\gamma _3} = 0\;, \\ \;\;\;\;\;\;\;\;\;{\omega _1}{\rm{ = }}{\omega _2} = {\omega _3} = 0。 \end{array} $ |
为了提高计算速度, 本文使用指数映射的近似映射-Cayley变换[16], 即用下式取代式(7)
| $ \begin{array}{l} {g_{i + 1, j}} = {g_{i, j}}{\rm{cay}}(\Delta t{\xi ^t}_{i + 1/2, j}) = \\ {g_{i, j}}{({I_4}-\Delta t{\xi ^t}_{i + 1/2, j}/2)^{-1}}({I_4} + \Delta t{\xi ^t}_{i + 1/2, j}/2), \end{array} $ | (7') |
这里I4表示4阶单位矩阵。
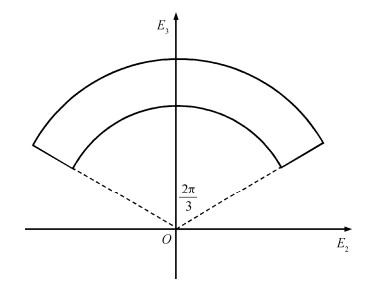
从图 2可见, Hamel场变分积分子虽不能精确地保持能量, 但可使能量长时间稳定在一个很小区间内。本例能量取值为99, 振幅区间长度仅为0.7, 说明该数值格式有好的长时间能量表现。
|
| 图 2. 梁的动能、势能和总能量 Figure 2. Evolution of kinetic energy, potential energy and total energy |
几何精确梁的角动量和线动量如图 3所示, 说明该算法保持角动量和线动量。

|
| 图 3. 梁的角动量和线动量 Figure 3. Evolution of angular momentum and linear momentum |
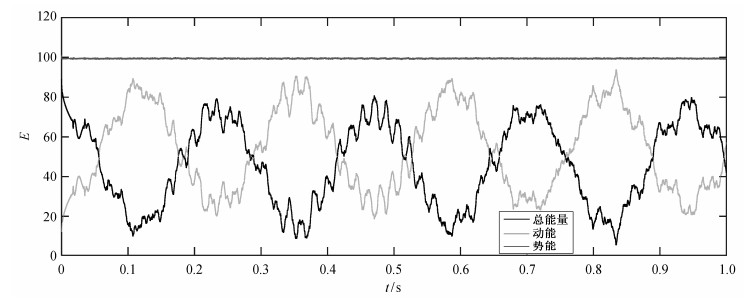
图 4是旋转矩阵正交性验证结果, 误差数量级达到10-14, 说明该算法精确地保持李群结构。
|
|
图 4.
|
对于中线的节点, 每隔10个节点取一个截面, 给出梁分别在不同时间点处的运动状态(图 5)。
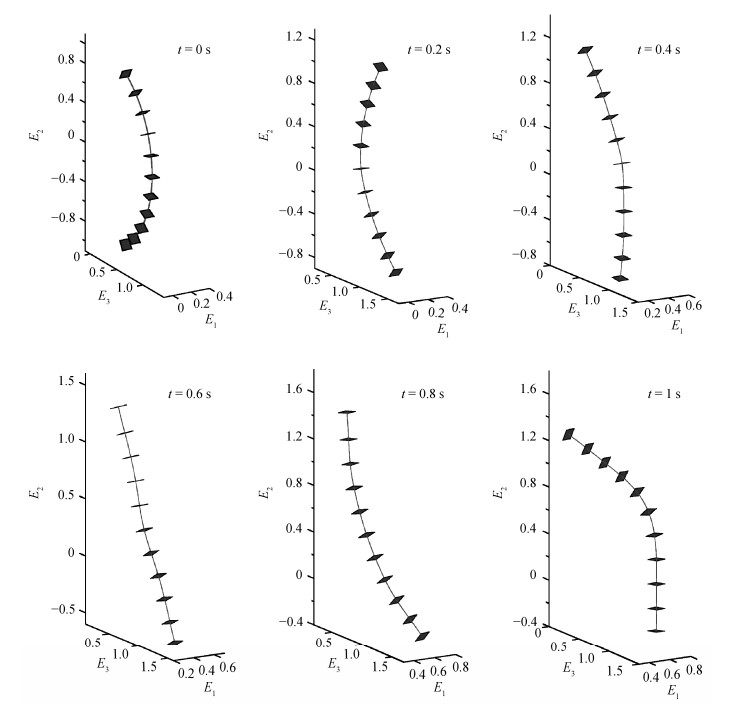
|
| 图 5. 梁分别在时间t=0, 0.2, 0.4, 0.6, 0.8和1 s的状态 Figure 5. Snapshot of the motion and deformation at t=0, 0.2, 0.4, 0.6, 0.8, and 1 s |
4 结论
本文通过Hamel场变分积分子, 得到几何精确梁的离散运动方程, 该算法具有保持能量、动量和几何结构的特点。与以往几何精确梁的李群变分积分子[10]不同, 在协变场论的观点下, 将时空等同离散和变分, 可有效地利用势能的对称性进行约化。本文最后以R3中的几何精确梁为例进行仿真, 结果表明该算法能够长时间保持能量、动量以及李群结构。下一步我们将进行算法分析, 与已有算法对比, 并将Hamel场变分积分子应用于Chaplygin-Timoshenko雪橇等无穷维非完整力学系统。
致谢:感谢Dmitry Zenkov在论文写作过程中的帮助。
| [1] | Deepak T, Amir L, Christopher D R. Geometrically exact models for soft robotic manipulators. IEEE Transactions on Robotics , 2008, 24 (4) : 773–780 DOI:10.1109/TRO.2008.924923 . |
| [2] | Bishop T C, Cortez R, Zhmudsky O O. Investigation of bend and shear waves in a geometrically exact elastic rod model. Journal of Computational Physics , 2004, 193 (2) : 642–665 DOI:10.1016/j.jcp.2003.08.028 . |
| [3] | Reissner E. On one-dimension, large-displacement, finite-strain beam theory. Stud Appl Math , 1973, 52 : 87–95 DOI:10.1002/sapm.v52.2 . |
| [4] | Antman S S. Kirchhoff problem for non-linearly elastic rods. Quart J Appl Math , 1974, 32 (3) : 221–240 DOI:10.1090/qam/1974-32-03 . |
| [5] | Antman S S, Jordan K B. Qualitative aspects of the spatial deformation of nonlinearly elastic rods. Proc Roy Soc Edinburgh Sect A , 1975, 73 (5) : 85–105 . |
| [6] | Simo J C, Ju J W. Strain-and stress-based conti-nuum damage models -I. Formulation. International Journal of Solids and Structures , 1987, 23 (7) : 821–840 DOI:10.1016/0020-7683(87)90083-7 . |
| [7] | 吴坛辉, 洪嘉振, 刘铸永. 非线性几何精确梁理论研究综述. 中国科技论文 , 2013, 8 (11) : 1126–1130. |
| [8] | Marsden J E, West M. Discrete mechanics and var-iational integrators. Acta Numerica , 2001, 10 : 357–514 DOI:10.1017/S096249290100006X . |
| [9] | Lew A, Marsden J E, Ortiz M, et al. An overview of variational integrators // Franca L P, Tezduyar T E, Masud A. Finite element methods: 1970s and beyond. Barcelona: CIMNE, 2004: 98-115 |
| [10] | Demoures F, Gay-Balmaz F, Leyendecker S, et al. Discrete variational Lie group formulation of geo-metrically exact beam dynamics. Numerische Mathematik , 2015, 130 (1) : 73–123 DOI:10.1007/s00211-014-0659-4 . |
| [11] | Ball K R, Zenkov D V. Hamel's formalism and variational integrators. Geometry, Mechanics and Dynamics: The Legacy of Jerry Marsden , 2015, 73 : 477–506 . |
| [12] | Shi Donghua. Hamel's field varational integrator. to appear , 2016 . |
| [13] | Simo J C, Vu-Quoc L. A three-dimensional finite-strain rod model, part Ⅱ: Computational aspects. Computer Methods in Applied Mechanics and Eng-ineering , 1986, 58 (1) : 79–116 DOI:10.1016/0045-7825(86)90079-4 . |
| [14] | Shi Donghua, Zenkov D V, Bloch A M. Hamel's formalism for classical field theory. to appear , 2016 . |
| [15] | Demoures F. Lie group and Lie algebra variational integrators for flexible beam and plate in R3 [D]. Lausanne: Ecole Polytechnique Federale de Lausanne, 2012 |
| [16] | Lewis D, Simo J C. Conserving algorithms for the dynamics of Hamiltonian systems on Lie groups. Journal of Nonlinear Science , 1994, 4 (1) : 253–299 DOI:10.1007/BF02430634 . |
 2016, Vol. 52
2016, Vol. 52