文章信息
- 李嘉琪, 王曙光, 宁杰远
- LI Jiaqi, WANG Shuguang, NING Jieyuan
- 应用迭代叠加法分离震源谱的理论探讨
- Theoretical Investigation on Earthquake Source Spectra Isolation by Iteratively Stacking Separation
- 北京大学学报(自然科学版), 2016, 52(3): 427-436
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(3): 427-436
-
文章历史
- 收稿日期: 2015-02-03
- 修回日期: 2015-11-10
- 网络出版日期: 2016-05-19
2. 中国地震局地震预测研究所, 北京 100036
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 100036
地震台站记录的地震波形包含震源区、传播路径和台站响应信息。从记录的地震波形中分离出地震的震源谱, 进而定量地分析震源区性质, 对于判断地震危险性具有十分重要的意义, 是地震学与地球内部物理学中重要的研究课题。
在震源模型中, 远场记录的震源谱可以近似地用频谱的低频水平(low frequency level)和拐角频率(corner frequency)表达[1]。由于地震矩可以用破裂尺度和应力降表达[2-3], 因此远场记录的震源谱可用于求取应力降。基于一些假设, 对单台记录的地震波形可以直接求取应力降[4-7]。随着高质量地震数据的获取以及宽频带地震学的快速发展, 人们更多地应用多台站‒多事件记录叠加求取区域甚至全球的应力降。
根据地震波的传播和衰减特征, Atkinson等[8]采用分段式模型, 从台站记录的位移谱中分离出路径项。Moya等[9]假设路径项已知, 采取遗传算法, 从位移谱中同时反演出震源参数和台站项。一些研究者利用类似方法, 求取不同地区的地震应力降[10-12]。近年来, Shearer等[13]提出先独立分离出震源谱, 再引入震源模型求取应力降的分步求解方法。这种方法对所有台站记录的同一地震位移谱进行叠加, 以得到更准确的震源项; 对同一台站记录的所有地震的位移谱进行叠加, 以得到更准确的台站项; 对路径长度基本上相同的位移谱进行叠加, 以得到更准确的路径项。通过对多个台站观测的多个事件记录的迭代叠加, 最终得到稳定的震源项、路径项和台站项。该方法可以独立得到不受台站项、路径项和震源项模型影响的震源谱, 并且在实际计算中收敛速度快, 因而广泛应用于地震应力降的研究中[13-16]。
研究人员对Shearer等[13]的分离方法的应用条件进行了多种测试[15-18]。对帕克菲尔德地区地震事件的输入/输出一致性检验[15]表明, 拐角频率在高频区间(大于20 Hz)存在输入/输出不一致的现象, 应力降也普遍存在输入/输出不一致的情况。同时, 台阵中相近台站得到的震源谱曲线也存在一定的差异。因此, 在进一步的应用中, 他们根据测试结果, 选取输入/输出一致性较强的频率区间进行计算[15-16], 并对应力降进行平滑处理, 更多地关注应力降的趋势性变化[17-18]。同时, 迭代叠加分离的应力降统计分析表明, 在台站数量较少且分布不均匀的情况下, 得到的应力降数值偏大[13]。为了确定这种方法的适用条件, 并更好地在实际工作中应用它, 有必要研究该方法的严格适用条件及合理使用方案。
本文通过推导迭代叠加法确定震源谱的解析表达式, 探讨该方法是否可以应用于更普遍的观测条件。首先通过三台站-三事件的例子, 展示震源谱迭代分离的具体过程。进一步地, 得到任意台站-事件条件下震源谱的普遍表达式, 并讨论其中各项取值对应力降计算的影响。在此基础上, 对如何正确地基于迭代叠加法计算应力降进行讨论。
1 多台站‒多事件震源谱迭代分离方法台站记录的地震波主要包含震源、传播路径、台站以及噪声等信息。Shearer研究组[13, 19-21]提出一种基于台站迭代叠加求取震源项的方法, Yang等[14]将这种方法应用于应变降的研究中。
在频率域对地震波的位移谱取对数, 台站j对事件i记录到的位移谱dij可以表示为
| $ {d_{ij}} = {e_i} + {t_k}_{(i,j)} + {s_j} + {r_{ij}}, $ | (1) |
其中, ei为震源项, tk(i, j)为路径项, sj为台站项, rij是残差项。为了体现路径长度的影响, 不同长度的路径项用下角标k标识。
为了提高计算精度, Shearer等[13]和Yang等[14]假设每个地震与相邻地震震源性质相似, 从而将所关注的地震与周围地震分为一组。下面的分析类似一组地震与所有台站记录进行分离的情形, 具体做法主要参照Yang等[14]的工作, 计算过程简单介绍如下。
在对观测位移谱的迭代分离中, 假设震源项、路径项和残差项的第一步均为零,
| $ {e_i}^1 = {t_k}{_{(i,j)}^1} = {r_{ij}}^1 = {\rm{ }}0。 $ | (2) |
假设m个地震事件, n个地震台站, k个路径离散步长情况下, 对任意台站j记录到的所有位移谱dij进行叠加, 得到第一步的台站项:
| $ s_j^1 = \frac{1}{m}\sum\limits_{i = 1}^m {{d_{ij}}} 。 $ | (3) |
第二步的迭代, 按照相同项叠加求取平均的方法进行。第p步的各项表示为
| $ e_i^p = \frac{1}{n}\sum\limits_{j = 1}^n {\left[ {{d_{ij}} - t_{k(i,j)}^{p - 1} - s_j^{p - 1} - r_{ij}^{p - 1}} \right]} , $ | (4) |
| $ t_k^p = \frac{1}{{{N_k}}}\sum {\left[ {{d_{ij}} - e_i^p - s_j^{p - 1} - r_{ij}^{p - 1}} \right]} , $ | (5) |
| $ s_j^p = \frac{1}{m}\sum\limits_{i = 1}^m {\left[ {{d_{ij}} - e_i^p - t_{k(i,j)}^p - r_{ij}^{p - 1}} \right]} , $ | (6) |
| $ r_{ij}^p = {d_{ij}} - e_i^p - t_{k(i,j)}^p - s_j^p。 $ | (7) |
迭代的收敛判据为:以下三式表达的迭代结果与上一步的差值小于设定的阈值。
| $ \begin{array}{l} \sum\nolimits_i {\left| {e_i^p - e_i^{p - 1}} \right|} \;,\\ \sum\nolimits_i {\left| {t_{k(i,j)}^p - t_{k(i,j)}^{p - 1}} \right|} \;,\\ \sum\nolimits_j {\left| {s_j^p - s_j^{p - 1}} \right|。} \end{array} $ |
通过以上步骤得到的震源项为相对值, 即各事件震源项与所有震源项平均值的差。得到所有震源项的平均值后, 可以进一步计算各个事件震源项的绝对值。
2 迭代叠加法分离震源谱的解析表达式参照Yang等[14]的计算流程, 首先针对三台站‒三事件的简单情形, 给出每一步迭代过程的震源项、路径项、台站项和残差项的表达式, 接着给出震源项的普遍表达式。
以三台站‒三事件的情况为例说明。设震源项、路径项和台站项为已知:震源项为E1, E2, E3; 台站项表示为S1, S2, S3; 路径项按震中距大小分为两组, 震中距较大的分为一组, 在第一个下角标中标注2加以区分, 具体形式为T2(1, 2), T2(1, 3)和T2(2, 2), 其余为一组, 在第一个下角标标注1加以区分; 残差项相应地表示为Rij, 其中下角标i, j (=1, 2, 3)分别对应于地震和台站。
各个台站的记录按照第1节的方法表达, 如第一个和第二个台站记录到的第一个事件可以表示为
| $ \left\{ \begin{array}{l} {D_{{\rm{11}}}} = {E_{\rm{1}}} + {T_{{\rm{1}}({\rm{1}},{\rm{ 1}})}} + {S_{\rm{1}}} + {R_{{\rm{11}}}},\\ {D_{{\rm{12}}}} = {E_{\rm{1}}} + {T_{{\rm{2}}({\rm{1}},{\rm{ 2}})}} + {S_{\rm{2}}} + {R_{{\rm{12}}}}。 \end{array} \right. $ | (8) |
按照第1节介绍的迭代方法, 第一步迭代的台站项可以表示为
| $ \begin{array}{l} s_j^1 = \frac{1}{3}({D_{1j}} + {D_{2j}} + {D_{3j}}) = \frac{1}{3}\sum\limits_{i = 1}^3 {{D_{ij}}} \\ \;\;\;\; = \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {{E_i} + {T_{k(i,j)}} + {R_{ij}}} \right)} + {S_j},\;\\ \;\;\;\;(j = 1,\;2,\;3), \end{array} $ | (9) |
由于假设震源项、路径项和残差项的第一步均为零, 所以第一步迭代得到的台站项(如第一个台站的台站项s11)不仅包含台站项的本身的真实值S1, 还包括所有震源项的平均值
迭代得到的第二步震源项为
| $ \begin{array}{l} e_i^2 = \frac{1}{3}\sum\limits_{j = 1}^3 {\left( {{D_{ij}} - s_j^1} \right)} = \left( {{E_i} - \frac{1}{3}\sum\limits_{i = 1}^3 {{E_i}} } \right) + \\ \;\;\;\;\;\;\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{T_{k(i,j)}}} - \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{T_{k(i,j)}}} } \right)} } \right) + \\ \;\;\;\;\;\;\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{R_{ij}}} - \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{R_{ij}}} } \right)} } \right)\\ \;\;\;\;\;\;(i = 1,\;2,\;3), \end{array} $ | (10) |
第二步迭代得到的震源项, 形式上表现为三项之和:一个事件的震源项与所有震源项平均的偏离值、该事件所涉及的路径项的平均值与所有路径项平均值的偏离值以及这个事件涉及的残差项平均值与所有事件残差项平均值的偏离值。
相应地, 可以得出迭代得到的第二步路径项。路径项按照震中距分组, 假设同一震中距区间内路径项相同。
第一组的路径项为
| $ \begin{array}{l} {t_1}^2 = \left[ {\left( {{D_{11}}-{e_1}^2-{s_1}^1} \right) + \left( {{D_{21}}-{e_2}^2-{s_1}^1} \right) + } \right.\\ \;\;\;\;\left( {{D_{22}}-{e_2}^2-{s_2}^1} \right) + \left( {{D_{31}}-{e_3}^2-{s_1}^1} \right) + \\ \left. {\;\;\;\;\left( {{D_{32}}-{e_3}^2-{s_2}^1} \right) + \left( {{D_{33}}-{e_3}^2-{s_3}^1} \right)} \right]/6, \end{array} $ | (11) |
整理后得
| $ \begin{array}{l} {t_1}^2 = [({T_{1(1,1)}}-{T_{2(1,2)}} + {T_{1(2,2)}}-{T_{2(2,3)}}-\\ \;\;\;\;{T_{1\left( {3,1} \right)}} + {T_{1(3,3)}}) + ({R_{11}}-{R_{12}} + \\ \;\;\;\;{R_{22}}-{R_{23}}-{R_{31}} + {R_{33}})]/18。 \end{array} $ | (12) |
第二组的路径项为
| $ \begin{array}{l} {t_2}^2 = - {\rm{ }}[({T_{1(1,1)}}-{T_{2(1,2)}} + {T_{1(2,2)}}-{T_{2(2,3)}}-\\ \;\;\;\;{T_{1\left( {3,1} \right)}} + {T_{1(3,3)}}){\rm{ }} + ({R_{11}}-{R_{12}} + \\ \;\;\;\;{R_{22}}-{R_{23}}-{R_{31}} + {R_{33}})]/9。 \end{array} $ | (13) |
相应步长区间内的各个路径项均更新为该区间内路径项的平均值:
| $ \begin{array}{l} t_{{\rm{1}}({\rm{1}},{\rm{ 1}})}^2 = t_{{\rm{1}}({\rm{2}},{\rm{ 1}})}^2 = t_{{\rm{1}}({\rm{2}},{\rm{ 2}})}^2 = t_{{\rm{1}}({\rm{3}},{\rm{ 1}})}^2\\ \;\;\;\;\;\;\; = t_{{\rm{1}}({\rm{3}},{\rm{ 2}})}^2 = t_{{\rm{1}}({\rm{3}},{\rm{ 3}})}^2 = t_{\rm{1}}^2, \end{array} $ | (14) |
| $ t_{{\rm{2}}({\rm{1}},{\rm{ 2}})}^2 = t_{{\rm{2}}({\rm{1}},{\rm{ 3}})}^2 = t_{{\rm{2}}({\rm{2}},{\rm{ 3}})}^2 = t_{\rm{2}}^2。 $ | (15) |
路径项包含各种步长的路径内容以及相应的残差项内容。由于前面对台站项和震源项的迭代计算中包含对不同路径长度的路径项取平均, 所以这一步迭代得到的路径项与具体的台站和事件分布直接相关。也就是说, 不同的震中距分布, 第二步迭代得到的路径项完全不同。并且, 第一组路径项包含第二组路径项的信息(同样, 第二组路径项也包含第一组路径项的信息)。
第二步的台站项为
| $ \begin{array}{l} s_1^2 = \frac{1}{3}\sum\limits_{i = 1}^3 {\left[ {{D_{i1}} - e_i^2 - t_{k(i,1)}^2} \right]} \\ \;\;\;\; = \frac{1}{3}\sum\limits_{i = 1}^3 {{E_i}} + \frac{1}{3}\sum\limits_{i = 1}^3 {{T_{k(i,1)}}} + {S_1} + \frac{1}{3}\sum\limits_{i = 1}^3 {{R_{i1}}} + \\ \;\;\;\;\;\;[({T_{2(1,2)}} + {T_{2(2,3)}} + {T_{1(3,1)}}) - ({T_{1(1,1)}} + {T_{1(2,2)}} + {T_{1(3,3)}}) + \\ \;\;\;\;\;\;({R_{12}} + {R_{23}} + {R_{31}}) - ({R_{11}} + {R_{22}} + {R_{33}})]/18, \end{array} $ | (16) |
| $ \begin{array}{l} s_2^2 = \frac{1}{3}\sum\limits_{i = 1}^3 {\left[ {{D_{i2}} - e_i^2 - t_{k(i,2)}^2} \right]} \\ \;\;\;\; = \frac{1}{3}\sum\limits_{i = 1}^3 {{E_i}} + \frac{1}{3}\sum\limits_{i = 1}^3 {{T_{k(i,2)}}} + {S_2} + \frac{1}{3}\sum\limits_{i = 1}^3 {{R_{i2}}} , \end{array} $ | (17) |
| $ \begin{array}{l} s_3^2 = \frac{1}{3}\sum\limits_{i = 1}^3 {\left[ {{D_{i3}} - e_i^2 - t_{k(i,3)}^2} \right]} \\ \;\;\;\; = \frac{1}{3}\sum\limits_{i = 1}^3 {{E_i}} + \frac{1}{3}\sum\limits_{i = 1}^3 {{T_{k(i,3)}}} + {S_3} + \frac{1}{3}\sum\limits_{i = 1}^3 {{R_{i3}}} - \\ \;\;\;\;\;\;[({T_{2(1,2)}} + {T_{2(2,3)}} + {T_{1(3,1)}}) - ({T_{1(1,1)}} + {T_{1(2,2)}} + {T_{1(3,3)}}) + \\ \;\;\;\;\;\;({R_{12}} + {R_{23}} + {R_{31}}) - ({R_{11}} + {R_{22}} + {R_{33}})]/{\rm{18}}。 \end{array} $ | (18) |
由于上一步迭代路径项形式的复杂性, 第二步迭代得到的台站项与上一步相比, 除明确表达的震源项的平均、相关路径项和残差项的平均以及台站项自身, 还包括与台站、事件分布有关的路径以及残差的影响。
第二步迭代得到的残差项表示为
| $ \begin{array}{l} r_{ij}^2 = {D_{ij}} - e_i^2 - t_{k(i,j)}^2 - s_j^2\\ \;\;\;\; = \left[ {{T_{k(i,j)}} - \frac{1}{3}\sum\limits_{i = 1}^3 {{T_{k(i,j)}}} - \frac{1}{3}\sum\limits_{j = 1}^3 {{T_{k(i,j)}}} + \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{T_{k(i,j)}}} } \right)} } \right] + \\ \;\;\;\;\;\;\left[ {{R_{ij}} - \frac{1}{3}\sum\limits_{i = 1}^3 {{R_{ij}}} - \frac{1}{3}\sum\limits_{j = 1}^3 {{R_{ij}}} + \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{R_{ij}}} } \right)} } \right]\\ \;\;\;\;\;\;(i = 1,\;2,\;3;\;j = 1,\;2,\;3), \end{array} $ | (19) |
第三步的迭代结果为
| $ {r_{ij}}^2 = {D_{ij}}-{e_i}^2-{t_{ij}}^2-{s_j}^2, $ | (20) |
| $ \begin{array}{l} {e_i}^3 = {D_{ij}}-{t_{ij}}^2-{s_j}^2-{r_{ij}}^2 = {D_{ij}}-{t_{ij}}^2 - {s_j}^2-\\ \;\;\;\;\left( {{D_{ij}}-{e_i}^2 - {t_{ij}}^2-{s_j}^2} \right){\rm{ }} = {e_j}^2, \end{array} $ | (21) |
| $ \begin{array}{l} {t_{ij}}^3 = {D_{ij}}-{e_i}^3-{s_j}^2-{r_{ij}}^2 = {D_{ij}}-{e_i}^2-{s_j}^2-\\ \;\;\;\;\left( {{D_{ij}}-{e_i}^2-{t_{ij}}^2-{s_j}^2} \right){\rm{ }} = {t_{ij}}^2, \end{array} $ | (22) |
| $ \begin{array}{l} {s_j}^3 = {D_{ij}}-{e_i}^3-{t_{ij}}^3-{r_{ij}}^2 = {D_{ij}}-{e_i}^2-{r_{ij}}^2-\\ \;\;\;\;\left( {{D_{ij}}-{e_i}^2-{t_{ij}}^2-{r_{ij}}^2} \right){\rm{ }} = {s_j}^2, \end{array} $ | (23) |
| $ \begin{array}{l} {r_{ij}}^3 = {D_{ij}}-{e_i}^3-{t_{ij}}^3-{s_j}^3 = {D_{ij}}-{e_i}^2-\\ \;\;\;\;{t_{ij}}^2-{s_j}^2 = {r_{ij}}^2 \end{array} $ | (24) |
式(20)~(24)说明, 第三步迭代得到的震源项与第二步相同, 即震源项的迭代在第三步得到收敛, 这与Yang等[14]利用实际资料计算的收敛情况一致。
因此, 从理论上讲, 第二步迭代得到的震源项就是迭代叠加法最终分离得到的震源项:
| $ \begin{array}{l} {e_i} = \left( {{E_i} - \frac{1}{3}\sum\limits_{i = 1}^3 {{E_i}} } \right) + \\ \;\;\;\;\;\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{T_{k(i,j)}}} - \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{T_{k(i,j)}}} } \right)} } \right) + \\ \;\;\;\;\;\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{R_{ij}}} - \frac{1}{3}\sum\limits_{i = 1}^3 {\left( {\frac{1}{3}\sum\limits_{j = 1}^3 {{R_{ij}}} } \right)} } \right)\\ \;\;\;\;\;(i = 1,\;2,\;3)。 \end{array} $ | (25) |
为了表达简洁, 我们用下角标上加横杠的方式表达对于该下角标的遍历求和, 并做求取平均的计算。台站和事件确定后, 路径长度唯一确定, 这种情况下, 我们将tk(i, j)简单地表示为tij。对于三台站‒三事件的简单例子, 可以表示为
| $ \begin{array}{l} s_j^1 = {D_{\bar i\;j}} = {E_{\bar i}} + {T_{\bar i\;j}} + {S_j} + {R_{\bar i\;j}}\\ \;\;\;\;(j = 1,\;2,\;3), \end{array} $ | (26) |
| $ \begin{array}{l} e_i^2 = ({E_i} - {E_{\bar i}}) + ({T_{i\;\bar j\;}} - {T_{\overline {ij} \;}}) + ({R_{i\;\bar j\;}} - {R_{\overline {ij} \;}})\\ \;\;\;\;(i = 1,\;2,\;3), \end{array} $ | (27) |
| $ \begin{array}{l} t_{k(i,j)}^2 = g_k^{\rm{2}}({T_{k(i,j)}}) + g_k^{\rm{2}}({R_{ij}})\\ \;\;\;\;(k = 1,\;2), \end{array} $ | (28) |
| $ s_j^2 = {E_{\bar i}} + {T_{\bar i\;j}} + {S_j} + {R_{\bar i\;j}} + h_j^{\rm{2}}({T_{ij}}) + h_j^{\rm{2}}({R_{ij}}), $ | (29) |
| $ \begin{array}{l} r_{ij}^2 = ({T_{ij}} - {T_{i\;\bar j}} - {T_{\bar i\;j}} + {T_{\bar i\bar j}}) + ({R_{ij}} - {R_{i\;\bar j}} - {R_{\bar i\;j}} + {R_{\bar i\bar j}})\\ \;\;\;\;(i = 1,\;2,\;3;j = 1,\;2,\;3), \end{array} $ | (30) |
其中, gk2和hj2分别为与台站和事件分布相关的函数, 表征其在迭代第二步中对离散步长以k标识的路径项以及第j个台站项的影响。
通过以上分析可以得到, 迭代过程中只有函数gk2和hj2与台站和地震事件的相对位置有关。因此, 以上的震源项(式(27))和残差项(式(30))与台站和地震事件的数量以及相对位置无关, 为任意台站地震事件数量和分布条件下的普遍表达式。考虑到式(21)~(24)实际上也适用于任意台站和事件数量的情况, 所以对任意的m个地震、n个台站, 迭代叠加法分离的震源谱的普遍表达式为
| $ \begin{array}{l} {e_i} = ({E_i} - {E_{\bar i}}) + ({T_{i\;\bar j\;}} - {T_{\bar i\bar j}}) + ({R_{i\;\bar j\;}} - {R_{\bar i\bar j}})\\ \;\;\;\;\;\;(i = 1,\;2,\;3,\;...,\;m;\;j = 1,\;2,\;3,\;...,\;n)\;, \end{array} $ | (31) |
也就是
| $ \begin{array}{l} {e_i} = \left( {{E_i} - \frac{1}{m}\sum\limits_{i = 1}^m {{E_i}} } \right) + \\ \;\;\;\;\;\left( {\;\frac{1}{n}\sum\limits_{j = 1}^n {{T_{k(i,j)}}} - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{1}{n}\sum\limits_{j = 1}^n {{T_{k(i,j)}}} } \right)} } \right) + \\ \;\;\;\;\;\left( {\frac{1}{n}\sum\limits_{j = 1}^n {{R_{ij}}} - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{1}{n}\sum\limits_{j = 1}^n {{R_{ij}}} } \right)} } \right)\\ \;\;\;\;\;(i = 1,\;2,\;3,\;...,\;m;\;j = 1,\;2,\;3,\;...,\;n)。 \end{array} $ | (32) |
为了测试前面得到的震源谱分离的普遍表达式, 并探讨其在区域地震研究中的应用, 参照Yang等[14]的计算程序, 我们编制了数值计算程序, 计算过程包括3个部分:正演计算、反演计算和还原计算。程序的正演计算方法是, 从已发表文献中读取相关的台站项、路径项和震源项模型及参数, 作为已知输入, 合成位移谱。程序的反演计算方法是, 按照第2节的迭代叠加过程, 对正演合成的位移谱进行操作, 得到单个事件的震源谱分离结果(实际上得到的反演结果是震源、路径和残差三项偏离值的和(式(32)), 而不只是震源项信息)。进一步地, 我们对震源谱分离结果进行拟合, 还原得到单个事件的震源参数, 并与正演计算中输入的参数进行对比, 以此测试震源谱分离表达式的正确性。
正演计算中, 位移谱通过震源项、路径项和台站项的模型参数叠加计算得到。选取正演计算的频率范围为1~50 Hz, 路径项离散距离的步长设为100 km。从文献中选取的震源项[13]、路径项[22]和台站项[23]模型及所使用的参数如表 1所示。按照式(1)的表述, 应用表 1中的模型和参数计算得到台站项、路径项和震源项, 并合成得到位移谱。由于一般情况下观测记录的极低频数值和高频数值存在很大误差, 类似于实际工作的处理方式, 因此在得到正演结果后, 进一步的拟合计算只利用频率范围为2~40 Hz的数据。
| 参数 | 数值 | 文献 | 用途 |
| P波速度(vp)/(km·s-1) | 6 | Yang等[14] | 通用 |
| S波速度(vs)/(km·s-1) | Shearer等[13] | 通用 | |
| 密度(ρ)/(kg·cm-3) | 2.7 | Andrews[24] | 通用 |
| 衰减常数(Q0) | 100 | Oth等[22] | 路径项 |
| 衰减系数(η) | 0.8 | Oth等[22] | Q(f)=Q0fη |
| 震级参数(A) | 42403 | Kanamori[25] | 震源项 |
| 震级参数(B) | 10.7 | Shearer等[13] | Mw=A·log10M0-B |
| 辐射因子(Rϕφ ) | 42475 | Yamada等[26] | 震源项/P波均值 |
| 高频衰减率(n) | 2 | Brune[3] | 震源项 |
还原计算参照Shearer等[13]的方法, 震源谱模型采用
我们首先检验不同台站项对分离震源谱的影响。台站项输入模型选用第四纪、第三纪和中生代3种典型沉积地层上方台站的频率响应[23]。台站项的选取参照文献[23]。因为Bonilla等[23]的台站项数值只在0.5~24 Hz范围内, 所以具体的选取方式为:在0.5~24 Hz范围内完全采用Bonilla等[23]的台站项数值; 在24~50 Hz范围内采取相同的数值(即0.5~24 Hz范围内的最小值)。假设4个事件, 3个台站, 事件位置(东经和北纬)分别为(125.0, 35.0), (126.0, 33.0), (126.0, 33.5)和(125.0, 34.0)。台站位置分别为(125.0, 36.0), (124.9, 33.1)和(123.9, 32.0)。为了突出台站项的影响, 输入的震源模型中, 事件的矩震级都取3.0, 拐角频率分别为4.4, 9.5, 16.3和19.8 Hz。我们进行了4组对比测试, 前3组为3个台站选取相同的台站项, 分别为第四纪、第三纪和中生代; 第4组为3个台站分别选取3种不同的台站项。正演计算、反演计算和还原计算的结果如图 1所示。
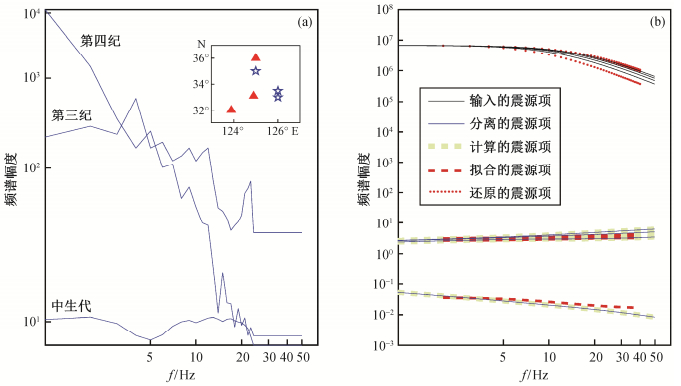
|
| (a)中小图表示台站和事件的位置, 红色三角形表示台站, 蓝色五角星表示地震事件; (b)中黑色实线和蓝色实线表示矩震级均为3.0, 拐角频率分别为4.4, 9.5, 16.3和19.8的4个地震的震源项输入模型和分离的震源项, 绿色虚线为应用解析表达式(式(32))计算的分离震源谱, 红色虚线表示通过拟合震源谱表达式得到的相对震源谱; 红色点线为还原的震源谱 图 1. 不同台站项模型输入条件下4个地震震源项的分离和震源参数拟合以及拟合结果与解析表达式及震源项输入模型的对比 Figure 1. Comparison among the input sources, analytical results of isolated sources, and the results given by iteratively stacking separation for different station terms |
测试结果表明, 震源谱的迭代叠加分离计算与台站项无关。对3个台站项选用3种不同类型台站响应的组合(图 1(a))进行正演计算得到位移谱, 并进一步得到震源谱分离结果(图 1(b)中蓝色曲线)后, 与应用解析表达式(式(32))直接计算得到的震源谱分离预测结果(图 1(b)中灰色虚线)完全相同, 充分说明台站项不影响应用迭代叠加法分离震源谱。这一结果的意义在于, 在应用迭代叠加法分离震源谱的计算过程中, 不用考虑台站响应的差异。
还原的震源谱(图 1(b)中红色点线)与输入的震源谱(图 1(b)中黑色实线)存在差异, 说明传统的求取震源谱的方法[13-14]会受到其他因素的影响, 这与根据式(32)得到的推论相同。
3.3 路径项对震源谱分离结果的影响为了显示路径项的影响, 我们在下面的计算测试中假定台站位置均匀分布, 设计事件位置分别为均匀分布、线性分布和个别事件零星分布3种情况。由于台站与事件的互易性, 这种测试也对应于事件位置分布均匀、台站位置分布非均匀的情况。为了突出不同拐角频率下台站项对震源谱迭代叠加分离计算的影响, 假设4个地震事件矩震级均为3.0, 对应震源模型的拐角频率输入值分别为12.0, 13.8, 15.1和16.3 Hz。图 2显示台站和事件的几何分布、震源谱分离结果与拟合结果的对比以及震源谱输入模型与拟合结果的对比。
对于事件位置均匀、线性和零星分布3种情况(图 2(a)), 得到3组完全不同的震源谱分离结果(图 2(b)中蓝色实线), 表明路径项对于震源谱分离结果有影响。图 2(c)显示非均匀的事件分布使反演得到的震源谱与输入模型之间产生了一定的偏离。因此, 台站和事件分布不均匀时, 迭代叠加法不能给出震源谱的正确结果。相应地, 拟合的拐角频率与输入模型之间也有差别(表 2)。
| 震源谱参数 | fc/Hz | Δσ/MPa | ||||||
| 事件1 | 事件2 | 事件3 | 事件4 | 事件1 | 事件2 | 事件3 | 事件4 | |
| 初始模型输入值 | 12.0 | 13.8 | 15.1 | 16.3 | 20 | 30 | 40 | 50 |
| 均匀分布拟合值 | 12.4 | 14.3 | 15.6 | 16.7 | 22 | 34 | 44 | 54 |
| 线性分布拟合值 | 17.3 | 16.7 | 9.5 | 11.2 | 60 | 54 | 10 | 16 |
| 零星分布拟合值 | 16.3 | 17.3 | 17.3 | 9.5 | 50 | 60 | 60 | 10 |
| 路径修正拟合值 | 12.4 | 14.1 | 15.4 | 16.5 | 22 | 32 | 42 | 52 |
4 路径项对求取拐角频率和应力降的影响及消除
震源项分离的普遍表达式包含路径项和残差项的影响。当地震事件和台站数量足够多且分布均匀时, 震源项表达式(式(32))中包含的路径项接近零。这个条件在Shearer等[13]对南加州的应力降研究以及Allmann等[16]对全球的应力降研究中是成立的, 也就是在这种情况下分离得到的震源项只包括该地震事件震源项与所有地震事件震源项平均值的偏离。下面具体地讨论路径项在不同地震事件和台站分布情况下, 对求取拐角频率和应力降的可能影响。
参照Shearer等[13]选取的震源模型, 拐角频率fc表达为应力降的函数[1]:
| $ {f_{\rm{c}}} = \frac{{0.42\beta }}{{{{({M_0}/\Delta \sigma )}^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}}} $ |
其中, β是剪切波速度, M0是地震矩, Δσ是应力降, 利用得到的拐角频率以及表 1和2中给出的计算参数, 可以进一步计算应力降。
计算结果表明, 当台站和事件分布不均匀时, 通过拟合迭代叠加法结果得到的应力降与输入的应力降差异明显。需要说明的是, 拟合迭代叠加法给出的震源谱时, 与拐角频率相对应的应力降格点搜索步长为2 MPa, 搜索范围为10~60 MPa。也就是说, 如果拟合得到的应力降是10和60 MPa, 意味着拟合不收敛。例如, 在台站和事件线性分布和零星分布情况下, 对于模型输入的应力降为20, 30, 40, 50 MPa的拟合结果分别为60, 54, 10, 16 MPa和60, 60, 60, 10 MPa, 就属于这种情况。
在针对区域地震的应力降研究中, 有时难以保证台站和事件均匀分布。地震事件沿断层线性分布, 或者个别地震事件零星分布的情况是存在的。尤其在应用流动地震台研究余震时, 地震台数量有限, 主震断层两端的地震事件分别偏离整个流动台阵。在这种条件下, 应用迭代叠加法分离震源谱会面临这种台站路径分布不均匀产生的影响, 路径项对应力降的拟合有很大的影响。这时, 可以将反演得到的分离震源谱减去路径项, 进而类似地应用迭代叠加方法计算拐角频率和应力降。
假定路径项先验已知, 从分离得到的震源谱中, 按照分离震源项的普遍表达式中对于路径项的表述
| $ \left( {\frac{1}{n}\sum\limits_{j = 1}^n {{T_{k(i,j)}}} - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{1}{n}\sum\limits_{j = 1}^n {{T_{k(i,j)}}} } \right)} } \right) $ |
减去路径项的影响。3种台站‒事件分布情况下, 去除路径项影响后得到相同的路径修正拟合值: 22, 32, 42和52 MPa, 对应于20, 30, 40和50 MPa的初始模型输入值, 拟合得到的应力降误差范围为4%~10%。尽管拟合值数值并不大, 但存在普遍偏大的情况。这主要是因为求取的低频水平值是震源谱前5个低频采样点对应的幅值的平均值。当地震台站不是宽频带地震台站, 或者地震事件的拐角频率较小时, 与输入的数值相比, 求取的低频水平值偏小, 拟合的拐角频率将偏大, 由此导致拟合的应力降偏大。在利用实际数据反演应力降时, 应在选用仪器、利用资料和采纳方法时予以精选, 或在结果解释时予以校正。
5 结论和讨论台站记录的地震位移谱包含代表源区特征的震源项、代表传播路径衰减特征的路径项和代表台站附近区域特征的台站项。本文基于对多台站‒多事件位移谱迭代叠加分离求取震源项过程的解析表达式分析, 得到分离震源项的普遍表达式。最终分离得到的单个事件震源谱为三项偏离值的和:该事件震源项与所有事件震源项平均的偏离值、事件与所有台站间路径项平均值和所有事件同类项平均值的偏离值以及与路径项偏离形式一致的与残差项相关的偏离值。结果表明, 分离的震源谱与台站项无关, 但是会受到与多事件‒多台站位置分布非均匀性相关的路径项影响。
为了在台站和事件分布不均匀情况下利用快速收敛的迭代叠加法得到震源谱拟合应力降, 本文提出利用独立得到的路径项减震源谱分离结果, 可以得到类似台站和事件分布均匀情况下的震源谱分离结果, 从而进一步计算应力降, 以满足台站和事件分布不均匀情况下应力降反演的需求。不过, 应当尽量选取信噪比较高的台站记录, 以避免台站和事件分布不均匀情况下残差项的影响。
同时,本文通过表达式分析得出震源项与台站项无关的结果, 增加了研究地震应力降可用资料的范围, 如受沉积层影响的流动地震台观测记录, 以及不能完全去除不同类型地震仪的仪器响应影响的固定地震台观测记录。
另外,本文的研究结果有助于流动地震台站建设。为避免台站和事件分布不均匀情况下路径项对应用迭代叠加法反演震源谱的不利影响, 需要在地震活动区周围均匀地布设地震台阵, 或借助固定地震台网设计流动地震台阵。要求流动地震台站和固定地震台站的分布整体上是均匀的, 比如环形, 甚至不完整的环形(环形的内外径设计要兼顾地震的震级)地震台阵也能满足计算要求。这时, 由于不同地震的路径项非常接近, 路径项的影响就自动消除了。不仅如此, 由于各个台站的噪音水平基本上维持恒定(尽可能兼顾时间段或加一个噪声水平限定), 因此形式上完全相同的残差项的影响也会在很大程度上消除。当地震台阵满足以上要求时, 可以利用快速的迭代叠加法计算应力降。随着中国地震台网的建设, 中国固定台网已能满足本文提出的要求。如果需要研究更小震级地震的应力降, 可以布设更密集的临时地震台阵。如果仅从反演地震应力降的角度出发, 只需要临时地震台阵和固定地震台网构成不完整的环形条带。
致谢:在论文完成过程中, 与陈棋福研究员、杨文正博士进行了有益的讨论, 在此表示感谢。
| [1] | Madariaga R. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America , 1976, 66 (3) : 639–666 . |
| [2] | Eshelby J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences , 1957, 241 : 376–396 DOI:10.1098/rspa.1957.0133 . |
| [3] | Brune J N. Tectonic stress and the spectra of seismic shear waves from earthquakes. Journal of geophy-sical research , 1970, 75 (26) : 4997–5009 DOI:10.1029/JB075i026p04997 . |
| [4] | Wu Z L, Kim S G, Chen Y T. High-frequency fall-off of source spectra of deep-focus earthquakes from Wigner-distribution estimation. Physics of the Earth and Planetary Interiors , 1997, 99 (3) : 221–229 . |
| [5] | 秦嘉政, 钱晓东. 武定6.5级地震序列的地震应力降研究. 地震研究 , 2001, 24 (1) : 17–22. |
| [6] | 郑建常, 潘元生, 万连初, 等. 青岛崂山ML 4.1地震序列应力降变化研究. 地震地磁观测与研究 , 2008, 29 (4) : 17–23. |
| [7] | 董瑞树, 刘志平, 冉洪流. 伊舒断裂带南、北段震源参数研究. 地震地质 , 1996, 18 (1) : 59–65. |
| [8] | Atkinson G M, Mereu R F. The shape of ground motion attenuation curves in southeastern Canada. Bulletin of the Seismological Society of America , 1992, 82 (5) : 2014–2031 . |
| [9] | Moya A, Aguirre J, Irikura K. Inversion of source parameters and site effects from strong ground motion records using genetic algorithms. Bulletin of the Seismological Society of America , 2000, 90 (4) : 977–992 DOI:10.1785/0119990007 . |
| [10] | 刘杰, 郑斯华, 黄玉龙. 利用遗传算法反演非弹性衰减系数、震源参数和场地响应. 地震学报 , 2003, 25 (2) : 211–218. |
| [11] | 华卫, 陈章立, 郑斯华. 2008年汶川8地震地磁观测与研究. 地球物理学报 , 2009, 52 (2) : 365–371. |
| [12] | 赵翠萍, 陈章立, 华卫, 等. 中国大陆主要地震活动区中小地震震源参数研究. 地球物理学报 , 2011, 54 (6) : 1478–1489. |
| [13] | Shearer P M, Prieto G A, Hauksson E. Compre-hensive analysis of earthquake source spectra in southern California. Journal of Geophysical Re-search: Solid Earth , 2006, 111 (B6) : 3197–3215 . |
| [14] | Yang W Z, Peng Z G, Ben-Zion Y. Variations of strain-drops of aftershocks of the 1999 İzmit and Düzce earthquakes around the Karadere-Düzce branch of the North Anatolian Fault. Geophysical Journal International , 2009, 177 (1) : 235–246 DOI:10.1111/gji.2009.177.issue-1 . |
| [15] | Allmann B P, Shearer P M. Spatial and temporal stress drop variations in small earthquakes near Parkfield, California. Journal of Geophysical Re-search: Solid Earth , 2007, 112 (B4) : 1–10 . |
| [16] | Allmann B P, Shearer P M. Global variations of stress drop for moderate to large earthquakes. Journal of Geophysical Research: Solid Earth , 2009, 114 (B1) : 1–22 . |
| [17] | Prieto G A, Parker R L, Vernon F L, et al. Uncertainties in earthquake source spectrum esti-mation using empirical Green functions. Earth-quakes: Radiated Energy and the Physics of Faulting , 2006, 170 : 69–74 DOI:10.1029/GM170 . |
| [18] | Kane D L, Prieto G A, Vernon F L, et al. Quantifying seismic source parameter uncertainties. Bulletin of the Seismological Society of America , 2011, 101 (2) : 535–543 DOI:10.1785/0120100166 . |
| [19] | Warren L M, Shearer P M. Investigating the frequency dependence of mantle Q by stacking P and PP spectra. Journal of Geophysical Research: Solid Earth , 2000, 105 (B11) : 25391–25402 DOI:10.1029/2000JB900283 . |
| [20] | Warren L M, Shearer P M. Mapping lateral variations in upper mantle attenuation by stacking P and PP spectra. Journal of Geophysical Research: Solid Earth , 2002, 107 (B12) : ESE 6-1–ESE 6-11 DOI:10.1029/2001JB001195 . |
| [21] | Prieto G A, Shearer P M, Vernon F L, et al. Earthquake source scaling and self-similarity estimation from stacking P and S spectra. Journal of Geophysical Research: Solid Earth , 2004, 109 (B8) : 217–228 . |
| [22] | Oth A, Bindi D, Parolai S, et al. S-wave attenuation characteristics beneath the Vrancea region in Romania: new insights from the inversion of ground-motion spectra. Bulletin of the Seismological Society of America , 2008, 98 (5) : 2482–2497 DOI:10.1785/0120080106 . |
| [23] | Bonilla L F, Steidl J H, Lindley G T, et al. Site amplification in the San Fernando Valley, California: variability of site-effect estimation using the S-wave, coda, and H/V methods. Bulletin of the Seis-mological Society of America , 1997, 87 (3) : 710–730 . |
| [24] | Andrews D J. Objective determination of source parameters and similarity of earthquakes of different size. Earthquake Source Mechanics , 1986, 37 : 259–267 DOI:10.1029/GM037 . |
| [25] | Kanamori H. The energy release in great earth-quakes. Journal of Geophysical Research , 1977, 82 (20) : 2981–2987 DOI:10.1029/JB082i020p02981 . |
| [26] | Yamada T, Mori J J, Ide S, et al. Radiation efficiency and apparent stress of small earthquakes in a South African gold mine. Journal of Geophysical Research: Solid Earth , 2005, 110 (B6) : 251–268 . |
 2016, Vol. 52
2016, Vol. 52





