

北京大学学报(自然科学版) 第61卷 第1期 2025年1月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 61, No. 1 (Jan. 2025)
doi: 10.13209/j.0479-8023.2024.038
国家重点研发计划(2021YFC2203003, 2022YFA1402704, 2021YFC2203002)和国家自然科学基金(11834005, 12247101)资助
收稿日期: 2024–02–05;
修回日期: 2024–04–03
摘要 极端质量比旋近 EMRI 指质量比在 104~107 之间的双星系统, 其中小质量天体被捕获后绕大质量黑洞旋近, 期间损失的能量以引力波的形式向外辐射。旋近结束前的最后一年估计能产生 105 个旋近周期, 因此可提供丰富的引力波相位演化信息。小质量天体处在大质量黑洞的强引力环境中, 运动轨迹能反映大质量黑洞周围的时空结构, 其波形可用来限制引力理论和无毛定理等。大质量黑洞一般处在星系中心, 星系所处的天文学环境会在波形中留下痕迹。多个波源能给出大黑洞的质量和自旋分布, 用于限制宇宙演化和星系演化等。基于上述科学意义, EMRI 成为空间引力波计划 LISA、太极和天琴的重要观测目标, 因此对 EMRI 的数据分析成为一个重要任务。EMRI 波形的高维度和复杂性对数据分析方法要求较高, 目前还没有公认的满意答案。首先回顾 LISA 模拟数据挑战赛中提出的方法和最近的讨论, 然后总结 EMRI 数据分析的难点, 并提出改进方法, 最后讨论未来研究发展中可能用到的几个线索。
关键词 极端质量比旋近; 信号探测; 参数估计; 频谱法; 匹配滤波
极端质量比旋近(Extrem Mass-Ratio Inspiral, EMRI)指一个小质量天体(可能是黑洞、中子星或白矮星等)被位于星系中心的大质量黑洞[1](一般认为是 104~107M⊙)捕获后不断旋近的双星系统[2–3]。EMRI 旋近期间损失的能量以引力波(gravitational wave, GW)的形式连续向外辐射, 结束旋近前最后一年可以观测到约 105 个轨道周期[4], 因此引力波波形中包含丰富的相位演化信息, 对引力波天文学有重要意义[5–6]。例如, 小质量天体处在大质量黑洞的强引力环境中, 其轨道演化可以刻画出大质量黑洞周围的时空结构[7–8], 可基于波形还原轨道演化过程, 用来检验引力理论和无毛定理等[9–11]; 大质量黑洞所处的星系环境效应也会影响波形[12]; 若干波源可以给出大质量黑洞的质量和自旋等分布信息, 用于限制星系演化等过程[5–6]。因此, EMRI 成为空间引力波探测计划 LISA (Laser Interferometer Space Antenna)[13]、太极[14–15]和天琴[16]的重要目标波源, EMIR 数据分析成为一个重要任务。
EMRI 的精确物理波形需要考虑小质量天体的自引力(Self-force)效应[17]。数据分析中常用的是唯像近似的半相对论性kludge波形, 包括以下 3 种方法。1)Analytical kludge (AK)[18]: AK 用后牛顿近似描述轨道演化, 同时考虑近心点进动和 Lense-Thir-ring 进动效应, 给出首阶四极矩波形; 2)Numerical kludge (NK)[19]: NK 用克尔测地线方程描述轨道演化, 与基于 Teukolsky 方程计算的更精确波形高度匹配, 计算速度优于 Teuko-lsky 方法, 但是比 AK慢; 3)Augmented Analytical kludge (AAK)[20–23]: AAK用 AK 的参数拟合 NK 的轨道频率, 融合 AK 计算速度快和 NK 精度高的优势。
参考 LISA 数据挑战赛(Mock LISA Data Chal-lenge[24–27]/LISA Data Challenge[28], MLDC/LDC), 本文主要介绍 AK 波形。AK 波形的高维度和复杂性(主要是多个谐波(harmonics)的叠加)使得探测统计量对应的参数空间结构比较复杂。一般认为, 存在一个高维尖锐主峰和数量众多的相互之间间隔明显的次峰环绕在主峰周围[29], Chua 等[30]将该特征比喻为干草堆里一根针, 用干草比喻次峰, 用针比喻信号所在位置的尖锐主峰。参数之间潜在的关联与简并[31]使得通过优化(optimization)或推断(inference)探测统计量得到全局极值点的难度较大。空间引力波探测器使用消除激光频率噪音的时间延迟技术(time delay interferometer, TDI)[32] , 由此产生的计算量使得计算探测统计量非常耗时。总之, EMRI 数据分析是一个在物理(波形的物理特征)和计算方面(匹配滤波需要至少百万次地计算不同位置的探测统计量)都很有挑战性的问题。
AK 波形[18]中包括 14 个参数: m, M, l, S/M2, e0, 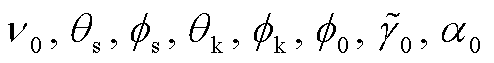 和 D。μ 和 M 分别是小质量天体和大质量黑洞的质量, λ 是小质量天体的轨道角动量与大黑洞自旋角动量的夹角, S/M2 是大黑洞自旋角动量, e0 和 v0 分别是轨道的初始偏心率和转动频率, θs 和 fs 是 EMRI 在黄道坐标系中的余纬和经角, θk 和 fk 是黄道坐标系中大质量黑洞自旋的方向, f0,
和 D。μ 和 M 分别是小质量天体和大质量黑洞的质量, λ 是小质量天体的轨道角动量与大黑洞自旋角动量的夹角, S/M2 是大黑洞自旋角动量, e0 和 v0 分别是轨道的初始偏心率和转动频率, θs 和 fs 是 EMRI 在黄道坐标系中的余纬和经角, θk 和 fk 是黄道坐标系中大质量黑洞自旋的方向, f0,  和a0 分别是轨道转动、近日点进动和轨道平面进动的初始相位角, D 是引力波波源在太阳系质心坐标系的距离。
和a0 分别是轨道转动、近日点进动和轨道平面进动的初始相位角, D 是引力波波源在太阳系质心坐标系的距离。
描述 EMRI 轨道演化的 5 个物理量分别是轨道转动的相位 f、频率 v、近日点进动在轨道平面的方位角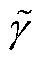 、轨道偏心率 e 和轨道平面进动在轨道平面的方位角 α, 其时间演化用一组常微分方程(ordi-nary differential equations, ODEs)[18]描述:
、轨道偏心率 e 和轨道平面进动在轨道平面的方位角 α, 其时间演化用一组常微分方程(ordi-nary differential equations, ODEs)[18]描述:
 (1)
(1)
需要指出, 以上 ODEs 的求解需使用与 MLDC/ LDC 一致的 5 阶 Cash-Karp Runge-Kutta 求解器[33], 原因是引力波波形对轨道演化非常敏感, 使用其他自适应的求解器不能得到与 LDC 一致的波形。得到 ODEs 的解后, 每个谐波的极化波形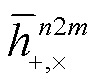 以如下形式[29,34]给出:
以如下形式[29,34]给出:
 (2)
(2)
其中 n, m 分别是每个谐波相对 ODEs 给出的轨道运动相位基准值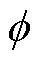 和轨道平面进动(Lense-Thirring 进动)相位基准值 α 的倍数。由于 AK 给出的是四极矩波形, 所以每个谐波相对 ODEs 给出的近心点进动相位基准值
和轨道平面进动(Lense-Thirring 进动)相位基准值 α 的倍数。由于 AK 给出的是四极矩波形, 所以每个谐波相对 ODEs 给出的近心点进动相位基准值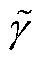 的倍数始终为 2。LDC 中, n=1, 2, 3, 4, 5, m=–2, –1, 0, 1, 2, 共包含 25 个谐波。式(2)使用基于大黑洞自旋角动量方向和引力波传播方向的坐标系重新表述了 AK 波形[29], 相比于使用基于小天体轨道角动量和引力波传播方向的坐标系的原始波 形[18], 可以更清晰地反映谐波的线性叠加特征,即每个谐波都有独立的振幅和相位, 方便参数空间的降维。
的倍数始终为 2。LDC 中, n=1, 2, 3, 4, 5, m=–2, –1, 0, 1, 2, 共包含 25 个谐波。式(2)使用基于大黑洞自旋角动量方向和引力波传播方向的坐标系重新表述了 AK 波形[29], 相比于使用基于小天体轨道角动量和引力波传播方向的坐标系的原始波 形[18], 可以更清晰地反映谐波的线性叠加特征,即每个谐波都有独立的振幅和相位, 方便参数空间的降维。
TDI 的信道 X, Y, Z 之间的噪音相关, 可通过进一步组合得到噪音互不相关的 A, E 和 T 信道[32]:
 (3)
(3)
一代 TDI 的 X, Y, Z 信道分别是 8 个延迟单臂响应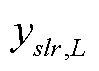 的线性叠加[35]:
的线性叠加[35]:
 (4)
(4)
其中, 下角标 s 和 r 分别表示发射和接受激光的卫星; 下角标 l 表示连接两个卫星的单臂, 其符号表示方向; 下角标 L 表示贡献延迟的臂, 其符号表示方向。由于 TDI 的特征延迟量探测器臂长(LISA 设计值是 250 万 km)小于多数 EMRI 波源产生的引力波(频率为 ω)的波长, 所以利用泰勒展开, 可以从单臂响应得到延迟单臂响应, 即
 。
。
单臂响应 yslr[35]可以表示为
 (5)
(5)
其中, 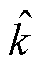 和
和 分别表示引力波传播方向与臂长 l 方向的基矢,
分别表示引力波传播方向与臂长 l 方向的基矢, 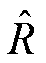 是卫星的位置向量, 单臂 l 对应的引力波应变为
是卫星的位置向量, 单臂 l 对应的引力波应变为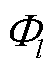 ,
, 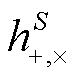 是两种极化模式的波形,
是两种极化模式的波形, 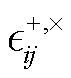 是太阳系质心坐标系中的极化张量,
是太阳系质心坐标系中的极化张量,  表示两个矢量的运算
表示两个矢量的运算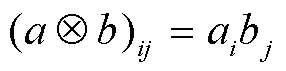 , “:”表示两个二维张量的运算
, “:”表示两个二维张量的运算 。
。
引力波数据分析方法大致分为两类: 依赖模板或不依赖模板。频谱图方法在信号探测时不依赖模板, 利用还原的信号轨迹估计参数时需要模板; 匹配滤波依赖模板; 机器学习方法在训练神经网络时依赖模板, 探测信号时不依赖模板, 估计参数时需要模板。
Gair 研究团队[36–42]在 2005—2008 年发展了频谱图的系列方法, 主要思路是基于给定的误报率水平, 首先用噪音数据拟合频谱图幅值的阈值, 然后在数据(可能包含引力波信号)的频谱图中搜索超过阈值的区域或像素, 最后通过分析这些超出噪音背景的像素的特征, 从中提取 EMRI 信号的信息。上述工作采用相同的方法将时间序列转换到频谱图, 即先将两年数据切分成若干连续的两周的数据段, 再分别做快速傅里叶变换(fast Fourer transformation, FFT), 得到每个数据段的频谱图, 最后按时间顺序, 将分段的频谱图拼接起来得到完整数据的频谱图。该系列方法按照设计目的与功能可以分为 3 个层次。
1)第 1 层次仅实现信号探测[36–38]。设计一系列不同尺寸的方形盒子, 依次用多个尺寸相同的方形盒子覆盖整个频谱图, 每一个盒子的幅值用所在区域内像素点幅值的平均值表示。拟合阈值时, 假定方形盒子之间相互独立[36], 其频谱没有重叠。对于数据(可能包含引力波信号)对应的频谱图, 如果某个盒子的幅值超过阈值, 就表示存在 EMRI 信号。考虑到方形盒子频谱之间的重叠效应[37], 通过蒙特卡洛模拟出其真实的自由度数目。此方法可以探测到距离为 2Gpc 左右显著的 EMRI 信号(小质量天体质量为 10M⊙, 大质量黑洞质量为 106M⊙)。
2)第 2 层次[39–41]不仅实现信号探测, 还能估计8 个参数, 即 6 个与 ODEs 相关的参数 μ, M, λ, S/M2, e0 和 v0 以及天区方位角 和
和 。第 1 层次使用一个阈值参数, 只能大致拟合出频谱图中明显超过噪音背景的像素, 第 2 层次[40]使用 3 个阈值参数, 分别是黑色像素(高亮)、灰色像素(中间亮度)的阈值以及区分出亮度超过灰色像素的像素点, 可在频谱图中拟合出连续的信号轨迹(track), 从中提取的频率演化信息可用来估计 6 个与 ODEs 相关的参数(μ, M, λ, S/M2, e0 和 v0), 从中提取的强度变化的信息可用来估计天区方位角
。第 1 层次使用一个阈值参数, 只能大致拟合出频谱图中明显超过噪音背景的像素, 第 2 层次[40]使用 3 个阈值参数, 分别是黑色像素(高亮)、灰色像素(中间亮度)的阈值以及区分出亮度超过灰色像素的像素点, 可在频谱图中拟合出连续的信号轨迹(track), 从中提取的频率演化信息可用来估计 6 个与 ODEs 相关的参数(μ, M, λ, S/M2, e0 和 v0), 从中提取的强度变化的信息可用来估计天区方位角 和
和 。此方法可以探测到距离为 2.6Gpc 左右显著的 EMRI 信号, 相比于第 1 层次, 探测距离略远。该方法应用在 MLDC-1.3 数据集中, 能够还原出 4 个信号, 漏掉 1 个信噪比较小的信号, 另外, 其参数估计误差比匹配滤波的结果略大。
。此方法可以探测到距离为 2.6Gpc 左右显著的 EMRI 信号, 相比于第 1 层次, 探测距离略远。该方法应用在 MLDC-1.3 数据集中, 能够还原出 4 个信号, 漏掉 1 个信噪比较小的信号, 另外, 其参数估计误差比匹配滤波的结果略大。
3)第 3 层次[42]是第二层次的拓展, 拟合信号轨迹时利用谐波啾啾(chirp)的频谱特征, 用多项式拟合出信号轨迹对应的频率、频率一阶导数和频率二阶导数, 最终除了能估计 8 个参数(μ, M, λ, S/M2, e0和 v0,  和
和 ), 还能估计出大黑洞自旋方向和引力波传播方向之间的夹角。该方法应用在 MLDC-1.3 数据集中, 能够还原出全部 5 个信号, 其参数误差相比匹配滤波的结果略大。
), 还能估计出大黑洞自旋方向和引力波传播方向之间的夹角。该方法应用在 MLDC-1.3 数据集中, 能够还原出全部 5 个信号, 其参数误差相比匹配滤波的结果略大。
频谱方法的优点是计算量小, 计算速度快。缺点是拟合阈值的过程非常依赖手动调节参数; 只能估计 ODEs 相关的参数和天区方位角, 不能估计其他参数, 因此不能重构完整波形; 并且, 其估计参数的误差一般大于匹配滤波的对应结果。频谱方法适合用在数据分析的第一阶段, 搜索信噪比较大的 信号。
2008—2013 年期间, EMRI 数据分析中有 4 个用马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)实现的匹配滤波的应用。
1)Gair 等[29,43]首先对 3 个月长度的数据运行多个短的 MCMC, 运用退火(annealing)等机制, 尽量快地找到很多探测统计量的次极大值点; 然后通过分析次极大值点的信息, 提取起主导作用的谐波信息; 重复数次该过程, 将现阶段最优次极大值点的位置作为下一段 MCMC 的初始位置, 利用拟合的占主导作用的谐波信息, 加速和限制新的匹配过程, 逐渐增加匹配数据的长度; 最后, 通过运行满足马尔科夫性质和细致平衡原理的 MCMC, 匹配完整的两年数据, 得到最终的参数估计值。
该工作给出 13 维探测统计量的解析构造方式以及用最强的 3 个谐波(top3)解析地估计 3 个初始相位参数 和 a0, 实现探测统计量降维的方法。进一步给出 8 维探测统计量的构造方式, 即按照与白矮星一样的 F 统计方式[44], 先对单个谐波进行降维, 再利用不同谐波波形间重合度低的假设, 将单个谐波的探测统计量相加, 得到 EMRI 的探测统计量。该方法运用在 MLDC-1.3 数据集中, 能够还原出所有 5 个信号。
和 a0, 实现探测统计量降维的方法。进一步给出 8 维探测统计量的构造方式, 即按照与白矮星一样的 F 统计方式[44], 先对单个谐波进行降维, 再利用不同谐波波形间重合度低的假设, 将单个谐波的探测统计量相加, 得到 EMRI 的探测统计量。该方法运用在 MLDC-1.3 数据集中, 能够还原出所有 5 个信号。
2)Cornish[45]使用与 Gair 等[29,43]类似的退火(an-nealing)机制, 还使用局部优化和遗传算法等方法来增强 MCMC 的搜索能力。
由于直接匹配完整的两年数据的计算量大, 该工作提出切割数据(heterodyne)的方法。在匹配滤波之前, 先将原始数据在频域切分成若干份, 使每一份子数据仅包含一个相对窄频段的信息, 在不损失信息的前提下, 调整采样率, 减少各个子数据的长度, 最后将处理好的子数据保存备用。在匹配滤波时, 判断 MCMC 每一步的波源参数对应的频率演化范围, 选择对应频段的子数据来匹配。相比于完整的数据, 子数据的匹配滤波计算量小, 并行实现可以显著地加速匹配滤波。该方法修改了白矮星频域波形FastGB, 对 EMRI 实现类似的频域波形计算, 与时域波形生成速度相比, 提高约 1000 倍。将该方法运用在 MLDC-1.3 和 MLDC-3 数据集中, 能够还原出所有 5 个信号。
3)Wang 等[46]提出 EMRI 的一种唯象波形。利用 EMRI 缓慢演化以及其谐波频谱类似啾啾(chirp)的特征, 可以在小于 3 个月的时间范围内, 用多项式来拟合谐波的非线性演化(式(1))。使用该唯象波形, 在匹配滤波时可以较容易地拟合出占主导作用的谐波和相应的唯象参数(振幅、频率、频率一阶导数和频率二阶导数), 之后再使用 MCMC 或粒子群方法, 将唯象参数转换为物理参数(质量和自旋等)。该工作采用与 Arnaud 等[26]类似的方法构造 8维探测统计量来实现降维。以 NK 为物理波形, 该工作用 3 个月长度的模拟数据验证了唯象波形在数据分析中的有效性。
4)Ali 等[34,47]使用 Parallel Tempering MCMC (PTMCMC)实现匹配滤波, 通过调节温度梯子的不同设置, 得到最佳搜索效果。由于调用 LISASimu-lator 来生成 TDI, 精度高, 但计算量特别大, 所以Ali 等[46]主要分析两个月长度的数据。将该方法运用在多组模拟数据、MLDC-1.3 和 MLDC-4 数据集中, 能够还原单个 EMRI 信号以及部分还原多个重叠的EMRI 信号。
2023 年以来, 有两篇文献讨论相关问题。
1)Bandopadhyay 等[48]主要讨论太阳质量双黑洞系统的数据分析问题, 同时提出迭代地使用灵 敏度越来越高的 semi-coherent 探测统计量来实现EMRI 的匹配滤波。前一阶段低灵敏度、大范围的搜索结果可用来缩小下一阶段高灵敏度搜索的参数范围, 逐步减小搜索目标尖峰的难度。文献[48]给出几点相当重要的总结: ①EMRI 波形多个谐波叠加的特征导致无法解析地令探测统计量的一阶导数等于零来最大化外部参数(振幅和初始相位等); ②数据长度越长, 匹配滤波的灵敏性越高, 灵活性越低, 匹配成功的难度越大。
2)Ye 等[49]使用分层次搜索(Hierarchcal Search)缩小信号可能所处的参数空间范围的方法, 这里的参数指与 ODEs(式(1))相关的 6 个参数(μ, M, λ, S/M2, e0 和 v0), 其微小变化会改变 ODEs 的解, 从而改变引力波波形。EMRI 波形的高维度和引力波波形对相位的敏感性, 使得对 ODEs 相关的参数大范围搜索相当困难。虽然 MLDC 给出的参数范围相对较 窄[40], 但利用现有的 MCMC 方法, 直接在此范围内搜索仍然很困难, 需要进一步缩小。该工作得出以下结论: 每个 ODEs 相关的参数范围为~100σ 的信号邻域, 是现有方法的一般适用范围, 非常有必要通过分层次搜索, 从给定的大范围中估计出信号所处的较窄范围。
匹配滤波是最精细的数据分析方法, 可以给出完整的参数估计, 也适用于低信噪比信号。但是, 对 EMRI 而言, 其参数空间的维数较高(14 维), 现阶段还没有公认的有效的降维方法, 因此其高维空间的匹配滤波难度较大; EMRI 的波形、TDI 和内积等计算量较大, 一般匹配滤波需要百万次甚至更多次地计算不同位置的模板对应的探测统计量, 从中挑选与给定数据匹配程度最高的模板及其位置, 因此对探测统计量的快速计算有较高的要求。这两点使得 EMRI 的匹配滤波在物理和计算两个角度都比较困难。
借助于最近兴起的机器学习和深度学习技术, 卷积神经网络(convolutional neural network, CNN)已应用于 EMRI 数据分析中。Zhang 等[50]将时域信号作为 CNN 的输入, 实现对信噪比为 50 的 3 个月长度的天琴模拟数据的信号探测。Zhao 等[51]将频域信号作为 CNN 的输入, 实现对信噪比为 50~ 120 的一年长度的 LISA 模拟数据的信号探测, 其中使用了 TDI-1.5。Yun 等[52–53]将 Q 变换的频谱图作为CNN 的输入, 实现对信噪比为 50~100 的半年长度的太极模拟数据的信号探测[52]以及大黑洞质量、自旋和轨道偏心率的参数估计[53], 其中使用 TDI-2.0 和另外一个 CNN 模型 VGG 来估计参数[53]。
神经网络方法的优势是使用训练好的神经网络可以非常快速地给出对新信号的探测和部分参数估计的结果, 效率远高于匹配滤波等方法。但是, 目前的研究中, 在训练网络时, 采用的训练集相比EMRI 的高维参数空间显得不充分, 其中一些参数的范围设定很窄, 一般性和普适性稍显不足; 同时, 仅能处理潜在信号信噪比较高的情形, 对信噪比更低的一般情形尚未探索。考虑到最近几年深度学习革命性的发展, 相信会在未来的 EMRI 数据分析中发挥更重要的作用。
本节讨论 EMRI 参数空间的降维方法及其改进、匹配滤波的难点及其应对策略。
EMRI 的参数空间维数是 14, 高维的匹配滤波难度大, 因此需要考虑降维。假设参数集 包含所有 14 个参数; 参数集 θ 包含除距离 D 之外的 13 个参数, 即
包含所有 14 个参数; 参数集 θ 包含除距离 D 之外的 13 个参数, 即 ; 参数集
; 参数集 包含除距离
包含除距离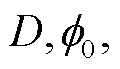
 和
和 外的 10 个参数,
外的 10 个参数, 
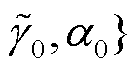 。14 维极化波形为
。14 维极化波形为 , 应变响应为
, 应变响应为 , TDI响应为
, TDI响应为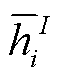 ; 13维极化波形为
; 13维极化波形为 , 应变响应为
, 应变响应为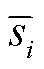 , TDI 响应为
, TDI 响应为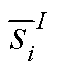 ; 10 维复极化波形为
; 10 维复极化波形为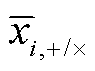 , 应变响应为
, 应变响应为 , TDI 响应为
, TDI 响应为 。指标 i 表示第 i 个谐波,
。指标 i 表示第 i 个谐波, 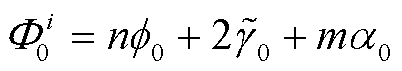 表示第 i 个谐波的初始相位, 两个独立 TDI 信道为
表示第 i 个谐波的初始相位, 两个独立 TDI 信道为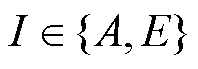 。
。
引力波数据分析中衡量两个信号 线性相关性的内积定义为
线性相关性的内积定义为
 (6)
(6)
其中, f是频率, Sn(f)是给定探测器的噪音功率谱密度, 上角标~表示傅里叶变换后的频域信号, *表示取复共轭。
首先参考 Gair 等[29]给出 13 维探测统计量的解析构造方式。给定信道 I 的数据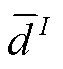 , 则探测统计量可以写为
, 则探测统计量可以写为
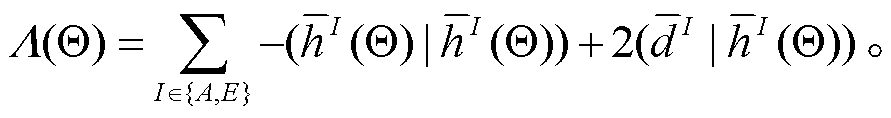 (7)
(7)
令探测统计量对参数 D 的一阶导数等于零, 得到

 (8)
(8)
D 的估计值 为
为
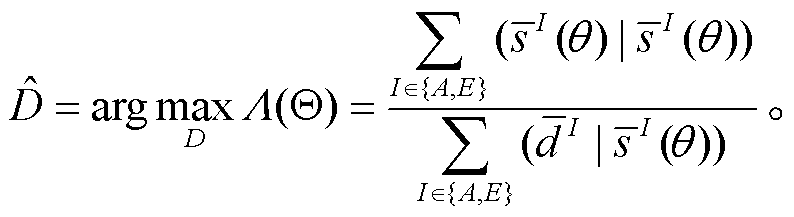 (9)
(9)
然后讨论 Gair 等[29]提出的基于 top3 谐波的降维方法。基于如下极化波形分解:
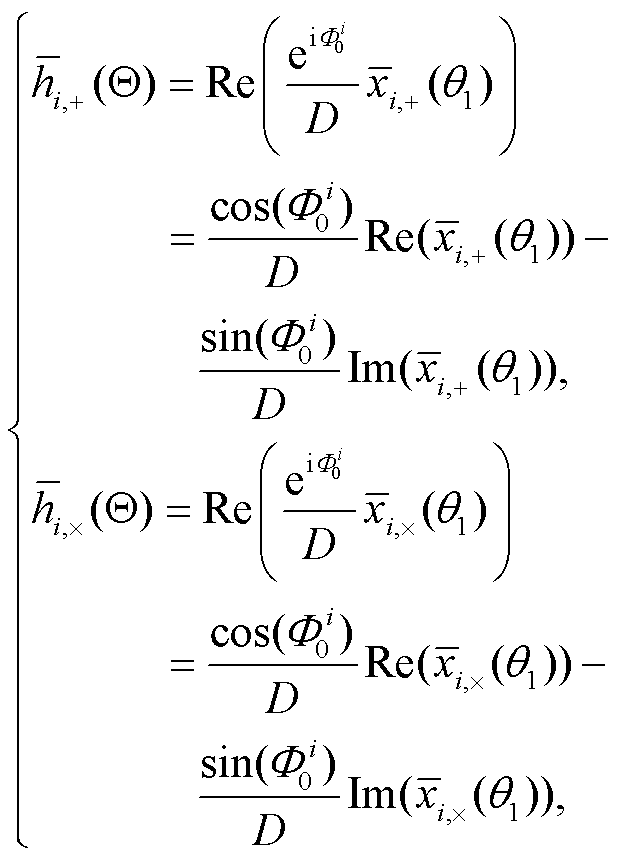 (10)
(10)
结合探测器响应函数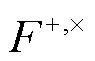 , 得到应变响应
, 得到应变响应
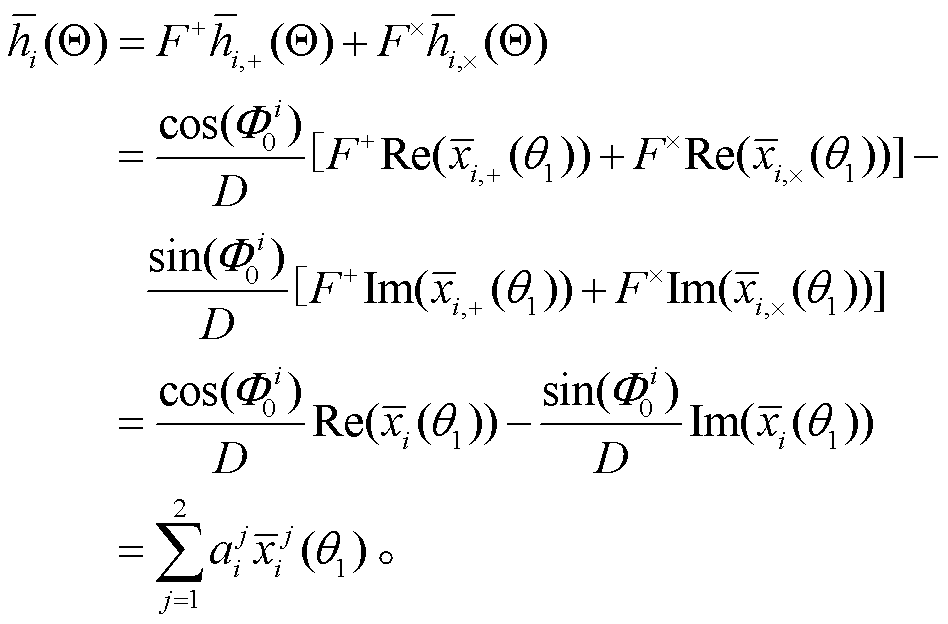 (11)
(11)
因为 TDI 的延迟只作用于含时项, 所以上述线性展开对 TDI 响应同样适用, 即
 (12)
(12)
此处每个谐波的 TDI 响应展开为两个线性项的叠加。基于以上分解, Gair 等[29]使用 F 统计[44], 对top3 谐波组成的探测统计量进行降维。首先使用 F统计估计线性项系数, 得到每个谐波的初始相位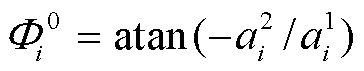 , 然后求解一个线性方程组解析地估计出 3 个初始相位
, 然后求解一个线性方程组解析地估计出 3 个初始相位 和 a0, 最后将其带入13 维探测统计量(式(8))进行匹配滤波。此时, 待搜索参数空间不再包含 3 个初始相位和距离参数, 使用式(9)估计距离 D。需要指出, 使用 top3 谐波的 6 个线性系数估计 3 个初始相位(
和 a0, 最后将其带入13 维探测统计量(式(8))进行匹配滤波。此时, 待搜索参数空间不再包含 3 个初始相位和距离参数, 使用式(9)估计距离 D。需要指出, 使用 top3 谐波的 6 个线性系数估计 3 个初始相位(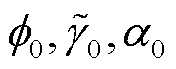 )存在自由度不一致的问题。每个谐波线性展开的两个系数满足如下条件:
)存在自由度不一致的问题。每个谐波线性展开的两个系数满足如下条件:
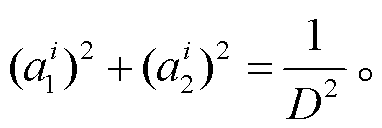 (13)
(13)
top3 谐波可以引入 3 个类似的条件。求解上述线性方程组时, 考虑这些限制条件可以平衡自由度, 对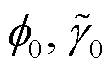 和
和 的估计会更精确。top3 谐波一般只占EMRI 整体信噪比的 90%左右, 考虑到匹配滤波对波形非常敏感, 有必要修正基于 top3 谐波估计的f0,
的估计会更精确。top3 谐波一般只占EMRI 整体信噪比的 90%左右, 考虑到匹配滤波对波形非常敏感, 有必要修正基于 top3 谐波估计的f0,  和
和 数值, 使其包含其他较弱谐波的影响。
数值, 使其包含其他较弱谐波的影响。
另外, Gair 等[4,29]和 Wang 等[46]都按白矮星的方式构造单个谐波的探测统计量, 在不同谐波波形重合度低的假设下, 求和得到 EMRI 探测统计量。这种方式的降维会导致 和 D 的估计依赖于谐波的选择。当使用匹配滤波的最终结果 10 维
和 D 的估计依赖于谐波的选择。当使用匹配滤波的最终结果 10 维 的最优匹配值估计参数
的最优匹配值估计参数 和 D 时, 每个谐波的线性项系数(式(12))都能给出一个距离 D 的估计值(式(13)), 每 3 个谐波的线性项系数都能给出一组
和 D 时, 每个谐波的线性项系数(式(12))都能给出一个距离 D 的估计值(式(13)), 每 3 个谐波的线性项系数都能给出一组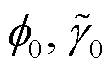 和
和 的估计值。然而, 事实上所有谐波共享一组相同的初始相位值和波源距离。使用单个谐波的探测统计量分别与数据匹配时存在类似的问题。估计参数
的估计值。然而, 事实上所有谐波共享一组相同的初始相位值和波源距离。使用单个谐波的探测统计量分别与数据匹配时存在类似的问题。估计参数 和 D 时出现多值的情形, 干扰了估计完整的波源参数, 影响重构完整波形。
和 D 时出现多值的情形, 干扰了估计完整的波源参数, 影响重构完整波形。
因为 EMRI 波形由多个谐波线性叠加组成, 而F 统计仅对单个谐波的波形适用, 所以直接应用F统计方法[44], 解析地对初始相位等参数降维, 是不可行的。Bandopadhyay 等[48]也给出相同的观点。参考式(8)和(9), 仅对距离 D 解析降维是可行的, 因此我们使用式(8)作为匹配滤波的探测统计量, 对 13 维参数空间进行降维。对初始相位等参数降维的解决办法是, 首先对波形做线性展开, 将含时项与非含时项分离; 然后在探测统计量(式(8))的内积中应用该线性展开, 实现式(8)中的参数(变量)分离; 最后使用嵌套的两种数值方法, 分别优化(或推断)分离后的两类参数(对含时项有贡献的参数和对非含时系数有贡献的参数, 简称含时参数与非含时参数)。需要注意的是, 本文一直使用 13 维探测统计量(式(8))作为匹配滤波的目标函数, 同时为对应下面不同分解方式中含时参数的数目, 将式(8)称为10 维/8 维/7 维探测统计量。
3.2.1 10维探测统计量
10 维探测统计量的含时参数集是 , 非含时参数是
, 非含时参数是 和
和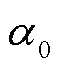 。我们使用与式(12)类似的线性 展开:
。我们使用与式(12)类似的线性 展开:
 (14)
(14)
系数 对应的限制条件为
对应的限制条件为 。式(8)中两种内积的第 i 和 j 个谐波的分量可以整理为
。式(8)中两种内积的第 i 和 j 个谐波的分量可以整理为
 (15)
(15)
将此分解带入式(8), 可以得到变量分离的 13 维探测统计量:
 (16)
(16)
其中, N 为谐波数目。
3.2.2 8维探测统计量
描述大黑洞自旋方向的两个参数(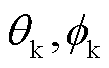 )只对不含时的振幅有贡献[29], 对波形进一步地线性展开, 将
)只对不含时的振幅有贡献[29], 对波形进一步地线性展开, 将 与
与 整理为非含时系数, 与含时参数实现分离。参数集
整理为非含时系数, 与含时参数实现分离。参数集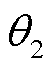 表示除
表示除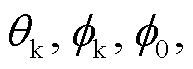
 和
和 外的 8 个参数, 即
外的 8 个参数, 即 ; 参数集
; 参数集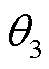 包含ODEs 相关的 6 个参数(m, M, l, S/M2, e0, v0), 即
包含ODEs 相关的 6 个参数(m, M, l, S/M2, e0, v0), 即 ; 8 维极化复波形为
; 8 维极化复波形为 , 应变响应为
, 应变响应为 , TDI 响应为
, TDI 响应为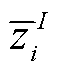 。此处含时参数集是
。此处含时参数集是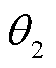 , 非含时参数是
, 非含时参数是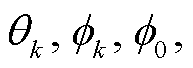
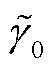 和
和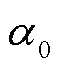 。8 维极化复波形的分解方式为
。8 维极化复波形的分解方式为
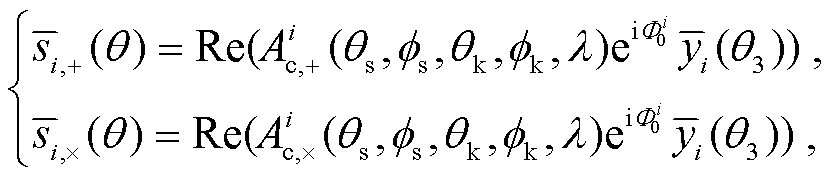 (17)
(17)
指标 i 表示第 i 个谐波, 下角标 c 表示该变量不含时。引力波波形的时变部分为
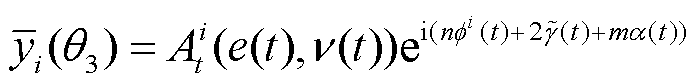 , (18)
, (18)
下角标 t 表示该变量含时。上述极化波形分解与探测器响应函数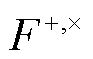 相结合, 可得到应变响应
相结合, 可得到应变响应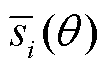 :
:
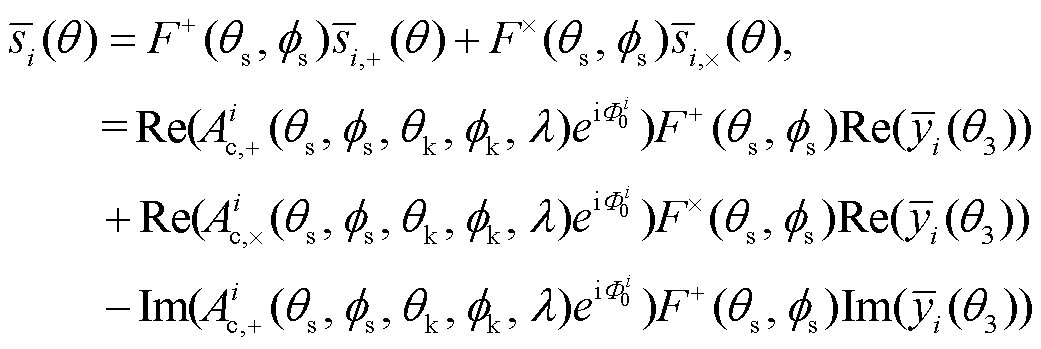
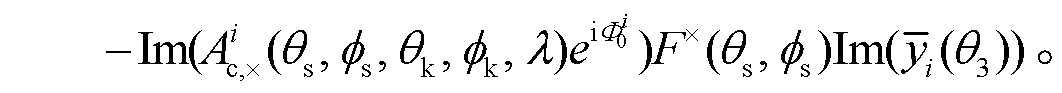 (19)
(19)
以上波形的线性展开对 TDI 响应也适用, 即
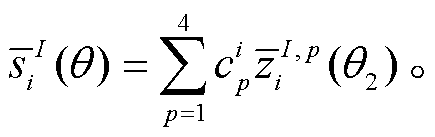 (20)
(20)
基于上述分解, 式(8)中的两种内积第 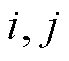 个谐波的分量可以整理为
个谐波的分量可以整理为
 (21)
(21)
通过式(16)可以得到变量分离的 13 维探测统计量(式(8))。
3.2.3 7维探测统计量
参数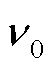 是小质量天体轨道转动的初始频率, 对所有谐波贡献一个相同的相位平移, 可以通过时域滑动(time sliding)或频域旋转(phase rotation)最大化探测统计量估计
是小质量天体轨道转动的初始频率, 对所有谐波贡献一个相同的相位平移, 可以通过时域滑动(time sliding)或频域旋转(phase rotation)最大化探测统计量估计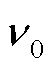 [4,45]。通过事先分析探测器的低频特征, 可以选择一个合适的
[4,45]。通过事先分析探测器的低频特征, 可以选择一个合适的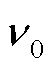 作为基准值。使用
作为基准值。使用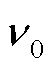 基准值与其他
基准值与其他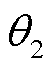 参数计算 8 维波形
参数计算 8 维波形 , 在一定范围内滑动平移该波形, 找到使得 8 维探测统计量(式(8))最大化的平移量, 该平移量对应的频率和偏心率即为参数 v0 和 e0的最优拟合值。需要注意的是, 此时 8 维参数集合
, 在一定范围内滑动平移该波形, 找到使得 8 维探测统计量(式(8))最大化的平移量, 该平移量对应的频率和偏心率即为参数 v0 和 e0的最优拟合值。需要注意的是, 此时 8 维参数集合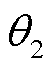 中, v0 被固定为基准值,
中, v0 被固定为基准值,  是基准值对应时刻的偏心率。
是基准值对应时刻的偏心率。
3.2.4 用局部优化方法优化非含时项中的参数
完成 10 维/8 维/7 维探测统计量中含时参数与非含时参数的变量分离后, 可以嵌套优化以上探测统计量。具体地, 我们用全局方法来优化或推断含时参数; 对于全局优化方法中每一步给定的含时参数, 用相对简单的局部优化方法来优化非含时参数。10 维探测统计量中的非含时参数是 和
和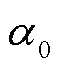 , 8 维/7 维探测统计量中的非含时参数是
, 8 维/7 维探测统计量中的非含时参数是 和fk。
和fk。
图 1 展示 13 维探测统计量(式(8))关于 θk 和 fk的 2 维切面以及 和
和 的 3 维子空间中任意选取的 3 个切面的轮廓(以表 1 中 LDC-1.2 真值为基准参数)。可以看出, 非含时参数对应子空间的结构相对简单。通过对
的 3 维子空间中任意选取的 3 个切面的轮廓(以表 1 中 LDC-1.2 真值为基准参数)。可以看出, 非含时参数对应子空间的结构相对简单。通过对 和
和 子空间中若干不同切面的验证, 我们发现上述结论总是成立。因此, 在嵌套优化中, 使用局部优化方法来优化非含时参数, 使得 13 维探测统计量(式(8))最大化是可行的。
子空间中若干不同切面的验证, 我们发现上述结论总是成立。因此, 在嵌套优化中, 使用局部优化方法来优化非含时参数, 使得 13 维探测统计量(式(8))最大化是可行的。
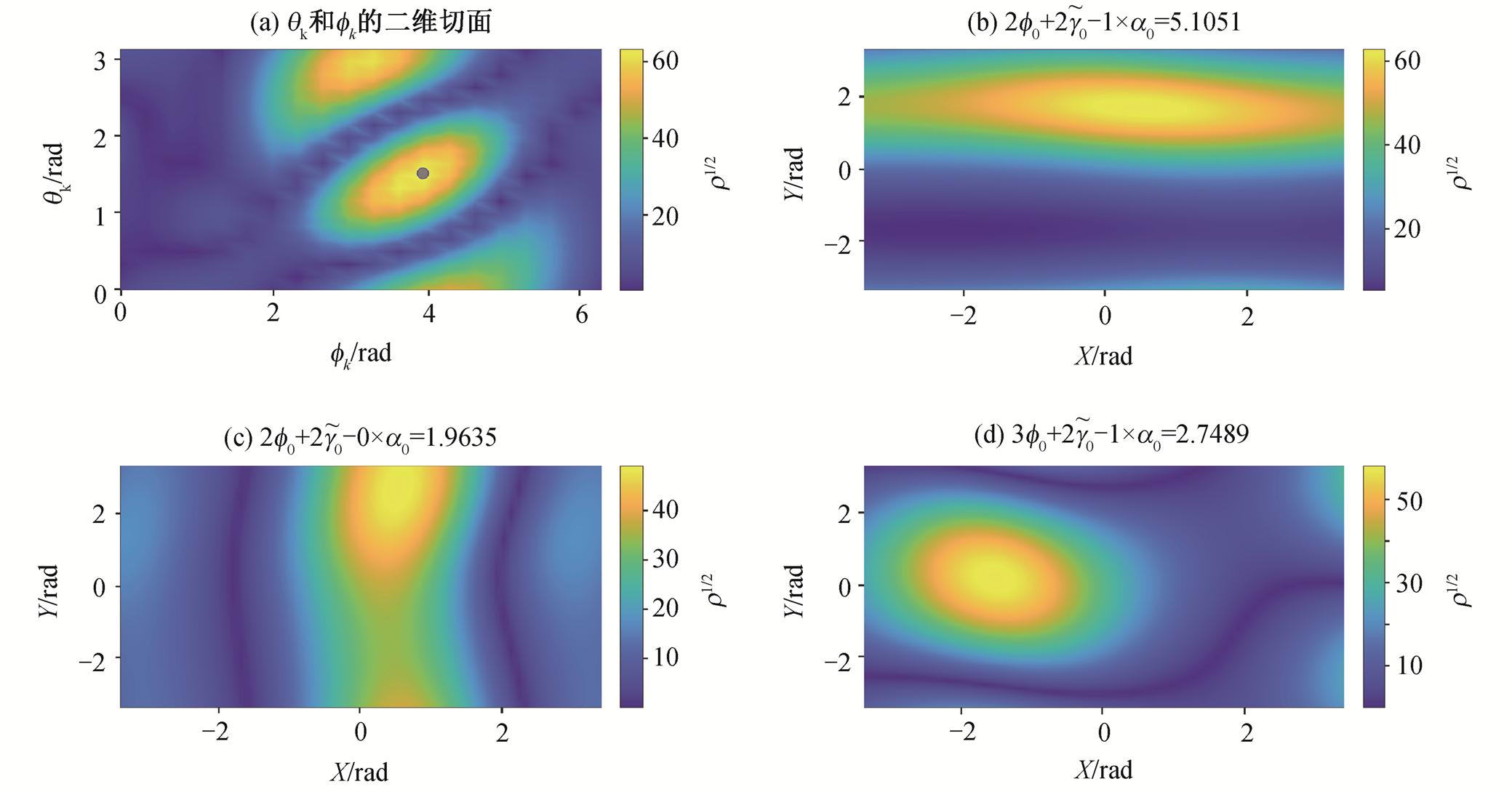
图1 非含时参数 和
和 对应的13维探测统计量(式(8))的切面轮廓
对应的13维探测统计量(式(8))的切面轮廓
Fig. 1 Illustration of the cross-sectional profiles for f0, a0, θk and fk in the 13-dimension detection statistics (Eq. (8))
a0, θk and fk in the 13-dimension detection statistics (Eq. (8))
表 1 费舍尔矩阵误差估计值
Table 1 Error estimation based on Fisher Information Matrix

参数半年数据两年数据(SNR=47)LDC -1.2 真值MLDC参数范围宽度单位 SNR=50SNR=40SNR=30 μ4.87×10−26.09×10−28.12×10−21.95×10−329.491.0太阳质量 M3.58×1034.48×1035.97×1031.83×1021.1349×1061.0x105太阳质量 Λ9.47×10−31.18×10−21.580×10−24.76×10−42.1422π弧度 S/M23.15×10−33.94×10−35.26×10−31.55×10−40.96970.2无单位标量 e01.84×10−42.30×10−43.07×10−48.42×10−60.22870.1无单位标量 v03.202×10−94.00×10−95.34×10−91.60×10−97.3805×10−4[1, 2] yr赫兹 θs2.42×10−33.02×10−34.03×10−33.86×10−30.4989π弧度 1.719×10−32.14×10−32.85×10−31.94×10−32.23282π弧度 1.53×10−21.91×10−22.54×10−21.60×10−21.5221π弧度 2.28×10−22.85×10−23.80×10−22.38×10−23.94672π弧度 7.60×10−29.50×10−21.27×10−11.43×10−12.04152π弧度 9.52×10−21.19×10−11.59×10−11.76×10−15.6597π/2弧度 5.90×10−27.38×10−29.84×10−29.01×10−21.17552π弧度
给定全局优化方法每一步的 (10 维搜索)或
(10 维搜索)或 (8 维或 7 维搜索)数值, 为了确保局部优化方法一定可以找到非含时参数对应子空间的极值, 选择多个不同的初始位置是必要的, 从中选出 13 维探测统计量(式(8))最大化的点即为
(8 维或 7 维搜索)数值, 为了确保局部优化方法一定可以找到非含时参数对应子空间的极值, 选择多个不同的初始位置是必要的, 从中选出 13 维探测统计量(式(8))最大化的点即为 或
或
 的最优拟合值。借助以上对探测统计量(式 8)的变量分解, 每一次局部优化的计算时间一般在毫秒量级, 多次调用不会显著地增加计算时间。
的最优拟合值。借助以上对探测统计量(式 8)的变量分解, 每一次局部优化的计算时间一般在毫秒量级, 多次调用不会显著地增加计算时间。
相比于振幅, 引力波波形对相位更敏感。因为相位的微小变化会引起波形的显著变化, 会导致探测统计量(式(7)或(8))的显著变化, 所以参数空间中, 在信号所处位置附近表现为一个尖峰。按照是否对相位敏感, 可将 EMRI 的波形参数分为两类: 敏感参数和非敏感参数。敏感参数是与 ODEs 相关的参数集 , 其中 e0 和 v0 是 ODEs 的初值(另外 3 个初始角度不影响每个谐波波形的形态, 只是对其进行平移), μ, M, λ和S/M2 是 ODEs 的超参数。根据费舍尔矩阵(Fisher Information Matrix, FIM)误差的几何意义, 参数值越小(相对真值), 表明该参数对探测统计量的尖峰贡献越大。参数集 θ 中各个参数的 FIM 误差估计值见表 1, 可见参数集 θ3 中各参数的 FIM 误差相对值比其他参数小约 2~3 个数量级, 因此敏感参数集 θ3 导致式(8)的参数空间中信号所在位置是一个 6 维的主极大尖峰。
, 其中 e0 和 v0 是 ODEs 的初值(另外 3 个初始角度不影响每个谐波波形的形态, 只是对其进行平移), μ, M, λ和S/M2 是 ODEs 的超参数。根据费舍尔矩阵(Fisher Information Matrix, FIM)误差的几何意义, 参数值越小(相对真值), 表明该参数对探测统计量的尖峰贡献越大。参数集 θ 中各个参数的 FIM 误差估计值见表 1, 可见参数集 θ3 中各参数的 FIM 误差相对值比其他参数小约 2~3 个数量级, 因此敏感参数集 θ3 导致式(8)的参数空间中信号所在位置是一个 6 维的主极大尖峰。
EMRI 的波形由多个强弱不等的谐波叠加构成。一般来说, 在模板与数据匹配的过程中, 模板中的谐波能同时与数据匹配是很困难的。占主导的信噪比大的谐波会较早得到好的匹配结果, 此时信噪比小的谐波的匹配情况依然糟糕, 此处会形成一个次极大峰(部分匹配)。因为谐波的数量多, 所以在参数空间中会出现数量众多的次极大峰, 分布在主极大尖峰周围; 当匹配好的谐波数量越来越多时(接近完整匹配), 对应的次极大峰的高度会越来越接近主极大尖峰的高度。次极大峰的广泛存在使得匹配主极大尖峰变得困难, 全局优化方法经常长时间困在某一个次极大峰而不能最终收敛到主极大尖峰。但是, 一定数量的次极大峰可以提供主极大尖峰的一些信息, 比如 Ye 等[49]通过分析符合一定条件的次极大峰位置的密度, 缩小信号的参数范围; Chua 等[31]通过分析次极大峰位置的拓扑连接, 为搜索主极大尖峰提供有用信息。
Bandopadhyay 等[48]讨论了 semi-coherent 方法在 EMRI 数据分析中的应用潜力。一般来说, 匹配滤波使用的数据长度越长, 其敏感性越高, 灵活性越低, 需要的计算量越大, 因此数据分析的难度越大。semi-coherent 方法在连续引力波信号的数据分析中广泛应用[48], 旨在解决与 EMRI 相同的完整数据计算量大和灵敏性高导致的匹配难度大的问题, 因此对 EMRI 数据分析有很大的借鉴意义。该方法先分析分段数据, 得到每个数据段中信号的粗略信息, 然后通过一定的方式, 将分段信息整合在一起,或利用分段信息限制, 或提升下一步更大长度数据的分析。从表 1 可以看到, 对于相同的波源参数对应的FIM 误差估计值, 半年信号的数值比两年信号的数值大一个量级左右, 表明半年数据中敏感参数贡献的探测统计量(式(8))的主极大尖峰的尖锐度有很大程度的减弱。
图 2 展示 13 维/10 维探测统计量(式(8))使用两年或半年数据时每个敏感参数的 1 维切面(以表 1 中LDC-1.2 真值为基准参数), 可以看出, 在数据长度相同的情况下, 10 维探测统计量对应的尖峰尖锐度比 13 维探测统计量(式(8))有一定程度的弱化, 在探测统计量维数相同的情况下, 半年数据对应的尖峰的尖锐度比两年数据有显著的弱化。
总的来说, EMRI 匹配滤波使用的探测统计量(式(8))在信号所处位置表现为 6 维尖峰, 定位难度较大, 可以通过降维或先分析短数据、再增加数据长度直至完整数据的分层次方法来降低难度, 后者的效果更显著。
对于 EMRI 匹配滤波这种多模态的全局优化问题, 在高维参数空间中得到其全局极值点难度较大, 优化过程经常会卡在某次极大位置, 而不能收敛到期待的全局极大值点。高维参数空间的内禀性质一般只体现在内部(intrinsic)参数中, 有外部(extrinsic)参数参与的全局优化会对内部参数收敛到其全局极大值点造成干扰, 使得优化过程收敛缓慢。基于这种一般性的考虑, 期待使用低维的探测统计量可以加速 EMRI 的匹配滤波收敛到全局最优匹配位置。从我们最近的工作中可以看到, 与 10 维相比, 8 维和 7 维的探测统计量可以在更大的参数范围内定位到信号所处位置的主尖峰[54–55], 体现在 EMRI 匹配滤波中使用低维探测统计量的优势。但是, 低维探测统计量的计算量明显增加, 尤其是 7 维。文献[55]中仅实现信号已知时, 7 维探测统计量对应的匹配滤波, 受限于计算资源, 未知信号的情形未能实现, 只做了定性的讨论。期待未来的工作中通过使用图形处理器(graphics processing unit, GPU)来加速代码, 克服计算瓶颈, 进而展示低维匹配滤波的更多优势。
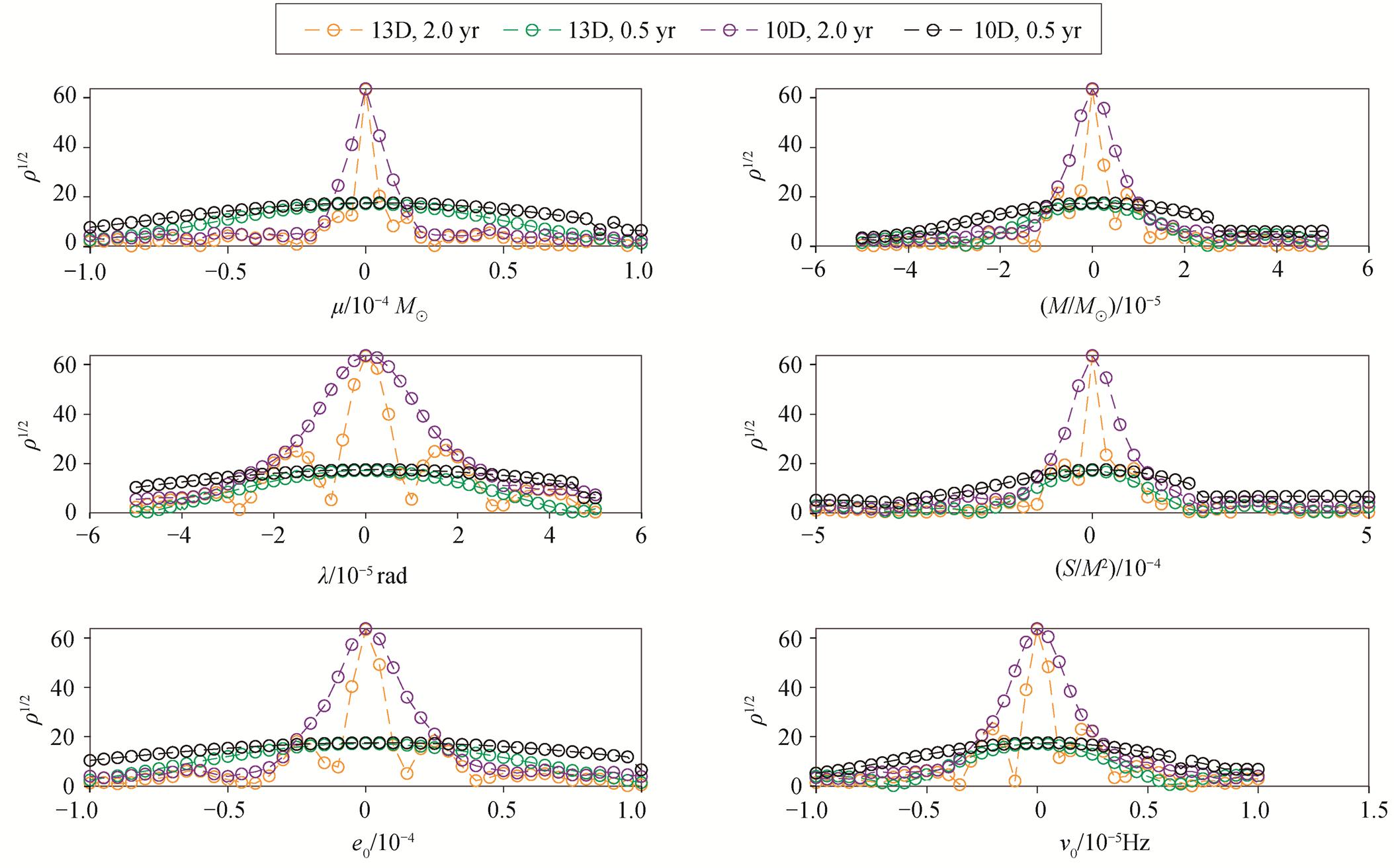
噪音模型为MLDC
图2 探测统计量对应不同维度和数据长度时每个敏感参数的 1 维切面
Fig. 2 1D peak of the detection statistics using different data duration and dimension
多个谐波的波形计算和一代 TDI 中 24 个单臂响应是计算观测量 最耗时的部分, 可以通过并行来加速, 用 OpenMP 实现。匹配滤波使用的随机推断–优化方法, 计算多个独立位置的 10 维/8 维/7 维探测统计量(式(8))时, 也可以通过并行来加速, 用MPI 来实现。也可以借助 GPU[22–23,56–57]来加速计算, 尤其是使用基于机器学习和深度学习的方法时, 可以调用支持 GPU 的计算平台。
最耗时的部分, 可以通过并行来加速, 用 OpenMP 实现。匹配滤波使用的随机推断–优化方法, 计算多个独立位置的 10 维/8 维/7 维探测统计量(式(8))时, 也可以通过并行来加速, 用MPI 来实现。也可以借助 GPU[22–23,56–57]来加速计算, 尤其是使用基于机器学习和深度学习的方法时, 可以调用支持 GPU 的计算平台。
以 LISA 15 秒的采样间隔为例, 两年数据大约有 4×106~222 个采样点。对于引力波数据分析中常用的时间序列操作(如快速傅里叶变换和插值等), 其运行时间与向量长度正相关, 因此分段数据的计算会更快。下面讨论数据分段的方式以及如何利用分段数据做匹配滤波。对于数据 和模板
和模板 分成N 段的情形:
分成N 段的情形:
 (22)
(22)
探测统计量(式(8))中两种内积则可表述为
 (23)
(23)
根据设计好的分段方式, 事先将数据 切分好。对匹配滤波中每一步的位置, 首先求得 ODEs的解, 然后根据同样的分段方式, 切分 ODEs 的解(时间序列)。首先分别计算每一段 ODEs 解对应的波形和TDI, 然后计算每个谐波分段的内积
切分好。对匹配滤波中每一步的位置, 首先求得 ODEs的解, 然后根据同样的分段方式, 切分 ODEs 的解(时间序列)。首先分别计算每一段 ODEs 解对应的波形和TDI, 然后计算每个谐波分段的内积 和
和 , 最后根据式(23)得到完整数据的内积
, 最后根据式(23)得到完整数据的内积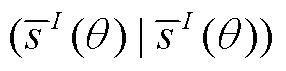 和
和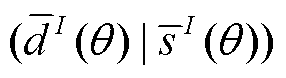 。通过上述数据先分段、模板随之分段的方式, 波形和 TDI 的计算对应的向量长度被缩短, 因此计算时间会相应地减少。将分段 ODEs 的解拼接起来, 仍然反映一个连续的轨道演化过程, 因此没有破坏信号在任意相邻数据段间的频率和相位的连续性。时域数据分段的缺点是, TDI 插值时会在数据段间的边界产生一些零点, 类似人为引入的数据缺口(gap)。频域数据分段的缺点是, 相邻频段之间可能存在频谱泄露, 需要小心处理边界效应。分段数据给出的傅里叶变换频率分辨率相比于完整数据有所降低, 加速效果依赖于能获得的核数或用 GPU 实现。
。通过上述数据先分段、模板随之分段的方式, 波形和 TDI 的计算对应的向量长度被缩短, 因此计算时间会相应地减少。将分段 ODEs 的解拼接起来, 仍然反映一个连续的轨道演化过程, 因此没有破坏信号在任意相邻数据段间的频率和相位的连续性。时域数据分段的缺点是, TDI 插值时会在数据段间的边界产生一些零点, 类似人为引入的数据缺口(gap)。频域数据分段的缺点是, 相邻频段之间可能存在频谱泄露, 需要小心处理边界效应。分段数据给出的傅里叶变换频率分辨率相比于完整数据有所降低, 加速效果依赖于能获得的核数或用 GPU 实现。
关于 EMRI 数据分析方法, 目前还没有公认的满意答案。Gair 等[29]描绘了从短数据到长数据的分层次分析的基本方法, 较好地平衡了短数据灵活性高、计算量小与长数据限制能力强、计算量大的优缺点。Cornish[45]提出切分数据的方式, 为分层次匹配滤波的实现与加速提供了另外一种思路。Bando-padhyay 等[48]进一步论证和丰富了这一观点。Chua等[31]讨论了 EMRI 参数间复杂的关联、简并和多波源间的混淆问题, 还讨论了次极大峰的聚类方法等, 以及如何利用 EMRI 波形为谐波叠加的特征设计更有效的探测统计量[58]。这些讨论为后续的工作提供了许多新思路。基于 surrogate 波形或 surrogate 探测统计量的方法[56–57]可能在加速 EMRI 数据分析中起到重要作用。
EMRI 数据分析目前使用的是 Kluge 唯象波形, 主要是 AK 和 AAK。随着 EMRI 精确波形的发展以及将 EMRI 用于高精度检验新物理或天文学效应的需求不断增加[12], 在数据分析中使用高精度波形是将来一定会遇到的情况, 比如基于 Teukolsky 方程和 KRZ 度规的 XSPEG 波形[59–60]。为了克服高精度波形带来的大计算量, Gair 等[29]和 Chua 等[30]发展了在稀疏的基准点使用高精度波形, 在其周围使用低精度波形, 用高斯过程来解析地消除低精度波形的误差的方法。高斯过程的作用类似插值, 是对低精度波形的修正。这种方法利用低精度波形计算量小的特点, 克服使用高精度波形计算量大的缺点, 对EMRI 数据分析的发展有重要意义。
针对 EMRI 复杂的参数空间的推断或优化, 现有的可以处理多模态(multimodality)参数空间的方法[61–65]还需要更多的测试与验证。我们最近测试了粒子群方法[66–67]在 EMRI 数据分析中的效果, 取得一定的进展[54–55]。目前, 我们的方法可以有限度地解决 EMRI 数据分析的问题, 但是能处理的情形局限于数据长度短(可以处理半年数据, 但 LDC-1.2的数据长度是两年)、信噪比高(可以处理信噪比为50 左右的信号, 但相同参数的 LDC 半年信号信噪比是 14)和搜索范围窄(μ, M, S/M2的参数范围与MLDC 相同, 但 λ和e0 的参数范围比 MLDC 窄), 需要进一步的提升与完善。
总而言之, EMRI 的数据分析方法还在发展中, 距离最终完全解决还需要做出很多努力。
致谢 本文的计算工作在中国科学院科学与工程计算国家重点实验室高性能计算机系统上完成; 中国科学院数学与系统科学研究院刘润球研究员提供计算资源, 同时给予指导; 钱莹博士耐心地解答使用集群时遇到的问题; 中国科学院力学研究所徐鹏研究员和中国科学院空间科学中心唐文林副研究员给予指导; 兰州大学博士研究生滕厚强和上海交通大学博士研究生恽倩云参与讨论。谨致谢忱。
参考文献
[1] 范会敏, 胡一鸣, 訾铁光. 极端质量比旋近及其探测. 中山大学学报(自然科学版), 2021, 60(1/2): 31–40
[2] Seoane P A, Gair J R, Freitag M, et al. Astrophysics, detection and science applications of intermediate- and extreme mass-ratio inspirals. Classical and Quantum Gravity, 2007, 24(17): 113–169
[3] Seoane P A. The gravitational capture of compact objects by massive black holes [EB/OL]. (2020–11–05)[2024–02–05]. https://arxiv.org/abs/2011.03059v1
[4] Gair J R, Barack L, Creighton T, et al. Event rate estimates for LISA extreme mass ratio capture sources. Class Quant Grav, 2004, 21(20): 1595–1606
[5] Fan Huimin, Hu Yimin, Barausse E, et al. Science with the TianQin observatory: preliminary result on extre-me-mass-ratio inspirals. Phys Rev D, 2020, 102(10): 063016
[6] Babak S, Gair J, Sesana A, et al. Science with the space-based interferometer LISA. Ⅴ: extreme mass-ratio inspirals. Phys Rev D, 2017, 95(10): 103012
[7] Babak S, Glampedakis K. Mapping spacetimes with LISA: inspiral of a test-body in a ‘quasi-Kerr’ field. Class Quant Grav, 2006, 23(12): 4167–4188
[8] Barack L, Cutler C. Using LISA EMRI sources to test off-Kerr deviations in the geometry of massive black holes. Phys Rev D, 2007, 75(4): 042003
[9] Gair J, Yunes N. Approximate waveforms for extreme-mass-ratio inspirals in modified gravity spacetimes. Phys Rev D, 2011, 84(6): 064016
[10] Xin Shuo, Han Wenbiao, Yang Shucheng. Gravitational waves from extreme-mass-ratio inspirals using general parametrized metrics. Phys Rev D, 2019,100(8): 084055
[11] Zi Tieguang, Zhan Jiandong, Fan Huimin, et al. Sci-ence with the TianQin observatory: preliminary results on testing the no-hair theorem with extreme mass ratio inspirals. Phys Rev D, 2021, 104(6): 064008
[12] Berry C P L, Hughes S A, Sopuerta C F, et al. The unique potential of extreme mass-ratio inspirals for gravitational-wave astronomy [EB/OL]. (2019–03–08) [2024–02–05]. https://arxiv.org/abs/1903.03686v1
[13] Seoane P A, Audley H, Babak S, et al. Laser interfer-ometer space antenna [EB/OL]. (2017–02–23)[2024–02–05]. https://arxiv.org/abs/1903.03686v1
[14] Hu Wenrui, WuYueliang. The Taiji program in space for gravitational wave physics and the nature of gra-vity. Natl Sci Rev, 2017, 4(5): 685–686
[15] Luo Ziren, Guo Zongkuan, Jin Gang, et al. A brief analysis to Taiji: science and technology. Results Phys, 2020, 16: 102918
[16] Luo Jun. TianQin: a space-borne gravitational wave detector. Class Quant Grav, 2016, 33(3): 035010
[17] Pound A, Wardell B, Warburton N, et al. Second-order self-force calculation of gravitational binding energy in compact binaries. Phys Rev Lett, 2020, 124(2): 021101
[18] Barack L, Cutler C. LISA capture sources: approximate waveforms, signal-to-noise ratios, and parameter esti-mation accuracy. Phys Rev D, 2004, 69(8): 082005
[19] Babak S, Fang Hua, Gair J R, et al. Kludge’ gravita-tional waveforms for a test-body orbiting a Kerr black hole. Phys Rev D, 2007, 75(2): 024005
[20] Chua A J K, Gair J R. Improved analytic extreme-mass-ratio inspiral model for scoping out eLISA data analy-sis. Class Quant Grav, 2015, 32(23): 232002
[21] Chua A J K, Moore C J, Gair J R. Augmented kludge waveforms for detecting extreme-mass-ratio inspirals. Phys Rev D, 2017, 96(4): 044005
[22] Chua A J K, Katz M L,Warburton N, et al. Rapid generation of fully relativistic extreme-mass-ratio-inspiral waveform templates for LISA data analysis. Phys Rev Lett, 2021, 126(5): 051102
[23] Katz M L, Chua A J K, Speri L, et al. Fast extreme-mass-ratio-inspiral waveforms: new tools for milliher-tz gravitational-wave data analysis. Phys Rev D, 2021, 104(6): 064047
[24] Babak S, Baker J G, Benacquista M J, et al. The mock LISA data challenges: from challenge 1B to challenge 3. Class Quant Grav, 2008, 25(18): 184026
[25] Babak S, Baker J G, Benacquista M J, et al. The mock LISA data challenges: from challenge 3 to challenge 4. Class Quant Grav, 2010, 27(8): 084009
[26] Arnaud K A, Babak S, Baker J G, et al. An overview of the second round of the Mock LISA data challenges. Class Quant Grav, 2007, 24(19): 551–564
[27] Porter E K. An overview of LISA data analysis algori-thms [EB/OL]. (2009–10–02)[2024–02–05]. https://arxiv. org/pdf/0910.0373
[28] Baghi Q. The LISA data challenges [EB/OL]. (2022–04–26)[2024–02–05]. https://arxiv.org/abs/2204.12142v1
[29] Gair J R, Babak S, Porter E K, et al. An algorithm for detection of extreme mass ratio inspirals in LISA data. Class Quant Grav, 2009, 26(13): 135004
[30] Chua A J K, Korsakova N, Moore C J, et al. Gaussian processes for the interpolation and marginalization of waveform error in extreme-mass-ratio-inspiral para-meter estimation. Phys Rev D, 2020, 101(4): 044027
[31] Chua A J K, Cutler C J. Nonlocal parameter degeneracy in the intrinsic space of gravitational-wave signals from extreme-mass-ratio inspirals. Phys Rev D, 2022, 106(12): 124046
[32] Tinto M, Dhurandhar S V. Time-delay interferometry. Living Rev Rel, 2014, 17(6): lrr-2014-6
[33] William H, Brian P, Saul A, et al. Numerical recipes in Fortran 90: the art of parallel scientific computing, 2nd ed. New York: Cambridge University Press, 1996
[34] Ali A. Bayesian inference on EMRI signals in LISA data [D]. Auckland: The University of Auckland, 2011
[35] Babak S. LISA data challenge manual [EB/OL]. (2019–07–11) [2025–01–08]. https://lisaldc.lal.in2p3.fr/static /data/pdf/LDC-manual-002.pdf
[36] Wen Linqing, Gair J R. Detecting extreme mass ratio inspirals with LISA using time-frequency methods. Class Quant Grav, 2005, 22(10): 445–452
[37] Gair J R. Detecting extreme mass ratio inspirals with LISA using time-frequency methods II: search charac-terization. Class Quant Grav, 2005, 22(18): 1359–1371
[38] Wen Linqing, Chen Yanbei, Gair J R. Extracting infor-mation about EMRIs using time-frequency methods. AIP Conf Proc, 2006, 873(1): 595–604
[39] Gair J R, Jones G. Detecting LISA sources using time-frequency techniques // 11th Marcel Grossmann Mee-ting on General Relativity. Berlin, 2006: 1236–1238
[40] Gair J R, Jones G. Detecting extreme mass ratio inspi-ral events in LISA data using the hierarchical algorithm for clusters and ridges (HACR). Class Quant Grav, 2007, 24(5): 1145–1168
[41] Gair J R, Mande I, Wen Linqing. Time-frequency ana-lysis of extreme-mass-ratio inspiral signals in mock LISA data. J Phys Conf Ser, 2008, 122(1): 012037
[42] Gair J R, Mande I, Wen Linqing. Improved time-frequency analysis of extreme-mass-ratio inspiral si-gnals in mock LISA data. Class Quant Grav, 2008, 25(18): 184031
[43] Gair J R, Porter E K, Babak S, et al. A constrained metropolis-hastings search for EMRIs in the Mock LISA data challenge 1B. Class Quant Grav, 2008, 25(18): 184030
[44] Jaranowski P, Krolak A, Schutz B F, et al. Data analysis of gravitational-wave signals from spinning neutron stars. 1. the signal and its detection. Phys Rev D, 1998, 58(6): 063001
[45] Cornish N J. Detection strategies for extreme mass ratio inspirals. Class Quant Grav, 2011, 28(9): 094016
[46] Wang Yan, Shang Yu, Babak S, et al. EMRI data analysis with a phenomenological waveform. Phys Rev D, 2012, 86(10): 104050
[47] Ali A, Christensen N, Rover C, et al. Bayesian infer-ence on EMRI signals using low frequency approxi-mations. Class Quant Grav, 2012, 29(14): 145014
[48] Bandopadhyay D, Moore C J. LISA stellar-mass black hole searches with semicoherent and particle-swarm methods. Phys Rev D, 2023, 108(8): 084014
[49] Ye Changqin, Fan Huimin, Hu Yimin, et al. Identifica-tion of gravitational-waves from extreme mass ratio inspirals. Phys Rev D, 2024, 109(12): 124034
[50] Zhang Xueting, Messenger C, Korsakova N, et al. Detecting gravitational waves from extreme mass ratio inspirals using convolutional neural networks. Phys Rev D, 2022, 105(12): 123027
[51] Zhao Tianyu, Zhou Yue, Shi Ruijun, et al. Dilated con-volutional neural network for detecting extreme-mass-ratio inspirals. Phys Rev D, 2024,109 (8): 084054
[52] Yun Qianyun, Han Wenbiao, Guo Yiyang, et al. De-tecting extreme-mass-ratio inspirals for space-borne detectors with deep learning [EB/OL]. (2023–09–13) [2024–02–05]. https://arxiv.org/abs/2309.06694
[53] Yun Qianyun, Han Wenbiao, Guo Yiyang, et al. The de-tection, extraction and parameter estimation of extre-me-mass-ratio inspirals with deep learning. Sci China Phys Mech Astron, 2025, 68 (1): 210413
[54] Zou Xiaobo, Mohanty S D, Luo Honggang et al. Swarm intelligence methods for extreme mass ratio inspiral search: first application of particle swarm optimiza-tion. Universe, 2024, 10(2): 96
[55] Zou Xiaobo, Mohanty S D, Luo Honggang et al. Search for extreme mass ratio inspirals using particle swarm optimization and reduced dimensionality likelihoods. Universe, 2024, 10(4): 171
[56] Strub S H, Ferraioli L, Schmelzbach C, et al. Bayesian parameter estimation of galactic binaries in LISA data with Gaussian process regression. Phys Rev D, 2022, 106(6): 062003
[57] Strub S H, Ferraioli L, Schmelzbach C, et al. Accele-rating global parameter estimation of gravitational waves from galactic binaries using a genetic algorithm and GPUs. Phys Rev D, 2023, 108(10): 103018
[58] Chua A J K. One-stop function for gravitational-wave detection, identification, and inference. Phys Rev D, 2022, 106(10): 104051
[59] Xin S, Han W B, Yang S C. Gravitational waves from extreme-mass-ratio inspirals using general parametri-zed metrics. Physical Review D, 2019, 100(8): 084055
[60] Zhang C, Han W B, Yang S C. Analytical effective one-body formalism for extreme-mass-ratio inspirals with eccentric orbits. Communications in Theoretical Phy-sics, 2021, 73(8): 085401
[61] Foreman-Mackey D, Hogg D, Land Dustin, et al. Em-cee: the MCMC hammer. Publications of the Astrono-mical Society of the Pacific, 2013, 125(925): 306–312
[62] Feroz F, Hobson M P. Multimodal nested sampling: an efficient and robust alternative to MCMC methods for astronomical data analysis. Mon Not Roy Astron Soc, 2008, 384(2): 449–463
[63] Speagle J S. DYNESTY: a dynamic nested sampling package for estimating Bayesian posteriors and evi-dences. Mon Not Roy Astron Soc, 2020, 493(3): 3132–3158
[64] Earl D J, Deem M W. Parallel tempering: theory, applications, and new perspectives [EB/OL]. (2005–08–17)[2024–02–05]. https://arxiv.org/pdf/physics/05 08111v1
[65] Green P J, Hastie D I. Reversible jump MCMC. Bio-metrika, 1995, 82(4): 711–732
[66] Kennedy J, Eberhart R C. Particle swarm optimization // Proceedings International Conference on Neural Networks Proceedings of ICNN’95 — International Conference on Neural Networks. Perth, 1995: 1942–1948
[67] Bratton D, Kennedy J. Defining a Standard for particle swarm optimization // IEEE Swarm Intelligence Sym-posium. Honolulu, 2007: 120–127
An Overview of EMRI Data Analysis
Abstract The Extreme Mass-Ratio Inspiral (EMRI) refers to binary system with a mass ratio between 104 and 107, where the smaller object loses energy as it inspirals closer to a massive black hole, emitting gravitational waves. It is estimated that there are 105 cycles during the last year before plunge, providing rich information on the evolution of gravitational wave phases. The motion of the smaller object in the strong gravitational field of the massive black hole can reflect the surrounding spacetime structure. The massive black hole is typically located at the center of a galaxy, in which the galaxy environment leaves traces in the EMRI waveform, thus EMRI can be used to constrain the gravitational theories, no-hair theorem and so on. Multiple sources can provide constraints on the mass and spin distribution of massive black holes, contributing to the understanding of cosmic and galactic evolution. Due to this significance, EMRI has become an important target for space gravitational wave missions such as LISA, Taiji, and TianQin. Consequently, the EMRI data analysis has become a crucial task. However, due to the high dimensionality and complexity of the waveform, relevant methods are still under discussion. This article initially reviews the framework and discussions regarding EMRI data analysis conducted during the Mock LISA Data Challenge (MLDC). It subsequently provides a comprehensive overview of the challenges encountered and the corresponding improvements proposed based on the authors’ research. Finally, the article offers some clues and suggestions regarding potential advancements in EMRI data analysis methods.
Key words EMRI; signal detection; parameter estimation; spectral method; matched filtering