文章信息
- 魏云鹏, 赵红颖, 辛甜甜, 郑鸿云
- WEI Yunpeng, ZHAO Hongying, XIN Tiantian, ZHENG Hongyun
- 应用于无人机视频影像密集匹配的特征描述方法
- Feature Description Method in Dense Matching of UAV Video Images
- 北京大学学报(自然科学版), 2016, 52(6): 990-998
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(6): 990-998
-
文章历史
- 收稿日期: 2015-05-31
- 修回日期: 2015-09-02
- 网络出版日期: 2015-09-02
图像匹配是在两幅或多幅图像之间寻找同名匹配点, 是图像融合、图像配准、三维重建和模式识别的基础, 在计算机视觉、数字摄影测量、遥感、地图学以及军事技术等诸多领域有广泛应用[1-4]。图像匹配的方法一般分为基于灰度相关的匹配算法和基于特征的匹配算法。基于灰度相关的匹配算法中较为常用的是块匹配法[5]、比值匹配法[6]和网格匹配法[7]。块匹配法精度受模块大小影响, 模块较大时精度较高, 同时时间消耗也很大; 比值匹配法精度比较低; 网格匹配法分为粗匹配和精匹配, 在粗匹配基础上再进行精匹配, 从而要求粗匹配精度要高, 这样才能保证精匹配精度。基于灰度相关的匹配算法的计算量比较大, 不同光照条件对图像灰度的影响非常大, 直接影响匹配精度。基于特征的匹配算法是通过图像的特征进行匹配, 不仅根据图像的灰度信息, 也结合图像中一些点的结构信息。典型的特征提取和特征匹配算法有Susan算子[8]、Harris算子[9]和SIFT算子[10]等。SIFT及其改进的SURF[11]、Affine-SIFT[12]、GLOH[13]、PCA-SIFT[14]、DASIY[15]系列算子通过建立尺度空间以及统计区域极值点的梯度方向直方图, 构建高维的特征描述符, 其匹配精度最高, 但计算量非常大。DASIY算子[15]比较适合稠密匹配, 速度比SIFT快很多, 但只适用于宽基线的影像稠密匹配。由于无人机拍摄的影像对之间的基线非常小, DASIY算子不适用。
密集匹配是三维重建的必要前提, 是在两幅图像之间为每个像素确定对应的像素, 建立稠密对应场[16]。但是, 对于真实的影像对来说, 由于拍摄位置不同, 使得影像对之间存在遮蔽现象, 即有些像素点在相应的影像对图像中并不存在对应点。对于此类遮蔽问题, 一般多采用设立约束条件的方法来解决。常见的约束条件有极线约束、相容性约束、唯一性约束、连续性约束、顺序性约束、视差梯度约束等[16]。在不同情况下, 不同传感器获得的数据特征及存在问题各不相同, 目前还没有发现一种适合任何数据的通用匹配方法, 因此需根据不同的数据, 选择与之相适应的约束策略。
在无人机密集匹配方面, 蔡龙洲等[17]通过改进FAST算法来提取特征点, 并利用RANSAC计算单应矩阵, 再利用极线约束和单应约束, 通过归一化互相关关系, 稳健匹配出所有点; 王竞雪等[18]利用像方特征点和物方面元两种匹配基元, 通过多视影像进行选择性匹配, 实现密集匹配。由于无人机视频图像密集匹配或准密集匹配需要处理的数据量非常大, 因此要完成相应的密集匹配, 必须提高匹配的效率, 减少匹配所消耗的时间。本文提出一种适用于无人机视频图像的特征描述和特征匹配方法, 该方法利用Harris算子检测角点, 之后生成角点的特征描述符并完成初匹配, 最后进行密集匹配, 生成密集匹配点对。
1 无人机视频影像密集匹配 1.1 无人机视频影像特点无人机航拍视频影像与卫星影像数据的区别表现在3个方面: 1)拍摄高度低, 多在几百米高度飞行, 单帧图像视场较小, 所包含的地物较少; 2)视频图像帧间重叠度高, 图像数据量比较大; 3)图像的分辨率普遍较高, 对地物内部纹理信息表达清晰, 能够提供丰富的地物信息。
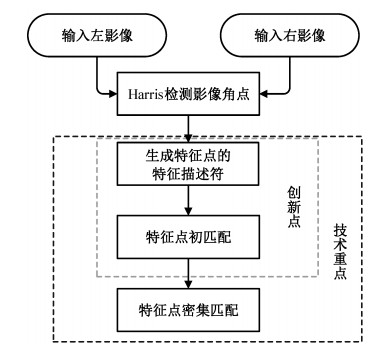
1.2 无人机视频影像密集匹配技术流程密集匹配流程如图 1所示。在无人机视频影像密集匹配过程中, 首先输入一对无人机视频影像(左/右遥感影像); 利用Harris角点检测算子, 检测每幅影像的角点, 并利用S-DASIY算子, 生成每个角点的特征描述符, 通过相应的匹配规则, 完成左/右影像特征点的初匹配, 得到初匹配特征点对, 以初匹配特征点为种子点, 进行特征点生长, 最终得到密集匹配的特征点对。
|
| 图 1. 密集匹配流程 Figure 1. Dense matching flow diagram |
在匹配过程中考虑到的技术问题如下。
1) Harris算子提取的角点。角点是图像的局部特征, 具有旋转和仿射不变性, 几乎不受光照条件的影响, 且在图像中占的比例很小。在没有严重丢失图像信息的情况下, 角点所处理的信息量很小, 提取角点消耗的时间也很少。本文在对图像进行Harris角点检测时, 设定检测窗口为3×3, 如果检测点为3×3邻域内角点响应函数的极值点, 若该响应函数值大于设定的阈值, 则该点为角点。
2) S-DASIY特征检测与特征描述。
3)特征点的匹配规则以及特征点生长和约束条件。
2 S-DASIY特征检测与特征描述方法DASIY算子特征描述可用于宽基线影像的稠密匹配, 能大大提高匹配速度, 并保证匹配精度。但是, 对于无人机视频图像来说, 由于数据量非常大, 要想完成密集匹配, 需进一步减少特征提取和匹配所消耗的时间。受DASIY描述符的设计启发, 本文针对无人机视频影像这一密集图像数据源, 设计一种快速简单的特征描述符S-DASIY。
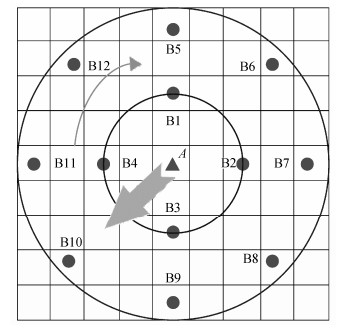
因为无人机视频图像帧之间的基线很小, 影像对中特征点变化比较小, 所以S-DASIY描述符没有在尺度空间上进行特征点的提取和描述, 而是直接通过图像的灰度信息和结构信息对特征进行描述。S-DASIY特征描述方法如图 2所示。计算A点特征描述符的步骤如下。
|
| 图 2. 特征描述 Figure 2. Feature description |
1)计算A点的点梯度:
| $ {\rm{grad }}f(x, y)=\frac{{\partial f}}{{\partial x}}\boldsymbol{i}+\frac{{\partial f}}{{\partial y}}\boldsymbol{j}. $ | (1) |
梯度的模为
| $ \left| {{\rm{grad }}f(x, y)} \right|=\sqrt {{{\left({\frac{{\partial f}}{{\partial x}}} \right)}^2}+{{\left({\frac{{\partial f}}{{\partial y}}} \right)}^2}} $ | (2) |
梯度的方向角为
| $ \theta ={\frac{\partial f}{\partial x}}/{\frac{\partial f}{\partial y}}\;. $ | (3) |
2)统计A点5×5邻域内0°, 90°, 180°和270°共4个方向上的4个点(图 2中B1, B2, B3和B4)的梯度主方向
3)统计A点9×9邻域内0°, 45°, 90°, 135°, 180°, 225°, 270°和315°共8个方向上的8个点(B5, B6, B7, B8, B9, B10, B11和B12)的梯度主方向
在第2和3步中统计每个点的梯度主方向
| $ P_{{G_1}}^n=\sum {({G_1}, \;..., \;{G_8}})=\sum\limits_{i=-1}^1 {\sum\limits_{j=-1}^1 {{\rm{grad}}\;f(x+i, y+j)} } $ | (4) |
其中, n=(1, 2, …, 12)代表 12个不同的点, Gi为梯度方向, G1, …, G8为8个不同的梯度方向。
4)统计上述12个点的梯度主方向, 得到A点的梯度主方向(图 2中箭头所示)。以A点梯度主方向为轴, 对上述12个周围点的梯度主方向进行调整, 得到12个点的特征方向, 即12个点的梯度主方向与A点梯度主方向的夹角(沿顺时针方向)。
特征点A的梯度主方向GT为
| $ {G^{\rm{T}}}=\sum {({G_1}, \cdots, {G_8}})=\sum\limits_{i=0}^{12} {(P_{{G_1}}^i)} $ | (5) |
获得GT后, 调整
| $ P_{{G_2}}^n=\sum {(G_1^{\rm{T}}, \;..., G_8^{\rm{T}}}) $ | (6) |
其中,
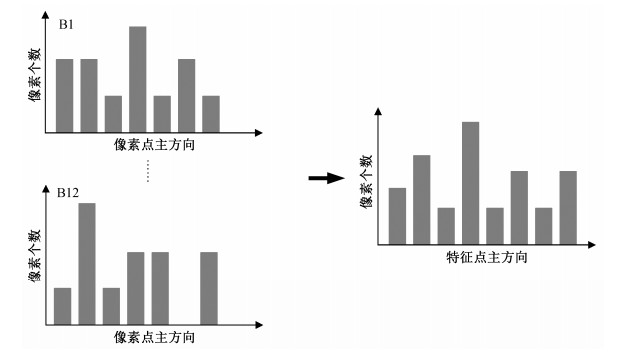
图 3为特征点梯度主方向统计的过程。
|
| 图 3. 特征点主方向统计 Figure 3. Main direction of feature points statistics |
5)最后, 生成A点25维的特征描述符DA :
| $ {D_A}=\left\{ {{G_A};\;{N_1}, \;{N_2}, \;..., {N_{12}};\;P_{G2}^1, \;P_{G2}^2, \;..., \;P_{{G_2}}^{12}} \right\} $ |
其中, GA为A点的点梯度,
在无人机图像中,
| $ \begin{array}{l} \;\;\;m(x, y)\\ =\sqrt {{{(I(x+1, y)- I(x - 1, y))}^2}+{{(I(x, y+1)- I(x, y - 1))}^2}}, \end{array} $ | (7) |
| $ \begin{array}{l} \theta(x, y)=\arctan((I(x, y+1)-I(x, y-1))/\\ \;\;\;\;\;\;\;\;\;\;\;\;\;(I(x+1, y)-I(x- 1, y))), \end{array} $ | (8) |
其中, m(x, y)为点(x, y)梯度的模, θ(x, y)为点(x, y)的梯度, I(x, y)为图像点(x, y)的灰度值。
特征点描述过程中所选的12个周围点均匀分布在特征点各个方向上, 这样可以很好地统计特征点周围的特征。以统计的特征点梯度主方向为基准, 重新调整12个点的梯度主方向, 确保生成的特征描述符具有旋转不变性, 消除图像旋转、抖动带来的影响, 使得对特征点对的描述更具相似性和唯一性。
3 特征点匹配与生长在密集匹配过程中, 首先利用主运动约束来估计无人机影像对之间的相对运动量, 完成影像对间特征点的初匹配; 然后通过初匹配得到的匹配点计算出影像对之间的单应矩阵和基本矩阵; 最后通过单应约束和极限约束实现特征点生成, 生长的种子点为初匹配所得到的匹配点。
3.1 特征初匹配 3.1.1 主运动约束对于小型无人机拍摄的视频图像, 主运动约束通过视频图像帧相对运动来估计无人机的全局运动。主运动约束在无人机电子稳像、运动目标识别等领域应用广泛。无人机运动估计方法一般分为3类:基于图像块、图像特征和像素灰度值。基于图像块的运动估计运算量大; 基于图像特征的运动估计在特征匹配中存在一些错误匹配, 影响匹配精度; 像素灰度值运动估计运用图像大量灰度信息, 且运算比较简单。本文采用灰度投影与块匹配相结合的方法来估计无人机全局运动。 灰度投影法根据图像灰度的总体分布变化来估计图像序列的帧间运动量[19]。灰度投影方法只适用于行列方向运动估计, 对于存在旋转的视频图像计算精度不高, 故通过选择若干个16×16个大小的图像块来估算视频图像帧之间的旋转角度。
图 4中, A, B, C, D和E为图像标记物(大小为16×16), 图像发生旋转后, 上述5个标记位置变为A', B', C', D'和E '。
| $ \left[{\begin{array}{*{20}{c}} {x'}\\ {y'} \end{array}} \right]=\left[{\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ {-\sin \theta }&{\cos \theta } \end{array}} \right]\left[{\begin{array}{*{20}{c}} x\\ y \end{array}} \right]+\left[{\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right]. $ | (9) |

|
| 图 4. 图像旋转 Figure 4. Image rotation |
我们利用上述方法估计无人机视频图像帧之间的全局运动, 通过该运动来限制图像对应点的匹配区域。这样, 既可以减少匹配时间, 还可以提高匹配精度。
3.1.2 匹配规则初匹配:根据两个特征点的25维特征向量的欧氏距离, 判别两点是否为匹配点。25维特征描述向量中方向特征向量和数量特征向量分别采用不同的距离阈值来限制。具体规则如下: 1)计算待匹配特征点之间25维特征向量中前13维特征向量的欧氏距离; 2)计算待匹配特征点间最后12维特征向量的欧氏距离; 3)若前两者计算的欧氏距离都小于规定阈值, 则确认此两点为匹配点。 初匹配过程中阈值选择:规则1中阈值取15, 规则2中阈值取8。阈值的确定主要考虑25维特征描述向量中方向特征和数量特征, 相比较的两个特征点的25维特征描述向量欧氏距离越短(对应阈值越小), 表明特征越相近, 匹配的概率越大, 但阈值太小, 相应的匹配点对数量会降低, 因此阈值确定需要考虑匹配精度和匹配点对数量双重因素。本文采用的阈值是通过多组无人机视频影像数据匹配试验所得到的经验值, 规则1中阈值(15)比规则1中阈值(8)大, 主要是受到点梯度特征向量的影响。
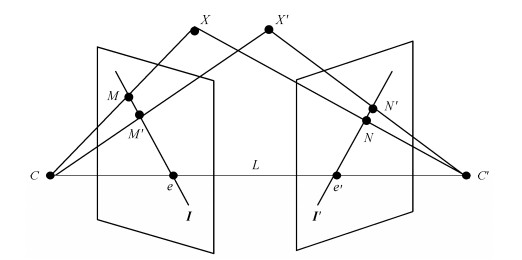
3.2 密集匹配 3.2.1 极几何约束和单应约束1)极几何约束。 极几何是同一场景两幅图像之间的几何关系, 它独立于场景结构, 只与相机内、外部参数有关[16]。 图 5中, C和C'为摄像机的光心; X和X'为拍摄场景中的景物; M和M'为X和X'在左图像中的成像; N和N'为X和X'在右图像中的成像; C与C'的连线L为基线, 基线与影像的交点e和e'为对极点; M和M'与e点的连线l以及N和N'与e'的连线l'称为极线。
|
| 图 5. 极几何原理图 Figure 5. Schematic of epipolar geometry |
对于左图像极线I, 在右图像上存在对应极线I'; 对于I上一点x, ∀x∈I在I'上都存在一点I'与之对应(x, ∀x∈I'), 根据极几何约束关系, 基本矩阵F满足:
| $ \mathit{\boldsymbol{I=FX}} $ | (10) |
| $ \mathit{\boldsymbol{I'=}}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{X'}}{\rm{.}} $ | (11) |
可以得到基本矩阵F的关系式: xTFx=0。 2)单应约束。 计算图像间变换单应矩阵的目的是实现图像之间对应点的坐标转换。相机在不同位置对空间中同一场景进行拍摄, 获取不同角度的图像。以两幅图像I1和I2(视频中对应为每一帧图像)为例, I1和I2两幅图像上相应位置上的点M=(X1, Y1, 1)T与N=(X2, Y2, 1)T之间存在如下对应关系:
| $ \boldsymbol{M}=\lambda \boldsymbol{HN}, $ | (12) |
其中, l为非零常数, H为单应矩阵。 在本文中, 通过初匹配获得影像对, 再通过RANSAC方法消除部分误匹配点, 并解算左/右像对对应的基本矩阵F以及影像对之间的单应矩阵H。通过左/右极线的对应关系(基本矩阵F)以及左/右像点对应关系(单应矩阵H)来限制影像对特征点的匹配范围, 减少匹配误差, 提高后续密集匹配的精度。
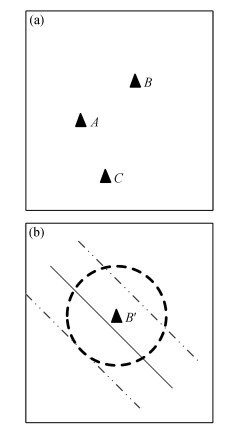
3.2.2 特征点生长密集匹配点对需要从初匹配的点对中生长而来, 在点对生长过程中, 利用极几何约束和单应约束条件, 缩小影像对之间特征点匹配的搜索区域, 以减少特征点匹配所消耗的时间。以图 6为例, 在左图像中A点为初匹配的特征点, 在A点3×3的邻域范围内寻找与A点差值最大的两个点B和C, 通过基本矩阵F和单应矩阵H分别计算B和C在右图像的位置区域。右图像中3条平行线为B点对应的极线, B′是通过单应矩阵得到的B点对应点。极线垂直方向上2个像素区域与B′圆形区域(半径为2个像素)间的重叠区域为B点在右图像上的匹配区域, 即在该区域内寻找与B点相匹配的点。C点也进行相应的处理, 其对应的匹配区域在右图像上未标出。
|
| 图 6. 影像对左图像(a)和影像对右图像(b) Figure 6. Left image of the image pairs (a) and right image of the image pairs (b) |
特征点匹配的过程中依然采用特征描述符S-DASIY以及前文所述的匹配规则。将新匹配的点对加入到种子点中, 依次生长, 直到没有新的匹配点为止。
4 实验结果 4.1 实验数据本文实验数据为小型无人机拍摄的航空视频影像。实验中采用3组影像数据(图 7), 分辨率分别为1280×720, 1600×1200和1920×1088。实验中使用的计算机配置为:处理器, Intel (R) Core (TM)2 Duo CPU E7300 @2.66 GHz; 内存(RAM), 4 G; 显卡, NVIDIA GeForce 9800 GT; 操作系统: windows7 64位; 程序运行平台, Microsoft Visual Studio 2010。

|
| (a)分辨率为1280×720; (b)分辨率为1600×1200; (c)分辨率为1920×1088 图 7. 实验采用的3组影像对 Figure 7. Three experimental data groups |
4.2 实验步骤
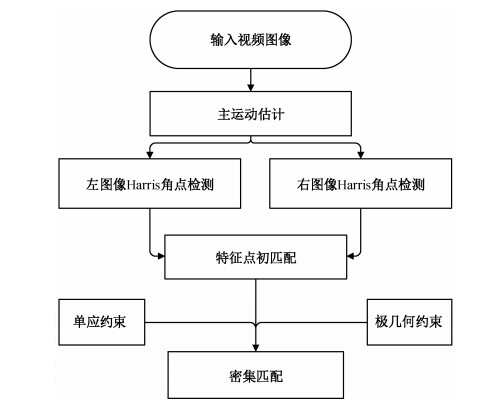
本实验对无人机视频图像进行处理, 实现密集匹配。具体实验步骤: 1)首先输入无人机视频图像的相邻图像帧, 进行去噪处理; 2)运用灰度投影与块匹配相结合的方法来估计主运动; 3)利用Harris角点检测算法检测角点, 并生成角点的特征描述符; 4)通过主运动约束完成特征点的初匹配; 5)利用RANSAC算法取出异常值, 计算基本矩阵F和单应矩阵H; 6)特征点生长, 实现密集匹配。实验流程如图 8所示。
|
| 图 8. 实验流程 Figure 8. Experimental flow diagram |
4.3 实验结果与分析
通过3组实验数据, 得到相应的密集匹配点对。在主运动约束的情况下, 计算左图像的每个特征点与右图像相应区域内(10×10)特征点特征描述符的欧氏距离, 将距离小于阈值(本文取阈值为15)的特征点确认为匹配点, 最终得到初匹配点对。3组数据中: 1280×720数据检测到的角点比较少, 是因为地物背景比较均匀, 建筑物比较少; 在1600×1200数据和1920×1088数据中, 角点个数在4000个左右, 甚至更多(本文限制角点数量最多为5000个)。3组数据的初步生长点对为11000。具体的数据对比见表 1。
| 数据 | Harris检测 角点数 | 初匹配 点对 | 初步生长 点对 | 密集匹配 点对 |
| 1280×720 | 左2636, 右2055 | 1860 | 11209 | 1142023 |
| 1600×1200 | 左3864, 右4262 | 3236 | 12958 | 1421633 |
| 1920×1088 | 左5000, 右5000 | 4275 | 13155 | 1343420 |
图 9为数据1920×1088的密集匹配结果图。通过初步生长点对为种子点, 进行密集点匹配生长, 在单应约束和极几何约束的条件下, 3组数据得到的密集匹配点对分别是1142023, 1421633和1343420(见表 1)。

|
| (a) Harris检测角点匹配点对; (b)初步生长匹配点对; (c)最终生成的密集匹配点对(在每个影像对中匹配点对连线, 绿色为初匹配点对, 红色为密集生长点对); (d)为(c)密集匹配点对的部分显示图, 即(d)是以影像对左图像的像素横坐标在201~210范围内与右图像匹配的点对 图 9. 密集匹配结果 Figure 9. Result of dense match |
在生成特征描述符时间消耗方面, 本文选择与处理速度比较快的siftGPU相比较(表 2)。siftGPU是GPU版本的SIFT描述子提取和匹配的开源程序[20], 利用大量显卡图形处理单元并行处理, 其运行速度比CPU环境串行处理的SIFT提高很多, 在处理批量图像方面速度也比其他方法快, 是当前处理速度最快的特征提取和匹配算法之一。
| 图像数据 | 消耗时间/s | |
| siftGPU | 本文算法(S-DASIY) | |
| a1 (1280×720) | 0.88 | 0.120 |
| a2 (1280×720) | 1.22 | 0.222 |
| a3 (1280×720) | 1.05 | 0.198 |
| b1 (1600×1200) | 3.11 | 0.439 |
| b2 (1600×1200) | 3.25 | 0.523 |
| b3 (1600×1200) | 2.29 | 0.349 |
| c1 (1920×1088) | 1.02 | 0.523 |
| c2 (1920×1088) | 1.10 | 0.553 |
| c3 (1920×1088) | 0.99 | 0.487 |
对于不同分辨率视频图像分辨, 各选取3组影像对进行比较。从表 2中可以看出, S-DASIY算子在生成特征点消耗的时间比siftGPU明显少很多。siftGPU算子在图像建立梯度空间时消耗大量时间, 而无人机拍摄的视频图像, 帧与帧之间的亮度变化和几何畸变都比较小, 因此S-DASIY算子没有建立梯度空间, 而是根据特征点周围的灰度信息来生成相应的特征描述符, 减少了特征生成所消耗的时间。我们发现, 对于分辨率1280×720的3组数据和1600×1200的3组数据, 本文算法效率提高6倍左右; 对于分辨率1920×1088的3组数据只提高2倍左右。通过分析发现, siftGPU处理时间与图像所生成的梯度空间所占用显存空间大小相关, 由于受图像长宽影响, siftGPU在处理图像时分配内存不同, 这就是对于1920×1088分辨率数据, siftGPU消耗时间少的主要原因。在相同分辨率的3组数据中, 处理时间也会有波动, 主要与图像所检测到的特征点数量相关, 即检测到特征点多, 处理时间长, 检测特征点少, 处理时间短, siftGPU与S-DASIY一致。
5 结论针对无人机视频影像大量数据的密集匹配, 本文提出快速的特征描述和特征匹配方法。该方法结合Harris角点生成特征点的特征描述符, 并通过匹配规则进行匹配。在几组不同分辨率的无人机影像对的密集匹配实验中, 该方法明显减少特征生成所消耗的时间, 对于无人机视频影像这种高重叠度、大数据量的图像匹配重建有非常好的效果。初匹配的特征点数据主要受限于Harris角点数量, 影像对在极几何约束和单应约束的条件下进行特征点生长, 得到几万个特征匹配点对, 为三维重建、DEM等提供了很好的密集点云数据。
| [1] | Zitová B, Flusser J. Image registration methods: a survey. Image and Vision Computing, 2003, 21: 977–1000 DOI:10.1016/S0262-8856(03)00137-9 . |
| [2] | Bentoutou Y, Taleb N, Kpalma K, et al. An automatic image registration for applications in remote sensing. IEEE Transactions on Geoscience and Remote Sen-sing, 2005, 43(9): 2127–2137 DOI:10.1109/TGRS.2005.853187 . |
| [3] | Li J M, Yan D M, Wang G, et al. An improved sift algorithm for unmanned aerial vehicle imagery. IOP Conference Series: Earth and Environmental Science, 2014, 17(1): 682–691 . |
| [4] | Gong M, Zhao S, Jiao L, et al. A novel coarse-to-fine scheme for automatic image registration based on SIFT and mutual information. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4328–4338 DOI:10.1109/TGRS.2013.2281391 . |
| [5] | 李忠新.图像镶嵌理论及若干算法研究[D].南京:南京理工大学, 2004 http://cdmd.cnki.com.cn/Article/CDMD-10288-2005031592.htm |
| [6] | Gupta R, Hartley R I. Linear pushbroom cameras. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(9): 963–975 DOI:10.1109/34.615446 . |
| [7] | 李志刚, 纪玉波, 薛全. 边界重叠图象的一种快速拼接算法. 计算机工程, 2000, 26(5): 37–38. |
| [8] | M.Smith S, M.Brady J. SUSAN -a new approach to low level image processing. International Journal of Computer Vision, 1995, 23(1): 45–78 . |
| [9] | Harris C, Stephens M.A combined corner and edge detector//Proc of Fourth Alvey Vision Conference.Manchester, 1988: 147-151 |
| [10] | Lowe D G. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004, 60(2): 91–110 DOI:10.1023/B:VISI.0000029664.99615.94 . |
| [11] | Bay H, Tuytelaars T, Van Gool L.Surf: speeded up robust features//Computer Vision-ECCV 2006.Berlin: Springer, 2006: 404-417 |
| [12] | Morel J, Yu G. ASIFT: a new framework for fully affine invariant image comparison. SIAM Journal on Imaging Sciences, 2009, 2(2): 438–469 DOI:10.1137/080732730 . |
| [13] | Mikolajczyk K, Schmid C. A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615–1630 DOI:10.1109/TPAMI.2005.188 . |
| [14] | Ke Y, Sukthankar R.PCA-SIFT: a more distinctive representation for local image descriptors//IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington, DC, 2004: 506-513 |
| [15] | Tola E, Lepetit V, Fua P.A fast local descriptor for dense matching//IEEE Conference on Computer Vision and Pattern Recognition.Anchorage, AK, 2008: 1-8 |
| [16] | 郑志刚.高精度摄像机标定和鲁棒立体匹配算法研究[D].合肥:中国科学技术大学, 2008 http://cdmd.cnki.com.cn/Article/CDMD-10358-2008091647.htm |
| [17] | 蔡龙洲, 余涛, 谢东海, 等. 基于无人机图像的密集匹配方法研究. 测绘科学, 2013, 38(5): 126–128. |
| [18] | 王竞雪, 朱庆, 王伟玺. 多匹配基元集成的多视影像密集匹配方法. 测绘学报, 2013, 42(5): 691–698. |
| [19] | 钟键.基于对极几何的图像匹配研究[D].长沙:中南大学, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10533-2010188574.htm |
| [20] | Wu C.SiftGPU: a GPU implementation of scale invariant feature transform (SIFT)[R].Chapel Hill, NC: University of North Carolia at Chapel Hill, 2007 |
 2016, Vol. 52
2016, Vol. 52




