文章信息
- 尚克明, 杜健, 孙振旭
- SHANG Keming, DU Jian, SUN Zhenxu
- 长大编组高速列车横风气动特性研究
- Investigation on Aerodynamic Characteristics of Long-Grouped High Speed Train Subjected to Crosswind
- 北京大学学报(自然科学版), 2016, 52(6): 977-984
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(6): 977-984
-
文章历史
- 收稿日期: 2015-05-21
- 修回日期: 2015-06-08
- 网络出版日期: 2016-04-13
2. 中国科学院力学研究所, 流固耦合系统力学实验室, 北京 100190
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190
列车高速运行时引起的空气动力学问题十分复杂, 特别是列车在大风条件下高速运行时, 存在不容忽视的安全风险[1]。列车在横风条件下运行时, 气动特性会发生显著变化, 即高速列车横风效应。这一效应引起的横向气动力和倾覆力矩不仅会使列车产生共振, 导致结构疲劳, 严峻条件下会增加列车横摆超限以及脱轨的可能性。兰新铁路多次发生列车被大风吹翻的事故, 造成人员伤亡和严重的经济损失[2]。京沪高速铁路沿线最大风速有可能超过30 m/s, 横风的威胁很大[3]。研究表明, 当列车的运行速度超过200 km/h, 横风风速大于30 m/s时极有可能导致列车脱轨或倾覆[4-5]。因此, 横风会对列车高速运行的安全性、稳定性和舒适性带来重大影响。随着运行速度的提高, 这一影响会越来越剧烈, 对高速列车运行安全性造成极大威胁。
当前针对高速列车横风效应的研究, 主要分为试验研究和数值模拟研究。早期受计算条件的限制, 试验研究较多。1986年, Baker[6]对铁路客运列车进行了一系列1:50缩比模型风洞试验, 研究车辆在横风作用下的气动特性。2003年, Sucuki等[7]利用风洞试验研究横风作用下车辆的气动特性, 发现横风对车辆的作用不仅与车辆的外形有关, 还与车辆下部结构的外形有关, 此后对气动力进行评价时, 开始考虑自然风的风向、风速和列车的运行速度。2004年, Sanquer等[8]发展一种新的试验方法来研究横风对高速列车的作用, 此方法能测定车辆每一个部分所受的气动力, 并能可靠地评估横风作用下列车所受的气动力。随着计算机技术和计算流体力学的发展, 人们开始将风洞试验和数值模拟结合起来评估高速列车的空气动力学特性。Khier等[9]采用分离式的原始变量SIMPLE算法求解黏性流体动力学方程(N-S方程), 对横风攻角不同情况下的流场结构进行讨论。Orellano等[10]通过数值模拟和试验研究高速列车的横风稳定性, 分析不同来流攻角对列车气动力的影响, 并给出横风作用下列车周围气流的运动轨迹。Hemida等[11]利用大涡模拟的方法研究35°和90°侧偏角下列车流场机理, 并与试验结果进行对比分析, 并讨论了横风侧偏角和尾涡结构对列车气动力的影响。郗艳红等[12]针对三编组列车模型, 采用分离涡方法, 模拟恒定风场中高速列车绕流的非定常流动, 在时域和频域内分析车辆气动特性的瞬态性质。刘加利等[13]针对列车车厢截面, 首先进行不同横风风速下高速列车非定常气动特性的分析, 进而将该截面拓展到整节车厢, 并结合多体动力学方法, 研究了横风对高速列车运行安全性的影响。
从研究对象上来看, 试验研究以及数值模拟研究的对象通常为简化模型, 或者较少编组模型(单节车厢或者三编组列车); 从数值模拟方法上来看, 高速列车横风气动特性研究可以采用定常方法或者非定常方法。针对前者, 通常采用雷诺平均方法; 针对后者, 通常采用的方法包括非定常雷诺平均方法、分离涡方法或者大涡模拟方法。不同方法对计算网格的要求各不相同, 在求解流场结构的精度上也存在差异。大涡模拟对计算网格要求最高, 由此获得的流场细节也更为详细。现有研究结果表明, 横风条件下定常流动模拟的气动力与气动力矩与非定常流动模拟结果的均值尽管有一定差异, 但整体误差在一定范围内。从流场结构来看, 定常方法获得的流场与非定常方法得到的流场具有大体相似的结构。
中国当前线上运行列车多为八编组或者十六编组, 横风条件下不同编组的气动力特性以及流场特性等均为主机厂家关注的重点。然而, 常规研究中风洞不可能复现长大编组工况, 数值分析时受限于非定常方法对网格的要求, 也不可能对长大编组进行非定常的细致分析。本文针对长大编组下列车的流场特性和气动力特性进行分析, 采用折中的方法, 将定常雷诺平均方法作为本文的CFD分析方法, 既可以大致捕捉长大编组流场特性, 获得不同编组的气动特性, 也能降低数值分析难度, 提升数值分析效率。
1 计算方法本文采用RANS方法进行长大编组高速列车横风气动力特性分析, 选取合适的湍流模式对正确预测列车的气动力非常关键。双方程模式(如k-ε模式[14])可以较好地模拟远离壁面充分发展的湍流流动, 但在近壁面附近会对湍流的输运作用估计过度, 使流动分离延迟或不发生流动分离, 从而降低求解存在逆压梯度和流动分离问题的精度。Wilcox的经典k-ω双方程模式[15]在求解壁面边界层流动以及自由剪切流方面具有非常良好的性能, 可以更广泛应用于各种压力梯度下的边界层问题, 但对自由来流中的ω值过度敏感, 而k-ε模式不存在这种问题。为了综合两种模型的优点, 本文采用Menter[16]提出的k-εSST模式。这是一种在工程上广泛应用的混合模式, 在近壁面保留了原始的k-ω 模型, 在远离壁面的地方应用k-ε模型。
在本文工况下, 流场的可压缩性与热传导效应均可以忽略, 因而流动方程可以写为
| $ \begin{array}{*{20}{c}} {\frac{{\partial {u_i}}}{{\partial {x_i}}}=0}\\ {\rho \left({\frac{{\partial {u_i}}}{{\partial t}}+\frac{{\partial \left({{u_i}{u_j}} \right)}}{{\partial {x_j}}}} \right)=- \frac{{\partial p}}{{\partial {x_i}}}+\frac{\partial }{{\partial {x_j}}}\left({\left({\mu+{\mu _t}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}}} \right)} \end{array} $ |
其中, ρ, ui和p分别是密度、速度和压强; μt为涡黏系数, 在k-ωSST模型中, 其表达式为
| $ {\mu _{\rm{t}}}=\frac{{{a_1}\rho k}}{{\max({a_1}\omega, \Omega {F_2})}}, \;\;{a_1}=0.31. $ |
k-εSST模式的两个输运方程形式为
| $ \begin{array}{l} \frac{{\partial(\bar \rho k)}}{{\partial t}}+\frac{\partial }{{\partial {x_j}}}(\bar \rho {{\tilde u}_j}k)=\frac{\partial }{{\partial {x_j}}}\left({\left({{\mu _l}+{\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right)+{P_k} - \bar \rho {\beta _k}k\omega \\ \frac{{\partial(\bar \rho \omega)}}{{\partial t}}+\frac{\partial }{{\partial {x_j}}}(\bar \rho {{\tilde u}_j}\omega)=\frac{\partial }{{\partial {x_j}}}\left({\left({{\mu _l}+{\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right)+\gamma \frac{\omega }{k} \cdot {P_k} - \\ {\rm{ }}\;\bar \rho {\beta _\omega }{\omega ^2}+\frac{{2\bar \rho(1 - {F_1}){\sigma _{\omega 2}}}}{\omega }\frac{{\partial k}}{{\partial {x_i}}}\frac{{\partial \omega }}{{\partial {x_i}}}\;. \end{array} $ |
k-εSST模型中的常数ϕ可以表示为
| $ \phi={F_1}{\phi _1}+(1 - {F_1}){\phi _2}. $ |
F1在近壁面区域趋近于1, 模型近似于k-ω模型; 远离壁面时F1趋近于0, 模型转化为k-ε模型。这样可以将两种模型取长补短。其中
| $ \begin{array}{*{20}{c}} {{\sigma _{k1}}=0.85, {\sigma _{\omega 1}}=0.5, {\beta _1}=0.075, }\\ {{\beta ^*}=0.09, {\gamma _1}=0.553;}\\ {{\sigma _{k2}}=1.0, {\sigma _{\omega 2}}=0.856, {\beta _2}=0.0828, }\\ {{\beta ^*}=0.09, {\gamma _2}=0.440.} \end{array} $ |
开关函数F1和F2定义为到壁面最小距离的函数:
| $ \begin{array}{*{20}{c}} {{F_1}=\tanh \left\{ {{{\left\{ {\min \left[{\max(\frac{{\sqrt k }}{{{\beta ^ * }\omega y}}, \frac{{500v}}{{{y^2}\omega }}), \;\frac{{4{\sigma _{\omega 2}}k}}{{C{D_{k\omega }}{y^2}}}} \right]} \right\}}^4}} \right\}, }\\ {{F_2}=\tanh \left\{ {{{\left[{\max(\frac{{2\sqrt k }}{{{\beta ^ * }\omega y}}, \;\frac{{500v}}{{{y^2}\omega }})} \right]}^2}} \right\}, }\\ {{\rm{C}}{{\rm{D}}_{k\omega }}=\max \left({\frac{{2\bar \rho {\sigma _{\omega 2}}}}{\omega }\frac{{\partial k}}{{\partial {x_i}}}\frac{{\partial \omega }}{{\partial {x_i}}}, \;{{10}^{ - 20}}} \right), }\\ {{P_k}=\min \left({{\tau _{ij}}\frac{{\partial {u_i}}}{{\partial {x_j}}}, \;20{\beta ^ * }k\omega } \right).} \end{array} $ |
y表示到物面的最小距离。
为了便于分析, 定义无量纲的列车气动阻力系数CD, 升力系数CL, 侧向力系数CS和倾覆力矩系数CMx如下:
| $ \begin{array}{l} {C_{\rm{D}}}=\frac{{{F_x}}}{{\frac{1}{2}\rho {V^2}{S_x}}}, {C_{\rm{L}}}=\frac{{{F_z}}}{{\frac{1}{2}\rho {V^2}{S_x}}}, \\ {C_{\rm{S}}}=\frac{{{F_y}}}{{\frac{1}{2}\rho {V^2}{S_x}}}, {C_{{M_x}}}=\frac{{{M_x}}}{{\frac{1}{2}\rho {V^2}{S_x}L}}, \end{array} $ |
式中, Fx为列车空气阻力; Fz为列车气动升力; Fy为列车侧向力; Mx为列车倾覆力矩; ρ为空气密度; V为列车运行速度; Sx为参考面积, 这里取列车最大迎风面积; L为参考长度。
2 计算模型和条件本文的计算面向十六编组, 采用头车+中间车(14节)+尾车+转向架+车顶附件+受电弓模型形式, 计算模型如图 1所示。计算建模采用真实的几何外形, 包括转向架、受电弓、风挡和空调, 以便实现对列车气动性能的准确模拟。

|
| 图 1. 整车计算模型 Figure 1. Computational model |
本文计算采用TRIM网格进行生成。TRIM网格对复杂外形的适应性比较好, 通过设置不同大小的区域加密可以完成高速列车复杂模型的网格生成, 同时也能较好地保证生成网格质量。为了准确地捕捉列车壁面附近的边界层流动, 在列车壁面附近和地面、轨道等位置进行边界层网格生成。边界层总厚度为30 mm。为了与六面体网格更好的衔接, 保证网格质量, 共设置6层边界层网格, 增长比为1.2, 网格的厚度及其与列车表面的正交性和贴体性, 保证了壁面函数的应用于边界层模拟的准确性。加密尾流、列车表面和受电弓三处对流场影响比较大的区域的网格。总网格数约6000万单元。列车截面网格示意图见图 2。

|
| 图 2. 截面网格示意图 Figure 2. Mesh configuration in longitudinal section |
采用相对运动条件模拟列车附近的外流场。设定列车静止, 地面移动, 空气来流以与列车运行速度反向等值的速度v绕流列车, 横风以速度vw垂直地吹向列车。主流方向空气来流的速度是vt与vw的合成速度vm, vm=vt+vm, 速度三角形如图 3所示。

|
| 图 3. 横风作用的速度三角形 Figure 3. Velocity triangle in cross-wind conditions |
采用速度入口边界, 设定速度为主流合速度; 采用压力出口边界, 给定出口压力为1 atm; 列车表面采用无滑移边界; 地面设为移动壁面, 设定为列车运行速度, 与列车运行方向相反; 计算域上表面亦采用压力出口边界。本文横风计算工况如表 1所示。
| 工况 | 横风风速/(m · s-1) | 列车运行速度/ (km · h-1) |
| 1 | 15 | 250 |
| 2 | 25 | 200 |
| 3 | 30 | 160 |
| 4 | 40 | 120 |
3 结果分析 3.1 流场特性分析
流场特性是气动力特性的根源。横风条件下高速列车的流场结构非常复杂, 列车表面的流动现象非常丰富。本节以工况2(列车运行速度为200 km/h, 横风速度为25 m/s)为例进行说明。
图 4为列车不同部位的表面压力分布。横风效应使列车承受压力分布呈现非常强的非对称性。如图 4(a)所示, 鼻锥正前方的滞止区域向横风迎风侧发生较明显的移动。同样, 如图 4(c)和(d)所示, 在受电弓、转向架的横风迎风侧也出现较明显的正压区域。在横风背风侧, 由于大量涡系的产生、发展和脱落, 背风侧出现大面积的负压区, 车身基本上为负压。如图 4(d)所示, 在受到横风作用时, 列车迎风面宽度增加, 会有更多的气流流向车身底部与地面之间的空隙, 造成车身底部结构承受的阻力增大, 各个转向架在横风作用下承受气动阻力均有大幅增加。

|
| 图 4. 列车不同部位表面压力分布 Figure 4. Pressure contour on different locations |
图 5为车身表面的表面流线。如图 5(a)所示, 在横风作用下, 从迎风侧开始向背风侧观察, 迎风侧基本上不会发生流动分离, 这是因为列车壁面之间的倒角足够光顺, 流动基本上沿着壁面向下游发展。在背风侧上拐角位置, 流动则发生分离(图 5(b)), 在尾车流线型背风侧也存在非常明显的分离线, 这些流动分离使得横风条件下尾流区的流动更加紊乱。

|
| 图 5. 列车首尾车表面流线 Figure 5. Surfaces streamlines on the leading and trailing car |
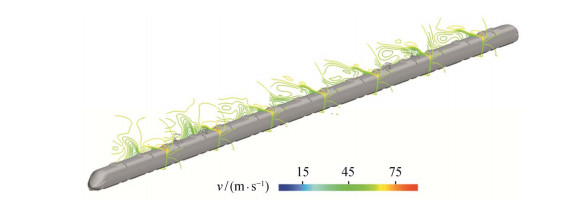
为了更好地研究背风侧涡出现的强度以及这些涡的发展趋势, 下面给出不同截面位置上的速度等值线(图 6)。在图 6中, 从第一中间车中部位置开始, 向下游每隔50 m取一个新的截面, 直到最后一节中间车, 覆盖列车的整个区域, 显示列车背风侧尾流漩涡的产生、发展以及与列车表面脱离的情况。列车背风侧产生多个漩涡, 沿车身向后, 各漩涡的起始位置呈底部、中部和顶部交替变化。可以看出, 背风侧涡的来源主要包括两类:从列车底部流经的气流在离开列车背风侧壁面时, 围绕背风侧壁面形成第一个涡, 该涡受流线型的影响不大, 所以早在头部流线型位置的地方就开始形成; 另一类是从列车上壁面流经的气流在离开背风侧壁面上端拐角位置时形成的涡, 该涡受车体截面形状影响较大, 在车体截面部分, 因为车体截面是一个比较典型的钝体, 流动经过时即形成典型的钝体绕流, 因而在背风侧壁面拐角位置形成大尺度的流动分离, 出现较大的涡。这两类不同的涡在绝大多数横截面上都可以观察到, 各个截面上的涡联合在一起形成两种独立的涡系。沿着流动方向向车体下游, 这两个涡系强度均变得越来越大, 且其涡核中心位置越来越偏离列车壁面。
|
| 图 6. 不同截面位置速度等值线 Figure 6. Velocity contour lines on different cross sections |
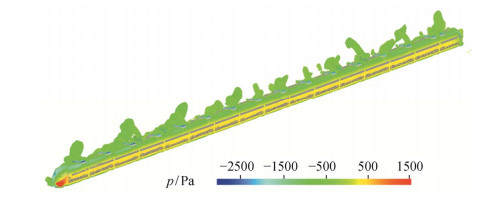
图 7为列车整车的Q等值面, 其中Q=100。从Q等值图上可以看到横风条件下背风侧大尺度的脱落涡结构, 转向架区域流场特征也比较复杂。受转向架复杂结构的影响, 在区域内也有较多不同尺度的涡结构。
|
| 图 7. 列车整车Q等值面图 Figure 7. Iso-surface of Q along the train |
3.2 气动力特性分析
在横风作用下, 由于相对于来流的迎风面积增加, 各节车厢的气动力均大幅提高。横风作用下列车的运行安全性存在重大危险, 极端严峻条件下有可能造成列车倾覆等恶性事故。在列车运行承受气动力中, 侧向力以及滚转力矩与列车的倾覆息息相关。下面重点分析十六编组列车承受侧向力和滚转力矩的特性。
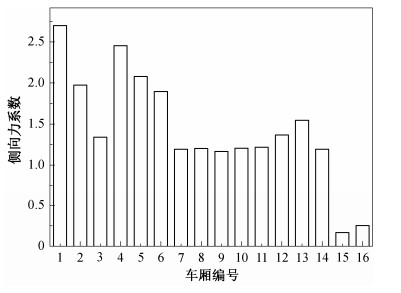
仍以工况2为例进行分析。首先给出不同车厢的侧向力系数比较, 如图 8所示。可以看到, 不同编组间侧向力最为严峻的车厢是头车, 侧向力系数最大, 而倒数第1和第2节车厢侧向力系数最小, 较为安全。从整车模型图上可以看到, 第4节和第13节车厢上面放置升弓, 而第5节和第12节车厢上面放置降弓, 由于放置受电弓后增大了车厢的侧向受力面积, 这4节车厢的侧向力系数明显大于周围车厢。然而, 这4节车厢的侧向力系数仍然小于头车。滚转力矩系数的比较也具有类似的规律, 说明在气动力分析时考察最严峻场景, 可以重点分析头车的运行安全性。
|
| 图 8. 不同车厢的侧向力系数比较 Figure 8. Comparison of side force coefficients for different coaches |
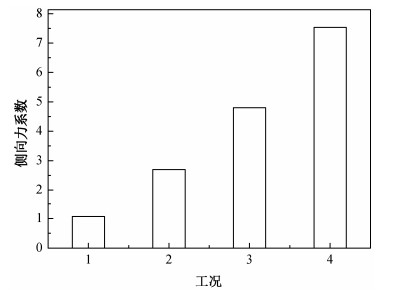
图 9为不同工况下头车侧向力系数的比较。可以看到, 随着运行速度降低, 横风风速增大, 来流侧偏角越来越大, 列车承受的侧向力则大幅增加。
|
| 图 9. 头车侧向力系数比较 Figure 9. Comparison of side force coefficients of the leading car |
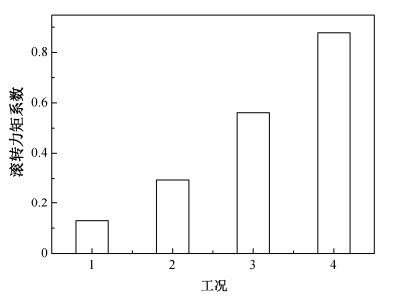
图 10为不同工况下头车滚转力矩系数的比较。可以看到, 滚转力矩系数具有与侧向力系数一样的规律。横风侧偏角越大, 列车承受的气动环境越恶化。随着横风侧偏角增大, 头车侧向力系数逐渐增大, 滚转力矩系数也逐渐增大, 增加了对行车安全的威胁。
|
| 图 10. 头车滚转力矩系数比较 Figure 10. Comparison of overturning moment coefficients of the leading car |
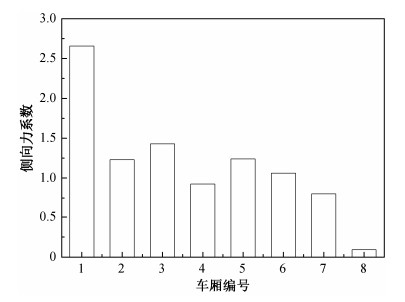
为了研究长大编组列车相对于短编组列车的横风气动力差异, 本文对三编组以及八编组列车的侧向力系数进行比较。三编组列车经常用于高速列车风洞试验, 而八编组列车和十六编组列车是当前线路上比较广泛的列车编组方式。因为不同编组形式涉及受电弓的安装问题, 本文假定三编组列车中间车上无受电弓, 八编组列车则按照实际运行情况在第2和第5中间车上方分别设置升弓与降弓。图 11和12为三编组列车以及八编组列车承受侧向力的情况。
|
| 图 11. 八编组列车不同车厢的侧向力系数比较 Figure 11. Comparison of side force coefficients for different coaches of 8-grouped train |
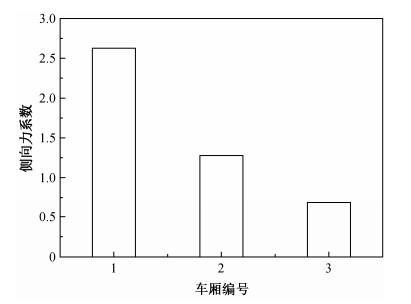
|
| 图 12. 三编组列车不同车厢的侧向力系数比较 Figure 12. Comparison of side force coefficients for different coaches of 3-grouped train |
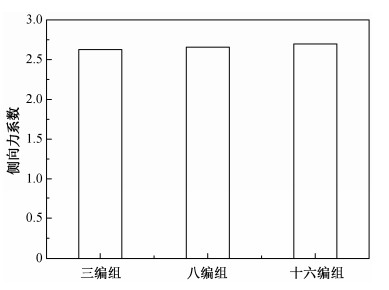
为了详细比较头车侧向力系数, 图 13给出不同编组列车头车侧向力系数的比较。可以看到, 不同编组情况下, 列车头车承受侧向力系数非常一致, 说明头车侧向力几乎不受编组条件影响。另外, 比较所有编组不同车厢的侧向力, 可以发现头车侧向力最大, 说明研究列车的安全性时, 可以仅考察短编组下的头车受力情况。
|
| 图 13. 不同编组列车头车侧向力系数比较 Figure 13. Comparison of side force coefficients of the leading car for high speed trains with different groups |
比较各编组条件下中间车厢的侧向力还可以发现, 十六编组条件下的尾车和最后一节中间车厢、八编组条件下尾车以及三编组尾车承受侧向力远小于其他车厢, 具有共性。此外, 放置受电弓升弓的列车其侧向力由于受力面积的增大也大幅增加。不同编组条件下中间车厢侧向力均值差异较大, 通常情况下列车上游中间车厢承受侧向力较大, 而越靠近尾车区域, 侧向力系数越小, 因而当编组情况发生变化时, 中间车厢的受力分布状况也会发生变化, 说明简单采用短编组列车来评估整体列车受力是不可靠的。为了准确地评估长大编组列车的气动力特性, 必须对具体编组情况进行分析。
4 结论本文基于定常RANS分析方法, 针对当前线路运行的长大编组高速列车进行横风运行特性分析。计算模型为十六编组实车模型, 包含受电弓、转向架、风挡、空调等附属结构, 得到以下结论。
1)横风使得高速列车表面压力出现强非对称性, 滞止区域的偏移造成迎风侧出现大幅正压区, 背风侧出现大幅负压区。迎风面积的增大也造成列车车体、转向架等部位承受较大阻力。
2)横风条件下, 列车表面流动现象非常丰富, 列车首尾流线型存在较多流动分离、再附等现象, 且受横风侧偏角影响较大。在列车背风侧出现两个以上的复杂分离涡系, 从列车头车下部开始, 向列车下游发展并逐渐远离列车车体。分离涡系是列车承受非定常气动力的根源。
3)列车头车是侧向力、滚转力矩最严峻的车厢, 且随着横风侧偏角增大, 侧向力、滚转力矩逐渐增大, 列车行车环境逐渐恶化。如果仅需要评估列车的横风安全性, 则可以研究短编组列车横风特性, 且只需针对头车进行安全特性分析即可。
4)不同编组下列车中间车厢侧向力分布差异较大, 通常情况下列车上游中间车厢承受侧向力较大, 而越靠近尾车区域, 侧向力系数越小。为了准确评估长大编组列车的气动力特性, 必须针对具体编组情况进行气动力分析。
| [1] | 田红旗. 高速列车空气动力学. 北京: 中国铁道出版社, 2007. |
| [2] | 高广军, 田红旗, 姚松, 等. 兰新线强横风对车辆倾覆稳定性的影响. 铁道学报, 2004, 26(4): 36–40. |
| [3] | Coleman S A, Baker C J. High sided road vehicles in crosswind. Journal of Wind Engineering and Indus-trial Aerodynamics, 1990, 36(2): 1383–1392 . |
| [4] | Hoppmann U U, Stefan K, Thorsten T, et al. A short term strong wind prediction model for railway application: design and verification. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(10): 1127–1134 DOI:10.1016/S0167-6105(02)00226-X . |
| [5] | Fujii T, Maeda T, Ishida H. Wind-induced accidents of train/vehicles and their measures in Japan. Quarterly Report of RTRT, 1999, 40(1): 50–55 DOI:10.2219/rtriqr.40.50 . |
| [6] | Baker C J. Train aerodynamic forces from moving model experiments. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 24(3): 227–252 DOI:10.1016/0167-6105(86)90024-3 . |
| [7] | Suzuki M, Tanemoto K, Maeda T. Aerodynamic characteristics of train/vehicles under crosswind. Journal of Wind Engineering and Industrial Aero-dynamics, 2003, 91: 209–218 DOI:10.1016/S0167-6105(02)00346-X . |
| [8] | Sanquer S, Barré C, de Virela M D, et al. Effect of cross winds on high-speed trains: development of a new experimental methodology. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7): 535–545 . |
| [9] | Khier W, Breuer M, Durst F. Flow structure around trains under side wind conditions: a numerical study. Computers and Fluids, 2000, 29(3): 179–195 . |
| [10] | Orellano A, Schober M. On side-wind stability of high speed trains. Vehicle System Dynamics Supplement, 2004, 40(Suppl 1): 143–160 . |
| [11] | Hemida H, Krajnovic S.Numerical study of the unsteady flow structures around train-shaped body subjected to side winds//European Conference on Computational Fluid Dynamics.Delft, 2006: 1-12 |
| [12] | 郗艳红, 毛军, 高亮, 等. 基于分离涡方法的高速列车横风非定常气动特性. 中南大学学报:自然科学版, 2015, 46(3): 1129–1139. |
| [13] | 刘加利, 于梦阁, 张继业, 等. 基于大涡模拟的高速列车横风运行安全性研究. 铁道学报, 2011, 33(4): 13–21. |
| [14] | Launder B E, Spalding D B. The numerical computation of turbulent flows. Computer Methods in Applied Mechanics and Engineering, 1974, 3(2): 269–289 DOI:10.1016/0045-7825(74)90029-2 . |
| [15] | Wilcox D C. Multiscale model for turbulent flows. AIAA Journal, 1988, 26(11): 1311–1320 DOI:10.2514/3.10042 . |
| [16] | Menter F R.Zonal two equation k-ω turbulence models for aerodynamic flows//23rd Fluid Dyna-mics, Plasmadynamics, and Lasers Conference.Orlando, FL, 1993: AIAA Paper 93-2906 |
 2016, Vol. 52
2016, Vol. 52




