文章信息
- 杨阳, 沈泽昊, 郑天立, 丁雨賝, 李本纲
- YANG Yang, SHEN Zehao, ZHENG Tianli, DING Yuchen, LI Bengang
- 中国当前城市空气综合质量的主要影响因素分析
- Influence Major Factors Analysis of Comprehensive Air Quality in the Cities in China
- 北京大学学报(自然科学版), 2016, 52(6): 1102-1108
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(6): 1102-1108
-
文章历史
- 收稿日期: 2015-05-12
- 修回日期: 2015-08-19
- 网络出版日期: 2016-11-06
大气环境质量是大气污染物和气象因素变化共同作用的结果, 对人体健康和生态环境影响巨大[1-2]。由于针对高度聚集的人群, 城市大气环境质量问题更受关注[3]。改善城市空气质量涉及社会生产生活的多个方面[4], 如城市经济发展将对城市消耗燃料的总量、类型构成、污染物排放量及处理技术产生影响, 城市绿地面积等影响城市内部对大气污染物的吸附和降解能力[5]。另一方面, 区域地形通过大气水平和垂直交换影响大气污染物的扩散条件[6]。因此, 为了对城市大气污染治理和环境改善进行科学决策, 需要对影响城市大气环境的多方面因素进行综合分析。
已有的研究主要从两个方面探讨大气质量与影响因素之间的关系: 1) 开展环境质量评价, 利用各类环境监测数据的时空统计对大气环境质量进行宏观描述分析, 如探讨大气污染物排放的时间序列或者空间分布[7]、大气污染物排放对大气环境质量的影响[8]; 2) 利用多变量模型评价排放以外的因素对城市空气质量的影响[9], 如影响城市空气中污染颗粒的各类因素[10]、天气和气候等对城市空气质量的影响[11]。人工神经网络具有很强的非线性拟合能力以及强大的自学习能力[12], 在城市空气质量模拟研究中已得到应用。然而, 以往的研究存在以下问题: 1) 仅以大气污染物和气象因子作为网络输入, 无法显示其他因素对大气环境质量的影响[13]; 2) 该方法不具备因子选择能力, 需要结合其他方法来选取关联因子, 构建优化的模型结构[14-17]。
本研究采用逐步回归法, 以我国78个主要城市为研究对象, 从城市气候因子、城市发展因子、城市治理因子和城市地形因子中筛选出与空气质量存在较强关系的因子, 在对比不同网络特性及模拟结果后, 选择学习速度快且能避免反复迭代的RBF (radial basis function, 径向基函数)人工神经网络模型, 用于构建模型, 探讨城市社会经济结构、自然环境和空间属性与城市空气质量之间的联系; 基于统计关系, 定量探讨影响我国城市空气质量的多方面因素及其相对贡献, 利用RBF人工神经网络模型模拟我国主要城市空气质量的宏观格局, 以期为城市空气质量治理提供决策依据。
1 数据与方法 1.1 研究区域与数据选取最低为地级的城市作为研究对象。这是由于地级市之间具有较为显著的历史、社会、经济背景差异, 国家统计部门对其经济和社会发展的年度状况可提供完整的统计数据, 以其作为研究对象有较强的代表性和可操作性。同时, 出于数据完整性的考虑, 选择2010年为研究年份。
人口、产业结构、土地资源等城市发展因子和城市环境状况因子数据来自《中国城市统计年鉴2011》[18]。研究区域气候数据来源于“中国气候科学数据共享服务网”中的“中国地面气候资料年值数据集” (http://data.cma.cn/data/index/6d1b5efbdcbf9a58.html), 提取研究城市气象台站的23个气候指标的2010年平均数据。城市地形因子以美国地质调查局(USGS)发布的SRTM3 (http://dds.cr.usgs.gov/srtm/version2_1/)为数据源。该数据球面坐标系统为WGS1984, 像元大小为3″, 在ArcGIS Desktop 9.5 (www.esri.org)中做Albertz等积割圆锥投影后, 重采样成空间分辨率为1000 m的数字高程模型, 利用《中国区域经济统计年鉴2011》提供的城市中心地理坐标并设置30 km缓冲区, 以此计算各城市区域内的地形值。由于数据来源不同, 不同数据中缺失不同的城市数据, 对数据进行整理, 去除不完整数据后, 共获得173个城市的完整数据。
城市大气空气质量来源于2010年国家环境保护部公布的指标:主要城市空气质量污染物浓度、空气质量等级以及优良天数占全年比例。
由于本研究的目的是探讨城市的自然、社会和经济结构对城市空气质量的影响, 故采用同一年份的空气质量数据进行分析。近5年来以2010年公布的城市空气质量排名信息最为丰富, 共有78个城市提供了完整的信息, 故使用78个城市2010年的空气质量数据, 包括ρ(SO2)年平均值、ρ(NO2)年平均值、ρ(PM10)年平均值、空气质量等级、优良天数占全年比例等5个指标。以这78个城市为我国城市样本, 进行空气质量和影响因素的筛选及后续模型的构建。对因子汇总的结果如表 1所示。
| 因子类别 | 观测指标 |
| 空气质量 | ρ(SO2)年平均值、ρ(NO2)年平均值、ρ(PM10)年平均值、空气质量等级、优良天数占全年比例 |
| 气候 | 极大风速、极大风速的风向、极端最低气压、极端最低气温、极度最高气压、极端最高气温、降水距平百分率、降水量、年平均本站气压、年平均风速、平均气温、年平均气温距平、年平均饱和水汽压、年平均相对湿度、年平均最低气温、年平均最高气温、日降水量≥0.1 mm的日数、日照百分率、日照时数、最大风速、最大风速的风向、最大日降水量、最小相对湿度 |
| 地形 | 平均海拔、海拔落差、海拔标准差、地形变异度(CV) |
| 城市发展 | 地区生产总值、人均地区生产总值、地区生产总值增长率、总人口、人口密度、建成区面积、城市建设用地占市区面积比重、第二产业占GDP的比重、第三产业占GDP的比重、公路客运量、公路货运量、煤气(人工、天然气)供气总量、液化石油气总量、城市道路面积、人均城市道路面积、工业SO2排放量、工业烟尘排放量 |
| 城市环境状况 | 绿地面积、人均绿地面积、建成区绿化覆盖率、环境治理费用 |
1.2 数据处理方法 1.2.1 空气质量数据综合
由于所得5个空气质量指标之间存在显著相关性, 故对原数据进行主成分分析[19], 在保证数据信息损失最小的前提下, 经线性变换舍弃小部分信息, 以少数的综合变量取代原始的多维变量[20-21]。在此基础上, 将提取出的前2个主成分因子的得分与对应的特征值和所提取主成分因子总的特征值之和的比值相乘, 然后求和得到城市空气质量综合得分, 以此分析影响空气质量的各类因素[22]。
1.2.2 空气质量影响因子筛选采用多元线性回归模型, 利用城市气候、地形、社会经济发展和环境质量四方面共48个指标解释城市空气质量综合得分, 并使用逐步回归的方法进行筛选, 以降低模型预测变量之间的共线性。定量评价不同指标对城市空气质量影响的显著性。
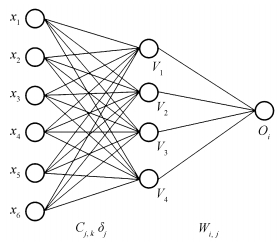
1.3 RBF人工神经网络模型建模RBF人工神经网络模型是近年来应用于土壤、水、大气等生态环境质量评价的一类人工神经网络模型[23]。它是前向型神经网络的一种, 具有强大的矢量分类功能、良好的非线性拟合功能和灵活快速的自组织计算能力, 能以任意精度逼近任意非线性函数[24]。目前选择RBF人工神经网络模型的算法主要有聚类算法和随机选择中心点等。该模型的一个明显不足是缺少确定合适的模型输入变量的方法[25]。为此, 我们利用逐步回归完成模型输入变量的筛选, 得到对城市空气质量具有独立、显著影响的城市自然环境与环境管理、社会经济结构等方面的指标[26-27]。
在RBF人工神经网络模型中(图 1), 隐含层单元输出:
| $\begin{gathered} R_j^u = \exp \left[{\frac{1}{2}\sum\limits_{k = 1}^N {{{\left( {\frac{{X_k^u-{C_{j, k}}}}{{\sigma _j^2}}} \right)}^2}} } \right], \\ V_j^u = \frac{{R_j^u}}{{\sum\nolimits_{j = 1}^L {R_j^u} }}, \end{gathered} $ |
Xk为输入层的输入; Cjk=(Cj1,
Cj2, …, Cjn)T为基函数的中心; σj为基函数的宽度;
|
| 图 1. RBF人工神经网络模型结构 Figure 1. The structure of RBFN |
输出层单元的输出:
| $O_i^N = \sum\limits_{j = 1}^L {W_i^jV_j^n}, $ |
Oi为输出层的输出, Vj为隐含层输出, Wj为从隐含层单元到输出层单元的连接权。
1.4 人工神经网络构建从78个城市中分层随机选取30个城市作为特征城市[28], 其分布如表 2[24]所示, 以保证综合得分能够对选取城市的空气质量有较为准确的衡量。为避免量纲影响, 对全体指标进行归一化处理[29], 将所有数值都归一化到[-1,1]区间, 转换方式为
| $y = 2 \cdot \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} - 1, $ |
x为归一化前的30个城市综合质量得分, xmax为30个城市综合质量得分中的最大值, xmin为30个城市综合质量得分中的最小值, y为归一化后的数据。
在此基础上, 对这30个城市的相关数据进行训练, 设置的停止训练误差为10-3, 当训练次数达到26次时, 误差小于10-6, 训练停止。
因子分析使用SPSS 20.0, 逐步回归使用R软件3.0.1版本。RBFN网络模型在MATLAB (2012a)中构建和运行。
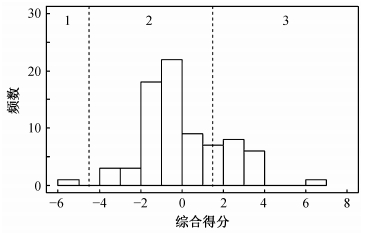
2 结果与讨论 2.1 城市空气质量得分主成分分析得到的前2个主成分累计承载了5个原始空气质量指标78.7%的信息。图 2反映78个城市空气质量综合得分的频率分布, 值域为[-6.0, 7.0]。综合得分数值越小表示空气质量越好, 数值越大表示空气质量越差。其中空气质量等级为1的城市其综合得分小于-4.5, 平均得分为-5.0;空气质量等级为2的城市综合得分值域为[-4.5, 1.5], 平均得分为-0.8;空气质量等级为3的城市其综合得分大于1.5, 平均得分为2.7。
|
| 图 2. 城市空气质量综合得分的频率分布 Figure 2. Histogram of urban air quality composite scores |
2.2 城市空气质量主要影响因素
利用城市空气质量的综合得分对气候因子、城市发展因子、城市环境治理因子和城市地形因子分别进行逐步回归, 剔除不显著因子, 并参考已有文献筛选因子, 然后将最终所得10个因子综合起来建立回归模型, 得到的回归结果及解释量如表 3所示。所有因子对空气质量综合得分的解释程度达到56.0%, 建成区面积对于综合得分的解释量最高, 达到14.7%;年平均饱和水汽压次之, 解释量为12.8%;城区海拔落差的解释量为8.8%;第二产业占GDP的比重解释量为7.2%。其中风速、风向等普遍认为与空气质量有较大关系的因子都在逐步回归中被剔除, 这可能是由于风速、风向的多周期变化存在, 并与污染物排放时空分布之间不存在一致性的联系(如风速最大时并不一定是污染物排放最多的时间), 因此, 尽管在特定时刻风速、风向与城市大气污染有较强的关系, 但在年际时间尺度上, 这个效应可能被平均或掩盖。
| 因子类别 | 因子 | 回归系数 | 标准差 | t | p |
| 气候 | 年平均饱和水汽压 | -2.576×10-2 | 8.071×10-3 | -3.192 | 0.002** |
| 年平均最高气温 | 1.423×10-2 | 7.377×10-3 | 1.929 | 0.058 | |
| 城市发展 | 地区生产总值/元 | -4.327×10-8 | 1.905×10-8 | -2.272 | 0.026* |
| 建成区面积/km2 | 9.451×10-3 | 2.493×10-3 | 3.791 | 0.001** | |
| 第二产业占GDP的比重 | 3.716×10-2 | 1.602×10-2 | 2.32 | 0.023* | |
| 公路客运量/104人 | -1.345×10-5 | 1.204×10-5 | -1.117 | 0.268 | |
| 环境治理 | 人均城市道路面积/m2 | -3.340×10-3 | 2.830×10-2 | -0.118 | 0.906 |
| 人均绿地面积/m2 | -8.972×10-3 | 4.810×10-3 | -1.865 | 0.067 | |
| 地形 | 海拔落差 | 2.498×10-3 | 8.869×10-4 | 2.817 | 0.006** |
| 海拔标准差 | -1.069×10-2 | 4.847×10-3 | -2.205 | 0.030* | |
| 空气质量 | 综合得分 | 8.654×10-8 | |||
| 注: *表示p < 0.05, **表示p < 0.01 | |||||
年平均最高气温和年平均饱和水气压从南向北均呈递减格局; 建成区面积以几个一线城市和直辖市为首, 其他城市的分布格局相对分散; 地区生产总值的分布格局与建成区面积相似, 不同之处在于地区生产总值与一、二线城市的规模基本一致; 第二产业占总产值的比例呈现从东向西依次递减的趋势; 公路客运量基本呈现中部地区向四周递减的格局; 人均城市道路面积的分布比较随机, 规律不明显; 人均绿地面积与人均城市道路面积的分布格局较为相似[29]; 城区海拔落差与城区海拔标准差都呈现平原地区低、山地高的特点。
2.3 城市空气质量模拟根据构建的RBF人工神经网络模型, 对78个城市的空气质量进行模拟验证, 模拟结果与实际综合得分(2.1节中城市空气质量得分)进行对比, 发现二者在地理空间上差距不大(图 3)。从整体上来看, 空气质量为四级的地级市在全国均匀分布, 未呈现明显的经、纬度分布特征。沿海城市空气质量平均较优, 内陆城市空气质量相对较差; 珠江三角洲区域的城市空气质量为全国最优, 长江三角洲区域的城市次之, 京津冀区域的城市空气质量则普遍较差。长江流域城市的空气质量普遍好于黄河流域城市[30]。为了验证模拟模型的稳定性和可靠程度, 使用模拟综合得分与实际综合得分1:1的坐标图来验证模型的模拟准确度, 模拟综合得分与实际综合得分比例为0.775, 拟合优度达0.658, p < 2.2×10-14, 因此模型整体上有较好的模拟准确性。

|
| 图 3. 78个城市模拟综合得分与实际综合得分对比 Figure 3. The map of 78 cities comparing predicted grade with the grade divided by composite score |
将城市模拟得分与影响因子相对比, 发现气候因子、城市发展因子、城市治理因子和地形因子对于城市空气质量有不同的影响。年平均相对湿度、年平均最高气温、年平均饱和水汽压等气候因子较大的城市空气质量较好。建成区面积、地区生产总值、第二产业占总产值的比例、公路货运量和公路客运量等城市发展因子较大的城市空气质量较差。在城市治理因子中, 人均城市道路面积越大的城市空气质量越不好, 而人均绿地面积越大的城市空气质量更好。海拔落差和海拔标准差较大时, 城市空气质量也较差。
对比发现, 城市空气质量的模拟值与2010年实际观测值之间存在一定的区域性差异。究其原因, 一方面可能是空气污染的年际差异所致, 另一方面, 也可能是一些区域性的环境因素未纳入网络中造成的[31]。如长江三角洲地区城市的模拟空气质量好于2010年空气质量的实际观测值, 而已有文献认为长江三角洲地区城市空气质量受周围农民燃烧秸秆的习惯影响较大[10]。渤海和黄海周边城市空气质量实际观测值优于模拟得分, 推测原因可能是模型没有考虑海洋吸纳空气污染物和面海空间对空气污染的稀释作用。
利用该模型对173个城市的空气质量得分进行模拟, 结果如图 4所示。沿海地区空气质量相对较优, 平均气温较低的省份(如黑龙江、辽宁)城市空气质量也相对较好。珠江三角洲城市群的空气质量优于长三角城市群, 京津冀城市群的空气质量最差。环渤海地区由于能源结构、产业布局等各方面的原因, 导致其空气质量问题难以解决。黄河中下游地区的城市, 普遍空气质量堪忧。

|
| 图 4. 173个城市的模拟综合得分分布 Figure 4. The distribution of predicted grade of 173 cities |
我国的城市空气质量基本上呈现“南优北劣”的特点, 珠江三角洲城市群的空气质量优于长江三角洲, 京津冀城市群的空气质量最差。另外, 黄河中下游地区和环渤海地区的城市也比长江中下游的城市空气质量差。对比发现, 长江三角洲城市群的实际情况比RBF人工神经网络模型模拟结果差, 而濒临渤海和黄海城市的实际情况比模拟结果好, 推测可能与城市周边的环境有关。基于RBF人工神经网络模型的模拟结果说明, 气候因子、城市发展因子、地形因子都对城市空气质量起负作用, 而城市治理因子的上升有助于城市空气质量改善。
3 结论1) 利用多元统计方法, 筛选得到城市自然环境、社会经济结构和环境治理10个因子, 包括年平均饱和水汽压、年平均最高气温、地区生产总值、建成区面积、第二产业占GDP的总量、公路客运量、人均城市道路面积、人均绿地面积、海拔落差和海拔标准差, 由此构建的城市空气质量RBF人工神经网络模型可以较好地模拟城市空气质量, 表明城市所处的自然环境条件、经济结构和发展阶段、城市的环境治理投入等不仅对城市空气质量具有不同程度的贡献, 同时也对污染气体排放和稀释降解方面有影响。
2) 年平均饱和水气压、城市建成区面积、城区海拔落差和第二产业占GDP的百分比是影响当前中国城市空气综合质量的主要因素, 分别可以解释城市空气质量变异性的14.7%, 12.8%, 8.8%和7.2%, 总共10个因子对中国当前城市空气质量的解释程度达到56.0%。
3) 使用模拟综合得分与实际综合得分1:1的坐标图来验证RBF人工神经网络模型的模拟准确度, 模拟综合得分与实际综合得分比例为0.775, 拟合优度达0.658, P < 2.2×10-14, 说明模型的模拟准确性较好, 揭示了城市空气质量的影响因素, 为城市空气质量控制的机理性研究提供线索。
4) 城市空气质量综合得分的模拟值与实际观测值之间存在一定的区域性差异, 可能是一些区域性的环境因素未纳入网络中造成的, 比如长江三角洲地区城市空气质量受周围农民燃烧秸秆习惯的影响较大。
| [1] | WANG Shuxiao, HAO Jiming. Air quality manage-ment in China: issues, challenges, and options. Journal of Environmental Sciences (China), 2012, 24(1): 1001–0742 . |
| [2] | 邵超峰, 鞠美庭, 张裕芬, 等. 突发性大气污染事件的环境风险评估与管理. 环境科学与技术, 2009, 32(3): 200–205. |
| [3] | Wahid H, Ha Q P, Duc H, et al. Neural network-based meta-modelling approach for estimating spatial distribution of air pollutant levels. Applied Soft Computing, 2013, 13(10): 4087–4096 DOI:10.1016/j.asoc.2013.05.007 . |
| [4] | 薛佳平, 田伟利, 张清宇. 杭州市机动车Nox排放清单的建立及其对空气质量的影响. 环境科学研究, 2010, 23(5): 613–618. |
| [5] | Westerlund J, Urbain J P, Bonilla J. Application of air quality combination forecasting to Bogota. Atmosphe-ric Environment, 2014, 89(1): 22–28 . |
| [6] | 程好好, 曾辉, 汪自书, 等. 城市绿地类型及格局特征与地表温度的关系. 北京大学学报:自然科学版, 2009, 45(3): 495–501. |
| [7] | 余波, 周英, 刘祖涵, 等. 基于混沌理论的兰州市近10 a空气污染指数时间序列分析. 干旱区地理, 2014, 37(3): 570–578. |
| [8] | De Gennaro G, Trizio L, di Gilio A. Neural network model for the prediction of PM10 daily concentrations in two sites in the Western Mediterranean. Science of the Total Environment, 2013, 463 . |
| [9] | 周国亮, 刘希玉, 武鲁英. BP神经网络模型在空气质量级别评价中的应用. 计算机工程与设计, 2009, 30(2): 392–394. |
| [10] | 吴立新, 吕鑫, 秦凯, 等. 秸秆焚烧期间徐州市空气污染物时空分布特征分析. 地理与地理信息科学, 2014, 30(1): 18–31. |
| [11] | 李婧, 智颖. 呼和浩特市空气颗粒物影响因素研究. 中国环境监测, 2014, 3(7): 26–30. |
| [12] | 李名升, 孙媛, 陈远航, 等. 污染排放与环境质量关系模型构建与应用. 环境科学, 2014, 35(3): 1198–1204. |
| [13] | Ching J. A perspective on urban canopy layer modeling for weather, climate and air quality appli-cations. Urban Climate, 2013, 3(1): 13–39 . |
| [14] | Cheng Shuiyuan, Li Li, Chen Dongsheng, et al. A neural network based ensemble approach for impro-ving the accuracy of meteorological fields used for regional air quality modeling. Journal of Environmen-tal Management, 2012, 112(7): 404–414 . |
| [15] | 李双成, 吴绍洪, 戴尔阜. 生态系统响应气候变化脆弱性的人工神经网络模型评价. 生态学报, 2005, 25(3): 25–27. |
| [16] | Wang Jun, Sheng Zheng, Zhou Bihua. Lightning potential forecast over Nanjing with denoised sounding-derived indices based on SSA and CS-BP neural network. Atmospheric Research, 2014, 137(1): 245–256 . |
| [17] | Font A, Baker T, Mudway I S. Degradation in urban air quality from construction activity and increased traffic arising from a road widening scheme. Science of the Total Environment, 2014, 497/498(1): 123–132 . |
| [18] | 国家统计局. 中国统计年鉴2011. 北京: 中国统计出版社, 2012. |
| [19] | Voukantsis D, Karatzas K, Kukkonen J, et al. Intercomparison of air quality data using principal component analysis, and forecasting of PM10 and PM2.5 concentrations using artificial neural networks, in Thessaloniki and Helsinki. Science of the Total Environment, 2011, 409(1): 1266–1276 . |
| [20] | Eder B, Bash J, Foley K, et al. Incorporating principal component analysis into air quality model evaluation. Atmospheric Environment, 2014, 82(1): 307–315 . |
| [21] | 胡开明, 李冰, 王水, 等. 太湖流域(江苏省)水质污染空间特征. 湖泊科学, 2014, 26(2): 200–206. |
| [22] | Yuan Hongchun, Shen Xiaoqian, Chen Xinjun. Pre-diction of fishing ground based on RBF neural net-work. Procedia Engineering, 2011, 15(1): 3240–3244 . |
| [23] | 师华定, 高庆先, 庄大方, 等. 基于径向基函数神经网络(RBFN)的内蒙古土壤风蚀危险度评价. 环境科学研究, 2008, 21(5): 1001–6929. |
| [24] | Russo A, Raischel F, Lind P G. Air quality prediction using optimal neural networks with stochastic vari-ables. Atmospheric Environment, 2013, 79(1): 822–830 . |
| [25] | 赵宏, 刘爱霞, 王恺, 等. 基于GA-ANN改进的空气质量预测模型. 环境科学研究, 2009, 11(1): 1276–1281. |
| [26] | Han Honggui, Chen Qili, Qiao Junfei. An efficient self-organizing RBF neural network for water quality prediction. Neural Networks, 2011, 24(1): 717–725 . |
| [27] | 谢正苗, 王艳平, 周广柱. 基于BP网络的城市空气质量中长期预测研究. 科技通报, 2010, 26(2): 245–248. |
| [28] | Luna A S, Paredes M L, de Oliveira G. Prediction of ozone concentration in tropospheric levels using artificial neural networks and support vector machine at Rio de Janeiro, Brazil. Atmospheric Environment, 2014, 98(1): 98–104 . |
| [29] | 徐祥德, 丁国安, 卞林根. 北京城市大气环境污染机理与调控原理. 应用气象学报, 2007, 17(6): 815–828. |
| [30] | Jiang D, Zhang Y, Hu X, et al. Progress in developing an ANN model for air pollution index forecast. Atmospheric Environment, 2004, 38(40): 7055–7064 DOI:10.1016/j.atmosenv.2003.10.066 . |
| [31] | De Ridder K, Kumar U, Lauwaet D, et al. Kalman filter-based air quality forecast adjustment. Atmos-pheric Environment, 2012, 50(1): 381–384 . |
| [32] | Huo Z, Feng S, Kang S, et al. Artificial neural net-work models for reference evapotranspiration in an arid area of northwest China. Journal of Arid Envir-onments, 2012, 82(1): 81–90 . |
 2016, Vol. 52
2016, Vol. 52




