文章信息
- 宫健华, 盖增喜
- GONG Jianhua, GE Zengxi
- SS前驱震相有限频效应研究
- Finite-Frequency Effects of SS Precursor
- 北京大学学报(自然科学版), 2016, 52(6): 1014-1024
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(6): 1014-1024
-
文章历史
- 收稿日期: 2015-06-07
- 修回日期: 2015-06-24
- 网络出版日期: 2016-09-29
410 km和660 km间断面是两个主要的地幔间断面, 研究它们的形成、形态以及与周围物质的相互作用情况对于研究地球内部过程具有重要的意义。
矿物学研究表明, 410 km间断面的形成主要由橄榄石的α相至β相的相变引起, 具有正的Cla-peyron斜率; 660 km间断面的形成主要由橄榄石的γ相至钙钛矿和镁方铁矿的相变引起, 具有负的Clapeyron斜率[1-2]。因此, 在温度较低的地区(如俯冲带), 410 km间断面会向上抬升, 660 km间断面则向下沉降; 在温度较高的地区则相反。因此, 410 km和660 km间断面的起伏状况可以用来推测转换带内部的温度和化学状态。
660 km间断面关系到地球动力学中一些重要的争论, 如:俯冲板片是否可以穿过660 km界面进入下地幔[3]; 660 km界面是否是能量与物质的隔断面, 从而关系到地幔符合分层对流模型还是全对流模型; 地幔柱的起源来自转换带内部还是下地幔或核幔边界, 即地幔柱是否穿透660 km界面[4]。这些都是层析成像和地球动力学模拟研究中关心的重要问题, 研究660 km间断面的起伏状况可以为上述问题提供必要的约束。
研究410 km和660 km间断面的两种主要方法是接收函数法[5-8]和SS/PP前驱震相方法[9-16]。接收函数法可以对台站下方的间断面进行成像, 在有密集台网或测线的地方, 可以得到较为连续的间断面起伏状况, 但是局限在陆地上有台站分布[5, 7]或海洋中有海底地震仪的地方[6], 不适合全球尺度的研究。SS/PP前驱震相方法有较好的全球覆盖率, 但是由于有较大的菲涅尔带, 所以分辨率较低。
有关SS/PP前驱波的研究, 经历了从基于射线理论的叠加到尽可能利用波形信息的转变。早期利用叠加方式对全球410 km和660 km间断面进行成像[14], 得到大尺度的间断面起伏情况。之后利用τ-p变换和Radon变换得到局部地区地幔间断面的深度[17]。为了解决间断面深度与转换带内速度之间的折中关系, Gu等[18]和Houser等[19]利用SS-SdS到时差对转换带速度结构和410 km, 660 km间断面深度进行联合反演。Lawrence等[20]利用拟合SS前驱波波形的方式得到全球平均的转换带速度模型。此外, 还有人利用SdS震相与SS震相的振幅比来计算地幔间断面的反射率, 得到全球大尺度地幔间断面的反射率图像[21-24]。随着全球地震数据的增多, 人们开始尝试借鉴勘探地震学的一些成像方法对地幔间断面进行成像。Shearer等[15]和Schmerr等[25]利用偏移方法得到局部地区地幔间断面分辨率较高的成像结果。Wang等[26]、Ma等[27]和Burdick等[28]将勘探中的广义Radon变换、逆时偏移等技术应用到地球内部间断面的成像。Rychert等[29]利用合成理论地震图的方法, 探讨利用SS前驱波探测地幔间断面地区的各向异性特征。随着方法的改进和数据量的增多, 利用前驱波的研究逐渐从全球大尺度结构向区域小尺度精细结构转变。
传统的SS/PP前驱震相方法都是利用射线理论, 将间断面震相的到时扰动转化为反射点处的界面起伏。以SS前驱震相为例, 到时扰动δT与反射点处界面起伏δh之间的关系可以写成
| ${\rm{\delta }}T=\frac{{2{\rm{\delta }}h\cos i}}{c}, $ | (1) |
其中, i为射线到达间断面的入射角, c为间断面下方S波的速度。我们规定δh > 0对应界面上升, δh < 0对应界面下沉。所以, δT > 0对应到时延迟, δT < 0对应到时提前。射线理论的不足之处在于基于高频(0波长)近似, 但是实际情况下SS的波长可达上百公里, 当间断面存在较小尺度的起伏时, 波前愈合效应将导致实际观测的δT偏离射线理论的估计值。
一些学者曾对SS/PP前驱震相对地幔间断面起伏的敏感性进行数值模拟。Chaljub等[30]模拟660 km间断面处存在半周期正弦函数形状起伏时的S660S地震波形, 发现起伏界面的横向尺度越小, 波前愈合效应越明显。Neele等[31]正演410 km间断面处存在界面起伏情况下的P410P地震波形, 并根据射线理论, 将P410P到时扰动转化为反射点处的界面起伏, 发现与正演模型相比, 利用射线理论得到的界面起伏产生较大假象。Neele等[32]提出一种利用振幅和走时信息反演界面起伏状况的方法, 由于真实的振幅信息在单个地震图上很难获得, 这种方法在实际应用中有较大困难。
Dahlen[33]基于有限频理论, 推导了边界敏感核的表达式, 建立δT与δh之间的显式关系。Lawrence等[12]利用Dahlen推导出的敏感核, 反演全球410 km和660 km间断面的起伏状况, 但在反演过程中只考虑了第一菲涅尔带的影响。
Deng等[34]推导接收函数的边界敏感核, 正演了间断面存在起伏扰动情况下的地震波形, 并利用边界敏感核, 成功预测接收函数到时扰动, 说明了接收函数对地幔间断面起伏状况的敏感性。
本文首先计算SS前驱震相边界敏感核, 讨论影响敏感核形态的因素。然后, 利用敏感核分析SS前驱震相的波前愈合效应, 并利用SPECFEM软件[35-36]正演间断面存在起伏扰动情况下的SS前驱震相地震波形, 将模拟的SS前驱震相到时扰动与利用敏感核预测的到时扰动相比较, 说明有限频理论可以很好地解释SS前驱震相的波前愈合效应。接着, 利用边界敏感核反演界面起伏, 说明当考虑有限频效应时, 可以更充分地利用波形信息, 更好地恢复间断面上的起伏形态。最后, 讨论基于上述近似方法得到边界敏感核的不足之处, 为今后的研究提出改进方向。
为了简便, 本文以SH分量的S660S震相为例进行讨论, 选用PREM模型作为背景速度模型, 理论计算和数值模拟过程中震源和台站都设置在深度为0 km的位置。本文中的图片全部用GMT软件绘制[37]。
1 S660S边界敏感核的计算 1.1 计算方法简述Dahlen等[33, 38]利用Born散射理论、WKBJ近似和傍轴近似, 推导出的SS前驱震相的边界敏感核可以表示为
| $\begin{array}{l} K=\frac{1}{{\rm{\pi }}}\frac{{|\cos i|}}{c}\sqrt {\frac{{{{\cos }^2}i|{J_{{\rm{rs}}}}|}}{{|{J_{{\rm{xs}}}}{J_{{\rm{xr}}}}|}}} \;\cdot \\ \;\;\;\;\;\frac{{\mathop \smallint \nolimits_0^\infty {\omega ^3}|\dot m(\omega){|^2}\cos \omega({T_{{\rm{xs}}}}+{T_{{\rm{xr}}}} - {T_{{\rm{rs}}}}){\rm{d}}\omega }}{{\mathop \smallint \nolimits_0^\infty {\omega ^2}|\dot m(\omega){|^2}{\rm{d}}\omega }}, \end{array}$ | (2) |
其中Trs, Txs, Txr, Jrs, Jxs和Jxr分别为源到接收点、源到散射点和接收点到散射点的走时和Jacobian系数,
| ${\rm{\delta }}T=\int_\Sigma K \;{\rm{\delta }}h\;{\rm{d}}{x^2}, $ | (3) |
其中, Σ代表地幔间断面。在已知敏感核和起伏形态的情况下, 可以根据式(3)预测SS前驱震相的到时扰动。
本文利用Tian等[39]介绍的算法(包括运动学射线追踪和动态射线追踪), 计算式(2)中的边界敏感核。计算S660S敏感核主要依赖于以下4项的确定: 1)i; 2)Txs+Txr −Trs; 3)
| $\dot m(\omega){|^2}=({\omega ^2}{\tau ^2}/2{\rm{\pi }})\exp(- {\omega ^2}{\tau ^2}/4{{\rm{\pi }}^2}), $ | (4) |
其中τ为特征周期, 不同的τ使得震源时间函数有不同的频率分部范围。确定以上4项后, 就可以通过数值积分的方法得到边界敏感核。
1.2 影响边界敏感核的因素在震源和台站深度确定的情况下, 影响边界敏感核的因素主要有两个:震中距和震源时间函数。这是因为在敏感核的表达式中, i, Txs+Txr−Trs和
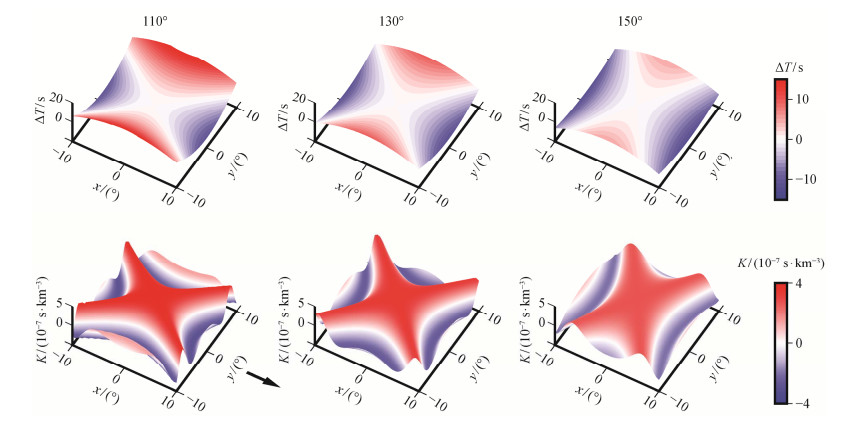
图 1展示震源时间函数相同的情况下不同震中距S660S菲涅尔带和边界敏感核的形态。震源时间函数功率谱固定为τ=20 s时的Gaussian型震源时间函数功率谱, 震中距分别为110°, 130°和150°。
|
| x, y轴为经纬度, 箭头指向台站方向 图 1. 震中距为110°, 130°和150°的S660S的菲涅尔带(第一行)和边界敏感核(第二行) Figure 1. Fresnel zones (the first line) and boundary topography sensitivity kernels (the second line) of S660S for epicenter distance of 110°, 130° and 150° |
S660S的菲涅尔带呈“马鞍”型, 这是因为在射线路径平面内, 当间断面上的散射点向着震源或台站的方向移动时, 得到的新射线路径将有更大的部分通过高速的下地幔, 传播时间更短, 使得Txs+Txr −Trs < 0;相反, 当间断面上的散射点沿着垂直于射线平面的方向向两侧移动时, 新的射线路径路程更长, 使得Txs+Txr −Trs > 0。又因为S660S边界敏感核表达式中包含偶函数cos函数, 所以相应的敏感核呈“X”形状。
随着震中距的增加, 菲涅尔带变“平坦”, 意味着第一菲涅尔带将增大, 同时敏感核的幅值减小, 意味着随着震中距的增加, S660S对间断面起伏状况的敏感度降低, 到时扰动
| ${\rm{\delta }}T=\int_\Sigma K \;{\rm{\delta }}h\;{\rm{d}}{x^2}$ |
是对更大范围内界面起伏状况的平均体现。
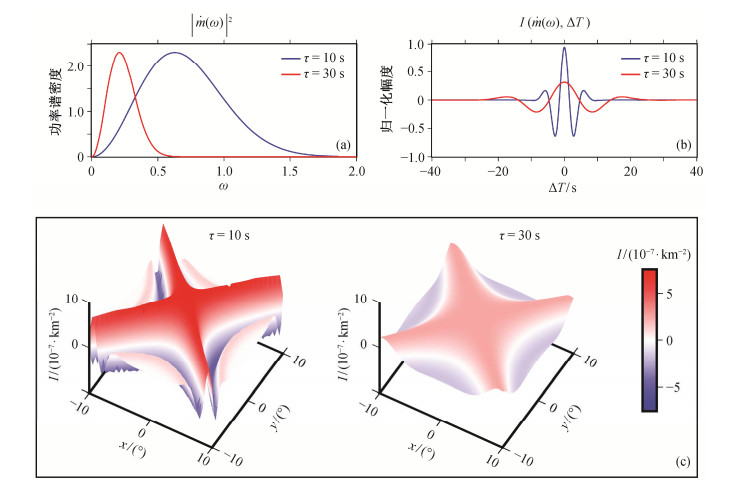
图 2显示相同震中距、不同震源时间函数情况下敏感核的形态。我们选取τ=10 s和τ=30 s的Gaussian型震源时间函数功率谱进行计算, 震中距为130°。图 2(a)显示两种震源时间函数的功率谱。当τ较小时, 震源时间函数中含有更多的高频成分。将敏感核公式的积分部分定义为I:
| $I(\dot m\left(\omega \right), {\rm{\Delta }}T)=\frac{{\mathop \smallint \nolimits_0^\infty {\omega ^3}|\dot m(\omega){|^2}\cos \omega({T_{{\rm{xs}}}}+{T_{{\rm{xr}}}} - {T_{{\rm{rs}}}}){\rm{d}}\omega }}{{\mathop \smallint \nolimits_0^\infty {\omega ^2}|\dot m(\omega){|^2}{\rm{d}}\omega }}, $ | (5) |
|
| (a)震源时间功率谱; (b)敏感核积分项I; (c)边界敏感核。震中距固定为130° 图 2. 不同频率成分的敏感核 Figure 2. Boundary topography sensitivity kernels for different frequency component |
其中, ΔT=Txs+Txr −Trs。I随ΔT的变化情况如图 2(b)所示, 其中主瓣大于0的部分即为通常所说的第一菲涅尔带。向两侧延伸, 第一个小于0的部分为第二菲涅尔带。随着ΔT的增加, I逐渐衰减为0。τ越小, I的幅值越大, 主瓣宽度越小, 相应的敏感核幅值也更高, 形状更“紧凑”, 意味着S660S对反射点附近的界面起伏情况更加敏感, 更容易分辨出横向尺度较小的结构。
2 S660S有限频效应由于到时差δT是敏感核K与界面起伏扰动δh的乘积在间断面上的积分, 所以敏感核形状的改变或起伏扰动形状的改变都会影响δT的大小。因此, 我们改变震中距、震源时间函数和起伏扰动的横向尺度来测试不同因素对δT的影响。
2.1 起伏界面选用Gaussian函数控制660 km间断面的起伏扰动形状, 其形状可以表达为
| ${\rm{\delta }}h(x, \;y)={h_0}\exp \left[{-\frac{{{{(x-{x_0})}^2}}}{{G_x^2}}-\frac{{{{(y - {y_0})}^2}}}{{G_y^2}}} \right], $ | (6) |
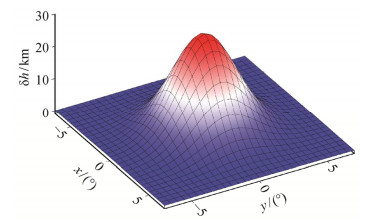
其中, h0控制Gaussian型起伏扰动的高度, x和y代表 660 km间断面上某一点的经纬度, x0和y0为Gaussian起伏扰动中心点的经纬度, Gx和Gy控制Gaussian起伏扰动的横向尺度。图 3展示h0=30 km, x0=y0=0, Gx=Gy=3情况下Gaussian起伏扰动的立体形状。
|
| h0=30 km, x0=y0=0, Gx=Gy=3 图 3. Gaussian型起伏扰动三维形态 Figure 3. 3D profile of the Gaussian shape topographyperturbation |
2.2 理论计算
首先, 讨论在震源时间函数固定的情况下, 震中距和间断面起伏扰动横向尺度改变时δT的变化情况。
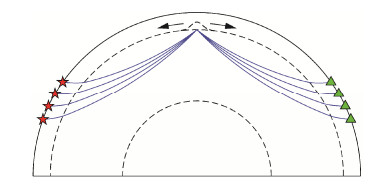
选取震中距为110°, 120°, 130°和140°四组共中心点的地震台站对, 将Gaussian型起伏扰动的中心设置在共中心点的位置, 通过改变Gx和Gy来调整Gaussian型起伏扰动的横向尺度。图 4显示震源、台站和Gaussian型起伏扰动的相对位置。
|
| 红色五角星代表震源, 绿色三角形代表台站; 为了明显起见, Gaussian型起伏扰动的径向起伏被放大10倍 图 4. 理论计算过程中台站、震源和660 km间断面处起伏扰动的相对位置示意图 Figure 4. The sketch showing the location of the receivers, the sources and the Gaussian shape topography pertur-bation implemented on the 660 km discontinuity for theoretical calculation |
图 5显示不同震中距δT随异常体尺度的变化曲线。规定Gx=Gy, 并令

|
| 虚线表示相应震中距下射线到时扰动的理论估计值 图 5. 不同震中距下δT随起伏异常横向尺度σ的变化曲线 Figure 5. The curve of traveltime perturbation δT versus lateral dimension of topography perturbation σ for different epicentre distances |
然后, 固定震中距, 选取τ=10, 20, 30 s的Gaussian型震源时间函数功率谱, 计算δT随间断面起伏扰动横向尺度的变化曲线, 震中距设定为130°, 结果如图 6所示。从图 6可以看出, 当起伏扰动横向尺度增大时, δT均逐渐增大, 并最终与射线理论吻合。有所不同的是, τ越小(也就是震源时间函数中所含的高频成分越多), δT趋向于射线理论估计值的速度越快, 这与射线理论的高频假设相吻合。

|
| 震中距为130°, 虚线表示射线理论下的到时扰动 图 6. 不同震源时间函数下δT随起伏异常横向尺度σ的变化曲线 Figure 6. The curve of traveltime perturbation δT versus lateral dimension of topography perturbation σfor different source time functions |
2.3 数值模拟
利用Specfem Global软件可以实现三维地球模型下的波场正演。为了验证SS前驱震相的波前愈合效应, 通过Specfem Global软件模拟660 km界面存在Gaussian型起伏扰动情况下SS前驱震相波形, 同时模拟标准PREM模型下的SS前驱震相波形。将两组波形做互相关, 得到模拟记录的S660S到时扰动量。
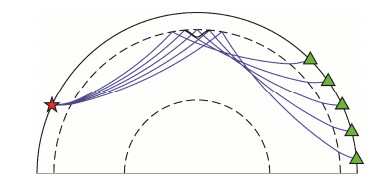
模拟过程中, 震源、起伏扰动中心位置和台站设置在赤道平面上, 震源设置在0°E, Gaussian型起伏扰动的中心位置设置在65°E, h0=−30 km, Gx=Gy=3, 台站设置在110°-150°E之间, 间隔0.25°, 共161个台站。震源、起伏扰动和台站的相对位置如图 7所示。
|
| 红色五角星代表震源, 绿色三角形代表台站; 为了明显起见, Gaussian型起伏扰动的径向起伏被放大10倍 图 7. 数值模拟过程中台站、震源和起伏扰动的相对位置示意图 Figure 7. The sketch showing the location of the receivers, the source and the Gaussian shape topography pertur-bation implemented on the 660 km discontinuity for numerical modeling |
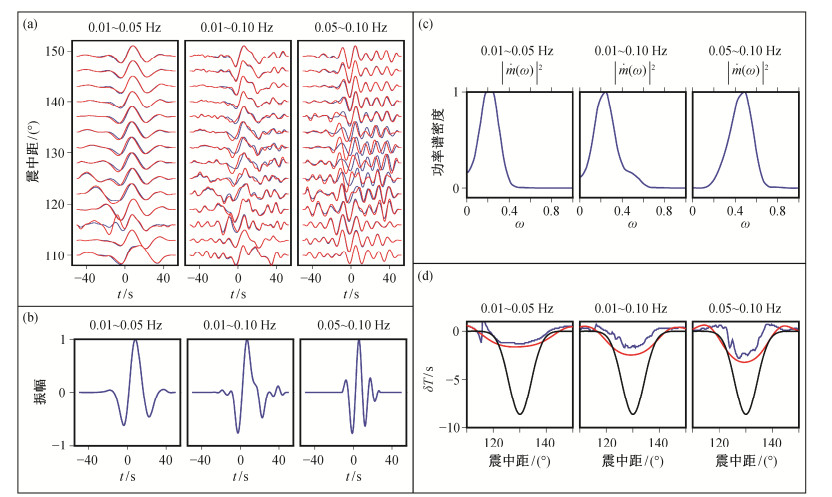
将地震波形按照0.01~0.05, 0.01~0.1和0.05~0.1 Hz的频带范围进行带通滤波, 得到标准PREM模型下地震波形和带有起伏扰动的地震波形, 如图 8(a)所示。可以看到, 在120°~140°之间两组波形有明显差异。将两组波形做互相关, 得到到时扰动量δT, 再利用式(3)计算有限频理论下的δT, 得到实测δT和理论δT随震中距的变化曲线, 如图 8(d)所示。在计算理论到时扰动量时, 将同一组波形按照S660S的理论到时对齐后进行叠加, 如图 8(b)所示, 对得到的波形求功率谱, 将其近似作为视震源时间函数, 带入边界敏感核的表达式(式(1)),计算边界敏感核。叠加后的S660S波形和相应的功率谱如图 8(c)和(d)所示。
|
| (a)不同频带滤波后S660S波形, 红线为带有起伏扰动的S660S波形, 蓝线为标准PREM模型下的S660S波形; (b)各频段S660S叠加波形(归一化); (c) S660S叠加波形功率谱(归一化); (d)射线理论(黑)、有限频理论(红)和模拟记录测量(蓝)得到的不同频带下S660S到时扰动量随震中距的变化曲线 图 8. 不同频率的合成数据的处理结果 Figure 8. Results of synthetic data for different frequency band |
从图 8(d)可以看出, 模拟和理论计算得到的到时扰动幅度远小于射线理论下的到时扰动幅度, 说明S660S的波前愈合效应较为明显。从变化趋势看, 在震中距由小变大的过程中, 模拟S660S到时扰动量由正(到时延迟)变负(到时提前), 在130°附近达到最低, 之后逐渐变大, 最后恢复为正值。两侧正的到时扰动说明, 当间断面存在向下凹陷的起伏扰动时, 却能观测到前驱震相到时延迟的现象, 因此在反演过程中不能忽略敏感核函数中的负值, 否则利用观测数据反演就可能出现假象。
可以利用有限频理论对S660S到时扰动量随震中距的变化趋势进行解释。当震中距小于130°时, S660S的反射点落在起伏扰动中心的左侧, 起伏扰动与相应边界敏感核的相对位置如图 9所示。震中距越小, 起伏扰动中心与边界敏感核的中心相距越远, 使得起伏扰动覆盖到边界敏感核为负的区域。积分时, 此部分与起伏扰动覆盖在边界敏感核正值区域的结果相抵消, 使得到时扰动量的绝对值偏小, 在δh < 0的情况下, 甚至会出现积分为正的情况。当震中距向130°靠近时, 起伏扰动主要覆盖在边界敏感核为正值的区域, 会得到较大的到时扰动。

|
| 五角星为震源所在位置, 绿色三角形为台站, 中央黑色三角形代表S660S反射点位置, 等高线代表起伏扰动 图 9. 震中距小于130°时边界敏感核和起伏扰动的相对位置示意图 Figure 9. Relative location of boundary topography sensitivity kernel and the topography perturbation on 660 km discontinuity for epicentre distance less than 130° |
但是, 模拟到时扰动存在一些不能用理论到时扰动解释的现象。首先, 在0.01~0.05 Hz频段, 115°附近S660S震相与S660SS震相相交, 引起波形的变化。在进行互相关时, δT会出现不连续的现象。本文计算的敏感核只针对S660S单一震相, 因而无法拟合这种现象。其次, 在0.05~0.1 Hz频段, 模拟到时扰动在120°和140°附近出现快速上升的现象, 而理论到时扰动曲线的变化较为平缓。另外, 与实测扰动量相比, 理论扰动量的幅值偏大。
3 数值模拟数据的反演根据传统走时理论, 可以将SS前驱震相的到时差直接转换成间断面深度的起伏。然而, 在考虑有限频效应时, 需要对观测数据进行反演, 才能得到间断面的深度。反演过程包括模型的线性化和线性反演。
3.1 模型线性化利用边界敏感核可以建立间断面起伏扰动与到时扰动之间的线性关系, 进而可以由到时扰动δT反演间断面的起伏扰动δh。根据公式
| $ {\rm{\delta }}T=\int_\Sigma K \;{\rm{\delta }}h\;{\rm{d}}{x^2} $ |
将间断面网格化, 假设每个子网格内δh不变, 可以构建δT与δh之间的线性关系, 从而在已知δT和敏感核K的情况下, 对δh进行反演。
假设将间断面划分为N个子网格, 每个子网格内界面起伏的平均高度为δhi, 对于第m次观测, 若有到时扰动δTm, 则δTm与δhi之间可以线性化表示为
| $ \begin{align} & \text{ }\!\!\delta\!\!\text{ }{{T}_{m}}=\int_{\Sigma }{{{K}_{m}}}\text{ }\!\!\delta\!\!\text{ }h\text{d}S \\ & \ \ \ \ \ \ \approx \sum\nolimits_{i}{\mathop{\int }^{}}{{K}_{m}}\Delta {{h}_{i}}\text{d}{{S}_{i}} \\ & \ \ \ \ \ \ =\sum\nolimits_{i}{\Delta }{{h}_{i}}\mathop{\int }^{}{{K}_{m}}\text{d}{{S}_{i}} \\ & \ \ \ \ \ \ =\Delta {{h}_{i}}{{k}_{mi}}, \\ \end{align} $ | (7) |
其中, kmi为敏感核在第i个网格内的积分。对于M个观测记录N个子网格, 则有
| $\left[{\begin{array}{*{20}{c}} {{\rm{\delta }}{T_1}}\\ \vdots \\ {{\rm{\delta }}{T_M}} \end{array}} \right]=\left[{\begin{array}{*{20}{c}} {{k_{11}}}& \cdots &{{k_{1N}}}\\ \vdots &{}& \vdots \\ {{k_{M1}}}& \cdots &{{k_{MN}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\Delta {h_1}}\\ \vdots \\ {\Delta {h_N}} \end{array}} \right], $ | (8) |
其中kmn为第m个边界敏感核在第i个子网格内的积分, 可以通过增加合理的正则化方法对δh进行线性反演。
3.2 反演实例在660 km间断面处设置向下凹的Gaussian型起伏扰动, 利用SPECFEM软件正演带有起伏扰动情况下的S660S地震波形, 与标准PREM模型下的S660S波形进行互相关计算, 得到S660S的到时扰动δT。然后, 利用视震源时间函数计算敏感核, 根据上述线性化过程, 对660 km界面的起伏状况进行反演。
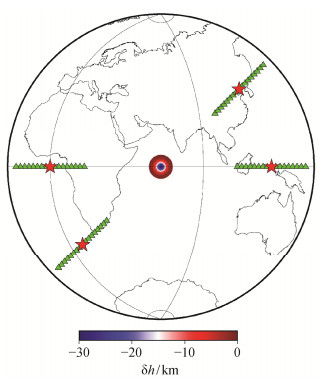
Gaussian型起伏扰动的中心位置设置在0°N, 65°E, 其中h0=−30 km, Gx=Gy=3。设置4个模拟震源S1~S4, 分别放置在与起伏中心相距65°, 方位角为270°, 90°, 45°和225°处, 对应的4组台站R1~R4分别设置在地震起伏中心大圆弧上, 震中距为110°~150°, 间隔0.25°。震源、台站和起伏界面的相对位置如图 10所示。反演区域为7°S-7°N, 58°-72°E, 将该区域离散为1°×1°的网格。
|
| 中心圆形部分为起伏扰动所在位置 图 10. 反演中使用的4次模拟地震S1~S4和相应的4组观测记录R1~R4位置示意图 Figure 10. Location of the four simulated earthquakes S1‒S4 and four sets of corresponding receivers R1‒R4 |
在反演过程中加入平滑, 并对边界进行固定, 按照式(8)构建以下反演方程组:
| $\left[{\begin{array}{*{20}{c}} K\\ {\lambda L}\\ {\mu E} \end{array}} \right]\Delta h=\left[{\begin{array}{*{20}{c}} {\delta T}\\ 0\\ 0 \end{array}} \right], $ | (9) |
其中K为敏感核矩阵, L为Laplace平滑算子, E为边界阻尼算子。将4组模拟数据分别进行0.01~0.05, 0.01~0.1和0.05~0.1 Hz的带通滤波, 每组模拟数据得到3组针对不同频段的到时扰动δT, 分别计算3个频段的敏感核, 组成4次地震、3个频段的敏感核矩阵K。λ=0.2, μ=1。反演结果如图 11所示, 最大起伏扰动的幅度为20.7 km。

|
| 图 11. 实际起伏模型(a)和反演结果(b) Figure 11. Real topography perturbation (a) and the inversion result of the topography perturbation (b) |
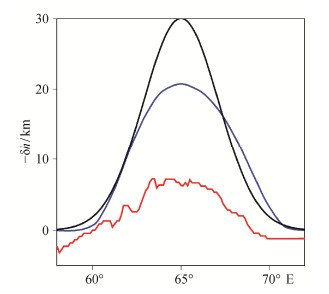
图 12为反演结果在赤道面上的横截面。由于波前愈合效应, SS前驱波的到时比射线理论的预测到时小, 导致与真实值相比, 利用射线理论将到时扰动量转化为间断面的起伏扰动量偏小幅度较大, 仅为真实的1/3左右。利用有限频原理反演得到的结果更接近实际情况, 能较好地恢复实际界面的起伏范围。但是, 与真实间断面起伏状况相比, 有限频的反演结果仍有一些差异, 主要表现在有限频反演结果仍比真实间断面小。这主要是因为在计算边界敏感核时, 我们将视震源时间函数的功率谱作为)
|
| 黑线代表真实起伏界面形态, 蓝线为反演结果, 红线为将R1组台站记录到的S660S波形进行0.01~0.1 Hz带通滤波得到的δT, 利用射线理论换算得到的反射面的起伏形态 图 12. 真实起伏扰动(黑)、反演结果(蓝)和射线理论下得到的结果(红)在赤道面上的投影 Figure 12. Real topography perturbation (black), the inveriosn topography (blue) and the topography predicted by ray theory (red) on the equatorial section |
从图 12可以看到, 根据射线原理将模拟观测的到时扰动转化为间断面起伏时, 结果并不连续, 这主要是由测量的模拟观测数据的到时扰动随震中距的变化不连续造成的。利用互相关方法测量到时扰动量时, 由于记录的采样间隔为0.1 s, 所以测得的到时扰动量也以0.1 s为分度值, 并不是连续变化的量。还有, 由于其他震相(如S660SS)对S660S的干扰, 会使S660S的波形发生改变, 因此到时扰动量会发生突变。
4 结论和讨论本文基于有限频理论, 计算S660S边界敏感核, 能够较好地解释SS前驱震相的波前愈合效应。同时利用边界敏感核, 可以对数据进行对频段滤波, 利用不同频率的到时信息对间断面起伏状况进行反演, 纠正射线理论带来的假象, 提高分辨率, 更好地恢复间断面的真实起伏状态。利用有限频理论计算的边界敏感核表达式中, 各项物理意义清晰, 便于理解。有限频方法计算效率高, 适用于大量数据的反演。
但是, 此方法是一种近似方法, 是基于WKBJ近似、傍轴近似等假设, 计算时背景速度模型需采用一维速度模型, 不考虑震源机制解的影响, 一个敏感核只针对单一震相, 计算得到的敏感核的准确性依赖于震源时间函数的选取。正确的边界敏感核是反演结果好坏的前提条件, 更精确地计算敏感核可以利用Adjoint[35-36, 40-41]和Normal Mode[34]等方法, 考虑震源和三维速度结构的影响[42], 计算针对地震图任意时间窗内的敏感核。利用这些方法, 可以更精确地拟合实际记录中的到时扰动, 更好地反演间断面的起伏状况。
致谢:感谢邓凯博士在数值模拟方面的帮助以及江燕老师关于有限频问题的讨论。
| [1] | Ito E, Takahashi E. Post-spinel transformations in the system Mg2SiO4-Fe2SiO4 and some geophysical implications. J geophys Res, 1989, 94: 10637–10646 DOI:10.1029/JB094iB08p10637 . |
| [2] | Ringwood A E. Composition and petrology of the earth's mantle. New York: McGraw-Hill, 1975. |
| [3] | Fukao Y, Obayashi M. Subducted slabs stagnant above, penetrating through, and trapped below the 660-km discontinuity. J Geophys Res, 2013, 118(11): 5920–5938 DOI:10.1002/2013JB010466 . |
| [4] | Montelli R, Nolet G, Dahlen F A, et al. Finite-frequency tomography reveals a variety of plumes in the mantle. Science, 2004, 303: 338–343 DOI:10.1126/science.1092485 . |
| [5] | Lawrence J F, Shearer P M. A global study of transition zone: thickness using receiver functions. J geophys Res, 2006, 111 DOI:10.1029/2005JB003973 . |
| [6] | Shen Y, Sheenhan A F, Dueker K G, et al. Mantle discontinuity structure beneath the southern East Pacific Rise from P-to-S converted phases. Science, 1998, 280: 1232–1235 DOI:10.1126/science.280.5367.1232 . |
| [7] | Tauzin B, van der Hilst R D, Wittlinger G, et al. Multiple transition zone seismic discontinuities and low velocity layers below western United States. J Geophys Res, 2013, 118: 2307–2322 DOI:10.1002/jgrb.50182 . |
| [8] | Vinnik L P. Detection of waves converted from P to SV in the mantle. Phys Earth Planet Int, 1977, 15: 39–45 DOI:10.1016/0031-9201(77)90008-5 . |
| [9] | Deuss A J, Woodhouse J H. A systematic search for mantle discontinuities using SS-precursor. Geophys Res Lett, 2002, 29(8) DOI:10.1029/2002GL014768 . |
| [10] | Deuss A J. Global observations of mantle disconti-nuities using SS and PP precursor. Surv Geophys, 2009, 30: 301–326 DOI:10.1007/s10712-009-9078-y . |
| [11] | Gu Y J, Dziewonsku A M. Global variability of transition zone thickness. J geophys Res, 2002, 107 DOI:10.1029/2001JB000489 . |
| [12] | Lawrence J, Shearer P. Imaging mantle transition zone thickness with SdS-SS finite-frequency sensiti-vity kernels. Geophs J Int, 2008, 174: 143–158 DOI:10.1111/gji.2008.174.issue-1 . |
| [13] | Sheare P M. Constraints on upper mantle discon-tinuities from observations of long-period reflected and converted phases. J Geophys Res, 1991, 96: 18147–18182 DOI:10.1029/91JB01592 . |
| [14] | Shearer P M. Global mapping of upper mantle reflectors from long-period SS precursors. Geophys J Int, 1993, 115: 878–904 DOI:10.1111/gji.1993.115.issue-3 . |
| [15] | Shearer P M, Flanagan M P, Hedlin M A H. Experiments in migration precessing of SS precursor data to image upper mantle discontinuity structure. J Geophys Res, 1999, 104: 7229–7242 DOI:10.1029/1998JB900119 . |
| [16] | Shearer P M, Masters T G. Global mapping of topography on the 660-km discontinuity. Nature, 1992, 355: 791–796 DOI:10.1038/355791a0 . |
| [17] | An Y, Gu Y J, Sacchi M D. Imaging mantle discontinuities using least squares Radon transform. J Geophys Res, 2007, 112 DOI:10.1029/2007JB005009 . |
| [18] | Gu Y J, Dziewonsku A M, Ekstrom G. Simultaneous inversion for mantle shear velocity and topography of transition zone discontinuities. Geophys J Int, 2003, 154: 559–583 DOI:10.1046/j.1365-246X.2003.01967.x . |
| [19] | Houser C, Masters G, Flanagan M, et al. Deter-mination and analysis of long-wavelength transition zone structure using SS precursors. Geophys J Int, 2008, 174: 178–194 DOI:10.1111/gji.2008.174.issue-1 . |
| [20] | Lawrence J F, Shearer P M. Constraining seismic velocity and density for the mantle transition zone with reflected and transmitted waveforms. Geochem Geophys Geosyst, 2006, 7 DOI:10.1029/2006GC001339 . |
| [21] | Chambers K, Deuss A, Woodhouse J H. Reflectivity of the 410-km discontinuity from PP and SS precursors. J Geophys Res, 2005, 110 DOI:10.1029/2004JB003345 . |
| [22] | Shearer P M, Flanagan M P. Seismic velocity and density jumps across the 410-and 660-kilometer discontinuities. Science, 1999, 285: 1545–1548 DOI:10.1126/science.285.5433.1545 . |
| [23] | Bai L, Zhang Y, Ritsema J.An analysis of SS precursors using spectral-element method seismo-grams Geophys J Int, 2012, 188: 293-300 |
| [24] | Bai L, Ritsema J. The effect of large-scale shear-velocity heterogeneity on SS precursor amplitudes. Geophys Res Lette, 2013, 40: 6054–6058 DOI:10.1002/2013GL058669 . |
| [25] | Schmerr N, Thomas C. Subducted lithosphere beneath the Kuriles from migration of PP precursor. Earth and Planetary Science Letters, 2011, 311: 101–111 DOI:10.1016/j.epsl.2011.09.002 . |
| [26] | Wang P, de Hoop M V, van der Hilst R D, et al. Imaging of structure at and near the core mantle boundary using a generalized radon transform: 1.construction of image gathers. J Geophys Res, 2006, 111: B12304 . |
| [27] | Ma P, Wang P, Tenorio L, et al. Imaging of structure at and near the coremantle boundary using a generalized radon transform: 2.statistical inference of singularities. J Geophys Res, 2007, 112: B08303 . |
| [28] | Burdick S, de Hoop M V, Wang S, et al. Reverse-time migration-based reflection tomography using teleseismic free surface multiples. Geophys J Int, 2014, 196: 996–1017 DOI:10.1093/gji/ggt428 . |
| [29] | Rychert C, Harmon N, Schmerr N. Synthetic waveform modelling of SS precursors from aniso-tropic upper-mantle discontinuities. Geophys J Int, 2014, 196: 1694–1705 DOI:10.1093/gji/ggt474 . |
| [30] | Chaljub E, Tarantola A. Sensitivity of SS precursors to topography on the upper-mantle 660-km discon-tinuity. Geophys Res Lett, 1997, 24: 2613–2616 DOI:10.1029/97GL52693 . |
| [31] | Neele F, de Regt H, VanDecar J. Gross errors in upper-mantle discontinuity topography from under-side reflection data. Geophys J Int, 1997, 129: 194–204 DOI:10.1111/gji.1997.129.issue-1 . |
| [32] | Neele F, de Regt H. Imaging upper-mantle discon-tinuity topography using underside-reflection data. Geophys J Int, 1991, 137: 91–106 . |
| [33] | Dahlen F A. Finite-frequency sensitivity kernels for boundary topography perturbations. Geophs J Int, 2005, 162: 525–540 DOI:10.1111/gji.2005.162.issue-2 . |
| [34] | Deng K, Zhou Y. Wave diffraction and resolution of mantle transition zone discontinuities in receiver function imaging. Geophys J Int, 2015, 201: 2008–2025 DOI:10.1093/gji/ggv124 . |
| [35] | Komatitsch D, Tromp J. Spectral-element simula-tions of global seismic wave propagation -Ⅰ. validation.Geophys J Int, 2002, 149: 390–412 DOI:10.1046/j.1365-246X.2002.01653.x . |
| [36] | Komatitsch D, Tromp J. Spectral-element simula-tions of global seismic wave propagation -Ⅱ.3D models.Oceans, rotation, and self-gravitation. Geophys J Int, 2002, 150: 303–318 DOI:10.1046/j.1365-246X.2002.01716.x . |
| [37] | Wessel P, Smith W H F.The generic mapping tools [EB/OL].(2001)[2013-01-01].http://gmt.soest.hawaii.edu |
| [38] | Dahlen F A, Hung S H, Nolet G. Frechet kernels for finite-frequency traveltimes -Ⅰ.Theory. Geophs J Int, 2000, 141: 157–174 DOI:10.1046/j.1365-246X.2000.00070.x . |
| [39] | Tian Y, Hung S H, Nolet G, et al. Dynamic ray tracing and traveltime corrections for global seismic tomography. Journal of Computational Physics, 2007, 266: 672–687 . |
| [40] | Colombi A, Nissen-Meyer T, Boschi L, et al. Seismic waveform sensitivity to global boundary topography. Geophs J Int, 2012, 191: 832–848 DOI:10.1111/gji.2012.191.issue-2 . |
| [41] | Liu Q, Tromp J. Finite-Frequency sensitivity kernels for global seismic wave propagation based upon adjoint methods. Geophs J Int, 2008, 174: 265–286 DOI:10.1111/gji.2008.174.issue-1 . |
| [42] | Zhao L, Chevrot S. SS-wave sensitivity to upper mantle structure: implicatiosn for the mapping of transition zone discontinuity topographies. Geophys Res Lett, 2003, 30 DOI:10.1029/2003GL017223 . |
 2016, Vol. 52
2016, Vol. 52




