文章信息
- 吕洪凤, 崔梅蕾
- LÜ Hongfeng, CUI Meilei
- 离子色谱保留模型同时检验果汁中7种有机酸
- Determination of Seven Organic Acids in Juice by Retention Model in Ion Chromatography
- 北京大学学报(自然科学版), 2016, 52(5): 785-792
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(5): 785-792
-
文章历史
- 收稿日期: 2015-04-14
- 修回日期: 2015-07-30
- 网络出版日期: 2016-05-09
水果的种类、产地、新鲜程度都会影响果汁的有机酸组成及含量, 因此对果汁中有机酸的检测不仅有助于鉴别果汁的真伪, 还能区分果汁原料的优劣[1]。测定果汁中有机酸的方法有很多, 包括光谱法、酶法、色谱法、毛细管电泳法等。其中, 离子色谱法因具有准确性高、选择性好、分离快速等优点, 在果汁有机酸的检测中发挥着越来越重要的作用。
由于淋洗条件的设置多依靠反复试验, 使得离子色谱的应用受到一定的限制[2], 而离子色谱保留模型可以很好地解决这一问题[3]。在单一淋洗液的情况下, 常用的保留模型有LSSM, EEPM和Dry-Lab等[3-4]。傅厚暾等[5]对矿物质离子的离子色谱分离进行计算机模拟; Karu等[6-7]利用等度和梯度保留模型, 对药物中的大分子有机酸在离子色谱中的保留行为做了一系列研究。但是, 尚未见到离子色谱保留模型在小分子有机酸分离中的应用。
本研究选择单一淋洗液, 首次将离子色谱保留模型应用于果汁中有机酸的分析, 在优化的等度模型下, 得到线性梯度模型所需的参数, 并依据线性梯度模型对保留时间的预测, 结合重复实验, 确立最优色谱条件。在该条件下, 对苹果汁中常见的7种有机酸进行检测, 并对3种不同的苹果汁进行分析。
1 实验部分 1.1 仪器、试剂与材料 1.1.1 实验材料与试剂“寇老西”牌苹果醋(248 mL装), “汇源”牌百分百苹果汁(200 mL装), “都乐”牌百分百果汁(250 mL装), 以上果汁均购于某大型超市。
奎宁酸、乳酸、苹果酸、酒石酸、富马酸、柠檬酸、抗坏血酸标样。其中, 奎宁酸(纯度为98%)、乳酸(纯度为85%)、苹果酸(纯度为99%)、富马酸(纯度为99%)均购自百灵威, 酒石酸、柠檬酸、抗坏血酸均为优级纯, 购自国家标准信息中心。50%氢氧化钠溶液购自Sigma。去离子水由Milli-Q超纯水系统产生, 电阻率为18.2 MΩ·cm。
1.1.2 实验仪器Dionex ICS 3000离子色谱仪配有AS11-HC分离柱和AG11-HC保护柱、ASRS-ULTRA 4-mm抑制器、电导检测器、Chromeleon (版本为6.5)色谱工作站、Pesticarb SPE小柱(200 mg/3 mL)(天津博纳艾杰尔科技有限公司)。
1.2 实验步骤 1.2.1 10种有机酸分离的等度和梯度实验方法本部分实验验证等度和梯度实验模型(详见2.1.1和2.1.2节)在离子色谱检测有机酸过程中的适用性, 进行10种有机酸分离的等度实验和梯度实验, 并与重复实验相结合, 确定摸索最优色谱条件的方法。综合考虑价态和疏水性等因素, 本实验选取果汁中相对含量较高的10种有机酸(奎宁酸、乙酸、乳酸、琥珀酸、苹果酸、酒石酸、草酸、富马酸、柠檬酸和抗坏血酸)。
1)配制淋洗液。
取50%的氢氧化钠液体5.2~5.3 mL, 加入储液罐, 并用去离子水定容至1 L, 即配制成浓度为100 mmol/L (误差小于2%)的淋洗液。溶液配好后, 将储液罐放入超声器中超声脱气30分钟, 之后充入氮气, 以排除淋洗液中的CO2等气体。
2)配制标准溶液。
用万分之一电子天平准确称取奎宁酸、乙酸、乳酸、琥珀酸、苹果酸、酒石酸、草酸、富马酸、抗坏血酸各0.1 g, 柠檬酸0.2 g, 用去离子水分别定容至100 mL容量瓶中, 即为1000 mg/L (柠檬酸为2000 mg/L)的母液。
用移液腔吸取0.1 mL母液至10 mL比色管中, 并用去离子水定容, 即为10 mg/L工作液。将工作液倒入自动进样器小瓶中(工作液的液面高度需超过小瓶高度的1/2, 以保证进样针能进样), 置于自动进样器中。稳定仪器。
3)编写淋洗条件程序、进样分析。
通过编写淋洗条件程序控制淋洗条件。每次开机后, 仪器需稳定半小时, 稳定后自动进样器进样, 每次进样前先走一针(25 μL)去离子水, 以稳定系统。进入编辑界面, 导出色谱图, 并记录保留时间(即出峰时间)和死时间(水负峰的出峰时间)。
1.2.2 确立最优色谱条件通过等度模型的建立, 可以确定各有机酸在不同淋洗液浓度下的保留时间。运用等度模型得到的数据建立不同酸的梯度模型, 可以估算不同有机酸在线性梯度条件下保留时间, 结合重复实验, 可得到分离有机酸的最优色谱条件。利用上述方法确定的最优色谱条件, 对苹果汁中常见的7种有机酸进行检测。
配制奎宁酸、乳酸、苹果酸、酒石酸、富马酸、抗坏血酸和柠檬酸7种有机酸的标准混合液及果汁样品溶液。将有机酸标准混合液各7个浓度梯度进行色谱分离, 以各种有机酸的峰高-浓度和峰面积-浓度分别制作标准曲线, 求出回归方程。在相同的色谱条件下, 将果汁样品色谱图与有机酸标准混合液的色谱图进行对照, 根据保留时间确定果汁样品中的各种有机酸, 并测定峰高或计算峰面积, 将有机酸峰高的响应值或峰面积的积分值代入各自的回归方程, 求出其浓度。得到淋洗液为NaOH溶液、流速为1.0 mL/min、进样量为25 μL情况下的最优离子色谱条件(梯度程序), 如表 1所示。
| t/min | [NaOH]/(mmol· L-1) |
| 0 | 5 |
| 4.0 | 5 |
| 22.0 | 34 |
| 34.0 | 34 |
| 34.1 | 5 |
| 40.0 | 5 |
2 结果与讨论 2.1 确立理论模型
保留模型可用于离子色谱法检测无机阴离子时的保留时间预测, 但未见应用于小分子有机酸的报道。本研究首次将离子色谱的等度保留模型和梯度保留模型成功地运用于检测果汁中的有机酸, 系统列出各保留模型的建立过程, 并对该过程中数据点的选取、公式的数学处理等问题进行详细的分析。
2.1.1 等度模型简介1) LSSM模型。
主要用于淋洗液为单一组分的情况(如以NaOH或Na2CO3为淋洗液时):
| $ \log {k_{\rm{i}}} = \frac{1}{y}\log {K_{{\rm{A}},{\rm{E}}}} + \frac{x}{y}\log \frac{Q}{y} + \log \frac{w}{{{V_{\rm{m}}}}} - \frac{x}{y}\log [{\rm{E}}_{\rm{m}}^{y - }], $ | (1) |
下角标i表示等度(isocratic)条件; k为容量因子, k=(tR-tM)/tM; tR为保留时间, tM为死时间; x为被测离子所带电荷数, y为淋洗液离子所带电荷数; [Emy-]为淋洗液中竞争离子Ey-(本文中为OH-)的浓度; KA, E为被测离子Ax-和Ey-的离子交换选择系数; Q为固定相的离子交换容量; w为固定相的质量; Vm为柱中淋洗液的体积。
对某种被测离子, 当淋洗液组成和固定相一定时, x, y, KA, E, Q, w和Vm均为固定值, 因此式(1)可简化为
| $ \log {{k}_{\text{i}}}={{c}_{\text{i}}}-\frac{x}{y}\text{l}og[E_{\text{m}}^{y-}], $ | (2) |
其中ci为常数。
2) EEPM模型。
EEPM模型是在LSSM模型的基础上得出的, 与LSSM模型的区别在于, LSSM模型中的x/y为理论值, EEPM模型中bi为实验值。
| $ \log {k_{\rm{i}}} = {a_{\rm{i}}}- {b_{\rm{i}}}\log [E_{\rm{m}}^{y-}], $ | (3) |
ai和bi均为常数, 可由实验获得。
3) Drylab模型。
Drylab是一个商业化的HPLC优化和模拟软件, 也可用于IC中单一淋洗液的情况。这种情况下的模型为
| $ \log {k_{\rm{i}}} = A + B\log [{\rm{O}}{{\rm{H}}^-}] + C{(\log [{\rm{O}}{{\rm{H}}^-}])^2}, $ | (4) |
其中A, B和C均为常数。
本实验对3种保留模型在10种小分子有机酸分析中的表现做出评价, 并选出最合适的模型用于后续实验的预测。
2.1.2 梯度模型介绍梯度模型均由LSSM模型衍生出来, 主要表达式为
| $ \log {k_{\rm{g}}} = \log {C_{\rm{g}}} - \frac{x}{{x + y}}\log R, $ | (5) |
式中, 下角标g表示梯度(gradient), k为容量因子, tg为被测物的保留时间, R为淋洗梯度的斜率(单位为mmol/L/min), Cg为与淋洗液组成和固定相相关的常数。
被测物保留时间相应可由式(6)得到:
| $ {t_{\rm{g}}} = \left( {\frac{1}{u}} \right)\left\langle {\left( {\frac{1}{B}} \right){{\left[{(z{b_{\rm{i}}} + 1)B{a_{\rm{i}}}{t_0}u + C_{\rm{s}}^{(z{b_{\rm{i}}} + 1)}} \right]}^{\frac{1}{{z{b_i}}}}} - \frac{{C_{\rm{s}}^{1/Z}}}{B}} \right\rangle + {t_0}, $ | (6) |
t0为死时间; u为淋洗液的流速; B为标准化的梯度斜率, B=R/u, 单位为mmol/L/mL; z为梯度形状的调整参数(线性梯度时z=1); Cs为梯度淋洗开始时淋洗液的浓度; ai和bi均为常数, 可由等度条件实验获得。
该梯度模型只能用于线性梯度淋洗的条件下, 对于混合梯度淋洗的情况无法直接进行预测。本实验对该模型在小分子有机酸预测中的应用进行研究和分析。
2.1.3 等度淋洗模型实验结果综合考虑价态和疏水性等因素, 本实验选取果汁中相对含量较高的10种有机酸(奎宁酸、乙酸、乳酸、琥珀酸、苹果酸、酒石酸、草酸、富马酸、柠檬酸和抗坏血酸)。以不同浓度(4~40 mmol/L)的NaOH为淋洗液, 在淋洗液流速为1 mmol/L/min时得到10种有机酸在不同淋洗液浓度[OH]下对应的保留时间tR。死时间为2.80分钟。以淋洗液浓度[OH]为横坐标, 保留时间tR为纵坐标时, 实验数据点呈抛物线分布。由于死时间t0与[OH]无关, 因此采用ki(ki=(tR-t0)/t0)表征时间量, 可以得到更好的拟合优度。以log[OH]为横坐标, logki为纵坐标, 对奎宁酸、乙酸、乳酸3种酸分别做对数拟合, 拟合优度分别为0.99936, 0.99948和0.99947。可知, 拟合优度较高, 可以很好地预测不同浓度淋洗液的保留时间。
以奎宁酸和乙酸为例, 讨论计算点的选取。在奎宁酸的LSSM模型下, 以不同的浓度为参考值(即0.00%所在位置), 求出log ki=a-log[OH]中的待定系数a, 用所得公式求出预测的保留时间tR, pred, 计算用来表征保留时间的预测值tR, pred与实验值tR, act比较结果的误差d (%):
| $ d = ({t_{R, pred}}-{t_{R, act}})/\left( {{t_{R, pred}} + {t_{R, act}}} \right) \times 2 \times 100\% $ |
从结果可知, 各系列点的分布趋势大致相同。当参考点取[OH]为18, 16和14 mmol/L时, 偏离0.00%较远; 取10和8 mmol/L时, 偏离0.00%较近。
在乙酸的LSSM模型下, 进行相同的数据处理。对各系列点分别求和后, 可得取[OH]为10 mmol/L时, 所得和最小, 即偏离0.00%最近。由d的定义可知, 对于乙酸, 取10 mmol/L的[OH]浓度为参考点时, 实验的误差最小。
对以上两种酸的分析可得, 取不同的[OH]浓度为参考点时, 保留时间预测值不同, 相应地, 会得到相同趋势的d分布, 但是d对0.00%偏差最小的值所在位置不同。为方便起见, 统一取6 mmol/L点作为参考点。
2.1.4 等度模型计算方法(以奎宁酸为例)1)根据实验数据, 计算调整保留时间(其中t0为死时间, 在本实验中为2.80 min), 容量因子ki (ki=(tR, act-t0)/ t0), 并对[OH]和ki取对数(见表 2)。
| [OH]/(mmol·L-1) | tR, act | tR, act-t0 | log[OH] | ki | log ki |
| 18 | 3.21 | 0.41 | 1.2553 | 0.1464 | -0.8344 |
| 16 | 3.28 | 0.48 | 1.2041 | 0.1714 | -0.7659 |
| 14 | 3.35 | 0.55 | 1.1461 | 0.1964 | -0.7068 |
| 10 | 3.62 | 0.82 | 1 | 0.2929 | -0.5333 |
| 8 | 3.85 | 1.05 | 0.9031 | 0.375 | -0.426 |
| 6 | 4.25 | 1.45 | 0.7782 | 0.5179 | -0.2858 |
| 4 | 5.02 | 2.22 | 0.6021 | 0.7929 | -0.1008 |
2)以log[OH]为横坐标, logki为纵坐标, 对数据点进行线性拟合。可得到拟合方程y=0.8404-1.12373x, 拟合优度R2为0.99936。
3)以[OH]为6 mmol/L时的数据为计算点, 求出LSSM模型的表达式为
| $ \log {k_i} = 0.5826 - 1.1159\log \left[ {{\rm{OH}}} \right], $ |
根据此表达式求出不同浓度[OH]下, 保留时间的预测值(tR, pred), 并与实验值(tR, act)进行比较。以[OH]为6 mmol/L和10 mmol/L的数据为计算点, 求出EEPM模型的表达式为
| $ {\rm{log}}{k_i} = {\rm{ }}0.5826 - 1.1159{\rm{log}}\left[ {{\rm{OH}}} \right], $ |
并根据此表达式求出不同浓度[OH]下保留时间的预测值(tR, pred), 与实验值(tR, act)进行比较。以[OH]为6, 10和16 mmol/L的数据为计算点, 求出DryLab模型的表达式为
| $ {\rm{log}}{k_i} = 0.5392 - 1.0167{\rm{log}}\left[ {{\rm{OH}}} \right] - 0.0558{\left( {{\rm{log}}\left[ {{\rm{OH}}} \right]} \right)^2}, $ |
根据此表达式求出不同浓度[OH]下, 保留时间的预测值(tR, pred), 并与实验值(tR, act)进行比较。
最终结果见表 3。
| 有机酸 | LSSM | EEPM | DryLab | |||||
| dav/% | Eav/% | dav/% | Eav/% | dav/% | Eav/% | |||
| 奎宁酸 | 1.09 | 1.53 | 0.34 | 0.48 | 0.20 | 0.47 | ||
| 乙酸 | 1.12 | 1.40 | 0.44 | 0.62 | 0.04 | 0.16 | ||
| 乳酸 | 1.01 | 1.41 | 0.35 | 0.49 | -0.03 | 0.41 | ||
| 琥珀酸 | 1.11 | 1.45 | -0.10 | 0.53 | 0.13 | 0.57 | ||
| 苹果酸 | 1.21 | 1.68 | -0.14 | 0.35 | 0.09 | 0.32 | ||
| 酒石酸 | 1.53 | 2.00 | -0.19 | 0.56 | 0.16 | 0.67 | ||
| 草酸 | 2.04 | 2.54 | -0.21 | 0.72 | -0.05 | 0.38 | ||
| 富马酸 | 1.63 | 2.02 | -0.34 | 0.88 | 0.21 | 0.84 | ||
| 抗坏血酸 | -6.25 | 9.40 | -0.13 | 0.18 | 0.04 | 0.24 | ||
| 柠檬酸 | 4.13 | 5.59 | 0.17 | 0.31 | 0.04 | 0.27 | ||
| 说明:误差d=(tR, pred-tR, act)/(tR, pred+ tR, act)×2×100%, 百分比误差E=(|tR, pred-tR, act |/tR, pred×100%), tR, pred为保留时间的预测值, tR, act为实验值。 | ||||||||
通过考察LSSM, EEPM和DryLab 3种等度保留模型实验值与预测值之间的偏差, 可知DryLab的准确性最好, EEPM的准确性比DryLab稍差, LSSM的准确性最差。但是, 要得到模型中的参数, DryLab需要的实验次数最多, EEPM次之, LSSM最少。因此, 综合考虑实验规模和模型的准确性, 对果汁中10种常见有机酸进行预测时采用EEPM。该结论与Madden等[4]利用这3种模型在AS11柱中检测21种无机阴离子时所得的结论一致。在OH-做淋洗因子时, 小分子有机酸与无机阴离子在离子交换柱上的保留特性相似, 因此该结论可推广至其他样品中的小分子有机酸和无机阴离子的同时检测。
2.1.5 梯度淋洗模型实验结果1)色谱图及有机酸的选取。
由于梯度模型只适合于线性梯度下的状况, 因此接下来选取一个线性条件下有机酸的色谱图, 以其中苹果酸、酒石酸、抗坏血酸和富马酸在梯度淋洗时的预测保留时间和实验保留时间的对比来说明该保留模型在本实验中的有效性, 并说明该模型的计算方法。
图 1为4种有机酸在梯度淋洗下的色谱图。色谱条件:流速1 mL/min, 抑制电流50 mA。梯度条件: NaOH浓度在0分钟时为12.0 mmol/L, 在25分钟时为23.6 mmol/L。
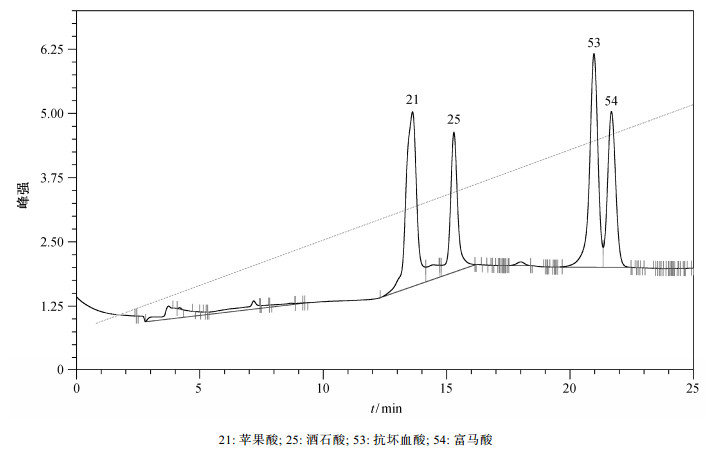
|
| 图 1. 4 种有机酸梯度淋洗下的色谱图 Figure 1. Ion Chromatography of malic, tartaric, ascorbic and fumaric organic acids in gradient elution |
2)梯度模型的计算方法(以苹果酸为例)。
由色谱图和梯度程序可知, 死时间为2.80分钟, 淋洗液的流速为1.0 mL/min, 淋洗液初始浓度为12.0 mmol/L, 最终浓度为23.6 mmol/L。根据梯度模型的计算方法可知:淋洗液的流速u=1.0 mL/ min, 淋洗梯度的斜率R=0.48 mmol/L/min, 标准化的梯度斜率B=0.48 mmol/L/mL, 梯度形状的调整参数z=1。
由等度部分数据处理可知, 在等度条件下(流速为1.0 mL/min时), 苹果酸的EEPM模型可计算的保留时间为
| $ \begin{array}{l} {t_{R, pred}} = 1 \times \{ \left( {1/0.48} \right) \times [\left( {2.1942 + 1} \right) \times 0.48 \times ({10^{3.1573}}) \times \\ \;\;\;\;\;\;\;\;\;\;\;2.80 \times 1.0 + {12^{\left( {2.1942 + 1} \right)}}{]^{\left( {1/3.1942} \right)}} -12/0.48\} + \\ \;\;\;\;\;\;\;\;\;\;\;2.80\\ \;\;\;\;\;\;\;\;\;\;\; = 13.7913{\rm{ }}\left( {min} \right), \end{array} $ |
即在图 1所示的梯度条件下, 利用线性梯度模型, 计算出苹果酸的保留时间为13.7913分钟。
用上述方法同样处理酒石酸、富马酸和抗坏血酸, 所得梯度模型误差数据如表 4所示。
| 有机酸 | tR, pred/min | tR, act/min | E/% | Eav/% |
| 苹果酸 | 13.79 | 13.62 | 1.23 | 1.28 |
| 酒石酸 | 15.52 | 15.3 | 1.42 | |
| 抗坏血酸 | 20.74 | 20.97 | 1.11 | |
| 富马酸 | 21.98 | 21.68 | 1.36 |
由百分比误差E可知, 该梯度模型对有机酸在色谱柱AS11-HC中进行梯度淋洗时的保留时间进行预测时, 有良好的表现。因此, 可根据预测的保留时间进行梯度的设计和优化, 能大大减少实验次数、缩短实验时间。
对于等度淋洗和线性梯度淋洗, 可以直接运用保留模型对有机酸离子的保留行为进行预测; 对于非线性梯度淋洗, 采用模型与反复实验结合的方法摸索最优色谱条件, 可以减少实验次数。该研究可以简化离子色谱检测有机酸的实验过程, 并为计算机模拟小分子有机酸在离子色谱柱中的保留行为提供理论依据。
2.2 最优色谱条件将有机酸标准混合液各浓度梯度进行色谱分离, 以各种有机酸的峰高-浓度和峰面积-浓度分别制作标准曲线, 求出回归方程。在相同的色谱条件下, 将样品色谱图与有机酸标准混合液的色谱图进行对照, 根据保留时间确定样品中的各种有机酸, 并测定峰高或计算峰面积, 将有机酸峰高的响应值或峰面积的积分值代入各自的回归方程, 求出其浓度。
2.2.1 制作标准曲线1)峰高-浓度的标准曲线。
以乳酸为例, 从色谱工作站中, 可以读出不同浓度(0.1, 1, 10, 20, 30, 40 mg/L)条件下乳酸峰形图各峰高的响应值, 分别为0.0688, 0.3128, 2.8489, 5.4103, 7.8501, 10.7889 μS。以乳酸溶液的浓度(mg/L)为x, 峰高的响应值(μS)为y, 做线性拟合, 可求出回归方程和相关系数。对不同浓度的其他各有机酸标准溶液分别进样, 进行色谱分离, 以峰高对浓度作图, 求出回归方程和相关系数(见表 5)。由回归分析可知, 在进样范围内, 各酸的线性关系良好。
| 有机酸 | 回归方程 | 相关系数 |
| 奎宁酸 | y=0.1745x-0.0231 | 0.9991 |
| 乳酸 | y=0.2654x+0.0739 | 0.9993 |
| 苹果酸 | y=0.2570x+0.0877 | 0.999 |
| 酒石酸 | y=0.2492x-0.0373 | 0.9967 |
| 抗坏血酸 | y=0.1643x+0.0110 | 0.9987 |
| 富马酸 | y=0.1411x-0.0150 | 0.9993 |
| 柠檬酸 | y=0.0630x+0.0599 | 0.9953 |
2)峰面积-浓度的标准曲线。
与步骤1相类似, 得到峰面积-浓度的标准曲线, 回归方程和相关系数见表 6。由表 6可知, 在进样范围内, 除酒石酸外, 其他酸的线性关系良好。
| 有机酸 | 回归方程 | 相关系数 |
| 奎宁酸 | y=0.0314x-0.0430 | 0.9902 |
| 乳酸 | y=0.0680x+0.0109 | 0.9959 |
| 苹果酸 | y=0.0499x-0.0070 | 0.9980 |
| 酒石酸 | y=0.0489x+0.0561 | 0.9586 |
| 抗坏血酸 | y=0.0375x+0.0211 | 0.9951 |
| 富马酸 | y=0.0329x-0.0096 | 0.9958 |
| 柠檬酸 | y=0.0375x-0.0595 | 0.9912 |
2.2.2 对果汁中7种有机酸的检验
1)保留时间的重复性。
用确定的色谱条件对有机酸标准混合溶液进样, 进行5次重复试验, 记录其保留时间, 进行统计分析, 求出平均值、标准差和变异系数CV结果见表 7。可见, 7种有机酸保留时间的标准差在0.007~0.115之间, 变异系数(CV)在0.06%~0.32%之间, 表明在确定的色谱条件下, 有机酸的保留时间基本恒定, 本方法具有很好的重复性。
| 有机酸 | 平均值/min | 标准差 | CV/% |
| 奎宁酸 | 4.653 | 0.007 | 0.16 |
| 乳酸 | 5.187 | 0.019 | 0.36 |
| 苹果酸 | 18.42 | 0.012 | 0.07 |
| 酒石酸 | 19.411 | 0.013 | 0.06 |
| 抗坏血酸 | 22.529 | 0.017 | 0.07 |
| 富马酸 | 22.939 | 0.014 | 0.06 |
| 柠檬酸 | 35.588 | 0.115 | 0.32 |
2)样品的重复性。
为考察方法的重复性, 对同一试样(都乐100%纯果汁)进行3次平行测定, 记录每种酸的峰高, 利用峰高-浓度回归方程计算每种酸的浓度, 并进行统计分析, 求出平均值、标准差和变异系数CV, 分析结果见表 8。由表 8可知, 该试样中检测出5种有机酸, 这5种有机酸含量的标准差在0.02~0.09之间, 除富马酸外, 变异系数CV在0.14%~0.79%之间。由于富马酸的含量微小, 影响了该有机酸分析结果的精密度。该实验表明, 除富马酸外, 分析结果的重复性好, 精密度高。
| 有机酸 | 平均值/(mg·L-1) | 标准差 | CV/% |
| 奎宁酸 | 16.30753 | 0.022369 | 0.14 |
| 乳酸 | 19.77437 | 0.050121 | 0.25 |
| 苹果酸 | 169.9993 | 0.899335 | 0.53 |
| 酒石酸 | - | - | - |
| 抗坏血酸 | 1.51586 | 0.011995 | 0.79 |
| 富马酸 | 0.09128 | 0.035626 | 39.02 |
| 柠檬酸 | - | - | - |
| 说明: -表示未检出。 | |||
3)回收率实验。
取汇源100%苹果汁样品两份, 其中一份作为本底, 另外一份添加一定量的有机酸标准混合液后测定各组分的含量, 考察测定方法的回收率。
取100 mg/L的混合酸标样0.3 mL置于比色管中, 定容至10 mL, 即成为3 mg/L的混标, 取1 mL苹果汁原汁放入其中混合; 另一个比色管中放入10 mL去离子水, 取1 mL苹果汁原汁放入其中混合, 作为本底。每份样品进行3次平行测定, 考察测定方法的回收率。结果如表 9所示, 所有有机酸的回收率都在96%以上, 比较理想。说明该方法的分析结果重现性好, 精密度高, 在该色谱条件下对果汁中的有机酸含量进行定量分析结果可靠。
| 有机酸 | 本底值/ (mg · L-1) |
添加值/ (mg · L-1) |
平均测定值/ (mg · L-1) |
回收率/% |
| 奎宁酸 | 20.6514 | 1 | 21.6184 | 96.71 |
| 乳酸 | 3.0617 | 1 | 4.0653 | 100.36 |
| 苹果酸 | 153.35 | 1 | 154.3227 | 97.27 |
| 酒石酸 | 0 | 1 | 1.0058 | 100.58 |
| 抗坏血酸 | 0.065 | 1 | 1.0437 | 97.87 |
| 富马酸 | 0 | 1 | 1.0164 | 101.64 |
| 柠檬酸 | 3.1737 | 2 | 5.2197 | 102.3 |
4)对果汁的定量分析。
取“寇老西”牌苹果醋(248 mL装), “汇源”牌百分百苹果汁(200 mL装), “都乐”百分百果汁(250 mL装) 3种苹果汁进行有机酸的测定。结果见表 10。从表 10可知, 利用本文提出的优化模型和分析果汁标准样内7种有机酸的最优色谱条件, 可以同时检测到果汁中的4~5种有机酸。除苹果汁外, 可推广至其他果汁的有机酸分析。
| mg/L | |||
| 有机酸 | 都乐 | 寇老西 | 汇源 |
| 奎宁酸 | 16.30753 | 0.45443 | 22.71652 |
| 乳酸 | 19.77437 | - | 3.37 |
| 苹果酸 | 169.9993 | 24.39 | 168.69 |
| 酒石酸 | - | - | - |
| 抗坏血酸 | 1.51586 | 0.50976 | 0.71303 |
| 富马酸 | 0.09128 | - | - |
| 柠檬酸 | - | 2.72301 | 3.49109 |
| 注: -表示未检出。 | |||
2.2.3 对果汁样品的前处理
先将Pesticarb PC2003 SPE小柱预先用去离子水润洗5分钟, 然后用甲醇活化15分钟, 最后用去离子水以1 mL/min的速度冲洗5分钟, 将甲醇冲洗干净。
量取果汁样品约20 mL置于比色管中。用注射器取2 mL样品注入SPE小柱中, 控制流速为1 mL/min, 使样品缓慢流过小柱, 重复该过程, 收集洗脱液于比色管中备用(前3~4 mL抛弃)。将洗脱液稀释10倍供测定。处理前后的果汁颜色差异很大, 说明色素成分去除比较彻底, 可以进行离子色谱检测。
3 结论本研究首次将离子色谱的等度保留模型和梯度保留模型成功地运用于检测果汁中的有机酸。对于等度淋洗和线性梯度淋洗, 可以直接运用保留模型对有机酸离子的保留行为进行预测; 对于非线性梯度淋洗, 采用模型与反复实验结合的方法摸索最优色谱条件, 可以减少实验次数。本研究可以简化离子色谱检测有机酸的实验过程, 并为计算机模拟小分子有机酸在离子色谱柱中的保留行为提供理论依据。本研究只对苹果汁进行了分析, 可推广至其他果汁的有机酸分析。
| [1] | Saccani G, Gherardi S, Trifirò A, et al. Use of ion chromatography for the measurement of organic acids in fruit juices. J Chromatogr A , 1995, 706 : 395–403 DOI:10.1016/0021-9673(95)00206-3 . |
| [2] | Zakaria P, Dicinoski G, Ng B, et al. Application of retention modelling to the simulation of separation of organic anions in suppressed ion chromatography. J Chromatogr A , 2009, 1216 (38) : 6600–6610 DOI:10.1016/j.chroma.2009.07.051 . |
| [3] | Madden J, Haddad P. Critical comparison of retention models for the optimisation of the separation of anions in ion chromatography: Ⅱ. suppressed anion chromatography using carbonate eluents. J Chroma-togr A , 1999, 850 (2) : 29–41 . |
| [4] | Madden J, Avdalovic N, Jackson P, et al. Critical comparison of retention models for optimisation of the separation of anions in ion chromatography: Ⅲ. anion chromatography using hydroxide eluents on a Dionex AS11 stationary phase. J Chromatogr A , 1999, 837 (2) : 65–74 . |
| [5] | 傅厚暾, 赵俐敏, 陈芳. 离子色谱线性梯度淋洗分离阴离子的计算机模拟. 分析化学 , 2006, 34 (8) : 1101–1105. |
| [6] | Karu N, Hutchinson J, Dicinoski G, et al. Deter-mination of pharmaceutically related compounds by suppressed ion chromatography: Ⅳ. interfacing ion chromatography with universal detectors.. J Chroma-togr A , 2012, 1253 : 44–51 DOI:10.1016/j.chroma.2012.06.101 . |
| [7] | Karu N, Dicinoski G W, Hanna-Brown M, et al. Determination of pharmaceutically related compounds by suppressed ion chromatography: Ⅱ. interactions of analytes with the suppressor. J Chromatogr A, , 2012, 1224 : 35–42 DOI:10.1016/j.chroma.2011.12.022 . |
 2016, Vol. 52
2016, Vol. 52




