北京大学学报自然科学版   2016, Vol. 52 Issue(4): 741-755

文章信息

阎绍泽, 向吴维凯, 黄铁球
YAN Shaoze, XIANG Wuweikai, HUANG Tieqiu
计及间隙的运动副和机械系统动力学的研究进展
Advances in Modeling of Clearance Joints and Dynamics of Mechanical Systems with Clearances
北京大学学报(自然科学版), 2016, 52(4): 741-755
Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 741-755

文章历史

收稿日期: 2016-06-04
修回日期: 2016-07-06
网络出版日期: 2016-07-12
 Abstract              PDF               Figures               Tables
引用本文
阎绍泽, 向吴维凯, 黄铁球. 计及间隙的运动副和机械系统动力学的研究进展[J]. 北京大学学报(自然科学版), 2016, 52(4): 741-755.
YAN Shaoze, XIANG Wuweikai, HUANG Tieqiu. Advances in Modeling of Clearance Joints and Dynamics of Mechanical Systems with Clearances[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 741-755.
计及间隙的运动副和机械系统动力学的研究进展
阎绍泽1, 向吴维凯1, 黄铁球2     
1. 摩擦学国家重点实验室, 清华大学机械工程系, 北京 100084;
2. 北京交通大学机械与电子控制工程学院, 北京 100044
收稿日期：2016-06-04；修回日期：2016-07-06；网络出版日期：2016-07-12
基金项目：国家自然科学基金(11272171)和高等学校博士学科点专项科研基金(20120002110070)资助
通信作者： 阎绍泽, E-mail: yansz@tsinghua.edu.cn
摘要： 基于近年来计及间隙影响的运动副建模以及含间隙机械系统动力学的研究, 综述间隙运动副连续接触模型、经典碰撞模型、连续接触力模型以及旋转副三维间隙模型等的研究进展, 介绍间隙模型在机械系统动力学非线性特性分析、性能评价与可靠性评估等方面的应用情况, 详细探讨考虑黏滞-滑动过程和接触表面形貌的间隙建模、共形接触建模、不确定参数的含间隙系统动力学分析、运动精度评估以及运动副间隙设计等未来应重点研究的若干关键技术问题。
关键词： 间隙运动副     碰撞     摩擦     动力学     性能评价    
Advances in Modeling of Clearance Joints and Dynamics of Mechanical Systems with Clearances
YAN Shaoze1, XIANG Wuweikai1, HUANG Tieqiu2     
1. State Key Laboratory of Tribology, Department of Mechanical Engineering, Tsinghua University, Beijing 100084;
2. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044
Corresponding author: YAN Shaoze, E-mail: yansz@tsinghua.edu.cn
Abstract: Recent developments in modeling of clearance joints and dynamics of mechanical systems with clearances are reviewed. Different modeling approaches for clearance joints are summarized firstly, which comprise the massless link approach, the non-smooth dynamics approach, the contact force approach and the 3D revolute joint approach. Then, applications of these approaches in the study of the nonlinear dynamics, and performance and reliability evaluation of the mechanical systems with clearances are systematically reviewed. Finally, the key problems and priorities which need to be further studied are proposed, including the modeling of clearace joints considering stick-slip phenomenon, contact surface profile and conformal contact condition, the dynamic analysis and kinematic accuracy evaluation of mechanical systems with both clearances and uncertainties, and the design for clearance joints.
Key words: clearance joint     impact     friction     dynamics     performance evaluation    

机器和机构是典型的机械多体系统, 运动副间隙是影响机械多体系统动力学特性的主要因素之一[1-3]。运动副间隙的产生因素是多方面的, 如运动副配合间隙、制造加工与装配误差、运动副构件相互摩擦与磨损而导致的间隙等。间隙的存在增加了机械系统的自由度, 从而降低了系统的运动精度。间隙运动副中的各构件间相互碰撞、分离及摩擦, 使得系统具有典型的非线性特性(如碰撞振动与干摩擦黏滑振动等), 造成速度波动, 运动副反力增加, 并引发机械振动和噪音等一系列问题, 导致系统性能下降。间隙也会加速运动副的磨损进程, 降低机构或机器的可靠性及使用寿命。

虽然机械多体系统动力学经历了40余年的发展, 但在分析与预测含间隙机械系统动力学特性时仍显不足。目前, 含间隙机械多体系统动力学理论研究已成为力学、机械工程、航空航天工程、车辆工程等领域的研究热点之一。由于间隙运动副中构件间存在频繁的碰撞与分离过程, 导致含间隙机械多体系统的约束条件或自由度不断改变, 因此, 含间隙机械多体系统是一个典型的变拓扑结构系统。具有变拓扑结构特性的含间隙系统建模更为复杂。

建立计及间隙影响的运动副模型, 需要考虑间隙运动副的变拓扑结构特性与接触模式、碰撞特性、接触变形与接触力的关系、阻尼、摩擦、表面粗糙度、构件的加工误差和系统装配误差、工作环境(如温度)等因素。涉及几何学与变拓扑结构理论、表面工程与摩擦学、碰撞理论与接触力学、固体力学、机械设计、制造工艺等多种学科。从计及间隙影响的机械多体系统动力学整体看, 需要考虑将间隙模型嵌入系统动力学方程的方法、柔性结构离散方法及数值计算的稳定性、精度与效率、非线性动力学特性分析等问题。含间隙机械系统动力学研究最终是分析机械装备的动力学特性和稳定性, 为系统结构参数设计服务, 使得机械系统在许可的精度下性能稳定、无故障长寿命运行。

运动副间隙影响着机械装备的性能和使用寿命, 如在航天工程中, 由于运动副间隙设计不完善而导致飞行故障的案例屡见不鲜。美国的哈勃太空望远镜由于热循环引起太阳能帆板运动副的“卡死-滑动”周期性运动的故障, 导致对定点的扰动, 得到的图像模糊不清, 美国国家航空航天局(NASA)为此更换了太阳翼的连接结构[4-5]。我国发射的东三通信卫星, 由于连接非线性的存在, 在轨运行时展开后的太阳翼出现颤振和频率漂移[6-7]。在轨遥测数据表明, 航天器在轨运行的特征频率比地面理论计算及试验值明显低[6], 即产生运行的频率漂移。除去多体系统刚体运动, 仅考察带有间隙的固定连接引发的动力学问题, 如我国某型号卫星在振动试验中也发现频率漂移现象, 分析表明, 连接结构非线性是产生此现象的原因之一[8-10]。美国NASA[11-12]和日本航天研究机构[13]分别对卡西尼号卫星和红外空间天文卫星(ASTRO-F)的频率漂移现象进行研究, 结果表明, 间隙是造成频率漂移的直接原因。若航天器上可展开附件(如太阳电池阵)由于频率漂移导致与卫星姿态控制系统产生频率耦合, 将会产生严重后果[7]。因此, 研究间隙建模及含间隙系统动力学, 对发展高端装备和大型精密卫星等航天器具有重要意义。

1 间隙运动副连续接触模型

早期对含间隙机构建模的目的主要是对机构运动精度进行分析, 其研究隶属运动学范畴。20世纪70年代, Earles等[14]提出间隙运动副的连续接触模型, 假定间隙碰撞过程极为短暂, 且在系统运动过程中构件主要处于接触状态, 因此采用无质量杆描述间隙。连续接触模型将间隙视为无质量的刚性杆即间隙杆, 将原来的含间隙机构转化为多杆无间隙机构[15]。为了使连续接触模型能够描述构件分离, 一些学者对该类模型进行改进, 将无质量杆角度的突变作为运动副构件分离的标志, Earles等[16]提出间隙副元素的分离判别式。由于连续接触模型没有考虑运动副的刚度、阻尼、摩擦系数和恢复系数, 所以难以描述运动副元素间的动力学特性以及碰撞对系统动力学的影响, 但连续接触模型建模方法简单, 易于计算, 可用于机器初始设计时的误差和精度分析。

2 间隙运动副经典碰撞模型

间隙运动副经典碰撞模型是一种基于单边约束的碰撞模型, 该模型将间隙副元素的运动分为接触、碰撞与分离3种状态[17]。假设碰撞物体表面为刚性, 两构件碰撞接触以单边约束条件表征, 即碰撞体不能相互刺穿, 碰撞过程中系统位形不发生改变, 在碰撞前后碰撞体有速度阶跃和能量损失, 可采用动量定理和恢复系数计算碰撞分离后的动量分配[18]。这种间隙模型是一种刚性碰撞模型, 在碰撞前后碰撞体速度不连续, 且假定碰撞瞬时完成, 略去碰撞过程细节, 因而不能预示含间隙运动副中碰撞力变化与接触变形过程, 只能采用反作用力冲量衡量冲击造成的严重程度。该模型适合于接触刚度很大的机械系统全局动力学特性分析问题。

恢复系数代表碰撞过程中能量耗散的程度, 其数值取决于材料性质和碰撞速度等因素的综合影响。确定恢复系数是间隙运动副经典碰撞模型构建的关键。从碰撞前后的速度、冲量、能量损失等出发, 对恢复系数有不同的定义形式[19-20]。

Newton等[21]利用两物体碰撞前后的法向速度比给出恢复系数的定义, 通过该系数将碰撞前后系统的运动学状态建立联系。研究发现, 采用单边约束的碰撞模型处理考虑Coulomb干摩擦的碰撞问题时, 可能引发系统动力学方程不协调。Kane等[22]求解复合摆与固定表面碰撞问题时, 发现在某些参数条件下系统动能增加, 称为Kane动力学之谜。为解决考虑干摩擦的碰撞问题, Brach[23]利用切向冲量比描述碰撞体的切向运动, 但是该系数具有不稳定性。Smith[24]利用切向运动的平均速度定义冲量比, 采用纯代数方程求解考虑干摩擦的碰撞问题。Keller[25]指出, 导致碰撞过程能量增加的原因在于, 摩擦引起的切向冲量依赖于切向运动模式。因此, 在分析考虑摩擦的碰撞过程时, 需要放弃碰撞瞬时性假设, 分析碰撞过程中切向微运动规律。Poisson利用碰撞过程中压缩阶段与恢复阶段的法向冲量比来定义恢复系数, 与Newton定义不同, 该系数刻画碰撞体动力学状态之间的关系[19], 但在某些特殊的情况下, 利用其计算考虑摩擦的碰撞过程时, 仍然会出现能量增加的现象。Stronge[20]提出基于碰撞过程中能量变化定义的能量恢复系数, 并利用该系数求解考虑摩擦的碰撞过程。

3种恢复系数在考虑单向滑动的碰撞过程中能给出相近的响应结果, 当碰撞构件发生黏滞与可逆滑动过程时, 能量恢复系数对能量耗散的刻画更为合理[26]。含摩擦的多体系统可能存在Painlevé疑难奇异性, 即多体系统的后续运动可能存在无解(非协调状态)或者多解(不确定状态), Zhao等[27-28]对Painlevé疑难展开理论与实验分析, 通过线性互补方法给定系统奇异条件, 利用Stronge恢复系数刻画碰撞过程, 证明了Painlevé系统中切向冲击的存在, 以及多体系统处于非协调状态时其后续运动的切向冲击特征。应用上述碰撞理论的研究, 可进一步完善间隙副经典碰撞模型。

3 间隙运动副连续接触力模型

间隙运动副连续接触力模型是一种基于力约束的碰撞模型。该模型将含间隙运动副元素的运动状态分为自由运动状态与接触变形状态, 当两构件接触时, 将构件之间的接触变形和接触力视为从零开始连续变化。该模型将接触体的接触区域局部柔化, 构建碰撞体接触面间刺穿深度与碰撞力的函数关系, 同时表征能量耗散的阻尼力和切向摩擦力。该间隙模型可以计及碰撞体间的法向接触力、切向接触力以及阻力矩, 考虑变形位移和变形速度的综合作用, 不仅能够求解系统运动过程中间隙铰轴销与孔体的碰撞力, 还能给出碰撞力与碰撞加速度的显式表达式, 并且易于集成到多体系统的动力学方程中。

旋转副是机械多体系统中最为常见的运动副, 其间隙连续接触力模型可分为平面间隙模型和三维间隙模型。旋转副平面间隙模型是基于组成运动副销轴和孔体轴线平行的假设, 而实际机械系统中运动副不但存在径向间隙, 还存在轴向间隙, 所以会出现销轴和孔体的轴线不平行的情况。为此, 需要建立旋转副的三维间隙。对于轴向间隙相对较小的场合, 采用平面间隙模型可以满足一定的精度要求。间隙运动副连续接触力模型的关键是描述运动副中的副反力与局部变形量的关系, 因此, 下面针对平面间隙模型中的法向接触力、法向阻尼、切向摩擦以及旋转运动副的三维间隙建模等方面的研究进展进行分析。

3.1 法向接触力

法向接触力包括与变形位移相关的等效弹簧力和与变形速度相关的等效阻尼力。对法向接触力的研究起始于不考虑等效阻尼力的Hertz接触模型, 在考虑材料属性与几何特征的基础上, 构造碰撞体接触面间刺穿深度与碰撞力的函数关系[29]。表 1给出几种法向接触力与变形关系式, 其中简化的接触力模型是一种常用的法向接触力模型[18, 30]:

$ {F_{\rm{N}}}{\rm{ = }}K{\delta ^n}, $ (1)

式中, FN为法向接触力, K为接触刚度系数, δ为刺穿深度, n为幂指数(n≥1)。

表 1. 法向接触力与变形关系式 Table 1. Elastic contact force model
接触力模型 表达式 符号含义 适用范围
简化的接触力模型[30] FN=Kδn FN
K
δ		 低速碰撞
Goldsmith接触力模型[31] $ {F_{\rm{N}}}{\rm{ = }}{F_{\max }}{\left( {\frac{{\delta-{\delta _{\rm{p}}}}}{{{\delta _{\max }}-{\delta _{\rm{p}}}}}} \right)^n} $ δp
δmax		 软接触材料, 高速碰撞
ESDU-78035接触力模型[32] $ \delta = {F_{\rm{N}}}\left( {\frac{{{\sigma _i} + {\sigma _j}}}{L}} \right)\left[{\ln \left( {\frac{{4L\left( {{R_i}-{R_j}} \right)}}{{{F_{\rm{N}}}\left( {{\sigma _i} + {\sigma _j}} \right)}}} \right) + 1} \right], \sigma = \frac{{1 -{\nu ^2}}}{E} $ L:圆柱体长度,
v:泊松比,
E:弹性模量		 圆柱平行接触
Liu接触力模型[33] $ {F_{\rm{N}}}{\rm{ = }}\frac{{{\rm{\pi }}{E^*}L\delta }}{2}{\left( {\frac{\delta }{{2\left( {c + \delta } \right)}}} \right)^{1/2}} $ E*:等效弹性模量,
c:半径间隙		 共形接触
表选项

由式(1)表征的法向接触刚度为

$ {K_{\rm{v}}}{\rm{ = }}\frac{{{\mathop{\rm d}\nolimits} {F_{\rm{N}}}}}{{{\mathop{\rm d}\nolimits} \delta }} = Kn{\delta ^{n-1}}。 $ (2)

由式(2)可以看出, 随着法向变形(刺穿深度)的增加, 接触刚度逐渐增加, 这与运动副间隙接触力定性分析一致。因此, 对于刺穿深度较小的场合, 可以采用该简化模型描述法向接触力。

ESDU-78035摩擦学数据库[32]提供了接触力和刺穿深度的多种隐式表达式, 分别适用于圆形区域和矩形区域接触。由于基于Hertz接触的法向接触力模型假设接触区域宽度远小于接触点的曲率半径, 因此, 在求解非共形接触问题时具有较高的精度, 但在求解共形接触问题时, 计算的接触刚度偏小[34]。

表 1给出的法向接触力模型仅描述了碰撞过程中材料的弹性变形, 并未考虑能量的耗散。koshy等[35]采用不同的接触力模型对含间隙曲柄滑块机构的动力学响应进行计算, 计算结果与实验结果对比发现, 只考虑材料弹性变形的接触力模型虽然结构简单, 但对碰撞过程的刻画不准确。运动副元素间碰撞过程的刻画需要考虑能量耗散问题, 否则将导致该方法分析结果失真[36]。事实上, 间隙运动副在接触碰撞时存在阻尼力, 即在碰撞过程中接触力与刺穿深度间存在迟滞现象, 阻尼力的确定需要探讨间隙运动副的能量耗散机制, 表 2给出几种考虑能量耗散的法向接触力模型。

表 2. 考虑能量耗散的法向接触力模型 Table 2. Contact force model with hysteresis damping
接触力模型 表达式 符号含义 适用范围
Kelvin-Voigt线性弹簧阻尼模型[31] $ {F_{\rm{N}}}{\rm{ = }}K\delta + D\dot \delta $ D:阻尼系数,
$ \dot \delta $:刺穿速度		 材料阻尼小的黏弹性接触
Hunt-Crossley接触力模型[30] $ {F_{\rm{N}}} = K{\delta ^n}\left[{1 + \frac{{3(1-c_e^{})\dot \delta }}{{2{{\dot \delta }^{(-)}}}}} \right] $ ce:恢复系数,
$ \dot \delta $(-)初始碰撞速度		 高恢复系数, 正碰撞, 不考虑摩擦
Lee-Wang接触力模型[37] $ {F_{\rm{N}}} = K{\delta ^n}\left[{1 + \frac{{3(1-c_e^{})\dot \delta }}{{4{{\dot \delta }^{(-)}}}}} \right] $ 满足碰撞边界条件的间歇机构接触
Lankarani-Nikravesh接触力模型[38] $ {F_{\mathop{\rm N}\nolimits} } = K{\delta ^n}\left[{1 + \frac{{3(1-c_e^2)\dot \delta }}{{4{{\dot \delta }^{(-)}}}}} \right] $ 高恢复系数, 碰撞能量耗散小
Flores接触力模型[39] $ {F_{\mathop{\rm N}\nolimits} } = K{\delta ^n}\left[{1 + \frac{{8(1-c_e^{})\dot \delta }}{{5c_e^{}{{\dot \delta }^{(-)}}}}} \right] $ 适用完全弹性或完全塑性
Gonthier接触力模型[40] $ {F_{\mathop{\rm N}\nolimits} } = K{\delta ^n}\left[{1 + \frac{{(1-c_e^2)\dot \delta }}{{c_e^{}{{\dot \delta }^{(-)}}}}} \right] $ 圆柱平行接触
表选项

为了考虑碰撞过程中能量耗散, Goldsmith[31]给出线性弹簧与线性阻尼模型(Kelvin-Voigt模型)来描述碰撞过程, Dubowsky等[41-42]采用线性弹簧阻尼模型模拟碰撞过程, 提出碰撞铰模型。Rogers等[43]采用线性弹簧阻尼模型, 研究含间隙平面机构动力学特性, 指出线性弹簧阻尼模型对材料阻尼较小的碰撞过程仿真精度较高, 但对高阻尼情况, 阻尼力需要考虑碰撞速度与接触刚度的影响。线性阻尼模型形式简单, 但不能反映碰撞过程碰撞力与相对刺穿深度的非线性关系, 且在碰撞开始时, 碰撞阻尼力非零且为最大值, 碰撞力合力不为零; 在碰撞结束时, 使得等效弹簧力和等效阻尼力的合力为拉力, 与接触的物理过程相违背[17, 30]。Hunt等[30]与Herbert[44]认为碰撞力与刺穿深度的n次方成正比, Hunt等[30]提出具有非线性阻尼的接触力模型(Hunt-Crossley模型)。与Hunt-Crossley模型类似, Lee等[37]提出改进的迟滞阻尼碰撞模型, 能较好地满足碰撞过程的边界条件。Lankarani等[38]在Hunt等[30]的研究基础上, 通过碰撞前后系统能量损失, 构建阻尼因子与恢复系数的关系, 提出Lankarani-Nikravesh连续接触力模型(L-N模型)。该模型考虑了碰撞过程中能量耗散, 反映碰撞体的材料性质、几何特征及运动状态对碰撞过程的影响。Gonthier等[40]通过计算碰撞力与刺穿深度曲线的斜率, 近似得到广义接触刚度系数, 并利用该系数, 对L-N模型中阻尼系数进行修正。分析表明:在较高恢复系数条件下, 通过该模型计算得到的碰撞压缩与恢复阶段的能量耗散基本上相当, 而当恢复系数较小时, 能量主要耗散于压缩阶段。

对于相对软的材料, 需要考虑塑性变形问题。Goldsmith[31]认为Hertz接触力模型能较好地刻画接触刚度较大且初始碰撞速度较低的碰撞过程, 但不适用于接触刚度小、初始碰撞速度高且需要考虑塑性变形的碰撞过程, 因此提出一种基于Hertz接触力模型的考虑材料塑性变形的接触力模型。针对接触中有塑性变形情况, Lankarani等[45]将L-N模型拓展到考虑高速碰撞与材料塑性变形的影响, Flores等[39]提出一种考虑弹性碰撞与非弹性碰撞过程的接触碰撞模型。

Hertz接触力模型适用于刻画大间隙、小载荷的碰撞过程, 若要精细模拟间隙碰撞问题, 还需要考虑间隙运动副共形接触问题, 发展间隙运动副的共形接触建模方法。为了解决运动副间隙共形接触建模问题, 陈鹿民等[46]提出一种多点接触碰撞模型及其离散算法, 根据Hertz接触理论和弹性基础假设, 将运动副间隙接触表面下的应力分布采用三次幂指数函数近似, 得到适用于光滑接触面和微小间隙运动副的等效弹簧阻尼器多点接触碰撞模型。Liu等[33]基于Winkler弹性基模型假设, 通过有限元方法, 对接触区域、压力分布与最大载荷进行分析, 提出一种适合于共形接触的法向接触力模型。

3.2 运动副的切向摩擦

间隙运动副接触位置的切向摩擦力一般采用Coulomb摩擦模型, 通过摩擦系数将法向接触力与摩擦力建立联系。由于Coulomb摩擦模型不连续, 且间隙运动副元素的接触和分离状态可能变化频繁, 导致采用传统Coulomb摩擦模型描述间隙运动副的切向摩擦力时存在明显不足, 数值计算的稳定性较低[47]。理论与实验表明, 摩擦力不仅与接触表面性质相关, 还受到滑动速度、材料性质以及温度等因素的影响, 而传统的Coulomb摩擦模型并未考虑这些因素的作用[48]。传统的Coulomb摩擦模型也不能表征两构件间的黏滞现象, 在碰撞过程中黏滞不仅导致构件间存在静摩擦力的变化, 也可能引起可逆滑动的发生。Ahmed等[49]认为合理的摩擦模型需要识别滑动与黏滞过程, 避免计算时碰撞系统能量的增加。

为了解决传统Coulomb摩擦模型的不足, 学者们引入一系列改进的Coulomb摩擦模型来刻画含间隙运动副中构件的摩擦力[50-53]。这些改进的模型大多引入平滑因子, 将摩擦力描述为切向速度的连续函数。改进的Coulomb摩擦模型只是从易于数值计算的角度对Coulomb摩擦力模型进行改进, 使摩擦力在速度上保持连续, 避免切向速度为零时摩擦力方向的突变, 提高了数值计算的稳定性。但是, 这些摩擦力模型不符合摩擦的物理本质, 并没有反映摩擦过程本身, 忽略了黏滞静摩擦力等因素的影响, 导致摩擦力物理表征的失真。

为了准确刻画接触过程中的黏滞、滑动及其转换过程, 一些学者引入系统的内部变量, 建立了动态摩擦模型。目前的动态摩擦模型主要有Dahl摩擦模型和LuGre摩擦模型等。Dahl[54]根据界面间的应力-应变关系, 将接触峰的平均变形量作为系统的内部变量, 描述构件的微小位移, 提出微分形式的动态摩擦模型, 避免了传统Coulomb摩擦模型的不连续性。Stribeck[55]研究发现, 在两个接触表面进入滑动阶段初始时刻的低速运动过程中, 摩擦力随着切向相对速度的增加而降低。虽然Dahl模型表征了预滑移, 描述了摩擦滞后, 但没有描述静摩擦力与Stribeck现象, 因此不能用于分析黏滞-滑动过程。Canudas等[56]采用接触面间弹性刚毛的平均偏移表征摩擦力的动态行为, 考虑刚毛平均偏移、变形速度与构件的切向速度对摩擦力的影响, 提出LuGre摩擦模型。LuGre摩擦模型不仅能准确地刻画构件间的Coulomb摩擦、可变静摩擦以及Stribeck摩擦现象, 而且可实现在不同的摩擦状态间连续平滑的转换。LuGre模型既能消除速度零点时摩擦力的不连续性, 又能较好地刻画含间隙机构中存在的黏滞-滑动现象与可变静摩擦力等问题。Muvengei等[57]将LuGre模型应用到含间隙多体系统动力学特性分析中, 发现含间隙运动副中转轴与轴套的碰撞过程存在大量的黏滞-滑动过程及其相互转换, 该过程对系统的非线性响应会产生较明显的影响。动态摩擦模型虽然能够全面地描述摩擦现象, 但模型较为复杂, 模型参数辨识尤为困难。因此, 动态摩擦模型应用于含间隙机械多体系统动力学分析尚有局限性, 针对间隙运动副中摩擦问题研究仍有待进一步完善。

3.3 旋转副的三维间隙建模

旋转运动副是一种典型的平面运动副, 其间隙模型一般为平面间隙模型, 这种模型基于转轴与孔体碰撞过程中轴线始终保持平行的假设条件, 忽略了其轴向间隙及其碰撞行为。由于实际的旋转副轴销和孔体很难实现严格的平行接触, 且圆柱表面的压力分布不均匀, 转轴与轴套间存在轴向边界效应的影响[30]。在平面机构中, 由于运动副间隙的存在, 转轴与孔体轴线可能发生倾斜, 轴销和孔体沿轴向也存在间隙, 使得在轴向产生复杂的碰撞过程, 从而引起平面机构脱离理想平面运动, 导致平面机构产生更为复杂的空间运动[58]。为了精细刻画含径向间隙和轴向间隙的运动副, 研究者提出旋转副三维间隙模型。Bauchau等[59]、Venanzi[60]和尉立肖等[61]提出旋转副的4种接触模式, 建立三维间隙模型, 分析间隙对机构运动精度的影响。张跃明等[62]根据轴销和轴套的约束关系, 给出间隙转动副11种接触模式, 分析各种模式的存在条件。Yan等[58]考虑转轴与轴套间的径向与轴向间隙, 基于运动副的几何特性分析, 给出构件间存在的13种接触模式及其存在条件(表 3), 提出平面旋转副的三维间隙铰模型; 针对径向与轴向存在的点、线、面等不同的接触行为, 分别给出非线性碰撞接触力表达式, 通过实验证实了平面旋转副由于间隙存在而呈现出的三维空间特性。此类模型更接近于真实的旋转运动副, 为分析实际机械系统的间隙运动副元素间的接触与碰撞复杂行为提供了理论基础。

表 3. 三维间隙接触模式[58] Table 3. Contact modesof 3D revolution joint[58]
编号 副元素接触图示 接触型式 说明 特征
1 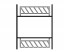自由状态 孔体部分与销轴部分不接触 δr_front>0, δr_back>0,
δa_front>0, δa_back>0
2 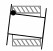一点 孔体部分与销轴部分的柱面上一点接触 δr_front≤0, δr_back>0,
δa_front>0, δa_back>0
3 两点 孔体部分与销轴部分的柱面上两点接触 δr_front≤0, δr_back≤0,
δa_front>0, δa_back>0
4 一线 孔体部分与销轴部分的柱面上一条母线接触 e3k//e3l
δr_front≤0, δr_back≤0,
δa_front>0, δa_back>0
5 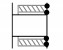一面 孔体部分与销轴部分的柱面的一个端面接触 e3k//e3l
δr_front>0, δr_back>0,
δa_front>0, δa_back≤0
6 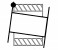一点 孔体部分与销轴部分的一个端面单点接触 δr_front>0, δr_back>0,
δa_front≤0, δa_back>0
7 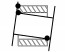三点 孔体部分与销轴部分的柱面上两点接触，同时与销轴部分的一个端面单点接触 δr_front≤0, δr_back≤0,
δa_front≤0, δa_back>0
8 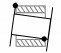两点 孔体部分与销轴部分的柱面上一点接触，同时与销轴部分的一个端面单点接触 δr_front>0, δr_back≤0,
δa_front≤0, δa_back>0
9 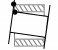两点 孔体部分的一端同时与销轴部分的柱面和端面接触 δr_front≤0, δr_back>0,
δa_front≤0, δa_back>0
10 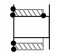一线一面 孔体部分与销轴部分的柱面和端面同时接触 e3k//e3l
δr_front≤0, δr_back≤0,
δa_front≤0, δa_back>0
11 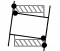四点 孔体部分与销轴部分的柱面上两点接触，同时与销轴部分端面两点接触 δr_front≤0, δr_back≤0,
δa_front≤0, δa_back≤0
12 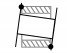两点 孔体部分与销轴部分的两端面同时接触 δr_front>0, δr_back>0,
δa_front≤0, δa_back≤0
13 三点 孔体部分与销轴部分的柱面上一点接触，同时与销轴部分的两个端面接触 δr_front≤0, δr_back>0,
δa_front≤0, δa_back≤0
注：δ为副元素的刺穿深度，r表示径向，a表示轴向，front表示前端面，back表示后端面。
表选项

4 含间隙机械系统动力学特性分析 4.1 间隙对系统动力学特性的影响分析

运动副间隙使机械多体系统产生复杂的动力学行为, 造成实际工程系统的性能与可靠性下降。预测与评估间隙对机械系统动力学特性的影响是国内外学者长期关注的问题。陈滨等[63]采用摄动法建立含间隙伸展机构动力学模型, 分析了间隙对机构运动特性的影响。马兴瑞等[6]和王天舒等[64]将绳索联动机构等效为一个被动控制器, 研究含铰间隙的太阳翼动力学行为。Li等[65]以考虑关节铰间隙的太阳电池阵为研究对象, 讨论关节阻尼与摩擦、重力场以及部件柔性对太阳翼展开过程动力学响应的影响。Zhang等[51]、Zhao等[66]和Bai等[67]研究含间隙太阳翼与空间机械臂动力学响应。何柏岩等[68]采用Hertz接触模型, 建立含间隙柔机械臂动力学模型, 分析间隙对机械臂动力学特性的影响。

齿面摩擦、齿侧间隙及时变啮合刚度是导致齿轮运动副产生复杂非线性振动的主要因素[69]。王三民等[69]以齿轮副啮合点间沿啮合线的相对位移为广义坐标, 建立计及摩擦、间隙及时变刚度等因素的直齿轮副非线性动力学模型。谷勇霞等[70]和Zhao等[71]以含谐波传动关节空间机械臂为研究对象, 分析空间机械臂运动精度与参数灵敏度。Yang等[72-74]综合考虑时变啮合刚度、齿侧间隙、齿面误差和啮合相位等非线性因素, 建立含行星减速器的空间机械臂关节精细模型, 分析运行过程中不同类型的扭转振动产生原因以及齿侧间隙对啮合冲击的影响。

阎绍泽等[18, 75-76]和陈鹿民等[77]对考虑间隙的可展结构动力学特性开展数值仿真与实验研究, 发现运动副间隙降低了系统稳定性, 且随着间隙值增大, 副反力幅值增加; 间隙导致系统具有初值敏感性, 呈现明显的非线性特征; 间隙内碰撞将激发结构的高频振动, 导致结构振动能量的转移; 杆件柔性对间隙运动副元素间的碰撞冲击具有缓冲作用。

由于间隙运动副的内碰撞及其变拓扑结构特性, 使得系统动力学行为较为复杂。运用时域和频域相结合的分析手段, 能够考察间隙局部非线性对系统全局非线性的影响, 以及间隙碰撞冲击特性与系统时频变化特征。宿月文等[78]利用快速傅立叶变换分析含间隙多体系统的动态时域响应, 得到系统的频谱, 分析了时域和频域的系统动态响应。Xun等[79]、Liu等[80]和荀剑等[81]基于时频分析方法分析含间隙可展结构振动信号的时频特征, 揭示了低频和高频段的不同振动特征, 对收拢和展开状态下太阳帆板实验数据时频分析表明:时频分析方法能够较好地表征含间隙可展结构的时频特征信息, 得到系统的频带以及各个频段衰减的速度和时间。

4.2 考虑润滑和磨损等因素的含间隙机械系统动力学分析

机器中的运动副一般注入润滑油, 若运动副元素间的相对速度较小, 则难以形成动压润滑; 另一方面, 在高速机械中运动副反力较大, 会从摩擦表面间挤出润滑油, 使得摩擦表面的凸起产生接触而处于边界润滑状态。在动态接触过程中, 间隙运动副将引起表面磨损[82]。可以看出, 考虑润滑的间隙副建模更为复杂。Ravn等[83]和Flores等[84]采用雷诺方程, 描述运动副间隙中的流体压力分布, 发现润滑膜降低了间隙运动副元素的碰撞, 增加了机构运动的稳定性。Dupac等[85]分析了间隙、杆件柔性与裂纹对曲柄滑块机构动力学响应与运动稳定性的影响, 将杆件柔性与裂纹通过旋转弹簧进行表征, 利用恢复系数描述间隙副碰撞过程, 发现间隙与裂纹导致系统呈现混沌响应, 激发杆件的高阶振型, 降低机构的运动稳定性。润滑可以在一定程度上降低间隙效应[83-84, 86-87], 润滑使得运动副中构件接触减少, 副反力幅值明显下降, 润滑油膜亦能降低运动副中摩擦力幅值与构件表面的磨损程度。

实际机械系统中含间隙运动副在长期运行中必然存在磨损。构件表面磨损后, 运动副间隙尺寸及其分布将呈现非规则特性[88]。这将引起机构动力学响应的改变, 这种变化又反作用于磨损过程, 造成系统复杂的动力学行为[89]。Tasora等[90]通过实验, 研究了含间隙转动副中的磨损情况, 证明了转轴表面磨损区域分布的不均匀性。Mukras等[91-92]将接触表面视为一系列弹簧即所谓的弹性基模型, 分析含间隙机构运动副中的磨损行为。由于该模型将接触表面等效为弹簧组并忽略接触面剪切效应, 因此可直接获取构件接触过程中的压力分布情况。Li等[93]考虑转轴与轴套磨损后构件几何特征分布不均匀导致的接触表面压力分布的非对称性, 提出非对称的Winkler弹性基模型。Xiang等[94]提出一种考虑动态磨损过程的含间隙运动副模型, 引入动态非线性接触刚度系数, 考虑非规则磨损间隙及构件曲率变化对接触力的影响, 计及材料的物理属性、几何特征与接触体变形过程, 基于构件间的接触压力与滑动距离, 利用Archard磨损模型对离散区内构件的磨损深度进行计算, 获取磨损造成的接触表面几何特征的变化, 通过余弦相关函数分析接触压力与滑动距离对运动副中磨损过程的影响。该模型的计算中, 转轴与轴套间接触和滑动行为的确定依赖于整个机构的运动过程, 实时更新间隙的尺寸与分布, 实现了含间隙运动副磨损深度的动态预测。Xiang等[94]发现, 在给定条件下, 曲柄转速较低时, 磨损区域较为集中; 当转轴与轴套发生连续碰撞时, 构件磨损率主要受接触压力的影响; 当转轴与轴套持续接触时, 构件的磨损率主要受滑动距离的影响。实际的机械系统运动副虽存在润滑, 但长期运行也会产生磨损, 而考虑润滑和磨损的间隙运动副建模的研究十分有限, 尤其缺少相关的实验研究。

4.3 含间隙机械系统的非线性特性分析

间隙导致接触表面存在复杂的碰撞与摩擦, 使得含间隙机械系统具有典型的非线性特性, 出现谐波共振等现象[95]。Moon等[96]实验研究含间隙空间桁架结构时发现, 在正弦激励条件下, 间隙导致桁架结构发生混沌振动。Rhee等[97]采用经典碰撞模型和庞加莱截面分析方法, 对含间隙四杆机构进行分析, 结果表明:随着运动副中摩擦系数的增加, 机构的非线性程度降低; 当摩擦系数较高时, 机构具有稳定的周期响应。卢绪祥等[98]采用分岔图、相图、庞加莱映射与功率谱图, 分析含间隙碰撞振动系统的非线性振动特性。Tang等[99]通过庞加莱映射, 分析含间隙四杆机构中存在的奇怪吸引子。Rahmanian等[100]利用分岔图, 分析含间隙多体系统的稳定区间。Farahanchi等[101]分析间隙值、摩擦系数与碰撞参数对曲柄滑块机构响应的影响, 指出机构响应存在混沌、暂态混沌与周期运动3种状态。赵永辉等[102]考虑操纵面自由度具有的间隙非线性, 建立二维翼段气动弹性系统无量纲分段线性运动方程, 研究表明, 操纵面铰链间隙非线性将导致整个系统的极限环振动, 随着来流速度的增加, 系统极限环振动的幅值和频率都存在跳跃现象。

大多数含间隙机械系统属于多参数系统, 参数的改变可能引起系统动力学响应发生本质变化, 导致周期解的个数及稳定性发生改变并产生分岔。含间隙系统存在多种分岔类型, 如叉式分岔[103]、倍周期分岔[104]、Hopf分岔[105]等, 且含间隙系统对参数和初值更为敏感, 很容易出现阵发性混沌[3, 106]。含间隙机构动力学行为的复杂性将导致如全局稳定流形定理等一些经典的分析方法失效[3, 105]。大部分学者在分析含间隙机械系统非线性特性时采用的间隙模型比较简单, 而运用接近真实的间隙模型, 进一步开展机械系统谐波共振、周期运动的稳定性和分岔等非线性动力学特性研究, 对提升实际机械装备动力学分析和设计水平具有重要意义。

4.4 含间隙机械系统性能评价与可靠性评估

由于机器或机构长时间运行, 其间隙运动副轴套和销轴会发生磨损, 使得间隙扩大, 引起系统运动精度以及系统动力学稳定性的改变, 导致性能退化, 因此, 需要进行性能评价和可靠性评估, 以预测机械系统运行精度和剩余使用寿命[107-109]。黄玮等[110]和孟宪举等[111]应用连续接触模型, 对含间隙运动副的机构精度和运动可靠性进行分析。Pan等[112]利用测试数据特征生成方法, 结合系统动力学方程, 给出含间隙的太阳电池阵同步机构的故障评估与可靠性预测方法。Wu等[113]结合系统动力学方程和Kaplan-Meier分析方法, 考虑杆长随机性与铰链磨损退化, 提出一种用于含间隙多体系统的可靠性评估方法。Xiang等[114]基于庞加莱映射理论与相点关联性分析, 提出一种含间隙机构的运动复杂度定量分析方法, 实现机构动力学特性的定量评价; 利用该方法对含间隙曲柄滑块机构开展参数影响研究, 发现间隙尺寸与曲柄转速和机构运动复杂度间分别满足玻尔兹曼函数与高斯函数关系。

5 研究展望

经过40多年的研究, 含间隙多体机械系统动力学在构件柔性(弹性)的表征、运动副非线性建模、多体动力学方程的数值解算方法, 以及多体机械系统的运动控制与振动抑制等诸多方面均取得较大成果, 但尚有很多问题有待进一步研究。

5.1 考虑黏滞-滑动过程的含间隙运动副建模

含间隙运动副摩擦力的刻画通常采用改进的Coulomb摩擦模型。该模型虽然解决了速度零点时摩擦力的连续性问题, 并保证数值计算的稳定性, 但违背了摩擦过程的物理本质, 且不能刻画可变静摩擦、Stribeck摩擦及黏滞-滑动效应在含间隙运动副中大量存在的摩擦现象, 导致理论描述摩擦机理失真。虽然少数学者通过引入动态摩擦模型来解决该问题, 但动态摩擦模型本身参数辨识困难, 且会给机构引入额外自由度, 不易在含间隙机构动力学分析中应用。因此, 有必要进一步考虑含间隙运动副中构件间的碰撞与摩擦机理, 建立考虑黏滞-滑动过程的含间隙运动副模型。同时, 对含间隙运动副构件碰撞过程中摩擦与磨损现象及能量耗散的实验测试与分析, 可以揭示间隙非线性行为, 还需开展相关实验研究, 并进行理论与实验对比验证。

5.2 间隙运动副的共形接触建模

目前含间隙运动副元素碰撞过程中, 碰撞力均基于理想接触表面确定, 而实际机构中广泛存在共形接触问题。对于高精度机械系统, 由于运动副间隙较小, 一般是运动副直径的1/100到1/10000, 具体数值视直径大小和精度而定[62]。尽管接触变形可能很小, 但是接触区域较大, 属于近似共形接触, 这时Hertz假设不再适用。因此, 这类间隙运动副内的接触碰撞属于相对碰撞速度很低的近似协调接触问题。基于弹性半空间理论的Hertz类接触力公式仅适用于非协调接触, 且只有几种简单表面之间的接触能得到解析表达式, 采用这类单点接触间隙模型解算共形接触问题可能会引起较大误差。含间隙运动副共形接触建模问题可以采用有限元方法解决, 但有限元方法需建立碰撞体接触后的准确动边界条件, 模型复杂, 计算量较大; 另外, 间隙有限元模型直接用于具有大位移运动的机构动力学解算, 需考虑到有限元方法处理刚体大位移的局限性。从运动副材料的物理本构出发, 运用接触力学和固体力学理论, 建立运动副间隙的共形接触模型有待进一步研究。

5.3 考虑接触表面形貌的运动副间隙建模

由于实际运动副接触表面上有众多的微凸峰, 当由微凸峰组成的两表面相互接近时, 接触仅仅发生在凸峰的顶部, 法向施加的压力越大, 凸峰压缩变形量越大, 接触力越大。随着磨损加剧, 微凸峰高度降低, 实际接触面增大, 接触刚度也相应提高。Song等[115]应用全反射方法对界面的真实接触面积进行测量, 将激光器作为光源, 使用改进后的Otsu图像处理方法对得到的图像进行处理, 发现在弹性变形范围内, 接触面积增长速率随正压力的增加而逐渐减小; 在相同正压力的情况下, 加载速度越快, 界面真实接触面积越小; 真实接触面积与正压力之间存在滞后现象; 粗糙表面之间的接触存在一定的随机性。Adams等[116]和Johnson[117]总结了粗糙表面间法向接触力和切向干摩擦力的研究状况。Aronov等[118-119]、Soom等[120]和Adams[121]采用Hertz接触力模型, 分别研究在粗糙表面上稳定滑动时法向随机振动和表面不平度引起的自激振动。Kalker等[122]研究存在摩擦和无摩擦条件下粗糙弹性表面的柔性接触仿真模型。Bengisu等[123]研究干摩擦力与接触表面粗糙度的关系, 研究结果揭示了干摩擦力能引起接触物体的黏滑(stick-slip)运动和自激振动, 对于给定法向载荷, 切向摩擦力只与真实接触面积在平均面上的切向和法向投影之比有关, 而与接触面积大小无关。借鉴考虑表面形貌接触问题的研究成果, 建立考虑表面形貌的间隙模型对机械系统动力学精细分析和动态设计具有重要意义。

5.4 考虑不确定参数的含间隙机械多体系统动力学分析及其运动精度评估

对于典型机械系统, 如果影响其工作性能指标的因素与理想值发生了偏差, 但系统仍可运行, 或其工作性能指标仍在允许的范围内, 可认为系统是稳健的。机械系统性能的影响因素分为可控因素和不可控因素。对于典型的机械多体系统, 可控因素主要包括构件尺寸及其误差、运动副间隙大小及其误差以及系统安装调试误差。不可控因素包括间隙所引起的碰撞、摩擦等。由于构件制造精度、不可避免的装配误差、相对运动构件间必不可少的运动副间隙、构件的弹性变形及输入运动误差等因素的影响, 使得机构的真实运动不同于(甚至严重偏离)其设计预定的理想运动。Deck等[124]实验研究表明, 无论如何调节几何参数和系统初始状态, 实验结果仍具有不确定性, 机构动态行为对初始状态和系统参数极度敏感, 这也是含间隙机构的内在本质。机械系统工作环境是时变的, 例如, 航天太阳电池阵和空间机械臂在轨运行的冷热交变环境变化以及各种干扰对运动副及系统具有较大影响[70-71, 125-127]。随机干扰因素会产生随机误差, 所以必需用概率统计理论和随机过程理论对系统运动精度进行分析。Yan等[76]基于连续接触力模型, 建立了含间隙四连杆机构动力学方程, 针对杆长误差、间隙误差及构件变形的影响, 利用Monte Carlo方法, 对含间隙机构运动进行概率分析, 分别采用偏差分布图和最大偏差分布图表征机构运动输出位置偏差的分布规律和输出运动过程中可能出现的最大偏差的分布情况。目前, 从概率统计的角度对含间隙机械系统进行相关分析的研究较少, 还需进一步开展机械系统的实际运动偏差的概率分析工作, 这对提高机械系统的运动精度具有重要意义。

5.5 运动副间隙设计

合理的运动副间隙设计是降低间隙对机械系统特性影响的有效方法之一。研究表明:减小间隙尺寸有助于降低含间隙运动副中的碰撞力[18, 75, 128]、减小磨损量[94]和降低系统运动的复杂度[114]。因此, 从动力学分析角度, 间隙越小越好。间隙设计不能仅考虑动力学问题, 还需考虑机械设计、表面与界面设计、制造工艺水平以及环境温度变化、工作载荷等因素的影响。运动副间隙主要由选取的公差配合确定, 例如, 对于名义直径尺寸为100 mm的旋转副, 选取H8/f7配合, 其轴与孔的尺寸差异(即间隙大小)为36~125 μm; 在需要滑动配合时, 选取H7/g6配合, 其轴与孔的尺寸差异为12~69 μm。因此, 公差配合要求越高, 运动副两副元素间的间隙越小; 反之, 运动副两副元素间的间隙越大。运动副要求有足够的间隙以保证副元素间的相对运动。当间隙较小时, 运动副不容易装配, 尤其在副元素的轴线相对有误差的情况下, 装配可能出现困难, 甚至形成过盈配合, 导致运动副失效。当间隙较大时, 运动副可轻易装入, 但此时副元素的轴线在机构运行的过程中必然会发生不重合或不平行, 使得机构在工作过程中会发生副元素碰撞, 动力学性能下降, 加速接触表面的磨损。在一般的机械设计中, 确定运动副公差配合时, 需考虑以下因素:尺寸公差、位置公差、形状公差和表面粗糙度。这些要素之间的大小关系应为:尺寸公差 > 形位公差 > 表面粗糙度。这是由于形位精度也包含尺寸精度, 若形位精度的值比尺寸精度的值大, 则会导致尺寸精度无法测量, 使得尺寸精度失去意义。同样, 若表面粗糙度的值比尺寸精度和形位精度的值大, 则会将二者“掩盖”, 亦无法测量。因此, 考虑间隙对机械系统动力学特性的影响时, 如何设计运动副的间隙配合也是值得深入研究的课题。

参考文献
[1] 王庚祥, 刘宏昭. 多体系统动力学中关节效应模型的研究进展. 力学学报 , 2014, 47 (1) : 31–50.
[2] 阎绍泽. 航天器中含间隙机构非线性动力学问题及其研究进展. 动力学与控制学报 , 2004, 2 (2) : 48–52.
[3] 曹登庆, 初世明, 李郑发, 等. 空间可展机构非光滑力学模型和动力学研究. 力学学报 , 2013, 45 (1) : 3–15.
[4] Nurre G S, Sharkey J P, Nelson J D, et al. Preserving mission, on-orbit modifications to hubble space telescope pointing control system. J of Guidance, Control, and Dynamics , 1995, 18 (2) : 222–229 DOI:10.2514/3.21373 .
[5] Foster C L, Tinker M L, Nurre G S, et al. Solar-array-induced disturbance of hubble space telescope pointing system. J of Spacecraft and Rockets , 1995, 32 (4) : 634–644 DOI:10.2514/3.26664 .
[6] 马兴瑞, 王本利, 苟兴宇, 等. 航天器动力学:若干问题进展及应用. 北京: 科学出版社, 2001 .
[7] 王伟方, 阎绍泽, 李刚, 等. 航天器及其太阳电池阵的结构频率漂移现象分析. 机械设计 , 2010, 27 (增刊1) : 180–182.
[8] 陈昌亚, 王本利, 王德禹, 等. 随振动量级增加卫星结构频率下移的分析. 上海航天 , 2004 (3) : 44–47.
[9] 卫洪涛, 孔宪仁, 王本利, 等. 非线性连接结构对一个典型卫星频率漂移的影响. 航天器环境工程 , 2012 (3) : 297–303.
[10] 薛宏伟, 林益明, 刘天雄. 航天器振动试验的频率漂移问题综述. 航天器工程 , 2005 (4) : 58–62.
[11] Smith K S, Peng C Y. Modal test of the Cassini spacecraft // 15th International Model Analysis Conference. Bethel, CT, 1997: 804-810
[12] Carney K, Yunis I, Smith K, et al. Nonlinear dynamic behavior in the Cassini spacecraft modal survey // 15th International Model Analysis Conference. Bethel, CT, 1997: 811-817
[13] Okuizumi N, Natori M C. Nonlinear vibrations of a satellite truss structure with gaps // 45th AIAA/ ASME/ ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference. Palm Springs, CA, 2004: 1867
[14] Earles S W E, Wu C L S. Motion analysis of a rigid link mechanism with clearance at a bearing using Lagrangian mechanics and digital computation // Conference on Mechanisms. London, 1972: 83-89
[15] 张策, 陈树勋, 王子良, 等. 弹性连杆机构分析与设计. 北京: 机械工业出版社, 1997 .
[16] Earles S W E, Wu C L S. Predicting the occurrence of contact loss and impact at a bearing from a zero-clearance analysis // 4th World Congress on the Theory of Machines and Mechanisms. Newcastle, England, 1975: 1013-1018
[17] 俞武勇, 季林红, 阎绍泽, 等. 含间隙机构运动副的动力学模型. 机械科学与技术 , 2001, 20 (5) : 665–669.
[18] 阎绍泽, 陈鹿民, 季林红, 等. 含间隙铰的机械多体系统动力学模型. 振动工程学报 , 2003, 16 (3) : 290–294.
[19] Seifried R, Schiehlen W, Eberhard P. Numerical and experimental evaluation of the coefficient of resti-tution for repeated impacts. International Journal of Impact Engineering , 2005, 32 (1) : 508–524 .
[20] Stronge W J. Impact mechanics. New York: Cam-bridge University Press, 2004 .
[21] Newton I, Bernoulli D, MacLaurin C, et al. Philo-sophiae naturalis principia mathematica. Glasgow: 1833 .
[22] Kane T R, Levinson D A. Dynamics, theory and applications. New York: McGraw Hill, 1985 .
[23] Brach R M. Formulation of rigid body impact problems using generalized coefficients. International Journal of Engineering Science , 1998, 36 (1) : 61–71 DOI:10.1016/S0020-7225(97)00057-8 .
[24] Smith C E. Predicting rebounds using rigid-body dynamics. ASME Journal of Applied Mechanics , 1991, 58 (3) : 754–758 DOI:10.1115/1.2897260 .
[25] Keller J B. Impact with friction. Journal of Applied Mechanics , 1986, 53 (1) : 1–4 DOI:10.1115/1.3171712 .
[26] Stronge W J. Comment: collision with friction, part B: Poisson's and Stronge's hypotheses. Multibody System Dynamics , 2010, 24 (1) : 123–127 DOI:10.1007/s11044-010-9204-0 .
[27] Zhao Z, Liu C S, Chen B. The Painlevé paradox studied at a 3D slender rod. Multibody System Dynamics , 2008, 19 (4) : 323–343 DOI:10.1007/s11044-007-9098-7 .
[28] Zhao Z, Liu C S, Ma W, et al. Experimental investigation of the Painlevé paradox in a robotic system. Journal of Applied Mechanics , 2008, 75 (4) : 1–11 .
[29] Hertz H. Über die berührung fester elastischer K rper. Journal für die Reine und angewandte Mathematik , 1882, 92 : 156–171 .
[30] Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact. Journal of Applied Mechanics , 1975, 42 (2) : 440–445 DOI:10.1115/1.3423596 .
[31] Goldsmith W. Impact: the theory and physical behavior of colliding solids. London: Arnold, 1960 .
[32] Engineering Sciences Data Unit Limited. Contact phenomena. Ⅰ: Stresses, deflections and contact dimensions for normally-loaded unlubricated elastic components. London: Engineering Sciences Data Unit, 1978 .
[33] Liu C S, Zhang K, Yang R. The FEM analysis and approximate model for cylindrical joints with clearances. Mechanism and Machine Theory , 2007, 42 (2) : 183–197 DOI:10.1016/j.mechmachtheory.2006.02.006 .
[34] Goodman L E, Keer L M. The contact stress problem for an elastic sphere indenting an elastic cavity. International Journal of Solids and Structures , 1965, 1 (4) : 407–415 DOI:10.1016/0020-7683(65)90005-3 .
[35] Koshy C S, Flores P, Lankarani H M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: computational and experimental approaches. Nonlinear Dynamics , 2013, 73 (1/2) : 325–338 .
[36] Flores P, Ambrósio J. Revolute joints with clearance in multibody systems. Computers & Structures , 2004, 82 (17) : 1359–1369 .
[37] Lee T W, Wang A C, et al. On the dynamics of intermittent-motion mechanisms. part 1: dynamic model and response. Journal of Mechanical Design , 1983, 105 (3) : 534–540 .
[38] Lankarani H M, Nikravesh P E. A contact force model with hysteresis damping for impact analysis of multibody systems. Journal of Mechanical Design , 1990, 112 (3) : 369–376 DOI:10.1115/1.2912617 .
[39] Flores P, Machado M, Silva M T, et al. On the continuous contact force models for soft materials in multibody dynamics. Multibody System Dynamics , 2011, 25 (25) : 357–375 .
[40] Gonthier Y, Mcphee J, Lange C, et al. A regularized contact model with asymmetric damping and dwell-time dependent friction. Multibody System Dynamics , 2004, 11 (3) : 209–233 DOI:10.1023/B:MUBO.0000029392.21648.bc .
[41] Dubowsky S, Freudenstein F. Dynamic analysis of mechanical systems with clearances-part 1: formation of dynamic model. Journal of Engineering for Industry , 1971, 93 (1) : 305–309 DOI:10.1115/1.3427895 .
[42] Dubowsky S, Freudenstein F. Dynamic analysis of mechanical systems with clearances-part 2: dynamic response. Journal of Engineering for Industry , 1971, 93 (1) : 310–316 DOI:10.1115/1.3427896 .
[43] Rogers R J, Andrews G C. Dynamic simulation of planar mechanical systems with lubricated bearing clearances using vector-network methods. Journal of Engineering for Industry , 1977, 99 (1) : 131–137 DOI:10.1115/1.3439126 .
[44] Herbert R G. Shape and frequency composition of pulses from an impact pair. Journal of Engineering for Industry , 1977, 99 (3) : 513–518 DOI:10.1115/1.3439270 .
[45] Lankarani H M, Nikravesh P E. Continuous contact force models for impact analysis in multibody systems. Nonlinear Dynamics , 1994, 5 (2) : 193–207 .
[46] 陈鹿民, 阎绍泽, 金德闻. 微小间隙转动副的接触碰撞模型及离散算法. 清华大学学报:自然科学版 , 2004, 44 (5) : 629–632.
[47] Pennestri E, Valentini P P, Vita L. Multibody dynamics simulation of planar linkages with Dahl friction. Multibody System Dynamics , 2007, 17 (4) : 321–347 DOI:10.1007/s11044-007-9047-5 .
[48] 温诗铸, 黄平. 摩擦学原理. 北京: 清华大学出版社, 2002 .
[49] Ahmed S, Lankarani H M, Pereira M F O S. Frictional impact analysis in open-loop multibody mechanical systems. Journal of Mechanical Design , 1999, 121 (1) : 119–127 DOI:10.1115/1.2829412 .
[50] Bai Z F, Zhao Y. Dynamic behaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model. International Journal of Mechanical Sciences , 2012, 54 (1) : 190–205 DOI:10.1016/j.ijmecsci.2011.10.009 .
[51] Zhang L X, Bai Z F, Zhao Y, et al. Dynamic response of solar panel deployment on spacecraft system considering joint clearance. Acta Astronautica , 2012, 81 (4) : 174–185 .
[52] Flores P. Dynamic analysis of mechanical systems with imperfect kinematic joints [D]. Portugal: Uni-versidade do Minho Para, 2004
[53] Ambrosio J A C. Impact of rigid and flexible multibody systems: deformation description and contact models // Schiehlen W, Valášek M. Virtual nonlinear multibody systems. Dordrecht: Kluwer Academic Publishcrs, 2002: 57-81
[54] Dahl P R. Solid friction damping of mechanical vibrations. AIAA Journal , 1976, 14 (12) : 1675–1682 DOI:10.2514/3.61511 .
[55] Stribeck R. The key qualities of sliding and roller bearings. Zeitschrift des Vereines Seutscher Inge-nieure , 1902, 46 (39) : 1432–1437 .
[56] Canudas C W, Olsson H, Astrom K J, et al. A new model for control of systems with friction. IEEE Transactions on Automatic Control , 1995, 40 (3) : 419–425 DOI:10.1109/9.376053 .
[57] Muvengei O, Kihiu J, Ikua B. Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints. Multi-body System Dynamics , 2012, 28 (4) : 369–393 DOI:10.1007/s11044-012-9309-8 .
[58] Yan S, Xiang W, Zhang L. A comprehensive model for 3D revolute joints with clearances in mechanical systems. Nonlinear Dynamics , 2015, 80 (1/2) : 309–328 .
[59] Bauchau O A, Ju C. Modeling friction phenomena in flexible multibody dynamics. Computer Methods in Applied Mechanics and Engineering , 2006, 195 (50) : 6909–6924 .
[60] Venanzi S, Parenti-Castelli V. A new technique for clearance influence analysis in spatial mechanisms. Journal of Mechanical Design , 2005, 127 (3) : 446–455 DOI:10.1115/1.1867512 .
[61] 尉立肖, 刘才山. 圆柱铰间隙运动学分析及动力学仿真. 北京大学学报:自然科学版 , 2005, 41 (5) : 679–687.
[62] 张跃明, 唐锡宽, 张兆东, 等. 空间机构间隙转动副模型的建立. 清华大学学报:自然科学版 , 1996, 36 (8) : 105–109.
[63] 陈滨, 潘寒萌. 含铰接间隙与杆件柔性的空间伸展机构单元的动力学建模与计算模, 第二部分:系统动态特性的计算模拟结果. 导弹与航天运载技术 , 1997 (3) : 33–40.
[64] 王天舒, 孔宪仁, 王本利, 等. 含铰间间隙的航天器附件展开过程分析. 哈尔滨工业大学学报 , 2001, 33 (3) : 283–286.
[65] Li J L, Yan S Z, Guo F, et al. Effects of damping, friction, gravity, and flexibility on the dynamic performance of a deployable mechanism with clea-rance. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science , 2013, 227 (8) : 1791–1803 DOI:10.1177/0954406212469563 .
[66] Zhao Y, Bai Z F. Dynamics analysis of space robot manipulator with joint clearance. Acta Astronautica , 2011, 68 (7) : 1147–1155 .
[67] Bai Z F, Zhao Y. A hybrid contact force model of revolute joint with clearance for planar mechanical systems. International Journal of Non-Linear Mecha-nics , 2013, 48 : 15–36 DOI:10.1016/j.ijnonlinmec.2012.07.003 .
[68] 何柏岩, 高峰, 王树新. 计及铰链间隙的机械臂动力学建模与仿真. 天津大学学报 , 2005, 38 (9) : 795–799.
[69] 王三民, 沈允文, 董海军. 含摩擦和间隙直齿轮副的混沌与分叉研究. 机械工程学报 , 2002, 38 (9) : 8–11.
[70] 谷勇霞, 赵杰亮, 阎绍泽, 等. 考虑谐波传动滞后的柔性空间机械臂运动精度. 机械工程学报 , 2013, 49 (23) : 74–79.
[71] Zhao J L, Yan S Z, Wu J N. Analysis of parameter sensitivity of space manipulator with harmonic drive based on the revised response surface method. Acta Astronautica , 2014, 98 (5) : 86–96 .
[72] Yang T F, Yan S Z, Han Z. Nonlinear model of space manipulator joint considering time-variant stiffness and backlash. Journal of Sound and Vibration , 2015, 341 : 246–259 DOI:10.1016/j.jsv.2014.12.028 .
[73] Yang T F, Yan S Z, Ma W. Joint dynamic analysis of space manipulator with planetary gear train trans-mission. Robotica , 2016, 34 (5) : 1042–1058 DOI:10.1017/S0263574714002045 .
[74] Yang T F, Yan S Z. Dynamic simulation of planetary gearbox. Key Engineering Materials , 2014, 584 : 220–224 .
[75] 阎绍泽, 申永胜, 陈洪彬. 考虑杆件柔性和铰间隙的可展结构动力学数值模拟. 清华大学学报:自然科学版 , 2003, 43 (2) : 145–148.
[76] Yan S Z, Guo P F. Kinematic accuracy analysis of flexible mechanisms with uncertain link lengths and joint clearances. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science , 2011, 225 (8) : 1973–1983 DOI:10.1177/0954406211401499 .
[77] 陈鹿民, 阎绍泽, 金德闻, 等. 含间隙铰空间可展桁架结构的动力学实验. 清华大学学报:自然科学版 , 2003, 43 (8) : 1027–1030.
[78] 宿月文, 朱爱斌, 陈渭, 等. 间隙约束副摩擦接触对多体系统动态特性的影响. 润滑与密封 , 2008 (8) : 16–19.
[79] Xun J, Yan S Z. A revised Hilbert-Huang trans-formation based on the neural networks and its application in vibration signal analysis of a deployable structure. Mechanical Systems and Signal Processing , 2008, 22 (7) : 1705–1723 DOI:10.1016/j.ymssp.2008.02.008 .
[80] Liu T, Yan S Z, Zhang W. Time-frequency analysis of nonstationary vibration signals for deployable structures by using the constant-Q nonstationary gabor transform. Mechanical Systems & Signal Processing , 2016, 75 : 228–244 .
[81] 荀剑, 阎绍泽. 基于小波变换的含间隙太阳能帆板动力学试验分析. 清华大学学报:自然科学版 , 2006, 46 (11) : 1844–1847.
[82] 王国庆, 刘宏昭, 孙百俊. 考虑边界润滑的间隙机构运动副接触磨损. 长安大学学报:自然科学版 , 2002, 22 (6) : 85–88.
[83] Ravn P, Shivaswamy S, Alshaer B J, et al. Joint clearances with lubricated long bearings in multibody mechanical systems. Journal of Mechanical Design , 2000, 122 (4) : 484–488 DOI:10.1115/1.1314867 .
[84] Flores P, Ambrósio J, Claro J C P, et al. Lubricated revolute joints in rigid multibody systems. Nonlinear Dynamics , 2009, 56 (3) : 277–295 DOI:10.1007/s11071-008-9399-2 .
[85] Dupac M, Beale D G. Dynamic analysis of a flexible linkage mechanism with cracks and clearance. Mechanism and Machine Theory , 2010, 45 (12) : 1909–1923 DOI:10.1016/j.mechmachtheory.2010.07.006 .
[86] Flores P, Ambrósio J, Claro J P. Dynamic analysis for planar multibody mechanical systems with lubricated joints. Multibody System Dynamics , 2004, 12 (1) : 47–74 DOI:10.1023/B:MUBO.0000042901.74498.3a .
[87] Tian Q, Liu C, Machado M, et al. A new model for dry and lubricated cylindrical joints with clearance in spatial flexible multibody systems. Nonlinear Dyna-mics , 2011, 64 (1/2) : 25–47 .
[88] Flores P. Modeling and simulation of wear in revolute clearance joints in multibody systems. Mechanism and Machine Theory , 2009, 44 (6) : 1211–1222 DOI:10.1016/j.mechmachtheory.2008.08.003 .
[89] Bai Z F, Zhao Y, Wang X G. Wear analysis of revolute joints with clearance in multibody systems. Science China Physics, Mechanics and Astronomy , 2013, 56 (8) : 1581–1590 DOI:10.1007/s11433-013-5125-2 .
[90] Tasora A, Prati E, Silvestri M. Experimental investigation of clearance effects in a revolute joint // Proceedings of the 2004 AIMETA International Tribology Conference. Rome , 2004 : 14–17 .
[91] Mukras S, Kim N H, Mauntler N A, et al. Comparison between elastic foundation and contact force models in wear analysis of planar multibody system. Journal of Tribology , 2010, 132 (3) : 1–11 .
[92] Mukras S, Kim N H, Mauntler N A, et al. Analysis of planar multibody systems with revolute joint wear. Wear , 2010, 268 (5) : 643–652 .
[93] Li P, Chen W, Zhu A B. An improved practical model for wear prediction of revolute clearance joints in crank slider mechanisms. Science China Techno-logical Sciences , 2013, 56 (12) : 2953–2963 DOI:10.1007/s11431-013-5401-4 .
[94] Xiang W W K, Yan S Z, Wu J N. A comprehensive method for joint wear prediction in planar mechanical systems with clearances considering complex contact conditions. Science China: Technological Sciences , 2015, 58 (1) : 86–96 DOI:10.1007/s11431-014-5685-z .
[95] Li Z, Cai G, Huang Q, et al. Analysis of nonlinear vibration of a motor-linkage mechanism system with composite links. Journal of Sound & Vibration , 2008, 311 : 924–940 .
[96] Moon F C, Li G X. Experimental study of chaotic vibrations in a pin-jointed space truss structure. AIAA Journal , 2012, 28 (5) : 915–921 .
[97] Rhee J, Akay A. Dynamic response of a revolute joint with clearance. Mechanism and Machine Theory , 1996, 31 (1) : 121–134 DOI:10.1016/0094-114X(95)00061-3 .
[98] 卢绪祥, 刘正强, 黄树红, 等. 含间隙碰撞振动系统的非线性振动特性. 动力工程学报 , 2012, 32 (5) : 388–393.
[99] Tang Y, Chang Z, Dong X, et al. Nonlinear dynamics and analysis of a four-bar linkage with clearance. Frontiers of Mechanical Engineering , 2013, 8 (2) : 160–168 DOI:10.1007/s11465-013-0258-6 .
[100] Rahmanian S, Ghazavi M R. Bifurcation in planar slider-crank mechanism with revolute clearance joint. Mechanism and Machine Theory , 2015, 91 : 86–101 DOI:10.1016/j.mechmachtheory.2015.04.008 .
[101] Farahanchi F, Shaw S W. Chaotic and periodic dynamics of a slider-crank mechanism with slider clearance. Journal of Sound and Vibration , 1994, 177 (3) : 307–324 DOI:10.1006/jsvi.1994.1436 .
[102] 赵永辉, 胡海岩. 具有操纵面间隙非线性二维翼段的气动弹性分析. 航空学报 , 2003, 24 (6) : 521–525.
[103] 胡海岩. 分段光滑机械系统动力学的进展. 振动工程学报 , 1995, 8 (4) : 331–341.
[104] Jin C M, Qiu Y, Fan L, et al. The non-linear dynamic behavior of an elastic linkage mechanism with clearances. Journal of Sound and Vibration , 2002, 249 (2) : 213–226 DOI:10.1006/jsvi.2001.3771 .
[105] 丁旺才, 谢建华. 碰撞振动系统分岔与混沌的研究进展. 力学进展 , 2005, 35 (4) : 513–524.
[106] Muvengei O, Kihiu J, Ikua B. Numerical study of parametric effects on the dynamic response of planar multi-body systems with differently located fric-tionless revolute clearance joints. Mechanism & Machine Theory , 2012, 53 (7) : 30–49 .
[107] Wu J N, Yan S Z. Fault severity evaluation and improvement design for mechanical systems using the fault injection technique and gini concordance measure. Mathematical Problems in Engineering , 2014 : 416048 .
[108] Wu J N, Yan S Z, Xie L Y, et al. Reliability apportionment approach for spacecraft solar array using fuzzy reasoning Petri net and fuzzy comprehensive evaluation. Acta Astronautica , 2012, 76 (4) : 136–144 .
[109] Wu J N, Yan S Z, Xie L Y. Reliability analysis method of a solar array by using fault tree analysis and fuzzy reasoning Petri net. Acta Astronautica , 2011, 69 (11) : 960–968 .
[110] 黄玮, 冯蕴雯, 吕震宙, 等. 考虑铰链运动副间隙的机构运动可靠性分析模型. 机械强度 , 2007, 29 (2) : 264–268.
[111] 孟宪举, 张策, 詹梅晶, 等. 含间隙连杆机构精度概率分析模型. 机械设计 , 2004, 21 (9) : 35–37.
[112] Pan Z H, Wu J N, Yan S Z, et al. Feature generation method for fault diagnosis of closed cable loop used in deployable space structures. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk & Reliability , 2014, 228 (6) : 631–640 .
[113] Wu J N, Yan S Z, Zuo M J. Evaluating the reliability of multi-body mechanisms: a method considering the uncertainties of dynamic performance. Reliability Engineering & System Safety , 2016, 149 : 96–106 .
[114] Xiang W W K, Yan S Z, Wu J N, et al. Complexity evaluation of nonlinear dynamic behavior of mechanisms with clearance joints by using the fractal method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science , 2014, 228 (18) : 3482–3495 DOI:10.1177/0954406214531251 .
[115] Song B J, Yan S Z, Xiang W W K. A measurement method for distinguishing the real contact area of rough surfaces of transparent solids using improved Otsu technique. Chinese Physics B , 2015, 24 (1) : 354–360 .
[116] Adams G G, Nosonovsky M. Contact modeling forces. Tribology International , 2000, 33 (5/6) : 431–442 .
[117] Johnson K L. The contribution of micro/nano-tribology to the interpretation of dry friction. Pro-ceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science , 2000, 214 (1) : 11–21 DOI:10.1243/0954406001522778 .
[118] Aronov V, D'Souza A F, Kalpakjian S, et al. Interactions among friction, wear, and system stiffness, part 1: effect of normal load and system stiffness. ASME J of Lubrication Technology , 1984, 106 (1) : 54–58 .
[119] Aronov V, D'Souza A F, Kalpakjian S, et al. Interactions among friction, wear, and system stiffness, part 2: vibrations induced by dry friction. ASME J of Lubrication Technology , 1984, 106 (1) : 59–64 .
[120] Soom A, Chen J W. Simulation of random surface roughness-induced contact vibrations at Hertzian contacts during steady sliding. J Tribology , 1986, 108 (1) : 123–127 DOI:10.1115/1.3261131 .
[121] Adams G G. Self-excited oscillations in sliding with a contact friction coefficient -a simple model. J Tribology , 1996, 118 (4) : 819–823 DOI:10.1115/1.2831614 .
[122] Kalker J J, Dekking F M, Vollebregt E A H. Simulation of rough, elastic contacts. J of Applied Mechanics , 1997, 64 (2) : 361–368 DOI:10.1115/1.2787315 .
[123] Bengisu M T, Akay A. Relation of dry-friction to surface soughness. J Tribology , 1997, 119 (1) : 18–25 DOI:10.1115/1.2832457 .
[124] Deck J F, Dubowsky S. On the limitations of predictions of the dynamic response of machines with clearance connections. ASME Journal of Mechanical Design , 1994, 116 (3) : 833–841 DOI:10.1115/1.2919457 .
[125] Li J L, Yan S Z. Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit. Applied Thermal Engineering , 2014, 71 (1) : 419–432 DOI:10.1016/j.applthermaleng.2014.07.015 .
[126] Li J L, Yan S Z, Cai R Y. Thermal analysis of composite solar array subjected to space heat flux. Aerospace Science & Technology , 2013, 27 (1) : 84–94 .
[127] Zhao J L, Wu J N, Yan S Z, et al. Dynamic modeling and motion precision analysis of spacecraft manipulator with harmonic drive considering the alternate thermal field in orbit. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering , 2015, 229 : 135–148 DOI:10.1177/0954410014527267 .
[128] Zhang Z, Xu L, Flores P, et al. A DOE-and Kriging-based model for studying on the dynamics of multibody mechanical systems with revolute joint clearance // ASME 2013 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers. San Diego, 2013: 15-21 http://webs.wichita.edu/?u=meweb&p=/facultyandstaff/lankarani/publications/