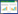传统结构力学理论和工程领域经常将细长构件的边界条件简化处理为简支、固支、自由等理想边界条件。然而, 很多实际结构(特别是复杂产品系统中的子结构)中, 由于材料性能不理想、结构设计的缺陷或受限制(重量、几何空间等)、结构加工工艺、结构承受苛刻的载荷条件等因素, 使得边界条件具有较大的不确定性, 在实际工程中体现出固支和简支根部的挠性变形, 自由端受单面约束限制, 边界非光滑产生干摩擦、碰撞, 以及发生干涉而卡死等现象。这些因素可能对产品的性能和可靠性产生很大程度的影响, 例如很多产品质量下降和性能失效的主要原因之一就在于边界连接问题。因此, 研究边界条件不确定性对结构力学性能的影响, 不仅具有很强的理论价值, 也是实际工程问题的需要。

对于经典边界条件下梁的动力学问题的研究已相当成熟。Trail-Nash等^[1]在理论上给出6类经典边界条件(简支-简支、简支-自由、自由-自由、固支-固支、固支-自由和固支-简支)下的频率方程及部分振型函数, Huang^[2]系统全面地解决了6类经典边界条件下的频率方程和振型函数问题。不同于上述6类经典边界条件, 当边界条件具有不确定性时, 首先需要对其不确定性进行描述和量化; 同时, 边界的不确定性将使得梁存在整体转动和/或平动自由度, 以及位移和力边界条件耦合, 使系统力学问题的求解非常复杂。对于悬臂梁根部存在挠性时的动力学问题, 文献[3-13]将悬臂梁根部退化成线弹性弹簧约束, 分析了根部挠性对梁动态特性和响应的影响, 但没有研究梁的整体运动特性。柔性多体系统动力学理论容易将边界不确定性参数化以便于工程分析, 又能同时描述系统的整体运动和相对变形, 所以得到广泛应用。基于柔性多体系统动力学理论, 文献[14]建立了挠性根部梁的严格非线性动力学模型; 文献[15]进一步建立整体转动状态下挠性根部梁的严格非线性动力学模型, 分析系统的分岔与屈曲行为; 文献[16]综合考虑整体转动和局部限制约束, 研究绕轴线自转悬臂梁自由端受单侧约束下的稳定性, 获得较丰富的非线性现象; 文献[17]建立任意边界梁的动力学模型, 得到广义边界条件下梁的横向振动代数特征方程、特征函数及特征值的退化表达式, 通过算例分析边界小扰动对固支-固支梁横向振动特征的影响规律。

本文考虑可移动简支支撑具有挠性/刚度不确定性时简支梁的振动特性与压缩稳定性问题, 采用柔性多体系统动力学理论的相对描述方式, 建立系统的大挠度非线性动力学模型, 分析边界不确定性/挠性对系统振动特性与压缩稳定性的影响规律, 以提升对具有边界不确定性结构力学性能的认识。

1 动力学建模

本文只考虑简支梁的轴向可移动简支支撑刚度存在不确定性/挠性(不可移简支不确定性可类似处理), 采用柔性多体系统相对描述理论, 将移动简支支撑刚度的不确定性参数化的思路进行动力学建模, 如图 1所示。图 1中, $O{\rm{ -}}\tilde X\tilde Y$为惯性坐标系, 单位矢量为i和j; O-XY为描述梁相对变形的浮动坐标系, 其运动由可移动简支边不确定性导致的支撑弹性变形引起, 相对于坐标系$O{\rm{ -}}\tilde X\tilde Y$的转角为α(t)。设梁长为L, 横截面积为A, 转动惯量为I, 密度为ρ, 弹性模量为E, 梁在可移动简支边受OX方向的压力F作用。

系统的建模基于以下3个基本假定: 1)柔性梁的变形运动在O-XY平面内; 2)只考虑梁的几何非线性, 而材料本构特性仍假设为线性的; 3)不考虑梁几何和物理参数的不确定性, 仅考虑可移动简支边支撑刚度的不确定性, 基于柔性多体系统相对描述理论将其参数化, 假设可移动简支边不确定性导致的支撑弹性力满足非线性强化弹性关系:

$ R = K(\mathit{\Delta }x) + \mathit{\Lambda} {(\mathit{\Delta }x)^3}, $

其中, K为线弹性刚度, Λ为非线性弹性刚度, 均为不确定性参数。

引入以下记号: 1)在浮动坐标系O-XY中, 柔性梁的变形使中轴线上原来自然状态下的(x, 0)点, 在t时刻变为(X, Y), 且中轴线转角为θ(x, t); 2)梁不可移动简支边端点到(X, Y)点的弧长为s(x, t), 记$\gamma (x, \; t)=\partial s (x, \; t)/\partial x$为梁中轴线的伸长率。

下面采用广义Hamilton原理, 建立系统的动力学方程。

在惯性坐标系$O{\rm{ -}}\tilde X\tilde Y$中, 梁的位移场为

$ \boldsymbol{r} = (X\cos \alpha-Y\sin \alpha )\boldsymbol{i} + (X\sin \alpha + Y\cos \alpha )\boldsymbol{j}, $

(1)

受完整几何约束

$ \left\{ \begin{array}{l} X' = \gamma \cos \theta, \\ Y' = \gamma \sin \theta \; \end{array} \right. $

(2)

作用, 式中X′和Y′表示对空间坐标x的偏导数。

梁的线性本构方程为

$ \left\{ \begin{array}{l} N = EA(\gamma-1), \\ M = EI\theta ', \end{array} \right. $

(3)

式中, N为轴力, M为弯矩。由梁的位移场(式(1))和本构关系(式(3))可计算得到梁的能量。

梁的动能为

$ T = (1/2)\int_{\;0}^{\;L} {\rho A\left[{{{(\dot X-Y\dot \alpha )}^2} + {{(\dot Y + X\dot \alpha )}^2}} \right]{\rm{d}}x}, $

(4)

式中, $\dot X$和$\dot Y$表示对时间坐标的偏导数。梁的势能为

$ U = (1/2)\int_{\;0}^{\;L} {\left[{EI{{(\theta ')}^2} + EA{{(\gamma-1)}^2}} \right]{\rm{d}}x} 。 $

(5)

移动简支不确定性导致的支撑弹性变形势能为

$ V = \left( {1{\rm{/}}2} \right)K{X^2}(L,t){\sin ^2}\alpha + \left( {1{\rm{/}}4} \right)\mathit{\Lambda} {X^4}(L,t){\sin ^4}\alpha , $

(6)

移动简支端压力P所作的虚功为

$ \delta W = F\delta \left[{L-X(L, t)\cos \alpha } 。\right] $

(7)

由广义Hamilton原理, 并采用Lagrange乘子法, 考虑约束方程(式(2))的影响, 有

$ \begin{array}{l} \int_{\, {t_1}}^{\, {t_2}} {\left\{ {\delta \left[{(T- U- V)- \int_{\, 0}^{\, L} {[P(X'-\gamma \cos \theta ) + } } \right.} \right.} \\ \left. {\left. {Q(Y'-\gamma \sin \theta )]{\rm{d}}x} \right] + \delta W} \right\}{\rm{d}}t = 0。 \end{array} $

(8)

式中, P和Q为Lagrange乘子, 其物理意义为梁在浮动坐标系中水平和垂直方向的内力, 与梁的轴力和剪力S有以下关系

$ \left\{ \begin{array}{l} P = N\cos \theta-S\sin \theta, \\ Q = N\sin \theta + S\cos \theta 。 \end{array} \right. $

(9)

将已求得的动能、势能及虚功表达式代入式(8), 即可得到系统的动力学方程组:

$ \left\{ \begin{array}{l} X'- \gamma \cos \theta = 0, \\ Y'- \gamma \sin \theta = 0, \\ EI\theta '' + \gamma [-P\sin \theta + Q\cos \theta] = 0, \\ EA(\gamma - 1) - [P\cos \theta + Q\sin \theta] = 0, \\ P' - \rho A\frac{{\rm{d}}}{{{\rm{d}}t}}(\dot X - Y\dot \alpha ) + \rho A(\dot Y + X\dot \alpha )\dot \alpha = 0, \;\;\;\;\\ Q' - \rho A\frac{{\rm{d}}}{{{\rm{d}}t}}(\dot Y + X\dot \alpha ) - \rho A(\dot X - Y\dot \alpha )\dot \alpha = 0, \\ \frac{{\rm{d}}}{{{\rm{d}}t}}\left\{ {\int_{\;0}^{\;L} {\rho A[-Y\dot X + X\dot Y + ({X^2} + {Y^2})\dot \alpha]{\rm{d}}x} } \right\} -FX(L, \;t)\sin \alpha \\ \quad + \frac{1}{2}K{X^2}(L, \;t)\sin 2\alpha + \frac{1}{2}\Lambda {X^4}(L, \;t){\sin ^2}\alpha \sin 2\alpha = 0, \end{array} \right. $

(10)

及其边界条件

$ \left\{ \begin{array}{l} X(0, \;t) = 0, \\ Y(0, \;t) = 0, \;\theta '(0, \;t) = 0, \;\\ Y(L, \;t) = 0, \;\theta '(L, \;t) = 0, \\ P(L, \;t) + KX(L, \;t){\sin ^2}\alpha + \\ \;\;\;\;\;\Lambda {X^3}(L, \;t){\sin ^4}\alpha + F\cos \alpha = 0。 \end{array} \right. $

(11)

考虑不可拉伸梁, 即$\gamma (x, t) \equiv 1$, 引进无量纲化参数, 设

$ \left\{ {\begin{array}{*{20}{l}} {\xi = x/L,\;u = (X - x)/L,\;v = Y/L,}\\ {p = P{L^2}/EI,\;q = Q{L^2}/EI,}\\ {\beta = \sqrt {\rho A{L^4}/EI} ,\;\mu = K{\rm{ /}}\rho AL,\;}\\ {\eta = \mathit{\Lambda} L/\rho A,\;f = F/\rho A{L^2}。} \end{array}} \right. $

(12)

显然, μ和η仍然为不确定性参数, 且与不确定性刚度参数K和Λ成正比。

记x为ξ, 则式(10)和(11)无量纲化为

$ \left\{ \begin{array}{l} u' = \cos \theta- 1, \;v' = \sin \theta, \\ \theta '' = p\sin \theta- q\cos \theta, \\ p' = {\beta ^2}\frac{{\rm{d}}}{{{\rm{d}}t}}(\dot u- v\dot \alpha ) - {\beta ^2}[\dot v + (x + u)\dot \alpha]\dot \alpha, \\ q' = {\beta ^2}\frac{{\rm{d}}}{{{\rm{d}}t}}[\dot v + (x + u)\dot \alpha] + {\beta ^2}(\dot u - v\dot \alpha )\dot \alpha, \\ \frac{{\rm{d}}}{{{\rm{d}}t}}\int_{\;0}^{\;1} {\{ - v\dot u + (x + u)\dot v + [{{(x + u)}^2} + {v^2}]\dot \alpha \} {\rm{d}}x} - \\ \;\;\;\;f[1 + u(1, \;t)]\sin \alpha + \frac{1}{2}\mu {[1 + u(1, \;t)]^2}\sin 2\alpha + \\ \;\;\;\;\frac{1}{2}\eta {[1 + u(1, \;t)]^4}{\sin ^2}\alpha \sin 2\alpha = 0, \end{array} \right. $

(13)

对应的边界条件为

$ \left\{ \begin{array}{l} u(0, \;t) = 0, \;v(0, \;t) = 0, \;\theta '(0, \;t) = 0, \;\\ v(1, \;t) = 0, \;\theta '(1, \;t) = 0, \\ p(1, \;t) + \mu {\beta ^2}[1 + u(1, \;t)]{\sin ^2}\alpha + \eta {\beta ^2}[1 + \\ \;\;\;\;u(1, \;t){]^3}{\sin ^4}\alpha + {\beta ^2}f\cos \alpha = 0。 \end{array} \right. $

(14)

不考虑轴向压缩载荷的作用, 假设梁及其可移动弹性支撑均为小变形, 则对式(13)及其边界条件(式(14))进行线性化, 可获得梁横向振动的线性化动力学模型:

$ \left\{ \begin{array}{l} {v^{(4)}} + {\beta ^2}\ddot v + {\beta ^2}x\ddot \alpha = 0, \\ \ddot \alpha + 3\int_0^1 {x\ddot v{\rm{d}}x} + 3\mu \alpha = 0, \\ v(0, \;t) = 0, \;v''(0, \;t) = 0, \;v(1, \;t) = 0, \;v''(1, \;t) = 0。 \end{array} \right. $

(15)

做线性变换

$ w = v + x\alpha, $

(16)

则式(15)中梁的变形方程可变换为

$ \left\{ \begin{array}{l} {w^{(4)}} + {\beta ^2}\ddot w = 0, \\ w(0, \;t) = 0, \;w''(0, \;t) = 0, \\ w'''(1, \;t)-\mu {\beta ^2}w(1, \;t) = 0, w''(1, \;t) = 0, \end{array} \right. $

(17)

此即简支-弹性支撑梁的经典线性动力学方程, 具有混合边界条件且未包含描述梁整体转动的变量, 不能描述刚性梁的转动。线性方程组(式(15))采用相对描述方式, 同时具有描述梁相对变形和整体转动的变量, 可描述刚性梁的整体转动, 且梁变形控制方程的边界条件非常简单, 更有利于近似解析分析。

2 边界不确定性对梁横向振动特性的影响

当简支梁可移动简支支撑刚度存在不确定性时, 其线性动力学模型为式(15), 其中μ是表征可移动简支支撑刚度不确定性的无量纲化参数。令

$ {(v, \;\alpha )^{\rm{T}}} = {({v_1}, \;{v_2})^{\rm{T}}}\exp ({\rm{i}}\omega t), $

(18)

将式(18)代入式(15), 即可得到系统线性自由振动的无量纲化特征方程组:

$ \left\{ \begin{array}{l} v_1^{(4)} - {\lambda ^4}{v_1} - ({\lambda ^4}/\mu {\beta ^2})x{{v'''}_1}\;(1) = 0, \\ {v_2} = (1/\mu {\beta ^2}){{v'''}_1}\;(1), \\ {v_1}(0) = 0, {v_1}^{\prime \prime }(0) = 0, {v_1}(1) = 0, {v_1}^{\prime \prime }(1) = 0, \end{array} \right. $

(19)

式中, $\lambda=\sqrt {\beta \omega } $。微分特征方程(式(19))有通解

$ {v_1} = cx + {c_1}\sin \lambda x + {c_2}\cos \lambda x + {c_3}{{\rm{e}}^{\lambda x}} + {c_4}{{\rm{e}}^{ - \lambda x}}, $

(20)

将式(20)代入式(19), 可得到代数特征值方程:

$ \sin \lambda + {\lambda ^3}(\cos \lambda - {\rm{cth}}\lambda \sin \lambda )/2\mu {\beta ^2} = 0, $

(21)

对应的振型函数为

$ \left\{ \begin{array}{l} {v_1}(x) = - 2(\sin \lambda \;{\rm{sh}}\lambda )x + {\rm{sh}}\lambda \sin \lambda x + \sin \lambda \;{\rm{sh}}\lambda x, \\ {v_2} = (\sin \lambda \;{\rm{ch}}\lambda - \cos \lambda \;{\rm{sh}}\lambda ){\lambda ^3}/(\mu {\beta ^2})。 \end{array} \right. $

(22)

由线性变换(式(16)), 可得到梁在惯性坐标系中的振型函数:

$ w(x) = {v_2}x + {v_1}(x)。 $

(23)

显然, 由于μ是不确定性参数, 因此特征值λ具有不确定性, 从而振型函数也具有不确定性。由于代数特征方程(式(21))不存在解析解, 所以采用数值方法分析移动简支不同支撑刚度对系统前3阶特征值的影响。为简单, 本文假设支撑刚度具有区间型不确定性, 且取不确定性参数$\mu {\beta ^2}$均值的±10%区间进行分析。

在不确定性参数$\mu {\beta ^2}$均值的±10%区间内对代数特征值方程(式(21))进行数值求解, 该不确定性参数均值对系统前3阶均值(No.1, No.2和No.3)频率的影响如图 2所示。

数值计算与图 2表明: 1)系统前3阶特征值随可移动简支支撑刚度的增加而升高, 随着支撑刚度的增加, 趋近于简支梁的前3阶特征值; 2)移动简支支撑刚度的分散性对不同阶特征值的影响不同, 随特征值阶数的升高逐渐向支撑刚度增加的方向偏移(曲线斜率最大的区域), 即简支支撑刚度小时, 对低阶(特别是第一阶)频率影响大, 简支支撑刚度大时, 对高阶频率影响大, 支撑刚度达到一定值后, 简支支撑的挠性对低阶频率的影响可忽略; 3)在不确定性参数$\mu {\beta ^2}$均值的±10%区间内, 第1阶特征值的分散性在±3%以内, 第2阶特征值的分散性在±1.5%以内, 第3阶特征值的分散性在±1.1%以内, 即随着特征值阶数的升高, 其相对分散性将下降。

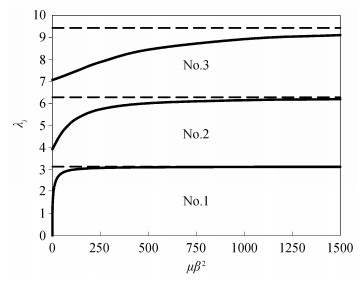
下面分析可移动简支支撑刚度对简支梁振型的影响。对于不同的支撑刚度, 梁在惯性坐标系中的振型函数如图 3所示, 各振型采用均方模1的方式进行标准化。实线是挠性简支支撑梁的振型, 虚线是理想简支梁的振型。

图 3表明: 1)当简支梁可移动简支支撑刚度较小(实际的简支-弹性支撑梁)时, 系统的第1阶振动形态主要体现为梁的整体转动, 对第2, 3阶端部的约束也较小, 与简支梁相应模态差别较大, 基本上破坏了其相对梁中间的对称或反对称性质; 2)随着简支梁可移动简支支撑刚度的增加, 其对梁端部的约束逐渐增强, 系统的第1阶振动形态逐渐体现为梁的第1阶横向弯曲振型, 各阶振型也逐渐趋近理想简支梁的振型, 且低阶比高阶趋近速度更快, 与前面的特征值随支撑刚度变化的趋势一致。

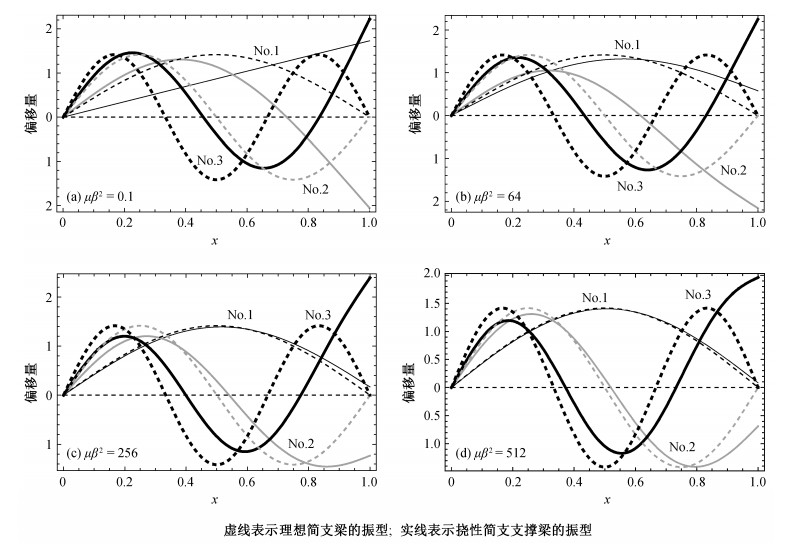
对于不同的支撑刚度, 梁在相对坐标系中的振型函数如图 4所示, 各振型同样采用均方模1的方式进行标准化。

图 4表明:可移动简支支撑刚度对简支梁相对坐标系中的第1阶振型影响很小, 但对第2, 3阶等高阶振型的影响非常显著, 在支撑刚度偏低的较大范围内, 前两阶振型都没有节点(与经典梁模态节点的基本定性性质^[18]不同), 表明多体系统动力学离散建模时, 需慎重采用结构的经典模态进行离散。

3 边界不确定性对简支梁轴向压缩稳定性的影响

移动简支支撑刚度具有不确定性的简支梁的无量纲化静力学方程组及其边界条件可由式(13)和(14)获得:

$ \left\{ \begin{array}{l} u' = \cos \theta- 1, \;v' = \sin \theta, \\ \theta '' = p\sin \theta- q\cos \theta, \\ q' = 0, \\ p =- {\beta ^2}\{ \mu [1 + u(1)]{\sin ^2}\alpha + \eta {[1 + u(1)]^3}{\sin ^4}\alpha + \\ \;\;\;\;\;f\cos \alpha \} \{ f - \mu [1 + u(1)]\cos \alpha - \eta [1 + \\ \;\;\;\;\;u(1){]^3}{\sin ^2}\alpha \cos \alpha \} \sin \alpha = 0, \\ u(0) = 0, \;v(0) = 0, \;\theta '(0) = 0, \;v(1) = 0, \;\theta '(1) = 0。 \end{array} \right. $

(24)

方程组(24)是强非线性连续体微分-代数方程组, 无解析解。本文仅考虑其梁的一阶失稳, 依据上节分析, 可采用简支梁的一阶模态离散方程组(24)的连续体微分方程组, 即设

$ v(x) = {v_1}\sin {\rm{\pi }}x, $

(25)

式中, v₁为广义坐标。方程组(24)中的几何约束方程

$ u' = \cos \theta-1, \;v' = \sin \theta $

(26)

在保留到广义坐标v₁的3阶项时, 可近似为

$ u' \approx-\frac{1}{2}{(v')^2}, \quad u(1) \approx-\frac{1}{2}\int_0^1 {{{(v')}^2}{\rm{d}}x} =-\frac{1}{2}{{\rm{\pi }}^2}v_1^2, $

(27)

$ \theta (x) = \arcsin (v') \approx v' + {(v')^3}{\rm{/}}6。 $

(28)

仍然保留广义坐标v₁、转角α及其耦合的3阶项, 则方程组(24)中梁的变形势能为

$ J = \frac{1}{2}\int_0^1 {{{(\theta ')}^2}- {\beta ^2}\left[{\mu {\alpha ^2} + f\left( {1-\frac{1}{2}{\alpha ^2}} \right)} \right]{{(v')}^2}{\rm{d}}x} 。 $

(29)

将式(25)和(28)代入式(29), 对广义坐标v₁变分, 并结合方程组(24)中转角满足的代数方程, 可获得移动简支支撑刚度具有不确定性简支梁的无量纲化近似静态平衡方程组:

$ \left\{ \begin{array}{l} [2({{\rm{\pi }}^2}-{\beta ^2}f) + {\beta ^2}(f-2\mu ){\alpha ^2} + {{\rm{\pi }}^4}v_1^2]{v_1} = 0, \\ [2(f-\mu ) + (\mu-2\eta ){\alpha ^2} + \mu {{\rm{\pi }}^2}v_1^2]\alpha = 0。 \end{array} \right. $

(30)

由式(30)可得到移动简支支撑刚度具有不确定性时压缩简支梁的稳定性。

1)当$f < {\rm{Min}}(\mu, \; {{\rm{\pi }}^2}/{\beta ^2})$时, 平凡解v₁稳定。

2)当$f \ge {\rm{Min}}(\mu, \; \; {{\rm{\pi }}^2}/{\beta ^2})$时, 平凡解v₁=0, α=0失稳, 此时存在两种情形。

情形1, $\mu < {{\rm{\pi }}^2}/{\beta ^2}$。当$\mu \le f \le (\mu + {{\rm{\pi }}^2}/{\beta ^2})/2$且弹性支撑非线性刚度系数$\eta > \mu /2$时, 平凡解${v_1}=0, \; \alpha=0$失稳, 叉式分岔到后屈曲解:

$ \left\{ \begin{array}{l} {v_1} = 0, \\ \alpha = \pm \sqrt {2(f-\mu )/(2\eta-\mu )} ; \end{array} \right. $

(31)

当$f \ge (\mu + {\pi ^2}/{\beta ^2})/2$且$\eta > \mu /2$时, 后屈曲解(式(31))演变为

$ \left\{ \begin{array}{l} {v_1} = \pm \sqrt {(4{\beta ^2}f- 2{\beta ^2}\mu- 2{{\rm{\pi }}^2})/{{\rm{\pi }}^4}- \mu {\beta ^2}}, \\ \alpha = \pm \sqrt {[2(f-\mu ) + \mu {{\rm{\pi }}^2}v_1^2]/2\eta -\mu } 。 \end{array} \right.\quad $

(32)

此时, 可移动弹性支撑非线性刚度较小, 使得$\eta \le \mu /2$, 方程(30)无解, 这是由该方程的简化所引起。

情形2, ${{\rm{\pi }}^2}/{\beta ^2} \le \mu $。当$f \ge {{\rm{\pi }}^2}/{\beta ^2}$时, 平凡解${v_1}=0, \; \alpha=0$失稳, 叉式分岔到后屈曲解:

$ \left\{ \begin{array}{l} {v_1} = \pm \frac{1}{{{{\rm{\pi }}^2}}}\sqrt {2({\beta ^2}f - {{\rm{\pi }}^2})}, \\ \alpha = 0。 \end{array} \right. $

(33)

平衡方程(30)的稳定性分析表明:当移动简支支撑刚度较小, 使得无量纲参数满足$\mu < {{\rm{\pi }}^2}/{\beta ^2}$时, 轴向压缩简支梁首先发生整体转动失稳, 随着压缩载荷的进一步增大, 梁才可能发生弯曲失稳; 当移动简支支撑刚度加大, 使得无量纲参数满足$\mu \ge {{\rm{\pi }}^2}/{\beta ^2}$时, 只发生梁的弯曲失稳, 而没有整体转动, 即简支梁支撑刚度的小不确定性不影响其轴向压缩稳定性。

下面对上述轴向压缩稳定性问题的近似解析分析进行初步验证和补充。首先是临界失稳值, 由于方程组(24)的初始平衡解是平凡解$\theta \equiv 0, \; \alpha \equiv 0$, 在其邻域线性化可得特征值问题:

$ \left\{ \begin{array}{l} \theta '' + {\beta ^2}f\theta = 0, \\ (f-\mu )\alpha = 0, \\ \theta '(0) = 0, \;\theta '(1) = 0。 \end{array} \right. $

(34)

特征方程(34)的特征值为

$ \left\{ \begin{array}{l} {f_{{\rm{c}}0, i}} = {(i{\rm{\pi }}/\beta )^2}\quad (i = 1, \;2, \;3, \;...), \\ {f_{{\rm{c0}}}} = \mu 。 \end{array} \right. $

(35)

显然, 近似分析的临界值与式(35)的前两阶相同, 即近似解析分析的失稳临界值是正确的。

由特征方程(34)和近似解析分析可知, 由平凡解$\theta \equiv 0, \; \alpha \equiv 0$失稳后分岔产生的屈曲解中, 压杆的初始整体刚性转动和杆的初始后屈曲解是解耦的, 互不影响, 因此退化为两个独立的稳定性问题。当可移动支撑刚度满足$\mu \ge {f_{{\rm{c}}0, 1}}={{\rm{\pi }}^2}/{\beta ^2}$时, 支撑刚度的小不确定性对其初始屈曲无影响, 因此退化为简支杆的屈曲问题, 关于该问题的研究已很成熟^[19], 本文不再讨论。当然, 若载荷大到一定程度使其一阶屈曲解发生二次分岔, 则支撑刚度不确定性的影响需要进一步研究。

若可移动支撑刚度满足$\mu < {f_{{\rm{c}}0, 1}}={{\rm{\pi }}^{\rm{2}}}/{\beta ^{\rm{2}}}$, 且载荷f超过临界值${f_{{\rm{c}}0}}=\mu $时, 压杆初始仅发生整体刚性转动, 满足非线性代数方程:

$ [f-(\mu + \eta )\cos \alpha + \eta {\cos ^3}\alpha]\sin \alpha = 0。 $

(36)

当$\eta \le \mu /2$且$f \ge \mu $时, 上式的稳定解为$\alpha={\rm{\pi }}$, 即可移动支撑非线性刚度小到满足$\eta \le \mu /2$时, 压杆将反转为拉杆, 此解不能由式(30)获得。

当$\eta > \mu /2$且$\mu \le f \le (\mu + {{\rm{\pi }}^2}/{\beta ^2})/2$时, 式(36)的稳定近似解为式(31)中的第2式, 初始分岔的精确解为

$ \left\{ \begin{array}{l} \alpha = \pm \arccos \left[{\frac{{\varphi (f, \;\mu, \;\eta ))}}{{\sqrt[3]{{18}}\eta }} + \frac{{\sqrt[3]{{2/3}}(\mu + \eta )}}{{\varphi (f, \;\mu, \;\eta )}}} \right], \\ \varphi (f, \;\mu, \;\eta ) = \sqrt[3]{{ - 9f{\eta ^2} + \sqrt 3 \sqrt {{\eta ^3}[27{f^2}\eta-4{{(\mu + \eta )}^3}]} }}。 \end{array} \right. $

(37)

当压缩载荷进一步增大, 特别是杆的整体刚性转动和屈曲耦合时, 需要由方程组(24)数值求解, 压杆的整体刚性转动和屈曲值有一定修正, 但分岔和屈曲的模式不会有太大的变化(可以由式(31)和(32)近似表示), 本文不再做进一步的分析。

4 结束语

本文面向实际工程普遍存在的边界不确定性, 应用柔性多体系统动力学相对描述理论, 建立了可移动简支刚度具有不确定性简支梁的非线性动力学模型, 解析结合数值分析了可移动简支刚度不确定性对系统振动特性和轴向压缩稳定性的影响, 得到以下结论和认识。

1)应用相对描述方式建立具有边界不确定性系统的动力学模型, 可以刻画边界不确定性导致的系统整体运动特性, 而绝对描述方式难以直观刻画此特性。

2)可移动简支支撑刚度对系统不同阶特征值的影响不同, 小刚度简支支撑相对对低阶(特别是第1阶)频率的影响大, 大刚度简支支撑相对对高阶频率的影响大, 支撑刚度达到一定值后, 可移动简支支撑的挠性对低阶频率的影响即可忽略。对于支撑刚度不确定性对系统振动频率的影响, 当移动简支支撑刚度参数KL³/EI的分散性在均值的±10%区间内时, 简支梁无量纲特征值参数$\lambda ({\lambda ^4}=\rho A{L^4}{\omega ^2}/EI)$的第1阶的分散性在±3%以内, 第2阶的分散性在±1.5%以内, 第3阶的分散性在±1.1%以内, 即随着特征值阶数的升高, 其相对分散性将下降。

3)对于惯性坐标系中的振型, 当简支梁可移动简支支撑刚度较小(实际的简支-弹性支撑梁)时, 系统第1阶振动形态主要体现为梁的整体转动, 第2, 3阶也与简支梁相应模态差别较大, 基本上破坏了梁模态的对称或反对称性质; 随着简支梁可移动简支支撑刚度的增加, 各阶振型也逐渐趋近理想简支梁的振型, 且低阶比高阶趋近速度更快。

4)对于相对坐标系中的振型, 与惯性坐标系中的影响不同, 可移动简支支撑刚度对第1阶振型影响很小, 但对第2, 3阶等高阶振型的影响非常显著, 在支撑刚度偏低的较大范围内, 前两阶振型都没有节点(与经典梁模态节点基本定性性质不同), 体现了整体运动对梁固有振动行为的影响特性, 表明在多体系统动力学离散建模时, 需要慎重采用结构的经典模态进行离散。例如应用假设模态法离散连杆机构时, 若简单采用梁的经典模态进行离散, 其计算精度可能难以保障。

5)对于可移动简支支撑刚度不确定性对轴向压缩简支梁稳定性的影响, 当移动简支支撑刚度较小, 满足$K{L^3}/EI < {{\rm{\pi }}^2}$时, 轴向压缩简支梁首先发生整体转动失稳, 随着压缩载荷的进一步增大, 梁才可能发生弯曲失稳; 当移动简支支撑刚度加大, 满足$K{L^3}/EI \ge {{\rm{\pi }}^2}$时, 系统只发生梁的弯曲失稳, 而没有整体转动, 即简支梁支撑刚度的小不确定性不影响其轴向压缩稳定性。

本文研究成果和认识对于梁构件约束边界设计、柔性多体动力学理论的建模及其应用具有重要意义。