文章信息
- 戈新生, 朱宁
- GE Xinsheng, ZHU Ning
- 基于Legendre伪谱法的3D刚体摆姿态轨迹跟踪控制
- Trajectory Tracking Control of 3D Rigid Body Pendulum Attitude Based on Legendre Pseudospectral Method
- 北京大学学报(自然科学版), 2016, 52(4): 619-626
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 619-626
-
文章历史
- 收稿日期: 2015-12-20
- 修回日期: 2016-02-03
- 网络出版日期: 2016-07-14
如图 2所示, 3D刚体摆绕一固定且无摩擦的支撑点

|
| 图 2. 3D刚体摆示意图 Figure 2. Schematic diagram of 3D rigid pendulum |
在惯性坐标系
| $J\mathit{\boldsymbol{\dot \omega }} = J\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{\omega }} + m\mathit{\boldsymbol{g\rho }} \times {\mathit{\boldsymbol{R}}^{\rm{T}}}{\mathit{\boldsymbol{e}}_3} + \mathit{\boldsymbol{u}},$ | (1) |
| $ \mathit{\boldsymbol{\dot R}} = \mathit{\boldsymbol{R\hat \omega }}, $ | (2) |
其中,
| $\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}} = \mathit{\boldsymbol{\hat ab}},$ | (3) |
其中斜对称矩阵
| $\mathit{\boldsymbol{\hat a}} = \left( {\begin{array}{*{20}{c}} 0&{ - {a_3}}&{{a_2}}\\ {{a_3}}&0&{ - {a_1}}\\ { - {a_2}}&{{a_1}}&0 \end{array}} \right)。$ |
令
| $J\mathit{\boldsymbol{\dot \omega }} = J\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{\omega }} + mg\mathit{\boldsymbol{\rho }} \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} + \mathit{\boldsymbol{u,}}$ | (4) |
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varGamma} = \boldsymbol{\varGamma} }} \times \mathit{\boldsymbol{\omega }}\mathit{\boldsymbol{。}} $ | (5) |
3D刚体摆在空间坐标系内存在两个平衡位置, 即悬垂平衡点和倒立平衡点[12-13], 意味着3D刚体摆的最优控制问题为从任意初始位置运动到目标平衡位置的姿态运动控制的过程。
2 Legendre闭环伪谱法求解在理想无干扰的环境中, 3D刚体摆可以根据控制目标, 利用Legendre伪谱法规得到的3D刚体摆的最优运动轨迹[7]。然后, 考虑3D刚体摆姿态控制过程中存在初始扰动的情况, 应用伪谱法并结合重规划策略, 设计状态闭环的轨迹跟踪控制器。将3D刚体摆姿态运动模型(式(1)和(2))在参考轨迹上线性化, 则有
| $\Delta \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{B}}\Delta \mathit{\boldsymbol{u}},$ | (6) |
其中,
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}}&{{\mathit{\boldsymbol{A}}_{12}}}\\ {{\mathit{\boldsymbol{A}}_{21}}}&{{\mathit{\boldsymbol{A}}_{22}}} \end{array}} \right],\mathit{\boldsymbol{B}} = {\left[ {{\mathit{\boldsymbol{B}}_1},\;{\mathit{\boldsymbol{B}}_2}} \right]^{\rm{T}}}, $ |
其中,
| $ {\mathit{\boldsymbol{A}}_{11}} = \left( {\begin{array}{*{20}{c}} 0&{\frac{{{J_2} - {J_3}}}{{{J_1}}}{\omega _3}}&{\frac{{{J_2} - {J_3}}}{{{J_1}}}{\omega _2}}\\ {\frac{{{J_3} - {J_1}}}{{{J_2}}}{\omega _3}}&0&{\frac{{{J_3} - {J_1}}}{{{J_2}}}{\omega _1}}\\ {\frac{{{J_1} - {J_2}}}{{{J_3}}}{\omega _2}}&{\frac{{{J_1} - {J_2}}}{{{J_3}}}{\omega _1}}&0 \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{A}}_{12}} = \left( {\begin{array}{*{20}{c}} 0&{ - \frac{{mgl}}{{{J_1}}}}&{\frac{{mgl}}{{{J_1}}}}\\ {\frac{{mgl}}{{{J_2}}}}&0&{ - \frac{{mgl}}{{{J_2}}}}\\ { - \frac{{mgl}}{{{J_3}}}}&{\frac{{mgl}}{{{J_3}}}}&0 \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{A}}_{21}} = \left( {\begin{array}{*{20}{c}} 0&{ - {\Gamma _3}}&{{\Gamma _2}}\\ {{\Gamma _3}}&0&{ - {\Gamma _1}}\\ { - {\Gamma _2}}&{{\Gamma _1}}&0 \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{A}}_{22}} = \left( {\begin{array}{*{20}{c}} 0&{{\omega _3}}&{ - {\omega _2}}\\ { - {\omega _3}}&0&{{\omega _1}}\\ {{\omega _2}}&{ - {\omega _1}}&0 \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{B}}_1} = \left( {\begin{array}{*{20}{c}} {\frac{1}{{{J_1}}}}&0&0\\ 0&{\frac{1}{{{J_2}}}}&0\\ 0&0&{\frac{1}{{{J_3}}}} \end{array}} \right), $ |
| $ {\mathit{\boldsymbol{B}}_2} = \left( {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right)。 $ |
根据线性化方程(6), 利用伪谱法设计姿态稳定控制器的目标, 就是通过确定输入修正量
| $ \begin{array}{l} \mathit{\pmb{\phi}}= \frac{1}{2}\Delta {\mathit{\boldsymbol{x}}^T}({t_f})\mathit{\boldsymbol{S}}\Delta \mathit{\boldsymbol{x}}({t_f}) + \\ \;\;\;\;\frac{1}{2}\int_{{t_0}}^{{t_f}} {\left[ {\Delta {\mathit{\boldsymbol{x}}^T}(t)\mathit{\boldsymbol{Q}}\Delta \mathit{\boldsymbol{x}}(t) + \Delta {\mathit{\boldsymbol{u}}^T}(t)\mathit{\boldsymbol{R}}\Delta \mathit{\boldsymbol{u}}(t)} \right]} \;{\rm{d}}t \end{array} $ | (7) |
最小。式(7)中, S是半正定的末端加权矩阵, Q是半正定的状态加权阵, R是正定的控制加权阵, 则相应的Hamilton函数为
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \frac{1}{2}\left[ {\Delta {\mathit{\boldsymbol{x}}^T}(t)\mathit{\boldsymbol{Q}}\Delta \mathit{\boldsymbol{x}}(t) + \Delta {\mathit{\boldsymbol{u}}^T}(t)\mathit{\boldsymbol{R}}\Delta \mathit{\boldsymbol{u}}(t)} \right]\; + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{\lambda }}^T}(t)\left[ {\mathit{\boldsymbol{A}}(t)\Delta \mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{B}}(t)\Delta \mathit{\boldsymbol{u}}(t)} \right], \end{array} $ | (8) |
式中,
| $ \left\{ \begin{array}{l} \dot \lambda (t) = - \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial \Delta \mathit{\boldsymbol{x}}}} = - \left[ {\mathit{\boldsymbol{Q}}\Delta x(t) + {\mathit{\boldsymbol{A}}^T}(t)\lambda (t)} \right],\\ \lambda ({t_f}) = \mathit{\boldsymbol{S}}\Delta \mathit{\boldsymbol{x}}({t_f})\;, \end{array} \right. $ | (9) |
又由
| $ \Delta {\mathit{\boldsymbol{u}}^*}(t) = - {\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^T}(t)\lambda (t)。 $ | (10) |
于是, 根据最优性必要条件, 有
| $ \left[ \begin{array}{l} \Delta \mathit{\boldsymbol{\dot x}}\\ {\mathit{\boldsymbol{\dot \lambda }}} \end{array} \right] = \left[ \begin{array}{l} \mathit{\boldsymbol{A}}(t)\\ - \mathit{\boldsymbol{Q}}(t) \end{array} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. \begin{array}{l} - \mathit{\boldsymbol{B}}(t){\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^T}(t)\\ - {\mathit{\boldsymbol{A}}^T}(t) \end{array} \right]\left[ \begin{array}{l} \Delta \mathit{\boldsymbol{x}}\\ \mathit{\boldsymbol{\lambda }} \end{array} \right], $ | (11) |
与之对应的边值条件为
| $ \left\{ \begin{array}{l} \Delta \mathit{\boldsymbol{x}}(t = 0) = \Delta \mathit{\boldsymbol{x}}({t_0}) = \Delta {\mathit{\boldsymbol{x}}_0},\\ \mathit{\boldsymbol{\lambda }}(t = {t_f}) = \mathit{\boldsymbol{S}}\Delta \mathit{\boldsymbol{x}}({t_f}) = \mathit{\boldsymbol{S}}\Delta {\mathit{\boldsymbol{x}}_f}。 \end{array} \right. $ | (12) |
由上述分析可知, 采用闭环控制算法设计姿态调节器时, 需要开环的最优控制两点边值问题能够时刻求解。由于3D刚体摆模型具有强非线性特性, 导致求解Riccati方程过程复杂, 运算量大。因此, 本节采用Legendre伪谱法将两点边值问题离散化, 将其求解微分方程组问题简化为求解一组线性代数方程。
首先进行线性变换, 用
| $ \left[ \begin{array}{l} \Delta \mathit{\boldsymbol{\dot x}}\\ {\mathit{\boldsymbol{\dot \lambda }}} \end{array} \right] = \frac{{{t_f} - {t_0}}}{2}\left[ \begin{array}{l} \mathit{\boldsymbol{A}}(\zeta )\\ - \mathit{\boldsymbol{Q}}(\zeta ) \end{array} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. \begin{array}{l} - \mathit{\boldsymbol{B}}(\zeta ){\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^T}(\zeta )\\ - {\mathit{\boldsymbol{A}}^T}(\zeta ) \end{array} \right]\left[ \begin{array}{l} \Delta \mathit{\boldsymbol{x}}\\ \;\mathit{\boldsymbol{\lambda }} \end{array} \right]。 $ | (13) |
在LGL (Legendre-Gauss-Lobatto)点ζη(η=0, 1, 2, …, N)上将状态变量
| $ \left\{ \begin{array}{l} \Delta \mathit{\boldsymbol{x}} \approx \Delta {\mathit{\boldsymbol{x}}^N}(\zeta ) = \sum\limits_{\eta = 0}^N {\Delta \mathit{\boldsymbol{x}}({\zeta _\eta }){\phi _\eta }(\zeta ),} \\ \mathit{\boldsymbol{\lambda }} \approx {\mathit{\boldsymbol{\lambda }}^N}(\zeta ) = \sum\limits_{\eta = 0}^N {\mathit{\boldsymbol{\lambda }}({\zeta _\eta }){\phi _\eta }(\zeta ){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \zeta \in [ - 1,\;1],} \end{array} \right. $ | (14) |
式中,
| $ \left\{ \begin{array}{l} \Delta \mathit{\boldsymbol{\dot x}}({\zeta _k}) \approx \Delta {{\mathit{\boldsymbol{\dot x}}}^N}({\zeta _k}) = \sum\limits_{\eta = 0}^N {\Delta \mathit{\boldsymbol{x}}({\zeta _\eta })\dot \phi (\zeta )} \\ \;\;\;\;\;\;\;\;\;\;\; = \sum\limits_{\eta = 0}^N {{D_{k\eta }}\Delta \mathit{\boldsymbol{x}}({\zeta _\eta }),} \\ \dot \lambda ({\zeta _k}) \approx {{\dot \lambda }^N}({\zeta _k}) = \sum\limits_{\eta = 0}^N {\lambda ({\zeta _\eta })\dot \phi (\zeta ) = \sum\limits_{\eta = 0}^N {{D_{k\eta }}\lambda ({\zeta _\eta })} ,} \end{array} \right. $ | (15) |
其中, D=(Dkh)为(N+1)×(N+1)阶导数矩阵:
| $ {D_{k\eta }} = \left\{ \begin{array}{l} \frac{{{L_N}({\zeta _\eta })}}{{{L_N}({\zeta _k})}} \cdot \frac{1}{{{\tau _\eta } - {\tau _k}}},\quad k \ne \eta ,\\ - \frac{{N(N + 1)}}{4},\quad \;\;\;\;\;k = \eta = 0,\\ \frac{{N(N + 1)}}{4},\quad \;\;\;\;\;\;\;k = \eta = N,\\ 0,\quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他。 \end{array} \right. $ |
两点边值问题在LGL点上离散化, 有
| $ \left\{ \begin{array}{l} \frac{2}{{{t_f} - {t_0}}}\sum\limits_{\eta = 0}^N {{D_{k\eta }}\Delta \mathit{\boldsymbol{x}}({\zeta _\eta }) - [\mathit{\boldsymbol{A}}({\zeta _k})\Delta \mathit{\boldsymbol{x}}({\zeta _k})} - \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{B}}({\zeta _k}){\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^T}({\zeta _k})\lambda ({\zeta _k})] = 0,\\ \frac{2}{{{t_f} - {t_0}}}\sum\limits_{\eta = 0}^N {{D_{k\eta }}\Delta \lambda ({\zeta _\eta }) + [\mathit{\boldsymbol{Q}}\Delta \mathit{\boldsymbol{x}}({\zeta _k}) + } \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{A}}^T}({\zeta _k})\Delta \lambda ({\zeta _k})] = 0\;。 \end{array} \right. $ | (16) |
为减小冗余, 用边界条件
| $ \mathit{\boldsymbol{CF}} = \mathit{\boldsymbol{D}}, $ | (17) |
式中,
| $ \mathit{\boldsymbol{C}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{C}}_{xx}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{C}}_{x\lambda }}{\kern 1pt} {\kern 1pt} \\ {\mathit{\boldsymbol{C}}_{\lambda x}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{C}}_{\lambda \lambda }} \end{array} \right], $ |
| $ {\mathit{\boldsymbol{C}}_{xx}} = {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&0& \ldots &0\\ {{\mathit{\boldsymbol{D}}_{10}}}&{{\mathit{\boldsymbol{D}}_{11}} - \mathit{\boldsymbol{A}}({\zeta _1}){\kern 1pt} }&{{\kern 1pt} \ldots }&{{\mathit{\boldsymbol{D}}_{1N}}}\\ {{\mathit{\boldsymbol{D}}_{20}}{\kern 1pt} }&{{\mathit{\boldsymbol{D}}_{12}}}& \ldots &{{\mathit{\boldsymbol{D}}_{2N}}}\\ {{\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} }&{{\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} }&{}&{{\kern 1pt} {\kern 1pt} \vdots }\\ {{\mathit{\boldsymbol{D}}_{N0}}{\kern 1pt} }&{{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{D}}_{N1}}{\kern 1pt} }&{{\kern 1pt} \ldots }&{{\mathit{\boldsymbol{D}}_{NN}} - \mathit{\boldsymbol{A}}({\zeta _N})} \end{array}} \right]_{n(N + 1) \times n(N + 1)}}, $ |
| $ {\mathit{\boldsymbol{C}}_{x\lambda }} = {\left[ {\begin{array}{*{20}{c}} 0&0&{...}&0\\ 0&{\mathit{\boldsymbol{B}}({\zeta _1}){\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^T}({\zeta _1})}&{...}&0\\ {{\kern 1pt} \vdots }&{{\kern 1pt} \vdots }&{}&{{\kern 1pt} \vdots }\\ 0&0&{...}&{\mathit{\boldsymbol{B}}({\zeta _N}){\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^T}({\zeta _N})} \end{array}} \right]_{n(N + 1) \times n(N + 1)}}, $ |
| $ {\mathit{\boldsymbol{C}}_{\lambda x}} = {\left[ \begin{array}{l} \mathit{\boldsymbol{Q}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Q}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Q}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\\ \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \mathit{\boldsymbol{S}} \end{array} \right]_{n(N + 1) \times n(N + 1)}}, $ |
| $ {\mathit{\boldsymbol{C}}_{\lambda \lambda }} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_{00}} + {\mathit{\boldsymbol{A}}^T}({\zeta _0}){\kern 1pt} }&{{\mathit{\boldsymbol{D}}_{01}}{\kern 1pt} }&{...}&{{\mathit{\boldsymbol{D}}_{0N}}}\\ {{\mathit{\boldsymbol{D}}_{10}}}&{{\mathit{\boldsymbol{D}}_{11}} + {\mathit{\boldsymbol{A}}^T}({\zeta _1}){\kern 1pt} }&{...}&{{\mathit{\boldsymbol{D}}_{1N}}}\\ { \vdots {\kern 1pt} }&{ \vdots {\kern 1pt} }&{}&{{\kern 1pt} \vdots }\\ {\bf{0}}&{\bf{0}}&{...}&\mathit{\boldsymbol{I}} \end{array}} \right]_{n(N + 1) \times n(N + 1)}}, $ |
式中, I是n×n的单位矩阵, 0是
通过求解线性方程组, 可以得到两点边值问题的解析解, 且无需对方程进行积分运算。因此, 算法的精度得到很好的保证, 并减少了运算时间, 大幅降低求解过程的计算量。
计算过程如下。
第1步, 选取算法采样周期。
第2步, 在参考轨迹上将3D刚体摆的运动模型线性化并确定初值
第3步, 对区间
第4步, 将代数方程组(17)的解代入方程(10), 求得最优控制修正量
第5步, 将实际控制输入方程u=u+Du*代入动力学方程(4), 求得3D刚体摆的实际运行轨迹x。
第6步, 令Dx*=x-Dx*, 在下一时刻, 重复步骤3~5, 直到
设3D刚体摆的质量为m=140kg, 转动惯量为J=diag (40, 45, 50) kg·m2, 支点与质心之间的距离为l=0.1 m。假设3D刚体摆在t=0时刻的干扰误差为
|Dwx(0)|≤0.1 rad/s,
|DGx(0)|≤0.1,
|Dwy(0)|≤0.1 rad/s,
|DGy(0)|≤0.1,
|Dwz(0)|≤0.1 rad/s,
|DGz(0)|≤0.1。
设3D刚体摆的初始位置角速度为
ω0=(0, 0, 0)Trad/s,
约化姿态为
设目标位置为悬垂平衡位置, 其角速度为
ωf=(0, 0, 0)Trad/s,
约化姿态为
插值点N=35, 仿真结果如图 3所示。
|
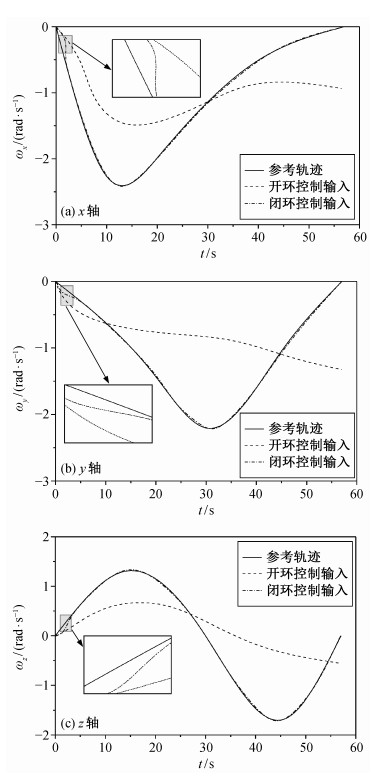
| 图 3. 3D刚体摆角速度变化曲线 Figure 3. Evolution of the angular velocity of the 3D pendulum |
图 3显示3D刚体摆的角速度沿三轴的变化曲线。可以看出, 在存在初始扰动的情况下, 开环控制的角速度受到初始扰动逐渐偏离最优参考轨迹运动, 失去控制效果; 而闭环反馈控制能够有效抵抗初始扰动的干扰, 迅速调整3D刚体摆的角速度变化, 沿最优轨迹使3D刚体摆到达目标悬垂平衡位置, 且角速度趋近于0。
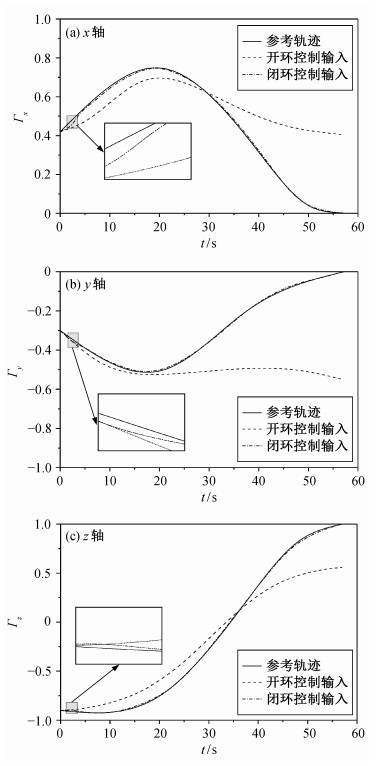
图 4显示3D刚体摆约化姿态变化曲线, 可以看出, 刚体摆受到初始扰动的影响, 开环控制不能有效地对3D刚体摆进行姿态调整, 逐渐偏离参考轨迹。利用提出的反馈控制方法, 3D刚体摆在受到初始扰动偏离最优路径轨迹, 能够迅速响应做出调整, 返回到最优运动轨迹, 且沿此路径最后到达悬垂平衡位置。
|
| 图 4. 3D刚体摆约化姿态变化曲线 Figure 4. Evolution of the reduced attitude of the 3D pendulum |
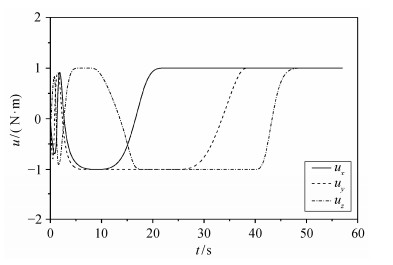
图 5所示的控制输入在[-1, 1]间切换, 根据最优控制问题的必要条件, 即得到的控制力矩是原姿态运动最优控制问题的最优解。图 6为3D刚体摆在最优控制输入下的空间姿态轨迹变化曲线。
|
| 图 5. 3D刚体摆控制力矩闭环反馈变化曲线 Figure 5. Closed-loop trajectory of the control torque of the 3D pendulum |

|
| 图 6. 3D刚体摆姿态运动空间轨迹 Figure 6. Motion of the vector between the pivot and the center of mass of the 3D pendulum |
同样, 在满足相同初始扰动存在的情况下, 设倒立平衡的初始角速度为
| $ {\mathit{\boldsymbol{\omega }}_0} = {\left( {0,0,0} \right)^{\rm{T}}}\;{\rm{rad/s,}} $ |
约化姿态为
| ${\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_0} = {( - 0.48,\; - 0.22,0.85)^T},$ |
设目标倒立平衡点角速度为
| ${\mathit{\boldsymbol{\omega }}_f} = {(0,\;0,\;0)^T}\;\;{\rm{rad/s,}}$ |
约化姿态为
| ${\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_f} = {(0,0, - 1)^T}。$ |
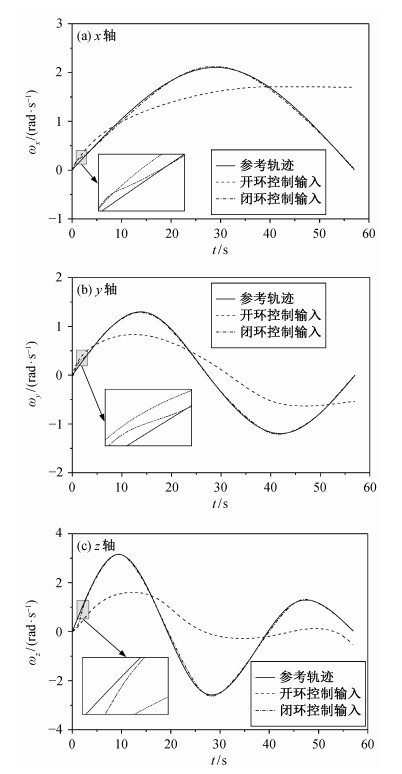
3D刚体摆在闭环反馈最优控制作用下, 倒立平衡仿真结果如图 7~10所示。
|
| 图 7. 3D刚体摆角速度变化曲线 Figure 7. Evolution of the angular velocity of the 3D pendulum |
|
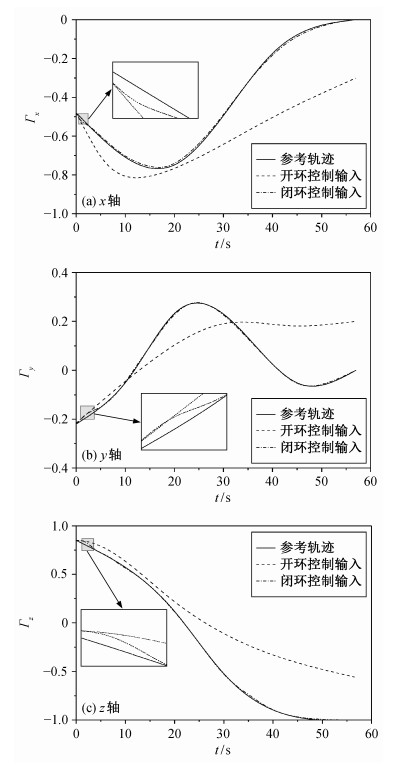
| 图 8. 3D刚体摆约化姿态变化曲线 Figure 8. Evolution of the reduced attitude of the 3D pendulum |
|
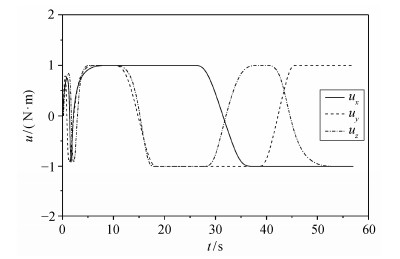
| 图 9. 3D刚体摆控制力矩闭环反馈变化曲线 Figure 9. Closed-loop trajectory of the control torque of the 3D pendulum |

|
| 图 10. 3D刚体摆姿态运动空间轨迹 Figure 10. Motion of the vector between the pivot and the center of mass of the 3D pendulum |
图 7所示的倒立情况下, 开环控制的角速度受到初始扰动, 逐渐偏离最优参考轨迹, 失去控制效果, 而闭环控制能够有效地抵抗初始扰动的干扰。在初段被干扰时, 该控制策略通过反馈作用能够迅速调整3D刚体摆的角速度变化, 沿最优轨迹使3D刚体摆到达目标倒立平衡点, 且角速度趋近于0。
图 8为倒立情况下3D刚体摆的约化姿态变化曲线, 说明在存在初始扰动的情况下, 闭环控制能够有效地抵抗初始扰动的干扰, 迅速调整3D刚体摆的空间姿态, 使3D刚体摆沿最有参考轨迹运动到目标倒立平衡点。相反, 开环最优控制则不能消除初始扰动的影响, 逐渐偏离最优轨迹, 无法运动到目标倒立平衡点。
图 9所示的最优控制输入力矩曲线在上下限间切换变化。图 10形象地反映了系统姿态在空间坐标内的运动轨迹。
4 结论本文针对3D刚体摆运动姿态稳定控制问题, 设计了Legendre伪谱法闭环控制器。仿真结果表明, 基于Legendre伪谱法闭环控制算法能够有效地抑制初始扰动给3D刚体摆运动过程带来的不利影响, 按照约束条件的要求达到目标平衡位置, 进一步证明了伪谱法求解3D刚体摆最优控制问题的可行性和有效性, 也为求解类似复杂约束系统的最优控制问题提供了新的途径。
| [1] | Shen J, Sanyal A K, Chaturvedi N A, et al. Dynamics and control of a 3D pendulum // Proceedings of the 43rd IEEE Conference on Decision and Control. Bahamas, 2004: 323-328 |
| [2] | Chaturvedi N A, Lee T, Leok M, et al. Nonlinear dynamics of the 3D pendulum. SIAM Journal on Applied Dynamical Systems , 2007, 7 (2) : 144–160 . |
| [3] | Gong Q, Ross I M, Kang W, et al. Connections between the convector mapping theorem and conver-gence of pseudospectral methods for optimal control. Computational Optimization and Applications , 2008, 41 : 307–335 DOI:10.1007/s10589-007-9102-4 . |
| [4] | 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述. 宇航学报 , 2008, 29 (2) : 397–406. |
| [5] | Fahroo F, Ross I M. Direct trajectory optimization by a Chebyshev pseudospectral method. Journal of Gui-dance, Control, and Dynamics , 2002, 25 (1) : 160–166 DOI:10.2514/2.4862 . |
| [6] | Shamsi M, Dehghan M. Determination of a control function in three-dimensional parabolic equations by Legendre pseudospectral method. Numeral Methods Partial Differential Equation , 2012, 28 : 74–93 DOI:10.1002/num.v28.1 . |
| [7] | 朱宁, 戈新生. 勒让德伪谱法求解三维刚体摆姿态运动最优控制问题. 力学与实践 , 2015 (4) : 481–487. |
| [8] | Lu P. Regulation about time-varying trajectories: precision entry guidance illustrated. Journal of Gui-dance, Control, and Dynamics , 1999, 22 (6) : 784–790 DOI:10.2514/2.4479 . |
| [9] | Yan H, Fahroo F, Ross I M. Optimal feedback control laws by legendre pseudospectral approximations // Proceedings of the American Control Conference. Piscataway , 2001 : 2388–2393 . |
| [10] | 庄宇飞, 黄海滨. 欠驱动航天器实时最优控制算法设计. 系统工程与电子技术 , 2013, 35 (7) : 1477–1485. |
| [11] | 庄宇飞, 马广富, 黄海滨. 欠驱动刚性航天器时间最优轨迹规划设计. 控制与决策 , 2010, 25 (10) : 1469–1473. |
| [12] | Chaturvedi N A, McClamroch N H. Asymptotic stabilization of the hanging equilibrium manifold of the 3D pendulum. International Journal of Robust and Nonlinear Control , 2007, 17 : 1435–1454 DOI:10.1002/(ISSN)1099-1239 . |
| [13] | Chaturvedi N A, McClamroch N H, Bernstein D S. Stabilization of a specified equilibrium in the inverted equilibrium manifold of the 3D pendulum // Procee-dings of the 2007 American Control Conference. New York , 2007 : 2485–2490 . |
 2016, Vol. 52
2016, Vol. 52




