文章信息
- 刘世兴, 邢燕, 刘畅, 郭永新
- LIU Shixing, XING Yan, LIU Chang, GUO Yongxin
- 对称约化对完整系统数值积分的影响
- The Affection of Symmetry Reduction to the Numerical Integration for Holonomic System
- 北京大学学报(自然科学版), 2016, 52(4): 592-596
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 592-596
-
文章历史
- 收稿日期: 2015-10-09
- 修回日期: 2016-03-01
- 网络出版日期: 2016-07-12
2. 辽东学院机械电子工程学院, 丹东 118001
2. School of Mechatronics Engineering, Eastern Liaoning University, Dandong 118001
自20世纪末期, 对称约化理论提出以来, 一直是几何动力学领域的热门课题之一, 并广泛应用于力学、物理学和工程科学等多个领域, 如固体力学、流体力学、场论、量子力学和广义相对论等[1]。对称约化的主要目的是利用系统的对称性消除动力学系统的部分局部坐标变量, 从而简化实际的动力学系统。对称约化的思想最早源于Routh[2]于1884年利用循环坐标对系统进行化简, 这种化简理论对应于现代的Lagrange约化理论。现代约化理论始于20世纪六七十年代Arnold[3-4]和Smale[5]的重要工作, Arnold开展了Lie群约化方法, Smale引入动量映射概念。Marsden等[6]在前人工作的基础上, 利用等变动量映射开展辛流形上的约化理论, 使现代约化理论走向成熟, 并得到广泛应用[7-8]。目前, 完整约束力学系统的几何动力学约化理论已经非常成熟, 大体上包括:辛约化[9]、Poission约化[1]和Lagrange约化[1, 10]。对称性约化理论在研究约束系统几何动力学及应用以及约束系统的保结构算法中发挥着非常重要的作用, 为研究约束系统几何数值积分的几何不变性质提供了新的途径。但是, 在现有的少量研究工作中, 对称约化理论在约束力学系统几何数值积分的研究中, 还没有发挥其应有的作用。较复杂的动力学系统经过对称约化得到一个简单的新的动力学系统, 系统方程的性质发生了变化, 变量所代表的物理含义有时也发生改变, 那么约化系统与原系统的内部联系, 特别是一些重要的性质是否能够很好地得以保留, 对原系统和约化后的系统分别做数值积分, 对称约化对数值积分的结果是否会受到影响?本文就这一问题展开探讨, 通过数值实验验证对称约化对数值积分的影响。首先, 简要介绍完整约束系统的辛约化理论; 然后, 简要介绍完整约束系统的数值积分方法, 并应用数值积分方法计算约化前和约化后系统的动力学方程, 比较约化前后动力学变量的数值结果; 最后得出结论。
1 完整约束系统的辛约化完整约束力学系统总可以表示为Hamilton形式。定义Hamilton系统为
| $\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = {}^\# {\rm{d}}H(x),$ | (1) |
这里
| $ \phi (g, \;z) = {\phi _g}(z), $ | (2) |
如果对于任意一个
| $\phi _g^ * \mathit{\Omega} = \mathit{\Omega}, $ | (3) |
则该作用
定义(辛约化) 辛流形
| ${\pi ^ * }{\mathit{\Omega} _P} = {\mathit{\Omega} _N}, $ | (4) |
这里
辛约化满足Marseden-Weinstein-Meyer辛约化定理[2, 6]。取点
定理 设Lie群
| $J:M \to {\mathcal{G}^ * }, $ |
如果存在正则值
| $\mu \in J(M) \subset {\mathcal{G}^ * }, $ |
且存在伴随余迷向子群
| ${G_\mu } = \left\{ {g \in G\left| {Ad_g^ * \mu = \mu } \right.} \right\}, $ |
则
| ${M_\mu }(x) = {J^{ - 1}}(\mu )\pi (x)$ |
上; 如果存在内映射
| ${i_\mu }:{J^{ - 1}}(\mu ) \to M$ |
和正则投影映射
| ${\pi _\mu }:{J^{ - 1}}(\mu ) \to {\hat M_\mu }, $ |
则一定存在具有辛结构
| ${\hat M_\mu } = {J^{ - 1}}(\mu )/{G_\mu }, $ |
满足
| $\pi _\mu ^ * \circ \mathit{\hat \Omega _\nu } = i_\mu ^ * \circ \mathit{\Omega} 。$ |
并且存在一个侵入映射
| ${\hat M_\mu } = {J^{ - 1}}(\mu )/{G_\mu }$ |
是
| $\pi :M \to M/G$ |
这个定理保证了约化后的商空间
完整约束系统总可以表示为Hamilton正则方程(1)的形式, 如取Hamilton函数
| $ z = {\left( {{p_1}, {\rm{ }} \ldots, {p_n};{q^1}, {\rm{ }} \ldots, {q^n}} \right)^T}, $ |
则方程(1)可以表示成如下坐标形式:
| $\frac{{{\rm{d}}z}}{{{\rm{d}}t}} = {\mathit{\boldsymbol{J}}^{ - 1}}\frac{{\partial H(z)}}{{\partial z}}, $ | (5) |
这里,
| $\begin{array}{l} \frac{{{z^{i + 1}} - {z^i}}}{\tau } = {J^{ - 1}}{\left( {\frac{{\partial H}}{{\partial z}}} \right)_{\frac{{{z^{i + 1}} + {z^i}}}{2}}}\\ (i = 0, \;1, \;...\;, \;n - 1), \end{array}$ | (6) |
这里
众所周知, 平面Kepler问题是典型的二体问题, 且满足机械能守恒和角动量守恒。令
| $q = ({q_1}, \;{q_2})$ |
为该二体问题的广义坐标, 并取
| $p = ({p_1}, \;{p_2}) = ({\dot q_1}, \;{\dot q_2}), $ |
则可以得到系统的Hamilton函数:
| $H({p_1}, \;{p_2}, \;{q_1}, \;{q_2}) = \frac{1}{2}(p_1^2 + p_2^2) - \frac{1}{{\sqrt {q_1^2 + q_2^2} }}, $ |
从而得到系统的Hamilton方程:
| $\left\{ \begin{array}{l} {{\dot p}_1} = - \frac{{{q_1}}}{{{{(q_1^2 + q_2^2)}^{3/2}}}}, \;\;\;\;{{\dot q}_1} = {p_1};\\ {{\dot p}_2} = - \frac{{{q_2}}}{{{{(q_1^2 + q_2^2)}^{3/2}}}}, \;\;\;\;{{\dot q}_2} = {p_2}。\; \end{array} \right.$ | (8) |
在Lie群变化下, 方程(8)可以约化为一维谐振子的运动方程:
| $ {u''_{}} + u = 1/d, $ | (9) |
这里,
| $\begin{array}{l} {q_1} = r\cos \theta, \;\;{q_2} = r\sin \theta 。\\ d = L_0^2 = {({q_1}{{\dot q}_2} - {q_2}{{\dot q}_1})^2} = {({r^2}\dot \theta )^2} \end{array}$ |
是系统的角动量,
″=d2/dθ 2。
令
| $H({p_u}, \;u) = \frac{1}{2}(p_u^2 + {u^2}) - \frac{u}{d} - \frac{{{H_0}}}{d}, $ | (10) |
这里,
| ${H_0} = \frac{1}{2}(p_1^2 + p_2^2) - \frac{1}{{\sqrt {q_1^2 + q_2^2} }} = \frac{1}{2}({\dot r^2} + {r^2}{\dot \theta ^2}) - \frac{1}{r}, $ |
是原二体系统的机械能。从而得到方程(9)对应的Hamilton方程:
| ${p'_u} = - u + 1/d, {\rm{ }}u' = {p_u}。$ | (11) |
取如下初始条件:
| $\begin{array}{l} {q_1}(0)1 - e, \;\;{q_2}(0) = 0, \;\;{{\dot q}_1}(0) = 0, \\ {{\dot q}_2}(0) = \sqrt {(1 + e)/(1 - e)}, \;\;\;e = 0.6。 \end{array}$ |
从而系统的总能量
| ${H_0} = - 1/2, $ | (13) |
总角动量
| ${L_0} = \sqrt {1 - {e^2}} = 0.8, \;\;d = L_0^2。$ |
我们采用上面的辛差分格式(式(6)), 并取步长
|
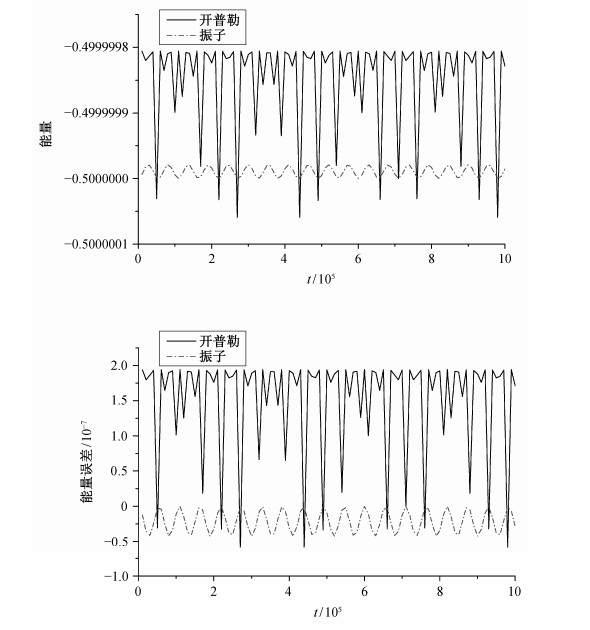
| 图 1. 系统的总能量和能量误差 Figure 1. Total energy and error of system |
|
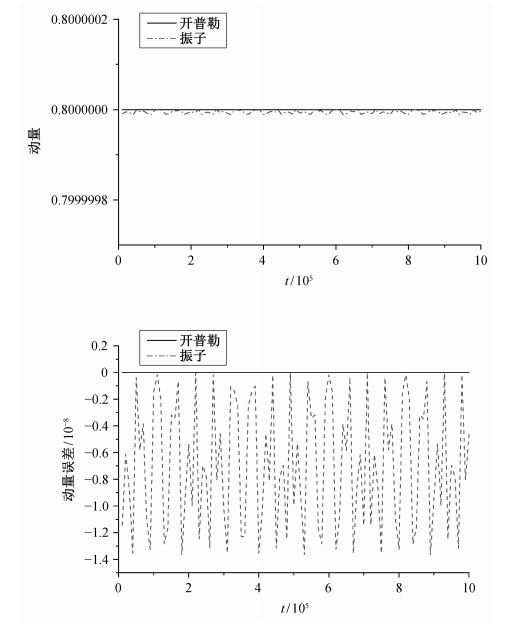
| 图 2. 系统的总动量和动量误差 Figure 2. Total momentum and error of system |
从图 1和2可以看出, 虽然在原体系框架下计算得到的总能量没有在约化后的体系中得到的结果好, 但是总动量的数值结果却优于约化体系中的数值结果。因此, 在约化前体系下和约化后体系下的数值结果并没有本质上的区别。并且, 我们求得的系统的总能量和总动量都在数值计算的误差允许范围内, 数值结果都很好地保持了原有系统的守恒量。区别在于, 我们在约化后的体系下进行数值研究, 由于体系的自由度减少, 从而减少了编程计算的难度, 同时也减少计算机机时。因此, 对于完整系统, 无论是在原体系框架下, 还是在约化后的系统中, 都可以得到满意的数值结果, 但在约化体系下, 可以获得简洁的计算机程序, 并减少计算机工作时间。这对于复杂的完整动力学系统来说, 对动力学系统进行对称约化, 以减少动力学系统的自由度数, 可以有效地进行数值计算, 从而在约化系统下间接地研究原系统的动力学性质。
| [1] | Marsden J E, Ratiu T S. Introduction to mechanics and symmetry. 2nd edition. New York: Springer-Verlag, 1999 . |
| [2] | Routh E J. Advanced Rigid Dynamics. London: MacMillian, 1884 . |
| [3] | Arnold V I. Mathematical methods of classical mechanics. New York: Springer-Verlag, 1978 . |
| [4] | Arnold V I. Dyanmical systems Ⅲ. Berlin: Springer-Verlag, 1988 . |
| [5] | Smale S. Topology and mechanics. Inv Math , 1970, 11 : 45–64 DOI:10.1007/BF01389805 . |
| [6] | Marsden J E, Weinstein A. Reduction of symplectic manifolds with symmetry. Rep Math Phys , 1974, 5 : 121–130 DOI:10.1016/0034-4877(74)90021-4 . |
| [7] | Koon W S, Marsden J E. Optimal control for holonomic and nonholonomic mechanical systems with symmetry and Lagrangian reduction. SIAM J Control and Optim , 1997, 35 : 901–929 DOI:10.1137/S0363012995290367 . |
| [8] | Weinstein A. A universal phase space for particles in Yang-Mills fields. Lett Math Phys , 1978, 2 : 417–420 DOI:10.1007/BF00400169 . |
| [9] | Libermann P, Marle C M. Symplectic geometric and analytical mechanics. Dordrecht: D Reidel Publishing Company, 1987 . |
| [10] | Holm D D, Marsden J E, Ratiu T S. Euler-Poincaré models of ideal fluids with nonlinear dispersion. Phys Rev Lett , 1998, 349 : 4173–4177 . |
| [11] | 冯康, 秦孟兆. 哈密尔顿系统的辛几何算法. 杭州: 浙江科学技术出版社, 2003 . |
| [12] | Hairer E, Lubich C, Wanner G. Geometric numerical integration: structure-preserving algorithms for ordi-nary differential equations. Berlin: Springer-Verlag, 2002 . |
 2016, Vol. 52
2016, Vol. 52