文章信息
- 李嘉琪, 王曙光, 蔡晨, 宁杰远
- LI Jiaqi, WANG Shuguang, CAI Chen, NING Jieyuan
- 一种定量地消除波速横向变化影响的三叉震相一维波速结构反演计算方案
- A Computational Scheme for Quantitatively Removing the Effects of Lateral Velocity Variation on 1-D Triplicated Wave Velocity Inversion
- 北京大学学报(自然科学版), 2016, 52(3): 420-426
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(3): 420-426
-
文章历史
- 收稿日期: 2015-02-01
- 修回日期: 2015-11-10
- 网络出版日期: 2016-05-19
2. 中国地震局地震预测研究所, 北京 100036;
3. Department of Earth and Planetary Sciences, Washington University, Saint Louis, MO 63130-4899
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 100036;
3. Department of Earth and Planetary Sciences, Washington University, Saint Louis, MO 63130-4899
随着地震台站的日益增多, 全球地震层析成像技术得到日益深入的应用[1-3], 人们由此对地球内部结构有了前所未有的认识。但是, 地震台站密度不高、全球地震活动性不均匀等因素限制了全球地震层析成像的分辨率精度, 因而不能很好地用于讨论区域精细结构, 如俯冲海洋岩石圈的影响和最终去向、地幔物质的运动及能量传递、火山岩浆的产生和运移等。
当研究区域内有密集的台站或者发生震级合适的地震时, 利用区域地震层析成像方法可以获取更高分辨率的地球内部波速结构, 得到一些区域下方俯冲带在深部延伸的清晰图像[4-6]。但是, 由于射线覆盖不够密集, 地幔过渡带等一些区域的细结构仍然存在分辨率不高的问题。更为突出的是, 区域地震层析成像受到研究区域外波速异常对震相到时污染的影响。
三叉震相由射线路径相近的3组震相组成。利用密集台站对三叉震相的观测结果, 可以很好地约束地幔一维波速结构, 尤其能够很好地约束地幔波速梯度带的起伏、跃变和层厚, 在约束地幔细结构方面, 是一种不可或缺的方法。
利用三叉震相反演地球内部结构, 已取得一些重要的研究结果[7-11]。但是, 这个方法同样面临研究区域外波速异常对震相到时污染的问题[9]。不仅如此, 对于三叉震相方法来说, 研究区域内的局部速度异常实际上也会影响其反演结果。二者叠加, 共同构成波速结构的横向变化对三叉震相一维反演的影响。Wang等[12]定量地分析了研究区域外波速异常对观测波形和到时存在的污染现象, 认为传统的一维反演方法得到的结果在一些情况下与真实结果有不可忽略的偏差。
本文在进一步研究波速结构的横向变化对应用三叉震相反演研究区内一维波速结构影响的具体方式及污染程度的基础上, 通过理论分析, 提出一种在一维波速结构反演中, 定量消除波速结构横向变化对震相到时污染的解决方案。同时, 利用射线追踪法初步实现此方案, 并对污染消除效果进行初步检验。
1 三叉震相和一维波速结构反演当地震波的传播路径上有波速突变界面时, 界面上方的直达波在界面产生的反射波以及通过界面的折射波将被不同震中距的台站记录, 形成三叉震相[7-9]。通过拟合观测波形得到三叉震相信息, 可以反演得到对应的一维波速结构。由于是3种震相的射线路径在间断面附近相交, 因而会对间断面的位置和形态特征有非常强的约束。
一般来说, 反演过程是通过波形拟合, 由浅至深, 逐层确定波速数值。首先拟合确定浅层的波速, 然后拟合确定下一层的波速。在确定下一层的波速时, 该层以上的波速结构沿用之前已经确定的数值。依此类推, 随着不同射线穿透深度的增加, 可以逐层得到各个深度的波速。当射线足够密集时, 可以得到精细分层的波速结构。
本文探讨波速的横向变化对利用三叉震相到时进行波速结构一维反演的影响及消除方法, 后续工作将进一步把该方法扩展到利用三叉震相波形反演一维波速结构的情形。不失一般性, 设定地震位于120 km深度, 并设0~200 km深度的波速与IASP91模型[13]一致, 一维波速结构的反演从200 km深度开始。采用IASP91模型作为初始波速模型, 利用Tau-p程序进行射线追踪, 正演计算得到每一条射线的路径、到时和转折点位置, 进而找出转折点(turning point)最接近200 km深度的射线。应用格点搜索方法, 找出计算到时和观测到时残差最小的波速扰动值, 最终求得200 km深度的波速。按照此方法, 由浅至深, 逐层得到各个深度转折点附近的波速, 并作为该深度层的波速。
2 区域外波速异常对一维反演结果影响的理论测试利用三叉震相反演一维波速结构, 是由浅至深逐步反演的, 每一个深度的波速基本上由每条射线转折点附近的速度确定。在目标区域外的射线路径上, 可能有偏离一维结构的波速异常体。以利用中国东北台阵研究太平洋板块发生的地震为例, 主要矛盾来自震源区俯冲板块的高速异常及接收台站下方的低速异常。下面将分别讨论这两种情况的影响。同时, 为了衡量目标区域内局部异常对计算结果的影响, 还将讨论目标区域内局部波速异常对一维波速结构反演的影响。
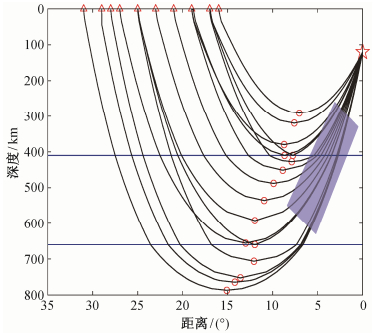
2.1 震源区附近高速异常的影响为了定量讨论震源区附近高速异常的影响, 我们在图 1中紫色影区所示的位置, 设计3.5%的高速异常, 大致代表俯冲板块处的高速异常。
|
| 红色三角代表台站, 五角星代表地震; 黑色实线是由Tau-p计算的射线路径, 其中红圈代表穿透深度的最低点; 两条蓝线代表 410和660 km的间断面; 紫色影区代表高速异常体, 其异常值比IASP91模型高出3.5%;横坐标1°表示地球周长的1/360 图 1. 震源区附近存在高速异常体的区域二维剖面示意图 Figure 1. 2-D profile of the study region with high velocity zone near sources |
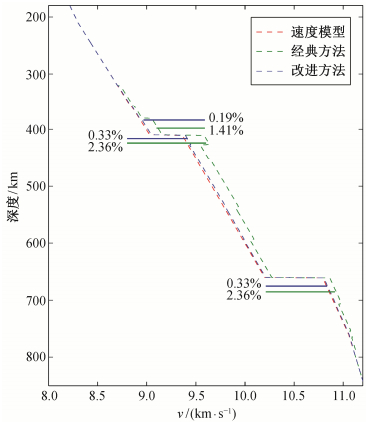
按照由浅至深逐层反演波速结构的计算方案, 转折点深度在400~800 km的射线将通过这一目标区域外的高速异常区。由于传统方法没有把目标区域外的波速异常纳入计算, 因此蓝色区域内的波速异常会被归算到目标区域转折点附近深度的波速异常中(图 2中绿色虚线所示)。在具体计算中, 我们根据射线穿过波速异常区的路径长度, 折算该区域内速度异常导致的到时差。进一步地, 按照射线在转折点速度层内的长度, 将该到时异常假象归算到反演的转折点所在深度范围内的速度异常假象。计算结果表明, 与真实的波速结构(图 2中红色虚线)相比, 传统方法得出的结果在400 km深度附近存在约1.41%的高速异常假象; 在410~600 km深度存在高速异常假象, 最大值为2.36%;在660~720 km深度波速异常假象的最大值为0.66%。在410~600 km深度出现最大的波速异常假象, 是因为在这个深度范围内增加相等的深度时, 转折点对应射线经过目标区域外高速异常体的路径长度(对应图 1中黑色曲线在紫色影区中的长度)增加得更多。类似地, 660~720 km深度波速异常假象小, 是因为相对来说, 射线经过目标区域外高速异常体的路径长度变化小。
|
| 百分比表示两种反演方法在不同深度偏离真实值的最大异常值(下同) 图 2. 震源区附近存在高速异常体情况下, 三叉震相反演的一维波速结构对比 Figure 2. 1-D triplicated velocity inversion of study region with high velocity zone near sources |
2.2 接收区附近低速异常的影响
在利用传统的三叉震相一维反演方法时, 如果某个深度(如200 km)以上的波速采用参考模型, 若接收台阵下方浅部(200 km以上)存在波速异常, 则通过浅部异常体的到时延迟会被归算为200 km深度以下的射线转折点所在的深度, 造成波速降低的假象。
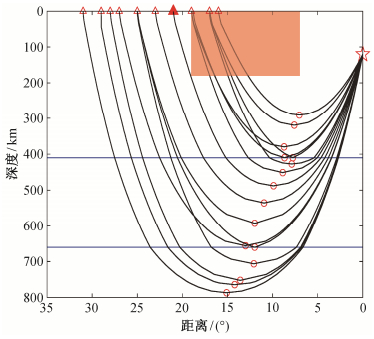
设接收区附近地下200 km内存在3.5%的低速异常(图 3中橙色影区), 转折点在200~300 km深度的假象异常值为-1.57%;在300~400 km深度的异常假象相对较小; 在450~550 km深度出现最大约1.52%的波速异常假象。图 3中红色实心三角所示台站记录到的射线恰好未经过波速异常区, 这条射线对应的转折点位于约450 km深度。此后, 为了补偿200~450 km深度计算结果与真实结果的累积偏离, 导致对450 km以下深度波速的高估。因为计算步骤中深度是逐步增加的, 所以对450 km以下深度波速的高估值会逐步减小, 高估值与射线通过200~450 km深度时因低速异常假象而多算的累积走时有关(图 4中绿色虚线所示)。

|
| 图 4. 接收台站附近存在低速异常体情况下, 三叉震相反演的一维波速结构对比 Figure 4. 1-D triplicated velocity inversion of study region with low velocity zone near receivers |
2.3 目标区浅部局地波速异常对深部波速结构反演结果的影响
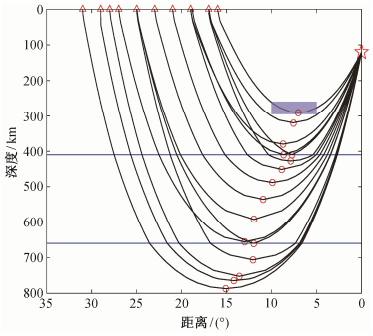
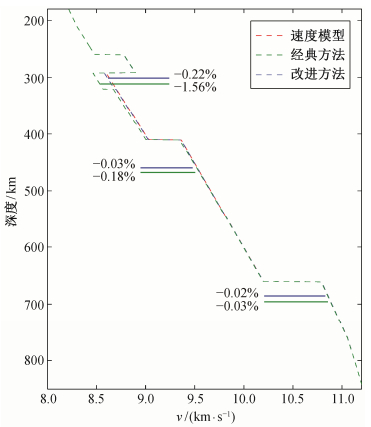
在一维反演过程中, 当目标区域内存在局地速度异常时, 将因其局地性而对其下的速度结构带来影响。为了考察其影响程度, 我们在约250 km深度设计波速高于IASP91模型3.5%的约500 km水平延伸距离的波速异常体(图 5中紫色影区)。由于高速异常体的局地性, 导致其下深度出现低速假象。穿过深部的射线需要补偿其上所有深度速度反演结果对走时产生的累积偏差, 由于每一个深度波速值的反演都起着负反馈的补偿作用, 所以深度越大, 影响越小。这种影响在410 km以下衰减到-0.18%, 660 km以下衰减到-0.03%, 但在250 km深度的真实异常体之下, 低速假象却衰减到不容忽视的-1.56%的量级(图 6)。
|
| 图 6. 反演区域内存在高速异常体情况下, 三叉震相反演的一维波速结构对比 Figure 6. 1-D triplicated velocity inversion of study region with high velocity zone |
当然, 这里讨论的是上层对下层的影响, 并不局限于浅部或高速异常。下面提出的假象消除方案也适用于消除这类波速异常的影响。
3 消除波速横向变化对计算结果影响的理论探讨Wang等[12]利用谱元法进行的三维波形正演测试表明, 区域外存在的异常体会对利用三叉震相反演一维波速结构产生很大影响。
如前所述, 区域外波速异常对一维反演结果影响的理论测试定量地说明, 波速横向变化在传统的一维波速结构反演中会产生与异常体相同量级的波速异常假象。然而, 传统的一维反演方法在反演结果稳定性方面有优势, 如果能解决区域外及区域内波速横向变化造成的假象问题, 将在研究地幔精细结构及相应的地球动力学问题方面有独特的优势。一种可选的解决方案是, 分析一维反演结果时设法去除波速横向变化的影响。但是, 这种方案难于实施, 因为区域外波速横向变化不仅影响经过异常区射线转折点位置的波速反演结果, 还会影响更大深度的波速反演结果。
下面探讨在反演过程中直接地、定量地消除波速横向变化影响的理论方案。首先, 参照先验结果(如层析成像结果), 从实际记录中去除每一条射线由于波速横向非均匀造成的影响, 得到十分接近一维波速结构的资料; 然后, 应用传统的三叉震相反演方法, 得到一维的波速结构; 最后, 还原之前由于去除而丢失的相对速度信息, 得到接近真实值的地下一维波速结构。下面将初步论证这种计算方案的合理性与可行性。
对于一个地区剖面上的真实二维波速结构, 可以认为是一个一维的标准速度模型M(z) (比如IASP91模型)叠加上一个二维的真实结构R(y, z)。层析成像得到的速度结构也可以拆分为一个一维的标准速度模型M(z)加上一个二维的相对速度结构T(y, z)。
首先应用地震层析成像的先验结果修改射线到时:将层析成像的结果剖分成网格, 计算由此产生的震相到时变化, 据此对实际的震相到时进行修改, 并应用于下一步的三叉震相一维反演中。
原地震图中的到时可以表示为f (M(z)+R(y, z)), 描述层析成像与一维标准模型之间差异的修正量可以表示为f (M(z)+T(y, z)) -f (M(z)), 修正后的震相到时可以表示为f (M(z)+R(y, z)) -[f (M(z)+T(y, z))-f (M(z))]。为了简洁, 表示为f (M+R) -[f (M+T)-f (M)]。
| $ \begin{array}{l} \;\;\;f(M + R) - [f(M + T) - f(M)]\\ = f(M + R - T) + {\left. {\frac{{{{\rm{\delta }}^{\rm{2}}}f}}{{{\rm{\delta }}{m^2}}}} \right|_{{m_3}}} \cdot \;({m_2} - {m_1})\; \cdot \;T, \end{array} $ | (1) |
其中,
| $ \begin{array}{l} {m_1} \in \left[ {M,M + T} \right],\\ {m_2} \in \left[ {M + R - T,M + R} \right],\\ {m_3} \in \left[ {min\left( {{m_1},{m_2}} \right),{\rm{ }}max\left( {{m_1},{m_2}} \right)} \right]。 \end{array} $ |
f表示到时, 具有
| $ \frac{{{{\rm{\delta }}^2}f}}{{{\rm{\delta }}{m^2}}} = \frac{{{d_i}}}{{m_i^3}} = f \cdot \frac{1}{{m_i^2}} $ | (2) |
因此,
| $ \begin{array}{l} \;\;\;\frac{{{{\rm{\delta }}^2}f}}{{{\rm{\delta }}{m^2}}}\; \cdot \;({m_2} - {m_1})\; \cdot T\\ \le f \cdot \;\left| {\frac{{\max ({m_2} - {m_1})}}{{\min ({m_i})}}} \right|\; \cdot \;\left| {\frac{{\max (T)}}{{\min ({m_i})}}} \right|, \end{array} $ | (3) |
其中,
| $ \begin{array}{l} \;\;\;f\left( {M + R} \right)-\left[ {f\left( {M + T} \right)-f\left( M \right)} \right]\\ \approx f\left( {M + R-T} \right)。 \end{array} $ | (4) |
因为
具体做法分为以下三步。
第一步, 应用地震层析成像结果修正到时。对于相对IASP91模型3.5%的波速异常, 我们直接假设地震层析成像结果提供了相对于IASP91模型3%的波速异常信息。在一维反演之前, 首先根据层析成像的结果对到时进行调整。对每一条射线, 分别计算层析成像(二维波速)模型和IASP91 (一维波速)模型的到时, 然后将二者的到时差从观测的射线到时中减去, 得到修正的到时。
第二步, 针对修正的到时, 应用传统的三叉震相方法反演一维波速结构。
第三步, 利用地震层析成像结果, 对第二步得到的一维波速结构进行修正, 得到沿着射线转折点连线的一维波速结构。
图 2显示, 利用改进的计算方案, 震源区高速异常带来的假象在200~410 km深度的最大偏离从1.41%变为0.19%, 在410~660 km深度的最大偏离从2.36%变为0.33%, 在660~800 km深度的最大偏离从0.66%变为0.10%。
图 4显示, 利用改进的计算方案, 接收区低速异常带来的假象在200~410 km深度的最大偏离从-1.57%变为-0.23%, 在410~660 km深度的最大偏离从1.52%变为0.22%, 在660~800 km深度的最大偏离从0.30%变为0.05%。
图 6显示, 利用改进的计算方案, 目标区浅部低速异常带来的假象在200~410 km深度的最大偏离从-1.56%变为-0.22%, 在410~660 km深度的最大偏离从-0.18%变为-0.02%, 在660~800 km深度的最大偏离从-0.03%变为0。
对于震源区、接收区以及浅部局地存在波速异常3种典型情形, 我们的计算方案都取得很好的效果。需要注意的是, 假象没有完全消除。分析其原因, 与地震层析成像结果有关。以震源区有高速异常为例, 地震层析成像对真实的3.5%高速异常的估计是3%, 少估算1/7。改进后方法的结果0.19%, 0.33%和0.10%也约为传统方法的假象异常值1.4%, 2.36%和0.66%的1/7。可见, 我们方法的改进程度与地震层析成像的精度有关。相对于模型速度的极性(高速或低速), 只要层析成像的结果与真实结构异常的极性相同, 就可以有效地改进三叉震相反演的一维波速结构。越接近真实的层析成像结果, 越有助于应用本文的方法定量地消除波速横向变化的影响。
5 结论和讨论利用三叉震相反演地幔波速结构, 在410 km和660 km间断面特征方面有独特的优势。但是, 对于俯冲带等有明显波速横向非均匀结构的区域, 利用三叉震相传统的一维反演结果会受到影响。本文利用走时信息, 定量地分析了3种典型的横向非均匀结构对一维波速结果的影响。
本文提出先减后加的计算方案, 首先利用层析成像的结果调整观测地震波形的到时信息, 得到更接近一维结构对应的地震震相到时; 然后应用传统的利用三叉震相一维反演方法进行深部波速结构反演; 最后对得到的结果进行补偿。
在进行初步的数学证明后, 本文利用正演数据做了初步测试。结果表明, 基于新的计算方案得到的反演结果明显优于传统的一维反演结果。这将使我们能够利用三叉震相, 得到更加真实的一维地幔波速结构, 有助于更深入、准确地理解地幔动力学过程。同时, 这种基于先验知识, 先去除、再补偿, 以便消除波速异常污染的研究方案, 对其他地震学反演问题也有借鉴意义。
本文的计算方案虽然是基于震相到时提出的, 但可以推广到利用波形资料进行的反演中。新的计算方案也需要基于地震观测资料的检验, 我们将在今后进一步予以讨论。
致谢:在论文完成过程中, 与北京大学博士研究生亢豆进行了有益的讨论, 也得到张献兵工程师的帮助, 在此表示感谢。
| [1] | Van der Hilst R D, Widiyantoro S, Engdahl E R. Evidence for deep mantle circulation from global tomography. Nature , 1997, 386 : 578–584 DOI:10.1038/386578a0 . |
| [2] | Fukao Y, Widiyantoro S, Obayashi M. Stagnant slabs in the upper and lower mantle transition region. Reviews of Geophysics , 2001, 39 (3) : 291–323 DOI:10.1029/1999RG000068 . |
| [3] | Grand S P. Mantle shear-wave tomography and the fate of subducted slabs. Philosophical Transactions of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences , 2002, 360 : 2475–2491 DOI:10.1098/rsta.2002.1077 . |
| [4] | Li X Q, Yuan X H. Receiver functions in north-east China: implications for slab penetration into the lower mantle in northwest Pacific subduction zone. Earth and Planetary Science Letters , 2003, 216 (4) : 679–691 DOI:10.1016/S0012-821X(03)00555-7 . |
| [5] | Huang J L, Zhao D P. High-resolution mantle tomography of China and surrounding regions. Journal of Geophysical Research , 2006, 111 (B9) : 4813–4825 . |
| [6] | Tang Y C, Obayashi M, Niu F L, et al. Changbaishan volcanism in northeast China linked to subduction-induced mantle upwelling. Nature Geoscience , 2014, 7 (6) : 470–475 DOI:10.1038/ngeo2166 . |
| [7] | Tajima F, Grand S P. Variation of transition zone high-velocity anomalies and depression of 660 km discontinuity associated with subduction zones from the southern Kuriles to Izu-Bonin and Ryukyu. Journal of Geophysical Research: Solid Earth , 1998, 103 (B7) : 15015–15036 DOI:10.1029/98JB00752 . |
| [8] | Wang T, Chen L. Distinct velocity variations around the base of the upper mantle beneath northeast Asia. Physics of the Earth and Planetary Interiors , 2009, 172 (3) : 241–256 . |
| [9] | Wang B S, Niu F L. A broad 660 km discontinuity beneath northeast China revealed by dense regional seismic networks in China. J Geophys Res , 2010, 115 (B6) : 1–12 . |
| [10] | Ye L L, Li J, Tseng T L, et al. A stagnant slab in a water-bearing mantle transition zone beneath north-east China: implications from regional SH waveform modelling. Geophysical Journal International , 2011, 186 (2) : 706–710 DOI:10.1111/j.1365-246X.2011.05063.x . |
| [11] | Takeuchi N, Kawakatsu H, Tanaka S, et al. Upper mantle tomography in the Northwestern Pacific region using triplicated P waves. Journal of Geophysical Research: Solid Earth , 2014, 119 (10) : 7667–7685 DOI:10.1002/2014JB011161 . |
| [12] | Wang T, Revenaugh J, Song X D. Two-dimen-sional/three-dimensional waveform modeling of sub-ducting slab and transition zone beneath Northeast Asia. Journal of Geophysical Research: Solid Earth , 2014, 119 (6) : 4766–4786 DOI:10.1002/2014JB011058 . |
| [13] | Kennett B L N, Engdahl E R. Traveltimes for global earthquake location and phase identification. Geo-physical Journal International , 1991, 105 (2) : 429–465 DOI:10.1111/gji.1991.105.issue-2 . |
 2016, Vol. 52
2016, Vol. 52