文章信息
- 高勇, 姜丹, 刘磊, 林星, 邬伦
- GAO Yong, JIANG Dan, LIU Lei, LIN Xing, WU Lun
- 一种地理信息检索的定性模型
- A Qualitative Method for Geographic Information Retrieval
- 北京大学学报(自然科学版), 2016, 52(2): 265-273
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(2): 265-273
-
文章历史
- 收稿日期: 2014-12-24
- 修回日期: 2015-01-30
- 网络出版日期: 2016-01-21
地理信息检索(geographic information retrieval, GIR)主要关注与地理位置相关的信息源的信息提取、存储、索引、查询、排序和浏览问题[1], 可以根据用户提交的请求, 从网页文本中检索在空间语义或空间范围上匹配的信息, 而这类信息通常以地名、地址等文本形式存在。地理信息检索扩展了传统信息检索(information retrieval, IR)的方法, 侧重于文档中与特定地理位置相关信息的处理[2], 其中的关键问题包括提取地理参照、地名去歧义、模糊地理信息处理、空间和文本索引、地理相似度排序、用户接口和结果评价等7个方面[3]。
当前的地理信息检索系统是将文档中的地理信息和主题信息分别提取、存储和匹配。其中, 主题信息部分沿用传统信息检索的方法, 基于文本关键字之间的共现程度评价文档与查询之间的主题相似度[4]。地理信息部分则基于传统GIS技术, 在地名辞典或地名库的帮助下, 将地名或地址等文本转换成以坐标表达的几何图形, 作为文档的地理范围(geographic footprint), 如中心点、外包矩形、凸包、简化多边形、点集等[5-9]。类似地, 检索请求中的地理约束条件同样被转化为定量的地理范围。在检索匹配的过程中, 主要基于文档和查询的地理范围之间的相对交叠面积或距离度量等方法[5, 10]进行空间相似度计算。最终, 将主题相似度与空间相似度集成[11-12], 对检索结果进行排序。
这种表达和相似度计算方法简化了地理信息处理的复杂性, 但却存在一些问题。主题与地理信息相互割裂的表达与处理办法, 忽略了两者的内在联系, 不符合人们日常表达和决策习惯, 使检索结果与用户实际信息需求存在一定的差异。采用单一的文档地理范围表达方法, 导致对文档地理范围的低估或高估。使用基于几何图形的地理范围定量化表达和基于交叠面积或欧氏距离的相似度计算方法, 会遗失大量的空间语义信息, 降低检索精度。
针对上述问题, 本文提出一种地理信息检索的定性模型, 基于命题逻辑和不确定性推理, 一体化建模主题信息和地理信息, 并评价文档相关性, 使其符合人类以概念化和自然语言形式使用地理空间知识的习惯, 从而可以很好地理解用户的地理信息检索请求和待检索的文档内容, 更准确地获取真正符合其检索需求的信息。
1 地理信息检索的定性表达方法 1.1 定性表达模型地理信息检索处理文档和查询两类数据, 它们都是用自然语言表达的文本形式, 其中包含主题和地理两类信息, 前者对应一系列文本关键词, 后者主要表现为文本地名、地址、IP地址、电话区号以及空间关系谓词或其组合。查询请求则可以表示为 < theme > < spatial relationship > < location > 三元组[3], 其中theme表示用户关心的主题信息, spatial relationship和location共同表示相关的地理空间范围约束。
为了更好地处理传统地理信息检索所缺失的语义特征, 这里以命题逻辑为基础, 建立主题信息与地理信息一体化的定性表达方法。命题逻辑是以逻辑运算符结合原子命题构成代表命题的公式, 以及允许某些公式建构成定理的一套形式证明规则。其中, 命题是能分辨真假的陈述句, 原子命题是能指派真假值的最小项。
首先将文档经过文本切割等预处理操作, 转换成一系列独立的信息单元, 每个单元均由 < 主题信息, 位置信息 > 组成, 表述一个独立的信息内容。基于命题逻辑, 将文档表达为命题的形式。相应地, 主题信息的每个关键词表达为一个主题命题, 位置信息则表达为地理空间命题的集合, 其中每个地理空间命题由地名、空间关系谓词及其逻辑连接符组成。进一步, 两类信息以命题逻辑组合, 形成一体化的表达方法。查询也采用相同的表达模型。
更一般地, 给定文档d, 基于主题信息与地理信息之间的关联性, 将其分割成一系列独立的信息单元, 则文档d的信息内容表示为
| $ d = \{ {u_i}|1 \le i \le n\} , $ | (1) |
其中, n为文档d包含的信息单元的数量, 如果n=0, 则d是一个空文档, 不包任何信息内容。信息单元ui包含主题部分ti与地理部分gi, 表示为
| $ {u_i} = \left( {{t_i},{g_i}} \right), $ | (2) |
相应地, 查询q基于信息单元表示为相同的结构。
1.2 主题信息的定性表达将信息单元ui的主题信息ti表示为该信息条目中出现的主题命题的集合, 即
| $ {t_i} = \{ {\rm{t}}{{\rm{p}}_i}(k)|1 \le k \le {\rm{N}}{{\rm{K}}_i}\} , $ | (3) |
其中, NKi是对应信息单元ui中表示主题内容的关键词数目; tpi(k)为主题命题语句, 可以是单个关键字或者是一个由关键字与连接符组成的复合主题命题语句。
基于命题逻辑, 主题命题语句由命题、逻辑连接符{∧, ∨, ﹁}组成, 定义其合成规则如下。
1) 单个关键字是原子主题命题语句。
2) 如果P是主题命题语句, 那么它的逆﹁P也是主题命题语句。
3) 如果P和Q是主题命题语句, 那么合取式P∧Q也是主题命题语句。
4) 如果P和Q是主题命题语句, 那么析取式P∨Q也是主题命题语句。
一般情况下, 文档中的一个信息单元可能包含多个主题关键词。在信息检索中, 由于文档内容经过分词等处理后得到的是词的罗列, 因此认为关键词是基于析取符号连接构成主题命题。由于查询是关键词的布尔逻辑, 所以只有在查询中存在合取和逆连接符。例如“军事新闻”是“军事”和“新闻”两个关键词的合取, “非官方消息”是“官方消息”的逆。这种情况在地理信息的表达中同样存在。
在该形式化表达的过程中, 需要引入领域本体, 对分词处理后的文档, 利用领域本体术语表对关键词汇进行识别、匹配和替换。
1.3 地理信息的定性表达信息单元ui中包含的地理信息内容gi, 表示为地理空间命题的集合, 即
| $ {g_i} = \{ {\rm{g}}{{\rm{p}}_i}(m)|1 \le m \le {\rm{N}}{{\rm{G}}_i}\} , $ | (4) |
其中, 地理空间命题gpi(m)是一个描述地理位置或范围的表达式, NGi是对应信息单元ui中地名的数目。地理空间命题可以继续细分, 直至地理空间元命题。每个地理空间元命题由一个空间关系谓词和一个地名组成。地理空间命题之间通过逻辑连接符相互关联、嵌套, 组成对地理范围的定性描述。
基于命题逻辑, 地理命题语句包括命题、逻辑连接符{∧, ∨, ﹁}和空间关系算子∮, 定义其合成规则如下。
1) 单个地名, 或由一个空间关系谓词修饰下的单个地名, 或由一个﹁操作符修饰下的单个地名, 是原子地理空间命题语句, 例如“北京”。
2) 如果∮是一元空间关系算子, p是地名, 那么∮p是地理空间命题语句, 例如“北京南部”、“上海周边”等。
3) 如果∮是二元空间关系算子, p和q是地名, 那么p∮q是地理空间命题语句, 例如“一环路和二环路之间”。多元空间关系算子依此定义, 例如“被太平洋、印度洋和大西洋包围”。
4) 如果P是地理空间命题语句, 那么它的逆﹁P也是地理空间命题语句, 例如“北京”和“非北京”。
5) 如果P和Q是地理空间命题语句, 那么合取式P∧Q也是地理空间命题语句。
6) 如果P和Q是地理空间命题语句, 那么析取式P∨Q也是地理空间命题语句。
值得注意的是, 本文引入的空间关系算子∮的操作元数量比通常所指的空间关系元数少1, 例如“······与······邻接”是二元空间关系, 而作为空间关系算子“与······邻接”是一元的。另外, 由于空间关系在不同场景下的模糊性不同[13], 本文所提出的表达和推理方法仅针对文本表示的地理信息检索领域。
在前人的研究中, 确定了地理空间中的空间关系谓词表达及其推理演算方法[14-15], 可以基于此建立空间关系算子集合。尽管空间关系算子同时支持对度量和方位关系的定量表达, 但在自然语言或网页文本中仍以定性描述为主要形式。
2 定性检索模型 2.1 相似度计算方法在地理信息检索中, 判断候选文档是否满足用户的检索请求, 需要进行文档和查询的相似度计算, 并据此排序检索结果, 这其中需要同时从主题和地理范围两个方面评价相似度。需要指出的是, 相似度的评价具有方向性, 即文档满足查询的程度与查询满足文档的程度并不完全相同。例如, 当查询“西餐厅”时, 检索结果返回“纽约披萨”是符合要求的; 反之, 检索“纽约披萨”时, 检索结果返回“西餐厅”则不那么符合要求。从推理的角度看, 相似度推理是方向相关的, 是d→q的推理过程置信度。
基于上述定性表达模型, 文档d由n个信息单元组成, 查询q包含m个子查询, 子查询是原子的、相互独立的, 并由逻辑连接符相连。据此提出基于证据理论和模糊逻辑的语义相似度计算模型, 将相似度求解过程分解为3个步骤。
1) 计算文档的每个信息单元ui与子查询qj的相似度, 记为Ru (ui, qj), 是ui与qj主题相似度和地理相似度的组合。
2) 将文档d中所有信息单元与子查询qj的相似度合成, 计算文档d满足子查询qj的程度, 记为Rq (d, qj)。
3) 将查询q的所有子查询的相似度合成, 形成最终文档d对查询q的满足程度, 记为R(d, q)。
在上述过程中, 涉及几个不同层次的相似度的计算, 可以将其区分为两个类别:信息单元的主题信息与地理信息、查询与子查询等是基于命题逻辑表达, 因此其相似度的合成函数采用模糊逻辑推理的方法; 文档是信息单元的集合表达, 因此将信息单元作为文档内容的证据, 基于证据理论合成信息单元相似度。下面将详细论述上述相似度的计算过程。
2.2 信息单元与子查询的相似度计算由于子查询可以表达为一个简单的信息单元, 因此信息单元ui与子查询qj的相似度Ru (ui, qj)可以归结为两个信息单元的相似度计算。每个信息单元均由主题部分和地理部分组成, 因此其相似度包括主题相似度、地理相似度及其组合3个部分。
在定性表达模型中, 各要素都是基于命题逻辑表达, 由命题变元基于逻辑连接符{∧, ∨, ﹁}连接。命题变元相似度的合成可以基于模糊逻辑推理完成。模糊逻辑是用于近似推理的逻辑[16], 是基于规则的, 规则的前提是基于逻辑算子建立的模糊集的组合, 规则的结论是一个具有相应隶属函数的模糊集。在匹配规则的过程中, 命题变元的逆是其模糊集合的补, 而命题变元的合取和析取分别采用最小算子和最大算子进行合并。
2.2.1 主题相似度两个信息单元在主题上的相似程度, 依赖于其传达的相同信息内容的程度, 是基于主题关键词之间语义相近程度的评价, 与主题词共现频率的评估并不相同。设a和b是两个主题关键词, 它们之间的主题相关性算子用⊕表示, 那么,
| $ \left\{ {\begin{array}{*{20}{l}} {a \oplus b = h(a,b)\;,}\\ {a \oplus \neg b = 1 - h(a,b)\;,} \end{array}} \right. $ | (5) |
其中h(a, b)为a和b的概念相似度函数。由于相似度的方向性, ⊕不满足交换律, 即a⊕b≠ b⊕a。
对于文档中的一个信息单元, 其主题信息X由关键词集合{x1, x2, …, xn}基于析取连接符构成。设a是一个关键词, 则X与a的主题相似度计算为
| $ \left\{ {\begin{array}{*{20}{l}} {X \oplus a = \max \{ {x_i} \oplus a|i = 1,2, \ldots ,n\} ,}\\ {X \oplus \neg a = 1 - \min \{ {x_i} \oplus a|i = 1,2, \ldots ,n\} \;。} \end{array}} \right. $ | (6) |
基于模糊逻辑的最大-最小方法, 两个主题信息X={x1, x2, …, xn}和Y={y1, y2, …, yk}的主题相似度计算为
| $ X \oplus Y = \min \{ X \oplus {y_i}|i = 1,2, \ldots ,k\} 。 $ | (7) |
设H={h1, h2}是一个检索查询的主题命题部分, 由两个关键词组成, 是连接子命题的逻辑连接符, 可以为∨或∧, 那么文档信息单元与查询的主题信息相似度计算为
| $ X \oplus H = \left\{ {\begin{array}{*{20}{c}} {\max \{ X \oplus {h_1},X \oplus {h_2}\} ,}&{\uplus = \vee \;,}\\ {\min \{ X \oplus {h_1},X \oplus {h_2}\} ,}&{\uplus = \wedge \;。} \end{array}} \right. $ | (8) |
任何复杂的查询命题, 总能分解为上述形式, 因此核心的问题是关键词之间语义相似度h(a, b)的计算。
领域本体中概念之间的相互关系提供了度量两个关键词之间语义相似度的途径, 因此基于概念加权最短距离[17]提出主题关键词语义相似度的计算方法。本体中的概念以及概念之间的联系形成一个树状或网状结构(概念语义网), 其中概念为节点, 概念之间的关系为连接。概念之间比较重要的关系有BT (广义词)关系、NT (狭义词)关系和RT (相关词)关系。两个概念之间最短路径定义为:在概念语义网中, 从一个概念出发, 经过最少中转节点到达另一个概念的路径。加权最短距离就是根据最短路径上概念两两间直接连接关系的强弱不同, 为对应连接设置不同的权重, 然后将最短路径上每条连接的加权距离值相加, 即得到两个概念之间的加权最短距离。
设a和b为两个主题关键字, 对应于本体中的概念, 其加权最短路径TD (a, b)为
| $ {\rm{TD(}}a,b{\rm{)}} = \left( {\frac{{{C_{a,{x_1}}}}}{{{L_{{x_1}}}}} + \frac{{{C_{{x_1},{x_2}}}}}{{{L_{{x_2}}}}} + \ldots + \frac{{{C_{{x_{n - 1}},{x_n}}}}}{{{L_{{x_n}}}}} + \frac{{{C_{{x_n},b}}}}{{{L_b}}}} \right), $ | (9) |
Cij表示连接两个相邻概念i和j的路径权重, 用i→j之间关系的强弱程度进行赋值。Li表示概念i在概念树中的深度。a→x1→x2→…→b为从概念a到概念b的最短路径。对式(9)的计算结果进行归一化, 作为最后的语义相似度值。可以用概念树中两个概念间可能的最大距离MD进行归一化, 也可以用对数表达式进行归一化。那么两个主题关键词a和b的概念相似度h(a, b)的计算公式为
| $ \begin{array}{l} h(a,b) = \frac{1}{{1 + \ln (1 + {\rm{TD}}(a,b))}}或\\ h(a,b) = 1 - \frac{{{\rm{TD}}(a,b)}}{{{\rm{MD}}}}. \end{array} $ | (10) |
在实际应用中, 需要对NT, BT和RT等关系进行加权, Tudhope等[17]的做法是wNT=wBT≤wRT, 也就是通过RT关系进行连接的两个概念, 要比通过NT或BT关系连接的两个概念在语义上离得远些。具体数值的确定过程都是凭经验, 例如可以设定wNT=wBT=0.5, wRT=0.8等。但这种关系权重设置方法并没有考虑概念相似度的有向性问题。由于a→b与b→a的语义相似度不同, 因此对BT和NT关系设置不同的权重, 并令其满足wNT < wBT < wRT。
例如, 某文档中包含“有色金属”和“煤矿”, 查询词为“铁矿”, 要计算主题相关性, 则可表达为
| $ \begin{array}{l} 铁矿 \oplus (有色金属 \vee 煤矿) = \\ (铁矿 \oplus 有色金属,\;铁矿 \oplus 煤矿)\;。 \end{array} $ |
根据煤矿领域语言词典的本体图, 我们设BT和NT两种关系的权重分别为0.6和0.4, RT关系设为1.0, 本题中两个概念之间最远加权距离为5.0, 则分别计算相似度为
| $ \begin{array}{l} 铁矿 \oplus 有色金属 = 1 - \frac{{\frac{{0.4}}{2} + \frac{{0.4}}{1} + \frac{{0.6}}{2}}}{{5.0}} = 0.82,\\ 铁矿 \oplus 煤矿 = 1 - \frac{{\frac{{0.4}}{2} + \frac{{0.4}}{1} + \frac{{0.6}}{2} + \frac{{0.6}}{3}}}{{5.0}} = 0.78\;。 \end{array} $ |
利用模糊集理论进行结果合并, 铁矿⊕(有色金属∨煤矿)=0.82。上述计算实例表明, 本文提出的主题相似度度量方法合理有效。
2.2.2 地理相似度两个信息单元的地理相似度, 是从语义的角度判断其地理信息内容之间的相关性。由于信息单元的地理信息是关于原子地理空间命题的语句, 因此地理相似度是两个信息单元中所包含的原子地理空间命题的函数。
一般情况下, 文档中的地理空间命题都是简单地名的形式, 有时可能包含空间关系谓词的简单组合。检索查询请求的情况与此相同。因此, 地理相似度的计算可以归结为两个地名之间语义相似度的计算。
地名的语义包括概念特征和位置特征。对于概念相似度, 采用以整体-部分关系进行组织的地名库为基础, 计算两个地名对应的概念在本体树上的层次距离[18], 即
| $ \begin{array}{l} {\rm{CS}}(p,o) = 1 - \left( {\sum\nolimits_{x \in \{ p.{\rm{PartOf}} - o.{\rm{PartOf}}\} } {\frac{\alpha }{{{L_x}}}} + } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\nolimits_{y \in \{ o.{\rm{PartOf}} - p.{\rm{PartOf}}\} } {\frac{\beta }{{{L_y}}}} + \sum\nolimits_{z \in \{ p,o\} } {\frac{\gamma }{{{L_z}}}} } \right), \end{array} $ | (11) |
其中, CS (p, o)是地名p和o的概念相似度, Lx, Ly, Lz分别代表x, y, z三个地名在本体树上的层数, p.partOf和o.PartOf分别代表地名p和o在本体树上所有祖先地名的集合, α, β, γ是调和系数, 一般令α=β=1.0, 而当p和o是兄弟关系时, 令γ=1.0, 否则γ=0。
位置相似度的计算基于“拓扑空间关系为主, 度量关系精化”[19]的原则。当地名p和o对应的空间范围尺度较大(如省级及以上级别)时, 可以直接采用拓扑关系语义相近度[20]进行评价, 无须通过距离进行精化。当空间范围尺度较小(如市级及以下级别)时, 采用综合考虑拓扑和度量的计算方法[21]。
第一步, 计算拓扑相似度:
| $ {\rm{Inclusion}}(p,o) = \left\{ {\begin{array}{*{20}{l}} {\frac{{NumDescendants\left( o \right) + 1}}{{NumDescendants\left( p \right) + 1}}}&{o \subseteq p,}\\ {0,}&{其他,} \end{array}} \right. $ | (12) |
其中NumDescendants (o)和NumDescendants (p)分别为地名o和p在本体树上子地名的数量。
第二步, 计算度量相似度:
| $ {\rm{Proximity}}(p,o) = \frac{1}{{1 + {\rm{Distance}}(p,o)/{\rm{diagnoal}}(p)}}, $ | (13) |
其中, Distance (p, o)为地名p与o之间的欧几里得距离, diagnoal (p)为地名p的MBR的对角线长度。
第三步, 判断是否为兄弟关系。当p和o具有相同的祖先时, 令Sibling (p, o)=1;否则令Sibling (p, o)=0。
第四步, 合并上述3个数值, 得到位置相似度LS (p, o):
| $ \begin{array}{l} LS(p,o) = b \times \{ Inside\left( {p,{\rm{ }}o} \right) + Proximity(p,o)\} + \\ \;\;\;\;\;\;\;\;\;\;\;(1 - b) \times Siblings\left( {p,o} \right), \end{array} $ | (14) |
其中, b是介于0与1之间的调和参数。
最后, 将概念相似度CS与位置相似度LS合成, 得到地理相似度g(p, o):
| $ g\left( {p,o} \right) = {w_g}LS\left( {p,o} \right) + {w_h}CS\left( {p,o} \right), $ | (15) |
其中, wg和wh是介于0和1之间的调和系数, 一般令wg和wh分别为0.6和0.4[22]。实际上, 上述各式中调和系数的取值均与查询及文档地理范围的尺度有关。
2.2.3 主题和地理相似度的组合将主题和地理的相似度组合形成一个综合的评价结果, 则文档d的一个信息单元ui与子查询qj的相似度Ru (ui, qj)可以表示为
| $ Ru\left( {{u_i},{q_j}} \right) = l\left( {R{u_g}\left( {{u_i},{q_j}} \right),{\rm{ }}R{u_t}\left( {{u_i},{q_j}} \right)} \right), $ | (16) |
其中Rug为地理相似度, Rut为主题相似度, l为合成函数。合成函数可以采用几何平均值、算术平均值、乘积、加权算术平均值、欧氏距离等方法。
2.3 文档与子查询的相似度计算对于文档d与子查询qj之间相似度评价Rq (d, qj)的计算, 可以将其建模为一个不确定性推理的过程, 合成文档所有信息单元与子查询的相似度。文档中的每个信息单元ui都可以看成是证明文档d与qj是否相关的一个证据, 证据之间是独立出现的。这样, ui与qj之间的相似程度可以视为证据来证明“文档d与子查询qj相关”的可信度。因此, 采用Dempster-Shafer (D-S)证据理论[23], 合并所有证据的可信度, 最终导出文档与子查询的相似度。
一般地, 对于GIR的检索模型, 需要证明的命题有两个: T=文档与查询相关, F=文档与查询不相关。基于D-S证据理论, 识别框Θ={T, F}。Θ是由互不相容的基本命题组成的完备集合, 表示对某一问题的所有可能答案, 但其中只有一个答案是正确的。Θ的幂集记做2Θ, 则有
| $ {2^{\rm{\Theta }}} = \{ \phi ,\;\{ T\} ,\;\{ f\} ,\;\{ T,\;F\} \} 。 $ | (17) |
对于2Θ中给定的命题(或子集) A, 基础信任分配函数m(A)表示证据对命题A的支持程度, 信任度函数Bel (A)表示对命题A的信任程度, 似然函数Pl (A)表示对命题A非假的信任程度, 也即对A似乎可能成立的不确定性度量。区间[Bel (A), Pl (A)]表示所有提交的证据给出的A为真的可信度的波动范围, 且有
| $ {\rm{Bel}}(A) = \sum\nolimits_{B|B \subseteq A} {m(B),} $ | (18) |
| $ {\rm{Pl}}(A) = \sum\nolimits_{B|B \cap A \ne \phi } {m(B)} , $ | (19) |
其中m函数满足
| $ \left\{ {\begin{array}{*{20}{l}} {m:{2^{\rm{\Theta }}} \to [0,\;\;1],}\\ {0 \le m(x) \le 1,\forall x \in {2^{\rm{\Theta }}},}\\ {\sum\nolimits_{x \in {2^{\rm{\Theta }}}} {m(x)} = 1,}\\ {m(\phi ) = 0\;。} \end{array}} \right. $ | (20) |
假设一个信息单元ui与子查询qj之间的相似度为α, 即Ru (ui, qj)=α (基于2.2节的方法计算), 如果把该信息单元视为一个证据, 那么它证明命题集合{T}成立的可信度为α。没有证据直接证明{F}命题组, 那么根据合成理论, 最好的方法是将1 -α赋给全集{T, F}, 即
| $ \left\{ {\begin{array}{*{20}{l}} {m(\{ T\} ) = \alpha ,}\\ {m(\{ F\} ) = 0,}\\ {m(\{ T,F\} ) = 1 - \alpha ,}\\ {m(\{ \phi \} ) = 0\;。} \end{array}} \right. $ | (21) |
那么, Rq (d, qj)可以由Ru (ui, qj)迭代导出。对于一个完整的文档, 依次加入文档中的信息单元作为证据, 计算每个证据的基础信任分配, 然后使用D-S的证据合成方法合成多个证据的确信度, 即
| $ {m_{i + 1}}(C) = \frac{{\mathop \sum \nolimits_{A \cap B = C} {m_i}(A){m^{i + 1}}(B)}}{{\mathop \sum \nolimits_{A \cap B \ne \phi } {m_i}(A){m^{i + 1}}(B)}}, $ | (22) |
其中, mi表示合成了i个证据后的m函数值, mi+1表示第i+1个证据出现后给出的基础信任分配。如果出现交集为空的元素, 依据D-S证据合成算法, 需要扣除交集为空集的计算结果, 然后对每个m函数值重新进行归一化。这样, 每个命题集合的m函数值迭代更新(表 1)。
| m函数 | mi+1({T}) | mi+1({T, F}) |
| mi({T}) | mi({T})﹒mi+1({T}) | mi({T})﹒mi+1({T, F}) |
| mi({T, F}) | mi({T, F})﹒mi+1({T}) | mi({T, F})﹒mi+1({T, F}) |
在所有的证据全部加入后, 得到最终每个命题集合的m, Bel和Pl函数值。对命题T和F支持的可信度p(T)和p(F)将分别满足:
| $ \left\{ \begin{array}{l} {\rm{Bel}}(\{ T\} ) \le p(T) \le {\rm{Pl}}(\{ T\} )\;,\\ {\rm{Bel}}(\{ F\} ) \le p(F) \le {\rm{Pl}}(\{ F\} )\;。 \end{array} \right. $ | (23) |
Bel ({T}), Pl ({T}), Bel ({F})和Pl ({F})是用于度量文档与子查询相似度的基本指标。可以直接使用Bel ({T})值作为相似度, 或更进一步地, 将相似度定义为
| $ \begin{array}{l} {\rm{Rq}}(d,{q_j}) = \frac{{{\rm{Bel}}(\{ T\} )}}{{{\rm{Bel}}(\{ F\} )}}2222\\ {\rm{Rq}}(d,{q_j}) = 1 - \frac{1}{{\ln \left( {{\rm{e}} + \frac{{{\rm{Bel}}(\{ T\} )}}{{{\rm{Bel}}(\{ F\} )}}} \right)}}。 \end{array} $ | (24) |
将文档与所有子查询的相似度进行合成, 得到最终文档与查询的相似度R(d, q)。查询和子查询都是基于命题逻辑表达, 查询根据其内部的逻辑结构, 分解为若干个形如 < theme > < spatial relationship > < location > 的原子的子查询, 且子查询之间通过逻辑连接符{∧, ∨, ﹁}相连。
由于文档d与子查询qj之间的相似度为Rq (d, qj), 则有
| $ Rq(d,{q_j}) = 1{\rm{ }} - Rq\left( {d,{q_j}} \right). $ | (25) |
设查询q由两个子查询{q1, q2}构成, 子查询通过的逻辑连接符连接, 可以为∨或∧, 那么文档d与q查询的相似度R(d, q)计算公式为
| $ R(d,q) = \left\{ \begin{array}{l} \max \{ {\rm{Rq}}(d,{q_1}),\;{\rm{Rq}}(d,{q_2})\} ,\;\uplus = \vee ,\\ \min \{ {\rm{Rq}}(d,{q_1}),\;{\rm{Rq}}(d,{q_2})\} ,\;\;\uplus = \wedge \;。 \end{array} \right. $ | (26) |
任意复杂的查询都可以先进行转换, 然后按照上述方法求解与文档的相似度。通过上述工作, 最终得到文档d与查询q的相似度R(d, q), 据此可排序候选文档。
3 实验实验文档集取自中国矿业网①, 所有文档都用中文自然语言编写, 内容限定为地质矿产专题领域。在限定领域的条件下, 一个有限且有效的领域本体相对容易制定, 在检索过程中, 该领域概念本体将作为专题知识库使用。信息单元的提取采取人工和机器相结合的方式进行, 先通过人工方式将文档内容分割成内容独立的若干段落, 再用中文分词工具对各个段落进行分词处理, 并提取相关的主题词信息和地名信息。通过上述处理, 整理汇编其中50个文档作为测试, 平均每个文档包含2~3个信息单元, 每个信息单元包含1个主题词和1个表示地理位置的地名。
① http://www.chinamining.com.cn
例如, 对于内容为“······我国铬铁矿储量分布于13个省(区), 但主要集中在西藏、内蒙古、新疆、甘肃。······我国铝土矿分布于20个省(区), 但主要集中在山西、贵州、河南和广西······”的文档, 可以表达为2个信息单元, 即
d={({铬铁矿}, {西藏, 内蒙古, 新疆, 甘肃}), ({铝土矿}, {山西, 贵州, 河南, 广西})}。
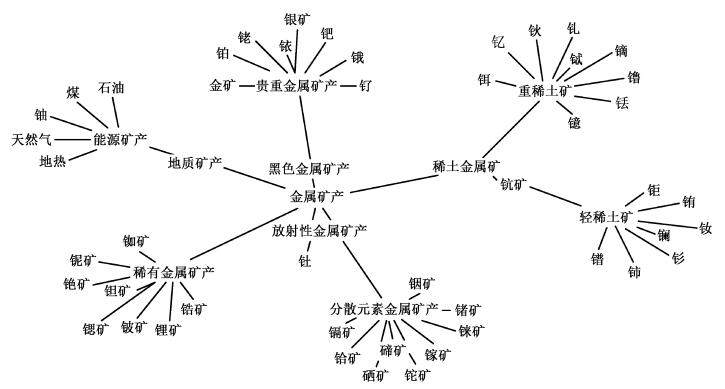
针对文档涉及的地质矿产领域, 建立一个简化的地质矿产资源类型本体, 如图 1所示。该领域本体中包含1个一级类别, 3个二级类别, 73个三级类别, 47个四级类别, 17个五级类别。
|
| 图 1. 实验中采用的地质矿产领域本体 Figure 1. Mineral ontology used in the experiment |
实验采用的地名库是覆盖县级行政区划的全国行政区地名库, 其中包含省级行政区划34个, 地级市地名360个, 县级地名2939个, 乡镇级地名20266个。
实验中采用传统的地理信息检索方法作为与定性检索方法的比较。该对比方法使用基于向量模型计算文档与查询的主题相似度, 采用外包矩形相交比率作为地理相似度, 对两者采用几何平均值方法合成。
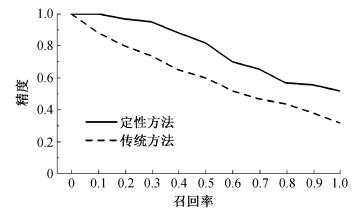
在该文档集上, 分别采用定性方法和传统方法进行多次查询, 查询过程中采用通用的 < theme > < location > 形式(这里基于简化的形式省略了 < spatial relationship > 部分), 例如“贵重金属矿产河北省”、“金属矿产石家庄市”等。每个查询的相关文档集采用人工方法判定。两种方法的查询结果采用11点标准召回率平均精度进行评估, 如图 2所示。实验表明, 定性方法表现出更好的检索精度, 并可以度量文档中比较细微的相似度差别, 较少出现定量方法那样完全不匹配的情况。
|
| 图 2. 两种检索方法的11点召回率精度对比评估 Figure 2. Comparison of 11-points recall rates of two GIR methods |
在一般情况下, 该定性方法可以取得比传统方法更好的结果, 特别是命题表达和定性推理规则更适用于处理中大空间尺度的查询。对于小尺度的查询, 例如街区尺度, 传统的定量方法则可以给出更精确的结果。因此, 更好的策略是在一个地理信息检索系统中同时集成定性和定量的方法。当查询的空间尺度较大(城市级别或更大)时, 采用定性方法更符合常识性空间认知, 检索处理也更容易、更快捷。当查询的空间尺度适中(区县级别)时, 组合使用定性和定量的方法, 首先使用定性方法进行空间范围的粗过滤, 然后使用定量方法精确处理。当查询的空间尺度很小(街区级别)时, 可以直接使用定量方法得到精确结果。
4 结论本文基于命题逻辑和不确定性推理, 提出一种地理信息检索的定性模型, 为提高现有地理信息检索技术的检索效率提供一种新方法。相比于传统的地理信息检索方法, 该定性方法顾及了语义信息, 没有对空间进行简化, 而是直接采用地理本体或地名库, 因而可以更加客观真实地刻画文档中的信息和用户的检索请求。所提方法中基于真实信息内容的推理匹配方法, 在大中尺度下得到的检索结果比传统定量方法更接近于使用者的常识性认知。并且, 该定性地理信息检索方法也可以同时支持传统的定量方法, 可以实现定量和定性检索模型的良好结合。
该定性检索方法仍需进一步完善, 还需要深入研究文本分割技术, 实现文档中信息单元的正确高效提取, 改善定性推理评价模型, 并完善地理知识库建设。
| [1] | Larson R R. Geographic information retrieval and spatial browsing // Smith L, Gluck M. Proceedings of the data processing clinic -geographic information systems and libraries: patrons, maps, and spatial information. Urbana-Champaign: University of Illi-nois, 1996: 81-124 |
| [2] | Jones C B, Purves R S. Foreword of GIR'06 // Workship on Geographic Information Retrieval, SIGIR'06. New York, 2006: 40-41 |
| [3] | Jones C B, Purves R S. Geographical information retrieval. International Journal of Geographical Information Science , 2008, 22 (3) : 219–228 DOI:10.1080/13658810701626343 . |
| [4] | Baeza-Yates R, Ribeiro-Neto B. Modern information retrieval. New York: ACM Press, 1999 . |
| [5] | Hill L L, Frew J, Zheng Q. Geographic names: the implementation of a gazetteer in a georeferenced digital library. D-Lib Magazine , 1999, 5 (1) : 1–19 . |
| [6] | Alani H, Jones C B, Tudhope D. Voronoi-based region approximation for geographical information retrieval with gazetteers. International Journal of Geographical Information Science , 2001, 15 (4) : 287–306 DOI:10.1080/13658810110038942 . |
| [7] | Frontiera P, Larson R, Radke J. A comparison of geometric approaches to assessing spatial similarity for GIR. International Journal of Geographical Information Science , 2008, 22 (3) : 337–360 DOI:10.1080/13658810701626293 . |
| [8] | Naaman M, Song Y J, Paepcke A, et al. Assigning textual names to sets of geographic coordinates. Computers, Environment and Urban Systems , 2006, 30 : 418–435 DOI:10.1016/j.compenvurbsys.2006.02.001 . |
| [9] | Liu Y, Yuan Y, Xiao D, et al. A point-set-based approximation for areal objects: a case study of representing localities. Computers, Environment and Urban Systems , 2010, 34 (1) : 28–39 DOI:10.1016/j.compenvurbsys.2009.05.001 . |
| [10] | Beard K, Sharma V. Multidimensional ranking for data in digital spatial libraries. International Journal on Digital Libraries , 1997, 1 (2) : 153–160 DOI:10.1007/s007990050011 . |
| [11] | Larson R R, Frontiera P. Spatial ranking methods for geographic information retrieval (GIR) in digital libraries // Heery R, Lyon L. Lecture notes in computer science 3232. Berlin: Springer, 2004: 45-57 |
| [12] | de Sabbata S, Reichenbacher T. A probabilistic model of geographic relevance // Proceedings of the 6th Workshop on Geographic Information Retrieval. Zürich: ACM, 2010: 23-24 |
| [13] | 金鑫, 耿海燕, 高勇, 等. 空间方位关系在不同场景下的模糊性探讨. 北京大学学报:自然科学版 , 2009, 45 (6) : 1025–1032. |
| [14] | Cohn A G, Renz J. Qualitative spatial representation and reasoning. Foundations of Artificial Intelligence , 2008, 3 : 551–596 . |
| [15] | 刘瑜, 龚咏喜, 张晶, 等. 地理空间中的空间关系表达和推理. 地理与地理信息科学 , 2007, 23 (5) : 1–7. |
| [16] | Zhang Yi, Gao Yong, Xue Lulu, et al. A common sense geographic knowledge base for GIR. Science in China Series E: Technological Sciences , 2008, 51 (Suppl 1) : 26–37 . |
| [17] | Tudhope D, Taylor C. Navigation via similarity: automatic linking based on semantic closeness. Information Processing and Management , 1997, 33 (2) : 233–242 DOI:10.1016/S0306-4573(96)00067-2 . |
| [18] | Jones C B, Alani H, Tudhope D. Geographical infor-mation retrieval with ontologies of place. Lecture Notes in Computer Science , 2001, 22 (3) : 322–335 . |
| [19] | Mark D M. Spatial representation: a cognitive view // Maguire D J, Goodchild M F, Rhind D W, et al. Geographical information systems: principles and applications. New York: John Wiley & Sons, 1999: 81-89 |
| [20] | Bruns T, Egenhofer M. Similarity of spatial scenes // Kraat M J, Molenaar M. Seventh Internaltional Symposium on Spatial Data Handling (SDH'96). Delft, 1996(4A): 31-42 |
| [21] | Andrade L, Silva M J. Relevance ranking for geographic IR // Workshop on Geographic Informa-tion Retrieval, SIGIR'06. Seattle, WA: ACM, 2006: 1-4 |
| [22] | Jones C B, Alani H, Tudhope D. Geographical information retrieval with ontologies of place // Proceedings of the International Conference on Spatial Information Theory: Foundations of Geo-graphic Information Science (COSIT). Morro Bay, CA: Springer Berlin/Heidelberg, 2001: 322-335 |
| [23] | Shafer G. A mathematical theory of evidence. Prince-ton, NJ: Princeton University Press, 1976 . |
 2016, Vol. 52
2016, Vol. 52




