文章信息
- 杜书恒, 师永民, 徐启, 方媛媛, 盛英帅
- DU Shuheng, SHI Yongmin, XU Qi, FANG Yuanyuan, SHENG Yingshuai
- 井震联合非均质储层改造规模的非线性表征方法
- Nonlinear Characterization Method of Fracturing Stimulation Scale on Heterogeneous Reservoir by Combining Logging and Seismic Data
- 北京大学学报(自然科学版), 2016, 52(2): 241-248
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(2): 241-248
-
文章历史
- 收稿日期: 2014-12-03
- 修回日期: 2015-01-29
- 网络出版日期: 2015-05-05
2. 中国石油天然气股份有限公司大庆油田分公司第十采油厂, 大庆 166405
2. The 10th Oil Production Plant, Daqing Oilfield Company, PetroChina, Daqing 166405
二次采油的关键问题在于厘清储层间连通关系, 以便采取水力压裂等增产措施, 建立油水井间有效驱动体系, 使水驱波及范围达到最大, 剩余油得到有效动用。水力压裂过程中产生的人工裂缝对原储层物性进行了较大规模的改造, 形成填砂裂缝, 达到充分改善原储层导流能力, 增加单井油气产量的目的[1-4]。因此, 在压裂前较准确地预测人工裂缝的展布情况, 对于提高措施效率和增产效益意义重大。
20世纪50年代以来, 相继出现描述人工裂缝展布规律的KGD[5], PKN[6]等二维模型和拟三维模型[7]等, 对压裂缝的展布情况做了一定程度上的预测。但这些模型大多只适用于海相均质地层, 假设条件均为井筒两端物性和岩石力学性质高度对称, 因而模拟结果仅为半缝长。然而, 对于中国陆相储层非均质性较强, 油水层连通关系复杂, 隔夹层发育现象普遍的情况, 半缝长的模拟结果远远不能满足预测陆相储层改造规模的需要, 亟需采用更为精确的模拟手段。另外, 线弹性理论中建立的压裂缝延伸缝高、缝宽计算模型[8-9]大多形式复杂, 涉及因素众多, 且有些参数不易获取, 限制了纵向上储层改造规模的判断精度, 给下一步开发层系的选取带来不便。
针对以上研究现状中的问题, 本文应用井震联合的手段建立大庆朝89区块三维物性参数、岩石力学参数及地应力场模型。同时, 考虑到油藏三维空间中的非均质性, 开展压裂缝的全缝长网格化定量模拟。最后对裂缝模拟过程中剖分的压裂层段网格的总应力值与对应的铺砂浓度值、裂缝宽度值、裂缝内净压力值进行归一化处理, 提出“相对应力”和“改造因子”的概念, 并给出二者间非线性经验关系式。根据研究区某井各压裂层段的归一化后总应力曲线, 结合关系式, 即可获取该井相应层段的“改造因子”曲线, 用以判断储层压裂后改造规模, 以便确定剩余油动用情况。
朝89区块位于朝阳沟背斜构造翼部, 其北部、东部和西部分别被3条正断层围限, 油藏内部断层不发育, 作为主力产层的扶余油层是松辽盆地大规模沉降前期形成的一套以河流相为主的沉积, 其中Ⅲ类区块含油面积为122 km2, 地质储量为7774.28×104 t, 空气渗透率为3.5 mD。
1 测井岩石力学参数计算正交偶极子阵列声波成像测井(X-MAC)将单极和偶极声波技术相结合, 能精确地进行各种地层的声波测量, 解决了慢速地层的横波测量问题, 是岩石弹性特性研究的理想工具[10-14]。我们对朝89区块内F111-67-1井开展了X-MAC测井, 对测井结果进行处理解释, 计算杨氏模量、泊松比等基本岩石力学参数(图 1)。

|
| 图 1. 朝89区块F111-67-1井X-MAC测井解释成果图 Figure 1. Logging interpretation results of well F111-67-1 in Chao 89 zone |
解释结果发现, 研究区储层杨氏模量、泊松比等岩石力学参数对自然伽马、声波时差、深侧向电阻率等常规测井曲线的变化较为敏感(图 1)。以下采用多元统计回归方法建立岩石力学参数与常规测井资料间的回归方程, 利用其求取工区内具有常规测井曲线井的“准岩石力学参数”, 为后期三维油藏模型的建立奠定基础。
经多元统计回归, 得出以下回归方程:
| $ \left\{ \begin{array}{l} \mu = 0.000{\rm{54AC}} + 0.0{\rm{14GR}} + 0.00{\rm{12LLD}},\\ R = 0.{\rm{9123}}, \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} E = 0.0{\rm{37AC}} + 0.{\rm{4721GR}} + 0.0{\rm{51LLD}},\\ R = 0.{\rm{9}}0{\rm{14}}, \end{array} \right. $ | (2) |
式中, μ为泊松比(无量纲), E为杨氏模量(GPa), AC为声波时差(μs/m), GR为自然伽马(API), LLD为深侧向电阻率(Ω·m)。
2 叠前地震波阻抗反演由地震反射剖面得到地层波阻抗剖面的过程称为地震波阻抗反演, 目的是提取声波阻抗体, 求取岩石力学参数[15-16]。相比叠后地震数据反演, 叠前反演不仅能得到纵波阻抗体, 还能得到横波阻抗信息[17]。
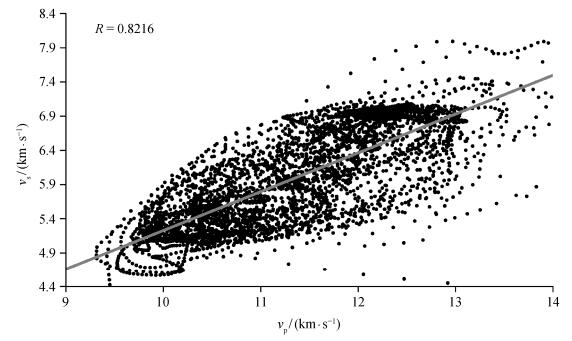
反演前, 先对地震数据进行动、静校正等常规处理, 以提高地震数据信噪比[18]。接着对区块内已有X-MAC测井信息的F111-67-1井进行纵横波速度交会分析(图 2), 相关系数R达到0.8216, 得到vs/vp平均值为0.61, 由此来控制联合反演得到纵波与横波数据体的初始模型。
|
| 图 2. 朝89区块F111-67-1井纵、横波速度vp与vs交会图 Figure 2. Cross-plot of P wave velocity and S wave velocity of well F111-67-1 in Chao 89 zone |
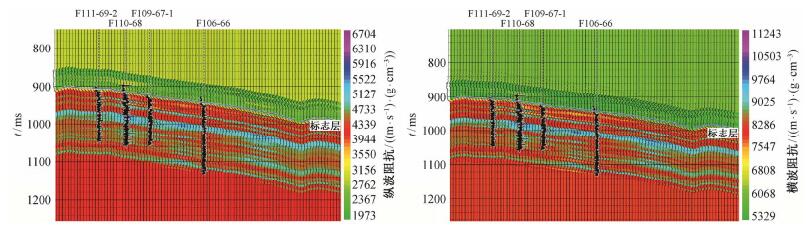
合成地震记录是将测井和垂直地震剖面资料经过人工合成转换成的地震记录, 目的是将深度域的测井信息拟合为时间域的波形, 与井旁地震道中的波形相对应[19]。基于研究区面积小、井位密、测井资料全且品质好的特点, 本次模型反演采用测井约束反演方法。利用研究区内F111-69-2, F110-68, F109-67-1和F106-66等井进行合成记录, 并反复修改模型, 以期与地震道达到最大程度吻合, 使反演结果精细度达到最大(图 3)。
|
| 图 3. 朝89区块叠前地震纵、横波阻抗反演结果 Figure 3. Wave impedance inversion results of pre-stack seismic data of Chao 89 zone |
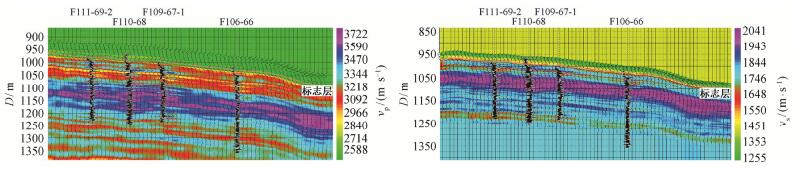
最后, 对已反演出的波阻抗模型以目的层顶面作为时深转换标准, 得到深度域纵横波速度反演数据体(图 4)。该深度域反演数据体可加入到储层地质建模软件中, 结合密度测井曲线, 在建模软件中计算得到杨氏模量、泊松比等弹性参数, 在井间以该地震反演弹性参数体做趋势约束, 在沉积微相控制下建立岩石力学参数泊松比和杨氏模量的三维模型, 为建立三维地应力场网格模型提供必要的数据准备。
|
| 图 4. 朝89区块叠前地震深度域纵、横波速度反演结果 Figure 4. Wave velocity inversion results in depth domain of pre-stack seismic data of Chao 89 zone |
3 应力场建模
建立应力场模型的思路是, 在根据式(1)和(2)建立的研究区井点岩体力学参数模型的基础上, 将井间地震反演弹性参数体模型作为趋势体, 将井间沉积微相模型作为约束条件, 建立井间三维岩体力学参数模型, 接着开展重力应力、构造应力、孔隙压力计算及多应力叠加, 获得总应力场模型。
3.1 沉积微相、物性参数及岩石力学参数模型建立考虑到朝89区块泥岩夹层分布广泛且厚度不均, 将模型X, Y, Z方向网格步长设置为5, 5, 0.2 m, 以期提高压裂缝预测的准确性。根据研究区油藏精细描述资料, 建立研究区三维油藏沉积微相模型(图 5)。在沉积微相约束下, 通过井震联合的手段, 结合研究区露头、地质知识库资料, 设置合成变差函数, 建立朝89区块孔隙度、渗透率、杨氏模量、泊松比、biot系数三维模型(图 5)。

|
| 图 5. 朝89区块物性参数、岩石力学参数、沉积微相三维模型 Figure 5. 3D models of physical parameters, rock mechanics parameters, sedimentary micro-facies in Chao 89 zone |
biot系数为一种表征多孔介质储层孔隙黏弹性的物理量, 主要用以确定孔隙对岩石变形的影响程度, 范围在0~1之间, 可用如下公式表示:
| $ {\rm{biot}} = 1 - \frac{{{K_{{\rm{dry}}}}}}{{{K_{\rm{s}}}}}, $ |
Kdry为干燥状态下岩石体积模量, Ks为组成岩石的矿物的体积模量。由于biot系数与孔隙度关系较密切, 实际计算中采用Krief等[20]提出的计算公式:
| $ {\rm{biot}} = 1 - {(1 - \phi )^{\frac{3}{{1 - \phi }}}} $ |
式中, φ为归一化孔隙度, 即
| $ \phi = ({\phi _0} - {\phi _{\min }})/({\phi _{\max }} - {\phi _{\min }})。 $ |
其中, φ0表示未归一化的孔隙度初始值。
3.2 应力场模型的建立依据各种应力计算公式, 在三维网格节点上分别求取每个节点的重力应力、构造应力和孔隙压力, 再进行矢量叠加, 得到空间连续变化的非均质应力场模型(图 6)。叠加后总应力公式[21]为
| $ \sigma = \mu ({\sigma _{\rm{v}}} - \alpha {D_{{\rm{tv}}}}{\gamma _{\rm{p}}})/(1 - \mu ) + \alpha {D_{{\rm{tv}}}}{\gamma _{\rm{p}}} + {\varepsilon _x}E + {\sigma _{\rm{t}}}, $ | (3) |

|
| 图 6. 朝89区块总应力三维模型 Figure 6. 3D model of total stress in Chao 89 zone |
σv表示上覆应力(MPa), σ表示总应力(MPa), μ表示泊松比, Dtv表示垂直深度(m), γp表示孔隙压力梯度(MPa/m), α表示biot系数, Dtvγp即孔隙压力, εx表示水平最大、最小地应力方向的应变, E表示杨氏模量(10 GPa), σt为构造应力附加量。
4 非对称压裂缝展布预测朝89区块示踪剂检测实验结果显示, NE17.5°方向油井出现示踪剂, 且示踪剂推进速度最快, 与F111-67-1井X-MAC测井得出的最大水平主应力方向相吻合, 证明裂缝在近南北向十分发育, 为该区天然裂缝和压裂缝的主方向。
本次采用的压裂模拟软件为国际上先进的网格化压裂定量模拟软件, 但其中物性参数、岩石力学参数及总应力网格化界面默认由测井数据读入, 即默认各参数只在纵向上发生变化, 而横向上井筒附近及井间均保持不变, 这显然不符合中国陆相非均质储层的实际情况, 将对压裂缝的预测产生误判。
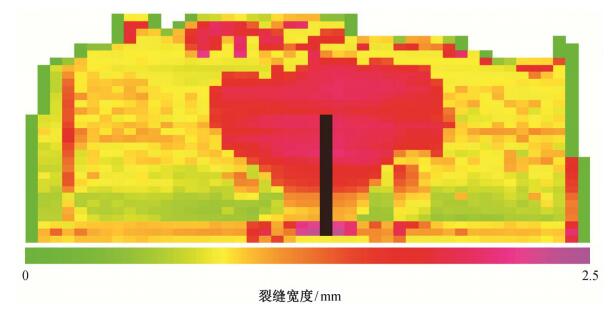
为达到预测非对称压裂缝展布的目的, 本次研究改进模拟方法, 在已建立的物性参数、岩石力学参数和总应力模型上, 沿最大水平主应力方向(即NE17.5°)进行截切, 得到经过单井井轨迹的剖面网格模型, 将相应物性参数、岩石力学参数和总应力剖面数据导入相同网格化精度的该压裂模拟软件中, 设计砂量、混砂比、排量等压裂施工工序参数, 预测压裂缝非对称展布情况, 实现储层地质模型与压裂预测软件相互对接, 充分尊重了研究区非均质储层的实际情况。以研究区F107-61-1井1156.6~1161.6 m压裂层段为例, 其压裂缝非对称展布情况如图 7所示。
|
| 黑色部分为井筒的射孔段; 随着压裂的实施, 裂缝向井筒的左右两端推进; 从左至右为全缝长, 从下至上为裂缝高度; 纵、横向网络步长分别为0.2 m和5 m 图 7. 朝89区块F107-61-1井1156.6~1161.6 m压裂缝非对称展布情况 Figure 7. Asymmetric fracture distribute of 1156.6‒1161.6 m in well F107-61-1, Chao 89 zone |
模拟结果(图 7)显示, F107-61-1井1156.6~1161.6 m压裂段全缝长230 m, 缝高6.5 m, 最大缝宽4.8 mm, 平均缝宽2.1 mm, 纵向上储层改造程度不均匀。中、上段改造程度较大, 对改善储层导流能力贡献较多; 下段改造程度较小, 对改善储层导流能力贡献较少。
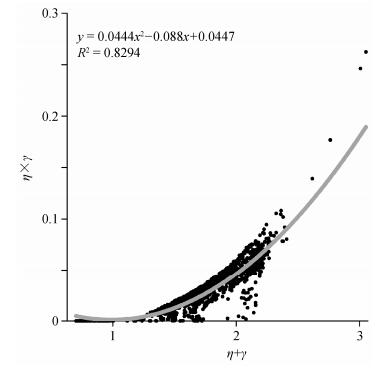
5 讨论考虑到纵向上储层改造规模不均的实际情况, 为有效提升产能, 以下提出扩大储层改造规模有针对性的措施依据。先对F107-61-1井1156.6~1161.6 m压裂缝模拟过程中的输入、输出数据做归一化处理, 再对该压裂层段1341个网格数据点做统计回归分析, 得出归一化总应力值(以下称“相对应力”, 用η表示)、归一化铺砂浓度、归一化裂缝宽度、归一化裂缝内净压力间的非线性经验关系式(图 8)。
|
| 图 8. (η+γ)与(η×γ)交会图 Figure 8. Cross-plot of (η+γ) and (η×γ) |
由于裂缝宽度代表压裂缝瞬时张开的大小, 铺砂浓度指示有效支撑缝的发育程度, 裂缝净压力决定裂缝得以延伸的力学条件, 因此这3个参数均对储层改造规模有重要影响。对3个参数做归一化处理后, 排除了不可控因素的影响, 其指示意义更加明确。取3个参数的乘积为“改造因子”, 作为压裂后储层改造规模大小的综合量度, 用γ表示。
以下以相对应力为例, 说明各参数归一化处理流程。
| $ \eta = \frac{{{\eta _0} - {\eta _{\min }}}}{{{\eta _{\max }} - {\eta _{\min }}}} $ |
其中, η为归一化后应力值, 即相对应力; η0为各网格应力初始值, ηmax为所有网格应力初始最大值, ηmin为所有网格应力初始最小值。
以(η+γ)为自变量, (η×γ)为因变量做交会分析, 二者相关系数平方R2达到0.8294, 相关性良好(图 8)。
将η, γ代入回归公式, 得到
| $ \begin{array}{l} 0.0444{\gamma ^2} + {\rm{ }}( - 0.9112\eta - 0.088)\gamma + \\ 0.0444{\eta ^2} - {\rm{ }}0.088\eta + {\rm{ }}0.0447 = 0。 \end{array} $ | (4) |
将γ作为未知量, 则式(4)的解即为改造因子:
| $ \begin{array}{*{20}{l}} {{\gamma _1} = {\rm{ }}(2278\eta + {\rm{ }}220 - (5140000{\eta ^2} + {\rm{ }}1100000\eta -}\\ {\;\;\;1217{)^{1/2}})/222,}\\ {{\gamma _2} = {\rm{ }}(2278\eta + {\rm{ }}220{\rm{ }} + {\rm{ }}(5140000{\eta ^2} + 1100000\eta -}\\ {\;\;\;1217{)^{1/2}})/222。} \end{array} $ |
由于相对应力η和改造因子γ均在[0, 1]范围内, 而γ2 > 1, 舍去该解。因此, 改造因子与相对应力间的关系式可表示为
| $ \begin{array}{l} \gamma = {\rm{ }}(2278\eta + {\rm{ }}220 - (5140000{\eta ^2} + 1100000\eta -\\ \;\;\;\;\;1217{)^{1/2}})/222。 \end{array} $ | (5) |
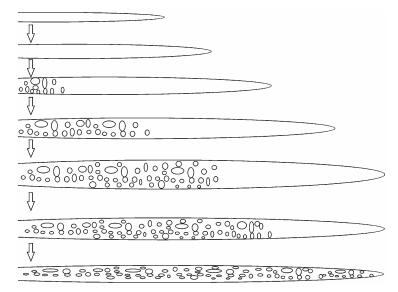
压裂过程中, 随着压裂缝的扩展, 携砂液中的支撑剂(通常为石英砂)除部分滤失入地层外, 其余皆充填于裂缝张开的地层中(图 9), 形成一条有效的支撑裂缝, 即填砂裂缝, 在很大程度上增加了地层的导流能力。
|
| 图 9. 填砂裂缝形成示意图 Figure 9. Schematic diagram of sand filling cracks |
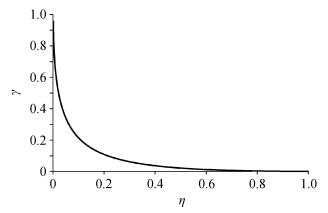
改造因子与相对应力间的关系曲线如图 10所示, 随着相对应力的增加, 改造因子(即储层改造的规模)呈非线性递减, 递减速度逐渐变慢。当相对应力值趋于0.65时, 改造因子基本上趋于0, 说明形成填砂裂缝的相对应力值范围为η介于0~0.65之间。
|
| 图 10. 相对应力η与改造因子γ关系曲线 Figure 10. Relation curve of relative stress and stimulation ratio |
矿场实践结果显示, 改造因子曲线可指示储层改造后各目的层段稳定产液量的相对大小, 为低渗透油藏开发选层提供依据。
6 结论1) 朝89区块储层非均质性较强, 岩性隔夹层、物性隔夹层发育较广泛, 将对压裂缝的延伸和扩展产生重要的影响。
2) 与半缝长裂缝定量预测相比, 井震联合地应力场建模进行全缝长非对称压裂缝预测的手段更加符合中国陆相非均质储层的地质特征, 对油田现场压裂施工设计具有较重要的指导意义。
3) 归一化铺砂浓度、归一化裂缝宽度、归一化裂缝内净压力3个参数均对储层改造规模有重要影响, 三者乘积(即改造因子)与归一化总应力值(即相对应力)可用非线性关系式表征。随着相对应力的增加, 改造因子呈非线性递减, 递减速度逐渐变慢。对于朝89区块而言, 形成填砂裂缝的相对应力值范围介于0~0.65之间。
4) 储层未进行正式压裂前, 在得到井点处总应力曲线的前提下, 对该曲线进行归一化处理, 代入非线性关系式得出改造因子曲线, 即可初步推测该井井筒附近纵向上储层改造规模分布情况, 可有效指导压裂参数优化设计。
| [1] | 徐晓春.水力压裂中地应力及岩石强度参数的研究[D].荆州:长江大学, 2012 |
| [2] | 张洪亮, 何川, 谭玉阳, 等. 基于模拟退火法的水力压裂裂缝参数反演. 北京大学学报:自然科学版 , 2013, 49 (4) : 585–590. |
| [3] | 冯彦军, 康红普. 水力压裂起裂与扩展分析. 岩石力学与工程学报 , 2013, 32 (增刊2) : 3169–3179. |
| [4] | 盛茂, 李根生. 水力压裂过程的扩展有限元数值模拟方法. 工程力学 , 2014, 31 (10) : 123–28. |
| [5] | Khristianovich S A, Zheltov Y P. Formation of vertical fractures by means of highly viscous liquid // Proceedings of the Fourth World Petroleum Con-gress. Rome, 1955: 579-586 |
| [6] | Perkins T K, Kern L R. Width of hydraulic fracture. J Petrol Technol , 1961, 13 : 937–949 DOI:10.2118/89-PA . |
| [7] | Cleary M P. Comprehensive design formulae for hydraulic fracturing// SPE Annual Technical Con-ference and Exhibition. Dallas, 1980: SPE 9259 |
| [8] | England A H, Green A E. Some two-dimen-sionalpunch and crack problems in classical elasticity // Proc CambridgePhil Soc. Cambridge, 1963: 59-89 |
| [9] | Runge C, Kutta H. Vorlesungen über numerisches rechnen. Berlin: Verlag von Julius Springer, 1924 . |
| [10] | 董经利. 多极子阵列声波测井资料处理及应用. 测井技术 , 2009, 33 (2) : 115–19. |
| [11] | 钟剑.阵列声波测井属性信息提取方法研究[D].成都:西南石油大学, 2011 |
| [12] | 李鹏举.声波测井资料高分辨率处理方法[D].大庆:大庆石油学院, 2003 |
| [13] | 张晓波, 高辉, 张剑. 现代声波测井技术应用. 石油仪器 , 2014, 28 (1) : 1–5. |
| [14] | 辛鹏来, 王东, 陈浩, 等. 多极子阵列声波成像测井技术研究. 应用声学 , 2013, 32 (4) : 237–245. |
| [15] | 王西文, 石兰亭, 雍学善, 等. 地震波阻抗反演方法研究. 岩性油气藏 , 2007, 19 (3) : 80–88. |
| [16] | 栾颖, 冯晅, 刘财, 等. 波阻抗反演技术的研究现状及发展. 吉林大学学报:地球科学版 , 2008, 38 (增刊1) : 94–98. |
| [17] | 曹孟起, 王九拴, 邵林海. 叠前弹性波阻抗反演技术及应用. 石油地球物理勘探 , 2006, 41 (3) : 323–326. |
| [18] | 王有新, 王延光. 地震勘探技术概述. 油气地球物理 , 2007, 5 (1) : 1–9. |
| [19] | 吴奎, 周东红, 吴俊刚, 等. 合成地震记录制作在油气勘探中的应用. 海洋石油 , 2012, 32 (1) : 28–32. |
| [20] | Krief M, Garat J, Stellingwerff J, et al. A petrophysical interpretation using the velocities of P and S waves full waveform sonic. The Log Analyst , 1990, 31 : 355–369 . |
| [21] | 吴文娟, 师永民, 王小军, 等. 超低渗油气藏非对称压裂数值模拟理论及应用. 北京大学学报:自然科学版 , 2012, 48 (6) : 895–901. |
 2016, Vol. 52
2016, Vol. 52




