文章信息
- 饶俊峰, 张显峰, 潘一凡
- RAO Junfeng, ZHANG Xianfeng, PAN Yifan
- 气溶胶光学厚度及Ångström指数遥感反演的不确定性对紫外线指数计算的影响
- Impact of the Uncertainty of the Remotely Sensed AOD and Ångström Exponent on the Calculation of Ultraviolet Index
- 北京大学学报(自然科学版), 2016, 52(2): 210-218
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(2): 210-218
-
文章历史
- 收稿日期: 2015-01-04
- 修回日期: 2015-04-10
- 网络出版日期: 2016-03-16
紫外线辐射对人体健康有重要影响, 过多地暴露在紫外线辐射下容易造成红疹、皮肤灼伤、皮肤光老化, 甚至致癌[1-4]。另一方面, 适度暴露在太阳光下有利于维生素D3合成[5]。因此, 长期监测紫外线辐射强度, 并预报紫外线指数, 提醒民众采取对应的防护措施, 合理控制出行时间是非常必要的。
由于纬度、海拔、大气状况等的差异, 不同地区的紫外线辐射差异很大[6]。对于紫外线辐射的监测预报, 目前主要有实验测量、辐射传输方程计算、经验预测等方法。站点观测只能代表仪器置放地点很小范围的真实情况, 而辐射传输方程法比经验预测要准确[6], 且较之站点观测能得到空间分布的紫外线辐射强度数据, 因此被广泛采用[7-12]。
辐射传输方程法计算较为复杂, 且需输入较多参数(包括臭氧含量、大气温度气压、地表状况、气溶胶等), 往往因没有充分考虑这些参数的不确定性降低了模型的估算精度[13]。卫星遥感反演能够在区域和全球尺度获得与紫外辐射相关的参数, 用以替代缺乏地面测量的地区。然而, 卫星遥感反演参数的不确定性也较大, 在全球不同区域研究卫星遥感反演参数的不确定性具有重要意义[14-16]。
气溶胶光学厚度(aerosol optical depth, AOD)是气溶胶颗粒对太阳辐射散射吸收的一种度量, 对紫外线辐射起削弱作用[17-22]。搭载在Terra卫星上的中分辨率成像光谱仪(MODIS)和多角度成像光谱仪(Multi-angle Imaging SpectroRadiometer, MISR)都能生产AOD产品, 并且可以通过Ångström定理计算Ångström指数。虽然MODIS能够提供更多的与地面观测站对比的数据(每1~2天覆盖全球), 但据Levy等[16]研究, MODIS计算得到的Ångström指数缺乏物理有效性, 与地面站测量差异很大。
首先, 统计2005-2013年间香港地区夏季和冬季的平均臭氧含量(Ozone)、AOD、气溶胶单次散射反照率(aerosol single scattering albedo, SSA)、地表反照率(Albedo)、大气可降水量参数(water vapor column, WVC)等辐射传输方程模拟所需基本参数。在此基础上, 将2005-2013年MISR/AOD产品以及据之计算的Ångström指数与AERONET地面站数据做对比, 分析卫星遥感反演产品的不确定性。然后, 利用辐射传输方程模拟与评估MISR数据不确定性对香港地区紫外线指数计算造成的影响。最后, 根据世界卫生组织(WHO)关于紫外线指数等级划分标准和对人体的伤害程度, 讨论MISR/ AOD产品以及据之计算的Ångström指数的不确定性对气象部门预报紫外线指数的影响。
1 数据和方法 1.1 数据和研究区域AERONET是由分布在全世界范围的大约700个精准校正的太阳光度计组成的观测网络, 可以提供每15分钟0.340~1.020 μm之间7个通道的无云AOD观测[23-25]。本研究选取香港两个AERONET站, 分别坐落于香港理工大学(PolyU, 22.30333°N, 114.17972°E)和鹤咀(Hok, 22.20970°N, 114.25800°E)。PolyU站代表城市气溶胶类型, Hok站代表乡村气溶胶类型。两站获取波长440和675 nm处的AOD数据用做MISR卫星遥感反演产品的参照。
2005年1月1日至2013年12月31日, MISR的443和670 nm处的AOD是从GIOVANNI (http://disc.sci.gsfc.nasa.gov/giovanni)应用获得的, 产品名称为“MIL3DAE”。该版本的气溶胶数据是Level3全球格网数据。本研究分别以PolyU和Hok站点经纬度为中心, 按照距离最临近法选择最近的可用格网点数据与地面站数据进行比较分析。
由于AERONET地面站测量是440和675 nm处的AOD, 为进行对比, 需将MISR的443和670 nm处的AOD分别转为440和675 nm处的AOD。利用Ångström定理可知:
| $ \frac{{{\rm{AO}}{{\rm{D}}_{{\lambda _2}}}}}{{{\rm{AO}}{{\rm{D}}_{{\lambda _1}}}}} = {\left( {\frac{{{\lambda _2}}}{{{\lambda _1}}}} \right)^{ - \alpha }} $ | (1) |
其中, λ1代表MISR的AOD相关波长(443和670 nm), λ2代表AERONET的AOD相关波长(440和675 nm), α是Ångström指数, α同样通过式(1), 由AERONET的440和675 nm处的AOD计算而得。
2005年1月1日至2013年12月31日的Ozone数据从NASA Reverb (http://reverb.echo.nasa.gov/reverb/)获得, 产品名称为“OMTO3e”, 也是Level 3全球格网数据。2005年1月1日至2013年12月31日354 nm SSA和354 nm Albedo以及WVC数据从NASA Reverb获得(表 1)。
| 参数类别 | 产品名称 | 数据级别 | 开始时间 | 结束时间 |
| AOD | MIL3DAE | Level 3 | 2005-01-01 | 2013-12-31 |
| Ozone | OMTO3e | Level 3 | 2005-01-01 | 2013-12-31 |
| SSA | OMAERUV | Level 2 | 2005-01-01 | 2013-12-21 |
| Albedo | OMAERUV | Level 2 | 2005-01-01 | 2013-12-21 |
| Water | MOD05_L2 | Level 2 | 2005-01-01 | 2013-12-21 |
| AERONET | PolyU | Level 2 | 2005-11-04 | 2013-06-18 |
| AERONET | Hok | Level 2 | 2007-10-17 | 2010-07-19 |
1.2 方法
气溶胶对紫外线辐射具有吸收和散射作用, AOD越大, 散射和吸收作用越强。TERRA卫星大约在地方时10:30左右过境香港。评价MISR/AOD产品的不确定性, 严格的做法是只选取地面站在卫星过境时间内的数据做平均。考虑到紫外线辐射指数等气象预报往往是日产品, 由卫星遥感反演提供的AOD参与辐射传输模型计算时, 代表的是全天的AOD, 综合考虑卫星遥感反演算法的不确定性以及用过境时的AOD替代全天AOD的不一致问题, 选择AERONET地面站当天测量时间06:00-18:00的AOD平均值与MISR产品做比较。
Ångström指数是描述AOD与波长之间依赖关系的指数, 一旦已知某波长上的AOD, 又知道Ångström指数, 那么其他波长处的AOD就可以根据Ångström定理计算得到。在物理意义上, Ångström指数与气溶胶的颗粒大小有关, 颗粒越小, Ångström指数越大, 反之亦然。实际应用中, 往往通过测量两个波长上的AOD计算其他波长的AOD, 因此, Ångström指数的不确定性会影响紫外线指数的计算。与确定MISR/AOD的不确定性相似, MISR的Ångström指数的不确定性也是通过对比AERONET的Ångström指数获得。基于同样的理由, 选择AERONET地面站当天测量时间在06:00-18:00的Ångström指数平均值与MISR的Ångström指数做比较。假设卫星产品数据与地面站真值的差值符合正态分布, 选择一个标准差的置信区间作为衡量不确定性的标准。结合标准差传递公式, 可以分别得到MISR/AOD与Ångström指数产品的不确定性。
本研究使用辐射传输方程计算开源软件包Libradtran 1.7进行模拟。为了区分这种不确定性在不同季节可能造成的影响, 选取紫外线辐射较强的夏季和冬季分别进行模拟。紫外线辐射(250~400 nm)除与气溶胶有关, 还与其他因素有关, 因此分别统计2005-2013年夏季(以太阳直射在香港PolyU站前后共30天计)和冬季(以太阳直射在南回归线前后共30天计)的平均Ozone, SSA, Albedo, WVC和AOD, 作为夏、冬季辐射传输方程计算的输入数据来模拟夏、冬季的基本辐射环境。辐射传输方程计算在无云条件下进行, 采用cdisort辐射传输方程[26], 计算250~400 nm之间每1 nm的光谱辐照度。人体皮肤的生理实验结果[27-30]表明, 紫外线不同波段对皮肤灼伤能力不同, 因此为了表征不同紫外线波段范围对人体皮肤的灼伤程度, 根据国际照明委员会(CIE)作用函数计算世界卫生组织用于公众天气预报的紫外线指数(global solar UV index, UVI)。
| $ {\rm{UVI}} = {k_{{\rm{er}}}} \times \int_{250\;{\rm{nm}}}^{400\;{\rm{nm}}} {{E_\lambda } \times {S_{{\rm{er}}}}(\lambda ){\rm{d}}\lambda } $ | (2) |
其中, ker=40 m2/W; Eλ是Libradtran在波长λ处的辐照度计算结果, 单位是W/(m2· nm); Ser是作用函数, 根据CIE 1998标准[31]计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{{\rm{er}}}}(\lambda ) = 1.0\;\;\;\;\;\;\;\;\;\;\;}&{(250\;{\rm{nm}} < \lambda \le 298\;{\rm{nm}})\;,}&{}\\ {{S_{{\rm{er}}}}(\lambda ) = {{10}^{0.094 \times (298 - \lambda )}}}&{(298\;{\rm{nm}} < \lambda \le 328\;{\rm{nm}})\;,}&{}\\ {{S_{{\rm{er}}}}(\lambda ) = {{10}^{0.015 \times (140 - \lambda )}}}&{(328\;{\rm{nm}} < \lambda \le 400\;{\rm{nm}})\;。}&{} \end{array}} \right. $ | (3) |
为了衡量AOD不确定性对UVI造成的影响, 在辐射传输模拟中, 以香港地方时06:00-18:00之间(720分钟), 每2分钟分别以夏、冬季AOD平均值和不确定性导致的最大波动范围上下边界AOD值(AOD443-σ(AOD443), AOD443+σ(AOD443))模拟计算UVI值(2×3×360)。定义三者的最大绝对偏差DUVI和最大相对偏差DUVIP, 用以描述UVI受气溶胶不确定影响的绝对变化和相对变化, 计算公式如下:
| $ \begin{array}{*{20}{l}} {{\rm{\Delta UVI = max(abs(UVI}}\left( {{\rm{AO}}{{\rm{D}}_{{\rm{443}}}}} \right){\rm{ - }}}\\ {\;\;\;\;\;\;\;\;\;\;\;{\rm{UVI(AO}}{{\rm{D}}_{{\rm{443}}}}{\rm{ - s}}\left( {{\rm{AO}}{{\rm{D}}_{{\rm{443}}}}} \right){\rm{)),}}}\\ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;{\rm{abs (UVI}}\left( {{\rm{AO}}{{\rm{D}}_{{\rm{443}}}}} \right){\rm{ - }}\\ \;\;\;\;\;\;\;\;\;\;\;{\rm{UVI(AO}}{{\rm{D}}_{{\rm{443}}}}{\rm{ + s}}\left( {{\rm{AO}}{{\rm{D}}_{{\rm{443}}}}} \right){\rm{)))}}, \end{array} \end{array} $ | (4) |
| $ \Delta {\rm{UVIP = DUVI/UVI}}\left( {{\rm{AO}}{{\rm{D}}_{{\rm{443}}}}} \right)。 $ | (5) |
基于与AOD同样的方法, 在香港地方时06:00-18:00之间(720分钟), 每2分钟分别以夏、冬季Ångström指数的平均值以及不确定性导致的最大波动范围上下边界Ångström指数值(αavg-σ(α), αavg+σ(α))模拟计算夏、冬季的UVI值(2× 3×360)。与式(4)和(5)相仿, 定义三者的最大绝对偏差为DUVI和最大相对偏差为DUVIP来表征Ångström指数不确定性对UVI的影响。
2 结果与分析 2.1 MISR/AOD与Ångström指数的不确定性分析 2.1.1 MISR/AOD的不确定性图 1是由PolyU和Hok两站数据合并后的AOD与地面站对比。合并算法是将两站不同时间测得的AOD和MISR对应时间在对应站点位置反演的AOD组成的点对集, 由原先的两个小集合合并成一个样本容量较大的集合。鉴于香港地区面积较小, PolyU站和Hok站所处位置又分属城市气溶胶类型和乡村气溶胶类型, 可以假设合并以后的数据集代表整个香港地区的情况。由图 1可知, AERONET的AOD与MISR相关性相对较高(440 nm处相关系数为0.74, 675 nm处相关系数为0.69), 说明MISR反演的AOD在较大程度上代表了大气的真实状况。另一方面, 从图 1也可看出二者之间存在明显误差, 并且不同光学厚度范围内卫星遥感反演精度存在差异, 因此有必要定量评价使用这些有明显偏差的卫星遥感反演数据计算得到的紫外线指数的可靠性。导致偏差的原因除MISR反演算法本身的不确定性外, 还与地面站AOD数据选取的时间范围设定有一定关系。表 2列出PolyU和Hok站与MISR/AOD分别对比的相关系数、回归方程斜率及平均偏差等。440和675 nm AOD的平均偏差(MBE)分别为−0.27和−0.12, 说明MISR/AOD产品过低估计了大气AOD。MISR/AOD与地面站AOD的差值为
| 站点 | 波长/nm | 斜率 | r | MBE | MABE | SD |
| Polyu | 440 | 0.41 | 0.74 | − 0.30 | 0.32 | 0.28 |
| 675 | 0.45 | 0.69 | − 0.14 | 0.15 | 0.18 | |
| Hok | 440 | 0.71 | 0.84 | − 0.13 | 0.13 | 0.14 |
| 675 | 1.05 | 0.88 | − 0.02 | 0.07 | 0.09 | |
| 两站合并 | 440 | 0.42 | 0.74 | − 0.27 | 0.29 | 0.27 |
| 675 | 0.48 | 0.69 | − 0.12 | 0.14 | 0.17 |
| $ {\rm{\Delta AOD = AO}}{{\rm{D}}_{\rm{M}}}{\rm{ - AO}}{{\rm{D}}_{\rm{G}}}, $ | (6) |

|
| 图 1. 香港地区AERONET AOD与MISR/AOD的线性回归关系 Figure 1. Regression relationship between AERONET AOD and MISR/AOD in Hong Kong |
根据标准差传递公式推导可得
| $ \begin{array}{l} \sigma {({\rm{AO}}{{\rm{D}}_{\rm{M}}})^2} = {\left( {\frac{{\partial ({\rm{AO}}{{\rm{D}}_{\rm{M}}})}}{{\partial (\Delta {\rm{AOD}})}}} \right)^2} \times \sigma {(\Delta {\rm{AOD}})^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\frac{{\partial ({\rm{AO}}{{\rm{D}}_{\rm{M}}})}}{{\partial ({\rm{AO}}{{\rm{D}}_{\rm{G}}})}}} \right)^2} \times \sigma {({\rm{AO}}{{\rm{D}}_{\rm{G}}})^2}, \end{array} $ | (7) |
| $ \sigma ({\rm{AO}}{{\rm{D}}_{\rm{M}}}) = \sqrt {\sigma {{(\Delta {\rm{AOD}})}^2} + \sigma {{({\rm{AO}}{{\rm{D}}_{\rm{G}}})}^2}} $ | (8) |
其中, σ(DAOD), σ(DAODM)和σ(DAODG)分别代表DAOD, MISR/AOD和地面站AOD的不确定性。假定DAOD是独立随机变量, 服从正态分布[13], 则MISR/AOD的不确定性(σ(AODM))可以认为是DAOD的标准差(SD)。根据Holben等[23]的研究, AERONET在440和675 nm处的AOD不确定性分别为0.02和0.01。因此, 式(8)可以进一步整理为
| $ \sigma ({\rm{AO}}{{\rm{D}}_{{\rm{M}}440}}) = \sqrt {{{0.27}^2} + {{0.02}^2}} = 0.2707, $ | (9) |
| $ \sigma ({\rm{AO}}{{\rm{D}}_{{\rm{M}}675}}) = \sqrt {{{0.17}^2} + {{0.01}^2}} = 0.1703。 $ | (10) |
据研究, MISR/AOD产品反演的不确定性在440与443 nm, 675与670 nm处几乎是一样的[13], 因此通过式(9)和(10)可以获得MISR 443和670 nm处AOD产品的不确定性。
2.1.2 MISR Ångström指数的不确定性通过采用与计算MISR/AOD不确定性类似的方法, 可以得到MISR反演的Ångström指数的不确定性。对比结果显示, MISR的Ångström指数与AERONET的指数之间相关性不好(r为0.10)。Román等[13]在伊比利亚半岛的研究也证实了MISR Ångström指数与地面站相关性差的结论(r=0.35)。从表 3可见MBE都是负值, 说明MISR反演的Ångström指数低估了实际的Ångström指数。
| 站点 | 斜率 | r | MBE | MABE | SD |
| Polyu | 0.12 | 0.05 | -0.18 | 0.49 | 0.58 |
| Hok | 1.16 | 0.43 | -0.27 | 0.45 | 0.43 |
| 两站合并 | 0.27 | 0.10 | -0.19 | 0.49 | 0.55 |
定义Δα为MISR Ångström指数与AERONET指数的差值, 同样假定Δα是独立随机变量且服从正态分布, 的不确定性(α(Δα))可以认为是Δα的标准差(SD), 表 3分别列出Polyu和Hok地面站以及两站合并后的Δα标准差, 类似于式(8), 可以得到MISR Ångström指数不确定性为
| $ \sigma ({\alpha _{\rm{M}}}) = \sqrt {\sigma {{(\Delta \alpha )}^2} + \sigma {{({\alpha _{\rm{G}}})}^2}}, $ | (11) |
其中,
| $ {\alpha _{\rm{G}}} = \ln \left( {\frac{{{\rm{AO}}{{\rm{D}}_{440}}}}{{{\rm{AO}}{{\rm{D}}_{675}}}}} \right)/\left( {\frac{{675}}{{440}}} \right)。 $ | (12) |
根据标准差传递公式可得
| $ \begin{array}{l} \sigma {({\alpha _{\rm{G}}})^2} = \frac{{\partial {{({\alpha _{\rm{G}}})}^2}}}{{\partial ({\rm{AO}}{{\rm{D}}_{440}})}} \times \sigma {({\rm{AO}}{{\rm{D}}_{440}})^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial {{({\alpha _{\rm{G}}})}^2}}}{{\partial ({\rm{AO}}{{\rm{D}}_{675}})}} \times \sigma {({\rm{AO}}{{\rm{D}}_{675}})^2}\;。 \end{array} $ | (13) |
| $ \begin{array}{l} \sigma ({\alpha _{\rm{G}}}) = \frac{1}{{\ln \left( {\frac{{675}}{{440}}} \right)}} \times \\ \sqrt {\sigma {{({\rm{AO}}{{\rm{D}}_{440}})}^2}/{\rm{AOD}}_{440}^2 + \sigma {{({\rm{AO}}{{\rm{D}}_{675}})}^2}/{\rm{AOD}}_{675}^2} \;。 \end{array} $ | (14) |
根据式(1):
| $ {\rm{AO}}{{\rm{D}}_{440}} = {\rm{AO}}{{\rm{D}}_{443}} \times {\left( {\frac{{440}}{{443}}} \right)^{ - \alpha }}, $ | (15) |
| $ {\rm{AO}}{{\rm{D}}_{675}} = {\rm{AO}}{{\rm{D}}_{443}} \times {\left( {\frac{{675}}{{443}}} \right)^{ - \alpha }}。 $ | (16) |
将式(15)和(16)代入式(13)得
| $ \begin{array}{l} \sigma ({\alpha _{\rm{G}}}) = \frac{1}{{\ln \left( {\frac{{675}}{{440}}} \right)}} \times \\ \sqrt {\frac{{{{\left( {\frac{{440}}{{443}}} \right)}^{2\alpha }} \times \sigma {{\left( {{\rm{AO}}{{\rm{D}}_{440}}} \right)}^2} + {{\left( {\frac{{675}}{{443}}} \right)}^{2\alpha }} \times \sigma {{({\rm{AO}}{{\rm{D}}_{675}})}^2}}}{{{\rm{AO}}{{\rm{D}}_{443}}^2}}} \;。 \end{array} $ | (17) |
由式(9)和(10)已知σ(AOD440)和σ(AOD675), 将式(17)代入式(11)得到MISR Ångström指数的不确定性:
| $ \begin{array}{l} \sigma ({\alpha _{\rm{G}}}) = \frac{1}{{\ln \left( {\frac{{675}}{{440}}} \right)}} \times \\ \sqrt {\frac{{{{\left( {\frac{{440}}{{443}}} \right)}^{2\alpha }} \times \sigma {{\left( {{\rm{AO}}{{\rm{D}}_{440}}} \right)}^2} + {{\left( {\frac{{675}}{{443}}} \right)}^{2\alpha }} \times \sigma {{({\rm{AO}}{{\rm{D}}_{675}})}^2}}}{{{\rm{AO}}{{\rm{D}}_{443}}^2}}} \;。 \end{array} $ | (18) |
由式(18)可知, MISR的Ångström的不确定性由443 nm处的AOD和Ångström指数确定。通过对式(18)分别求α和AOD443的一次偏导数
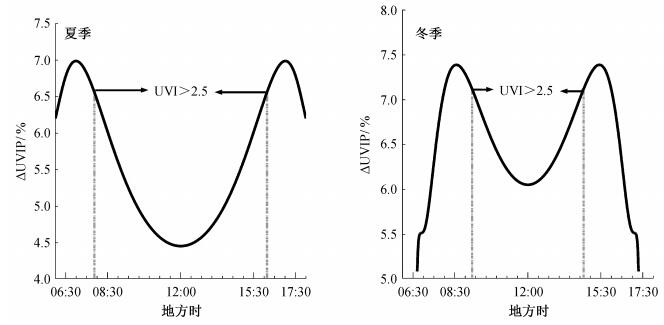
由图 2可知, 受MISR 443 nm处AOD的不确定性影响, 夏季紫外线指数的变动范围在4.5%~7.0%之间, 地方时12:00受AOD不确定性的影响最小, 在地方时约07:00和17:00的影响最大。冬季紫外线指数的波动范围在5.1%~7.4%之间, 地方时12:00的相对偏差为6.1%, 在地方时08:30和15:30的影响最大。由于UVI较小时, 紫外线辐射对于皮肤伤害较小, 所以一般关注UVI较大情况下UVI受气溶胶等因素影响的变化规律。图 2中UVI大于2.5的部分, 按照世界卫生组织的紫外线指数等级划分不再是“Low”的安全级别。在这种情况下, 不论是夏季和冬季, 紫外线指数相对变化都在地方时12:00的影响最小, 并且向两边递增。与夏季相比, 冬季受气溶胶影响紫外线指数相对变化更大。
|
| 图 2. MISR AOD443不确定性引起的紫外线指数的夏、冬季相对变化(DUVIP) Figure 2. DUVIP caused by MISR AOD443 uncertainty |
2005-2013年夏季443 nm AOD平均值为0.21, 由式(9)可知AOD不确定性为0.2707, 变化下界小于0, 所以在图 3中, 由变化下界引起的紫外线指数波动没有列出。由图 3可知, 随着气溶胶厚度增大, 气溶胶的削弱作用增强, 紫外线辐射减弱, 紫外线指数降低。紫外线指数受MISR 443 nm的不确定性影响, 最大绝对变化值(0.55)发生在正午, 这与相对变化在地方时12:00变化最小正好相反。由于紫外线指数是通过四舍五入取整得到, 所以最大差值0.55最多能导致紫外线指数±1的变化。按照世界卫生组织关于紫外线等级的分级(1~2:低; 3~5:中; 6~7:高; 8~10:很高; > 11:极高), AOD不确定性有可能造成波动前后的紫外线风险相差一个等级。

|
| 图 3. MISR 443 nm气溶胶光学厚度不确定性引起的夏季紫外线指数变化 Figure 3. UVI uncertainty caused by MISR AOD443 uncertainty in summer |
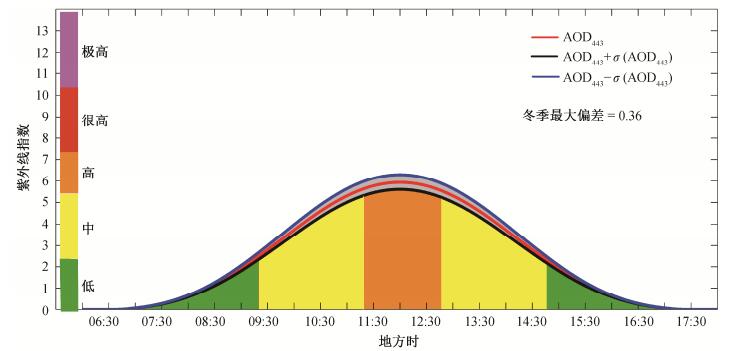
冬季紫外线辐射较弱, 由图 4可知, 正午紫外线指数大约在6~7之间。由于气溶胶散射可以减弱紫外线辐射, 因此MISR/AOD变化上界的紫外线指数较低, 变化下界的紫外线指数较高。与夏季相比, 冬季受AOD的影响变化也较小, 最大变化(0.36)发生在正午, 四舍五入之后最多造成紫外线指数±1的变化, 紫外线风险最多相差一级。
|
| 图 4. MISR 443 nm气溶胶光学厚度不确定性引起的冬季紫外线指数变化 Figure 4. UVI uncertainty caused by MISR AOD443 uncertainty in winter |
综合夏季和冬季情况, MISR/AOD的不确定性引起的紫外线指数波动在±1之内, 因此由MISR反演的AOD作为参数计算紫外线指数基本上可靠。
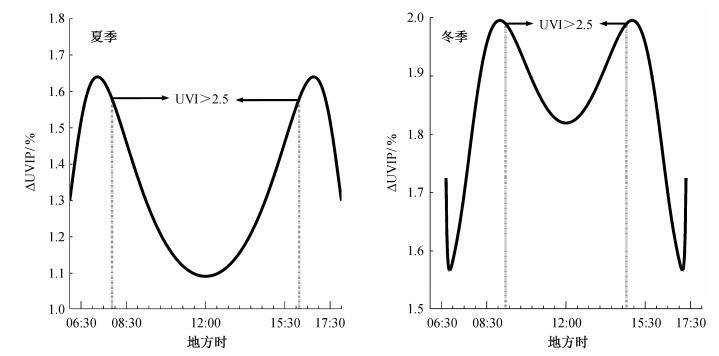
2.2.2 Ångström指数由图 5可知, UVI受Ångström指数不确定性影响较之气溶胶对紫外线的影响小(1.1%~2.0%之间), 夏季波动范围在1.1%~1.6%之间, 地方时12:00的百分比波动最小, 地方时07:15和16:45影响最大。UVI冬季波动范围在1.6%~2.0%之间, 在地方时09:00和15:00影响最大。这个结论与Román等[13]在伊比利亚半岛的实验结论(太阳高度角在0~90°变化时, 紫外线直射与散射辐射之和的变动范围在0.5%~2.0%之间)相近, 差别在于本文研究的是紫外线指数, 而不是紫外波长的辐照度以及加权和。基于与2.2.1节中气溶胶同样的原因, 当只考虑UVI大于2.5时, 不论夏、冬季, Ångström指数对UVI百分比变化的影响都在正午时最小, 同时向两边递增。从季节上看, 冬季受Ångström指数不确定性的影响比夏季大。
|
| 图 5. MISR Ångström指数不确定性引起的紫外线指数的夏、冬季相对变化(DUVIP) Figure 5. DUVIP caused by MISR Ångström exponent uncertainty |
就绝对变化而言, 夏、冬季紫外线指数的绝对变化都在地方时12:00最大, 分别为0.13与0.11。相对于夏季(最大偏差0.55), 冬季受气溶胶影响小(最大偏差0.36)。Ångström指数的不确定性造成的UVI不确定性小, 最多造成紫外线指数±1的变化。在世界卫生组织的紫外线指数风险分级标准下, MISRÅngström指数的不确定性对紫外线风险等级的计算影响很小。尤其是冬季, 紫外线辐射在正午时候大约在6~7之间, 紫外线对人体的灼伤作用有限, 小范围的波动不会有显著的影响。
3 结论本文通过对比2005-2013年间MISR气溶胶产品和AERONET地面站数据, 分别计算了MISR 443和670 nm处气溶胶光学厚度以及Ångström指数的不确定性。同时利用辐射传输方程, 评估了气溶胶光学厚度和Ångström指数不确定性造成的地表紫外线辐射指数的不确定性, 以及不同季节影响程度的差异。研究结果表明, 紫外线指数受气溶胶光学厚度和Ångström指数的不确定性影响具有一致的规律, 即当只考虑紫外线指数大于2.5时, 不论夏、冬季, 气溶胶光学厚度和Ångström指数的不确定性导致的紫外线指数的相对变化都在正午时刻达到最小。无论夏、冬季, 气溶胶光学厚度和Ångström指数不确定性导致的紫外线指数的绝对变化都在正午时刻达到最大。夏季与冬季相比, 无论是气溶胶光学厚度还是Ångström指数, 对紫外线指数百分比的影响都是冬季高于夏季, 对紫外线指数绝对值的影响都是夏季高于冬季。气溶胶光学厚度与Ångström指数相比, 不论夏季还是冬季, 都是气溶胶光学厚度不确定性对紫外线指数的影响更大, 说明紫外线指数对气溶胶光学厚度不确定性更敏感。
由于气溶胶光学厚度和Ångström指数造成的紫外线指数误差在±1范围内, 所以MISR气溶胶光学厚度和Ångström指数产品用于辐射传输方程法预测紫外线指数基本上是可靠的。不论是气溶胶光学厚度还是Ångström指数的不确定性, 在夏季和冬季基本上都不会影响到对民众发布的紫外线分级, 最差情况下会导致紫外线风险等级有一级的偏差。
不同气溶胶光学厚度范围内, 卫星遥感反演结果的精度存在差异。下一步工作中有必要将气溶胶光学厚度划分为若干区间, 分别计算MISR反演结果在不同气溶胶光学厚度区间上的不确定性, 以期弄清当气溶胶光学厚度介于哪些区间时, 使用MISR反演的气溶胶光学厚度用以计算紫外线指数更可靠。
致谢:感谢Janet Elizabeth Nichol博士提供AERONET数据以及他为建立和维护香港PolyU和Hok Tsui两个观测站做出的努力和贡献。同时感谢MISR和MODIS科学团队提供卫星数据。
| [1] | Sklar L R, Almutawa F, Lim H W, et al. Effects of ultraviolet radiation, visible light, and infrared radiation on erythema and pigmentation: a review. Photochemical & Photobiological Sciences , 2013, 12 (1) : 54–64 . |
| [2] | Norval M, Lucas R M, Cullen A P, et al. The human health effects of ozone depletion and interactions with climate change. Photochemical & Photobiological Sciences , 2011, 10 (2) : 199–225 . |
| [3] | Lucas R M, McMichael A J, Armstrong B K, et al. Estimating the global disease burden due to ultra-violet radiation exposure. International Journal of Epidemiology , 2008, 37 (3) : 654–667 DOI:10.1093/ije/dyn017 . |
| [4] | Juzeniene A, Brekke P, Dahlback A, et al. Solar radiation and human health. Reports on Progress in Physics , 2011, 74 (6) : 066701 DOI:10.1088/0034-4885/74/6/066701 . |
| [5] | Holick M F. Vitamin D: importance in the prevention of cancers, type 1 diabetes, heart disease, and osteo-porosis. The American Journal of Clinical Nutrition , 2004, 79 (3) : 362–371 . |
| [6] | Moreno J C, Serrano M A, Lorente M, et al. An empirical model of erythemal ultraviolet radiation in the city of Valencia, Spain. Photochemical & Photobiological Sciences , 2013, 12 (9) : 1707–1716 . |
| [7] | Den Outer P N, Slaper H, Tax R B. UV radiation in the Netherlands: assessing long-term variability and trends in relation to ozone and clouds. Journal of Geophysical Research , 2005, 110 (D2) : 169–190 . |
| [8] | Lindfors A, Kaurola J, Arola A, et al. A method for reconstruction of past UV radiation based on radiative transfer modeling: applied to four stations in northern Europe. Journal of Geophysical Research , 2007, 112 (D23) : 209–232 . |
| [9] | Walker D. Cloud effects on erythemal UV radiation in a complex topography[D]. Zürich: Eidgenössische Technische Hochschule, 2009 |
| [10] | Bilbao J, Román R, de Miguel A, et al. Long-term solar erythemal UV irradiance data reconstruction in Spain using a semiempirical method. Journal of Geophysical Research , 2011, 116 (D22) : 898–908 . |
| [11] | Antón M, Serrano A, Cancillo M L, et al. Experimental and forecasted values of the ultraviolet index in southwestern Spain. Journal of Geophysical Research , 2009, 114 (D5) : 1007–1012 . |
| [12] | Tourpali K, Bais A F, Kazantzidis A, et al. Clear sky UV simulations for the 21st century based on ozone and temperature projections from Chemistry-Climate Models. Atmospheric Chemistry and Physics , 2009, 9 (4) : 1165–1172 DOI:10.5194/acp-9-1165-2009 . |
| [13] | Román R, Bilbao J, de Miguel A. Uncertainty and variability in satellite-based water vapor column, aerosol optical depth and Ångström exponent, and its effect on radiative transfer simulations in the Iberian Peninsula. Atmospheric Environment , 2014, 89 : 556–569 DOI:10.1016/j.atmosenv.2014.02.027 . |
| [14] | Kahn R A, Garay M J, Nelson D L, et al. Satellite-derived aerosol optical depth over dark water from MISR and MODIS: comparisons with AERONET and implications for climatological studies. Journal of Geophysical Research , 2007, 112 (D18) : 1148–1154 . |
| [15] | Eck T F, Holben B N, Reid J S, et al. Optical properties of boreal region biomass burning aerosols in central Alaska and seasonal variation of aerosol optical depth at an Arctic coastal site. Journal of Geophysical Research , 2009, 114 (D11) : 1840–1846 . |
| [16] | Levy R C, Remer L A, Kleidman R G, et al. Global evaluation of the Collection 5 MODIS dark-target aerosol products over land. Atmospheric Chemistry and Physics , 2010, 10 (21) : 10399–10420 DOI:10.5194/acp-10-10399-2010 . |
| [17] | Ångström A. On the atmospheric transmission of sun radiation:Ⅱ. Geografiska Annaler , 1930, 12 : 130–159 DOI:10.2307/519561 . |
| [18] | Van de Hulst H C. Scattering in a planetary atmosphere. The Astrophysical Journal , 1948, 107 (2) : 220–246 . |
| [19] | IPCC. IPCC fourth assessment reports (AR4), working groupⅠreport: climate change 2007, the physical science basis. Gevera: WMO/UNEP Report, 2007 |
| [20] | 郑有飞, 石广玉. 太阳紫外线辐射预测计算模型研究. 太阳能学报 , 2001, 22 (4) : 461–465. |
| [21] | 张庆阳, 张沅, 胡英. 国外紫外线指数预报概况. 气象 , 2000, 26 (11) : 56–57. |
| [22] | 邓英姿, 董蕙青. 紫外线指数及其预报技术介绍. 广西气象 , 2000, 21 (3) : 38–40. |
| [23] | Holben B N, Eck T F, Slutsker I, et al. AERONET -a federated instrument network and data archive for aerosol characterization. Remote Sensing of Environ-ment , 1998, 66 (1) : 1–16 DOI:10.1016/S0034-4257(98)00031-5 . |
| [24] | Holben B N, Tanre D, Smirnov A, et al. An emerging ground-based aerosol climatology: aerosol optical depth from AERONET. Journal of Geophysical Research , 2001, 106 (D11) : 12067–12097 DOI:10.1029/2001JD900014 . |
| [25] | Smirnov A, Holben B N, Eck T F, et al. Cloud-screening and quality control algorithms for the AERONET database. Remote Sensing of Environ-ment , 2000, 73 (3) : 337–349 DOI:10.1016/S0034-4257(00)00109-7 . |
| [26] | Buras R, Dowling T, Emde C. New secondary-scattering correction in DISORT with increased efficiency for forward scattering. Journal of Quan-titative Spectroscopy and Radiative Transfer , 2011, 112 (12) : 2028–2034 DOI:10.1016/j.jqsrt.2011.03.019 . |
| [27] | McKinlay A F, Diffey B L. A reference action spectrum for ultraviolet induced erythema in human skin. CIE J , 1987, 6 (1) : 17–22 . |
| [28] | WHO. International commission on non-ionizing radiation protection. Global solar UV index: a practical guide. 2002 |
| [29] | Freeman R G. Data on the action spectrum for ultraviolet carcinogenesis. Journal of the National Cancer Institute , 1975, 55 (5) : 1119–1122 . |
| [30] | Kligman L H, Sayre R M. An action spectrum for ultraviolet induced elastosis in hairless mice: quantification of elastosis by image analysis. Photochemistry and Photobiology , 1991, 53 (2) : 237–242 DOI:10.1111/php.1991.53.issue-2 . |
| [31] | CIE Standard. Erythema reference action spectrum and standard erythema dose. CIE S 007/E-1998. Vienna: Commission Internationale del'Eclairage, 1998 |
 2016, Vol. 52
2016, Vol. 52




