文章信息
- 沈戈晖, 刘沛东, 邓志鸿
- SHEN Gehui, LIU Peidong, DENG Zhihong
- NB-MAFIA:基于N-List的最长频繁项集挖掘算法
- NB-MAFIA: An N-List Based Maximal Frequent Itemset Algorithm
- 北京大学学报(自然科学版), 2016, 52(2): 199-209
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(2): 199-209
-
文章历史
- 收稿日期: 2014-12-30
- 修回日期: 2015-01-14
- 网络出版日期: 2016-02-11
2. 北京大学信息科学技术学院智能科学系, 北京 100871;
3. 北京大学机器感知与智能教育部重点实验室, 北京 100871
2. Department of Machine Intelligence, School of Electronics Engineering and Computer Science, Peking University, Beijing 100871;
3. Key Laboratory Machine Perception (MOE), Peking University, Beijing 100871
近些年来, 由于应用的多样性和广泛性, 频繁模式挖掘受到研究者极大关注。自Agrawal等[1-2]提出频繁模式挖掘以来, 它便成为数据挖掘领域中的重要问题。频繁模式挖掘不仅在关联规则挖掘中处于核心地位, 而且还在相关性分析、因果分析、序列模式挖掘、情节挖掘、多维模式挖掘等任务上有重要作用[1]。
给定一个事务数据库DB, 假设DB包含的所有项的集合为I={i1, i2, ..., i|I|}。DB中有若干事务记录, 记为{T1, T2, ..., T|DB|}, 每个事务T都是I的一个子集, 即T⊆I。对于任意X⊆I, 如果事务T满足X⊆T, 称T包含X。定义t(X)={Y∈D|X⊆Y}。I的所有子集构成的集合(即I的幂集)构成一个格, 称为项集格。我们把包含X的事务数称为X的计数支持度, 记为X.count, 即|t(X)|。包含X的事务数在数据库中所占比例称为X的支持度, 记为X.support。给定一个最小支持度minSup (∈[0,1]), 称一个项集X是频繁的当且仅当X.support≥minSup, 即X.count≥minSup×|DB|。定义所有频繁项集的集合为FI (frequent itemsets), 长度为k的频繁项集称为频繁k-项集。
当一个事务数据库非常稠密, 并且最小支持度设定非常低时, 频繁项集的数量会非常巨大。我们知道, 对于一个长度为l的频繁项集, 它的2l -1个非空子集都是频繁的。因此频繁项集数量会随l呈指数型增长。在这种情况下, 挖掘出所有频繁项集是不现实的。一种可行方案是, 只挖掘所有频繁项集的一个子集, 通过这个子集可以方便地还原所有频繁项集。因此, 最长频繁项集(maximal frequent itemsets, MFI)和闭频繁项集(closed frequent itemsets, CFI)的概念被提出。如果一个频繁项集X满足它的真超集都是不频繁的, 则称X是最长频繁项集。如果一个频繁项集X满足它的真超集的支持度都不等于其自身的支持度, 则称X是闭频繁项集。根据定义, 显然有MFI ⊆ CFI ⊆ FI。在实际应用中, MFI的数量要比CFI少几个数量级, 而CFI的数量又比FI少几个数量级。如果我们只挖掘MFI, 再根据它还原FI, 而每个项集的支持度也可以通过扫描数据库得到, 比起挖掘所有的频繁项集, 可以大大减少挖掘过程的时间开销和内存开销。此外, 有的应用只需要MFI的信息就足够[3]。
自最长频繁模式被提出以来, 已有多种算法先后被提出并改进, 以期达到对最长频繁模式的高效挖掘。其中, Burdick等[4]以项的全序搜索树为搜索空间, 在深度优先搜索的基础上, 提出几个有效的剪枝策略: PEP, FHUT, MFIHUT以及Dynamic Reordering, 并同时使用高效的MFI超集检测策略LMFI[4-6], 得到一个整合算法: MAFIA[4-5]。由于MAFIA的剪枝策略有效地减少了搜索空间, LMFI策略也减少了检测当前项集是否是MFI的开销。因此, 相比已有的算法, 对于多数数据集, 特别是稠密数据集, MAFIA在运行时间上有很大的优势。但是, MAFIA在计算项集的支持度时, 使用位向量来表示项集, 使得每次计算支持度时都要花费一个|DB|位的位运算。当数据库包含很多事务记录时, 位运算所需计算代价就很大。因此, 基于位向量的表示方法不适用于挖掘大规模数据集。
基于Deng等[7]提出的新的项集表示结构N-List, 本文提出一个新的最长模式挖掘算法NB-MAFIA (N-List Based MAFIA)。我们采用基于全序搜索树和深度优先搜索的基本算法框架, 利用N-List数据结构来表示项集, 并快速计算项集支持度, 同时适当地结合MAFIA中的剪枝策略和超集检测策略, 得到一个更有效的最长频繁项集挖掘算法。与位向量相比, 用N-List表示项集有较高的压缩率。当数据集比较稠密时, N-List的长度会随着项集长度增加而显著减少, 进而对两个N-List的求交集运算会很快, 因此我们的算法特别适用于稠密的数据集。实验结果表明, NB-MAFIA算法在绝大多数情况下都优于MAFIA算法和FP-growth算法, 在稠密的数据集上, 相比已有的算法, NB-MAFIA算法的时间效率基本上是最好的。
1 相关工作迄今为止, 有很多研究致力于如何高效地挖掘所有频繁项集[7-22]和最长频繁项集[5, 23-29]。Apriori方法使用单纯的广度优先策略来遍历搜索树, 为了得到支持度信息, 它需要显式地生成候选项集并计数[2]。MaxMiner在使用广度优先搜索遍历的同时, 能够对可以裁剪的结点进行预测[23]。
当频繁项集的长度较长(超过15或20个项)时, FI和FCI的规模变得非常庞大, 传统方法因为要对过多的项集进行计数而变得不易实现。对于频繁k-项集, 基于Apriori的算法需要挖掘出2k个子集, 当项集比较长时, 算法的可扩展性就很差。另外, 由于未能及时获得较长项集的信息, 基于广度优先搜索的算法在进行有效的预测和剪枝时效果不佳。文献[23-24]分析了深度优先搜索策略的优越性。
数据库的表示形式直接影响项集生成和计数过程的效率, 从而成为影响挖掘效率的重要因素。生成项集Z=(X∪Y)的过程即为计算t(Z)=t(X)∩t(Y)的过程, 而计数则需计算Z的支持度。通常,数据库由很多记录组成, 每一个记录代表一个事务。我们也可以用垂直的结构来表示数据库和项集。对于项集X, 用t(X)中所有的事务编号(transaction identifiers, TIDs)来表示[10, 13-14, 17]。MAFIA正是基于这种表示方法, 对项集支持度计数过程进行优化。
Shenoy等[17]通过VIPER算法证实了基于垂直表示的方法有时可以比水平表示的最优算法表现得更加出色。但是, VIPER算法生成了所有频繁项集, 因此不适用于模式较长的最长频繁模式。Holsheimer等[30]和Savasere等[16]各自提出基于垂直表示的挖掘所有频繁项集的方法。Dunkel等[13]分析数据库的不同表示方法对算法性能的影响。Ganti等[14]展示了使用垂直表示方法的优越性。
Burdick等[4]提出MAFIA算法来挖掘最长频繁模式, 使用链表结构来组织频繁项集。每个项集I对应一个位向量, 位向量的长度是事务数据库中的事务数。如果I在某个事务中出现, 则位向量中对应的位置为1, 否则置0。由于数据库的所有信息都保存在位向量中, 在生成候选项集并计算其支持度时只需要使用与按位运算即可。同时, MAFIA针对搜索空间的剪枝提出了一系列有效的策略。Burdick等[5]对MAFIA进行改进和完善, 加入超集检测技术[6], 并且针对位向量提出更有效的压缩技术。
FP-growth方法[8]在挖掘频繁项集时不需要生成候选项集, 而是使用一个压缩程度很高的数据结构FP-tree来存储数据库, 并使用分治策略进行挖掘。实验证明, 该算法显著地提高了挖掘效率。Grahne等[28]基于FP-tree数据结构, 提出挖掘最长频繁模式的FPmax算法。FP-growth*算法[29]则用一种特殊的数据结构FP-array来优化FPmax算法在稀疏数据上的效率, 同时使用FP-tree的一个变种MFI-tree, 提高了检测一个频繁项集是否为最长频繁项集的效率。
Deng等[21]提出一种新的项集前缀树PPC-tree。基于PPC-tree, Deng等[7]进一步提出新的项集表示结构N-List及相应的频繁项集挖掘算法PrePost。PPC-tree有与FP-tree相似的结构和相同的压缩率。由于PPC-tree在前缀树的每个节点记录了前、后序遍历编号, 因此可以用对应的前缀树节点链表来表示项集, 这个链表称为N-List[7]。PPC-tree记录了数据库的所有信息, 在对数据库进行两次扫描, 构建好PPC-tree后, 即可从内存中删除整个数据库。与FP-growth算法相比, PrePost在递归寻找所有频繁项集过程中不需要反复构建局部前缀树, 也不需要反复扫描PPC-tree, 甚至可以在构建好所有频繁项的N-List后将PPC-tree删除。计算项集支持度的过程等价于将两个N-List做交运算, 该过程可以由一个复杂度为O(m+n)的算法来实现, 其中m和n分别为两个N-List的长度。同时, 相较于类似Tidset的垂直表示方式, N-List由于有较高的压缩率, 其长度一般远小于事务数, 因此用N-List来表示项集, 算法效率会有很大的提高。
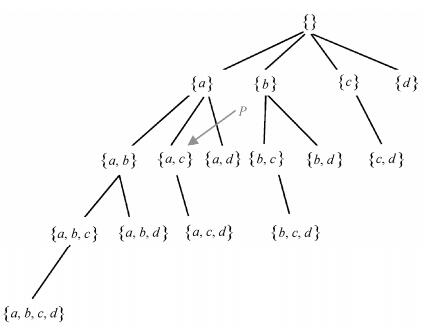
2 NB-MAFIA:基于N-List的最长频繁模式挖掘算法 2.1 最长频繁模式挖掘的基本框架对于一个事务数据库DB, 假设它包含的所有项的集合用I表示, I={i1, i2, ..., i|I|}。假设I中的元素有一个全序关系≤L(比如字典序或项的支持度升序等), 根据这个顺序, 如果项i出现在项j前面, 记为i≤Lj。对于一个由I={a, b, c, d}组成的事务数据库, 规定全序关系≤L为字典序(即a≤Lb≤Lc≤Ld)。图 1展示这个数据库中所有项集根据这个序关系生成的一个搜索树。除树的最上层的结点对应空集外, 树中其他结点都与数据库中一个非空项集相对应, 第k层(假定树的最上层为第0层)包含所有k-项集。我们利用一定的顺序来遍历这棵树, 从而找到所有最长频繁项集。为了满足N-List的性质, 本文规定全序关系≤L代表将项按支持度升序排列。
定义1[5] 对于搜索树中的结点C, 将它对应的项集称为这个结点的head集合, 记做C.head。
定义2[5] 对于搜索树中的结点C, 将所有从这个结点可扩展出的项称为该结点的tail集合, 记做C.tail。
显然, C.head与C.tail之间有如下的关系: C.tail={i∈I|∀j∈C.head, j≤Li}。
定义3[5] 对于搜索树中的结点C, 定义其head集合与tail集合的并集称为HUT (head union tail)集合, 记做C.HUT, C.HUT=C.head∪C.tail。
定义4[5] 对于搜索树中的结点C, 将C.tail中的每个项i称为C的一个1-扩展项。
定义5[5] 对于搜索树中的结点C, 称与C, 有相同父结点的结点为C的兄弟结点。所有在搜索树中位于C右边的兄弟结点的集合记做C.sibling+。
在图 1中, 对于{a, c}代表的结点P, 由上述定义可知, P.head={a, c}, P.tail={d}, P.HUT={a, c, d}, P.sibling+={{a, d}}。其中d是结点P的1-扩展项。
结合文献[1]提出的Apriori性质, 可以使用深度优先搜索(Depth-First Search, DFS)策略来遍历搜索树, 得到一个最基本的最长模式挖掘算法: DFS算法, 其伪代码如算法1所示。在每个结点C, 对于C.tail中的每个1-扩展项i, 检测项集{C.head}∪{i}的支持度, 如果其支持度大于minSup, 则向下递归进入相应结点。当C的所有由1-扩展项扩展得到的超集均不频繁时, C在频繁模式搜索树中是一个叶结点。此时检测当前的最长频繁模式集合MFI中是否有C.head的超集, 如果没有, 则C是一个最长模式, 将它加入到MFI中。
|
| 图 1. 包含4个项的字典序搜索树 Figure 1. Lexicographic subset tree for four items |
算法1 (DFS算法)
输入:一个交易数据库DB和最小支持度minSup
输出: DB的所有最长频繁模式集合MFI
MFI←∅
Root.head←∅
Root.tail←DB频繁项的集合
Call DFS (Root)
DFS (Current node C)
for C.tail中的所有项i do
C_extension.head←C.head∪{i}
C_extension.tail←{j∈C.tail|i≤Lj}
计算C_extension.support
If (C_extension.support≥minSup)
DFS (C_extension)
endif
endfor
if (C是叶结点并且MFI中不存在C.head的超集) do
MFI←MFI∪C.head
endif
2.2 PPC-tree和N-List的基本性质及在NB-MAFIA中的应用以下给出相关的概念和性质。关于N-List更详细的介绍和以下性质的证明可以参考文献[7]。某些性质描述与原文相比略有改动, 但其本质相同, 证明过程类似。
定义6 (PPC-tree) PPC-tree是一棵前缀树, 它有如下两个特点: PPC-tree有一个空的根节点, 利用输入数据生成的其他前缀树都是该根节点的子孙; PPC-tree的每一个节点除记录项的名称与支持度外, 还记录在整棵树的前序、后续遍历中该节点的顺序编号。根节点的前序编号总是最小的, 后续编号总是最大的。
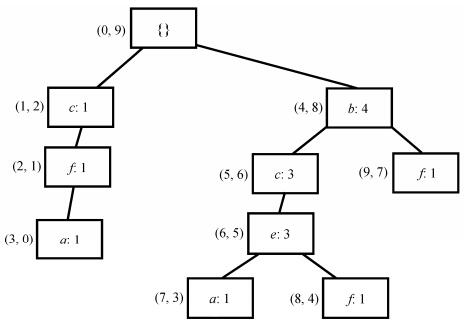
对表 1给出的事务数据库, 当最小支持度minSup=0.4时, 构建的PPC-tree如图 2所示。
| ID | Items | Ordered frequent items |
| 1 | a, c, g, f | c, f, a |
| 2 | e, a, c, b | b, c, e, a |
| 3 | e, c, b, i | b, c, e |
| 4 | b, f, h | b, f |
| 5 | b, f, e, c, d | b, c, e, f |
性质1 给出一个PPC-tree中两点N1和N2的前序编号和后序编号, 记做N1.pre-order, N1.post-order, N2.pre-order, N2.post-order。N1是N2的祖先当且仅当N1.pre-order < N2.pre-order且N1.post-order > N2.post-order。
定义7 (N-List) N-List是一个记录节点信息的列表, 在N-List中, 用 < (pre-order, post-order):support > 表示PPC-tree的一个节点, N-List就是将某些特定的节点按前序编号升序排列得到的列表。
定义8 (1-项集的N-List) 1-项集的N-List是将所有代表某特定项i的节点信息按序排列得到的列表, {i}的N-List简称为i的N-List。
定义9 (2-项集的N-List)假设一个2-项集为{i, j}, 且i的支持度大于j(即i在PPC-tree中位置更高), 将i的N-List记做{ < (x1i, y1i):z1i > , < (x2i, y2i):z2i > , …}, j的N-List记做{ < (x1j, y1j):z1j > , < (x2j, y2j):z2j > , …}, 则根据以下规则生成{i, j}的N-List。
1) 如果i的某个节点 < (xmi, ymi):zmi > 是j的某个节点 < (xnj, ynj):znj > 的祖先, 那么将 < (xmi, ymi):znj > 加入{i, j}的N-List。
2) 检查{i, j}的N-List, 将所有前序编号相同的节点信息通过将支持度相加的方式合并。
定义10 (k项集的N-List) k-项集的N-List需要通过两个k-1项集的N-List合并得到。设一k项集为i1i2...ikik+1ik+2(i1≤Li2≤L...≤Lik≤Lik+1≤Lik+2)。两个k-1项集分别为I1=i1i2...ikik+2, I2=i1i2...ikik+1。将I1的N-List记做{ < (x1i, y1i):z1i > , < (x2i, y2i):z2i > , …}, I2的N-List记做{ < (x1j, y1j):z1j > , < (x2j, y2j):z2j > , …}, 根据定义9中规则2, 类似地生成该k项集的N-List。
为了更好理解上述概念, 以图 2为例, 展示一些项集的N-List。根据定义8, {c}的N-List为{ < (1, 2):1 > , < (5, 6):3 > ), {e}的N-List为{ < (6, 5):3 > }, {f}的N-List为{ < (2, 1):1 > , < (8, 4):1 > , < (9, 7):1 > }。根据定义9, {cf}的N-List为{ < (1, 2):1 > , < (5, 6):1 > ), {ef}的N-List为{ < (6, 5):1 > }。类似地, {cef}的N-List为{ < (5, 6):1 > )。
性质2 两个长度分别为m和n的N-List求交集的时间复杂度是O(m+n)。
性质3 某k项集的支持度可以通过将该k项集的N-List的所有节点的支持度相加得到。
至此, 我们得到快速计算项集支持度的方法。当数据集较稠密时, PPC-tree对数据集的压缩率较高, 从而项集的N-List长度远小于事务的数量。同时, N-List的长度和合并时间会随着项集长度的增加而减少, 因此用N-List表示项集的方法在计算项集支持度时十分高效。这也是N-List相较于Tidset的优势所在。
2.3 NB-MAFIA算法 2.3.1 基本算法对于DFS算法, 其主要运行时间都用在计算1-扩展项集的支持度上。根据前面介绍的N-List的性质, 对于两个项集i1i2...iniu和i1i2...iniv, 其中i1≤Li2≤L...≤Lin≤Liu≤Liv, 假设它们的N-List分别为NL1和NL2, 那么我们可对NL1和NL2做求交集操作, 得到i1i2...iniuiv的N-List, 进而立即得到i1i2...iniuiv的支持度。因此, 对于当前搜索结点C, C.head={i1i2...in}, C.tail={ikik+1...im}(i1≤Li2≤L...≤Lin≤Lik≤Lik+1≤L...≤Lim), 为了得到C的所有1-扩展项集的支持度, 我们只需要记录项集i1i2...in-1in和i1i2... in-1ik, i1i2... in-1ik+1, ..., i1i2... in-1im的N-List, i1i2...in即为结点C所对应的项集, 后面项集组成的集合则为C.sibling+。基于这种思想, 我们可以将N-List与深度优先搜索策略相结合, 得到基于N-List的DFS算法, 其伪代码如算法2所示。
算法2 (基于N-List的DFS算法)
输入:一个交易数据库DB和最小支持度minSup
输出: DB的所有最长频繁模式集合MFI
MFI←∅
Root.head←∅
Root.tail←DB频繁项的集合(按照项的支持度升序排列)
运行PPC-tree construction算法, 得到所有频繁1-项集的N-List, 记为NL1
Call DFS_based_NList (Root, NULL, NULL)
DFS_based_NList (Current node C, C’s NList NL_cur, C.sibling+s’NLists[] NLS)
k←C.head中按项的支持度升序排列排在最后的项
for C.tail中的所有项ido
if (NL_cur==NULL)
NL_child[i]=NL1[i]
else
C_tmp←C.head∪{i}-{k}
NL_tmp←NLS中记录C_tmp的元素
NL_child[i]=NL_intersection (NL_cur, NL_tmp)
endif
endfor
for C.tail中的所有项i do
C_extension.head←C.head∪{i}
C_extension.tail←{j∈C.tail|i≤Lj}
C_tmp←C.head∪{i}-{k}
NLS_child←NL_child中所有在NL_child[i]后面的元素
If (NL_child[i].support≥minSup)
DFS_based_NList (C_extension, NL_child[i], NLS_ child)
endif
endfor
if (C是叶结点并且MFI中不存在C.head的超集) do
MFI←MFI∪C.head
endif
2.3.2 优化策略MAFIA使用的第一个重要剪枝策略是父结点等价剪枝(parent equivalence pruning, PEP)[5]。PEP剪枝主要基于项集搜索树的以下性质。
性质4 对于搜索树中的一个结点C, y为C.tail中的一个元素, 如果包含X=C.head的事务和包含Y=C.head∪{y}的事务完全相同, 即t(X)=t(Y), 那么对于C.tail的任意子集S, 项集I1=X∪S和I2=Y∪S的支持度相同。
证明 显然t(I2)⊆t(I1)。如果存在一个事务T包含I1但不包含I2, 因为I2只比I1多一个项y, 因此y∉T。但由于t(X)=t(Y), 且T包含X, 故T包含Y, 因此y∈T, 这就发生矛盾。因此有t(I2)=t(I1), 即I1与I2的支持度相同, 进而I1=X∪S一定不是最长频繁项集。
因此, 在对以C为根结点的子树进行搜索时, 可以直接将y从C.tail中删除, 并放入C.head, 不会影响搜索出的最长模式。
我们用到的另一个剪枝策略是HUTMFI剪枝[3]。假设当前搜索结点为C, 如果当前的MFI中已经存在C.HUT的超集, 那么以C为根结点的子树中必然没有最长频项集, 因此可以立即结束进一步的递归搜索。
另外, 将任何一个项集加入MFI时, 必须检测它的超集是否已经在MFI中存在, 这个检测操作比较频繁。我们使用MAFIA所使用的策略[5]来优化超集检测过程, 有效地改进算法效率。对于一个给定的结点C, MFI中只有一部分是C.head的超集, 称之为C的局部最长频繁项集(local MFI, LMFI)。对于任意的y∈C.tail, 我们会从y得到C的1-扩展项集并向下进行递归到结点C1。可以看到, 当前C1的LMFI显然是C的LMFI的子集, 并且C1的LMFI中的项集都要包含y。因此, 可以对C的LMFI进行一个排序, 将其中包含y的项集放在一起, 这些项集构成C1的LMFI。当以C为根结点的子树搜索完成时, 由于在这个子树上找到的最长频繁项集都是C的超集, 因此要把新加入MFI的项集加入到C的LMFI中。在判断是否要将一个项集加入MFI时, 只需要判断当前结点的LMFI是否为空即可。
算法3 展示采用上述优化方法的伪代码(为了清晰起见, 本节算法中没有加入与N-List相关的部分)。
算法3 (基于优化策略的算法)
输入:一个交易数据库DB和最小支持度minSup
输出: DB的所有最长频繁模式集合MFI
MFI←∅
Root.head←∅
Root.tail←DB频繁项的集合
Call DFS (Root)
DFS (Current node C)
//HUTMFI
If (MFI中存在C.HUT的超集)
return
endif
for C.tail中的所有项i do
C_extension.head←C.head∪{i}
C_extension.tail←{j∈C.tail|i≤Lj}
计算C_extension.support
//PEP
if (C_extension.support==C.support)
将i从C.tail删掉并加入C.head
else if (C_extension.support≥minSup)
对MFI中在C.LMFIleft和C.LMFIright之间的项集进行排序, 包含i的放在右边, 不包含i的放在左边。假设最靠左边包含i的项集标号为l。
C_extension.LMFIleft←l
C_extension.LMFIright←C.LMFIright
DFS (C_extension)
调整C.LMFIright使得所有新加入MFI的项集都在C的LMFI中
endif
endfor
if (C的LMFI为空集) do
MFI←MFI∪C.head
endif
2.3.3 NB-MAFIA算法伪码最后, 我们将算法2与算法3相结合, 形成NB-MAFIA算法。算法4给出NB-MAFIA算法的伪代码。需要注意的是, 算法2在第一个for循环中计算所有1-扩展项集的支持度, 我们在这个循环中同时执行PEP剪枝的步骤。
算法4 (NB-MAFIA算法)
输入:一个交易数据库DB和最小支持度minSup
输出: DB的所有最长频繁模式集合MFI
MFI←∅
Root.head←∅
Root.tail←DB频繁项的集合(按照项的支持度升序排列)
运行PPC-tree construction算法, 得到所有频繁1-项集的N-List, 记为NL1
Call NBMAFIA (Root, NULL, NULL)
NBMAFIA (Current node C, C’sNList NL_cur, C.sibling+s’NLists[] NLS)
//HUTMFI
If (MFI中存在C.HUT的超集)
return
endif
k←C.head中按项的支持度升序排列排在最后的项
for C.tail中的所有项i do
if (NL_cur==NULL)
NL_child[i]=NL1[i]
else
C_tmp←C.head∪{i}-{k}
NL_tmp←NLS中记录C_tmp的元素
NL_child[i]=NL_intersection (NL_cur, NL_tmp)
endif
//PEP
If (NL_child[i].support==C.support)
将i从C.tail删掉并加入C.head
else if (NL_child[i].support < minSup)
将i从C.tail删掉
endfor
for C.tail中的所有项i do
C_extension.head←C.head∪{i }
C_extension.tail←{j∈C.tail|i≤Lj }
C_tmp←C.head∪{i}-{k}
NLS_child←NL_child中所有在NL_child[i]后面的元素
对MFI中在C.LMFIleft和C.LMFIrigh之间的项集进行排序, 包含i的放在右边, 不包含i的放在左边。假设最靠左边包含i的项集标号为l
C_extension.LMFIleft←l
C_extension.LMFIright←C.LMFIright
NBMAFIA (C_extension, NL_child[i], NLS_child)
调整C.LMFIright使得所有新加入MFI的项集都在C的LMFI中
endif
endfor
if (C的LMFI为空集) do
MFI←MFI∪C.head
endif
3 实验通过比较NB-MAFIA与其他两个著名算法MAFIA[5]和FP-growth*[29]在不同数据集上挖掘最长频繁模式所用时间, 来验证其有效性。在每组实验中, 3个算法运行所得到的最长频繁模式完全相同, 保证了NB-MAFIA算法的正确性和完整性。我们根据2003年频繁项集挖掘评测比赛官方网站(http://fimi.ua.ac.be/experiments/fimi03/maximal)上提供的信息, 在每个数据集上选取合适的最小支持度用于测试。同时, 为了保证试验结果的公平, 我们在同一台机器上运行3个算法, 并比较结果, 避免由其他客观因素带来的性能差异。
3.1 实验设置我们使用6个真实数据集和两个仿真数据集来完成实验, 这些数据集都是在已有的关于频繁模式挖掘的论文中经常提及和使用的。6个真实数据集为Mushroom, Accidents, Pumsb, Retail, Kosarak和Connect。两个仿真数据集分别是T10I4D100K和T40I10D100K。这些数据集都由2003年频繁模式挖掘评测比赛官方网站(http://fimi.ua.ac.be/data/)提供。T10I4D100K和T40I10D100K由数据生成器IBM Almaden生成。生成T10I4D100K的标准为:平均事务长度(average transactions length, ATL)为10, 潜在的最长频繁项集的平均长度为4, 事务数和项的数量分别为100000和1000。T40I10D100K的标准与之类似。
考虑到不同算法在不同特征的数据集上的表现差异较大, 我们同时选择稠密的数据集和稀疏的数据集进行实验。在真实数据集中, Accidents, Pumsb和Connect都是十分稠密的数据集, 即使在较高的最小支持度下, 它们也包含大量的频繁项集。Mushroom虽然也比较稠密, 但是其整体规模较小(只包含一百多个项和几千个事务)。Kosarak的大小仅次于Accidents, 但比Accidents要稀疏得多。Retail是十分稀疏的数据集。两个仿真数据集T10I4D100K和T40I10D100K也是十分稀疏的。表 2为实验使用数据集的基本特征。
| 数据集 | #item | #trans | ATL |
| Accidents | 468 | 340183 | 33.8 |
| Mushroom | 119 | 8214 | 23.0 |
| Connect | 129 | 675557 | 43.0 |
| Pumsb | 7117 | 49046 | 74.0 |
| Kosarak | 36842 | 990007 | 7.1 |
| Retail | 16470 | 88162 | 10.3 |
| T10I4D100K | 870 | 100000 | 10.1 |
| T40I10D100K | 942 | 100000 | 39.6 |
实验的所有程序用C/C++编写。其中MAFIA的代码下载自http://himalaya-tools.sourceforge.net/Mafia/, FP-growth的代码下载自http://fimi.cs.helsinki.fi/src/。所有的实验在一台CPU配置为Intel i5-3230 2.6 GHz, 内存2 G的PC上进行。实验的操作系统为32bit Ubuntu 12.04。
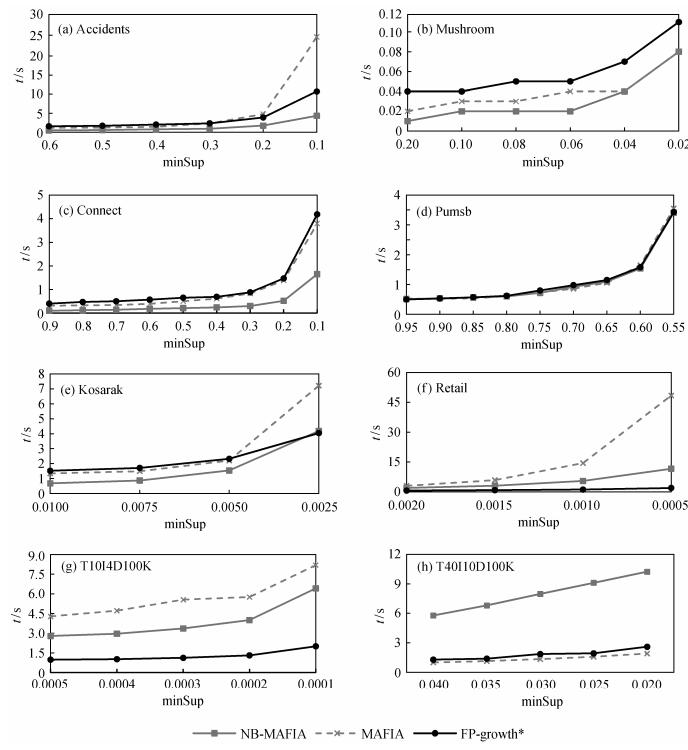
3.2 运行时间的比较和分析图 3展示了3个算法在8个数据集上, 基于不同的最小支持度设定的运行时间。由于3个算法在读入阶段都需要建立一定的数据结构来保证算法正确、有效地运行, 因此这一部分所用的时间是不可忽视的。由于最长频繁模式的数目有限, 加入输出时间对于总体运行时间不会有较大影响, 因此, 上述运行时间描述的都是程序运行的总时间。
|
| 图 3. 3种算法在8个数据集上的运行时间 Figure 3. Runtime of three algorithms for eight datasets |
图 3(a)为3个算法运行在Accidents数据集上的情况。在所有最小支持度下, NB-MAFIA的时间效率在3个算法中都是最好的。随着最小支持度的下降, MAFIA算法的运行时间增长非常快。当最小支持度高于0.3时, MAFIA的效率优于FP-growth*, 而在更低的最小支持度下, FP-growth*则比MAFIA所用时间少。图 3(b)是关于Mushroom数据集的比较。显然, NB-MAFIA仍然表现最为出色, 尽管在最小支持度低到4%后与MAFIA的运行时间基本上相同。FP-growth*则是三者中所用时间最多的。图 3(c)展示了3个算法运行在Connect数据集上的情况。NB-MAFIA依然具有最快的速度, 并且所用时间不到其他两个算法的一半。MAFIA和FP-growth*的时间效率十分接近。图 3(d)是针对Pumsb数据集的测试结果展示。对于这个数据集, 在所有最小支持度下, 3个算法的表现十分接近, 没有一个算法明显优于其他二者。我们的NB-MAFIA算法的表现也总不是最差的。图 3(e)是3个算法在Kosarak数据集上的情况。可以看到, NB-MAFIA的运行时间在所有最小支持度下都比MAFIA少。只有在最小支持度为0.25%时, NB-MAFIA的效率略逊色于FP-growth*算法。图 3(f)是3个算法在Retail数据集上的运行情况。在这个数据集上, FP-growth*的效果最稳定, 也最优秀。FP-growth*比NB-MAFIA快3~5倍。MAFIA的表现极差, 当最小支持度较低时, 它的效率甚至比FP-growth*要低一个数量级以上。相似的结果在图 3(g)关于T10I4D100K数据集的结果中也可以看到。图 3(h)是T40I10100K的结果, 只有在这一数据集上, NB-MAFIA的效率比其他两个算法都差。
通过上述实验结果可以看到, 在稠密的数据集Accident, Mushroom, Connect和Kosarak上, 我们的NB-MAFIA算法都明显优于其他两个算法, 而对于稠密的Pumsb数据集, NB-MAFIA也不比其他两个算法差。这主要是因为在稠密的数据集上, PPC-tree对于数据集有较高的压缩率[7], 我们可以用N-List来高效地表示项集、计算项集支持度。而对于稀疏的数据集, 虽然NB-MAFIA的表现不如FP-growth*, 但在多数情况下依然要优于MAFIA算法。由于NB-MAFIA是在MAFIA搜索框架的基础上改进得到的, 因此, 我们通过实验证明了NB-MAFIA对MAFIA的改进的确有效。NB-MAFIA表现较差的两个数据集T10I4D100K和T40I10D100K都是人造数据集, 并不能很好地表现实际应用中数据的特点。另外, 从实验结果来看, 对于挖掘所有频繁模式任务, PrePost算法在Retail和T10I4D100K数据集上的表现与FP-growth算法和FP-growth*算法相似, 甚至有比二者差的情况[7]。这从侧面印证了对于最长模式挖掘任务, NB-MAFIA和FP-growth*算法在两个数据集上效率的相对关系。由于两个算法所用数据结构的差异, 我们很难定量分析出导致两者效率差别的原因。
4 总结本文提出一个整合算法NB-MAFIA, 可以高效地完成最长频繁模式挖掘任务。NB-MAFIA是基于MAFIA算法的深度优先搜索策略, 并用N-List数据结构来表示项集, 同时适当地结合MAFIA中用到的剪枝策略和超集检测策略来提高搜索效率。由于N-List所具有的性质, 我们可以通过高效地对其进行求交集操作来获得项集的支持度。我们在多个真实和仿真数据集上进行测试, 验证了NB-MAFIA优越的性能。实验证明, 在稠密的数据集上, NB-MAFIA都有出色的表现, 在5个数据集中的4个数据集上都比MAFIA和FP-growth更加高效。在稀疏的数据集上, 整体上看, NB-MAFIA也比MAFIA有效。在真实的数据集上, NB-MAFIA都比MAFIA性能好。这说明我们的算法是对MAFIA的一个有效改进。我们未来的研究方向, 可以针对稀疏数据集对NB-MAFIA算法进行进一步改进; 也可以以N-List结构为基础, 改进闭模式挖掘、高效用模式挖掘等任务的效率; 还可以Deng等[22]提出的相较于N-List更简省有效的数据结构Nodeset为基础, 进一步提高NB-MAFIA的效率和可扩展性。
| [1] | Agrawal R, Imielinski T, Swami A. Mining association rules between sets of items in large databases // Buneman P, Jajodia S. SIGMOD93: Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. Washingdon, DC: ACM Press, 1993: 207-216 |
| [2] | Agrawal R, Srikant R. Fast algorithm for mining association rules // Bocca B J, Jarke M, Zaniolo C. VLDB94: The 20th International Conference on Very Large Data Bases. Santiago de Chile: Morgan Kaufmann, 1994: 487-499 |
| [3] | Rigoutsos I, Floratos A. Combinatorial pattern discovery in biological sequences: the teiresias algorithm. Bioinformatics , 1998, 14 (1) : 55–67 DOI:10.1093/bioinformatics/14.1.55 . |
| [4] | Burdick D, Calimlim M, Gehrke J. MAFIA: a maximal frequent itemset algorithm for transactional databases // Georgakopoulos D, Buchmann A. ICDE2001: Proceedings of the 17th International Conference on Data Engineering. Heidelberg: IEEE Computer Society, 2011: 443-452 |
| [5] | Burdick D, Calimlim M, Flannick J, et al. Mafia: a maximal frequent itemset algorithm. IEEE TKDE J , 2005, 17 (11) : 1490–1504 . |
| [6] | Gouda K, Zaki M J. Efficiently mining maximal frequent itemsets // Cercone N, Lin T Y, Wu X D. ICDM2001: Proceedings of the 2001 IEEE Interna-tional Conference on Data Mining. San Jose: IEEE Computer Society, 2001: 163-170 |
| [7] | Deng Z H, Wang Z H, Jiang J J. A new algorithm for fast mining frequent itemsets using N-lists. Science China Information Sciences , 2012, 55 (9) : 2008–2030 DOI:10.1007/s11432-012-4638-z . |
| [8] | Han J W, Pei J, Yin Y W. Mining frequent patterns without candidate generation // Chen W D, Naughton J F, Bernstein, P A. Proceedings of the 2000 ACM SIGMOD International Conferenceon Management of Data. Dellas: ACM Press, 2000: 1-12 |
| [9] | Pei J, Han J W, Lu H J, et al. H-Mine: hyper-structure mining of frequent patterns in large databases // Cercone N, Lin Y T, Wu X D. ICDM2001: Procee-dings of the 2001 IEEE International Conference on Data Mining. San Jose: IEEE Computer Society, 2001: 441-448 |
| [10] | Agrawal R, Mannila H, Srikant R, et al. Fast discovery of association rules // Fayyad U M, Piatetsky-Shapiro G, Smyth P, et al. Advances in knowledge discovery and data mining. AAAI/MIT Press, 1996: 307-328 |
| [11] | Aggarwal C C, Yu P S. Mining large itemsets for association rules. IEEE Data Eng Bull , 1998, 12 (1) : 23–31 . |
| [12] | Aggarwal C C, Yu P S. Online generation of association rules// Urban D S, Bertino E. ICDE1998: Proceedings of the 2001 IEEE International Confe-rence on Data Mining. Orlando: IEEE Computer Society, 1998: 402-411 |
| [13] | Dunkel B, Soparkar N. Data organization and access for efficient data mining // Kitsuregawa M, Papazoglou M P. ICDE1999: Proceedings of the 15th International Conference on Data Engineering. Sydney: IEEE Computer Society, 1999: 522-529 |
| [14] | Ganti V, Gehrke J, Ramakrishnan R. Demon: mining and monitoring evolving data. IEEE TKDE J , 2001, 13 (1) : 50–63 . |
| [15] | Park J S, Chen M S, Yu P S. An effective hash-based algorithm for mining association rules // Carey M J, Schneider D A. KDD1995: International Conference on Management of Data. San Jose: ACM Press, 1995: 175-186 |
| [16] | Savasere A, Omiecinski E, Navathe S B. An efficient algorithm for mining association rules in large databases // Dayal U, Gray P M D, Nishio S. VLDB94: Proceedings of 21th International Conference on Very Large Data Bases. Zurich: Morgan Kaufmann, 1995: 432-444 |
| [17] | Shenoy P, Haritsa J, Sudarshan S, et al. Turbo-charging vertical mining of large database // Chen W D, Naughton J F, Bernstein, P A. SIGMOD00: Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. Dallas: ACM Press, 2000: 22-33 |
| [18] | Toivonen H. Sampling large databases for association rules // Vijayaraman T M, Buchmann A P, Mohan C, et al. VLDB96: Proceedings of 22th International Conference on Very Large Data Bases. Mumbai: Morgan Kaufmann, 1996: 134-145 |
| [19] | Yip C L, Loo K K, Kao B, et al. Lgen --a lattice-based candidate set generation algorithm for I/O efficient association rule mining // Zhong N, Zhou L Z. PAKDD99: Methodologies for Knowledge Disco-very and Data Mining, Third Pacific-Asia Conference. Beijing, 1999: 54-63 |
| [20] | Zaki M J, Gouda K. Fast vertical mining using diffsets // Getoor L, Senator T E, Domingos P, et al. KDD2003: The 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington DC: ACM Press, 2003: 326-335 |
| [21] | Deng Z H, Wang Z H. A new fast vertical method for mining frequent itemsets. International Journal of Computational Intelligence Systems , 2010, 3 (6) : 733–744 DOI:10.1080/18756891.2010.9727736 . |
| [22] | Deng Z H, Lv S L. Fast mining frequent itemsets using nodesets. Expert Systems with Applications , 2014, 41 (10) : 4505–4512 DOI:10.1016/j.eswa.2014.01.025 . |
| [23] | Bayardo R J. Efficiently mining long patterns from databases // Haas M L, Tiwary A. SIGMOD1998: Proceedings ACM SIGMOD International Conference on Management of Data. Washingdon: ACM Press, 1998: 85-93 |
| [24] | Agarwal R C, Aggarwal C C, Prasad V V V. A tree projection algorithm for generation of frequent item sets. J Parallel and Distributed Computing , 2001, 61 (3) : 350–371 DOI:10.1006/jpdc.2000.1693 . |
| [25] | Gunopulos D, Mannila H, Saluja S. Discovering all most specific sentences by randomized algorithms // Kolaitis G P, Afrati N F. ICDT97: Proceedings of 6th International Conference Database Theory. Greece, 1997: 215-229 |
| [26] | Lin D I, Kedem Z M. Pincer search: a new algorithm for discovering the maximum frequent set // Schek H, Saltor F, Ramos I, et al. EDBT98: Proceedings of 6th International Conference on Extending Database Technology. Valencia, 1998: 105-119 |
| [27] | Zaki M J. Scalable algorithms for association mining. IEEE TKDE J , 2000, 12 (3) : 372–390 . |
| [28] | Grahne G, Zhu J F. High performance mining of maximal frequent itemsets // HPDM2003: Procee-dings of the 6th International Workshop High Performance Data Mining. San Francisco, 2003: 135-143 |
| [29] | Grahne G, Zhu J F. Fast algorithms for frequent itemset mining using FP-Trees. IEEE TKDE J , 2005, 17 (10) : 1347–1362 . |
| [30] | Holsheimer M, Kersten M L, Mannila H, et al. A perspective on databases and data mining // Fayyad U M, Uthurusamy R. KDD95: Proc Proceedings of the First International Conference on Knowledge Disco-very and Data Mining. Montreal: AAAI Press, 1995: 150-155 |
 2016, Vol. 52
2016, Vol. 52