文章信息
- 刘颖滨, 孙燕南, 荀恩东
- LIU Yingbin, SUN Yannan, XUN Endong
- 一种基于三维空间信息的字形匹配方法
- Chinese Calligraphy Alignment Based on 3D Point Set Registration
- 北京大学学报(自然科学版), 2016, 52(1): 81-88
- Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(1): 81-88
-
文章历史
- 收稿日期: 2015-06-03
- 修回日期: 2015-08-15
- 网络出版日期: 2015-09-30
字形匹配指按照一定的准则, 衡量汉字字形的相似程度, 从而建立对应关系并进行变换的过程, 是字形美化的关键步骤[1-2]。传统字形匹配方法有基于骨架的方法[3]、基于笔画还原的方法[4]和基于特征提取的方法[5]等。近年来, 点集匹配算法[6-11]发展较快, 并且已经被应用到字形匹配领域[12-14]。
记两个有限维空间中的点集{M, S}为待匹配点集, 其中S为目标点集, M为模型点集。在匹配过程中, S保持固定不变, M向S不断逼近。点集匹配问题可描述为找到一个变换T, 使得M经过变换后的结果点集R与目标点集S实现最优匹配。点集匹配算法分为基于刚体变换和基于非刚体变换两种。非刚体变换属于局部性几何形变, 自由度更高, 匹配效果较好。Myronenko等[9]提出的一致性点漂移算法(Coherent Point Drift, CPD)是一种具有代表性的基于非刚体变换的点集匹配方法。CPD算法将模型点集M中各点视作高斯混合模型(Gaussian Mixture Model, GMM)中各个高斯分量质心。在匹配过程中, M作为一个整体逐渐向S进行保持拓扑结构一致性的漂移运动。Sun等[13]和Lian等[14]使用CPD算法进行汉字笔画的抽取, 提出一种基于结构指导的快速一致点漂移算法(Structure-Guided Coherent Point Drift, SGCPD)。Jian等[12]提出一个统一的基于高斯混合模型的点集匹配算法框架, 利用概率统计方法将点集匹配转化为数值计算问题。现有的点集匹配算法[7-11]都可用此框架重新解释。该框架的核心思想是针对点集建立高斯混合模型, 从而将点集匹配问题转化为高斯混合模型间的相似度最大化问题。实验证明, 基于此框架的点集匹配算法具有内在的统计鲁棒性, 且易于实现[12]。
一般地, 通用的点集匹配算法适用于多维点集, 而在字形匹配领域, 目前基于点集匹配的方法[12-14]限于字形的二维点集。实验表明, 仅采用二维点集进行匹配的结果往往不够理想, 原因之一在于汉字字形内在的特殊性和复杂性。仅使用二维点集进行匹配时, 汉字字形轮廓中所蕴含的许多信息被忽略, 无法在匹配过程中发挥作用。本文将字形信息定义为超越二维几何信息的多维数据, 以期充分表达书写过程, 提升匹配精度。作为利用多维字形信息的第一步, 本文结合字形本身特征, 将字形二维点集M和S扩充为三维点集M′和S′, 然后再进行匹配, 具体步骤为: 1) 提取二维字形控制点集并扩充至三维; 2) 为三维字形点集建立GMM; 3) 通过最小化两个GMM之间的欧氏距离(L2)完成匹配; 4) 将匹配后的三维结果转化为二维, 经平滑处理后生成字形曲线。
本文的创新之处主要体现在: 1) 采用三维点集进行匹配, 尝试采用扩充维度的方法来改进匹配结果; 2) 仅使用字体信息, 不依赖其他附加信息; 3) 选用最小化高斯混合模型间的L2距离来求解匹配关系, 实现简单且稳定性好。
1 数据处理本文采用汉字字体轮廓的Bézier曲线[15]控制点集定义字形, 优势在于: 1) 控制点集可以从数学上精确定义轮廓曲线, 并且可以根据需要绘制(字形骨架点必须通过额外工作才能还原轮廓[14]); 2) 标准TrueType字库均采用Bézier控制点来定义曲线轮廓, 具有普遍性; 3) Bézier曲线便于进行插值和细分。
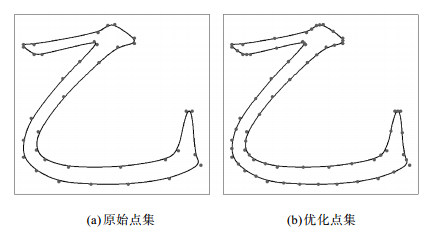
1.1 二维控制点集TrueType字体[16]使用直线和二次Bézier曲线定义字形轮廓。在设计字体时, 利用二次Bézier曲线的C1连续性条件, 往往会省略部分在曲线上的控制点以减小数据量。因此, TrueType字体轮廓的原始控制点可能疏密不均, 需要进行优化处理。为了统一表达, 本文将直线视为特殊的二次Bézier曲线, 认为字形轮廓由若干分段二次Bézier曲线连接而成。控制点集优化是还原完整的分段二次Bézier曲线控制点的过程, 包括还原被省略的控制点、将直线统一为二次Bézier曲线以及轮廓封闭处理3个步骤。在优化过程中, 还可以利用Bézier曲线任意细分而不改变原始曲线形状的性质, 对控制点集进行适当加密以便于匹配, 加密方法不在此赘述。图1为楷体“乙”字的原始控制点集以及经过优化后的结果。
|
| 图 1. 楷体“乙”控制点集优化 Figure 1. Optimization of the control points of “Yi” in Kaiti |
1.2 三维点集
实验表明, 直接采用字形的二维控制点集进行匹配, 结果往往不够理想, 原因在于汉字字形轮廓中蕴含的约束条件在匹配过程中很可能被破坏, 导致匹配结果不符合汉字的审美标准。例如, 单笔画匹配时, 某些较细的笔画轮廓两边的点对应错位; 整字匹配时, 某些笔画轮廓被匹配到其他笔画。为了弥补二维信息的不足, 本文将二维点集扩充为三维点集。扩充的基本思想在于利用字形本身特征生成第三维信息, 使点集分布在三维空间中, 以减少二维匹配产生的错误。扩充过程不改变原始的二维坐标。
以模型点集M为例, νi = [Xi Yi]表示M中第i个点, 对于∀νi∈M, 使得
| $ {\nu '_i} = \left\{ \begin{array}{l} {\nu _i}\;{{\mathit{\pmb{V}}}_1},\;\;t \ge 0\;,\\ {\nu _i}\;{{\mathit{\pmb{V}}}_2},\;\;t < 0\;, \end{array} \right. $ |
上式中, t = (arg max yi- arg min yi)- (arg max xi - arg min xi), i = 1, 2, …, k。
| $ {{\mathit{\pmb{V}}}_1} = \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1 & 0 & {\tan \theta } \end{array}\\ \begin{array}{*{20}{c}} 0 & 1 & 0 \end{array} \end{array} \right],\;\;{{\mathit{\pmb{V}}}_2} = \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1 & 0 & 0 \end{array}\\ \begin{array}{*{20}{c}} 0 & 1 & {\tan \theta } \end{array} \end{array} \right], $ |
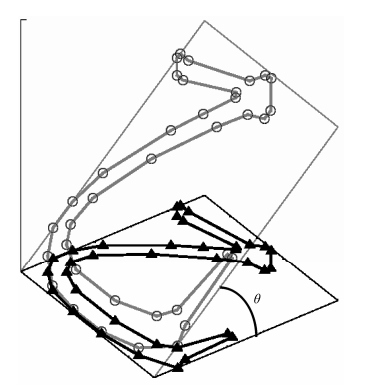
θ表示三维点集所在平面与XY平面所成的夹角。θ的取值对匹配结果有一定影响, 此处取经验值θ=π/4。利用上述方法将二维控制点集M和S扩充为三维点集M′和S′。图2为楷体“乙”的三维点集的生成过程。
|
| 图 2. 三维点集的生成 Figure 2. Generation of 3D point set |
2 建立高斯混合模型
作为常用的统计学方法, 高斯混合模型用若干个高斯概率分布的线性组合来表示数据的概率分布[17-18]。一个K阶的高斯混合模型的概率密度函数可以表示为
| $ P(X\left| \lambda \right.) = \sum\limits_{i = 1}^K {{\alpha _i}} N(x;{\mu _i};{\sum _i}), $ | (1) |
其中, X为D维随机变量; αi (i=1, 2, …, K)为每个高斯分布的权重, 且满足
汉字字形轮廓控制点的分布并不严格服从特定的概率密度函数, 但是, 由中心极限定理可知, 任意形状的概率分布都可以用若干个高斯密度函数的线性组合来逼近。在字形匹配研究中, 可对三维点集建立高斯混合模型, 从而将字形匹配问题转化为GMM的匹配问题。根据式(1), 令D=3, K为三维点集X中点的个数, 则X的GMM定义如下:
| $ {\rm{gmm}}(X) = {\rm{P}}(X|\lambda ) = \sum\limits_{i = 1}^K {{\alpha _i}} N(x;{\mu _i};{\sum _i}). $ | (2) |
选用GMM定义三维点集的优势在于: 1) 将字形匹配问题转化为GMM匹配问题, 可使问题得到简化; 2) GMM能精确表达三维点集的概率分布情况, 体现字形整体与局部的字形特征, 提升匹配精确度。
3 匹配算法通过定义并求解基于GMM的目标函数可以解决对应的三维点集的匹配问题。目标函数的定义可采用最小化欧氏距离(L2)、最大化对数似然函数[12]和最大化内核相关(Kernel Correlation)[19]等方法。其中, L2距离简单直观, 稳定性强, 而且在多维空间中存在明确定义, 比较适合三维字形匹配。本文采用最小化L2距离作为目标函数, 用GMM间的L2距离来衡量GMM间相似度, L2距离越小, 则GMM间的相似度越高, 字形的匹配度就越高。
对于三维模型点集M′ 和目标点集S′, 用T表示带参数的非刚体变换, 则目标函数定义如下:
| $ {d_{L2}}(S',\;M',\;\lambda ) = \int {{{({\rm{gmm}}(S') - {\rm{gmm}}(T(M',\;\lambda )))}^2}} {\rm{d}}x. $ | (3) |
至此, 问题转化为如何求解出一组最优的参数λ, 使得目标函数的值最小。最优的模型参数λ*可表示为
| $ {\lambda ^*} = \arg \min {d_{L2}}(S',\;M',\;\;\lambda ). $ | (4) |
本文采用的匹配算法框架如下。
输入: 模型点集M′, 目标点集S′, 参数化的变换T
输出: 使得目标函数(式(3))最小的最优的变换参数λ*
开始:
设置循环次数times, 循环计数变量count=0
初始化参数T(如从恒等变换开始)
定义目标函数(式(3))
重复:
将λ作为参数, 最小化目标函数
更新参数, 即λ←argminTdL2
count ← count +1
直到达到设定的循环次数count ≥ times
结束
上述算法中, 常用的变换模型T有薄板样条函数(Thin-plate Splines, TPS)[20]和高斯径向基函数(Gaussian Radial Basis Functions, GRBF)[21-22]等。本文采用TPS作为匹配时的变换模型, 将匹配后的三维结果平行投影到XY平面得到最终的二维结果R。由于R中轮廓曲线的分段连续性条件在匹配过程中可能被破坏, 所以根据模型点集M中的相应的分段连续关系, 对R进行局部平滑操作, 并生成最后的字形曲线。
4 实验结果本文选取“仿宋”和“楷体”两种字体的33个基本笔画进行字形匹配实验, 见表1。根据使用的变换模型、目标函数以及数据维度, 将实验所涉及的方法分别命名。本文提出的基于三维空间信息的字形匹配方法命名为TPS_L2_3D方法。另外选取具有代表性的TPS_L2和EM_GRBF方法(EM_GRBF方法即CPD方法)[12]作为对照实验, 两种方法都使用二维点集建立GMM。前者通过最小化L2距离完成匹配并以TPS作为变换模型; 后者通过最大化对数似然函数完成匹配, 以GRBF作为变换模型。TPS_L2方法简单且稳定性强, EM_GRBF匹配精确度高, 但容易受到噪声点的影响[12]。
| 编号 | 笔画 |
| 0 | 左点 |
| 1 | 斜竖 |
| 2 | 横折弯撇 |
| 3 | 竖弯 |
| 4 | 右点 |
| 5 | 斜竖折 |
| 6 | 横折弯 |
| 7 | 提 |
| 8 | 撇提 |
| 9 | 撇 |
| 10 | 横撇弯钩 |
| 11 | 横勾 |
| 12 | 竖折(折弯) |
| 13 | 竖钩 |
| 14 | 竖弯钩 |
| 15 | 斜弯钩 |
| 16 | 撇点 |
| 17 | 弯钩 |
| 18 | 竖 |
| 19 | 捺 |
| 20 | 卧钩 |
| 21 | 斜钩 |
| 22 | 撇折 |
| 23 | 横 |
| 24 | 竖折撇 |
| 25 | 横折钩 |
| 26 | 横折斜钩 |
| 27 | 竖折 |
| 28 | 横折(折直) |
| 29 | 横撇 |
| 30 | 横折折勾 |
| 31 | 横折弯钩(折直) |
| 32 | 横折弯钩(折弯) |
本文的实验结果分析主要从平均匹配概率和视觉效果两个方面来衡量。平均匹配概率(averaged assignment probability, AAP)[13]的定义如下:
| $ {\rm{AAP}}(S,\;R) = \frac{{\sum\limits_{i = 1}^n {{{\max }_{1 \le j \le m}}\{ pij\} } }}{n}, $ | (5) |
其中, S表示目标点集, R表示模型点集M匹配后的结果, m和n分别表示M与S的点集大小, pij表示M中第i个点与S中第j个点的匹配概率。AAP反映点集中各点的最优匹配概率的平均水平, 这一指标在一定程度上体现变换后的点集与目标点集的相似度。由于字形的特殊性, 匹配结果的美观程度也是评价匹配结果的一个重要标准。
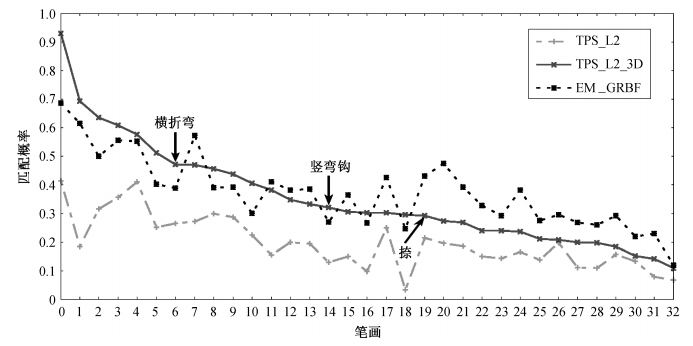
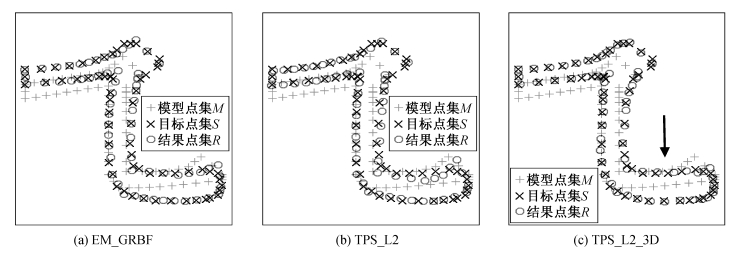
图3为3种方法在笔画实验中的平均匹配概率分布。从图3可以看出, 本文提出的TPS_L2_3D方法比TPS_L2方法在平均匹配概率上有显著提升; TPS_L2_3D的匹配结果与EM_GRBF结果相近, 部分笔画的平均匹配概率比EM_GRBF方法更高。以具体笔画为例, 图3中箭头标示的“竖弯钩”和“横折弯”这两个笔画的平均匹配概率都是TPS_L2_3D方法最高, 其对应的控制点匹配结果分别如图4和5所示。从图4和5可以看出, 就匹配的整体视觉效果而言, TPS_L2_3D的匹配结果比TPS_L2和EM_GRBF方法更接近目标点集, 这一点与平均匹配概率的数据分析结果一致; 在局部匹配上, 对于图4和5中箭头标示部分的匹配, TPS_L2_3D方法匹配的更为精细。
|
| 图 3. 平均匹配概率统计 Figure 3. Average alignment probability of strokes |
|
| 图 4. “竖弯钩”匹配结果 Figure 4. Alignment result of stroke “Shuwangou” |
|
| 图 5. “横折弯”匹配结果 Figure 5. Alignment result of stroke “Hengzhewan” |
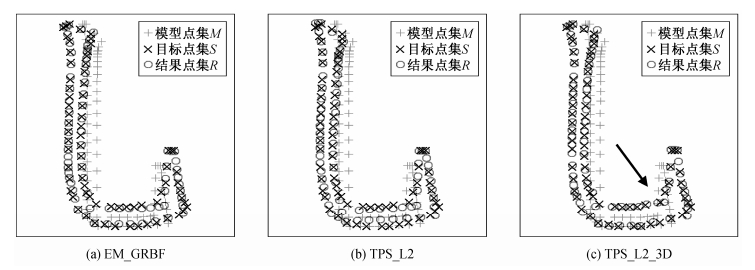
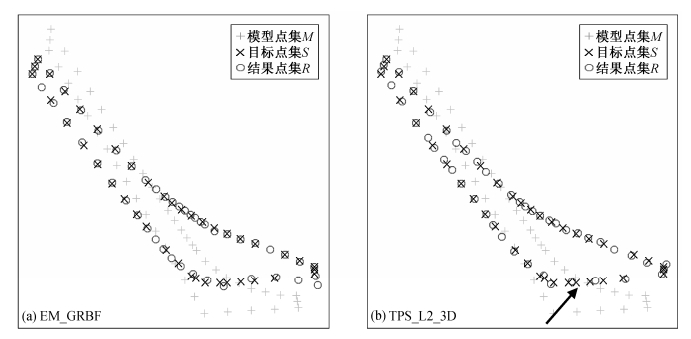
对于部分TPS_L2_3D平均匹配概率低于EM_GRBF的情况, 我们发现两种方法的匹配结果视觉上都具备目标字形的基本轮廓特征, 整体效果相似; TPS_L2_3D未造成明显的匹配错误, 甚至局部的匹配结果优于EM_GRBF。以图6笔画“捺”为例, 虽然其TPS_L2_3D平均最优匹配概率AAP值低于EM_GRBF, 但是TPS_L2_3D匹配结果却更好地保持了字形的基本轮廓特征。同时, 第三维信息的加入能够帮助提升局部点的匹配精度, 例如在箭头标示区域, TPS_L2_3D的匹配结果比EM_GRBF的匹配结果更美观。
|
| 图 6. “捺”匹配结果 Figure 6. Alignment result of stroke “Na” |
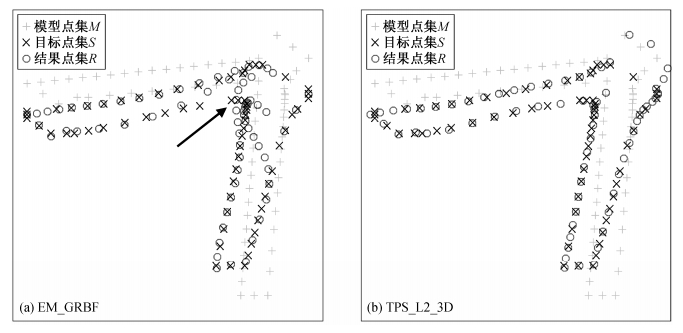
对于部分TPS_L2_3D匹配结果的平均匹配概率高于EM_GRBF的情况, 由于TPS_L2_3D方法稳定性强, 对于噪声点不敏感, 因此在匹配过程中能够较好地保持字形的整体拓扑结构。EM_GRBF方法对噪声点比较敏感, 算法的结果和效率受调整参数的影响较大[12], 因此可能会造成匹配结果偏离目标字形。如图7所示, 笔画“横折”的EM_GRBF匹配结果在箭头标示处出现明显的偏差, 而TPS_L2_3D匹配结果则明显占优。
|
| 图 7. “横折”匹配结果 Figure 7. Alignment result of stroke “Hengzhe” |
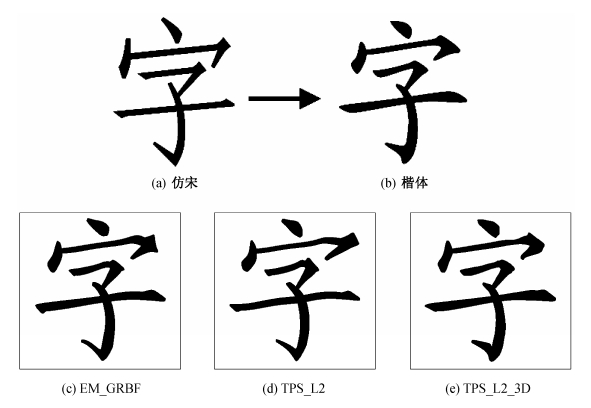
本文另外选取部分汉字, 进行从仿宋到楷体的整字匹配实验。以“汉”和“字”为例, 整字匹配结果经过光滑处理后得到的字形曲线分别如图8和9 所示。通过对比3种方法的匹配结果, 可见TPS_L2_3D的综合匹配结果最理想: 1) 整体效果最接近目标字形, 具备楷体的风格, 而另外两种方法仍带有较明显的仿宋体的特征; 2) 在拐角等关键点的匹配更为精准, 笔画流畅, 符合书写特点; 3) 算法效率高, TPS_L2_3D与TPS_L2的复杂度大致相同, 但在精确性和美观性方面, 前者的匹配结果比后者提升很多。

|
| 图 8. “汉”匹配结果 Figure 8. Alignment of character “Han” from Fangsong to Kaiti |
|
| 图 9. “字”匹配结果 Figure 9. Calligraphy alignment of character “Zi” from Fangsong to Kaiti |
5 总结和展望
采用基于高斯混合模型的三维点集匹配算法解决字形匹配问题, 是汉字字形匹配领域的一次创新。本文使用了多维数据定义字形信息, 从而改善了字形匹配结果。实验结果表明, 通过旋转变换来扩充第三维数据可以有效提升字形匹配精度, 从而验证了使用多维度信息对于改善字形匹配效果的可行性。从宏观上讲, 尽管字形本身是二维信息, 但是书写过程本质上包含多个维度的信息(如书写速度、力度等)。以往的研究中, 这些信息多抽象为书写规则或个人经验的形式进行描述; 字形匹配的工作也局限于二维几何信息, 多关注于书写结果的研究而忽略了书写过程。将来的研究中, 我们会尝试从多维度的视角来解决字形匹配问题, 通过收集书写过程的多维度信息, 发现规律并提取特征, 充分还原书写过程的多维度属性。
通过有效的多维度字形匹配, 有助于解决中文字形领域内的许多问题, 具有广阔的应用前景。除标准字体外, 还可以应用到手写汉字字形美化领域。在获取手写字的多维字形信息后, 可以通过字形匹配使手写字具备目标字形的特征, 从而达到美化字形的目的; 通过设置字形匹配的参数, 用户可以定制兼顾个人书写风格与特定目标字体风格的个性化字体。
| [1] | 庄崇彪, 金连文. 在线汉字书写正误及工整的智能评判算法. 信号处理 , 2005, 8 (4A) : 276–279. |
| [2] | 杨晓江. 汉字智能书写及其算法. 计算机工程 , 2003, 29 (21) : 154–155. |
| [3] | 刘云飞. 脱机手写体汉字识别中细化、特征提取和相似字识别算法研究[D]. 长春: 吉林大学, 2006 |
| [4] | 荀恩东, 吕晓晨, 安维华, 等. 面向书写教学的手写汉字图像笔画还原. 北京大学学报: 自然科学版 , 2015, 51 (2) : 241–248. |
| [5] | 孙华, 张航. 汉字识别方法综述. 计算机工程 , 2010, 36 (20) : 194–197. |
| [6] | 赵键. 点模式匹配算法研究[D]. 长沙: 国防科学技术大学, 2012 |
| [7] | Besl P J, McKay H D. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1992, 14 (2) : 239–256 DOI:10.1109/34.121791 . |
| [8] | Jian B, Vemuri B C. A robust algorithm for point set registration using mixture of Gaussians // ICCV. Beijing, 2005: 1246-1251 |
| [9] | Myronenko A, Song X B. Point-set registration: Coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2010, 32 (12) : 2262–2275 DOI:10.1109/TPAMI.2010.46 . |
| [10] | Chui H, Rangarajan A. A new algorithm for non-rigid point registration. CVPR , 2000, 89 (2) : 2044–2051 . |
| [11] | Myronenko A, Song X B. Non-rigid point setre-gistration: coherent point drift. NIPS , 2006, 32 (12) : 1009–1016 . |
| [12] | Jian B, Vemuri B C. Robust point set registration using gaussian mixture models. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2011, 33 (8) : 1633–1645 DOI:10.1109/TPAMI.2010.223 . |
| [13] | Sun Hao, Lian Zhouhui, Tang Yingming, et al. Non-rigid point set registration for chinese characters using structure-guided coherent point drift // IEEE International Conference on Image Processing (ICIP). Paris, 2014: 4752-4756 |
| [14] | Lian Zhouhui, Xiao Jianguo. Automatic shape morphing for Chinese characters // 5th ACM SIGGRAPH Conference and Exhibition on Computer Graphics and Interactive Techniques in Asia (SIGGRAPH ASIA 2012). Singapore, 2012: Article No. 2 |
| [15] | 张明星. 广义Bézier曲线与B样条曲线的研究[D]. 长沙: 中南大学, 2013 |
| [16] | 吴海辉, 樊庆林, 王虎, 等. TrueType字体技术的研究分析与应用. 电脑知识与技术(学术交流) , 2007, 1 (3) : 783–784, 794. |
| [17] | 管涛, 李玲玲. 高斯混合模型、求解算法及视觉应用综述. 中国图象图形学报 , 2012, 17 (12) : 1461–1471. |
| [18] | 赵玲丽. 基于高斯混合模型的语音转换技术研究[D]. 南京: 南京邮电大学, 2011 |
| [19] | Tsin Y, Kanade T. A correlation-based approach to robust point set registration // ECCV. Berlin: Springer, 2004: 558-569 |
| [20] | Bookstein F L, Principal W. Thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1989, 11 (6) : 567–585 DOI:10.1109/34.24792 . |
| [21] | Fornefett M, Rohr K, Stiehl H S. Elastic registration of medical images using radial basis functions with compact support // IEEE Computer Society Con-ference on Computer Vision and Pattern Recognition. Colorada, 1999: 402-407 |
| [22] | Powell M J D. Radial basis functions for multivariate interpolation: a review // Conf 1st Algorithms for Approximation (Inst Math Its Appl Conf Series). Oxford: ClarendonPress, 1987: 143-147 |
 2016, Vol. 52
2016, Vol. 52




