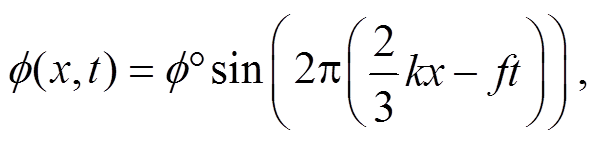 (1)
(1)
北京大学学报(自然科学版) 第60卷 第2期 2024年3月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 60, No. 2 (Mar. 2024)
doi: 10.13209/j.0479-8023.2024.014
国家重点基础研究计划(JCKY2018204B054)资助
收稿日期: 2023–02–27;
修回日期: 2023–03–24
摘要 为了克服传统螺旋桨推进航行器推进效率低、灵活性差和噪声大的缺点, 针对一种仿生柔性体推进的水下航行器的水动力特性进行数值研究, 分析柔性体波动的振幅和波数对水动力特性的影响、仿生表面对水动力性能的影响以及整体设计对水动力特性的影响。数值结果表明, 增大振幅将显著地增大静水推力, 同时增加推进阻力; 增加波数则显著地增加推进阻力, 并减小静水推力。此外, 使用仿生表面和现有的前尖端设计, 可以减小推进阻力。研究结果有利于进一步优化航行器, 提高航行器推进效率。
关键词 水下航行器; 仿生推进; 柔性体; 水动力特性
水下仿生航行器应具有低能耗、低噪声、机动灵活和推进效率高的特点, 其动力装置应可以克服传统螺旋桨推进器效率低、机动性差和噪声大的缺点[1–2]。鱼类通过流线型的身体和独特的推进模式、可以获得非凡的机动性和高效的推进效率。因此, 研究鱼类游动的推进机理并研发模仿其运动方式的水下仿生航行器一直都是研究热点[3–4]。
Webb[5]根据鱼类推进过程中摆动部位的不同, 把推进模式分为两类: 身体/尾鳍模式和中央鳍/对鳍模式。
身体/尾鳍模式是通过身体的波动和尾鳍的摆动来实现推进, 具有高效和高速推进的特点, 不足之处是灵活性较差。
Wolfgang 等[6]采用实验和数值模拟相结合的方式研究大斑马鱼推进机理, 发现大斑马鱼通过尾鳍抑制大尺度涡的产生, 从而提高推进效率和机动能力。Zhu 等[7]揭示了大斑马鱼和金枪鱼通过尾鳍提升推进效率另一种模式: 尾鳍制造同向涡, 配合鱼身制造的涡产生高推力。Singh 等[8]基于计算流体力学, 将水下航行器的仿胸鳍产生的力参数化, 结果表明远离质心的胸鳍可以为航行器提供更好的灵活性。Kern 等[9]通过三维数值模拟研究鱼体大幅摆动的水动力特性, 他们通过进化算法发现鱼身前部保持平直、尾部大幅度摆动的运动方式不仅推力大而且推进效率高。Rahman 等[10]以乌贼为研究对象, 将波动鳍简化成一对等摆幅波动的矩形鳍面, 通过计算鳍面上的压强分布, 分析鳍面尺寸、摆动频率和摆幅等参数对水动力特性的影响。
中央鳍/对鳍模式主要通过背鳍或胸鳍的柔性波动产生推力, 在这种推进方式下, 鱼类游动比较稳健, 灵活性强, 但推进效率较低。Zhang 等[11]对“蓝点魟”的波动胸鳍开展大量数值计算工作, 综合分析运动学参数、波动模式、鳍面形状和鳍条倾角对水动力特性的影响, 并从涡动力学角度揭示推力产生的机理。Hu 等[12]采用数值方法, 开展长鳍波动(背鳍/臀鳍/背腹鳍)推进鱼类的形态学、运动学和水动力学研究, 结合工程设计的需求, 进行验证性和探索性的分析工作。刘芳芳等[13]对二维柔性波动长鳍的流场进行数值计算, 结果表明在波动推进过程中, 鳍面阻力波动频率为鳍面波动频率的两倍。章永华等[14]根据鱼鳍二维波形波幅包络形式的不同, 将鱼鳍分为摆幅逐渐增大和摆幅保持不变两种情况, 并计算两种模式下雷诺数、频率、波速和平均振幅对鱼鳍水动力性能的影响, 结果表明, 随着频率、摆幅和波长的增大, 鳍产生的推力都会增加, 且在相同运动学参数下, 摆幅逐渐增大模式产生的推进力始终大于等摆幅模式。白亚强等[15]对静水中尼罗河魔鬼鱼的长背鳍波动推进过程进行数值模拟, 结果表明平均推力与波动频率的平方成正比。
综上所述, 国内外学者对鱼类推进模式进行了充分的研究, 也研制出多种仿生机器鱼[16–20]。本文设计一种新型的柔性体波动推进航行器模型, 并基于动网格方法进行三维数值模拟。首先, 我们对类鳍柔性体进行模拟, 在此基础上, 研究类鳍柔性体运动规律和仿生表面对水动力特性的影响, 并提出一种振幅衰减式波动推进方式, 从而可以减小推进阻力。
本文设计一种新型的由仿生柔性体波动推进的水下航行器(图 1), 包含两部分: 主体部件和运动部件。主体部件由 3 个柱体组成, 用于搭载电池、电机和控制系统等。运动部件由一对类似尼罗河魔鬼鱼长背鳍的柔性体组成, 长 1.5m, 宽 0.2m, 厚 0.01m, 用于航行器推进。
航行器启动时, 由与主体部件相连的 10 根连杆驱动柔性体波动来推动航行器。我们参照文献[15], 使用简谐运动定义柔性体的波动运动规律, 并对比文献中的结果来验证数值方法。
图 2 展示笛卡儿直角坐标系下的单个柔性体, x轴沿流向, y 轴沿柔性体展向, z 轴沿水深方向。柔性体运动规律以方程形式表示为
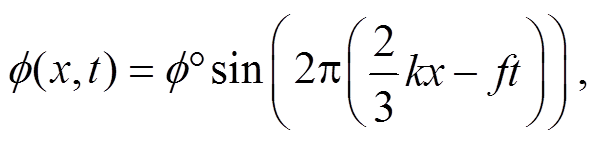 (1)
(1)
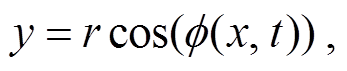 (2)
(2)
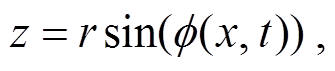 (3)
(3)
其中, 振幅f°为柔性体运动过程中与水平面的最大夹角; f(x, t)描述振幅f°沿 x方向随时间变化的规律, 表示不同位置不同时刻柔性体与水平面的夹角; f是波动频率; k是柔性体沿 x方向的波数; r 是柔性体的波动半径, 取值为 0~0.2m。本文考虑 3 种振幅f°= 15°, 30°, 40°, 5 种波动频率f=1, 2, 3, 4, 5Hz, 3 种波数 k=1, 2, 4。
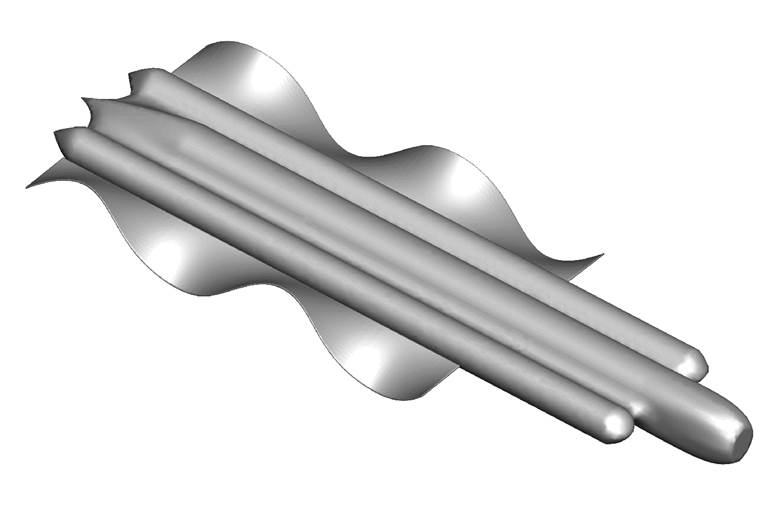
图1 水下航行器三维几何模型
Fig. 1 Schematic diagram of the undersea bionic vehicle
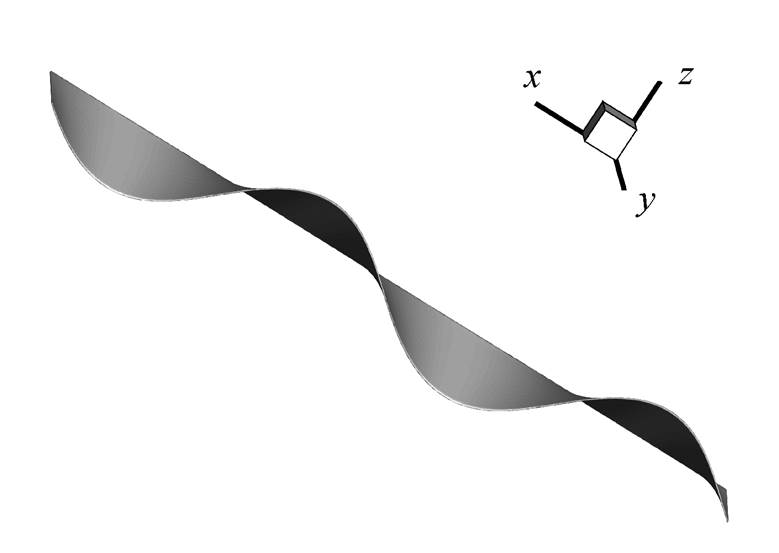
图2 柔性体三维几何模型
Fig. 2 Schematic diagram of the flexible body on both sides of the undersea vehicle
本文中数值计算的控制方程为三维不可压缩黏性流体的 RANS 方程:
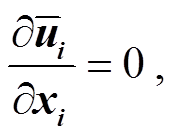 (4)
(4)
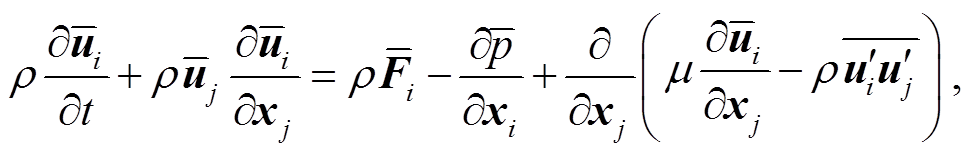 (5)
(5)
其中,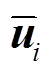 与
与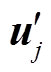 分别为时均速度与脉动速度, ρ 为流体密度, μ 为动力黏度,
分别为时均速度与脉动速度, ρ 为流体密度, μ 为动力黏度,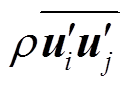 为雷诺应力项。
为雷诺应力项。
湍流模型使用标准的 k−ε两方程模型, 湍动能k 与耗散率 ε 对应的输运方程为
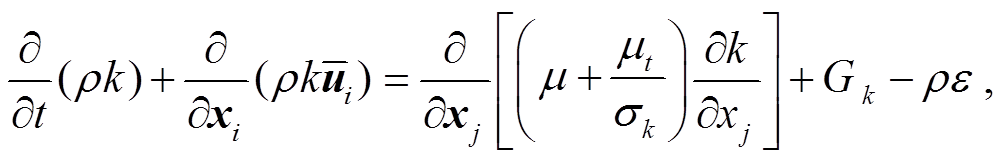 (6)
(6)
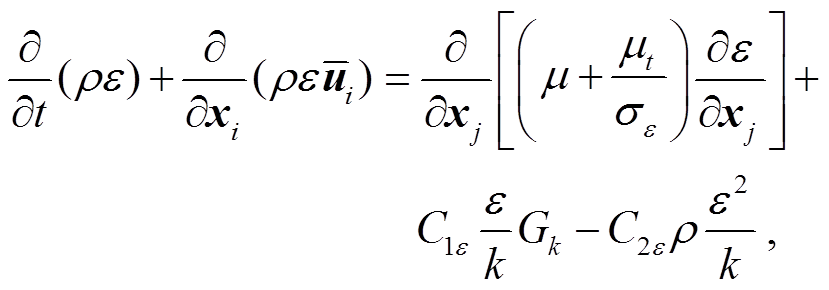 (7)
(7)
其中湍流黏度方程为
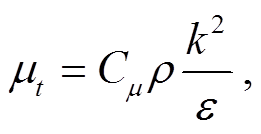 (8)
(8)
Gk 是由平均速度梯度引起的湍动能k的产生项, Cμ, C1ε 和 C2ε 为经验常数, σk 和 σε 分别是与湍动能和耗散率对应的 Prandtl 数。在实际计算中, 这些系数常取值为C1ε=1.44, C2ε=1.92, Cμ=0.09, σk=1.0, σε=1.3。
本文基于 ANSYS Fluent 求解 RANS 方程, 使用标准的 k−ε 湍流模型, 方程离散采用有限体积法, 压强–速度耦合使用 SIMPLE 算法, 时间离散采用一阶隐式格式, 其他采用二阶格式, 收敛残差设为1×10–5。时间步长为 0.02s, 每个时间步最大迭代次数为 20 次, 时间步数取 1000 步。
本文进行两类数值计算。
1)对不同运动规律柔性体的数值模拟。由于有静水和动水两种工况, 因此分别使用来流 0 和 10节(1 节=1.852km/h)两个速度条件描述入口。柔性体表面分别使用滑移壁面和无滑移壁面两种边界条件(对应是否使用仿生表面减阻)。靠近航行器的流场侧面使用无滑移壁面条件, 其余外流场侧面使用对称条件。出口使用压力出口条件, 参考压强为一个大气压。
2)对航行器整机的数值模拟。由于有进车和倒车两种工况, 所以都使用来流 10 节速度条件描述入口, 通过改变入口和出口位置, 实现进车和倒车工况的切换。柔性体表面和主体表面均使用无滑移壁面, 外流场侧面使用对称条件。
根据文献[15]的计算结果, 柔性体波动产生的平均推力与波动频率的平方成正比。因此, 我们选取波动频率 f=1, 2, 3, 4, 5 Hz, 在静水工况下对柔性体波动推进进行数值模拟, 并统计柔性体的平均推力, 验证数值方法的正确性。
图 3 展示不同运动规律的柔性体的静水推力随波动频率的变化情况, 由于工况较多, 我们只选择3 种运动规律(振幅f°=15°, 波数 k=1; 振幅f°=30°, 波数 k=2; 振幅f°=40°, 波数 k=4)的柔性体。从图 3 看出, 无论柔性体按哪种规律运动, 静水推力 T与波动频率 f 的平方均呈线性关系, 由此验证了文献[15]的结论以及本文所用数值方法的正确性。
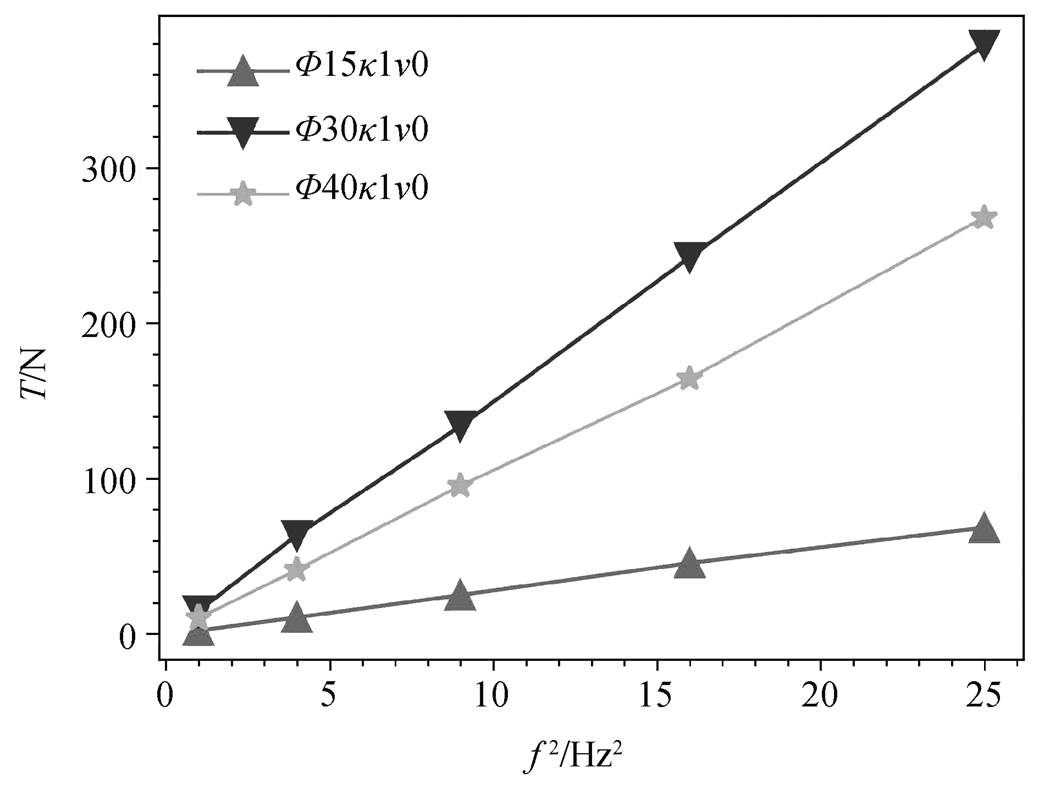
图3 静水推力 T与波动频率 f的关系
Fig. 3 Hydrostatic thrust force with respect to wave frequency
由于机械设备的限制, 柔性体很难高频波动推进, 因此计算中将波动频率 f 设置为 1Hz。
柔性体在静水中运动时, 其表面 x 方向的合力是柔性体产生的静水推力 T。在动水中运动时, 其表面 x 方向的合力减去柔性体静水推力可以反映柔性体推进阻力的大小。
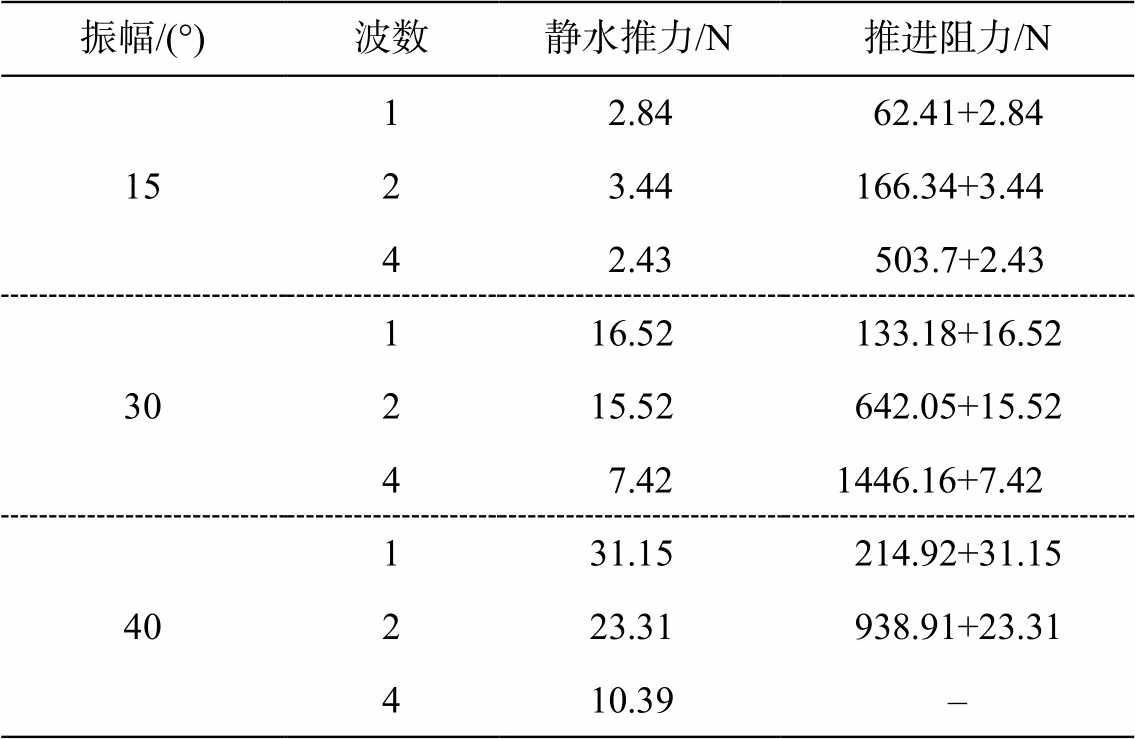
表 1 展示纯推力和推进阻力随振幅和波数的变化情况, 可以发现两点规律: 1)增加振幅, 静水推力显著增加, 同时增加推进阻力; 2)增加波数, 推进阻力显著增加, 同时减小静水推力。
图 4 为不同运动规律的柔性体在静水条件下y=0.15m 截面处的压强云图。可以看出, 增加振幅将显著增加压差, 在静水条件下表现为静水推力增加; 增加波数会将集中的正压和负压均匀地分布于多个波峰和波谷之间, 导致静水推力减小, 另一方面, 更均匀的受力有助于提高航行器的稳定性。
图 5 为不同运动规律的柔性体在动水条件下y=0.15m 截面处压强云图。通过对比各子图的压力分布, 我们发现与在静水条件下不同, 增加波数没有将集中的正负压均匀地分布为更小的正负压, 反而导致均匀分布的更大的正负压, 表现为增加波数导致推进阻力急剧增加。增加振幅同样导致更大的压差, 但在动水条件表现为推进阻力增加。
在动水条件下, 增加柔性体波数导致均匀分布在波峰波谷间的大压差, 从而导致推进阻力的急剧增加。因此, 我们在 x 方向引入振幅衰减函数, 改变柔性体运动规律, 以便缓解这一问题。
表1 不同运动规律的柔性体静水推力和推进阻力的统计
Table 1 Hydrostatic thrust forces and propulsion resistance forces of flexible body with different motions
振幅/(°)波数静水推力/N推进阻力/N 1512.8462.41+2.84 23.44166.34+3.44 42.43 503.7+2.43 30116.52133.18+16.52 215.52642.05+15.52 47.421446.16+7.42 40131.15214.92+31.15 223.31938.91+23.31 410.39–
图 6 为动水条件下振幅随 x 衰减的柔性体 y= 0.15m 截面处压强云图。可以看出, 由于振幅随x 衰减, 原本分布在各波峰波谷的正负压差变小了。通过统计其推进阻力, 得到其值分别为 213.38N (振幅不衰减时为 1070.67N)和 275.19N (振幅不衰减时为 1446.16N), 是振幅不衰减柔性体推进阻力的20%左右。同时, 推进阻力也小于振幅f°=15°波数k=3 时柔性体的推进阻力。因此, 引入振幅衰减机制有利于减小柔性体的推进阻力。
仿生表面减阻是众多减阻方法中非常有前景的减阻方式, 如使用特氟龙材料包裹航行器。我们将航行器壁面设置为滑移壁面, 模拟使用特氟龙等减阻材料包裹航行器的情形。设置方法分为两步: 1)通过无滑移壁面计算, 得到壁面的平均剪切应力 τ; 2)在 fluent 中选择壁面类型为 specified shear, 将剪切应力沿流向的分量设置为 0.95τx。不同运动规律的柔性体在不同壁面条件下的推进阻力如表2 所示, 可以看出, 使用仿生表面是一种可行的办法, 可以减小约 2%~3%的阻力。
图 7 为柔性体做振幅f°=30°, 波数 k=2 运动, 航行器分别以 10 节航速进车和倒车时, 四周的压力分布云图。
当航行器进车时, 前尖端有效地降低航行器前端高压区的压力, 并在尾端形成较大面积的局部高压, 减小航行器前后压差, 从而降低航行器的推进阻力。同时, 前尖端的存在可以有效地降低柔性体前缘高压区的压力, 从而降低柔性体受到的阻力。相反, 当航行器倒车时, 由于尾端缺少类似前尖端的结构, 在尾端形成大面积的高压区, 而在航行器前端形成的高压区面积小, 导致航行器受到很大的倒车阻力。航行器进车时, 所受推进阻力约为 1751N, 倒车时所受推进阻力约为 2998N。因此, 当前设计牺牲了航行器的倒车性能来降低进车时的推进阻力, 前尖端的设计可以有效地降低航行器所受的推进阻力, 也说明当前设计仍有优化的余地, 例如, 可以通过流线型设计来减小两侧柱体前端形成的局部高压。
表2 不同运动规律的柔性体在不同壁面条件下的推进阻力统计
Table 2 Propulsion resistance forces of flexible body with different motions under the condition of slip wall and nonslip wall
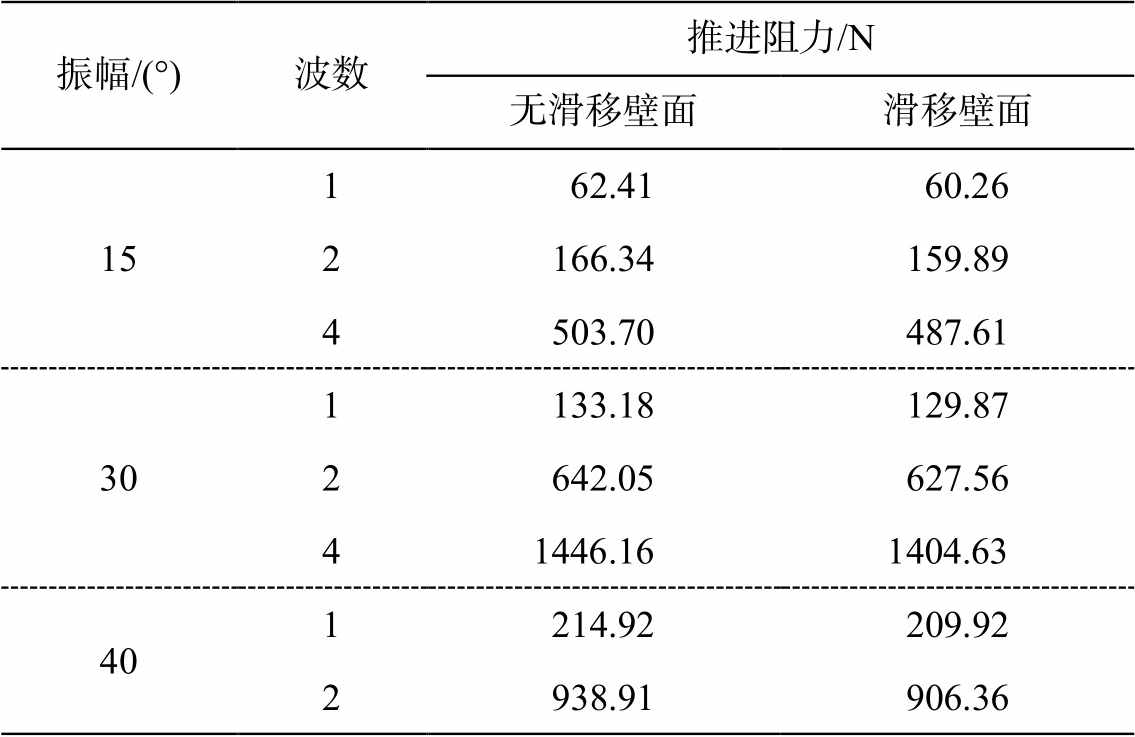
振幅/(°)波数推进阻力/N无滑移壁面滑移壁面 15162.4160.26 2166.34159.89 4503.70487.61 301133.18129.87 2642.05627.56 41446.161404.63 401214.92209.92 2938.91906.36
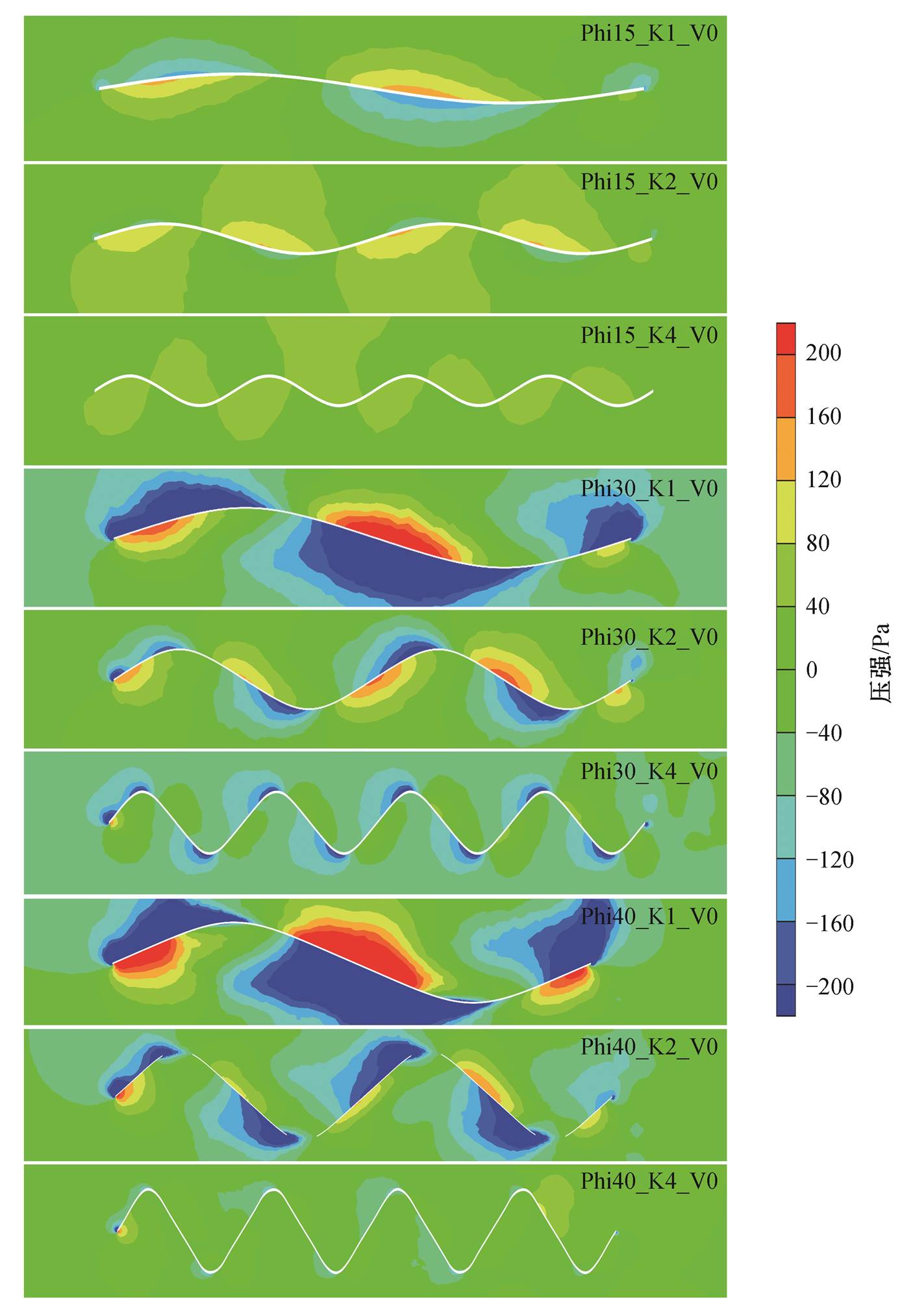
图4 不同运动规律的柔性体在静水条件下y=0.15 m截面处压强云图
Fig. 4 Pressure contours of flexible bodies with different motions aty=0.15 m section under hydrostatic conditions
本文采用数值计算的方式, 对自行设计的水下仿生航行器水动力特性进行研究, 分析柔性体运动规律对静水推力和推进阻力的影响, 并给出解释。我们发现, 增加柔性体波数, 推进阻力会增大, 静水推力会减小。这是因为静水条件下, 增加波数会使得集中的大压差变成分布在各波峰波谷周围的小压差, 从而导致静水推力减小。在动水条件下, 集中的大压差会变成分布在各波峰波谷周围的大压差, 导致推进阻力增大。增加振幅, 会使得压差增大, 因此表现为增加静水推力, 但也增加推进阻力。我们设计了一种振幅衰减的运动方式, 可以有效地降低航行器推进阻力。相较于波数为 1 的运动方式, 这种振幅衰减的运动方式产生的升力分布更均匀, 有利于提升航行器稳定性。受限于计算条件和实验条件, 本文未对新运动方式对稳定性的影响进行定量分析。此外, 我们通过对航行器的水动力特性的分析, 发现当前航行器设计虽然可以降低推进阻力, 但牺牲了航行器的倒车性能。将来的研究工作将围绕优化航行器主体设计来降低航行器的推进阻力以及优化振幅衰减式运动方式来提升航行器的稳定性展开。
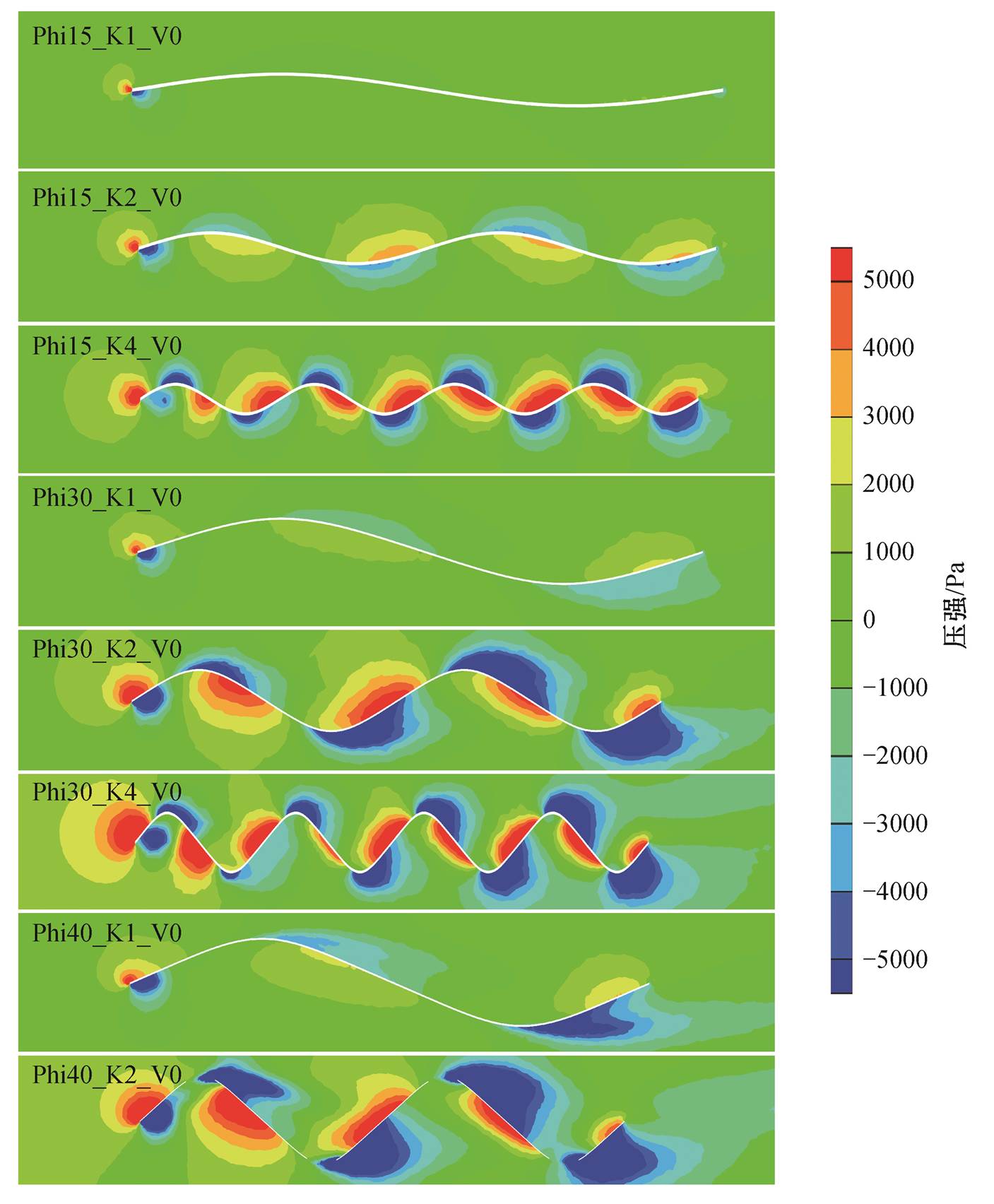
图5 不同运动规律的柔性体在自由来流速度10节条件下y=0.15 m截面处压强云图
Fig. 5 Pressure contours of flexible bodies with different motions at y=0.15 m section under the condition of flow velocity 10 knots
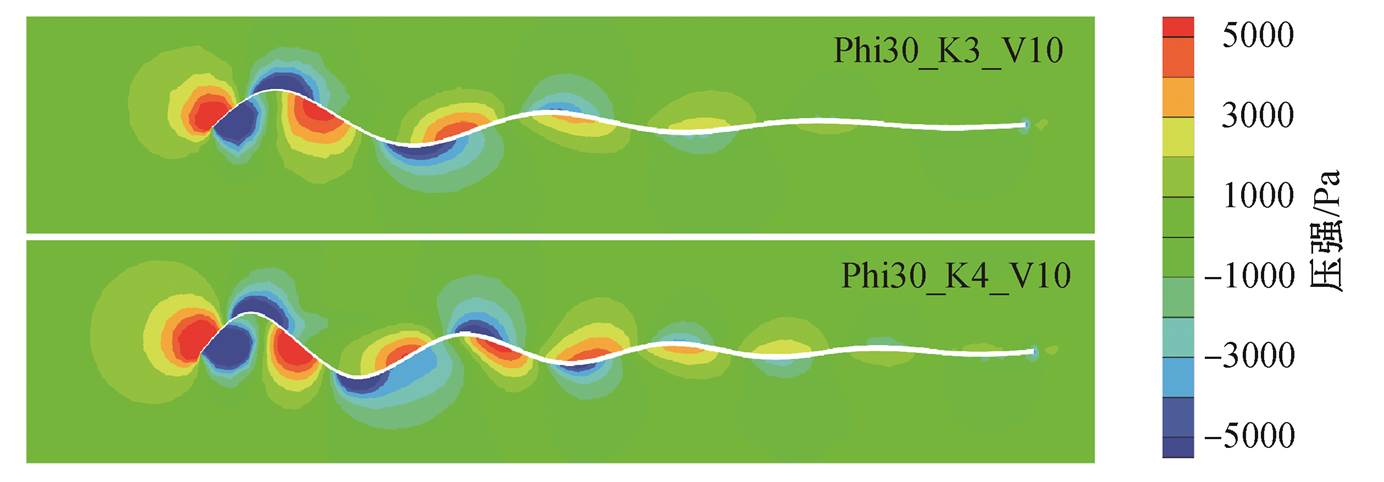
图6 振幅随x衰减的柔性体在来流10节条件下y=0.15 m截面处压强云图
Fig. 6 Pressure contours of flexible bodies with decaying f° at y=0.15 m section under the condition of flow velocity 10 knots
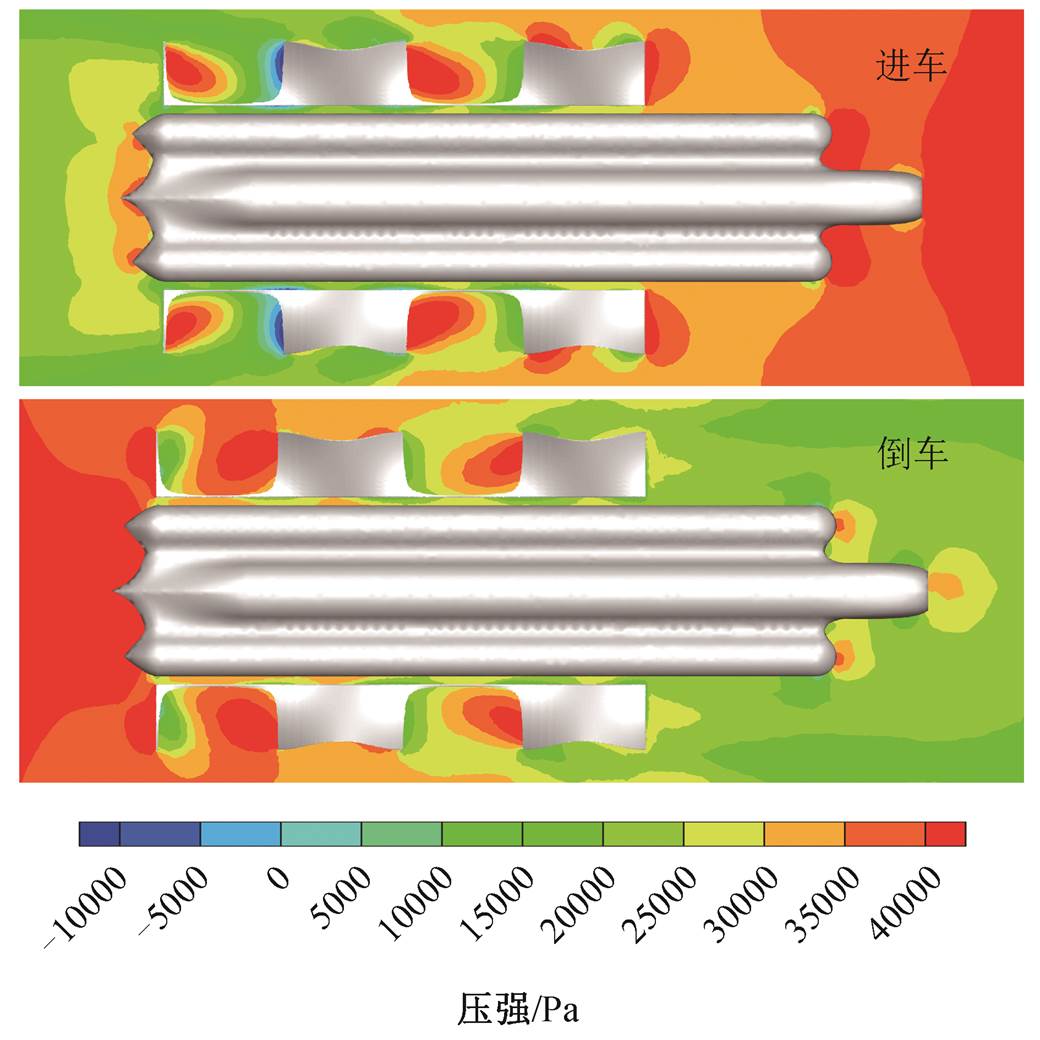
图7 进车和倒车工况下航行器周围压强云图
Fig. 7 Pressure contours around the vehicle as it moves forward and back
参考文献
[1] 喻俊志, 谭民, 王硕, 等. 高机动仿生机器鱼设计与控制技术. 武汉: 华中科技大学出版社, 2018
[2] 沈艳, 郭兵, 章洁, 等. 仿生机器鱼原理及应用. 北京: 电子工业出版社, 2017
[3] Chen J, Yin B, Wang C, et al. Bioinspired closed-loop CPG-based control of a robot fish for obstacle avoi-dance and direction tracking . Journal of Bionics Engi-neering, 2021, 18(1): 171–183
[4] 盛兆华, 杨朔. 仿鳐鱼水下航行器动态流体仿真. 水下无人系统学报. 2021, 29(3): 308–312
[5] Webb P W. Form and function in fish swimming. Scien-tific American, 1984, 251(1): 72–83
[6] Wolfgang M J, Anderson J M, Grosenbaugh M A, et al. Near-body flow dynamics in swimming fish. Journal of Experimental Biology, 1999, 202(17): 2303–2327
[7] Zhu Q, Wolfgang M J, Yue K P, et al. Three-dimensional flow structures and vorticity control in fish-like swimming. Journal of Fluid Mechanics, 2002, 468: 1–28
[8] Singh S N, Simha A, Mittal R. Biorobotic AUV maneuvering by pectoral fins: inverse control design based on CFD parameterization. IEEE Journal of Oceanic Engineering, 2004, 29(3): 777–785
[9] Kern S, Koumoutsakos P. Simulations of optimized anguilliform swimming. Journal of Experimental Bio-logy, 2006, 209(24): 4841–4857
[10] Rahman M M, Toda Y, Miki H, et al. Computational study on a squid-like underwater robot with two undu-lating side fins. Journal of Bionic Engineering, 2011, 8(1): 25–32
[11] Zhang Y H, He J H, Yang J, et al. A computational fluid dynamics (CFD) analysis of an undulatory me-chanical fin driven by shape memory alloy. Interna-tional Journal of Automation and Computing, 2006, 3(4): 374–381
[12] Hu T J, Shen L C, Wang G M, et al. A novel CFD-based approach of biopropulsor allocation optimization for underwater robots // Proceedings of the International Conference on Mechanical Engineering and Mecha-nics. Nanjing, 2005: 331–336
[13] 刘芳芳, 杨灿军, 苏琦, 等. 仿生鱼鳍运动仿真分析及试验研究. 机械工程学报, 2010, 46(19): 24–29
[14] 章永华, 何建慧, 贾来兵. 仿生蓝点魟胸鳍在两种波动模式下推进力的比较. 机械工程学报, 2012 (18): 166–176
[15] 白亚强, 张军, 翟树成, 等. 静水中波动推进水动力的数值模拟. 船舶力学, 2016, 20(6): 647–654
[16] 吴梦妍, 张瑶. 一种仿生波动鳍装置设计与实验研究. 海洋技术学报, 2021, 40(1): 63–70
[17] 张昕辰, 杨康, 孙玉龙, 等. 一种仿生鱼深海探测机器人的机构设计. 机械, 2022, 49(4): 68–73
[18] 马楷东, 张瑞荣, 郭鑫, 等. 仿双髻鲨头部的仿生机器鱼外型设计及其流场特性. 力学学报, 2021, 53(12): 3389–3398
[19] Zhong Y, Li Z, Du R. A novel robot fish with wire-driven active body and compliant tail. IEEE/ASME transactions on mechatronics, 2017, 22(4): 1633–1643
[20] Xie F, Li Z, Ding Y, Zhong Y, Du R. An experimental study on the fish body flapping patterns by using a biomimetic robot fish. IEEE Robotics and Automation Letters, 2020, 5(1): 64–71
Numerical Investigation of Hydrodynamic Characteristic of Undersea Vehicle with Low Noise
Abstract Given that the shortcomings of low propulsion efficiency, poor flexibility, and high noise of traditional propeller propulsion vehicles, numerical investigation of hydrodynamic characteristics of a new undersea vehicle propelled by bionic flexible bodies is conducted in three aspects: 1) the effect of amplitude and wave number of flexible body motions; 2) the effect of bionic surface of the vehicle; and 3) the effect of overall design of the vehicle. The numerical results show that increasing the amplitude will significantly increase the hydrostatic thrust and the propulsion resistance, while increasing the wave number will significantly increase the propulsion resistance and decrease the hydrostatic thrust. In addition, the front tip design of the vehicle and the bionic surface of the vehicle can reduce the propulsion resistance. These findings are beneficial to further optimize the vehicle and improve the vehicle propulsion efficiency.
Key words undersea vehicle; bionic propulsion; flexible body; hydrodynamic characteristic