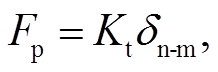(1)
北京大学学报(自然科学版) 第59卷 第6期 2023年11月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 6 (Nov. 2023)
doi: 10.13209/j.0479-8023.2023.087
国家自然科学基金(11932001)和天津市紧固连接技术企业重点实验室开放课题(TKLF2021-02-A-01)资助
收稿日期: 2022–12–02;
修回日期: 2023–02–20
摘要 针对目前有限元仿真手段在螺纹紧固件预紧过程研究中的不足, 借助 ANSYS 的 APDL, 将过盈配合法与直接扭转法相结合, 提出一种能够保证计算精度的高效预紧手段。首先通过模拟收口塑性成型过程, 获得收口加工前后的螺纹副结构有限元模型, 继而实现收口防松螺母的装配过程仿真。利用不同的预紧手段模拟装配过程, 获得螺纹副承载分布、接触应力状态和扭拉关系。通过对比未收口螺母的数值解与理论解, 验证所建模型以及仿真过程的可靠性。通过对比不同预紧手段的计算时间和数值结果, 证明联合预紧手段是可靠而有效的。
关键词 ANSYS; 预紧方法; 扭拉关系; 螺纹副受力; 收口防松螺母紧固件
螺栓连接结构是工程技术的重要基础组件, 普遍存在于火箭舱段、航空发动机等重大设备中。例如, 十二角法兰面螺母经镀银润滑、加工收口后, 大量用于发动机涡轮盘防松连接中[1]。螺栓紧固件依靠内、外螺纹形成配合关系, 再通过装配预紧过程产生轴向预紧力来实现连接及紧固作用。作为服役过程的初始状态, 预紧后对整体结构的强度、刚度、振型模态和断裂韧度等力学性能产生重要影响。预紧力过小易发生螺纹松动及疲劳断裂故障, 过大会发生螺纹咬合及过载断裂。因此, 研究螺栓连接结构预紧力及其施加手段极为重要。
早期研究的螺栓连接结构都是针对普通螺纹螺母, 以模型理论法[2–3]和光弹实验法[4]为主要研究手段, 通过对比已知预紧力作用下的螺纹副轴向承载分布来相互验证。后来有学者结合螺纹副和支承面特性, 对扭拉关系推导出理论表达式[5–6], 并进行试验研究[7–8]。但是, 可用于理论分析的物理模型十分有限, 尤其对收口防松螺母预紧扭拉关系及预紧后力学状态方面的研究, 目前几乎都是依靠试验手段[9–10], 并且试验后的收口螺母不能重复使用, 造成资源巨大浪费。
有限元软件的发展为螺纹结构的建模及分析提供了极大的便利。目前, 利用螺纹特性已经建立出轴对称二维模型[11]、三维[12]模型以及考虑螺纹升角的精细化三维[13]模型, 再通过划分网格, 即可建立有限元模型。王自勤等[14]利用 ADINA 模拟螺母收口加工过程, 基于热胀冷缩原理, 提出一种径向嵌入式的预装配仿真手段, 获得收口螺母在预紧前的力学状态。陈海平等[15]利用 ANSYS 研究螺纹副承载比, 获得良好的结果, 并分析螺纹牙型、螺距、旋合扣数和摩擦系数等因素的影响。利用 ABAQUS, Grimsmo 等[16]研究在轴向力作用下长螺栓结构发生螺齿或母体过载断裂的影响因素, 并与试验结果相互验证, Li 等[17]模拟收口加工过程, 研究收口量、材料性质以及螺纹类型等因素对锁紧性能的影响, 杨乾等[18]模拟收口螺母沿外螺纹旋入的预装配过程, 分析多种型号螺母收口量对锁紧力矩的影响。
在实际装配紧固件的过程中, 监控预紧力的主要手段包括扭矩控制法、扭矩/转角控制法和屈服点法等, 扭矩与转角是获得预紧力的主要因变量, 因此进行有限元仿真研究时也应选择合适的预紧手段。直接扭转法[19–22]可模拟真实装配过程, 能获得扭拉关系和连接刚度。预紧单元法在有限元软件中极为常见, 可直接调用便捷的的预紧力单元完成计算, 多用于研究螺纹副承载分布和接触应力分布。桂学文等[23]对比分析了这两种方法, 前者计算时间相当长, 而后者在预紧过程中未考虑切向力作用, 即无装配扭矩和转角, 且需对分离的两段螺栓分别处理。然而, 目前尚无关于收口螺母预紧过程的仿真研究。
本文以一款典型螺栓螺母紧固件[1]为研究对象, 提出一种温控预紧法作为过盈配合法的等效手段, 将拉、扭预紧方法联合仿真, 形成更有效的预紧手段。利用 ANSYS 参数化建模, 通过塑性成型并更新网格, 获得收口螺母有限元模型。利用不同的预紧手段, 计算螺纹副轴向承载分布、接触压力分布以及扭拉关系, 并验证联合预紧手段的高效性及可 靠性。
螺栓连接紧固结构是通过轴向预紧力产生作用, 因此装配预紧过程对结构后续各种工况的力学分析极为重要。在有限元计算中, 通过特殊方式施加预紧力, 现有的预紧方式如下。
直接扭转法 将螺母和螺栓头部的支承面置于刚好与被连接件接触且无挤压处(初始过盈 δ0n-m= 0), 两支承面间距为 zmm。将螺母沿外螺纹逐步旋入θn-m, 最终支承面间距变为 zmp, 产生初始预紧力Fp, 从而模拟真实预紧过程。预紧后, 被连接件压缩量–Δzmp=zmm–zmp, 螺杆伸长量 Δzbp=zmm–zmp+ δn-m, 其中 δn-m=θn-mPt/360º, Pt 为螺距。当螺杆和被连接件处于线弹性变形阶段时,
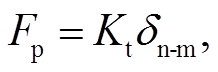(1)
其中, 总连接刚度 Kt 为常量。直接扭转法包括扭矩预紧法[19–20]和转角预紧法[21–22]两种, 前者能直接拟合出扭拉关系式, 而后者收敛更容易, 计算速度更快。由于有限元软件中的实体单元没有转角自由度, 因此通过施加轴向等效分布力、建立刚柔性约束[19]或使用 MPC 单元[20]等方式, 间接地施加扭矩或转角。然而, 扭矩预紧法和转角预紧法的计算时间都相当长, 在长期逐步加载过程中会累积计算误差, 可能导致在某个较大加载步时突然收敛困难, 使计算终止。
预紧单元法 螺杆截面法是预紧单元法的实现基础。将螺杆横向断开形成截面, 然后分别在两个截面施加轴向载荷 Fp, 也可对螺母支承面施加约束, 代替与被连接件的接触作用[15]。在有限元软件中, 在截面处直接设置预紧力单元, 简化了操作步骤。利用 ANSYS, 先将支承面置于 δ0n-m=0 处, 然后选择部分螺杆单元, 利用 PSMESH 命令建立预紧力截面, 由截面上的节点与面外控制节点自动构成PRETS179 预紧单元, 再利用 SLOAD 命令给定预紧力值进行求解, 最终支承面间距变为 zmp。预紧单元法命令流简单, 计算速度极快。然而, 螺杆在截面处被断开, 仅能承受轴向拉力作用, 难以被继续施拧, 限制了其在更复杂工况中的应用。该方法还无法得到 Δzbp, 因此主要用于研究预紧后的螺纹副应力状态。
过盈配合法 在初始建模时, 将任意支承面嵌入被连接件(δ0n-m>0), 产生过盈接触量 δon-m, 再通过软件自动收敛计算接触非线性平衡, 使螺栓拉伸 Δzbp, 被连接件压缩–Δzmp, 最终支承面间距变为zmp。该方法不能给出扭拉关系, 计算得出的预紧力与实际情况相差略大, 且若过盈量较大或支承面形貌复杂, 导致计算收敛困难。
等效外载法 将被连接件中的一个固定, 对另一个施加轴向载荷, 使螺栓中产生轴向拉力[16]。然而, 该方法改变了被连接结构, 无法得到 Δzmp, 也主要用于研究螺纹副应力状态。
模拟降温法 通过降温使螺杆收缩 δn-m, 其与温度变化 ΔT 的关系为
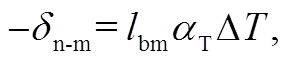(2)
其中, lbm 为螺孔总深度,αT 为螺栓材料热膨胀系数。结合式(1)和(2), 得到预紧力计算式为
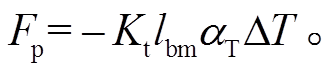(3)
降温属于人为附加的工况, 不能用于指导实际装配过程。此外, 螺杆中有热应力, 会对继续求解热力耦合问题带来影响。
对于过盈配合法, 可基于模拟降温法原理进行等效, 形成一种温控预紧法, 用于弥补原方法在旋入量极大或者接触面形貌复杂情况时的不足。首先将螺母置于出现过盈量 δn-m 处, 再利用式(2)升温ΔT0, 将螺杆沿轴向伸长, 使螺母支承面与被连接件分离, 继而逐渐降温–ΔT0 来抵消热应力。后续载荷步中求解热应力问题时, 只需重新定义材料热参数即可。
温控预紧法计算时间更长, 但其他方面与过盈配合法一致, 均避免了预紧单元法和模拟降温法的不足, 可以用来研究弯扭复杂工况及热应力问题。
表 1 给出几种仿真预紧方法的适用性。其中, 预紧方式可分为两类: 一类是通过施加环向扭转载荷的旋入式纯扭转预紧(直接扭转法 A 和 B), 计算得出全部预紧结果, 但计算量极大; 另一类是通过施加轴向载荷的嵌入式纯拉压预紧(方法 C～G), 均未考虑扭转变形, 无法获得扭拉关系。
表1 不同预紧方法的适用性
Table 1 Applicability of different pre-tighting methods
适用性ABCDEFG 预紧力(螺纹承载)√√√√√√√ 扭矩(扭拉关系)√√××××× 杆伸长量√√×√√√× 被连接件压缩量√√√√√×√ 预紧转角√√×√√×× 是否未改变结构√√×√√×× 后续可否施拧√√×√√×√
说明: A～G 依次表示扭矩预紧法、转角预紧法、预紧单元法、过盈配合法、温控预紧法、等效外载法和模拟降温法。
本文在直接扭转法 A 或 B 的基础上, 使用嵌入式预紧 D 或 E 代替一段前期旋入过程, 即拉–扭联合, 形成一种既高效又比较符合真实过程的仿真预紧手段。首先将螺母置于初始过盈 δ0n-m(或初始转角 θ0n-m)处, 计算初步预紧结果。利用 APDL 更新有限元模型, 以此为初始构型和预应力, 继续对螺母施加所需要的扭矩或微量转角达到目标过盈量 δn-m, 从而获得目标预紧状态的有限元计算结果。如果施加扭矩后螺母未发生明显转动, 说明 δ0n-m 设置过大, 需适当减小。
对于方法 A 和 B, δ0n-m=0; 对于方法 D 和 E, δ0n-m=δn-m。本文将“过盈–扭矩”联合预紧手段称为 D +A, 其余联合手段依此类推。
图 1 为由十二角法兰面螺母与普通螺栓组成的紧固件结构, 内外螺纹均为 MJ14×1.5, 被连接件为两个相同的带孔圆盘, 通过 APDL 建立几何模型, 并划分网格。螺母三段半径最大处分别为 8.5, 9.82和 11.5mm, 对应高度为 7.0, 8.5 和 2mm。螺杆直径为 14mm, 高度为 11mm, 螺杆紧邻高度为 3mm 的圆台。圆盘的高度为 7.5mm, 外径为 35.5mm, 孔径为 14.2mm。螺栓和螺母使用不同的高温合金材料。内螺纹表面镀银润滑, 螺纹副的摩擦系数设为 0.15, 两个支承面的摩擦系数均为 0.3。
在整体网格划分过程中, 首先精准地控制主要线的网格, 再使用三维实体单元, 对规则圆筒和柱体采用映射网格划分, 对其余不规则体采用自由网格划分(图 1)。在螺纹副、两圆盘之间、螺母支承面与下圆盘以及螺栓头部支承面与上圆盘这 4 组接触面上设置接触单元和目标单元。
图1 十二角法兰面螺母紧固件结构
Fig. 1 Fastener structure with the 12-point flange nut
基于图 1 紧固件有限元模型, 在螺母自由端两侧使用圆弧凹面模具, 模拟两点式收口塑性成型过程[14]。图 2 为卸载回弹后收口螺母的径向位移云图, 自由面收口呈近椭圆状, 收口量约为 0.301mm。继而利用热预装配方式[14], 获得预紧过程的初始有限元构型和预应力, 图 3 为此时紧固件应力云图。
对于表 1 中扭拉关系和螺纹承载等预紧问题,在一些特定约束的规则结构中, 可用理论模型进行计算, 从而对比验证有限元模型与仿真预紧过程的可靠性。
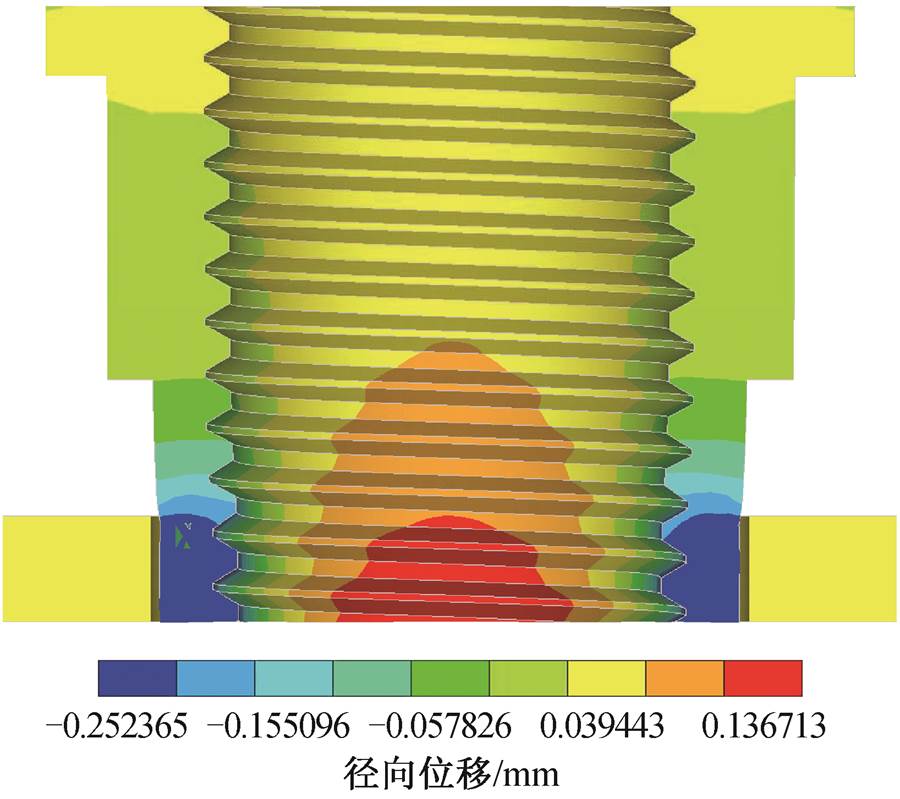
图2 卸载回弹后螺母径向位移云图
Fig. 2 Radial displacement nephogram of the nut after unloading and rebounding
图3 热预装配后紧固件Mises应力云图
Fig. 3 Mises stress nephogram of the fastener after hot-preassembling
Motosh[5]给出拧紧扭拉关系式:
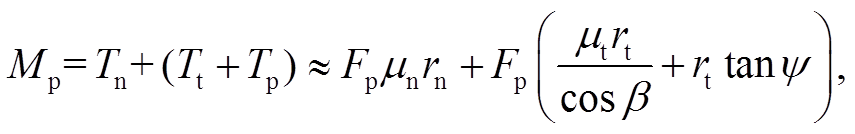(4)
式中, Tn表示克服支承面摩擦作用的扭矩, Tt表示克服螺纹副摩擦作用的扭矩, Tp 表示紧固件发生扭转弹性变形而形成预紧力的扭矩, β 为牙型半角, ψ 为螺纹升角, μn 和 μt 分别为螺母支承面与螺纹副的摩擦系数, 螺纹副有效接触半径 rt=0.5d2, dn, dh和d2 分别为螺母支承面外径、螺孔直径和螺纹中径。假设支承面的压力呈均匀分布, 则有效接触半径
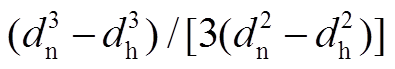。Nassar 等[6]基于螺纹升角的平衡关系, 提出一种更精确的形式:
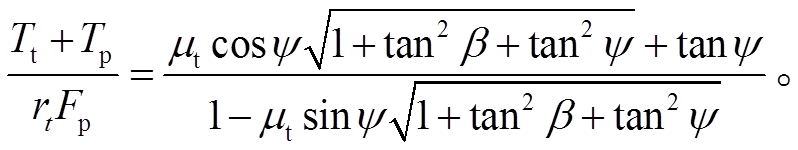(5)
当sinψ ≈ tanψ ≈ ψ (即 ψ 很小)时, 式(5)可以转化为式(4)。
在 Izumi 等[24]的研究中, 模拟真实工况对螺母外壁施拧, Mp/Fp 有限元数值结果比理论解明显偏小。然而, 在邓新建等[20]的研究中, 将螺栓头部和被连接件接触面全约束, 将 MPC 单元设置为支承面全部节点的耦合连接, 获得的多数有限元结果与理论解高度吻合, 但是当螺纹副摩擦系数增大至0.3 时, 会明显偏大。产生这种差别的原因是真实情况的支承面上压力分布与有效接触半径不同。
对于图 1 所示的 MJ14×1.5 螺纹紧固件, 将螺母外壁改为直径 17mm 的直圆筒外壁, 其他参数与网格保持不变, 由式(4)和(5)分别得到 Mp/Fp 的理论值为 3.7134 和 3.7220mm。使用文献[20]中的约束和耦合节点集, 利用扭矩预紧法 A 预紧仿真, 选取 Mp为 3×103, 1.8×104 和 3×104N·mm 对应的 3 个散点, 计算得到 Mp/Fp 分别为 3.7205, 3.7176 和 3.7314 mm。经过与理论解对比, 说明本文利用扭矩预紧法获得的结果是可靠的, 进而证明了本文建立的结构有限元模型的可靠性。
Sopwith[2]结合螺杆变形和螺齿变形几何协调条件, 解析推导出在轴向任意 s 处螺杆横截面的轴向合力为
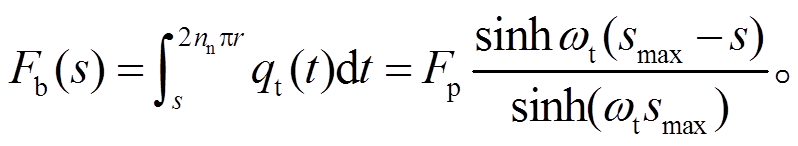(6)
山本晃[3]给出另一种形式:
(7)
两种理论解均可作为参考解[15,22]。
在模拟真实工况时, 文献[24]中螺纹副轴向承载分布有限元结果与理论解相差较大, 而在文献[23]中还出现第一扣螺纹承载比例少于第二扣的现象。这是因为理论模型假设各扣螺纹的啮合状态相同, 而真实情况的螺母支承面有径向位移, 使第一扣起始段接触不完全, 只有部分面有接触压力。因而, 需要研究螺母径向约束状态对承载分布趋势的影响。
同样地, 将图 1 模型的螺母外壁也改为直径 17mm, 计算得到 ωt=4.40。利用预紧单元法施加 Fp =24600N, 从支承面开始计扣数, 第 12 扣仅有 2/3圈。表 2 列出螺纹副的轴向承载比, 表中工况 2 与文献[15]中对二维轴对称模型施加的约束一致。可以发现, 与理论解相比, 工况 1 的第一扣偏小而最后一扣偏大, 与文献[24]中规律相同。工况 2 和 3 均与理论解相当吻合, 说明本文利用预紧单元法获得结果是可靠的, 同时验证了在理论分析中假设的各扣螺纹始终保持啮合。
表2 螺母轴向承载比例
Table 2 Proprtion of axial load distribution of the nut
扣数轴向承载比/% 工况1工况2工况3Sopwith解[2] 123.2035.4832.6531.42 220.7623.7621.8321.56 315.5214.0714.4514.79 411.428.469.7510.16 58.325.376.586.99 66.043.704.504.82 74.402.643.143.34 83.221.952.242.34 92.391.491.671.68 101.851.191.321.26 111.661.091.141.02 121.210.780.730.63
说明: 工况 1～3 分别对应螺母中无约束(真实情况)、支承面径向约束以及所有节点径向约束。
针对图 1 和 3 对应的螺母收口前后的紧固件有限元模型, 利用多种预紧手段, 对螺母旋入或嵌入的预紧过程进行仿真, 得到表 1 中预紧力等参量的数值结果, 进而对比拉扭联合预紧的优势。
首先考虑图 1 对应的普通螺母紧固件模型。利用方法 A, 对螺母十二角部位分别用单个载荷步施加 105和 4×105N·mm 扭矩, 计算得到预紧转角、预紧力和圆盘压缩量最大值, 结果如表 3 所示。以其中部分结果作为其他方法的加载条件, 所得结果也列在表 3 中。其中, D1 和 D3～D6 对应的初始转角θ0n-m 分别为5º, 11.38º, 15º, 35º 和 40º, D2 和 E2 均对应 10º。使用相同的计算环境, 且在关键载荷步中设置相同求解子步控制(NSUBST, 1, 10000, 1)。利用/OUTPUT 命令, 记录预紧过程每步仿真在求解器中的起止时刻, 计算得到的总时长 tc 见表 3。
从表 3 可以看出, 扭矩预紧法 A 所需时间最长, 预紧单元法 C 最短, 拉扭联合手段的耗时介于参与方法各自单独计算的耗时之间。在同一转角处, 扭转法 A 和 B 的结果高度吻合, 转角预紧法 B 耗时更少, 但需经过复杂的后处理才能获得扭矩值。过盈配合法 D 与温控预紧法 E 的结果也高度吻合, 均与扭转法结果偏差较大, 而过盈配合法 D 耗时更少, 应优先考虑使用。对比高、低扭矩结果可以发现, 扭转法 A 获得的预紧转角变为 4 倍, 其计算时间也为 4 倍, 而预紧单元法 C 均只需计算一个载荷步, 耗时相近。
表3 低扭矩和高扭矩时普通螺母不同预紧方法的结果
Table 3 Results of different pre-tightening methods the normal nut at lwo torque and high torque
预紧手段θn-m/(º)Fp/104N/10–2 mmtc/h 低扭矩A11.382.4601.3194.37 B{11.38}2.4611.3161.05 C—{2.46}1.2640.05 D1+A11.972.4801.3622.06 D1+B11.382.3511.2910.60 D2+A12.492.4981.4061.26 D{11.38}2.2891.3250.11 D3+A12.592.4971.4740.43 D4+A15.033.0431.7670.41 E2+A12.482.4981.4081.28 E{11.38}2.2901.3380.24 高扭矩A45.499.8775.24917.4 B{45.49}9.8795.2403.00 C—{9.877}4.6780.05 D5+A48.499.9635.4884.48 D6+A48.939.9735.6874.37 D{45.49}9.7714.6150.46
说明: { }表示作为加载条件, 下同。
对比联合法与扭矩预紧法 A 可以发现, D1+A和 D5+A 的预紧力结果 Fp 相对误差分别仅为 0.81%和 0.87%, 计算时间 tc 却分别节省 53%和 74%。随着初始转角减小, 与扭转法所得结果更接近, 但计算时间变长。此外, 由 D4+A 对应的结果可看出, 仿真施加扭矩已不足以克服摩擦阻力, 螺母无明显转动, 应减小初始过盈量 δ0n-m。
再考虑图 3 对应的收口螺母紧固件模型, 施加105N·mm 扭矩对应的载荷条件, 计算结果与耗时见表 4。可以看出, 对于收口螺母也可以观察到与表3相同的规律。另外, 在相同扭矩作用下, 收口后获得的转角和预紧力都降低, 这是由于在旋入扭矩中, 用于克服螺纹副摩擦阻力的比例增加。
考虑图 1 所示的结构, 由式(4)和(5)可分别得到 Mp/Fp的理论值为 4.209 与 4.218mm。
表4 低扭矩时收口螺母不同预紧方法的结果
Table 4 Results of different pre-tightening methods for the necking nut at low torque
预紧手段θn-m/(º)Fp/104N/10–2 mmtc/h A11.011.8441.2354.29 B{11.01}1.8431.2340.96 D{11.01}1.7801.1460.13 D1+A11.321.8481.2782.56 D2+A11.841.8671.2851.59
首先利用扭矩预紧法 A, 对十二角区域逐步施加扭矩 Mp 至 6×105N·mm, 图 4 显示预紧转角 θn-m 和预紧力 Fp 的变化情况。可以看出, 在一定范围内, θn-m 和 Fp 均随 Mp 线性递增。
根据图 4, 对于普通螺母, 选取 Mp∈[104, 3× 105]中的 8 个散点, 利用最小二乘法拟合得到扭拉关系为
(8)
决定系数 R2=0.999993。根据式(4)和(5), 标准螺纹螺母的扭拉关系式应为正比例函数, 而式(8)却出现非零常数项。其实, 如果选取不同的散点集, 拟合直线的斜率变化很小, 而常数项会在零值附近变化。选取 Mp 为 104, 105 和 3×105N·mm对应的 3 个散点, 可以计算得到 Mp/Fp 分别为 4.0723, 4.0649 和4.0745mm, 说明式(8)中常数项可以忽略。对于收口螺母, 选取 Mp∈[105, 3×105]中的 5 个散点, 拟合得到扭拉关系为
(9)
且 R2=0.999976。式(9)与文献[9]中试验结果呈线性是一致的, 式中常数项即为锁紧力矩。
从图 4 可知, 与普通螺母相比, 收口螺母在低扭矩时由于锁紧力矩的作用, 曲线出现明显的非线性变化; 在中高扭矩时, 曲线重合度很高, 说明收口对预紧转角的影响小。
此外, 式(8)中普通螺母有限元结果 4.0702mm比理论解小, 符合文献[24]得到的规律。若按照文献[20]的约束和耦合节点集计算, 在 3×103 和 3×104N·mm 散点处分别求得 Mp/Fp 为 4.304 和 4.297mm, 此结果比式(8)的结果更接近理论解。
利用本文提出的联合预紧手段 D+A, 将普通螺母或收口螺母从 θ0n-m 处开始, 逐渐施加到扭矩为105N·mm, 预紧力和预紧转角结果如图 5 所示; 将普通螺母逐渐施加到扭矩为 4×105N·mm, 预紧力结果如图 6 所示。
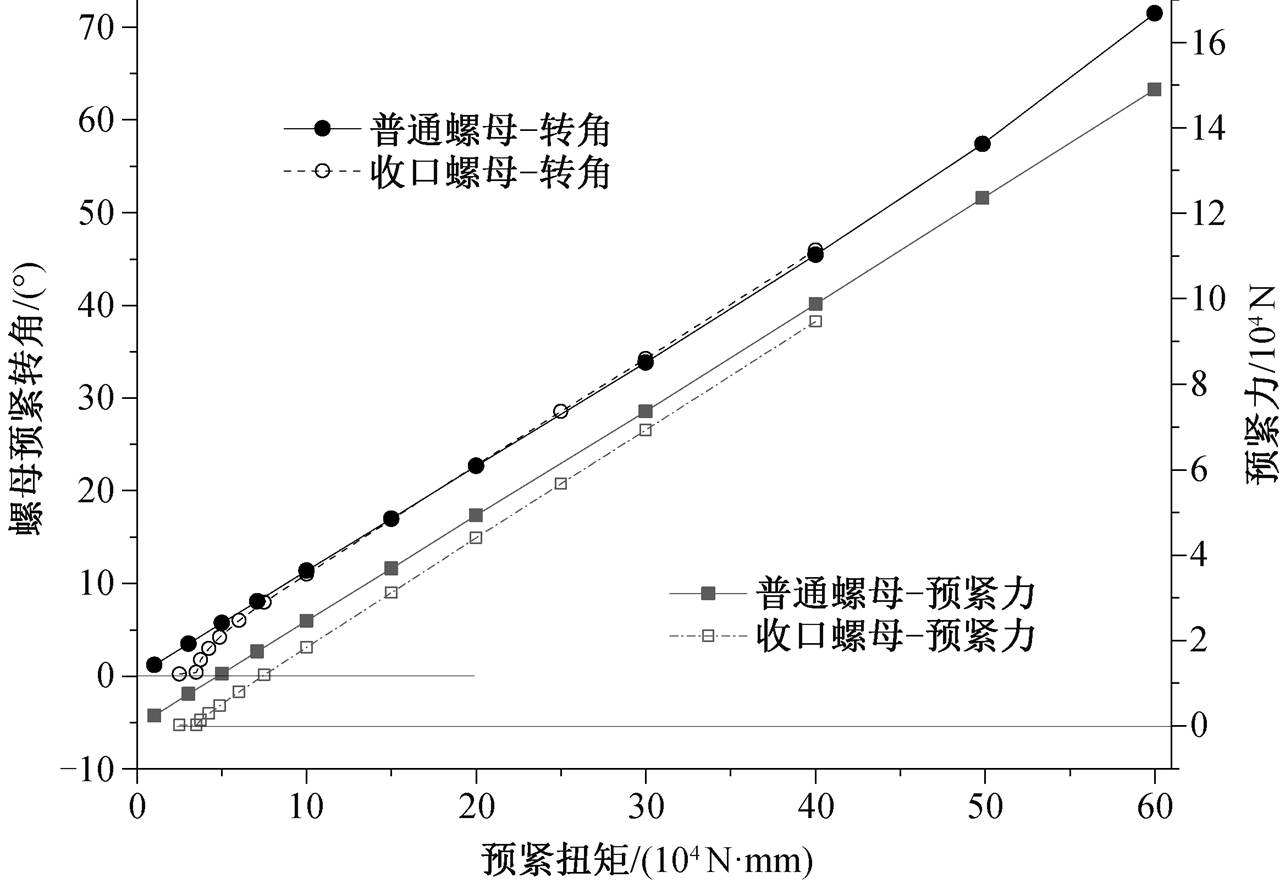
图4 预紧转角和预紧力随预紧扭矩的变化
Fig. 4 Rotation angle and preload change with the torque
根据图 5, 对于普通螺母和联合手段 D1+A, 选取 Mp∈[6×104, 105]中的 5 个散点, 对应的拟合扭拉关系为
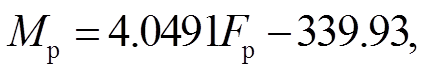(10)
且 R2=0.999991。选取区间中间的 3 个散点, 可计算得到 Mp/Fp 分别为 4.0309, 4.0341 和 4.0359mm, 说明式(10)中常数项也可以忽略。同样地, 对于联合手段 D2+A, 选取 Mp∈[9×104, 105]中的 3 个散点, 对应的拟合扭拉关系为 Mp=3.9951Fp+197.84。对于图 6 中更大初始转角对应的两条联合手段 D+ A 拟合曲线, 其直线段与扭矩预紧法 A 拟合曲线的偏离均很小。将表 3 中手段 A, D1+A 和D2+A 对应的预紧力代入式(8), 可得到扭矩为 101589, 405494和 401994N·mm, 相对于实际施加的扭矩, 误差仅为 1.6%, 0.49%和 1.4%。因此可以说明, 式(10)与(8)的计算结果基本上一致, 并且初始转角越小, 这种扭拉关系的一致性越好。
根据图 5, 对于收口螺母和联合手段 D1+A, 选取 Mp∈[6×104, 105]中的 5 个散点, 对应拟合扭拉关系为
水平线表示螺纹副尚未发生相对转动, 下同
图5 低扭矩时利用不同预紧手段的预紧力和预紧转角
Fig. 5 Results of the preload and rotation angle for low torque and different means
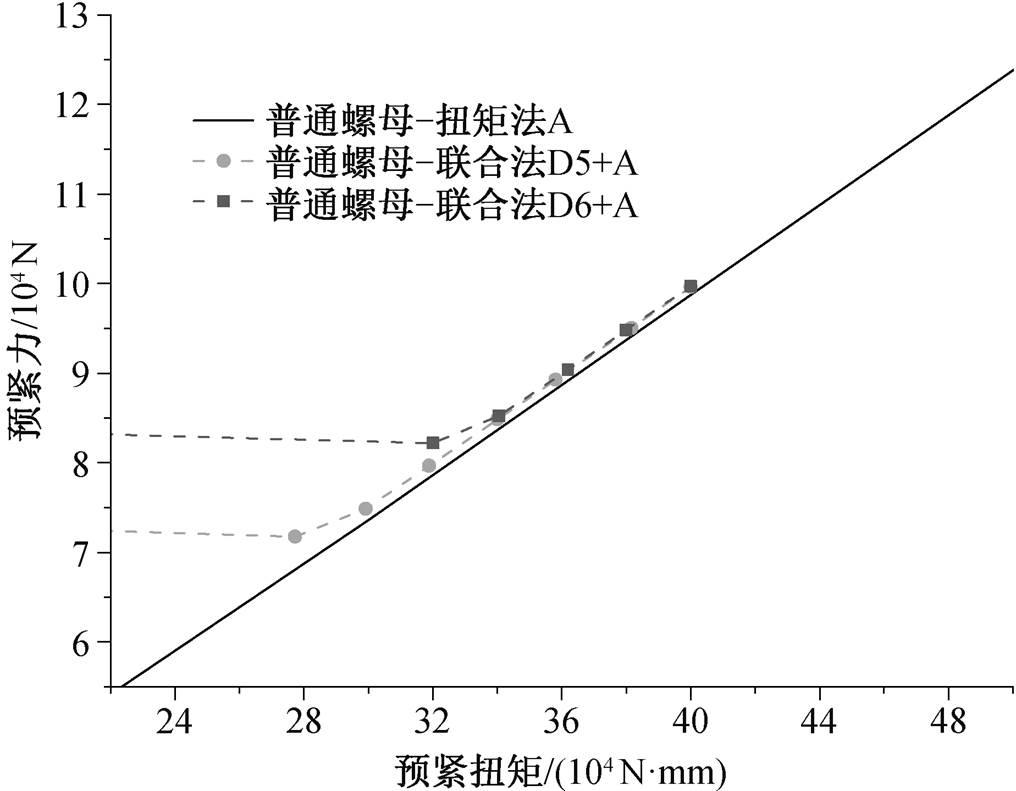
图6 高扭矩时利用不同预紧手段的预紧力结果
Fig. 6 Results of the preload for high torque and different means
(11)
且 R2=0.999991。可以发现, 式(11)与(9)的计算结果差别较大。为了分析此差别, 对于式(9), 重新选取图 4 中Mp∈[6×104, 105]中的 5 个散点, 则对应的拟合扭拉关系变为
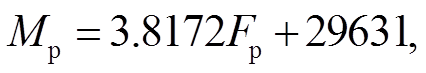(12)
且 R2=0.999953。式(12)与(9)差异明显, 说明收口螺母扭拉关系对取样范围有依赖性。出现差异的原因是, 随预紧力增加, 收口附近塑性临界区的受力状态发生非线性变化, 导致图 4 中收口螺母“预紧力–扭矩”关系直线段存在一定的非线性。式(12)与(11)的计算结果一致性却很好, 说明联合手段对收口螺母同样适用。
根据图 5, 利用 D+A 获得的预紧转角均明显大于扭矩预紧法 A 的结果, 这会影响与旋入量相关的计算结果。但是, θ0n-m 越小, 所得转角结果越接近扭矩预紧法对应的结果。
因此, 本文提出的高效联合预紧手段能够有效地获取目标预紧力, 可以通过扭矩控制法指导产品的装配预紧过程, 并且对收口螺母同样有效。
利用预紧后结果, 可用预紧单元法 C 计算得到螺纹副轴向承载分布的数值结果。下面针对十二角法兰面螺母, 使用表 2 中工况 1 分析真实情况。
利用不同的预紧手段, 对普通螺母和收口螺母分别施加表 3 和 4 中的载荷条件, 螺纹副轴向承载比分别如图 7(a)和(b)所示。可以看出, 各种预紧手段的计算结果及趋势较为吻合, 尤其 D1+A 手段与扭转法结果的吻合度十分高。将图 7(a)与表 2 中结果相比, 普通螺母前几扣的螺纹仍是主要承载处, 但第一扣螺纹承载大幅减小, 说明第一扣接触面积更少。图 7(b)中收口螺母的主要承载处已转移到收口附近, 且在收口沿轴向边缘处出现螺纹副反向挤压作用。
图 8 给出普通螺母在预紧力作用下的 Mises 应力云图。可以看出, 普通螺母的应力最大值位于内螺纹在螺母支承端最薄处, 此处在服役过程中极易发生磨损甚至断齿。由图 8(b)和(c)可知, 由 C 和 D两种嵌入预紧方式得到的螺母应力分布一致, 其中的微小差别是由预紧力略有不同(表 3)导致, 该现象与图 7(a)中方法 C 和 D 的结果高度吻合一致。
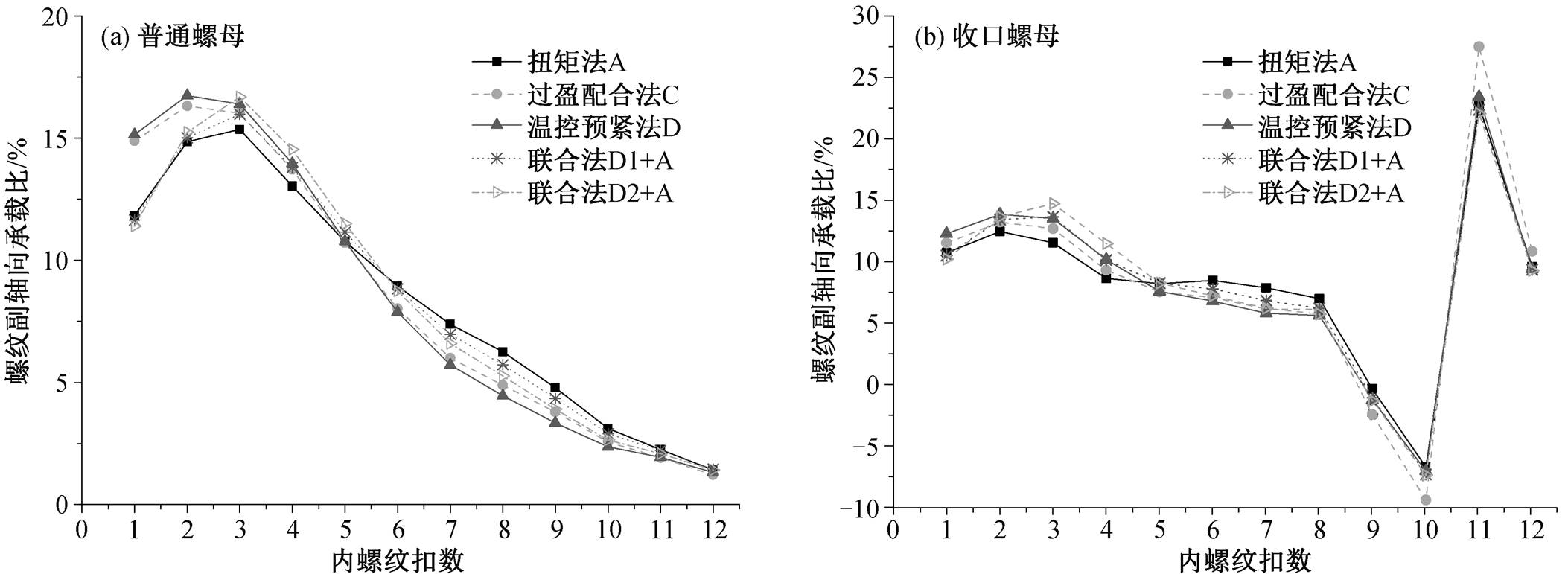
图7 普通螺母和收口螺母的轴向承载比
Fig. 7 Proprtion of axial load distribution for the normal nut and the necking nut
图 9 为对普通螺母施加 105, 4×105 以及 6×105 N·mm 扭矩后螺纹副的接触压力云图。图 9(c)中已有螺纹进入塑性变形, 与图 9(a)和(b)相比, 最大接触压力变为位于第二扣, 但主要受压区域仍是前几扣。图 10 给出施加 4×105N·mm 扭矩前后螺纹副接触压力云图。可以发现, 收口螺母的主要挤压位置已移至收口附近, 且在未预紧的旋入过程中便已出现润滑层界面失效的风险。
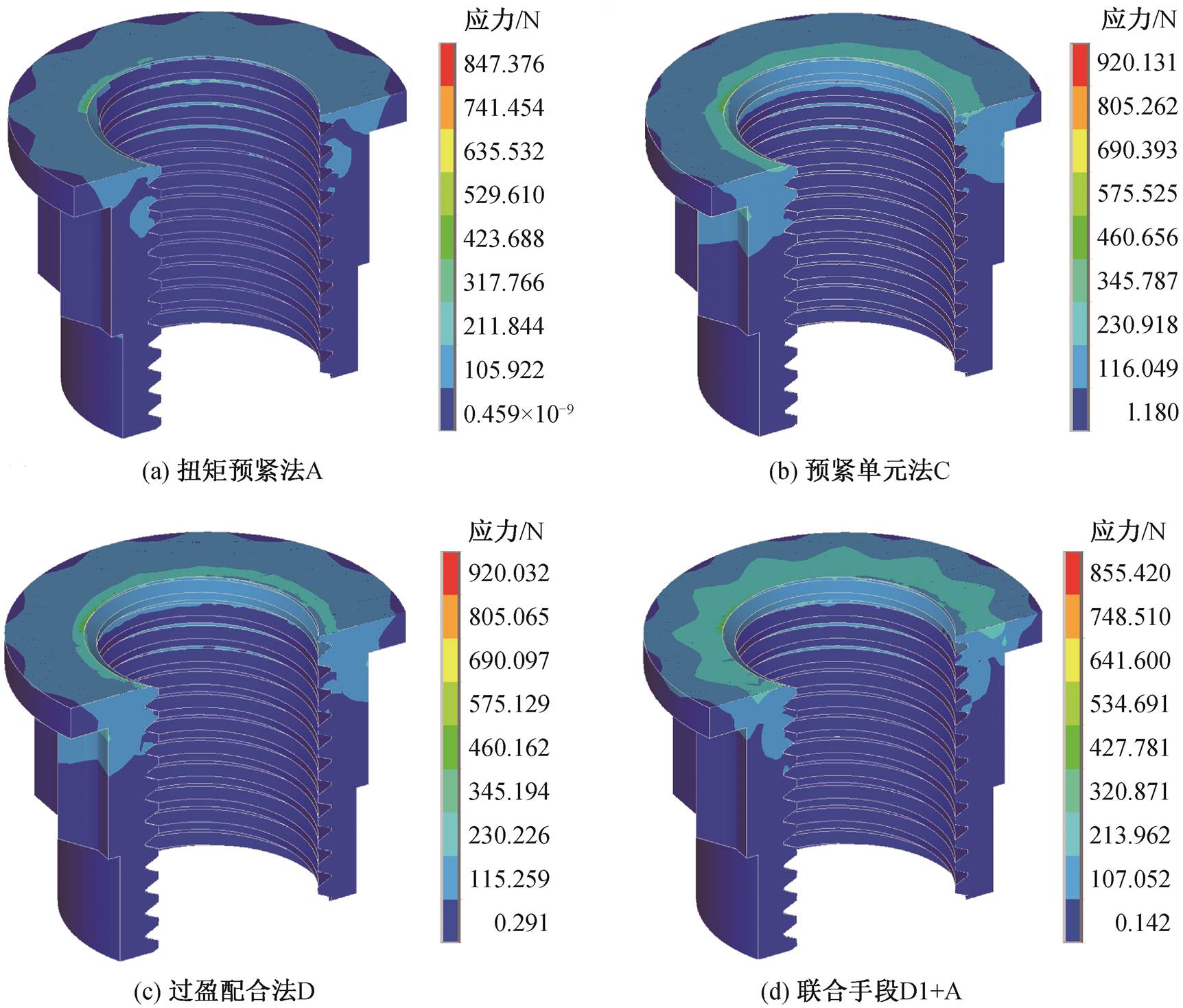
图8 预紧后螺母Mises应力云图
Fig. 8 Mises stress nephogram of the nut after pre-tightening
图9 普通螺母螺纹副接触压力云图
Fig. 9 Contact pressure nephogram of the normal nut thread pair
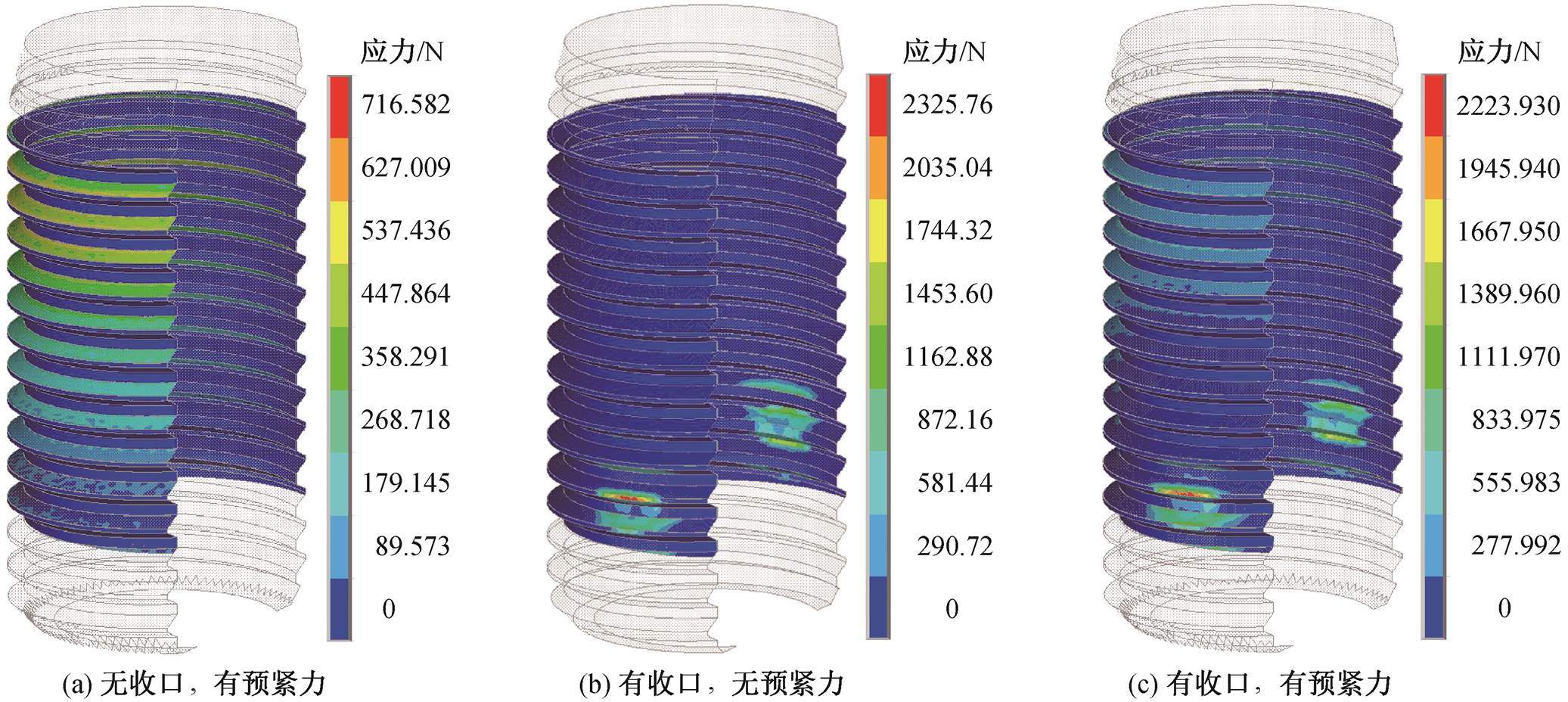
图10 不同状态组合对应螺纹副接触压力云图
Fig. 10 Contact pressure nephogram of the thread pair in different state combinations
本文提出一种高效、可靠的拉–扭联合预紧手段, 利用 ANSYS命令流操作, 实现收口加工过程及装配过程的仿真。通过对比螺纹副承载比、扭拉关系的理论解以及由不同预紧手段获得的数值结果, 得出以下结论。
1)通过构建与理论假设一致的结构、约束和耦合条件等, 获得与理论解一致的数值结果, 证明了有限元建模过程及各预紧仿真过程的可靠性。
2)扭矩预紧法耗时最长, 但能直接给出扭矩值; 预紧单元法耗时最短, 但存在截断面不能直接抗扭; 其余方法均可继续施加扭矩, 形成联合预紧手段。考虑到其中过盈配合法耗时最少, 本文利用命令流, 首次实现将过盈配合法与直接扭转法联合预紧, 获得令人满意的仿真效果。
3)通过对比本文的联合手段与扭矩预紧法可知, 普通螺母和收口螺母对应的预紧力、扭拉关系式和螺纹副轴向承载比等数值结果均高度一致, 因此本文联合手段是高效而可靠的, 可有效地指导扭矩控制法装配过程, 并能节省 50%以上的计算时间, 为研究施加拉–弯–扭、热、振动等复杂外载工况奠定基础。
4)本研究巧妙地实现了收口螺母的预紧过程仿真, 并获得与试验规律一致的线性扭拉关系式, 给出锁紧力矩。收口螺母在预紧力作用下, 前几扣的轴向承载分布比普通螺母更均匀且更小, 降低了第一扣的失效风险。在收口附近观察到反向挤压作用, 承载占比极高, 极易发生螺纹失效。
5)本文给出螺纹副接触压力和塑性应力分布的数值结果。利用这些结果, 可以协助分析镀银层的磨损、剥离或冷焊等界面的失效情况, 进而修正有限元计算模型参数, 研究收口螺母的防松性能及咬合失效分析。
参考文献
[1] 刘燕, 李文生, 修文波, 等. 基于有限元仿真方法的镀银层厚度均匀性研究. 电镀与精饰, 2021, 43 (11): 36–41
[2] Sopwith D G. The distribution of load in screw threads. Proceedings of the Institution of Mechanical Engi-neers, 1948, 159(1): 373–383
[3] 山本晃. 螺纹联接的理论与计算. 郭可谦, 高素娟, 王晓凤, 等, 译. 上海: 上海科学技术文献出版社, 1984
[4] Kenny B, Patterson A. Load and stress distribution in screw threads. Experimental Mechanics, 1985, 25(3): 208–213
[5] Motosh N. Development of design charts for bolts preloaded up to the plastic range. Journal of Enginee-ring for Industry, 1976, 98(3): 849–851
[6] Nassar S A, Yang X. Novel formulation of the tigh-tening and breakaway torque components in threaded fasteners. Journal of Pressure Vessel Technology, 2007, 129: 653–663
[7] 刘盛循, 张大平, 邓小伟, 等. 六角端面六角头螺栓扭矩系数理论计算. 大连理工大学学报, 2020, 60(3): 262–266
[8] 范俊伟, 杨璐, 班慧勇. 新型单边拧紧高强度螺栓摩擦型连接扭矩系数及抗剪性能试验研究. 工程力学, 2021, 38(1): 119–128
[9] 赵兵, 张守阳, 王辉. Inconel717螺栓与A286收口螺母配合扭拉试验研究. 实验力学, 2021, 36(5): 686–692
[10] 苗生沛, 张辉, 隋明丽. 高锁螺母力矩及预紧力测试技术研究. 航空标准化与质量, 2021(3): 20–23
[11] Tanaka M, Hongo K, Asaba E. Finite element analysis of the threaded connections subjected to external loads. Bulletin of JSME, 1982, 25: 291–298
[12] Jiang Y, Zhang M, Lee C H. A study of early stage self-loosening of bolted joints. Journal of Mechani- cal Design, 2003, 125(3): 518–526
[13] Yang G, Hong J, Zhu L, et al. Three-dimensional finite element analysis of the mechanical properties of he-lical thread connection. Chinese Journal of Mechani-cal Engineering, 2013, 26(3): 564–572
[14] 王自勤, 戴明, 解佳. 收口防松螺母有限元数值模拟//李伯虎. 全球化制造高级论坛暨 21 世纪仿真技术研讨会论文集. 贵阳: 世界图书出版社, 2004: 176–179
[15] 陈海平, 曾攀, 方刚, 等. 螺纹副承载的分布规律. 机械工程学报, 2010, 46(9): 171–178
[16] Grimsmo E L, Aalberg A, Langseth M, et al. Failure modes of bolt and nut assemblies under tensile loading. Journal of Constructional Steel Research, 2016, 126: 15–25
[17] Li M, Zhou L, Zhang M, et al. Numerical simulation of closing amount for aerial self-locking nuts with diffe-rent materials. Journal of the Institution of Engineers (India): Series C, 2021, 102(6): 1571–1579
[18] 杨乾, 张晓斌, 单垄垄, 等. 航空用镶嵌螺母收口量对锁紧力矩影响的数值仿真研究. 制造技术与机床, 2021(12): 64–68
[19] 姜凯, 郭连水. 基于有限元技术的螺纹联接扭矩系数分析与计算方法. 机械工程师, 2010(5): 62–64
[20] 邓新建, 刘检华, 张忠伟, 等. 楔形螺纹连接扭拉关系理论分析及拧紧特性. 机械工程学报, 2022, 57(19): 180–191
[21] 徐卫秀, 王淑范, 杨帆, 等. 考虑螺纹细节的螺栓预紧过程仿真分析研究. 宇航总体技术, 2018, 2(5): 50–56
[22] 颜庭梁, 李家春. 螺纹载荷分布计算方法研究及有限元分析. 机电工程, 2020, 37(5): 471–477
[23] 桂学文, 张京东, 廖日东. 螺栓预紧过程的有限元仿真研究. 强度与环境, 2021, 48(6): 9–16
[24] Izumi S, Yokoyama T, Iwasaki A, et al. Three-dimensional finite element analysis of tightening and loosening mechanism of threaded fastener. Enginee-ring Failure Analysis, 2005, 12(4): 604–615
Efficient Combined Simulation Research of Finite Element Analysis for Bolt Assembly Process
Abstract Current finite element (FE) simulating methods for pre-tightening process of thread fasteners have some shortcomings. In order to ensure the accuracy and efficiency simultaneously, the interference fit method and the direct torsion method are combined via ANSYS APDL to form a new pre-tightening means. Firstly, FE models of the thread pair structure before and after simulating the necking plastic forming process are obtained. Further assembly process simulation of the necking anti-loosening nuts is realized. Via different pre-tightening methods for simulating the assembly process, the thread pair load distribution, the contact stress state and the torsion-tension relationship can be obtained. Via comparing the numerical results of the zero closure amount nuts with some theoretical solutions, the reliabilities of the FE models and the simulation process are verified. Furthermore, the calculation time and numerical results of different pre-tightening methods are compared to prove the combined pre-tightening method is reliable and effective.
Key words ANSYS; pre-tightening method; preload-torque relationship; thread pair force; necking anti-loosening nut fastener