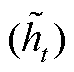 , 有利于得到时序数据中的短期依赖关系。更新门(zt)控制前一时刻的状态信息(ht−1)被带入当前状态(ht)的程度, 有助于得到时序数据中的长期依赖关系。单个门控单元的计算过程如下:
, 有利于得到时序数据中的短期依赖关系。更新门(zt)控制前一时刻的状态信息(ht−1)被带入当前状态(ht)的程度, 有助于得到时序数据中的长期依赖关系。单个门控单元的计算过程如下: 北京大学学报(自然科学版) 第59卷 第5期 2023年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 5 (Sept. 2023)
广东省重点领域研发计划(2020B1111020003)和国家自然科学基金(41976007)资助
doi: 10.13209/j.0479-8023.2023.051
收稿日期: 2022–09–23;
修回日期: 2023–04–17
摘要 为解决部分城市 PM2.5 浓度数据缺值严重, 无法通过训练自身数据得到预报模型的问题, 提出用相似城市的预报模型实现目标城市历史数据的填补。依据 23 个城市的气象数据、城市发展数据和 PM2.5 浓度数据, 建立基于自组织映射(SOM)和门控循环单元(GRU)神经网络的 PM2.5 日均浓度数据插值模型, 并分别利用该插值模型和传统插值方法(线性插值和样条插值)对不同类型的缺值数据进行填补, 对比两者的填补效果。实验结果表明, 基于 SOM 神经网络的城市匹配模型可以准确地匹配出目标城市的相似城市; 当缺值数据少于 5 天时, 利用传统插值方法的填补效果优于 GRU 插值模型; 当缺值数据多于 5 天时, GRU 插值模型更胜任长时间缺测数据的填补工作。
关键词 PM2.5; 自组织映射(SOM); 门控循环单元(GRU); 插值模型
PM2.5 是主要的大气污染物之一, 能被人体直接吸入, 危害人类健康[1–2], 还会对大气能见度和气候造成影响[3–4]。为了缓解PM2.5对城市经济、居民生活和环境质量的影响和限制, 各城市都十分重视PM2.5相关理论和防治的研究。除了解其主要来源和扩散途径, 以便安排对应治理措施外, 提前预测各区域 PM2.5 浓度变化, 做好对应的预防和示警也是工作的重点[5]。
PM2.5 浓度的时间序列易受扰动, 受气象要素(如风速和风向等)的影响大, 存在短时间内波动大的可能性。目前, PM2.5 预报方法主要有数值预报和统计预报两种[6]。数值预报主要基于大气扩散理论和物理化学过程, 不仅需要获取多种详细资料, 而且需要大型计算机的参与, 计算复杂度和消耗成本高。传统的统计预报方法通过分析空气污染资料的统计规律预报未来污染趋势, 相对快捷和简便, 但是模型中的相关因子会随着气候变迁而改变。
21 世纪, 机器学习进入成熟阶段, 很多科学家将其引入 PM2.5 预测研究中。彭斯俊等[7]根据武汉市 2013 年不同时段的 PM2.5 日平均浓度分布特征, 建立分时段自回归移动平均模型(autoregressive in-tegrated moving average model, ARIMA), 能较好地拟合 PM2.5 浓度变化趋势。杜续等[8]利用随机森林回归算法(random forest regression prediction, RFRP), 对西安市的 PM2.5 浓度数据建模, 并与 BP 神经网络(back propagation neural network, BPNN)模型对比, 实验证明 RFRP 模型不仅能保证更高的预测精度, 还能提高模型的预测效率。Li 等[9]基于北京市 12个站点的小时 PM2.5 浓度数据, 建立多种神经网络预报模型并对比预测效果, 结果显示 LSTM 模型的预测更加准确。张恒德等[10]利用 BP 神经网络对北京、天津和石家庄的 3 种模式预报资料进行集成预报, 并与单一模式预报效果对比, 发现BP神经网络集成模型对 PM2.5 的预报效果普遍优于其他 3 种单一模式。邹思琳等[11]利用多元线性回归、BP 神经网络和 LSTM 神经网络 3 种方法, 对北京 PM2.5 浓度值进行建模, 发现不论是对小时浓度数据建模还是对日均浓度数据建模, BP 和 LSTM 神经网络方法在4 种指标上的效果都优于多元线性回归模型(multi-ple linear regression, MLR)方法。Liu 等[12]选取处于不同地理和气候环境的北京、广州、长沙和苏州为研究区域, 利用一种多步预测模型对这 4 座城市的PM2.5 数据建立预报模型, 取得不错的效果。
虽然对 PM2.5 浓度的预测已经取得一些成绩, 但前人的研究大多针对某一特定的地区(如京津冀、长三角以及省会城市等数据资源丰富的地区)来优化预报算法, 忽略了因建站时间不长、设备故障和数据维护等原因而存在 PM2.5 浓度数据严重缺失的城市, 研究人员只能利用传统的插值方法填补缺测数据, 无法用神经网络进行训练和预报。基于上述情况, 本文以 PM2.5 浓度时间序列为研究对象, 提出基于混合神经网络的插值模型, 探究新型机器学习方法能否提供比传统插值方法更优质的插值方法, 以期为 PM2.5 浓度数据严重缺失城市的数据填补提供参考, 并为新型机器学习方法在气象预报领域的应用提供借鉴。
1.1.1 SOM网络
自组织特征映射(self-organizing map, SOM)网络的学习过程是无监督式自动寻找样本规律, 自组织、自适应地改变网络参数, 训练过程无需人工介入。该网络仅包含输入层和输出层, 输入向量从输入层输入, 网络将依据某种聚类法则进行竞争学习, 得出获胜神经元, 从而根据邻域半径和学习率, 自动调整权值向量, 使得权值向量更远离或更靠近输入向量, 通过不断地学习和调整, 直至所有输入样本聚集在合适位置。SOM 聚类方法已广泛应用于数据分类和数据挖掘等领域。例如, 吴聘奇等[13]利用 SOM 聚类方法对福建省 23 个城市进行职能分类, 杨黎刚等[14]结合 SOM 网络的自组织映射能力和人眼对低维模式的识别能力, 对电信客户进行细分, 取得良好的效果。SOM 算法的基本步骤如下。
1)初始化: 将权值向量 Wij 赋予区间[0, 1]内的随机值进行初始化,
Wij = (Wj1, Wj2, ... , Wjn), (1)
其中, i=1, 2, ..., N;j=1, 2, ..., M。
2)归一化: 对输入向量 Xki 和权值向量 Wij 进行归一化处理。
3)将样本输入网络: 计算输入向量与权值向量的点积 Xki·Wij, 点积值最大的输出神经元 g 赢得 竞争。
4)更新邻域半径和学习率: 领域半径 Ng(t)是以获胜神经元 g 为中心, 包含其他若干神经元的区域范围, 由迭代次数 t 决定, 一般初始邻域半径较大, 随着迭代次数的增加而单调地递减; 学习率 η(N, t)由邻域半径 N 和迭代次数 t 决定。
5)更新权值: 对获胜的神经元 g 邻域半径内所有神经元进行更新, 对学习后的权值重新归一化。
6)令 t=t+1, 直到 t 达到设定的迭代次数。
1.1.2 GRU网络
门控循环单元(gated recurrent unit, GRU)神经网络结构简单, 容易训练, 能很好地处理远距离依赖和反向传播中梯度消失问题。如图 1 所示, GRU 有重置门和更新门两个门控单元, 两个门的输入信息均为当前时间步输入和上一时间步隐藏状态。重置门(rt)控制前一时刻状态有多少信息被写入当前隐藏状态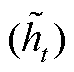 , 有利于得到时序数据中的短期依赖关系。更新门(zt)控制前一时刻的状态信息(ht−1)被带入当前状态(ht)的程度, 有助于得到时序数据中的长期依赖关系。单个门控单元的计算过程如下:
, 有利于得到时序数据中的短期依赖关系。更新门(zt)控制前一时刻的状态信息(ht−1)被带入当前状态(ht)的程度, 有助于得到时序数据中的长期依赖关系。单个门控单元的计算过程如下:
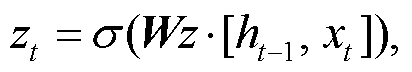 (2)
(2)
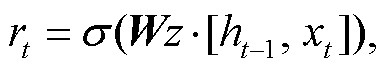 (3)
(3)
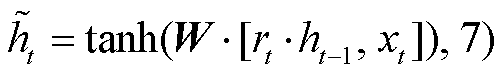 (4)
(4)
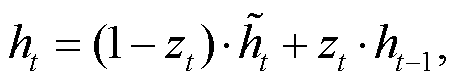 (5)
(5)
其中, t 代表时刻, xt 代表输入数据, W 为参数矩阵; σ和 tanh 代表激活函数, 能增加神经网络模型的非线性程度。
1.2.1线性插值
线性插值是一种使用比较广泛的插值方法, 根据一维数据序列中需要插值的点左右临近的两个数据进行数值估计, 依据这两个点的距离分配比例, 属于一种效果比较中庸的插值方法。
1.2.2样条插值
本文采用的样条插值方法为 2 阶 B 样条曲线插值, 是一种低阶次的插值方法, 具有计算简单、稳定性好以及收敛性有保证等特点, 同时能保证连接处的连续性及一阶导数的连续性。结合 PM2.5 浓度分布的时空特性, 发现高阶样条插值会出现过拟合的情况, 而 1 阶插值不能体现 PM2.5 浓度时间序列的周期震荡特性, 故选择 2 阶 B 样条曲线插值法作为对比项。
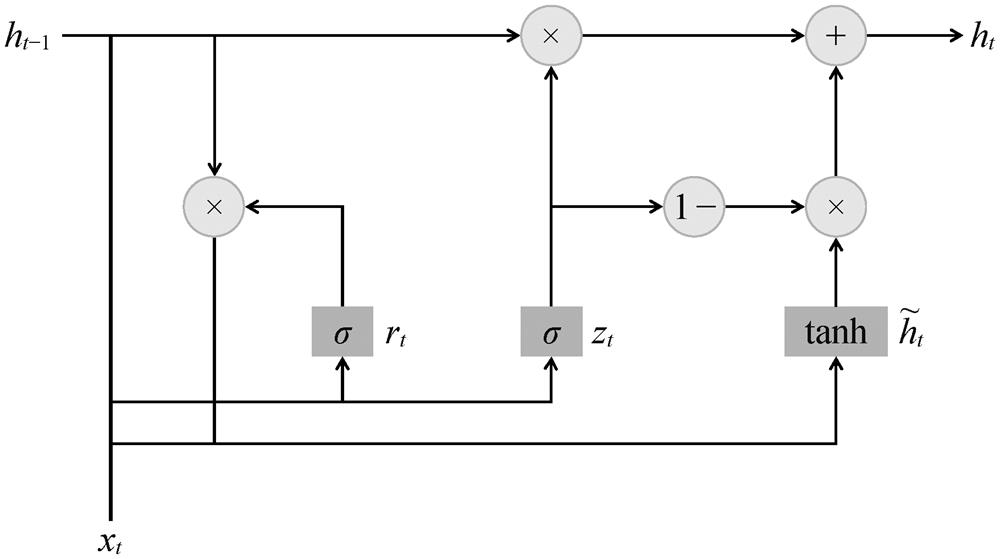
图 1 GRU的结构
Fig. 1 Structure of GRU
为了评估插值模型的数据填补效果, 本文选用均方根误差(root mean square error, RMSE)和相关系数(correlation coefficient, CC)作为评价标准, 计算公式如下:
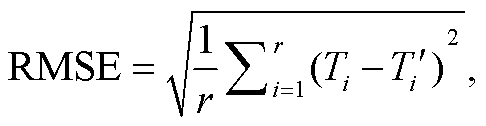 (6)
(6)
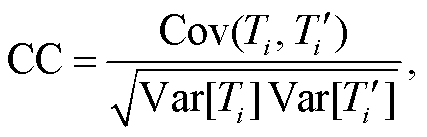 (7)
(7)
其中, r 为样本数, Ti 为实测值, 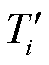 为插值结果。
为插值结果。
本研究所用气象数据和 PM2.5 浓度数据来源于http://beijingair.sinaapp.com/网站, 涉及 23 个城市, 其中气象数据为每 3 小时资料, PM2.5 浓度数据为整点的小时数据, 时间为 2016 年 1 月 1 日至 2019 年12月 31 日, 共 1461 天。GDP 和人口数据涉及时段为2016—2019 年, 来源于国家统计局官方网站(http:// www.stats.gov.cn/)和《中国城市统计年鉴》。数据预处理方式见表 1, 先将风速转化为东西向分量(u)和南北向分量(v), 再做日平均。如果某一城市存在多个气象站点, 则将多站点数据的当日均值作为该城市当日代表值。
由于后续建模过程涉及多种数据, 初始数据的特征不同, 通常具有不同的数量级和量纲。为了方便计算和提升神经网络模型的学习效率, 本文对数据分别进行标准化处理(式(8))和归一化处理(式(9)):
X1 = (X − μ) / S, (8)
X2 = (X − Xmin) / (Xmax − Xmin), (9)
其中, X为初始数据, X1为标准化数据, μ为数据平均值, S为数据标准差, X2为归一化数据, Xmax为数据最大值, Xmin为数据最小值。
图2示意本文实验设计的整体思路, 下面进行详细的阐述。
屈超等[15]及夏晓圣等[16]的研究结果表明, 气象条件是影响 PM2.5 浓度变化的重要因素。刘清等[17]发现, PM2.5 浓度值具有明显的季节差异, 以夏季为转折点, 呈现“夏优, 春秋继替”的特征。因此, 本文选用常规的气象观测数据温度、露点温度、风向、风速和海平面气压, 按照季节划分(3—5 月为春季, 6—8 月为夏季, 9—11 月为秋季, 12—2 月为冬季), 分别求取各季节数据的均值和方差来表征城市的气象数据特征。基于我国各地区 PM2.5 浓度的相关统计数据[18–19]进行分析, 结果表明中国经济最发达、城镇化和工业化进程最快速的京津冀、长三角和珠三角三大城市群是我国 PM2.5 污染最严重的区域。因此, 除选用常规的气象要素外, 还选用城市 GDP 和人口数据作为城市发展特征进行 SOM 城市匹配, 使得依靠这些城市特征得到的城市分组结果能够在一定程度上体现同组城市 PM2.5 浓度特征的相似性。
表1 数据来源及预处理方式
Table 1 Data sources and preprocessing methods

数据来源预处理方式城市 气象数据: 温度(T)、露点温度(Td)、风向、风速(v)、海平面气压(P); PM2.5浓度http://beijingair.sinaapp.com/利用 Akima 插值方法补全缺失值; 将北京时间 00 至 23 时的小时数据进行算数平均, 得到日均值安阳、北京、成都、重庆、广州、柳州、洛阳、上海、沈阳、石家庄、西安、张家口、郑州、舟山、深圳、长春、大同、鄂尔多斯、贵阳、酒泉、克拉玛依、汕头、厦门 GDP和人口国家统计局官方网站和《中国城市统计年鉴》年均值
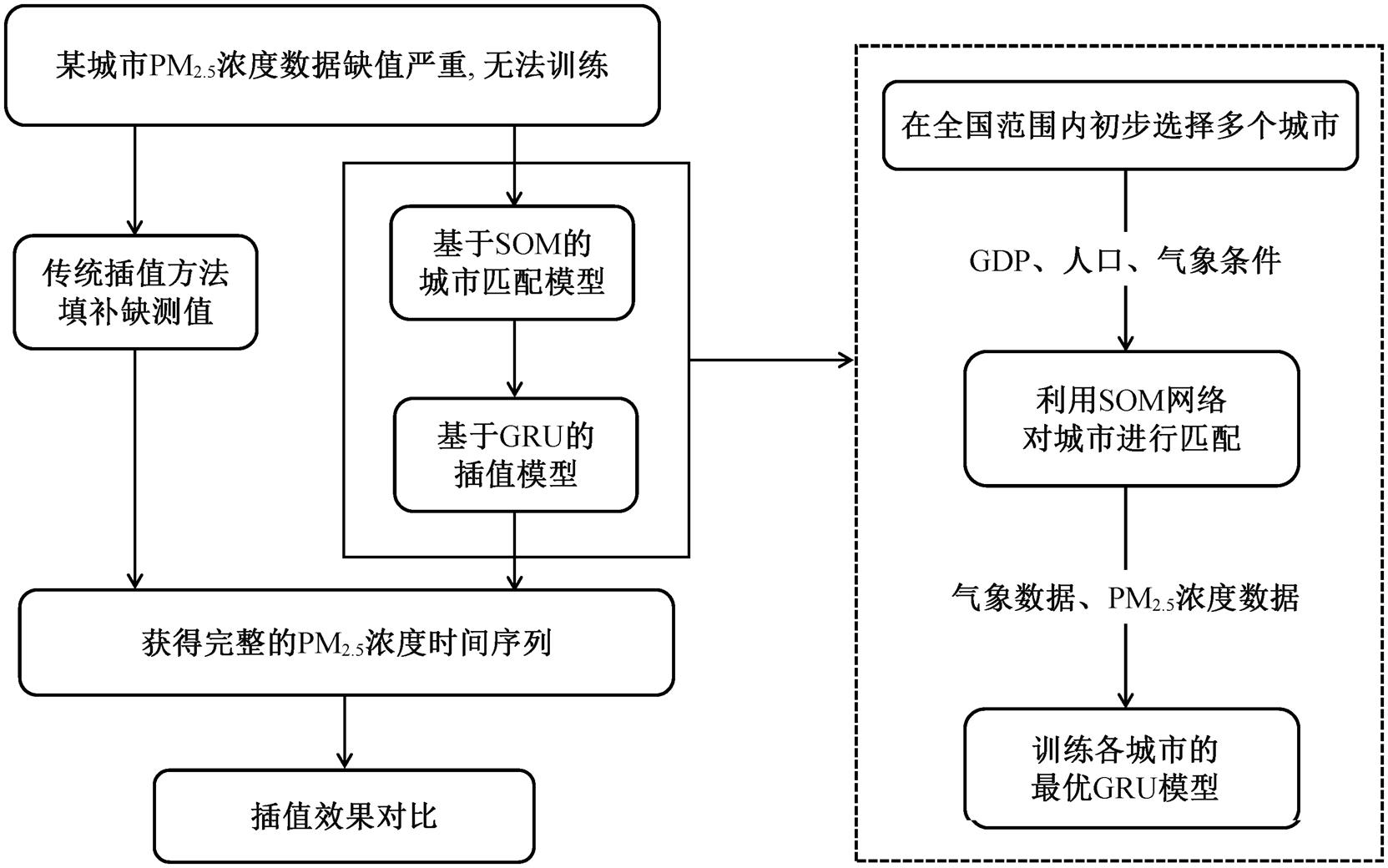
图2 实验设计流程
Fig. 2 Experimental design flow chart
据 3.1 节的结果, 一座城市包括 42 项城市特征, 即 5 项常规气象要素各季节的均值和方差、GDP 和人口数据。将 23 个城市的 42 项特征组成的数据进行标准化处理后输入 SOM 网络。由于每项特征对应一个输入神经元, 因此 SOM 网络输入层设置 42个神经元。输出层神经元格式可依据需求类别设定, 类别越多, 分组越细致, 相似度越高。迭代次数设置为 1000 次。
当前, 用于 PM2.5 浓度预报的数据主要包括能见度数据、气象数据和空气污染物质量浓度数据。考虑到本研究涉及的城市数量相对较多以及获取各个城市数据的难易程度, 本文选择常规气象要素数据和 PM2.5 浓度数据分别作为预报因子和预报量。以深圳城市为例, 各项特征数据的基本情况如表 2所示。黄春桃等[20]利用两种传统的机器学习模型(RF 和 XGBoost)和两种新型深度学习模型(LSTM 和GRU)对广州市的 PM2.5 和 PM10 日均浓度进行建模, 从 5 种评价指标角度看, GRU 模型都属于预测效果最好的情况。因此, 本文选用 GRU 模型和日均气象要素数据构建各城市的最优 PM2.5 预报模型, 经过多次实验, 选用前 7 天的气象数据(T, Td, u, v和 P)作为各城市 PM2.5 预报模型的输入值, 当天 PM2.5 浓度值作为输出值, 训练集选取 2016 年 1 月 1 日至2018 年 10 月 4 日时段的数据。模型包括一层 GRU层和两层全连接层。GRU 层的神经元个数为 100, 第一层全连接层的神经元个数也为 100, 第二层全连接层个数为 1。本文对 batch size 参数采用遍历循环的方式进行优化, 利用早停机制(early stopping)设置防止 epoch 过大, 出现过拟合现象。
假设深圳的 PM2.5 浓度数据存在严重缺值现象, 必须对历史缺测值进行填补, 才能正常利用神经网络方法建模。随机选取深圳市 10%的 PM2.5 数据做如下 4 种缺值假设: 每 8 天缺值最后 1 天(7+1 型)、每 12 天缺值最后 5 天(7+5 型)、每 14 天缺值最后 7天(7+7 型)以及每 21 天缺值最后 14 天(7+14 型)。使用基于 SOM 网络进行匹配后的相似城市 GRU 模型和传统的插值方法(线性插值和样条插值), 对上述 4 种缺值类型进行历史数据的填补。同时, 为了说明根据城市特征代表值进行城市匹配是有效的, 本文还设置另一组对比试验, 用除相似城市之外的其他城市的 GRU 模型为深圳缺值数据做插值, 插值效果用均方根误差和相关系数两个指标进行评估和对比。
依据分类原理, 可以将 23 个城市按需求进行分类。类别越多, 分类越细致, 每个类型间的相似度越高。本文尝试将类别数定为 23, 以便寻求与研究对象深圳最相似的两三个城市。结果表明, 汕头、贵阳和厦门是与深圳最相似城市。为了考虑得更全面, 将城市分为 3 组(表 3)。本文分别计算 3 组城市模型对深圳 7+1 型缺值数据的插值效果平均值, 得到第一组城市模型的 RMSE 均值为 20.64, CC 为0.54; 第二组城市的RMSE 均值为 24.67, CC 为0.39; 第三组城市的 RMSE 均值为 28.56, CC 为 0.42。可见深圳同组别城市模型的插值效果明显高于其他组别城市。
表 4 展示分别以 RMSE 和 CC 为标准, 对各城市模型 7+1 型缺值填补效果进行排序的前五名城市模型的组合, 去除重复城市后, 共计 8 个不同的城市模型。缺值数据的分布位置是随机选择的, 缺失长度为总长度的 10%。表 4 中的结果是对 5 组 7+1型随机缺失值进行填补后综合得到的, 8 个城市模型中, 有 4 个属于深圳同组相似城市。可以看出, 不论是按实测值与填补值之间的均方根误差排序, 还是按相关系数排序, 深圳同组相似城市 GRU 模型的插值效果都较为优秀。从整体插值效果来看, 最优秀的城市模型为汕头模型, 插值结果与实测值之间的均方根误差为 11.82, 相关系数为 0.56; 厦门模型次之, 均方根误差为 13.45, 相关系数为 0.57。如果仅依据 7+1 型插值结果, 就认为基于 SOM 匹配模型得到的相似城市分组结果在 PM2.5 浓度层面具有合理性, 论据相对单薄。因此, 本文进一步对7+5 型、7+7 型和 7+14 型缺值情况进行数据填补。从时间角度来看, 7+5 型属于短期缺测情况, 7+ 7 型属于中期缺测情况, 7+14 型属于长期缺测情况。
表2 深圳市气象数据和PM2.5浓度数据的统计信息
Table 2 Statistical information of meteorological data and PM2.5 concentration data in Shenzhen

要素单位区间平均值标准差 PM2.5浓度μg/m3[4.88, 102.33]26.1513.66 T (温度)℃[3.03, 32.70]23.645.28 Td (露点温度)℃[−7.83, 28.25]18.976.75 v (南北风分量)m/s[−1.30, 5.03]1.060.67 u (东西风分量)m/s[0.23, 5.29]1.190.69 P (海平面气压)hPa[9932.25, 10354.17]10128.9067.11
表3 SOM模型的城市分组结果
Table 3 City grouping results of SOM model

组别城市 第一组成都、重庆、广州、郑州、深圳、汕头、贵阳、厦门 第二组安阳、柳州、洛阳、上海、西安、舟山 第三组北京、沈阳、石家庄、张家口、长春、大同、鄂尔多斯、酒泉、克拉玛依
说明: 粗字体为与深圳最相似的城市。
表4 分别以RMSE和CC为排序标准的前五名城市模型组合(7+1型缺值)
Table 4 Top five city model combinations (7+1 type missing value) with RMSE and CC as the ranking criteria respectively

城市模型 RMSE/(μg·m−3)CC 汕头模型11.820.56 厦门模型13.450.57 大同模型14.610.52 酒泉模型14.860.42 克拉玛依模型14.940.51 柳州模型21.020.63 广州模型18.810.62 贵阳模型22.410.58
说明: 粗字体为深圳同组相似城市, 阴影为与深圳最相似的城市, 白底为其他组别城市, 下同。
表 5 对比线性插值方法、样条插值和各城市GRU 模型对深圳 4 种缺值类型的插值效果。可以看出, 针对 7+1 型和 7+5 型这类短期缺测的情况, 不论是均方根误差还是相关系数, 传统的线性插值和样条插值方法表现更优秀; 针对 7+7 型和 7+14 型这类中长期缺值的情况, 传统插值方法的优势降低, 其对 PM2.5 浓度变化趋势和数值的模拟效果不如深圳最相似城市模型。随着缺值时间的增长, 传统插值方法的均方根误差出现逐渐上升的趋势, 相关系数也逐渐降低, 其中样条插值的效果变化尤为剧烈, 而城市模型的表现相对稳定, 指标的浮动区间相对较小。在 7+14 型缺值情况下, 汕头模型对缺值数据趋势模拟的相关系数仍然保持在 0.45 以上, 而线性插值的相关系数已降低至 0.35, 样条插值的相关系数降为 0.1。
综上所述, 相对于其他城市模型, 基于 SOM 匹配模型得到的相似城市模型插值效果更优。这进一步印证了本研究进行城市匹配的意义, 城市之间的相似程度可在很大程度上代表模型通用的准确性。
图 3 对比汕头模型、线性插值方法和样条插值方法对每种缺值类型的一组随机缺失数据的插值结果与实测值。可以看出, 对于 7+1 型缺值情况, 传统的插值方法能较好地捕捉 PM2.5 浓度的变化趋势,对于 7+5 型、7+7 型和 7+14 型缺值情况, 虽然大多数时候传统插值方法能掌握 PM2.5 浓度的整体波动趋势, 但是忽略了很多高频的波动特征, 这一点在 7+7 型和 7+14 型的插值曲线中更明显。传统的插值方法只是学习了序列两端的特征, 从而建立起插值直线或曲线, 将很多高频的波动特征简化为升高或降低趋势, 这种简化处理忽略了高频信号, 随着缺值天数的增加, 弊端越发凸显, 最直接的体现就是均方根误差(RMSE)大幅增加, 相关系数(CC)降低(表 5)。图 3 的结果表明, 城市模型能很好地学习这种高频振荡的非线性变化的时间序列, 利用城市模型插值得到的序列能很好地表现出序列的波动特征, 插值序列的振荡周期与实测值的振荡周期较为一致, 起伏趋势也大致相同。
表5 传统插值方法和城市模型插值效果对比
Table 5 Comparison of effect between traditional interpolation methods and urban model interpolation methods

插值方法和城市模型 7+1型7+5型7+7型7+14型RMSE/(μg·m−3)CCRMSE/(μg·m−3)CCRMSE/(μg·m−3)CCRMSE/(μg·m−3)CC 线性插值法7.600.8410.510.6511.740.5012.090.35 样条插值法8.030.8414.780.4619.620.3631.760.10 汕头模型11.820.5611.120.5910.750.5811.050.47 厦门模型13.450.5713.680.5712.480.5512.970.52 大同模型14.610.5212.990.5313.670.4113.990.38 酒泉模型14.860.4213.760.4014.540.2514.280.28 克拉玛依模型14.940.5115.720.4814.800.4015.710.39 柳州模型21.020.6318.210.6320.610.5623.300.26 广州模型18.810.6217.010.6516.400.5919.680.42 贵阳模型22.410.5821.070.5620.610.5023.300.16
说明: 粗体数字代表该类型插值效果最优; 每种缺值类型的 RMSE 和 CC 数据是模型对 5 组随机缺值进行数据填补后得到的平均值。
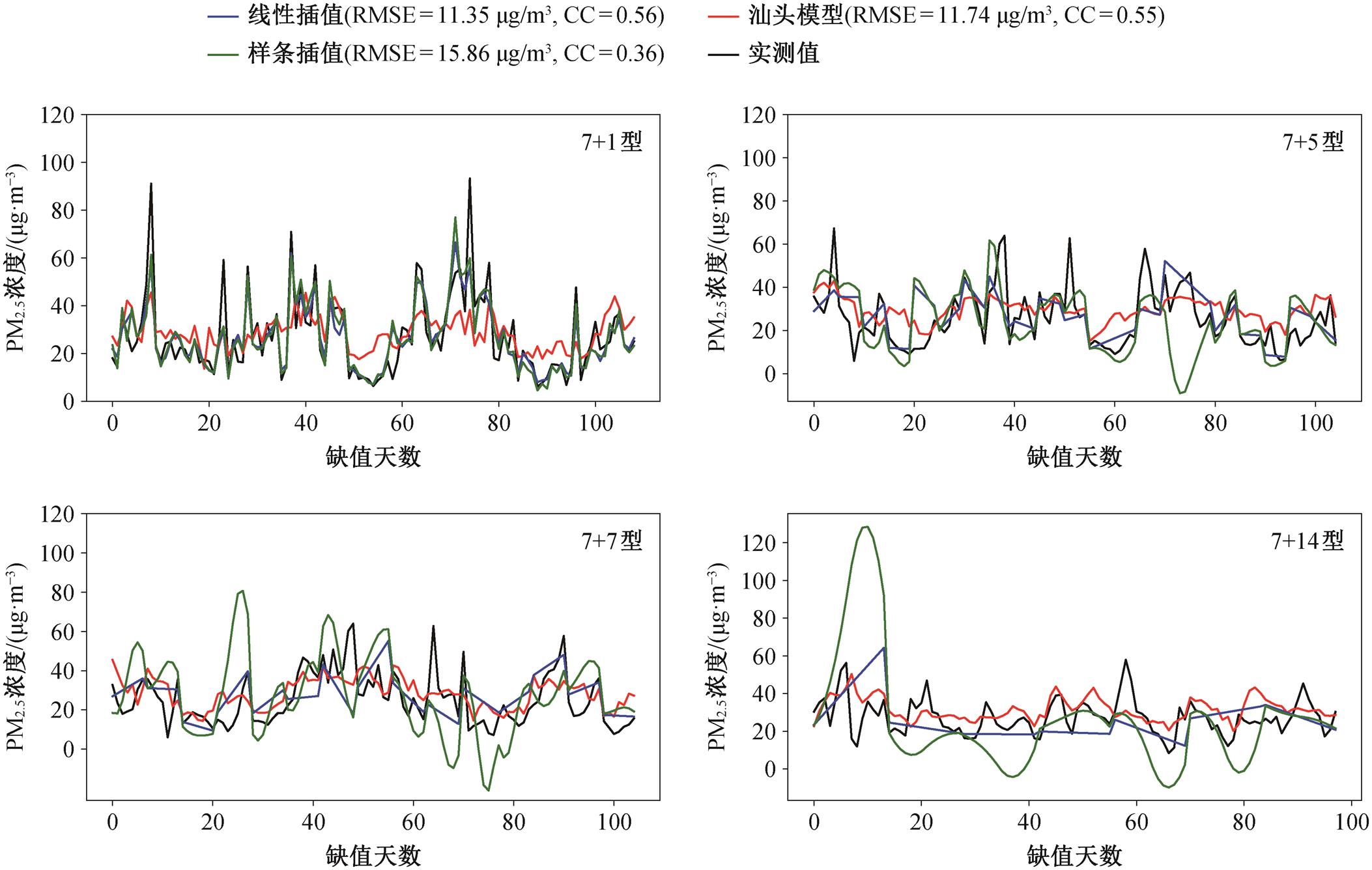
图3 汕头模型、线性插值方法和样条插值方法插值结果与实测值对比
Fig. 3 Comparison of interpolation results with measured values for Shantou model, linear method and spline method
本研究发现, 对 PM2.5 浓度序列这种短时间内高频振荡的, 具有很强非线性特征的序列来说, 用城市模型对中长期缺值型(7+7 型和 7+14 型)进行插值的效果会更好, 能够插值得到波动和振荡的序列; 对短期缺值型(7+1 型和 7+5 型)进行插值则无法体现 GRU 模型能够学习到序列波动特征的能力。因此, 用线性插值法能够更好地填补短期变化的起伏特征。
1)以城市发展水平数据和气象数据为基础建立的 SOM 城市匹配网络, 能够在一定程度上有效地反映各城市 PM2.5 浓度变化的相似情况。以深圳为例, SOM 城市匹配模型将其与汕头、厦门和贵阳归为同组, 这一点在后期的插值效果对比中也有所体现, 汕头模型对深圳缺值数据的填补效果的确为 最优。
2)对于短期缺测类型, 线性插值方法更具优势, 在均方根误差和相关系数方面有更好的表现; 对于中长期缺测类型, 城市模型能学习到 PM2.5 浓度时间序列的波动性和非线性, 并且不需要知道缺测值两端的数值, 对数据要求更低, 能更好地解决插值问题。
参考文献
[1] 陈熙勐, 张皓旻, 顾万清, 等. 我国PM2.5 主要成分及对人体健康危害研究进展. 中华保健医学杂志, 2019, 21(1): 83–85
[2] 郭新彪, 魏红英. 大气PM2.5 对健康影响的研究进展. 科学通报, 2013, 58(13): 1171–1177
[3] 张理博, 孙鹏, 罗淑年. 大气细颗粒物PM2.5的危害及其治理政策的研究. 环境科学与管理, 2020, 45 (4): 102–105
[4] 张瑾, 薛彩凤, 温彪, 等. 浅谈PM2.5 的危害及我国的控制历程与经验. 环境与可持续发展, 2021, 46 (1): 109–114
[5] 杨洪斌, 邹旭东, 汪宏宇, 等. 大气环境中PM2.5 的研究进展与展望. 气象与环境学报, 2012, 28(3): 77–82
[6] 尹文君, 张大伟, 严京海, 等. 基于深度学习的大数据空气污染预报. 中国环境管理, 2015, 7(6): 46–52
[7] 彭斯俊, 沈加超, 朱雪. 基于ARIMA模型的PM2.5 预测. 安全与环境工程, 2014, 21(6): 125–128
[8] 杜续, 冯景瑜, 吕少卿, 等. 基于随机森林回归分析的PM2.5 浓度预测模型. 电信科学, 2017, 33(7): 66–75
[9] Li X, Peng L, Yao X, et al. Long short-term memory neural network for air pollutant concentration predict-tions: method development and evaluation. Environ-mental Pollution, 2017, 231: 997–1004
[10] 张恒德, 张庭玉, 李涛, 等. 基于BP神经网络的污染物浓度多模式集成预报. 中国环境科学, 2018, 38(4): 1243–1256
[11] 邹思琳, 任晓晨, 王成功, 等. 时间精度与空间信息对神经网络模型预报PM2.5 浓度的影响. 北京大学学报(自然科学版), 2020, 56(3): 417–426
[12] Liu H, Long Z H, Duan Z, et al. A new model using multiple feature clustering and neural networks for forecasting hourly PM2.5 concentrations, and its app-lications in China. Engineering, 2020, 6(8): 944–970
[13] 吴聘奇, 黄民生. SOM网络在福建省城市职能分类中的应用. 经济地理, 2005(1): 68–70
[14] 杨黎刚, 苏宏业, 张英, 等. 基于SOM聚类的数据挖掘方法及其应用研究. 计算机工程与科学, 2007 (8): 133–136
[15] 屈超, 陈婷婷, 刘佳, 等. 中国典型城市PM2.5 浓 度时空演绎规律及影响因素分析. 环境科学研究, 2019, 32(7): 1117–1725
[16] 夏晓圣, 陈菁菁, 王佳佳, 等. 基于随机森林模型的中国PM2.5 浓度影响因素分析. 环境科学, 2020, 41(5): 2057–2065
[17] 刘清, 杨永春, 刘海洋. 中国 366 个城市空气污染综合程度的时空演变特征分析. 干旱区地理, 2020, 43(3): 820–830
[18] 王涛, 王明悦, 胡薇, 等. 中国 2018 年PM2.5 的空间分布特征——基于地理信息系统的研究. 环境与职业医学, 2020, 37(6): 553–557
[19] 战杨志豪, 谢旻, 罗干, 等. 2018 年冬季南京重霾污染特征及气象因素分析. 环境科学学报, 2020, 40 (11): 4038–4047
[20] 黄春桃, 范东平, 卢集富, 等. 基于深度学习模型的广州市大气PM2.5 和PM10 浓度预测. 环境工程, 2021, 39(12): 135–140
A PM2.5 Interpolation Method Based on Neural Network for Optimum City Matching
Abstract In order to solve the problem that some cities have serious PM2.5 concentrationdata deficiency and can not get prediction model by training their own data, this paper proposes a method to use prediction model of similar cities to fill in historical data of target city. Based on the meteorological data, urban development data and PM2.5 concentration data of 23 cities, an interpolation model of PM2.5 daily concentration data is established based on self-organizing map (SOM) and gated recurrent unit (GRU) neural network and use it and raditional interpolation (linear interpolation and quadratic interpolation) methods are used to fill missing data respectively. The comparision of filling effects show that the SOM city matching model can accurately match the similar cities of the target city. For the missing data less than 5 days, the filling effect of traditional interpolation methods are better than that of GRU interpolation model. For the missing data more than 5 days, the GRU interpolation model is more competent to fill in the missing data for a long time.
Key words PM2.5; self-organizing map (SOM); gated recurrent unit (GRU); interpolation model