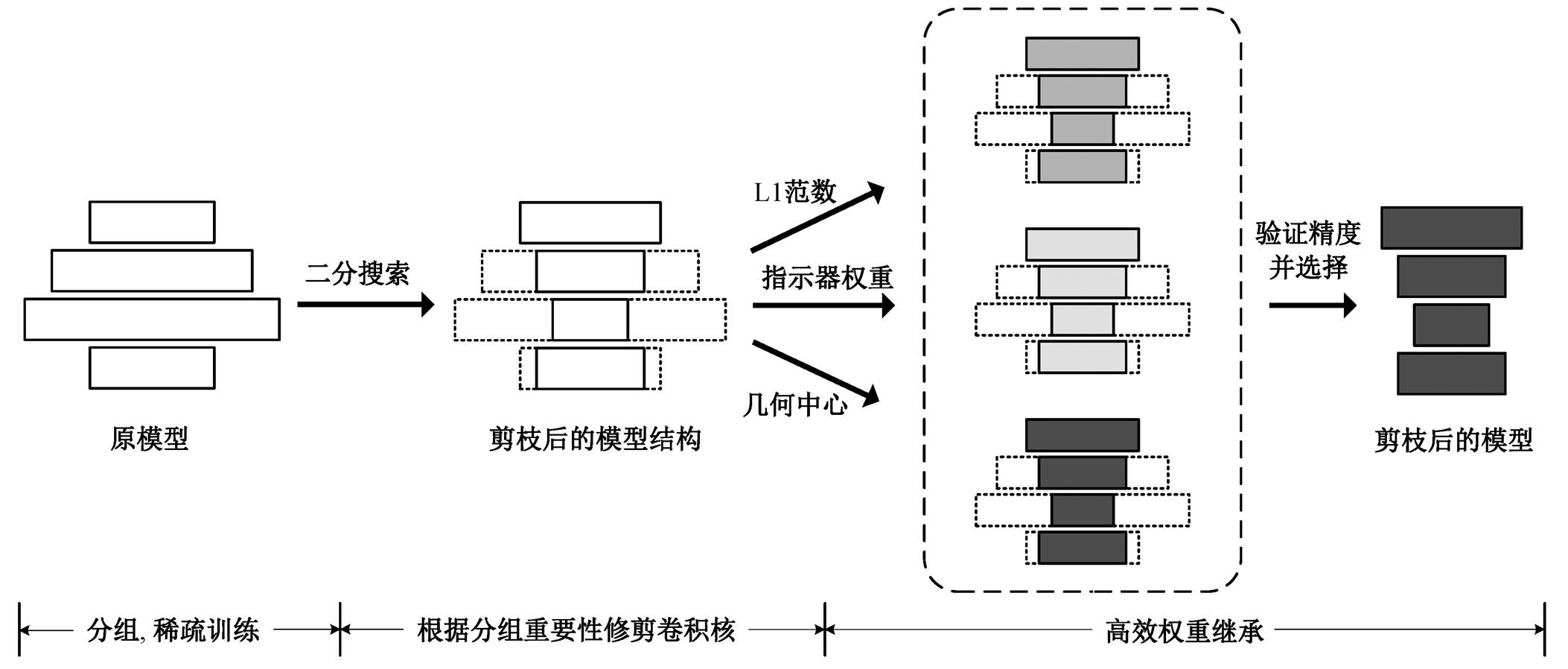
图1 自适应通道剪枝框架
Fig. 1 Framework of adaptive channel pruning
北京大学学报(自然科学版) 第59卷 第5期 2023年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 5 (Sept. 2023)
国家重点研发计划(2018YFE0203801)资助
doi: 10.13209/j.0479-8023.2022.115
收稿日期: 2022–09–14;
修回日期: 2022–11–11
摘要 目前的通道级剪枝方法往往需要复杂的搜索和微调过程, 并且容易陷入局部最优解, 针对此问题, 提出一种新颖的通道剪枝框架(AdaPruner), 只需通过一次稀疏训练, 就可以针对各种预算复杂度, 自适应地生成相应的子网络, 并高效地选择适合当前结构的初始化权重。在图像分类任务的多个数据集上实验结果表明, 该方法在常用的残差网络和轻量级网络上的性能都优于以往剪枝方法。
关键词 卷积神经网络; 通道剪枝; 稀疏化训练; 神经网络结构搜索; 图像分类
卷积神经网络[1–3]广泛应用在计算机视觉的各项任务中。然而, 深度神经网络在取得优异性能的同时, 也饱受计算成本过高等诟病, 阻止了卷积神经网络在端侧设备的部署。神经网络剪枝是常用的模型压缩手段, 可分为结构化剪枝和非结构化剪枝。非结构化剪枝技术[4–7]在更细的粒度修剪网络参数, 从而使模型的权重参数变成高度稀疏的矩阵, 即使在很高的压缩率下, 也能有良好的性能表现, 但需要特殊硬件和计算库的支持, 因此应用场景受限。结构化剪枝中最常用的是通道剪枝, 也称为卷积核剪枝。它通过修剪网络中冗余的卷积核, 实现减少网络的参数量, 从而加快模型的推理速度。因直接减少模型的宽度, 可以很方便地实现加速。
按照各层剪枝比例的设置, 通道剪枝可以分为逐层剪枝和全局剪枝两大类。逐层剪枝需要手工设置各层的剪枝率, 然后按照预先定义的权重评估准则, 逐层修剪不重要的卷积核。例如, Li 等[8]认为卷积核的 L1 范数可以反映其重要性, 提出在各层内按照卷积核的 L1 范数排序, 并修剪掉最不重要的通道。He 等[9]提出更好的卷积核评价标准——几何中位数, 裁剪掉每层最靠近几何中心点的权重。Luo 等[10]根据下一层的统计信息引导当前层的剪枝, 通过最小化下一层的特征重建误差贪心修剪。Lin 等[11]对激活输出进行奇异值分解, 并修剪最低秩特征图对应的滤波器。逐层修剪方法的显著问题在于依赖人工经验控制网络的修剪行为, 可靠性无法得到保证, 同时难以实现预算感知下的自动化剪枝流程。
全局剪枝可以实现自动确定网络各层的剪枝比例, 通过在全局范围内修剪最不重要的卷积核, 得到合适的网络结构。全局修剪的关键在于解决全局卷积核重要性排序。已有的排序方法主要包含稀疏训练, 损失函数展开以及自动搜索。Liu 等[12]通过对批归一化层进行正则化, 以稀疏训练的方式得到所有卷积核的重要性排序, 并根据阈值, 保留重要的通道。Liu 等[13]去掉某一卷积核, 对损失函数的改变应用泰勒展开, 利用 Fisher 信息得到全局滤波器的重要性。Liu 等[14]通过大量实验证明, 修剪之后的网络结构对模型性能的影响比初始化权重更重要, 找到合适的子网络架构是剪枝算法的关键，因此基于自动机器学习搜索网络架构的剪枝算法变得流行。He 等[15]将模型的压缩率和精度作为强化学习算法的反馈, 训练了一个可以自动对各层实现剪枝的智能体。Liu 等[16]首先随机采样子网络, 训练一个元网络, 专门为子网生成初始化权重, 然后应用遗传算法搜索满足约束的最优子网。Lin 等[17]引入人工蜂群算法, 直接搜索子网络的结构配置。Li等[18]提出一种快速验证子网精度的方法, 通过大量随机搜索寻找合适的子网。全局修剪的方法克服了手动设计的弊端, 但仍然面临迭代修剪和自动化搜索过程中计算代价昂贵的问题。
本文提出一种便捷高效的基于自适应剪枝率与高效权重继承的神经网络通道剪枝方法(AdaPrun-er), 只需要一次稀疏化训练, 就可以根据各种预算复杂度自动生成相应的子网络结构, 省去手动调参和迭代修剪的繁琐, 同时剪枝的计算代价和剪枝后模型的精度明显提升。
如图 1 所示, 本文提出的神经网络剪枝框架分为 4 个步骤: 1)将预训练网络所有的卷积层分组, 并在各组中插入相同的可训练参数; 2)通过稀疏化训练, 使各组的可训练参数有差异地变化, 获得稀疏化模型各组可训练参数的均值; 3)根据目标预算和各组均值, 使用二分法, 快速找到符合约束的子网; 4)更新批归一化层的统计量, 确定适合当前结构的初始化权重, 并进行微调。
基于机器学习的剪枝算法[15–17]是通过进化算法和强化学习搜索各层的通道数配置, 计算成本高, 且存在次优解。本文提出基于数据驱动的方式得到各层的重要性, 然后在全局范围内分配计算资源。考虑到目前流行的神经网络都包含残差结构[19–20], 跳连前后层的输出通道数需要保持一致才能相加,首先将网络中具有相同输出通道数的卷积层划分到同一组。如图 2 所示, 以 ResNet[19]中的一个卷积块为例, 将跳连前后的卷积层分到同一组, 方便相加, 其内部相同通道数的卷积层也在同一组。
图1 自适应通道剪枝框架
Fig. 1 Framework of adaptive channel pruning
划分好网络的分组后, 对各个分组插入可训练的参数, 即组重要性指示器。可训练参数通过输出通道数等于分组通道数的 1×1 深度可分离卷积 W实现, 并且全部初始化为 1。典型的卷积结构包括卷积层、批归一化[21]层和激活函数, 本文在批归一化层之后添加分组重要性指示器。因此卷积层的计算方式如下:
y=ReLU (W*BN (Conv (x))), (1)
式中, *表示卷积操作; x和y分别表示输入和输出的特征图, Conv 和 BN 分别表示卷积和批归一化运算, ReLU 表示激活函数。值得注意的是, 为了保持分组内卷积层的稀疏行为一致, 每个分组内部所有卷积层之后的重要性指示器共享同一组参数。
稀疏训练是剪枝常用的方法之一。为了抑制不重要的通道, 凸显不同分组的重要性, 本文对各组重要性指示器的权重施加 L1 范数正则化, 鼓励稀疏解。整体的损失函数如下:
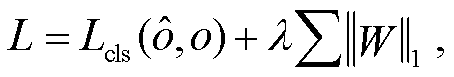(2)
式中,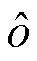
表示模型的预测结果, o 是标签, Lcls 表示网络原来使用的交叉熵损失函数, λ是用来控制训练和稀疏平衡的超参数。在训练过程中, 模型精度和稀疏度会逐渐达到平衡。
稀疏训练完成后, 各组重要性指示器的参数平均值发生显著改变。第 i 个分组的重要性指标 Mi为
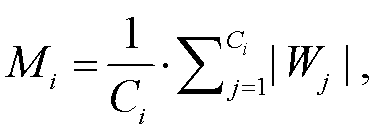(3)
式中, Ci表示第 i 组的输出通道数。各组的重要性表示为当前分组可训练参数的均值。由于组重要性指示器插入在批归一化层之后, 因此各组的重要性评价指标允许在全局范围内直接比较。
在获得各个分组的重要性评价指标后, 面临的一个显著问题是如何在目标计算量的约束下, 将重要性映射为实际的剪枝率。为了进行全局的资源分配, 首先计算每个组占整个网络重要性的百分比 Ii:
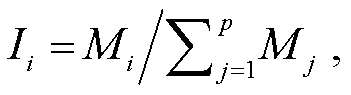(4)
式中, P 表示分组后的全部组数, Mi 表示第 i 组的重要性指标。
直观地看, 某个分组的重要性指标越大, 该组的重要性越高, 应当分配更多的计算资源; 均值越小, 说明该组越不重要, 可以在不显著影响性能的前提下修剪大量卷积核。因此, 本文假定每个分组实际的通道数保留比例 Ri 与重要性的百分比成正比:
(5)
式中,α表示待定的比例系数。给定任一浮点运算量 FLOPs, 求解 α 的过程比较繁琐, 并且无法实现剪枝流程的自动化。为了便捷高效地求解待定系数, 我们利用开源工具, 以二分查找的方式快速求得 α 值, 进而得到符合预算的子网络。具体的算法流程如算法 1 所示。
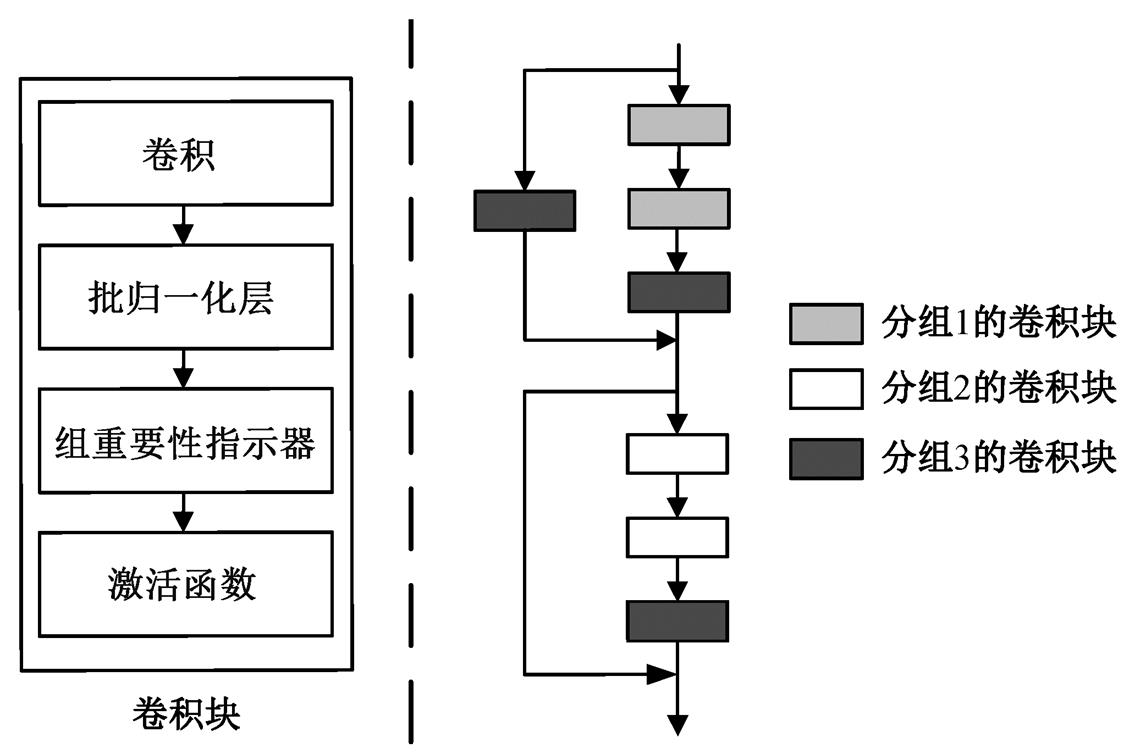
图2 包含组重要性指示器的卷积块和分组的示意图
Fig. 2 Schematic illustration of convolution block with group importance indicator and grouping
算法1二分法搜索符合约束的子网结构。
输入: 各分组重要性占比
, 模型复杂度计算公式
, 目标预算
参数: 初始化区间左值 l, 初始化区间右值 r, 误差容忍度 δ
输出: 待定比例系数 α
1. 初始化辅助函数两端的值 f(l)=
, f(r) =
2. 当l≤r时, 循环步骤3～6
3. 计算区间中点 α = (l+r)/2和对应的函数值
4. 若|f (α)|<δ, 则跳出循环
5. 若f (l) · f (α)<0, 则更新区间 r=α, f (r)= f (α)
6. 否则l=α, f (l)= f (α)
7. 循环结束, 返回 α
相比基于机器学习的剪枝算法, 本文提出的方法不需要对各层的剪枝率设置上限, 就能够精确地达到目标计算量, 也不会出现某一层过度修剪的问题。更重要的是, 本文提出的剪枝框架在一定程度上实现了“一劳永逸”, 只需一次稀疏化训练, 便能计算出各组重要性在整个网络中的占比, 针对不同的预算复杂度, 可以按照事先算好的比例, 全局分配计算资源, 得到一系列满足要求的子网络, 无需重复搜索。
经过分组、稀疏训练和二分搜索后, 利用本文提出的方法可以轻易地得到符合目标计算量的子网络结构。如果对不同初始化权重的子网都经过完整训练再验证其精度, 会造成很大的计算开销。本文提出一种可以快速评估初始化权重的方法, 无需重新训练全部参数。
首先考虑批归一化层的训练和测试过程中的不同。批归一化层按照如下指数滑动平均公式, 不断更新输入特征的均值 μ 以及方差 σ2, 以便测试时 使用。
(6)
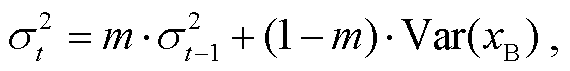(7)
式中, m 表示动量值, t 表示到目前训练的迭代轮数, E(xB)和 Var(xB)分别表示当前输入算得的均值和 方差。
原来的网络被修剪后, 一些通道被删去, 激活的均值 μ 和方差 σ2 相应地发生改变, 使用旧的统计量必定造成不匹配。由于误差是逐层累积, 重校准批归一化层格外必要, 可以有效地反映当前模型的真实潜力。神经网络结构搜索相关的文献[18,22]也提到这一点。重校准批归一化统计量的方式十分简单, 固定剪枝后网络的所有可学习参数, 打开批归一化层的训练模式, 将极少量数据(不需要标签)送入模型做前向传播, 就可以完成批归一化层的 校准。
本文采用 3 种常用的权重评价标准: 卷积核的L1 范数、几何中位数和指示器权重的绝对大小。
假设模型第 i 层的输入通道数为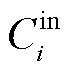
, 输出通道数为
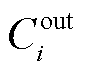, 则某一个卷积核的 L1 范数为
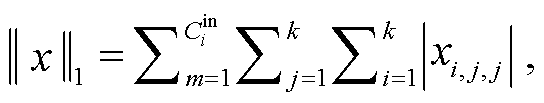(8)
计算该层每个卷积核对应的 L1 范数并降序排列, 保留前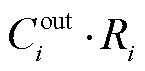
大的卷积核, 将其参数值作为子网络的初始化权重。
由于几何中位数(GM)是欧式空间中数据中心性的经典鲁棒估计量, 因此 GM 与其他数据共享通用性的信息。类似地, 如果一个卷积核越靠近它们的几何中心, 说明其包含的信息越冗余, 可以删除。首先按照下式计算该层所有卷积核的几何中心:
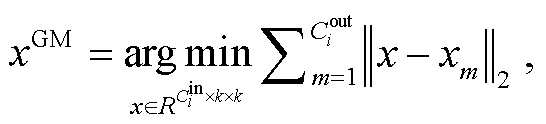(9)
然后, 修剪掉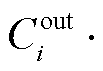
(1–Ri)个最接近几何中位数的卷积核, 把其余卷积核的参数值作为子网络的初始化权重。
得益于稀疏训练, 某个卷积核对应的组重要性指示器的权重反映其重要性。在层内直接对所有卷积核的指示器的权重排序, 保留前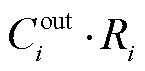大的卷积核, 把它们的参数值作为子网络的初始化权重。值得注意的是, 各种剪枝算法中提出的滤波器评价指标都可以应用在本文提出的修剪框架中。
因此, 对一个固定结构的剪枝后的网络, 分别使用各种预定义的权重继承方式初始化其参数, 再重新校准批归一化层的均值和方差, 然后不经过训练, 直接在验证集上测试其表现。表现最好的权重继承准则被认为是最具潜力的初始化方式, 可以进行最后的微调训练。
为了验证本文所提方法的有效性, 将自适应通道剪枝方法在不同数据集和不同网络结构上进行实验, 并与目前先进的通道剪枝方法对比, 最后进行消融实验, 对本文方法做详细分析。
在不同规模的图像分类数据集 CIFAR-10 和ImageNet 上, 针对多种网络结构进行实验, 所用数据集概况和网络结构如表 1 所示。
首先, 在 CIFAR-10 数据集上对 VGG-16网络进行实验, 结果如表 2 所示。可以看出, 与已有的剪枝算法相比, 本文的自适应剪枝方法在节省相似的浮点运算量的情况下取得更好的精度表现, 甚至比未剪枝的模型有所上涨, 这主要是由于模型压缩在一定程度上减少了过拟合的风险。表 3为各修剪算法在 ResNet-56 上的表现。因此, 本文提出的方法远优于传统的剪枝算法[9–11,23–24], 与基于搜索的剪枝方法[15,17]相比, 也展现出极具竞争力的表现。
进一步, 在 CIFAR-10 数据集上对 ResNet-110模型进行剪枝实验, 结果见表 4。可以看出, 本文方法比以往的剪枝算法取得更好的精度——复杂度均衡(运算量), 并且针对不同的计算量预算, 自适应剪枝算法只需一次稀疏训练就能达到“一劳永逸”的效果。
表1 实验使用的数据集和网络结构
Table 1 Datasets and network structure used in the experiment
数据集类别数训练数量/测试数量实验所用网络结构 CIFAR-101050000/10000VGG-16, ResNet-56, ResNet-110 ImageNet10001200000/50000ResNet-50, MobileNetV2
表2 CIFAR-10数据集上VGG-16模型应用各剪枝方法的对比
Table 2 Comparison of various pruning methods applied to VGG-16 on CIFAR10
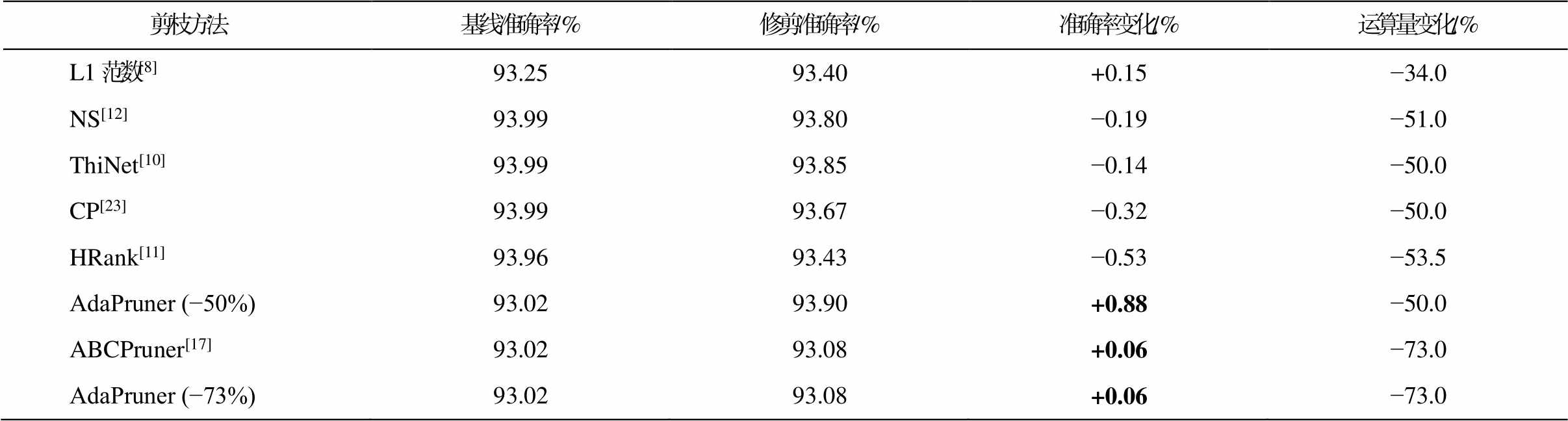
剪枝方法基线准确率/%修剪准确率/%准确率变化/%运算量变化/% L1范数[8]93.2593.40+0.15−34.0 NS[12]93.9993.80−0.19−51.0 ThiNet[10]93.9993.85−0.14−50.0 CP[23]93.9993.67−0.32−50.0 HRank[11]93.9693.43−0.53−53.5 AdaPruner (−50%)93.0293.90+0.88−50.0 ABCPruner[17]93.0293.08+0.06−73.0 AdaPruner (−73%)93.0293.08+0.06−73.0
说明: AdaPruner ( )中数字表示运算量变化, 粗体数字标示指标最优，下同。
表3 CIFAR-10数据集上ResNet-56模型应用各剪枝方法的对比
Table 3 Comparison of various pruning methods applied to ResNet-56 on CIFAR10
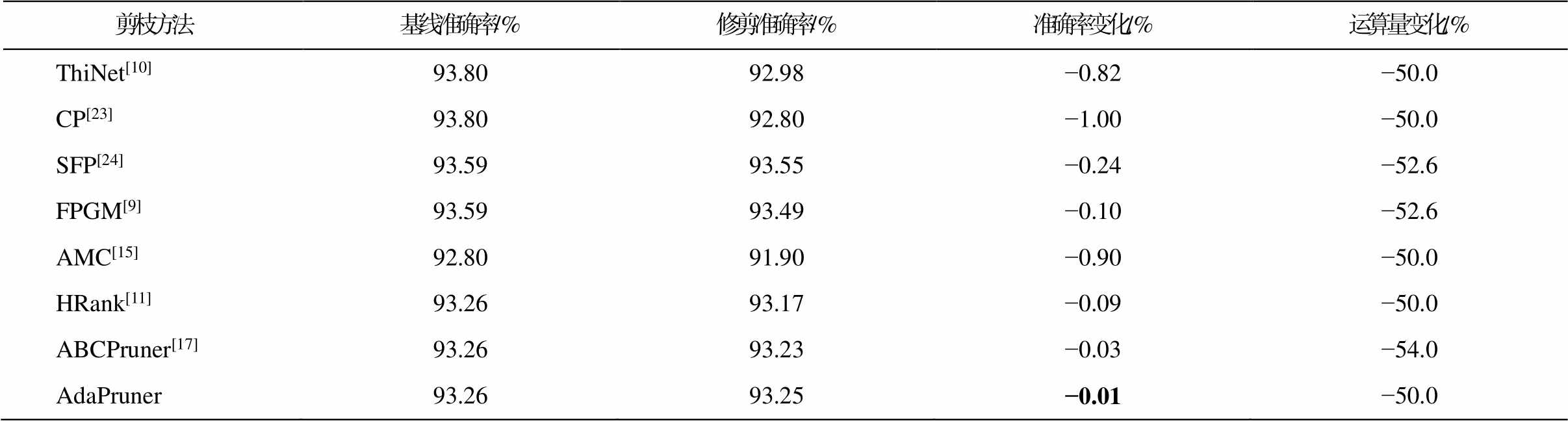
剪枝方法基线准确率/%修剪准确率/%准确率变化/%运算量变化/% ThiNet[10]93.8092.98−0.82−50.0 CP[23]93.8092.80−1.00−50.0 SFP[24]93.5993.55−0.24−52.6 FPGM[9]93.5993.49−0.10−52.6 AMC[15]92.8091.90−0.90−50.0 HRank[11]93.2693.17−0.09−50.0 ABCPruner[17]93.2693.23−0.03−54.0 AdaPruner93.2693.25−0.01−50.0
表4 CIFAR-10数据集上ResNet-110模型应用各剪枝方法的对比
Table 4 Comparison of various pruning methods applied to ResNet-110 on CIFAR10
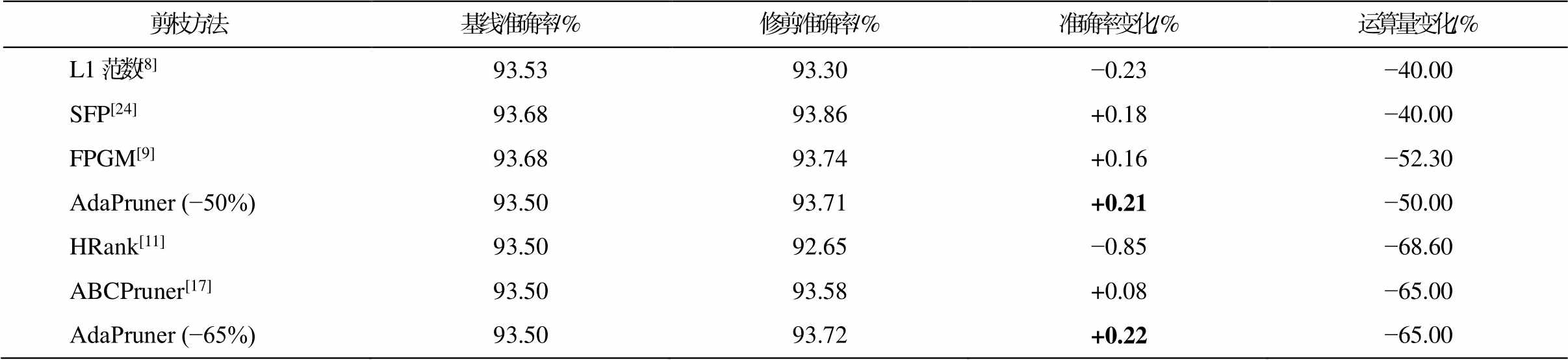
剪枝方法基线准确率/%修剪准确率/%准确率变化/%运算量变化/% L1范数[8]93.5393.30−0.23−40.00 SFP[24]93.6893.86+0.18−40.00 FPGM[9]93.6893.74+0.16−52.30 AdaPruner (−50%)93.5093.71+0.21−50.00 HRank[11]93.5092.65−0.85−68.60 ABCPruner[17]93.5093.58+0.08−65.00 AdaPruner (−65%)93.5093.72+0.22−65.00
为了在大规模的数据集上验证本文方法的有效性, 在标准的 ImageNet-1K 数据集上, 针对常用的残差网络和轻量化网络进行对比实验。首先对基准ResNet-50 网络进行不同计算量下的实验, 结果见表 5。可以看出, 保留原模型一半的浮点运算量时, 本文方法的 Top-1 准确率只下降不到 0.4%, 比之前的剪枝算法有明显的提升。保留原模型 1/4 的浮点运算量(即 1G 的 FLOPs)时, 相比目前先进的算 法[16,18], 本文方法也可以取得更好的精度。
轻量化模型[20]在边缘设备上的使用更广泛, 专门为节省参数和计算量设计, 因此压缩起来比普通网络更加困难。如表 6 所示, 在 ImageNet 数据集上, MobileNetV2 模型保留 70%计算量时, 本文方法比已有算法表现更好, 证明了自适应剪枝算法的有效性和广泛适用性。
为了解自适应通道剪枝方法对修剪后网络结构的影响, 通过可视化的方式分析剪枝后网络的结构特点以及与其他算法的对比。首先绘制稀疏训练前后 MobileNetV2 中各个分组重要性的占比。如图 3所示, 未稀疏前, 各组的重要性指示器权重初始化为 1, 占比也相同。经过稀疏化训练后, 不同分组的重要性比例出现显著的差异, 表明各组的剪枝率应当分别考虑。根据是否下采样把模型分为 6 个阶段。可以发现, 各阶段第一个分组的重要性占比在该阶段所有分组中最高, 这是因为每个阶段的第一个卷积层承担下采样和改变输出通道数的功能, 更多的信息被编码在通道中, 所以不能被过度修剪。本文方法可以根据各组重要性自适应调节剪枝比例, 因此, 比手动设置更合理, 比基于搜索的算法节省计算开销。
表5 ImageNet数据集上ResNet-50模型应用各剪枝方法的对比
Table 5 Comparison of various pruning methods applied to ResNet-50 on ImageNet
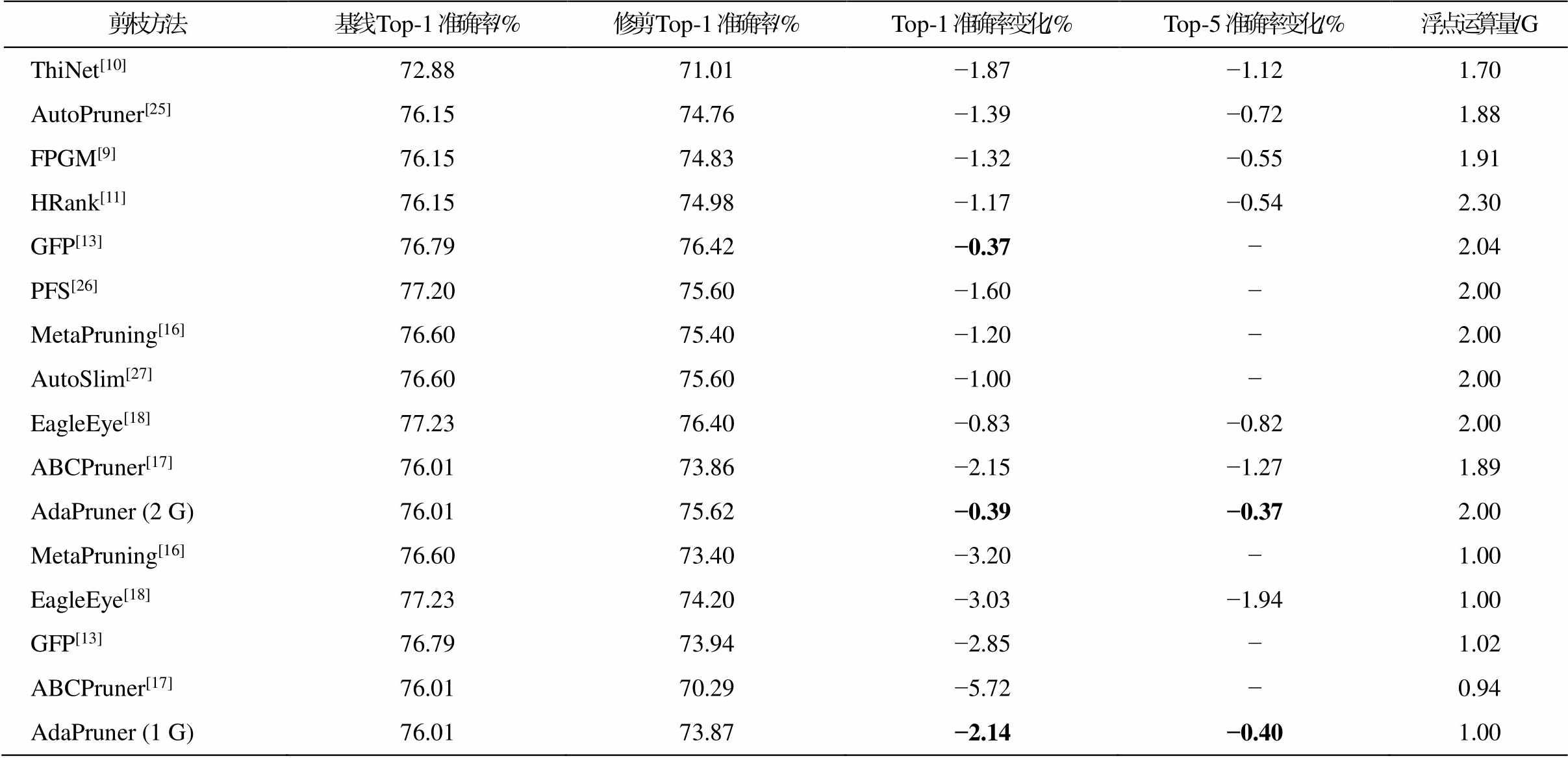
剪枝方法基线Top-1 准确率/%修剪Top-1 准确率/%Top-1 准确率变化/%Top-5 准确率变化/%浮点运算量/G ThiNet[10]72.8871.01−1.87−1.121.70 AutoPruner[25]76.1574.76−1.39−0.721.88 FPGM[9]76.1574.83−1.32−0.551.91 HRank[11]76.1574.98−1.17−0.542.30 GFP[13]76.7976.42−0.37−2.04 PFS[26]77.2075.60−1.60−2.00 MetaPruning[16]76.6075.40−1.20−2.00 AutoSlim[27]76.6075.60−1.00−2.00 EagleEye[18]77.2376.40−0.83−0.822.00 ABCPruner[17]76.0173.86−2.15−1.271.89 AdaPruner (2 G)76.0175.62−0.39−0.372.00 MetaPruning[16]76.6073.40−3.20−1.00 EagleEye[18]77.2374.20−3.03−1.941.00 GFP[13]76.7973.94−2.85−1.02 ABCPruner[17]76.0170.29−5.72−0.94 AdaPruner (1 G)76.0173.87−2.14−0.401.00
说明: AdaPruner ( )中数字表示浮点运算量。
表6 ImageNet数据集上MobileNetV2模型应用各剪枝方法的对比
Table 6 Comparison of various pruning methods applied to MobileNetV2 on ImageNet
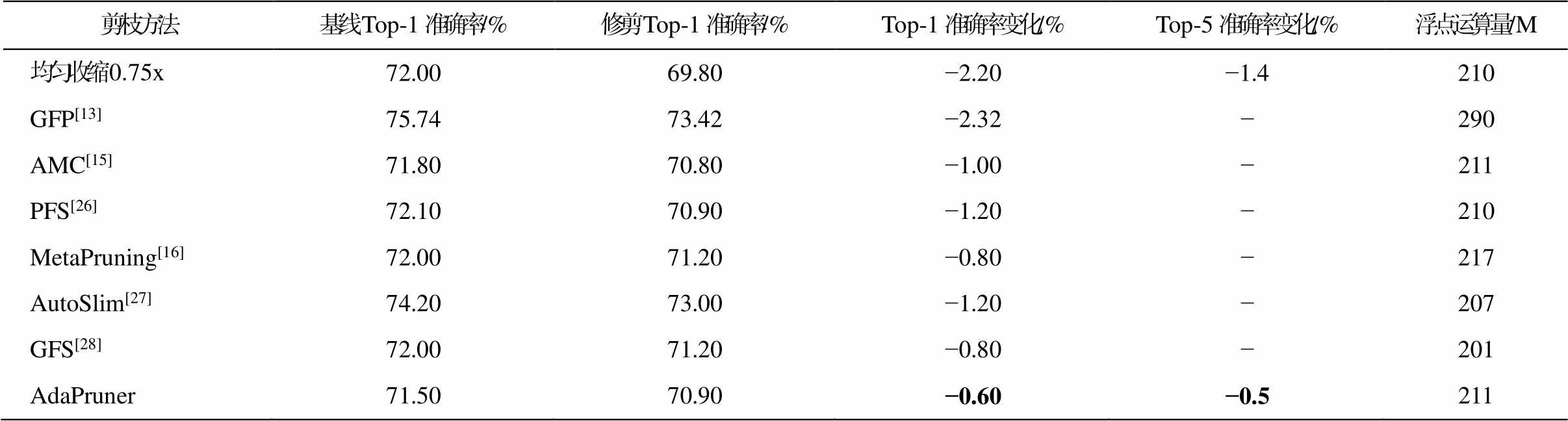
剪枝方法基线Top-1准确率/%修剪Top-1准确率/%Top-1准确率变化/%Top-5准确率变化/%浮点运算量/M 均匀收缩0.75x72.0069.80−2.20−1.4210 GFP[13]75.7473.42−2.32−290 AMC[15]71.8070.80−1.00−211 PFS[26]72.1070.90−1.20−210 MetaPruning[16]72.0071.20−0.80−217 AutoSlim[27]74.2073.00−1.20−207 GFS[28]72.0071.20−0.80−201 AdaPruner71.5070.90−0.60−0.5211
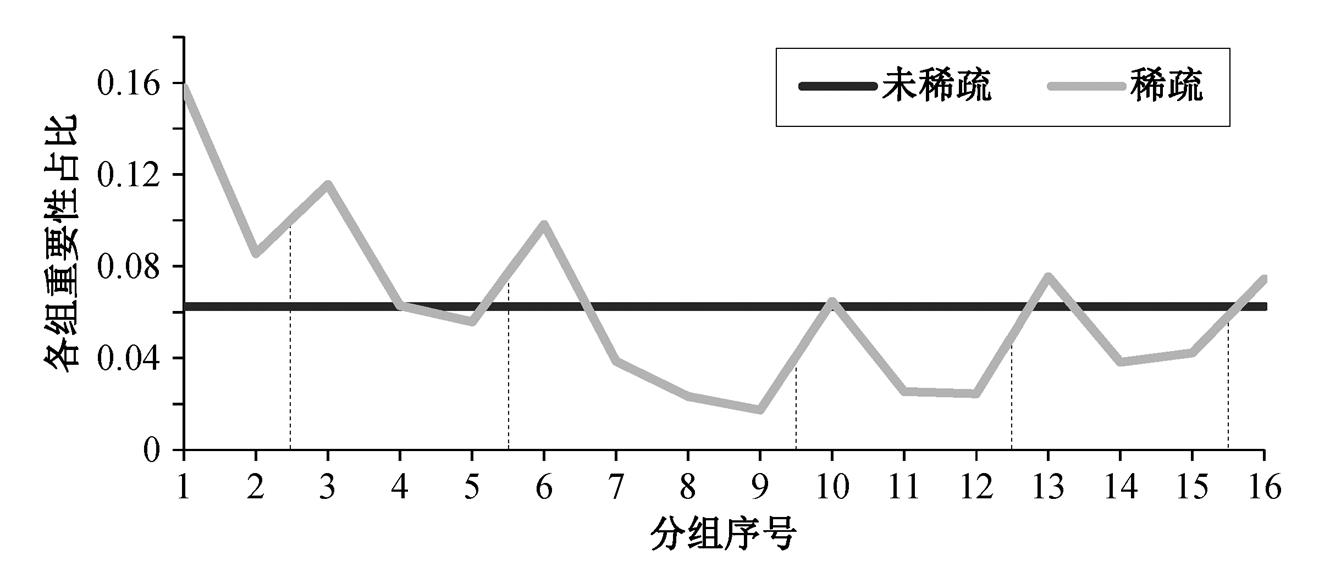
图3 稀疏训练前后分组重要性占比对比
Fig. 3 Comparison of group importance ratios before and after sparse training
将本文剪枝得到的 ResNet-50 网络结构与基于自动机器学习的剪枝算法ABCPruner[17]得到的网络结构进行对比, 分析两者的差异。图 4 显示两种方法压缩相近运算量时, 生成的子网各层的通道保留比例, 按照通道数不同, 把模型分成 4 个阶段。可以看出, 本文方法倾向在网络的首尾层和每个阶段的第一个卷积层保留更多的卷积核, 因为它们对分类更重要。基于智能搜索算法的剪枝方法[17]没有显著的特点, 可能是由于其采用的蜂群算法收敛不充分。
本文提出的基于自适应剪枝率和高效权重继承的通道剪枝算法综合考虑剪枝后模型的结构及其初始化权重, 使用稀疏训练的方式确定结构, 使用批归一化层重校准的方式快速验证初始化权重, 因此需要分别考虑这两部分对压缩后模型性能的影响。
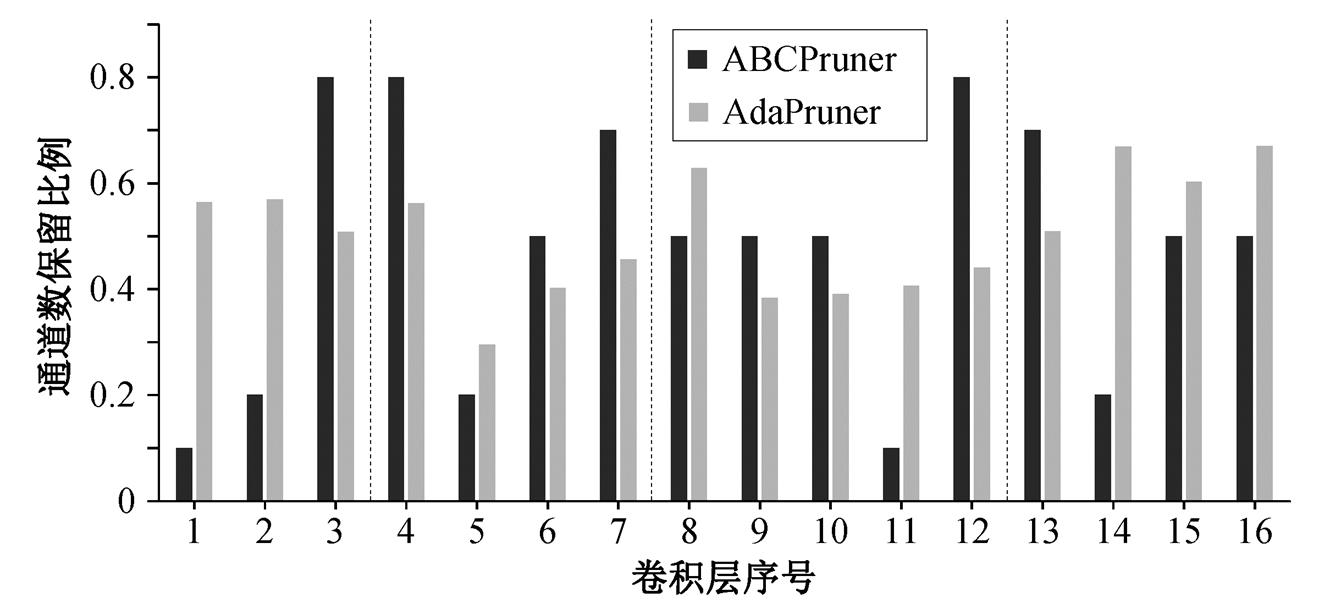
图4 不同剪枝算法生成的网络结构
Fig. 4 Comparison of network architecture generated by different pruning methods
为了证明自适应修剪产生的子网结构优于搜索产生的结构, 分别使用本文方法、ABCPruner[17]和随机剪枝方式, 在相同计算量约束下修剪 ResNet-110, 并且都使用 L1 范数作为权重选择的标准。按照相同的策略, 在 CIFAR-10 数据集上训练网络并比较精度, 结果如表 7 所示。可以看出, 自适应剪枝方法在网络结构方面优于基于自动机器学习的方法, 并且不需要反复搜索。基于搜索的算法甚至比随机修剪的性能差, 主要是因为它的搜索和验证过程都很复杂, 需要重新训练子网, 造成收敛不充分。
通过实验验证批归一化校准的必要性。使用本文方法对 ResNet-56 和 ResNet-110 分别生成剪枝模型结构, 然后按照随机化、L1 范数、指示器权重值大小和几何中心的准则, 分别初始化模型参数, 比较它们校准批归一化层后的精度以及微调训练后的精度, 实验结果如表 8 所示。可以发现, 经过校准后, 网络的精度与微调后的精度有很强的正相关, 表明其可以作为验证子网潜力的有效方法。此外, 本文提出的高效权重继承方法可以自动选择适合当前结构的初始化权重, 进一步提高了性能。
针对现有的通道卷积方法需要反复迭代修剪,搜索成本高昂, 性能表现不佳的问题, 本文提出一种基于自适应剪枝率与高效权重继承的神经网络通道剪枝框架 AdaPruner。它通过一次稀疏训练, 就能获得模型各个分组的相对重要性, 然后根据不同的预算要求, 动态地分配计算资源, 避免重复搜索。将剪枝网络的结构和权重结合起来考虑, 通过批归一化重校准的方式, 快速地选择适合当前结构的初始化参数。实验结果表明, 本文方法在普通的残差网络和轻量化网络上超越以往的剪枝算法, 取得更好的精度(复杂度平衡)。
表7 相同初始化权重下各剪枝方法的对比
Table 7 Comparison of various pruning methods with the same initialization weights
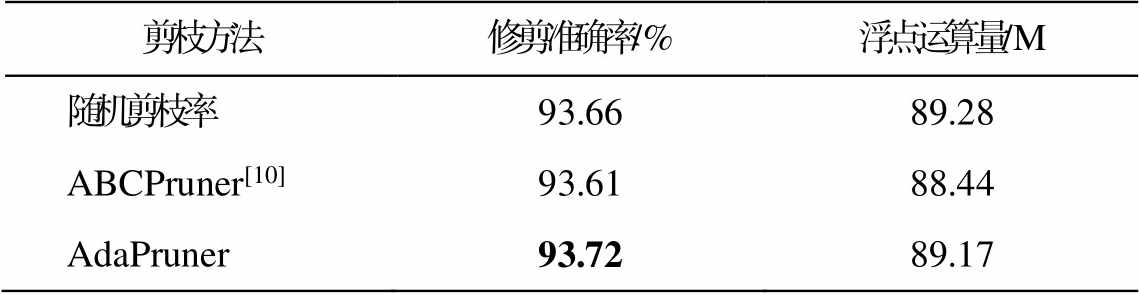
剪枝方法修剪准确率/%浮点运算量/M 随机剪枝率93.6689.28 ABCPruner[10]93.6188.44 AdaPruner93.7289.17
表8 相同结构下不同初始化权重的精度
Table 8 Accuracy of different initialization weights with the same architecture
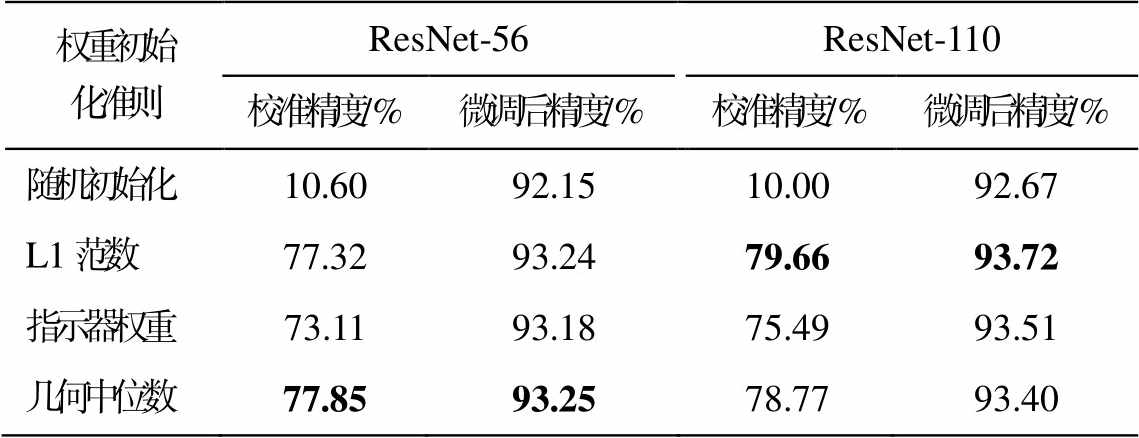
权重初始化准则ResNet-56ResNet-110校准精度/%微调后精度/%校准精度/%微调后精度/% 随机初始化10.6092.1510.0092.67 L1范数77.3293.2479.6693.72 指示器权重73.1193.1875.4993.51 几何中位数77.8593.2578.7793.40
未来的工作中, 我们将探索如何将本文提出的剪枝方案与量化和蒸馏等手段相结合, 在更高的压缩率下提升模型的性能。
参考文献
[1] Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions // IEEE Conference on Computer Vision and Pattern Recognition. Boston, 2015: 1–9
[2] Ren S, He K, Girshick R, et al. Faster R-CNN: towards real-time object detection with region proposal net-works. IEEE Transactions on Pattern Analysis & Ma-chine Intelligence, 2017, 39(6): 1137–1149
[3] Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation // IEEE Conferen-ce on Computer Vision and Pattern Recognition. Bos-ton, 2015: 3431–3440
[4] LeCun Y, Denker J, Solla S. Optimal brain damage // Advances in Neural Information Processing Systems. Denver, 1989: 598–605
[5] Hassibi B, Stork D G, Wolff G J. Optimal brain surgeon and general network pruning // IEEE International Conference on Neural Networks. San Francisco, 1993: 293–299
[6] Han S, Mao H, Dally W J. Deep compression: com-pressing deep neural network with pruning, trained quantization and Huffman coding [EB/OL]. (2015–11–20)[2022–09–11]. https://arxiv.org/abs/1510.00149v3
[7] Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural network // Proceedings of the 28th International Conference on Neural In-formation Processing Systems. Montreal, 2015: 1135–1143
[8] Li H, Kadav A, Durdanovic I, et al. Pruning filters for efficient convnets [EB/OL]. (2017–03–10)[2022–09–11]. https://arxiv.org/abs/1608.08710v3
[9] He Y, Liu P, Wang Z, et al. Pruning filter via geometric median for deep convolutional neural networks ace-leration // IEEE Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 4340–4349
[10] Luo J H, Wu J, Lin W. Thinet: A filter level pruning method for deep neural network compression // IEEE International Conference on Computer Vision. Venice, 2017: 5058–5066
[11] Lin M, Ji R, Wang Y, et al. Hrank: filter pruning using high-rank feature map // IEEE Conference on Com-puter Vision and Pattern Recognition. Seattle, 2020: 1529–1538
[12] Liu Zhuang, Li Jianguo, Shen Zhiqiang, et al. Learning efficient convolutional networks through network slim-ming // IEEE International Conference on Computer Vision. Venice, 2017: 2736–2744
[13] Liu L, Zhang S, Kuang Z, et al. Group fisher pruning for practical network compression // International Con-ference on Machine Learning. Vienna, 2021: 7021–7032
[14] Liu Z, Sun M, Zhou T, et al. Rethinking the value of network pruning [EB/OL]. (2019–03–05) [2022–09–11]. https://arxiv.org/abs/1810.05270
[15] He Y, Lin J, Liu Z, et al. AMC: automl for model compression and acceleration on mobile devices // Proceedings of the European conference on computer vision (ECCV). Munich, 2018: 784–800
[16] Liu Z, Mu H, Zhang X, et al. Metapruning: meta learning for automatic neural network channel pruning // IEEE International Conference on Computer Vision. Seoul, 2019: 3296–3305
[17] Lin M, Ji R, Zhang Y, et al. Channel pruning via auto-matic structure search [EB/OL]. (2020–06–29)[2022–09–11]. https://arxiv.org/abs/2001.08565v3
[18] Li B, Wu B, Su J, et al. Eagleeye: fast sub-net eva-luation for efficient neural network pruning // Euro-pean conference on computer vision. Cham: Springer, 2020: 639–654
[19] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition // IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, 2016: 770–778
[20] Sandler M, Howard A, Zhu M, et al. MobileNetV2: inverted residuals and linear bottlenecks // IEEE Con-ference on Computer Vision and Pattern Recognition. Salt Lake City, 2018: 4510–4520
[21] Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift // International Conference on Machine Learning. Lille, 2015: 448–456
[22] Yu J, Huang T S. Universally slimmable networks and improved training techniques // IEEE International Conference on Computer Vision. Seoul, 2019: 1803–1811
[23] He Y, Zhang X, Sun J. Channel pruning for ace-lerating very deep neural networks // Proceedings of the IEEE International Conference on Computer Vision. Venice, 2017: 1389–1397
[24] He Y, Kang G, Dong X, et al. Soft filter pruning for accelerating deep convolutional neural networks [EB/ OL]. (2018–08–21) [2022–09–11]. https://arxiv.org/ abs/1808.06866
[25] Luo J H, Wu J. Autopruner: an end-to-end trainable filter pruning method for efficient deep model infe-rence. Pattern Recognition, 2020, 107: 107461
[26] Wang Y, Zhang X, Xie L, et al. Pruning from scratch. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(7): 12273–12280
[27] Yu J, Huang T. AutoSlim: towards one-shot architec-ture search for channel numbers [EB/OL]. (2019–06–01)[2022–09–11]. https://arxiv.org/abs/1903.11728v2
[28] Ye M, Gong C, Nie L, et al. Good subnetworks pro-vably exist: pruning via greedy forward selection // International Conference on Machine Learning. Vien-na, 2020: 10820–10830
AdaPruner: Adaptive Channel Pruning and Effective Weights Inheritance
Abstract Previous channel pruning methods require complex search and fine-tuning processes and are prone to fall into local optimal solutions. To solve this problem, the authors propose a novel channel pruning framework AdaPruner, which can generate corresponding sub-networks adaptively for various budget complexities and efficiently select the initialization weights suitable for the current structure by sparse training once. Experimental results show that the proposed method achieves better performance than previous pruning methods on both commonly used residual networks and lightweight networks on multiple datasets for image classification task.
Key words convolutional neural network; channel pruning; sparse training; neural network architecture search; image classification