北京大学学报(自然科学版) 第59卷 第5期 2023年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 5 (Sept. 2023)
国家重点研发计划项目(2018YFE0203801)资助
doi: 10.13209/j.0479-8023.2023.065
收稿日期: 2022–10–07;
修回日期: 2023–01–13
摘要 提出一种基于知识蒸馏的脉冲神经网络(SNN)强化学习方法 SDN。该方法利用 STBP 梯度下降法, 实现深度神经网络(DNN)向 SNN 强化学习任务的知识蒸馏。实验结果表明, 与传统的 SNN 强化学习和 DNN 强化学习方法相比, 该方法可以更快地收敛, 能获得比 DNN 参数量更小的 SNN 强化学习模型。将 SDN 部署到神经形态学芯片上, 证明其功耗比 DNN 低, 是高性能的 SNN 强化学习方法, 可以加速 SNN 强化学习的收敛。
关键词 脉冲神经网络; 强化学习; 知识蒸馏
大脑是动物最重要的器官。自从 Legallois[1]定义了大脑区域的特定功能以来, 脑神经学吸引了许多研究人员进行仿造大脑系统的实验研究。1958 年, Rosenblatt[2]建立一个基于大脑神经元的感知机模型, 为神经网络(neural network, NN)的发展开辟了道路。Pisarchik 等[3]将猴子大脑神经元脉冲转化为控制外部设备的指令。Carpenter 等[4]构建的神经模式识别机架构为后来各种神经形态芯片(包括 True-North[5], Loihi[6]和 Tianjic[7])的设计提供了思路。
自 AlexNet[8]提出以来, 深度神经网络(deep neural network, DNN)在语音和图像处理等方面表现出优异性能。然而, DNN 的高性能基于非常高的功耗。与 DNN 相比, 脉冲神经网络(spiking neural network, SNN)[9]作为第三代神经网络, 具有更低的功耗和更强的生物可解释性, 有望以接近脑神经元范式的形式, 完成更复杂的认知问题。
基于 SNN 的应用正在逐步完善。在分类方面, Massa 等[10]使用 DVS 进行手势识别; 在目标检测方面, Kim 等[11]提出 Spiking Yolo。上述基于监督学习的应用通过学习标签, 在精度上取得良好的结果。基于 SNN 的强化学习研究也在进行中, Zheng 等[12]使用 STDP 训练硬件友好的 actor critical 网络; Yuan等[13]通过结合 hedonistic synapse 模型和 STDP 训练 SDC 网络; Azimirad 等[14]利用 STDP 训练 TCT 网络; Sharifizadeh 等[15]使用 R-STDP 训练 R-SNN 网络; Patel 等[16]基于 DNN 训练 DQN 网络, 然后将其转换为 SNN。多数传统研究中倾向于使用 STDP 及其改进算法来实现 SNN 强化学习, 这种方式的训练网络速度慢, 精度不高。
为有效地训练 SNN, Wu 等[17]提出 STBP 算法。实验结果表明, 在分类网络上, 通过 STBP 算法训练的 SNN 的性能和收敛速度明显优于 STDP 算法。然而, STBP 算法使用脉冲频率编码[18], 使得模型对应的输出精度很低, 导致直接使用 STBP 算法训练SNN 强化学习模型时, 在搜索动作空间这一行为上存在困难。本文把这种现象称为行动搜索空间的压缩。
本文从知识蒸馏[19]的概念中得到启发, 提出利用脉冲蒸馏网络(Spiking Distillation Network, SDN)来解决这一问题。将用 DNN 教师网络训练 DNN 学生网络的方式转变为用 DNN 教师网络训练 SNN 学生网络, DNN 负责强化学习的搜索动作空间行为, 然后 DNN 向 SNN 蒸馏, 避免让 SNN 搜索动作空间, 同时也进一步压缩 SNN 的容量。在蒸馏过程中, 利用高效的 STBP 算法来训练 SNN 强化学习模型, 可以避免利用 STBP 直接进行强化学习而造成动作搜索空间压缩的问题。
SDN 的训练是基于训练有素的 DNN 强化学习教师网络, 本文使用 DQN[20]和 DDQN[21]来训练DNN 教师网络。假设在一个智能体与环境交互的场景中, 环境每个时刻向智能体提供从当前时刻开始往前 T 个时刻对应的状态 S∈RT×H×W 以及奖励。时间维度是合并到通道维度上的。本文中, 环境提供的状态是图像, H和W分别表示图像的高度和宽度, 智能体根据状态选择下一动作a1或a2。智能体将获取的状态输入DNN 后, DNN预测所选动作a1和a2对应的Q值(Q 表示从当前时刻到游戏结束, 智能体可以获得的奖励总值)。智能体选择Q值最高的动作作为其下一动作。对应上述场景, DQN的损失函数表示如下:
![]() (1)
(1)
其中, QL 是层数为 L 的 DNN, γ 是对 DNN 预测结果的怀疑比例值, St 和 Rt 是从经验池中随机抽取的状态和奖励。DDQN 与 DQN 的不同之处在于, DDQN相对于 DNN 的参数更新会滞后一段时间, 从而使得 Q 值更加接近真实情况。
需要说明的是, SDN 并不限定强化学习 DNN 的训练方法, 也可以使用其他强化学习方法来训练本文中的 DNN 教师网络, 例如 DDPG[22], TD3[23]以及PPO[24]等。
SDN 是一个 DNN 教师网络向 SNN 学生网络蒸馏的训练框架(图 1)。与训练教师网络方法不同的是, 该框架内, 环境会分别为 DNN 教师网络和SNN 学生网络提供不同的状态, 且不提供奖励。
对于 DNN 教师网络, 环境为其提供从当前时刻开始往前 T 个时刻对应的状态, 即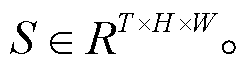 对于 SNN 学生网络, 这些状态为
对于 SNN 学生网络, 这些状态为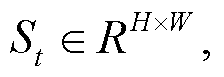 是按时间顺序提供, 而不是合并在通道维度, 这为 SNN 提供了额外的时间维度信息。
是按时间顺序提供, 而不是合并在通道维度, 这为 SNN 提供了额外的时间维度信息。
使用 Leaky Integrate-and-Fire (LIF)神经元[25]表示本文的 SNN 模型。LIF 神经元的输出由脉冲输入、膜电位和阈值电位决定。膜电位随着脉冲输入而累积, 当膜电位超过阈值电位时, LIF 神经元发放脉冲。膜电位将随着时间的推移产生泄漏而下降。LIF 神经元的表达式如下:
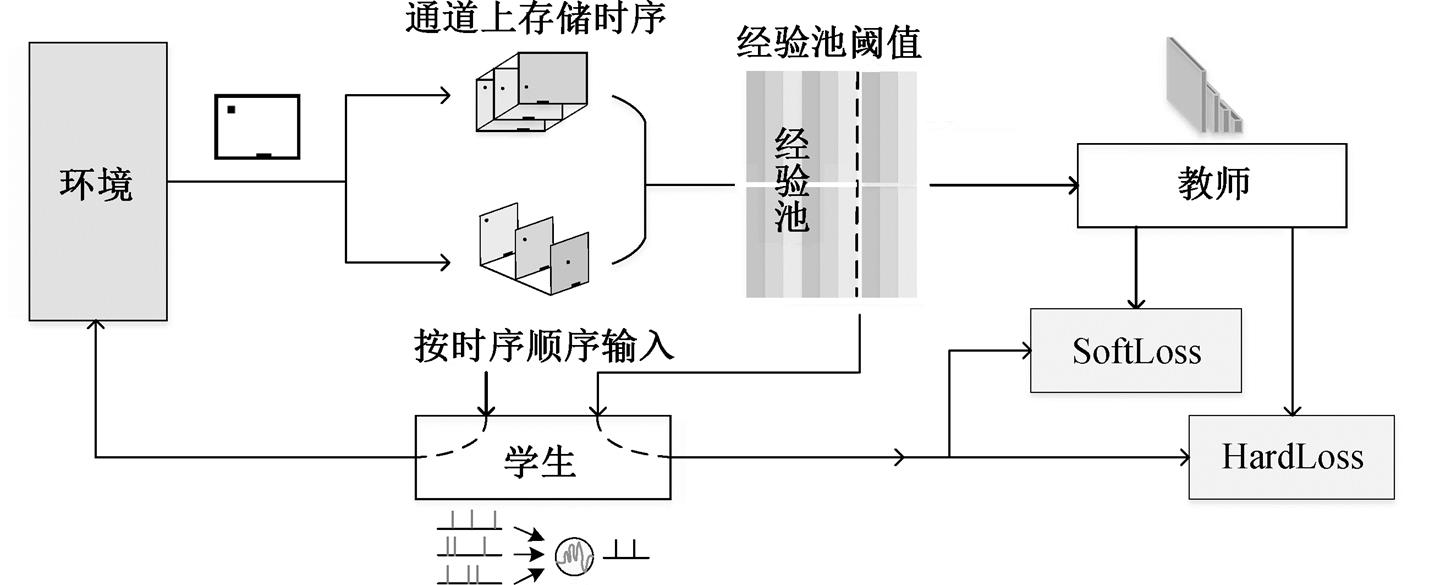
图1 SDN的架构
Fig. 1 Architecture of SDN
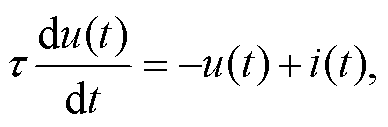 (2)
(2)
其中, u(t)是 LIF 神经元在时刻 t 的膜电位, τ 是泄漏比例, i(t)是输入脉冲和权重乘累加的结果。
为使用 STBP 算法[17], 本文将 LIF 神经元的表达分为 3 个部分: 计算 i(t)、膜电位积累 u(t)和发放脉冲(式(3)~(5))。经过脉冲层层发放, 网络输出层发放脉冲, 并统计脉冲个数(式(6))。最后进行脉冲频率解码(式(7)), 得到最终结果。
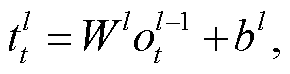 (3)
(3)
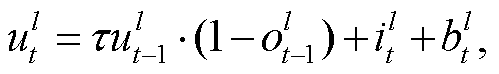 (4)
(4)
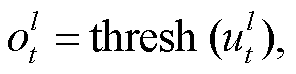 (5)
(5)
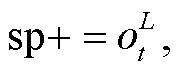 (6)
(6)
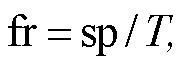 (7)
(7)
其中, t 是时间, l 是 SNN 学生网络层数的序号,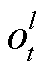 表示 SNN 第 l 层在t时刻的脉冲发放情况,
表示 SNN 第 l 层在t时刻的脉冲发放情况, ![]() 是阈值电位, sp 表示输出脉冲的个数, fr 表示脉冲频率编码的输出。
是阈值电位, sp 表示输出脉冲的个数, fr 表示脉冲频率编码的输出。
τ 是 STBP 中 LIF 神经元获取时间维度信息的重要参数, 它可以区分出不同时刻的输入。假设膜电位从时刻 0 到时刻 t 未超过阈值电位, 则时刻 t 的LIF 神经元膜电位为
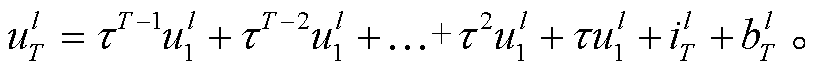 (8)
(8)
可以看出, τ 通过其自身的累乘, 对不同时刻的输入进行区分。
DNN 的卷积很难区分不同通道上不同时刻的输入, 因为所有通道上相同位置的像素将平等地相乘相加, 获得输出像素:
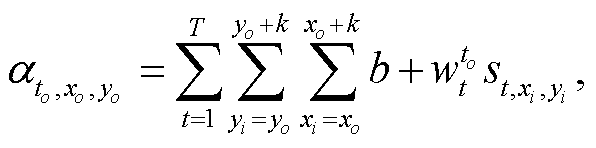 (9)
(9)
其中, ![]() 表示 DNN 输出中位置为
表示 DNN 输出中位置为 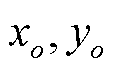 , 通道为to 处, 对应的像素值;
, 通道为to 处, 对应的像素值;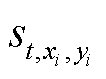 表示输入中位置为
表示输入中位置为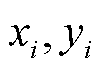 , 通道为 t 处, 对应的像素; k 表示卷积核大小;
, 通道为 t 处, 对应的像素; k 表示卷积核大小; 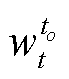 代表 DNN 中的权重。这意味着, 当 DNN 在处理通道上具有不同时间顺序的输入时, 尽管输出的每个像素都融合了不同时间维度的信息, 但每个通道的输出不再具有显著的时间顺序差异。
代表 DNN 中的权重。这意味着, 当 DNN 在处理通道上具有不同时间顺序的输入时, 尽管输出的每个像素都融合了不同时间维度的信息, 但每个通道的输出不再具有显著的时间顺序差异。
SDN 将首先积累经验池, 存储环境提供的 S 和st。st 被输入 SNN 学生网络, 获得输出 fr, 本文向环境提供 fr 作为下一步行动选择的判断依据。当经验池已满时, SDN 将利用存储在经验池中的内容来训练 SNN 学生网络。经验池的作用是破坏样本的相关性, 提高数据的利用率。
当 SDN 积累的经验池已满时, 从经验池中取出对应的环境状态S󠆴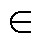 RT×H×W和 st, 分别输入 SNN 学生网络和 DNN 教师网络, 得到相应的输出 fr 和 o, 并计算这两个输出的损失函数。
RT×H×W和 st, 分别输入 SNN 学生网络和 DNN 教师网络, 得到相应的输出 fr 和 o, 并计算这两个输出的损失函数。
本文使用的损失函数是 SoftLoss 和 HardLoss 的组合[19]。将输出除以温度值, 使输出分布变得平缓, 然后用 Softmax 和 CrossEntropy 计算 SoftLoss。同时, 将教师网络的输出进行 OneHot 编码, 用 Soft-max 和 CrossEntropy 计算 HardLoss:
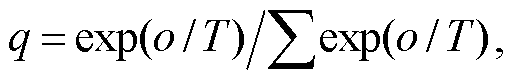 (10)
(10)
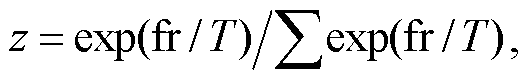 (11)
(11)
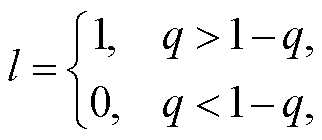
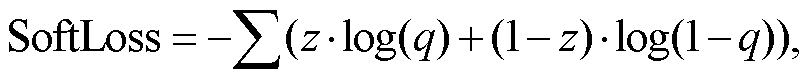 (12)
(12)
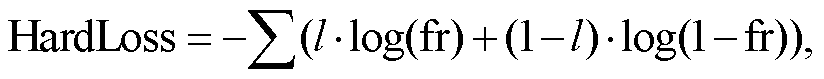 (13)
(13)
其中, o 表示 DNN 的输出, fr 表示 SNN 的输出, T 为温度值。
将 SoftLoss 和 HardLoss 按 λ 和 1 – λ 的比例相加, 得到最终的损失函数:
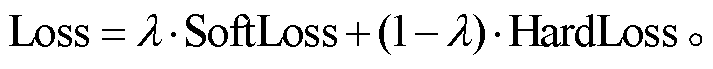 (14)
(14)
SoftLoss 和 HardLoss 的结合使 SNN 学生网络能够学习 DNN 教师网络提供的软标签, 从中学到更多的泛化信息, 加速收敛, 提高准确性。最后, 用损失函数对 SNN 执行 STBP[17]反向传播, 更新 SNN 的参数。
这里给出理论推导, 即直接使用 STBP 训练SNN 强化学习网络很难收敛。本文使用 DQN 和DDQN 训练 DNN, 并统计其输出和输出精度的变化。如图 2 所示, DNN 输出的动作值由一个小负数训练成一个大正数。然而, 脉冲频率编码的输出范围仅在 0~1 之间, 很难用如此大的变化范围来表示动作值。这使得 STBP 直接用 DQN 和 DDQN 算法训练 SNN 变得非常困难。
本文用仿射变换, 将 DNN 的输出 x 映射为STBP 脉冲频率编码的 SNN 输出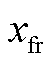 :
:
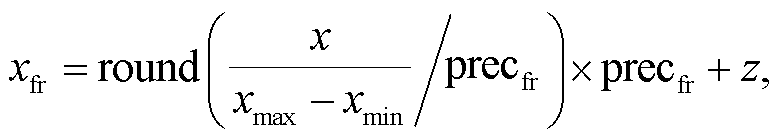 (15)
(15)
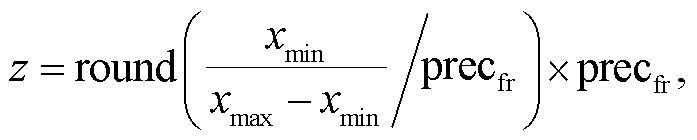 (16)
(16)
其中,precfr是 STBP 脉冲频率编码的精度。
为了使此仿射变换不造成误差, 需要至少指定
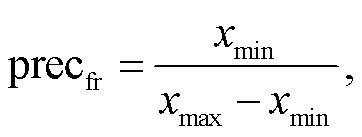 (17)
(17)
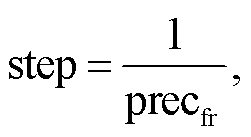 (18)
(18)
其中, step 是为获得脉冲频率编码结果, 网络需要推理的次数。可以看出, 为了不造成误差, 脉冲频率编码所需的 step 将达到 1×105, 意味着需要花费大量功耗和延时进行推理。从下面的实验中也可以得出, SDN 可以有效地避免这种搜索, 只需几个 step即可完成 SNN 强化学习的训练。
比较两种 SDN 的损失函数: MSE 函数和 Cross-Entropy 函数, 结果如图 3 所示。对于 MSE, 由于DNN 的输出范围不适合 SNN 输出的脉冲频率编码范围, 因此将 DNN 的输出映射到本文设置的范围, 以便通过 DNN 和 SNN 输出来计算损失函数。本文将映射范围分为 3 个单独的实验: 1)保留原有 DNN输出不变, 不进行线性映射; 2)使用 onehot 编码, 将 DNN 输出的最大值设为 1, 其他值均设为 0; 3)线性缩放 DNN 输出:
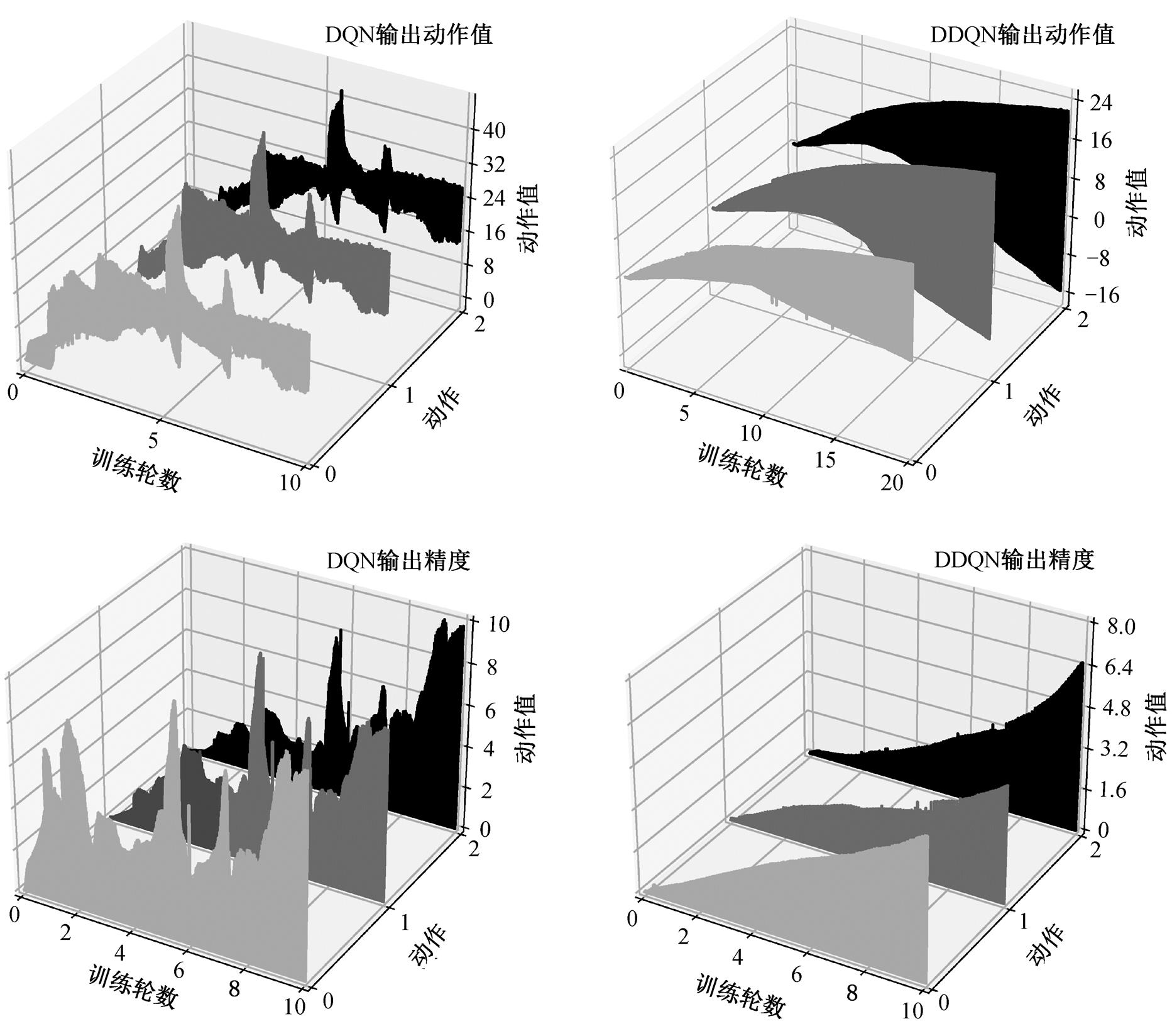
图2 DNN强化学习的动作空间搜索
Fig. 2 Search of action space in DNN reinforcement learning
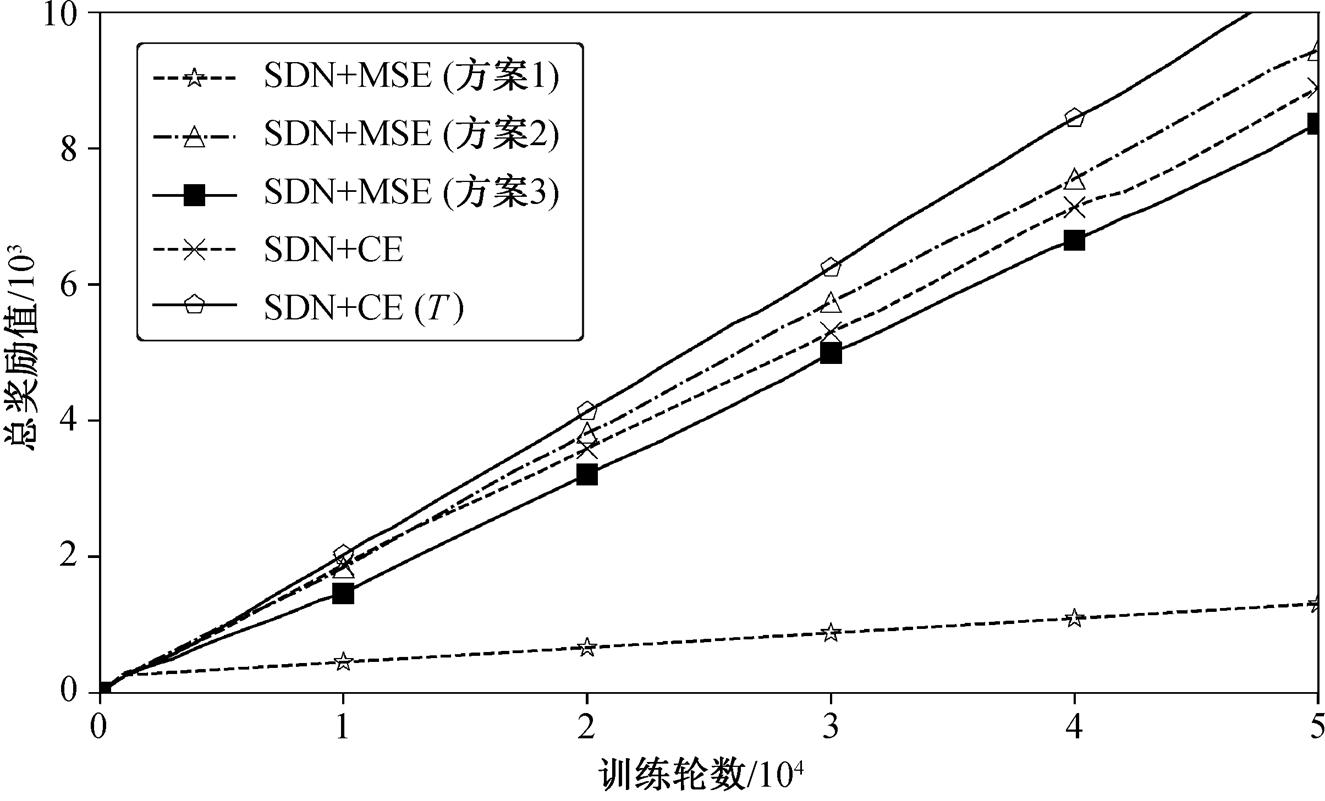
图3 SDN不同损失函数的对比
Fig. 3 Comparison of different SDN loss functions
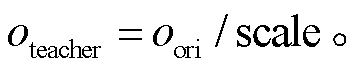 (19)
(19)
对于 CrossEntropy, 分别用 CrossEntropy 和带有温度(T)的 CrossEntropy 作为损失函数。
从图 4 可以看出, 带有温度(T)的 CrossEntropy获得的奖励值最大, 因此本文选择带有温度(T)的CrossEntropy 作为 SDN 的损失函数。
将 SDN 与其他 SNN 强化学习方法进行比较, 结果如图 4 所示。可以发现, STBP[17]与 DNN 直接结合使用, 并不能达到理想的学习效果, 而 SDN 的效果远远好于这种方式, 这与 STBP 脉冲频率编码影响动作搜索空间的解释吻合。
本文还对 SDN 与 DNN 至 SNN 的转换方法进行比较。分别设置 SNN 的时间步为 2, 4 和 16, 结果见表 1。可以发现, DNN 至 SNN 的转换方法获得的奖励比 SDN 少。因为 DNN 到 SNN 的转换后, SNN 只会重复输入同一帧而得出结果, 使得输入缺乏时间维度信息, 转换时会造成损失。SDN 直接使用 SNN训练, 含有时间维度信息, 易于收敛。
本文采用大容量 DNN 教师网络来训练小 SNN学生网络, 如图 5 所示。所有实验都在 Pong 游戏环境中执行。将 Pong 的实时游戏屏幕二值化作为环境的状态。在 Pong 游戏中, 使用 892KB 的 10 层教师网络, 而经过训练的 SNN 学生网络只有 3 层, 大小为 5KB, 压缩近 200 倍, 证明 SDN 具有训练小 SNN模型的能力。
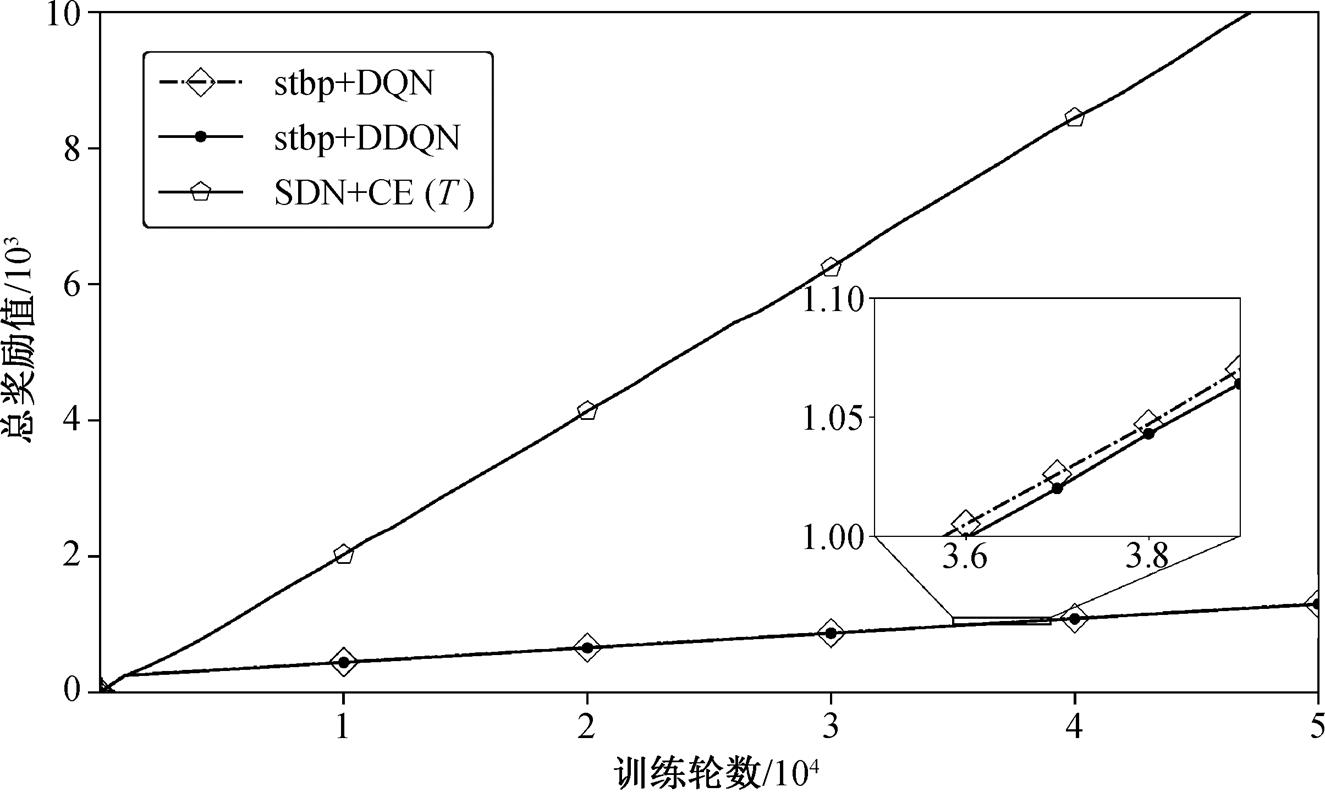
图4 SDN与其他SNN强化学习方法对比
Fig. 4 Comparison of SDN and other SNN reinforcement learning method.
表1 SDN与DNN至SNN转换方法的对比
Table 1 Comparison of SDN and DNN-to-SNN conversion method
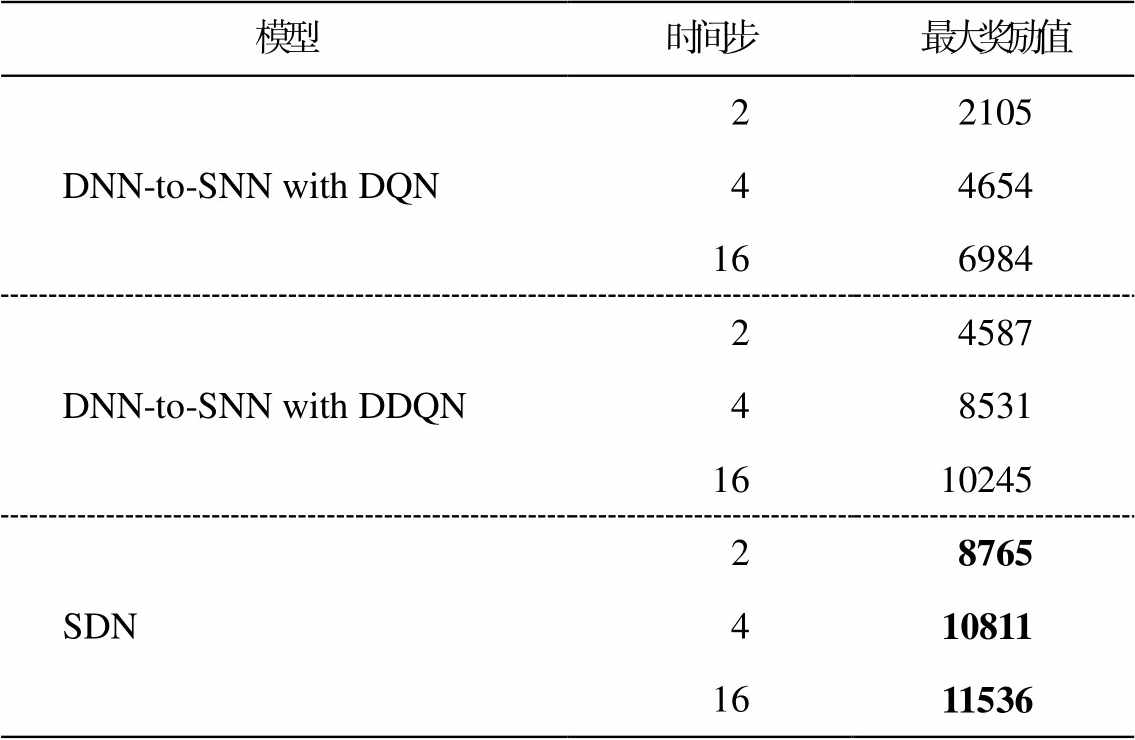
模型时间步最大奖励值 DNN-to-SNN with DQN 22105 44654 166984 DNN-to-SNN with DDQN24587 48531 1610245 SDN28765 410811 1611536
图5 Pong游戏
Fig. 5 Pong Game
将 DNN 强化学习方法与 SDN 进行比较, 结果如图 6 所示。由于结合了时间维度信息, SDN 的收敛速度比 DNN 快, 获得的奖励也比DNN 多。
为证明 SDN 在功耗方面的效果, 将其部署在神经形态学芯片 PAICORE[26]上, 并与其他设备部署功耗对比, 结果如表 2 所示。可以看出, 与NVIDIA RTX 2080 等大型设备相比较, SDN 的功耗仅为其1/600; 与 NVIDIA Jetson NX 等嵌入式设备相比, SDN 的功耗也为其 1/10。
本文提出一种新的 SNN 强化学习算法——脉冲蒸馏网络(SDN)。该方法将动作空间的搜索交给DNN 执行, 使 DNN 教师网络通过知识蒸馏方法来训练 SNN 学生网络。与传统的 SNN 和 DNN 强化学习算法相比, SDN 可以获得更好的性能。
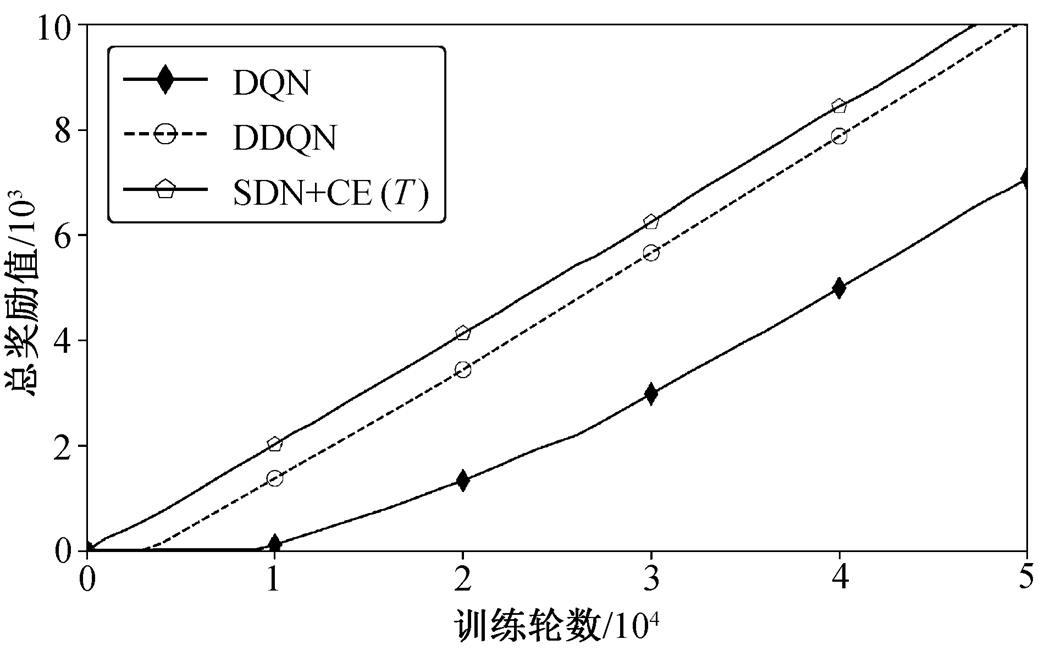
图6 SDN与DNN强化学习方法的对比
Fig. 6 Comparison of SDN and DNN reinforcement learning method
表2 SDN与DNN的网络功耗对比
Table 2 Power performance of SDN and DNN

模型设备功耗/W DNNRTX208064 RTX800062 Jetson NX1.429 SDNPAI Core0.103
实验结果证明, SDN 的收敛速度比传统的 SNN和 DNN 强化学习算法更快, 表明 SDN 具有高效性; 同时, SDN 中学生网络的容量远小于教师网络, 证明 SDN 具有压缩能力。将 SDN 部署在神经形态芯片 PAI Core 上, 测得 SDN 的功耗远远低于 DNN 模型。
未来的研究中, 可以将更多的 DNN 强化学习算法移植到 SDN 中, 如 A3C 和 DDPG 等, 并尝试使用其他蒸馏方法来提高 SDN 中 SNN 的准确性。
参考文献
[1] Legallois C. Expériences sur le principe de la vie, no-tamment sur celui des mouvemens du coeur, et sur le siège de ce principe. Paris: d’Hautel, 1812: 1–8
[2] Rosenblatt F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychological Review, 1958, 65(6): 386–389
[3] Pisarchik A N, Maksimenko V A, Hramov A E. From novel technology to novel applications: comment on “an integrated brain-machine interface platform with thousands of channels” by Elon Musk and Neuralink. Journal of Medical Internet Research, 2019, 21(10): e16356
[4] Carpenter G A, Grossberg S. A massively parallel architecture for a self-organizing neural pattern recog-nition machine. Computer Vision, Graphics, and Image Processing, 1987, 37(1): 54–115
[5] Akopyan F, Sawada J, Cassidy A, et al. Truenorth: design and tool flow of a 65 mw 1 million neuron programmable neurosynaptic chip. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2015, 34(10): 1537–1557
[6] Davies M, Srinivasa N, Lin T H, et al. Loihi: a neu-romorphic manycore processor with on-chip learning. IEEE Micro, 2018, 38(1): 82–99
[7] Pei J, Deng L, Song S, et al. Towards artificial general intelligence with hybrid Tianjic chip architecture. Nature, 2019, 572: 106–111
[8] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural net-works. Communications of the ACM, 2017, 60(6): 84–90
[9] Ghosh-Dastidar S, Adeli H. Spiking neural networks. International Journal of Neural Systems, 2009, 19(4): 295–308
[10] Massa R, Marchisio A, Martina M, et al. An efficient spiking neural network for recognizing gestures with a DVS camera on the Loihi neuromorphic processor // 2020 International Joint Conference on Neural Net-works (IJCNN). Glasgow, 2020: 1–9
[11] Kim S, Park S, Na B, et al. Spiking-yolo: spiking neural network for energy-efficient object detection // Proceedings of the AAAI Conference on Artificial In-telligence. 2020, 34(7): 11270–11277
[12] Zheng N, Mazumder P. Hardware-friendly actor-critic reinforcement learning through modulation of spike-timing-dependent plasticity. IEEE Transactions on Computers, 2016, 66(2): 299–311
[13] Yuan M, Wu X, Yan R, et al. Reinforcement learning in spiking neural networks with stochastic and deter-ministic synapses. Neural Computation, 2019, 31(12): 2368–2389
[14] Azimirad V, Sani M F. Experimental study of rein-forcement learning in mobile robots through spiking architecture of thalamo-cortico-thalamic circuitry of mammalian brain. Robotica, 2020, 38(9): 1558–1575
[15] Sharifizadeh F, Ganjtabesh M, Nowzari-Dalini A. En-hancing efficiency of object recognition in different categorization levels by reinforcement learning in modular spiking neural networks [EB/OL]. (2021–02–10) [2023–01–13]. https://arxiv.org/abs/2102.05401
[16] Patel D, Hazan H, Saunders D J, et al. Improved ro-bustness of reinforcement learning policies upon con-version to spiking neuronal network platforms applied to Atari Breakout game. Neural Networks, 2019, 120: 108–115
[17] Wu Y, Deng L, Li G, et al. Spatio-temporal backpro-pagation for training high-performance spiking neural networks. Frontiers in Neuroscience, 2018, 12: 331–333
[18] Gerstner W, Kistler W M. Spiking neuron models: Single neurons, populations, plasticity. Cambridge: Cambridge University Press, 2002
[19] Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network [EB/OL]. (2015–03–09) [2023–01–13]. https://arxiv.org/abs/1503.02531
[20] Mnih V, Kavukcuoglu K, Silver D, et al. Playing Atari with deep reinforcement learning [EB/OL]. (2013–12–19) [2023–01–13]. https://arxiv.org/abs/1312.5602
[21] Van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double Q-learning // Proceedings of the AAAI Conference on Artificial Intelligence. Phoenix, 2016: 2094–2100
[22] Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning [EB/OL]. (2015–09–09) [2023–01–13]. https://arxiv.org/abs/15 09.02971
[23] Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods // Inter-national Conference on Machine Learning. New York, 2018: 1587–1596
[24] Schulman J, Wolski F, Dhariwal P, et al. Proximal po-licy optimization algorithms [EB/OL]. (2017–07–20) [2023–01–13]. https://arxiv.org/abs/1707.06347
[25] Kuang Y, Cui X, Zhong Y, et al. A 64 K-neuron 64 m-1 B-synapse 2.64 PJ/SOP neuromorphic chip with all memory on chip for spike-based models in 65 nm CMOS. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(7): 2655–2659
[26] Burkitt A N. A review of the integrate-and-fire neuron model: I. homogeneous synaptic input. Biological cy-bernetics, 2006, 95(1): 1–19
Reinforcement Learning of Spiking Neural Network Based on Knowledge Distillation
Abstract We propose the reinforcement learning method of Spike Distillation Network (SDN), which uses STBP gradient descent method to realize the knowledge distillation from Deep Neural Network (DNN) to Spiking Neural Network (SNN) reinforcement learning tasks. Experiment results show that SDN converges faster than traditional SNN reinforcement learning and DNN reinforcement learning methods, and can obtain a SNN reinforcement learning model with smaller parameters than DNN. SDN is deployed to the neuromorphology chip, and the power consumption is lower than DNN, proving that SDN is a new and high-performance SNN reinforcement learning method and can accelerate the convergence of SNN reinforcement learning.
Key words spiking neural network (SNN); reinforcement learning; knowledge distillation