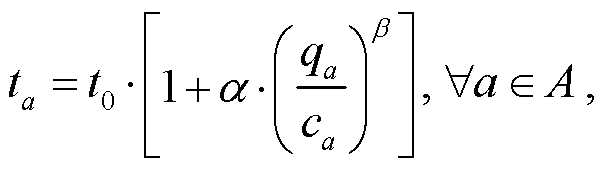 (1)
(1)
北京大学学报(自然科学版) 第59卷 第5期 2023年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 5 (Sept. 2023)
国家自然科学基金(72001017, 72288101, 72361137003, 72331001)资助
doi: 10.13209/j.0479-8023.2023.066
收稿日期: 2022–09–13;
修回日期: 2023–03–03
摘要 为了得到自动驾驶汽车(CAV)与人工驾驶汽车(HDV)并存条件下最优道路收费方案, 针对 CAV 在道路上的通行能力, 特别是对道路容量产生的影响进行量化分析, 获得道路容量与 HDV 流量和 CAV 流量之间的非线性关系。然后, 对传统的美国公路局路阻函数进行改进, 并基于改进后的路阻函数, 建立系统最优(system optimal, SO)流量分配模型, 对不同 CAV 占比条件下和不同 HDV 与 CAV 安全车距比值条件下的交通流进行系统最优分配。采用 Frank-Wolfe 算法, 对 SO 模型进行求解, 并考虑因 HDV 而产生的额外道路出行成本对不同条件下系统最优分配结果的差异性进行比较。基于最优收费理论, 针对不同规模道路网制定相应的收费方案。最后, 将模型与算法应用到 Nguyen-Dupuis 交通网络中。结果表明, 在 HDV 与 CAV 并存条件下, 以系统最优分配结果下的边际成本进行收费是道路交通系统最优拥堵收费方案, 可作为 HDV 与 CAV 并存条件下道路收费方案设计的依据。
关键词 自动驾驶汽车; 道路网络; 美国公路局路阻函数; 系统最优分配; Frank-Wolfe算法; 拥堵收费
未来城市交通由人工驾驶汽车(human-driven vehicles, HDV)时代逐步向更加智能化的自动驾驶汽车(connected autonomous vehicles, CAV)时代发展已是大势所趋[1]。与 HDV 相比, CAV 具有较多的优势, 能够优化部分 HDV 难以解决的问题, 如道路拥堵、驾驶安全和交通污染等。此外, CAV 依托先进的通信技术和自动化技术, 在将来可能改变人们的出行体验。研究表明, CAV 的普及会使道路交通拥堵得到极大的改善。首先, CAV 能够大幅度提高道路通行能力, 若道路交通流中 60%的车辆是 CAV, 其通行能力将提高一倍[2]。随着 CAV 车辆在道路交通流中占比的增大, 道路通行能力将逐步提高, 进而降低道路发生拥堵的概率。其次, CAV 可以提高出行效率, 并减少人为因素导致的交通事故[3]。第三, CAV 将减少人工操作, 出行者可以利用出行时间处理其他事务, 极大地节约出行时间成本[4–5]。第四, CAV 可以提高能源效率, 为轻型卡车节省7%~15%的燃油消耗, 为重型卡车节省 15%~21%的燃油消耗[6–8]。
目前, 针对 CAV 与 HDV 混合驾驶已开展很多研究。Berg 等[4]就 CAV 与 HDV 在道路容量、时间价值以及使用者偏好等方面进行异质性研究, 证明了 CAV 的突出作用。Chen 等[9–10]建议设立 HDV 向CAV 过渡期间的专用车道, 促使 CAV 的使用, 以便发挥 CAV 的更大优势。Wang 等[6]基于交叉嵌套的 Logit 模型和变分不等式研发的 RSRS-MSRA 算法解决了多类流量分配问题。CAV 与 HDV 流量分配的关键在于路径选择, 马华伟等[11]基于模拟退火算法, 对甩挂车的路径进行规划。然而, 上述基于 CAV 与 HDV 并存条件下交通运行特征的研究并不能缓解交通拥堵的现象。
道路拥堵收费是缓解道路拥堵问题的常用方法[12]。例如, Luo 等[13]提出采用补贴的形式, 加速从HDV 向 CAV 的转变。国外比较典型的模式有新加坡的“通行证方案”、挪威的“警戒线定价方案”、英国伦敦的“道路收费方案”和美国的“高乘载收费车道”等, 这些方案都是缓解道路拥堵的有效手 段[14]。国内典型的道路收费模式是高速公路采用的 ETC 收费系统。收费政策实施的关键是定价问题, 合理的定价方案能够被消费者接受[15–16]。目前对交通拥堵收费的研究大多基于 HDV 道路, 缺乏对 HDV 与 CAV 混合收费的研究。
本文将 CAV 与 HDV 混合交通流特征与城市拥堵收费设计问题相结合, 探讨 CAV 与 HDV 并存条件下如何在道路上进行系统最优分配, 并根据最优分配结果计算 HDV 的收费标准。首先探讨 CAV和 HDV 对拥堵道路通行能力的影响因素, 并结合混合交通流下的安全车距, 对美国公路局(Bureau of Public Road, BPR)路阻函数进行改进, 探究道路出行成本与 CAV 和 HDV 交通量之间的关系。然后, 用系统最优(system optimum, SO)流量分配模型, 结合新的道路阻抗函数, 描述 CAV 和 HDV 并存条件下的混合交通流分配问题。采用 Frank-Wolfe 算法, 对不同条件下的混合交通流 SO 模型进行求解, 得到不同条件下的系统最优分配结果。最后, 基于最优收费原理, 对当前条件下的系统最优分配结果与其他条件下的分配结果进行分析, 针对结果的差异, 计算拥堵道路上因 HDV 并存而额外产生的道路出行成本, 最终确定 CAV 与 HDV 并存条件下的最优拥堵收费方案。
BPR 函数描述路段行驶时间与路段交通负荷以及交叉口负荷与交叉口延误之间的关系。道路交通网络上的路段阻抗通常受出行时间、出行成本、出行安全、舒适度和便捷性等诸多影响因素, 其中出行时间是道路阻抗的主要因素影响[17]。在畅通的路段上, 出行时间往往与路段长度成正比, 但在城市拥堵的交通网络上, 完全畅通的路段较少, 因此车流密度与速度也是影响出行时间的重要因素。目前, BPR 函数广泛应用于交通领域。路段 a上的道路阻抗ta为
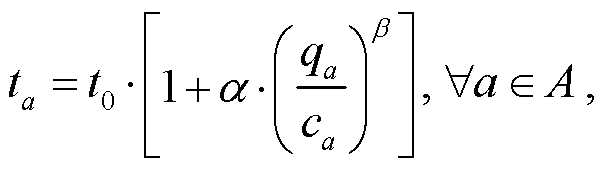 (1)
(1)
其中, A表示交通道路网; t0表示路段零流阻抗; qa表示路段a上的当前实际交通量; ca表示路段a上的道路容量; α和β为模型待定参数; 通常情况下取 α= 0.15, β=0.4。
传统的 BPR 函数针对的是单一交通流下的道路网阻抗, 在 CAV 与 HDV 并存条件下, 需要基于两种车辆对道路通行能力的影响进行分析。由于CAV 的安全车距小于 HDV 的安全车距, 因此在理论上, 同一条道路能容纳的 CAV 多于 HDV。
本文利用 CAV 占比、道路容量以及安全车距来改进 BPR 函数, 并基于安全车距进行混合交通量与原始交通量的等价转化。
CAV 占比 CAV 对道路通行能力的影响程度取决于 CAV 在混合交通流中的占比。CAV 在路段a 上的占比为
其中,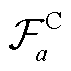 表示路段 a 上的 CAV 车流量,
表示路段 a 上的 CAV 车流量, 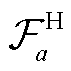 表示路段 a 上的 HDV 车流量。
表示路段 a 上的 HDV 车流量。
道路容量 假设所有车辆与车辆之间的间距不能低于法律规定的安全车距(由汽车生产公司测算刹车距离, 进而推断安全车距, 与驾驶员无关)[18], 某车辆后方跟随 CAV 的概率为 γa, 则后方跟随车是HDV 的概率为 1–γa。对于成对的车辆, CAV 跟随CAV 的概率为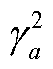 , HDV 跟随 CAV 的概率与 CAV 跟随 HDV 的概率为
, HDV 跟随 CAV 的概率与 CAV 跟随 HDV 的概率为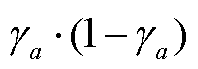 , HDV 跟随 HDV 的概率为
, HDV 跟随 HDV 的概率为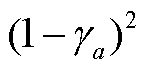 。因此, 在忽略车体长度的影响下, HDV和 CAV 并存条件下的道路容量函数为
。因此, 在忽略车体长度的影响下, HDV和 CAV 并存条件下的道路容量函数为
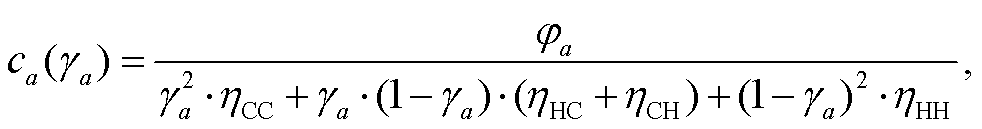 (3)
(3)
其中, φa表示路段 a 的路段长度, ![]() 表示 HDV 与HDV 之间的安全车距,
表示 HDV 与HDV 之间的安全车距, ![]() 表示 CAV 与 CAV 之间的安全车距,
表示 CAV 与 CAV 之间的安全车距, ![]() 表示 HDV 跟随 CAV 的安全车距,
表示 HDV 跟随 CAV 的安全车距, ![]() 表示 CAV 跟随 HDV 的安全车距。
表示 CAV 跟随 HDV 的安全车距。
安全车距 假设 HDV 与 CAV 保持相同的行驶速度, 并尽量与前车保持最小安全车距, 安全车距由后方车辆类型的操作反应时间决定, 则 CAV 跟随 HDV 与 CAV 的安全车距相等, HDV 跟随 CAV 与HDV 的安全车距也相等。当不考虑车身长度时, 道路长度可以容纳车辆数即为可以容纳的安全车距数量。当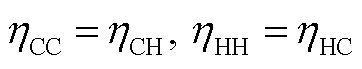 时, ca(γa)可简化为
时, ca(γa)可简化为
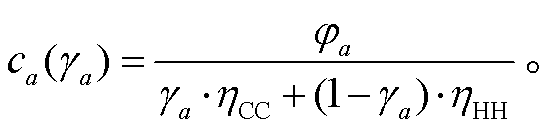 (4)
(4)
改进 BPR 函数 用 CAV 和 HDV 并存下的混合交通量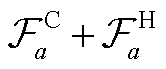 替代传统 BPR 函数的道路交通量qa。改进后的道路阻抗函数为
替代传统 BPR 函数的道路交通量qa。改进后的道路阻抗函数为
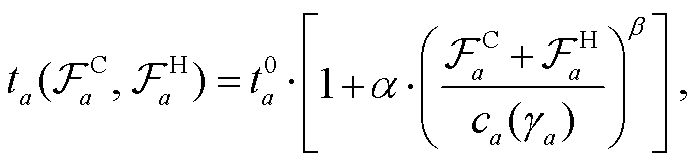 (5)
(5)
其中, 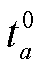 表示路段 a 上车流量为 0 时的道路阻抗。
表示路段 a 上车流量为 0 时的道路阻抗。
交通量等价转化 现存道路是 CAV 投入使用之前设计的, 现有的道路容量为 HDV 道路容量, 因此需要将道路阻抗函数变换成能用 HDV 道路容量表达的形式[19]。通过计算转化因子, 改变混合交通量的表达形式, 将 HDV 转化为等价 CAV, 或将CAV 转化为等价 HDV。基于道路的 HDV 容量, 对改进后的道路阻抗函数进行转化:
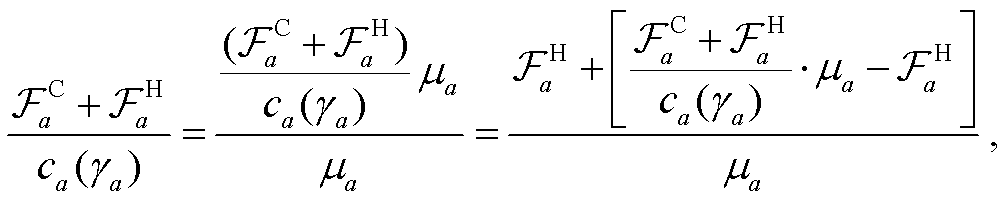 (6)
(6)
其中, μa 表示路段 a 上的纯 HDV 道路容量, 即 μa= ca(0)。基于式(2)做恒等变形, 可以得出![]()
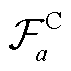 , 并将
, 并将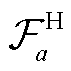 代入改进的道路阻抗函数, 可得
代入改进的道路阻抗函数, 可得
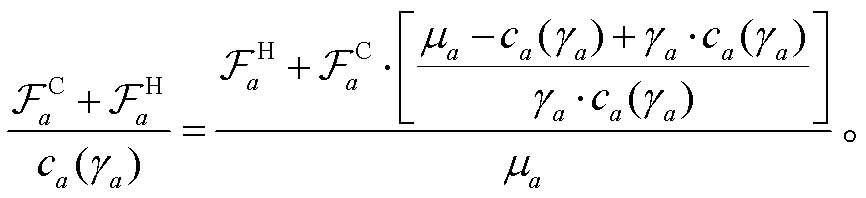 (7)
(7)
综上所述, 改进的道路阻抗函数为
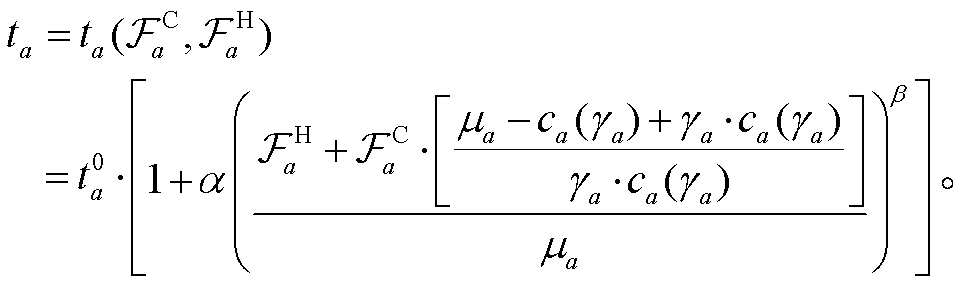 (8)
(8)
本文建立的混合交通流 SO 分配模型为
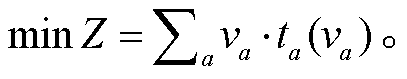 (9)
(9)
模型满足式(2)和(4)以及以下约束:
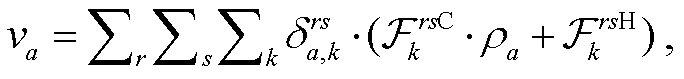 (10)
(10)
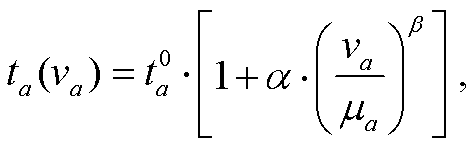 (11)
(11)
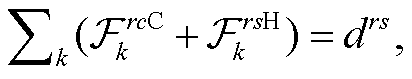 (12)
(12)
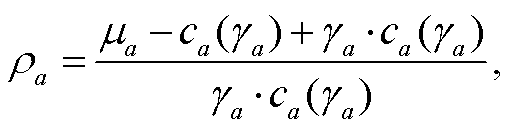 (13)
(13)
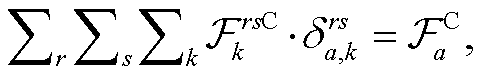 (14)
(14)
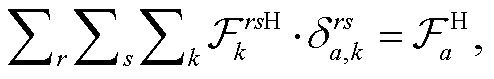 (15)
(15)
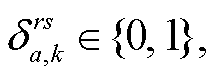 (16)
(16)
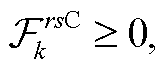 (17)
(17)
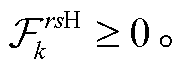 (18)
(18)
式(10)计算道路上 CAV 转化为等价 HDV 后的混合交通量 va; 式(11)计算路段 a 上混合交通量为va 的道路阻抗; 式(12)表示交通流平衡分配问题需要满足的交通流守恒条件, 即出发地到目的地(OD 对)之间各条路径交通量之和等于该 OD 对之间总交通量; 式(13)计算 CAV 转化为等价 HDV 的转化因子; 式(14)和(15)分别表示 CAV 和 HDV 在路径之间的交通量应与路段交通量满足累加关系; 式(16)~(18)分别定义各决策变量的取值范围。
由于我们是按转化因子将 CAV 转化为等价的HDV, 所以利用混合交通流计算道路阻抗时, BPR函数的模型参数可与单一交通流的取值一致。
SO 模型的目标函数包含道路混合交通流量和道路阻抗函数, 这两个中间变量之间是非线性关系, 因此该规划问题是一个非线性优化问题。针对上述非线性规划模型的求解, 采用基于梯度下降的启发式算法, 下降方向选取最速下降方向, 步长通过一维线搜索确定, 并进行循环迭代, 至达到停机准则, 得到(近似)最优解。
Frank-Wolfe 算法可用来求解非线性规划模型[20], 该算法利用线性规划逐步逼近非线性规划而求得最优解。Frank-Wolfe 算法主要由两个部分构成: 确定目标函数的可行下降方向; 利用分割法搜索最优 步长。
在交通流分配中, 首先获得拓扑化之后的 OD交通网络, 用 Dijkstra 算法得到有需求 OD 对的最短路径。然后, 通过全有全无分配, 将流量分配到最小阻抗路径上, 利用子过程的解与当前解的差值, 确定最速下降方向, 采用黄金分割法确定最优步长。最后, 按照最速下降方向不断迭代直至收敛。Frank-Wolfe 算法的具体步骤如下。
1)对整个交通网络初始化, 使所有道路的交通量为 0。基于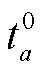 进行全有全无的分配, 获得初始交通流分配结果va。
进行全有全无的分配, 获得初始交通流分配结果va。
2)更新初始交通流分配后的路段阻抗, 令![]() 。
。
3)寻找并确定最速下降搜索方向, 进行基于ta 条件下的全有全无分配, 得出辅助路段流量集合ya(n)。
4)按照确定的最速下降方向进行一维线性搜索, 并通过黄金分割法求得满足 min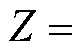
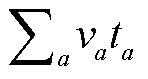 (va)目标函数下的最优步长 λ。
(va)目标函数下的最优步长 λ。
5)根据确定的最优步长, 对混合交通流分配结果进行移动: va(n+1)=va(n)+λ(ya(n)–va(n))。
6)收敛性验证。如果满足收敛准则(式(19)), 即误差小于规定的范围, 则结束计算过程, 得出最优解。否则令 n=n+1, 转向步骤 1, 进行下一次 迭代。
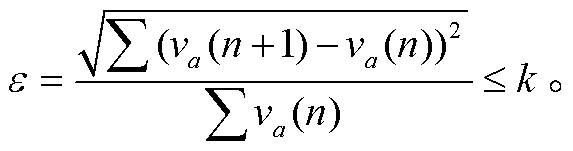 (19)
(19)
黄金分割法是通过对一维凸函数进行线性搜索而求得函数极小值的方法[21], 是以区间消去法原理为基础的试探性方法。类似于二分法, 黄金分割法的基本原理是按照 0.618 的比例将区间划分为 3 份, 舍弃区间函数值较大的区间, 从而把搜索区间缩小0.618 倍或 0.382 倍。缩小后的区间仍然包括函数极小值点, 不断进行迭代操作, 直至区间缩小至规定精度时, 即获得一维搜索的近似最优解(图 1)。综合利用 Frank-Wolfe 算法和黄金分割法, 可求解 SO模型。
人们在出行选择时, 以个人边际成本最小为依据, 不会考虑自身的出行选择给其他驾驶人员出行造成的额外成本。当出行利益大于其此次出行的边际成本时, 该出行者会选择此次出行[22]。通常情况下, 边际个人成本(marginal personal cost, MPC)小于边际社会成本(marginal social cost, MSC), 因此可以通过收取一定的费用, 弥补两者之间的差额, 具体表现形式见图 2。
根据式(4)和(8)可知, ca(γa)与 γa 成正比, ta 与 γa成反比, 因此, 当 γa=1 时, 系统总成本最低。令 γa ≠ 1 的边际成本曲线表示 MSC 曲线(式(20)), γa =1 的边际成本曲线表示 MPC 曲线(式(21))。
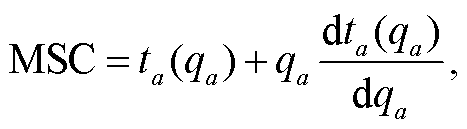 (20)
(20)
MPC = ta(qa)。 (21)
两条边际成本曲线与交通需求曲线相交于图 2 中 A和 B 两点, 分别对应交通需求为 D2 和 D1 的 MPC 和MSC。当道路交通需求固定不变时, 以 D2 为例, 与两条边际成本曲线相交于 A 和 M 两点。
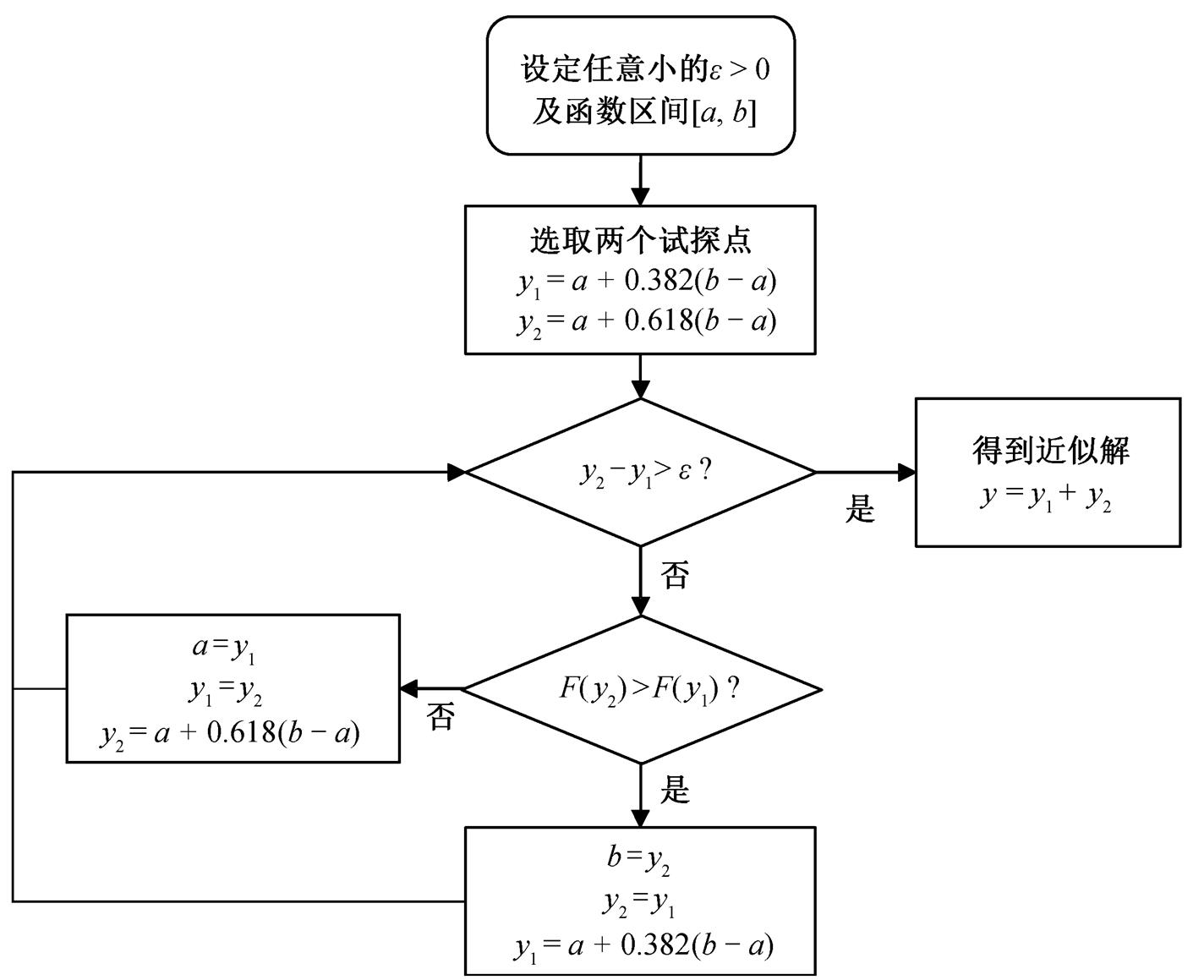
图1 黄金分割法流程
Fig. 1 Flowchart of the golden section method
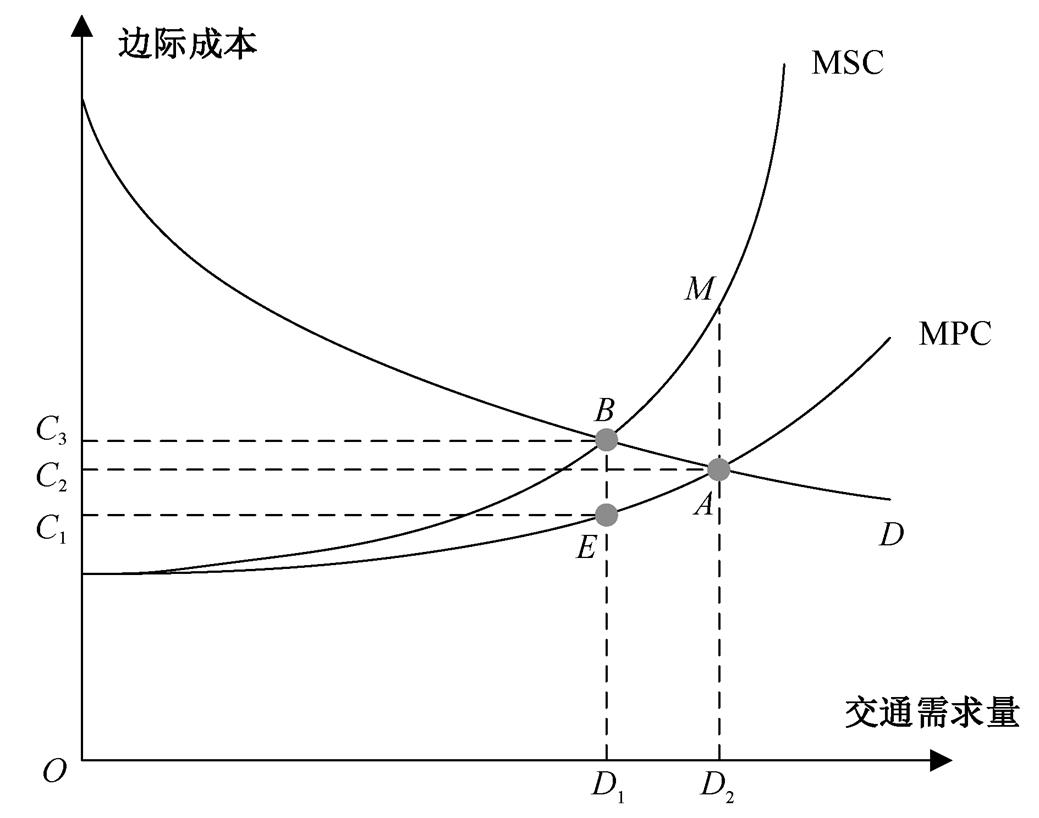
图2 拥挤定价关系示意图[12]
Fig. 2 Crowded pricing relationship diagram[12]
在模型中, OD 对之间的交通需求量是固定不变的, 当 γa 发生改变时, 导致混合交通量发生改变, 使 MSC 高于 MPC。最优拥堵收费水平用∆C 表示, 为该混合交通量下 MSC 和 MPC 之差:
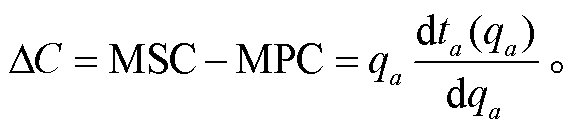 (22)
(22)
A 与 M 两点之间的边际成本差∆C 即为最优拥堵收费[23]。
以图 3 所示的 Nguyen-Dupuis 交通网络[19]为例进行数值验算。该混合道路交通网络系统共有 13个节点、19 条路段以及 4 个 OD 需求对(d12=9600veh/h, d13=19200veh/h, d42=14400veh/h, d43=4800 veh/h)。本文假设所有 OD 对的 CAV 占比 γa 相同。
为了探讨不同 CAV 占比 γa 以及 CAV 与 CAV之间安全车距对道路交通网络分配结果的影响, 首先固定 ηHH/ηCC, 并对 γa 在 0~1 之间取不同的值(步长为 0.2)进行计算; 然后固定 γa, 并对 ηHH/ηCC 在1~5 之间取不同的值(步长为 0.5)进行计算。计算结果表明, ρa 只与 ηHH/ηCC 有关, 并成反比关系。图 4示意 ηHH/ηCC 与 ρa 的关系, 本算例中按照 ηHH/ηCC= 2.5, γa=0.4 这一道路条件进行计算演示, 交通量转化因子 ρa= 0.4。
根据 CAV 占比, 将 OD 间的交通量划分为CAV交通量和 HDV 交通量。也就是, 将 d12=9600veh/h, d13=19200veh/h, d 42=14400veh/h 和 d43=4800veh/h按照 γa=0.4 可分为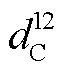 =3840veh/h,
=3840veh/h, 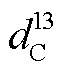 =7680veh/h,
=7680veh/h, 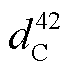 =5760veh/h,
=5760veh/h, 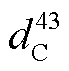 =1920veh/h,
=1920veh/h, 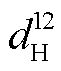 =5760veh/h,
=5760veh/h, 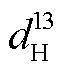 =11520veh/h,
=11520veh/h, 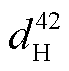 =8640veh/h 和
=8640veh/h 和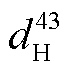 =2880veh/h, 共 8 种交通需求量, 经交通量转化因子 ρa 计算, 得出新的混合交通需求量 q12=7296veh/h, q13=14592veh/h, q42=10944veh/h 和 q43=3648veh/h。图 5 展示不同 CAV 占比与车间距比的混合交通流量, 可以发现, 固定交通需求转化的混合交通需求量与车间距比和 CAV 占比均负相关。
=2880veh/h, 共 8 种交通需求量, 经交通量转化因子 ρa 计算, 得出新的混合交通需求量 q12=7296veh/h, q13=14592veh/h, q42=10944veh/h 和 q43=3648veh/h。图 5 展示不同 CAV 占比与车间距比的混合交通流量, 可以发现, 固定交通需求转化的混合交通需求量与车间距比和 CAV 占比均负相关。
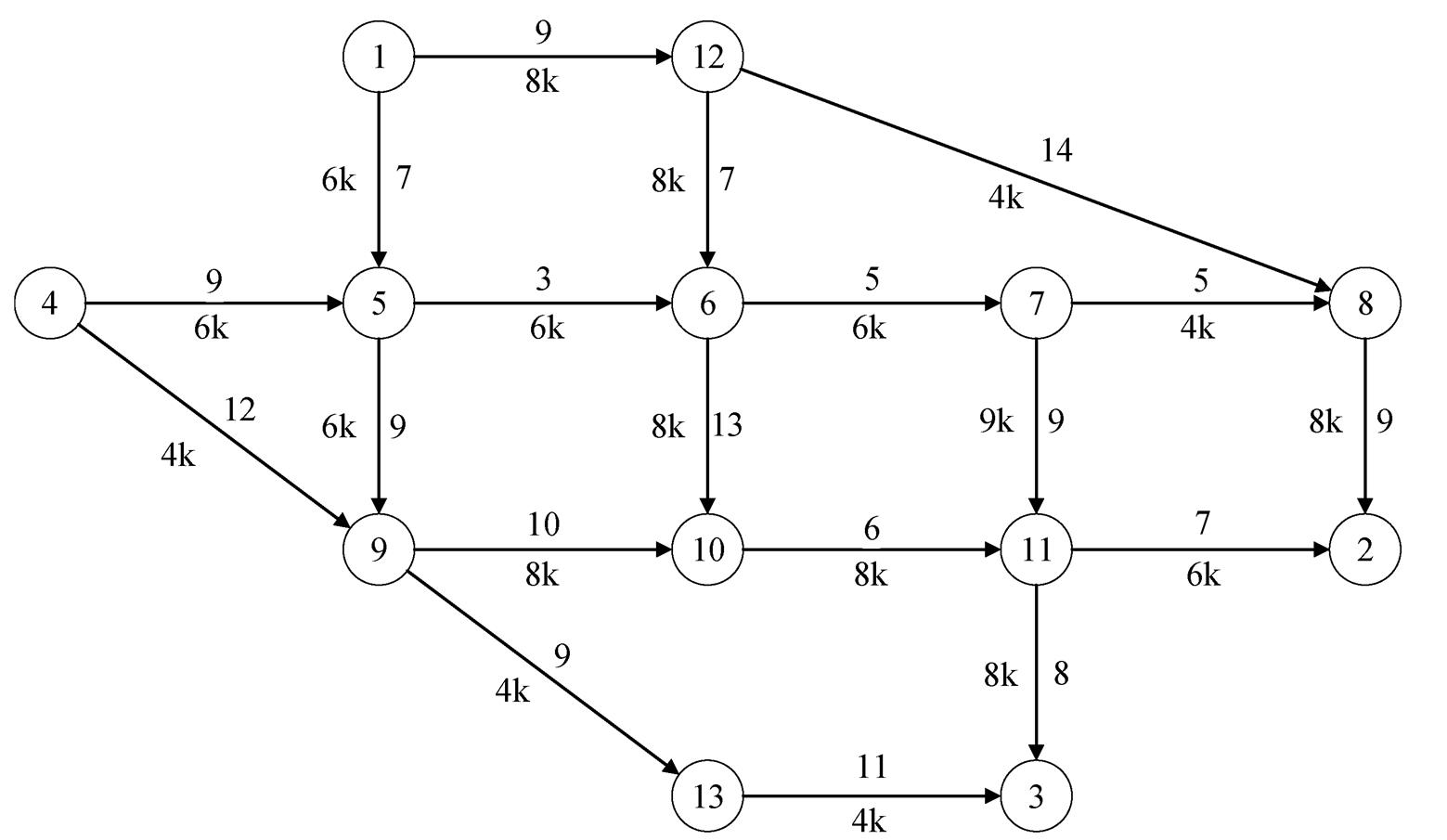
圆圈内数字为路网节点, 路网中所有路段均为单向路段, 箭头上方或右方表示路段零流阻抗, 下方或左方数字表示道路的HDV容量
图3 Nguyen-Dupuis交通网络
Fig. 3 Nguyen-Dupuis traffic network
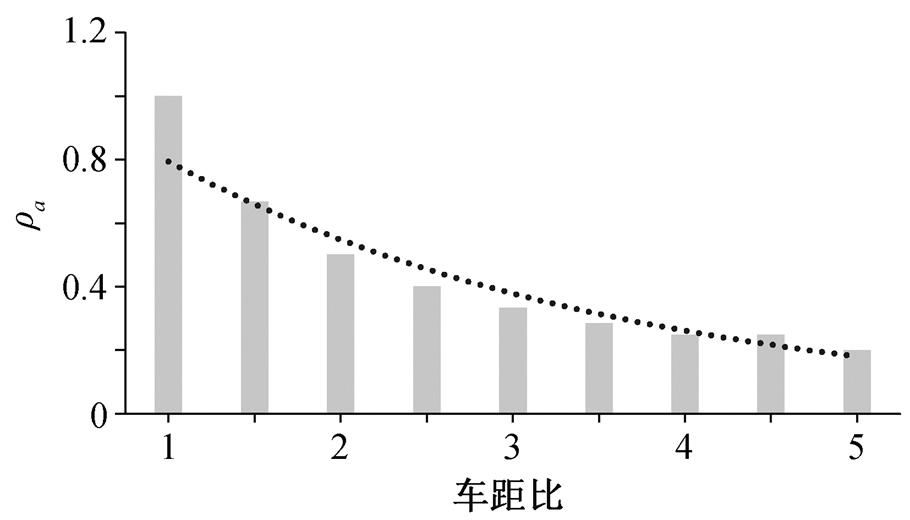
图4 不同安全车距下的ρa值
Fig. 4 Values of ρa under different safe distances
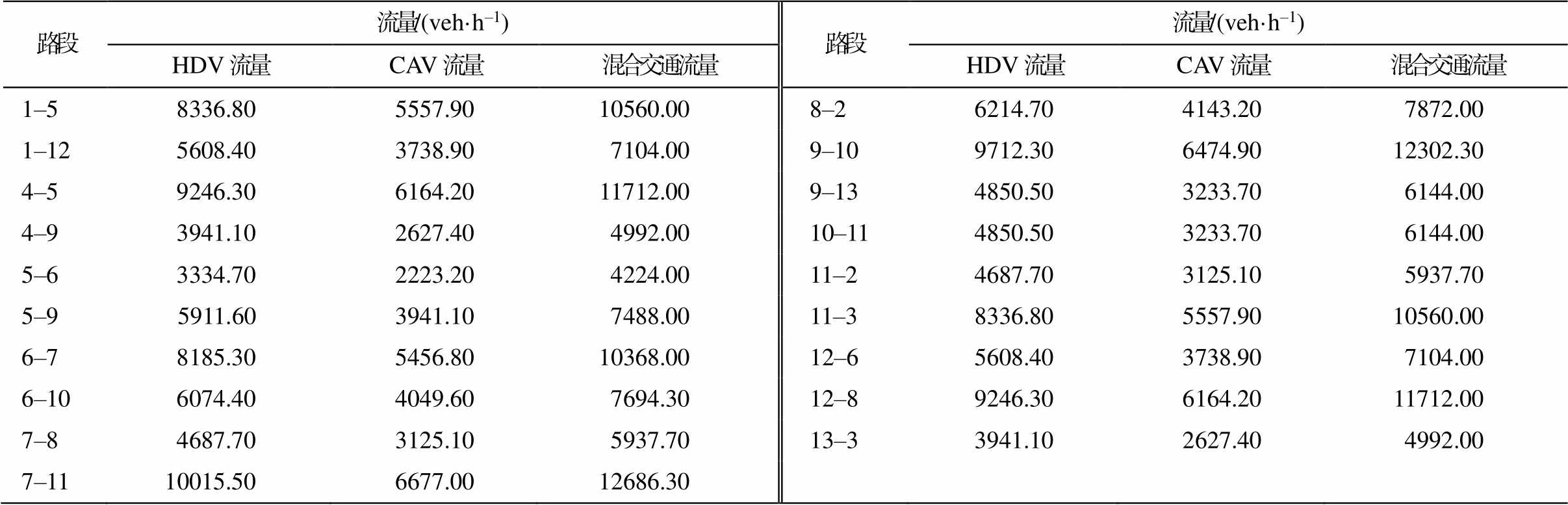
将所有路段的混合交通流量按 CAV 占比与转化系数的关系划分为 CAV 和 HDV, 根据混合交通需求量, 使用 Frank-Wolfe 算法求解 SO 模型, 得到混合交通流系统最优分配结果, 如表 1 所示。可以看出, 相较于本身的道路容量, 路段 1–5, 4–5, 6–7 和 12–8 的车流量较大, 分别超出道路容量 176%, 195%, 173%和 293%。相似地, 从表 2 可以看出, 这些路段的拥挤系数分别达到 1.76, 1.95, 1.73 和 2.93, 道路阻抗系数分别达到 7.32, 15.89, 12.81 和 15.89。特别是路段 12–8, 因零流阻抗较大, 且道路容量较小, 分配后拥挤系数远超其他路段。该交通流分配结果是系统总出行成本最小的分配结果, 系统总出行成本是各个路段出行成本的总和, 约为 2152635。
通过计算, 可以得到不同 γa 和 ηHH/ηCC 条件下的交通流分配结果以及该结果下系统最优分配的出行成本。由于本算例研究的是 CAV 和 HDV 的混合交通流道路, 且 CAV 之间的安全车距一般小于HDV 之间的安全车距, 所以忽略 γa=0 和 ηHH/ηCC=1的条件。系统最优成本关系如图 6 所示, 可以发现系统最优成本与 CAV 占比负相关, 与安全车距比也负相关。
随着 HDV 占比增大, 道路行驶成本提高, 对道路的压力加大。HDV 给道路通行带来额外的道路出行成本, 可采取收费的方式来弥补。基于最优收费理论, 应将额外产生的道路出行成本分摊至每个HDV 用户。假设 HDV 的安全车距是 CAV 安全车距的 2.5 倍。当 γa=1 时, 根据 SO 模型目标函数(式(9))计算得到系统最优成本为 742340。然而, 在相同安全车距比情况下, 当 γa=0.4 时, 系统总最优成本为2152635。期间产生的 1410295 额外成本可以分别按照路网、路段和 OD 对 3 种方式, 分摊至路网中的 HDV。
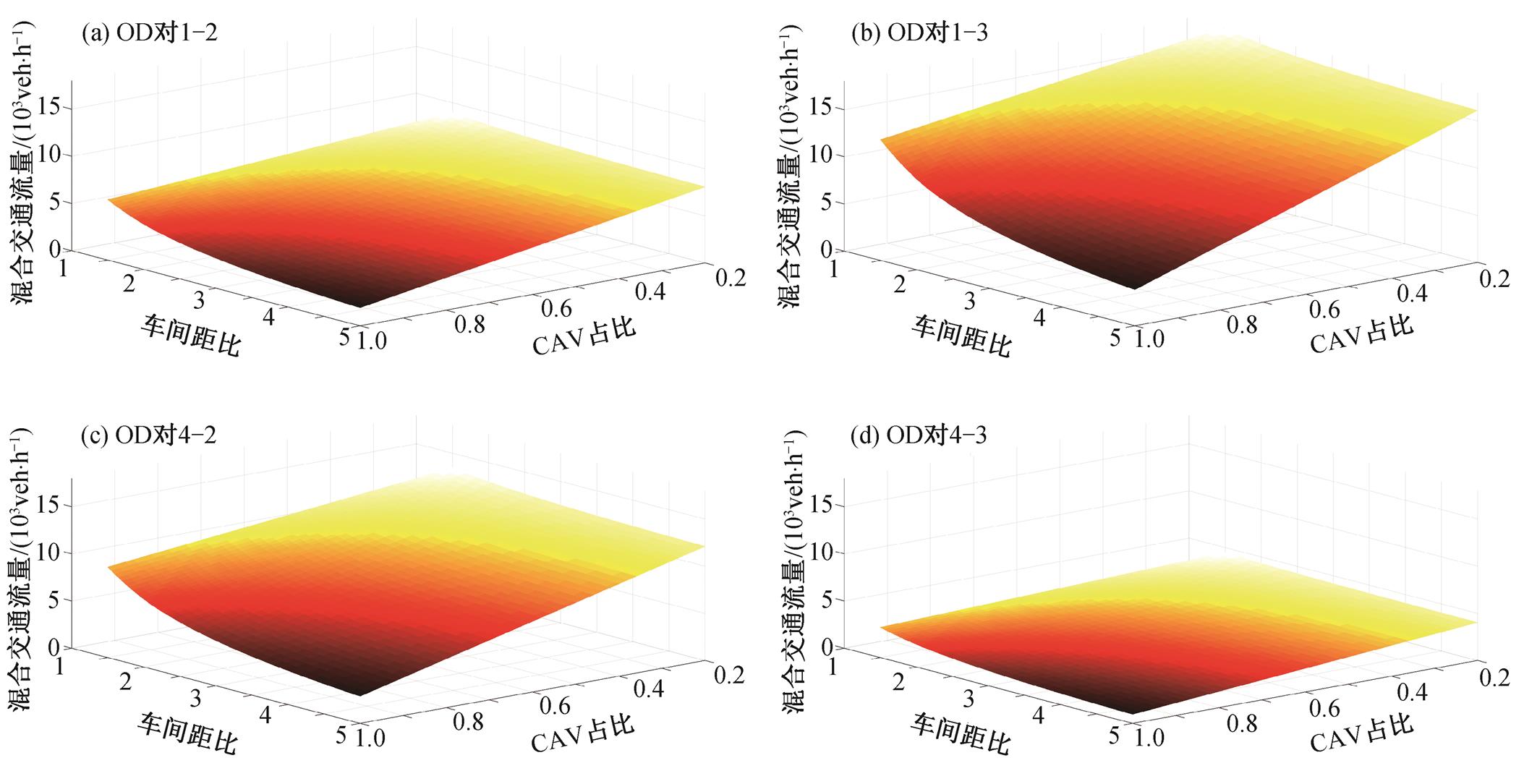
图5 混合交通OD需求量
Fig. 5 Mixed traffic OD demand
表1 交通流量分布
Table 1 Traffic flow distribution
路段流量/(veh·h–1)路段 流量/(veh·h–1)HDV流量CAV流量混合交通流量HDV流量CAV流量混合交通流量 1–58336.805557.9010560.008–26214.704143.207872.00 1–125608.403738.907104.009–109712.306474.9012302.30 4–59246.306164.2011712.009–134850.503233.706144.00 4–93941.102627.404992.0010–114850.503233.706144.00 5–63334.702223.204224.0011–24687.703125.105937.70 5–95911.603941.107488.0011–38336.805557.9010560.00 6–78185.305456.8010368.0012–65608.403738.907104.00 6–106074.404049.607694.3012–89246.306164.2011712.00 7–84687.703125.105937.7013–33941.102627.404992.00 7–1110015.506677.0012686.30
路网 道路交通网上额外产生的道路出行成本由该路网所有 HDV 平均分摊。即由 28800 辆 HDV (HDV 车辆数=(1–γa)·(d12+d13+d42+d43)=48000(1–0.4)veh/h=28800veh/h)平均分摊 1410295 成本, 即每辆 HDV 支付 48.97 的道路出行费用。该收费方案计算简便, 并且能弥补道路出行费用的差异, 但因每辆 HDV 实际行驶距离不同, 对所有 HDV 收取等额的费用, 对出行距离较短的 HDV 缺乏公平性。因此, 该收费方案适合各 OD 对之间不同的路径距离相近, 每辆车实际行驶距离相差不大的道路交通网。
路段 各路段额外产生的道路出行成本由该路段上所有 HDV 平均分摊。以算例中 γa=0.4, ηHH/ηCC =2.5 时的路段 1–5 为例, 当 γa=1 时, 道路成本为38017; 当 γa=0.4 时, 道路总成本为 77276。额外产生的 39259 成本应由路段 1–5 上的 8336.8 辆 HDV 平均分摊, 即每辆 HDV 需要支付 4.71 的出行费用。该方案解决了基于路网收费方案的部分缺陷, 每辆HDV 都能按照个人实际出行距离缴纳费用。该收费方案适合拥堵程度不高, 用户最优分配结果和系统最优分配结果相似的道路交通网络收费定价, 各车辆不会为达到系统最优而选择较远的路径。
表2 路段拥挤程度及出行成本
Table 2 Road congestion and travel costs
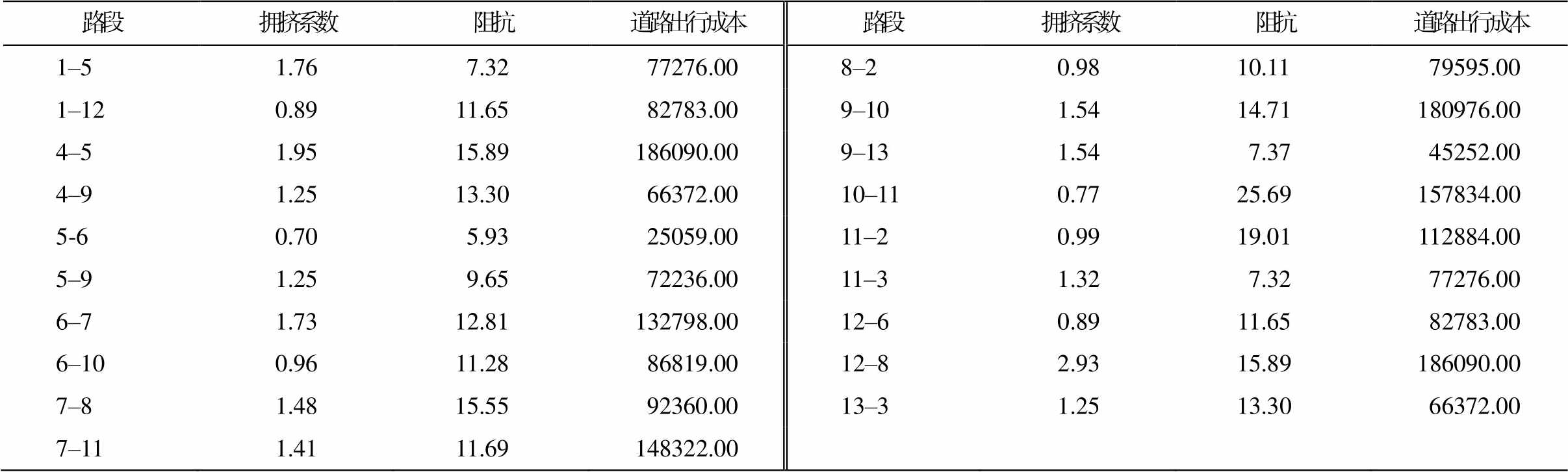
路段拥挤系数阻抗道路出行成本路段 拥挤系数阻抗道路出行成本 1–51.767.3277276.008–20.9810.1179595.00 1–120.8911.6582783.009–101.5414.71180976.00 4–51.9515.89186090.009–131.547.3745252.00 4–91.2513.3066372.0010–110.7725.69157834.00 5-60.705.9325059.0011–20.9919.01112884.00 5–91.259.6572236.0011–31.327.3277276.00 6–71.7312.81132798.0012–60.8911.6582783.00 6–100.9611.2886819.0012–82.9315.89186090.00 7–81.4815.5592360.0013–31.2513.3066372.00 7–111.4111.69148322.00
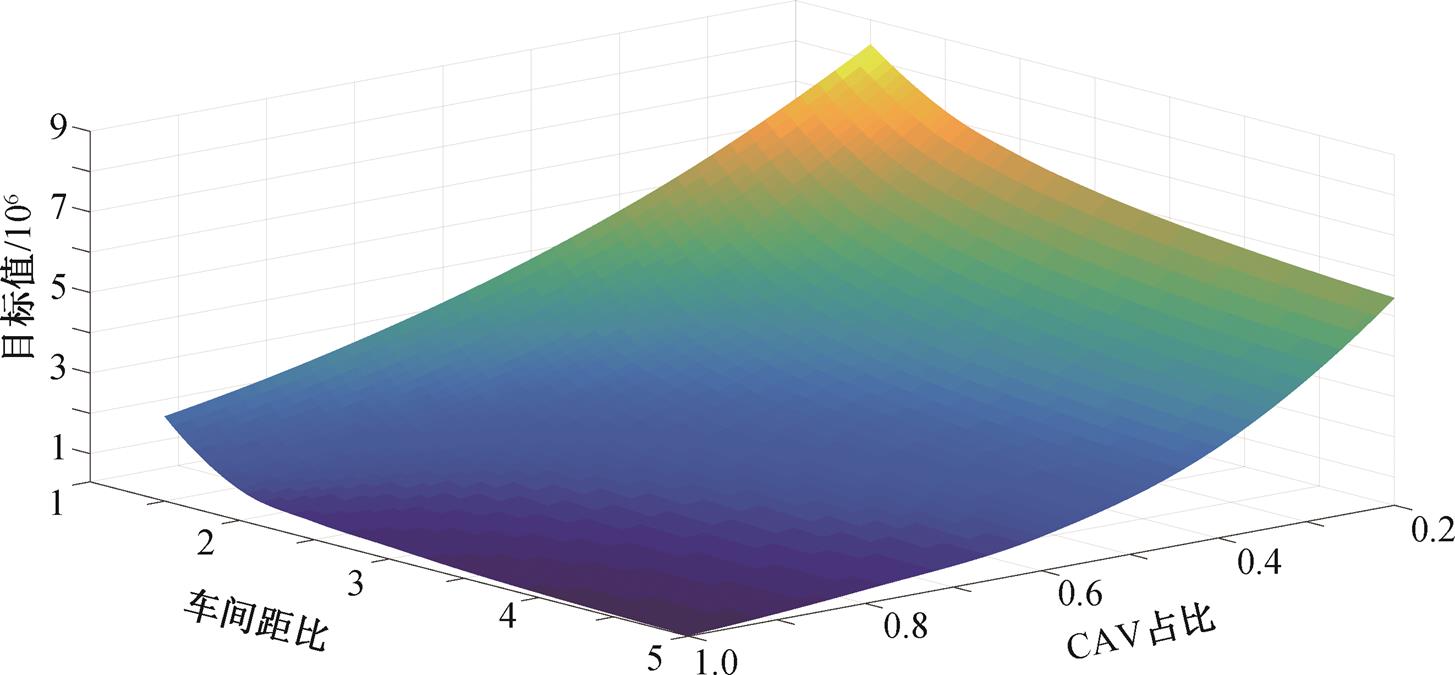
图6 系统最优成本关系
Fig. 6 Optimal cost relationship of the system
OD 对 每辆 HDV 分摊的道路出行成本应根据每辆车的出发地和目的地来决定, 即相同 OD的 HDV 用户平均分摊该 OD 对之间所有路径上额外产生的属于该 OD 对的道路出行成本。以 γa= 0.4, ηHH/ηCC =2.5 时的 OD 对 4–3 为例, 当 γa=1 时, OD对 4–3 上的车辆行驶路径为 4–9–13–3, 该路径上行驶产生的道路出行成本为 67131; 当 γa=0.4 时, OD对 4–3 上的车辆行驶路径仍为 4–9–13–3, 而此时这些车辆在该路径上行驶产生的出行成本为 79746, 将额外产生的 12614 成本分摊到 3941 辆 HDV 上, 即每辆从 4 到 3 的 HDV 需要支付 3.2 的出行费用。该方案比前两个方案更加公平, 适合大部分的道路交通网, 但计算过程复杂, 难以实现。对于复杂的道路交通网络, 分配在相同路段上的车辆可以来自不同的 OD 对, 难以确定每个路段上属于各 OD 对之间的交通量造成的额外成本。
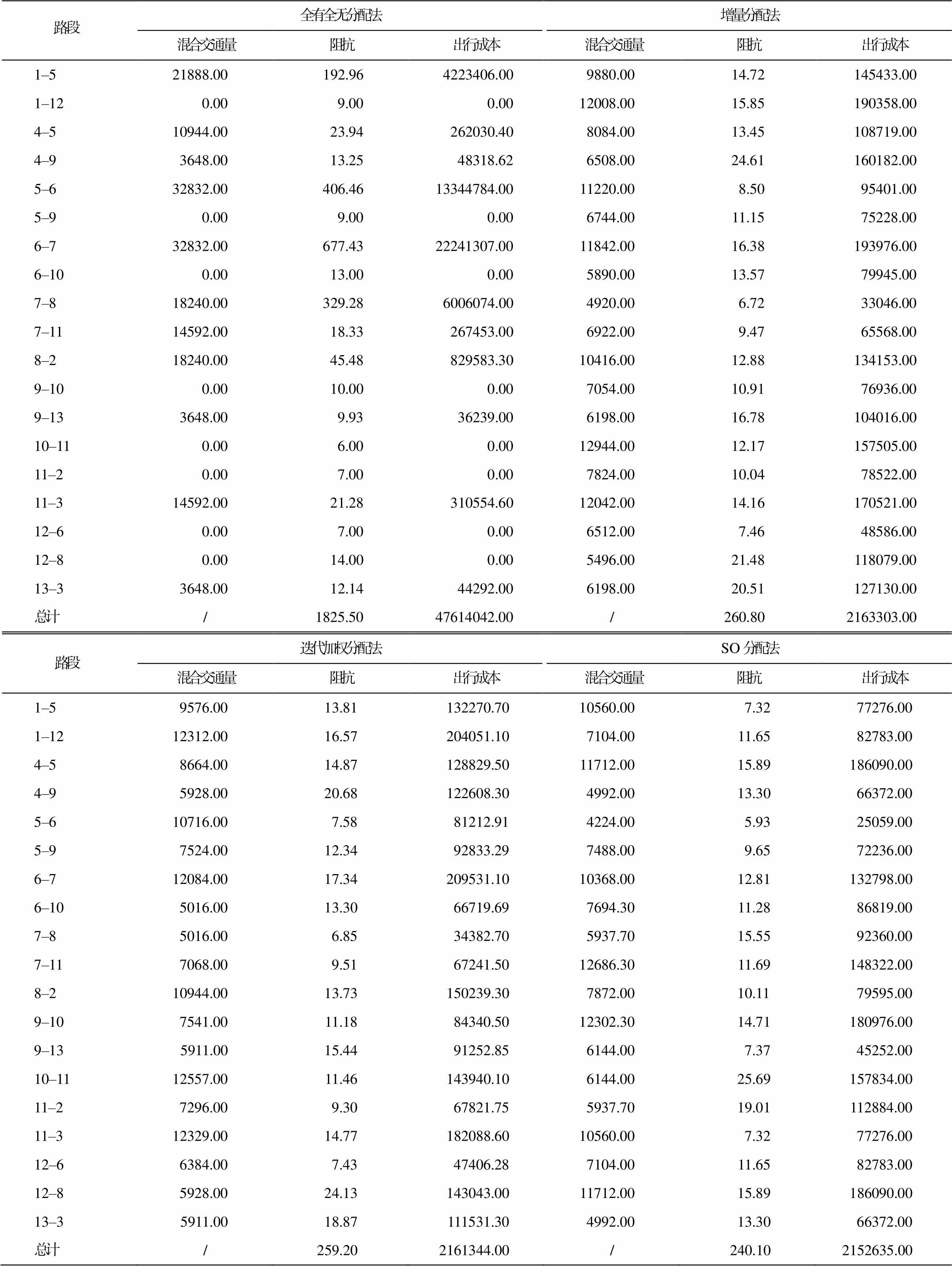
为了证明 SO 分配法在减少系统总出行成本方面的优势, 本文分别采用全有全无分配法、增量分配法和迭代加权分配法对案例进行计算, 并将结果与SO 分配法进行对比, 结果如表 3 所示。全有全无分配法中多个路段的车流量为 0, 致使道路资源被浪费, 因此全网总出行成本远高于其他方法。增量分配法、迭代加权分配法以及本文提出的 SO 分配法得到的总出行成本接近, 但 SO 分配法得到的路网总阻抗略低。因此, 本文提出的基于 SO 分配方法的人工和自动混合驾驶环境下的道路拥挤收费方案更合理。
本文结合安全车距对传统 BPR 函数进行改进, 建立混合交通流下的道路阻抗函数。根据改进后的道路阻抗函数建立 SO 模型, 采用 Frank-Wolfe 算法对模型进行求解, 结果表明, 与传统交通流分配方法相比, 本文方法显示出优势。系统最优成本曲线表明, CAV 对道路通行能力有一定的积极作用。结合最优收费模型设计的最优道路拥堵收费方案, 可以为混合驾驶汽车环境下的道路收费管理提供科学依据。
表3 交通流分配方法对比
Table 3 Comparison of traffic flow distribution methods
路段 全有全无分配法增量分配法 混合交通量阻抗出行成本混合交通量阻抗出行成本 1–521888.00192.964223406.009880.0014.72145433.00 1–120.009.000.0012008.0015.85190358.00 4–510944.0023.94262030.408084.0013.45108719.00 4–93648.0013.2548318.626508.0024.61160182.00 5–632832.00406.4613344784.0011220.008.5095401.00 5–90.009.000.006744.0011.1575228.00 6–732832.00677.4322241307.0011842.0016.38193976.00 6–100.0013.000.005890.0013.5779945.00 7–818240.00329.286006074.004920.006.7233046.00 7–1114592.0018.33267453.006922.009.4765568.00 8–218240.0045.48829583.3010416.0012.88134153.00 9–100.0010.000.007054.0010.9176936.00 9–133648.009.9336239.006198.0016.78104016.00 10–110.006.000.0012944.0012.17157505.00 11–20.007.000.007824.0010.0478522.00 11–314592.0021.28310554.6012042.0014.16170521.00 12–60.007.000.006512.007.4648586.00 12–80.0014.000.005496.0021.48118079.00 13–33648.0012.1444292.006198.0020.51127130.00 总计/1825.5047614042.00/260.802163303.00 路段 迭代加权分配法SO分配法 混合交通量阻抗出行成本混合交通量阻抗出行成本 1–59576.0013.81132270.7010560.007.3277276.00 1–1212312.0016.57204051.107104.0011.6582783.00 4–58664.0014.87128829.5011712.0015.89186090.00 4–95928.0020.68122608.304992.0013.3066372.00 5–610716.007.5881212.914224.005.9325059.00 5–97524.0012.3492833.297488.009.6572236.00 6–712084.0017.34209531.1010368.0012.81132798.00 6–105016.0013.3066719.697694.3011.2886819.00 7–85016.006.8534382.705937.7015.5592360.00 7–117068.009.5167241.5012686.3011.69148322.00 8–210944.0013.73150239.307872.0010.1179595.00 9–107541.0011.1884340.5012302.3014.71180976.00 9–135911.0015.4491252.856144.007.3745252.00 10–1112557.0011.46143940.106144.0025.69157834.00 11–27296.009.3067821.755937.7019.01112884.00 11–312329.0014.77182088.6010560.007.3277276.00 12–66384.007.4347406.287104.0011.6582783.00 12–85928.0024.13143043.0011712.0015.89186090.00 13–35911.0018.87111531.304992.0013.3066372.00 总计/259.202161344.00/240.102152635.00
本研究存在如下的局限性。1)本文探讨的CAV 环境下最优道路拥堵收费是固定需求下的道路拥堵收费。在收费政策制定后, 部分出行者会根据收费情况而改变其出行方式, 进而产生弹性需求。后续可针对弹性需求下的混合交通拥堵收费展开研究。2)本文研究的混合驾驶环境下交通流分配为静态系统最优分配, 结果缺乏实时验证。后续可对时变的混合交通流进行动态系统最优分配, 并基于动态系统最优分配结果开展动态道路拥堵收费定价相关的研究。
参考文献
[1] 唐立, 卿三东, 徐志刚, 等. 自动驾驶公众接受度研究综述. 交通运输工程学报, 2020, 20(2): 131–146
[2] Aghassi M, Bertsimas D, Perakis G. Solving asymmet-ric variational inequalities via convex optimization. Operations Research Letters, 2006, 34(5): 481–490
[3] Tientrakool P, Ho Y C, Maxemchuk N F. Highway capacity benefits from using vehicle-to-vehicle com-munication and sensors for collision avoidance // Ve-hicular Technology Conference (VTC Fall). San Fran-cisco, 2011: 1–5
[4] Berg V A C, Verhoef E T. Autonomous cars and dynamic bottleneck congestion: the effects on capacity value of time and preference heterogeneity. Trans-portation Research Part B, 2016, 94: 43–60
[5] Yu X, Vincent A C, Van Den B, et al. Autonomous cars and activity-based bottleneck model: How do inve-hicle activities determine aggregate travel patterns?. Transportation Research Part C, 2022, 139: 103641
[6] Wang J, Peeta S, He X. Multiclass traffic assignment model for mixed traffic flow of human-driven vehicles and connected and autonomous vehicles. Transpor-tation Research Part B, 2019, 126: 139–168
[7] 胡煜晗, 靳雅娜, 张世秋. 电动汽车替代燃油车的气候和健康影响及社会成本——基于单车视角的成本效益分析. 北京大学学报(自然科学版), 2021, 57(5): 916–926
[8] 于亚申, 胡煜晗, 张世秋. 老旧机动车淘汰更新及补贴政策的成本有效性分析——以北京市为例. 北京大学学报(自然科学版), 2022, 58(4): 763–770
[9] Chen Z, He F, Yin Y, et al. Optimal design of au-tonomous vehicle zones in transportation networks. Transportation Research Part B, 2016, 99: 44–61
[10] Chen Z, He F, Yin Y, et al. Optimal deployment of autonomous vehicle lanes with endogenous market penetration. Transportation Research Part C, 2017, 72: 143–156
[11] 马华伟, 胡明明, 胡笑旋. 基于模拟退火算法的甩挂运输路径规划. 中国管理科学, 2016, 24(增刊 1): 1–6
[12] 韩小亮, 邓祖新. 城市交通拥堵的经济学分析——基于计算经济学的模拟检验. 财经研究, 2006(5): 19–31
[13] Luo Q, Saigal R, Chen Z, et al. Accelerating the adoption of automated vehicles by subsidies: a dyna-mic games approach. Transportation Research Part B, 2019, 129: 226–243
[14] 曹芳萍, 潘焕学, 沈小波. 解决城市交通拥挤的道路收费理论及实践探索. 价格理论与实践, 2010(5): 28–29
[15] 赵雪峰, 吴伟伟, 吴德林, 等. 基于TPCBoost模型的新型交通服务定价研究——以纽约网约车为实例. 中国管理科学, 2022, 30(10): 210–223
[16] 邵晓双, 谭德庆. 社会地位效用及城市交通状况对私家车厂商市场策略的影响. 中国管理科学, 2016, 24(8): 37–44
[17] 何南, 赵胜川. 城市道路阻抗函数模型研究——以大连市为例. 公路交通科技, 2014, 31(2): 104–108
[18] Lazar D A, Samuel C, Ramtin P. Capacity modeling and routing for traffic networks with mixed autonomy // IEEE 56th Conference on Decision and Control (CDC). Melbourne, 2017: 8264516
[19] Liu Z, Song Z. Strategic planning of dedicated autonomous vehicle lanes and autonomous vehicle/toll lanes in transportation networks. Transportation Re-search Part C, 2019, 106: 381–403
[20] 徐猛, 屈云超, 高自友. Frank-Wolfe算法求解交通分配问题: 比较不同流量更新策略和线搜索技术. 交通运输系统工程与信息, 2008, 8(3): 14–22
[21] 宋巨龙, 钱富才, 彭刚. 利用平面上的黄金分割法求全局最优解. 数学的实践与认识, 2004, 34(11): 113–117
[22] 马万达, 韩印. 交通拥挤收费原理与对策研究. 交通与运输(学术版), 2007(1): 53–56
[23] 史峰, 李志纯. 拥挤道路使用收费的理论构架. 交通运输工程学报, 2002, 2(2): 78–82
Optimal Road Congestion Charging Model in Mixed Driving Environment of Connected Autonomous Vehicle and Human-Driven Vehicle
Abstract In order to get the optimal road congestion charging scheme in mixed driving environment of connected autonomous vehicles (CAV) and human-driven vehicles (HDV), this paper conducts a quantitative analysis of the impact of CAV on road networks (especially on road capacity), and analyzes the functional relationship between the road capacity and HDV flows as well as CAV flows. Secondly, the traditional Bureau of Public Road (BPR) Function is improved, and the system optimal allocation model is established based on the new BPR function. The system optimum (SO) assignment is performed on the traffic flow under the conditions of different CAV proportions and different HDV-CAV headways. Then, Frank-Wolfe algorithm is used to solve the SO model, by considering the extra traffic cost of HDV in the differences of SO results under different conditions. The corresponding road networks are formulated using the optimal toll theory charge plan. Finally, the model and the algorithm are applied to the Nguyen-Dupuis transportation network. The results show that under the coexisting condition of HDV and CAV, the marginal cost under the optimal allocation result of the system is the optimal congestion charging which can be the basis for the road toll scheme design under the coexistence of HDV and CAV.
Key words connected autonomous vehicles; road network; Bureau of Public Road (BPR) function; system optimum assignment; Frank-Wolfe algorithm; congestion charging