 (1)
(1)
doi: 10.13209/j.0479-8023.2023.036
国家自然科学基金(51721006, 42142047)和云南省高原湖泊流域污染过程与管理重点实验室开放基金(2016PL03)资助
收稿日期: 2022–07–11;
修回日期: 2022–09–05
北京大学学报(自然科学版) 第59卷 第4期 2023年7月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 4 (July. 2023)
摘要 基于现有研究中典型的水质响应非线性行为, 定义基于交叉样本熵、傅里叶变化、乱序计数和调整R2 的 4 种负荷削减–水质响应非线性强度指标。在典型水质响应样本的基础上进行指标的计算和比选, 为基于数值模拟的水质管理提供可参考的非线性强度衡量指标和非线性判断依据。研究结果表明, 4 种水质响应非线性强度指标虽然有一定的重叠, 但不可以互相替代, 它们分别指示季节差异、峰值变化、短期水质恶化以及水质均值变化等不同类型的非线性行为。结合计算结果, 给出使用 4 种非线性指标判断非线性行为的方法, 并讨论非线性定义的局限性以及所提指标的应用前景。研究结果有助于进一步区分和认识水体水质响应不同类型的非线性行为, 以便针对非线性水质响应行为的特定类型进行分析。
关键词 非线性; 水质响应; 负荷削减; 数值模拟
根据第二次全国污染物普查公报, 2017 年全国水污染物排放量化学需氧量为 2143.98 万吨, 总氮为 304.14 万吨, 总磷为 31.54 万吨, 与 2007 年相比, 分别下降 29.2%, 35.7%和 25.5%[1–2]。同时, 全国重点湖库水质 IV 类以及劣于 IV 类的比例从 71.5%降至 37.4%[3–4]。但是, 当前的水质管理依然面临诸多挑战。《水污染防治行动计划》提出, 到 2030 年, 全国七大重点流域水质优良比例将达 75%以上。在未来一段时间内, 进一步削减污染负荷仍是水质管理的主要任务之一[5–7]。
然而, 水质对污染负荷削减的响应并不是线性变化的, 这种非线性响应为水质管理带来困难[8]。负荷削减–水质响应的非线性关系来源于两个阶段: 1)从负荷输入到水体营养盐浓度[9–10]; 2)从营养盐浓度到藻类浓度[8,11–12]。由于水体底泥等内源释放现象, 加上复杂的湖沼学过程和水体流场的动态变化, 这两个阶段并不完全独立, 常常相互影响[13]。
尽管水体水质的非线性行为被现有研究(特别是水质预测研究)广泛提及, 但对其具体分析缺少足够的关注。为解决非线性问题, 水质预测模型逐渐采用机器学习等方法来提高预测精度, 如支持向量机[14–15]和人工神经网络[16]等。从理论上讲, 这些机器学习模型可以拟合任何非线性函数的形状, 因此在有充足训练数据的情况下, 这类研究并不关注水质响应属于哪种非线性函数。线性关系有明确的定义, 非线性关系却没有一个统一的表现形式。Su等[17]在大规模数值模拟实验的基础上, 归纳出水体水质响应非线性关系的 4 种主要类型: 1)负荷削减后, 水质不成比例地响应, 但水质随时间的变化规律没有改变(即水质时间序列的形状没有改变); 2)水质时间序列的峰值提前或滞后; 3)水质时间序列的峰值消失; 4)负荷削减后, 水质在有限时间内呈现短暂的恶化。
水质响应的非线性强度指标能够帮助人们判断非线性关系的强度和类型, 但目前缺乏相关指标。在实际的水质管理中, 不同水体可能表现出不同类型的非线性响应行为, 确定每一种水体属于何种非线性响应行为及其响应强度, 对水质管理有较强的现实意义。Janssen 等[18]在太湖的案例中使用调整R2 作为水质响应非线性强度的指标, 但没有明确该指标与具体非线性行为之间的关系。Su 等[17]在区分水质响应非线性行为类型时, 使用一种基于方差的非线性指标, 但该指标带有时间尺度, 不是一个可用于指示整体水质响应非线性行为的单一指标。
本研究旨在开发和讨论可以衡量负荷削减–水质响应非线性强度的指标, 在实践中用于非线性水质响应行为的判断和识别。鉴于基于水质监测和数值模拟模型的不同, 我们主要讨论针对特定水体已经建立水质数值模拟模型的情况。本研究基于现有文献中对负荷削减–水质响应非线性类型的描述, 定义 4 种非线性强度指标, 进而在水质响应代表性数值模拟样本中, 对 4 种非线性强度指标进行比较, 分析其重叠程度和区分度, 并对实际管理中如何应用这些指标提出建议和参考标准。
在本研究中, 将水质响应的非线性行为理解为“水质响应不成比例地对负荷削减进行响应”, 即负荷削减的边际效应不恒定。水质响应的非线性可以指两个负荷削减水平下水质响应的行为变化, 也可以指多个负荷削减水平下水质响应行为的变化。后者更关注湖泊特征, 而不是当前负荷水平下的水质响应, 对长期水质管理的意义更大, 因此本研究主要讨论后者。同时, 在指标选择过程中, 尽量避免解释性不强的黑箱指标。
针对多个负荷削减水平下水质响应的非线性行为, 本研究分别选取基于交叉样本熵、傅里叶变换、乱序计数和调整 R2 的 4 种水质响应非线性指标。其中, 前两种需要先单独考虑个别负荷削减水平响应的非线性, 然后汇总至多个负荷削减水平进行计算; 后两种可以直接计算多个负荷削减水平与水质响应的关系。
1.1.1基于交叉样本熵的水质响应非线性指标
交叉样本熵一般用于衡量两个带有随机性的时间序列的相似性[19–20]。本研究依据交叉样本熵的计算方法, 采用式(1)~(4)计算两个负荷削减水平下水质响应时间序列的相似性。
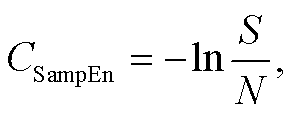 (1)
(1)
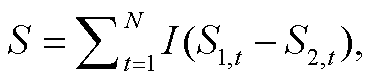 (2)
(2)
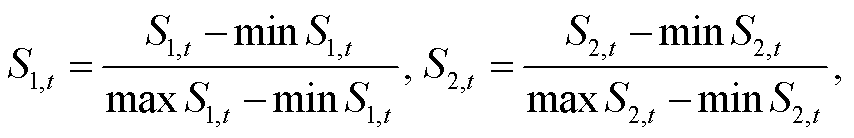 (3)
(3)
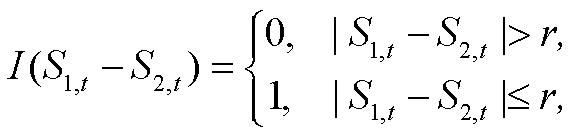 (4)
(4)
式中, CSampEn 为非线性指标, N 为时间序列长度; S1,t和S2,t为两个负荷削减水平下水质响应在 t 时刻的响应值; r 为识别精度, 一般为序列标准差的 10%, 本研究取 0.025。
上述指标的本质在于计算两个水质响应时间序列标准化之后的一致性。两个负荷削减水平下水质响应越相似, CSampEn 就越接近 0; 反之, 当任意时刻两个负荷削减水平下水质响应都不相似时, CSampEn为正无穷。由于计算过程中将水质时间序列标准化, 因此此处做如下假设: 虽然特定季节的响应可能是线性的, 但只要不同季节的响应程度不同, 水质响应的季节差异也是非线性的一种。
对于多个负荷削减水平, 首先计算相比于未削减情景, 各削减情景下基于交叉样本熵的水质响应非线性指标, 然后将所计算指标的平均值作为多负荷削减水平下基于交叉样本熵的水质响应非线性指标。
1.1.2基于傅里叶变换的水质响应非线性指标
在机器学习中, 傅里叶变换是常用的曲线形状特征提取方法[21–22], 可以将任意时间序列曲线分解, 并得到其频谱, 用频谱的主频描述时间序列曲线的形状特征。由于水质响应的非线性特征包括时间序列峰值改变的情况, 因此需要考虑将时间序列曲线形状的改变作为衡量非线性的一个方面。
采用快速傅里叶变化(fast Fourier transform, FFT)方法, 首先得到每一个负荷削减水平下的频谱, 并保留每一个负荷削减水平下的前 6 个主频。然后, 将所有负荷削减水平下(包括未削减情景下)的所有前 6 个主频进行并集运算, 通过并集集合元素的个数除以所有负荷水平下前 6 个主频的个数进行归一化。
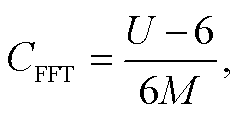 (5)
(5)
式中, U 为未削减情景以及所有负荷削减情景下前 6个主频并集的元素个数, M 为负荷削减情景的个数(不含未削减情景)。并集集合元素越多, 该指标越接近 1, 说明水质响应曲线的形状改变越大, 非线性越强; 当所有情景下的前 6 个主频都相同时, 该指标为 0。
1.1.3基于乱序计数的水质响应非线性指标
针对所有负荷削减水平下的时间序列曲线, 遍历所有时间, 观察水质是否依次变好, 将水质没有依次变好的时间占总时间的比例作为水质响应非线性的指标。当负荷削减水平逐渐增强时, 水质应当依次变好。然而, 水质响应的非线性会导致局部时段内的水质反而恶化。在线性情况下, 该指标为 0, 在强非线性情况下, 即任意时间都出现水质恶化的情况下, 该指标为 1。
1.1.4基于调整 R2的水质响应非线性指标
首先, 计算各负荷削减水平下水质响应时间序列的平均值, 与负荷削减水平组成数据集。然后, 在数据集上进行线性拟合, 并计算其调整 R2, 作为水质响应非线性的指标[18]:
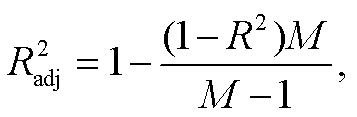 (6)
(6)
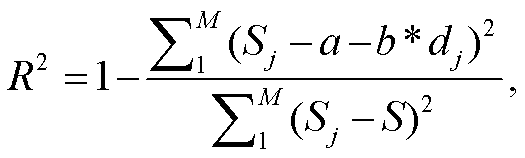 (7)
(7)
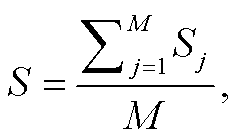 (8)
(8)
式中, a 和 b 分别为对(dj, Sj)进行最小二乘拟合所得到的截距和一次项系数, j=0, …, M, dj 为第 j 个负荷水平, M 为负荷削减情景的个数, Sj 为该水质响应的平均值。
式(6)~(8)计算的是观测到的水质响应和完全线性水质响应之间的偏离程度, 将偏离程度作为非线性强度的衡量指标。与 R2 相比, 调整 R2 可以更好地指示线性关系对观测数据的偏离程度。在完全线性的情况下, 调整 R2 为 1, 非线性越明显, 调整 R2越小, 最小为 0。
本研究水质响应数值模拟样本来自 15 种典型的水质非线性响应行为。Su 等[17]以滇池为湖泊原型, 考虑 3 种不同气候条件和负荷输入, 进行 35 万次数值模拟实验, 对负荷削减–湖泊水质响应的关系进行大数据分析聚类, 得到 15 种典型的水质非线性响应行为。我们根据上述 15 种典型非线性响应的时间序列(每种类型至少包含 TN, TP 和 Chla 中的一种水质指标), 获得 42 个水质响应样本(部分典型水质非线性响应行为只包含 3 个水质指标中的一个或两个), 每个水质响应样本包括未削减情景和 4 个不同负荷削减情景下的水质响应时间序列。负荷削减情景设计和典型水质响应非线性行为的获取方法以及各水质响应样本时间序列数据详见文献[17]。
为筛选出充分指示水质响应非线性程度的指标, 我们分析各个指标之间的共线性。若两个指标之间存在共线性, 意味着这两个指标之间存在比较强的相互替代关系, 则有一个指标是冗余的。共线性的判断通过计算两个指标分布的相关性来实现。同时, 分析各个非线性指标的分布情况, 对照水质响应的典型时间序列, 分析各个指标计算结果中最强非线性的特征, 判断是否能够依据不同指标识别所出现的非线性。理想的非线性指标应能明确地区分线性与非线性的水质响应关系, 而非所有情况下的计算结果差异不大。结合上述两点, 对照水质响应的时间序列, 对非线性指标进行筛选。
本研究中的计算在北京大学高性能计算平台上进行。
4种非线性指标的计算结果如表 1 所示。在 4个指标中, 基于交叉样本熵的非线性指标最小值与最大值之间的差距最大, 且四分位数之间的计算差异也比较明显, 说明基于交叉样本熵的非线性指标对水质响应非线性的区分度最高。
对 4 种非线性指标所指示的最强非线性进行比较, 结果如图 1 所示。基于交叉样本熵的非线性指标的最强非线性水质响应时间序列没有发生任何形状上的改变, 并且以直观上看水质响应较为线性(图 1(a))。对水质响应进行标准化(图 2), 可以看出, 基于交叉样本熵的非线性指标主要指示水质响应的时间差异性, 即虽然在局部时段内, 水质响应可能是线性的, 但在不同的时段, 水质响应的程度有所差异, 因此水质响应时间序列标准化后, 发现水质响应存在一定的非线性。相比之下, 基于傅里叶变化的非线性指标(图 1(b))可以较好地指示水质响应时间序列形状的变化, 包括峰值的提前和滞后, 并且是 4 个非线性指标中唯一发现明显时间序列改变的指标。基于乱序计数和调整 R2 的非线性指标的最强非线性样本为同一个样本(图 1(c)), 主要表现为存在短时间内负荷削减之后反而水质恶化的情况。这是基于乱序计数的非线性指标特定识别的情况, 由于这种情况的存在, 也会影响水质响应时间序列平均值与负荷削减之间的关系, 因此两个指标的最强非线性指向同一个样本。
4个指标计算结果的分布及相关关系如图 3 所示, 可以看出, 任意两个指标之间没有很强的相关关系, 即指标之间不能相互替代。其中, 基于乱序计数和基于调整 R2 的非线性强度指标在非线性较强的时候有一定的相关性, 但在非线性不强的时候, 这两个指标之间的相关性很弱。
虽然 4 个非线性指标没有很强的共线性, 但它们所指示的非线性有一定的重叠。例如, 基于傅里叶变化的非线性指标所指示的最强非线性样本, 其基于交叉样本熵、乱序计数以及调整 R2 的非线性指标的计算值分别为 1.911, 0.077 和 0.998, 都显示出有一定的非线性, 说明所指示的非线性存在部分重叠。
不过, 上面的共线性分析结果表明, 指标含义的重叠不足以导致指标相互替代。另一个证据是, 在 4 个指标分别指示的 5 个最强非线性的样本中, 并没有完全重叠的样本, 即没有一个样本的非线性强度在 4 个指标中都能排到前五位, 说明 4 个指标之间存在较强的区分度。
表1 4种非线性强度指标在典型水质数值模拟样本中的计算结果
Table 1 Statistics of the four indicators for nonlinearity strength on the typical numerical water quality simulation samples

统计指标基于交叉样本熵的非线性指标基于傅里叶变换的非线性指标基于乱序计数的非线性指标基于调整 R2的非线性指标 均值1.0406520.0505950.0442760.976651 方差0.7210190.0465040.0707880.060315 最小值0.045542000.710623 25%分位数0.511421000.984222 50%分位数0.9027360.0416670.0054790.997099 75%分位数1.6649960.0833330.0597600.999851 最大值2.6133630.1666670.2657531
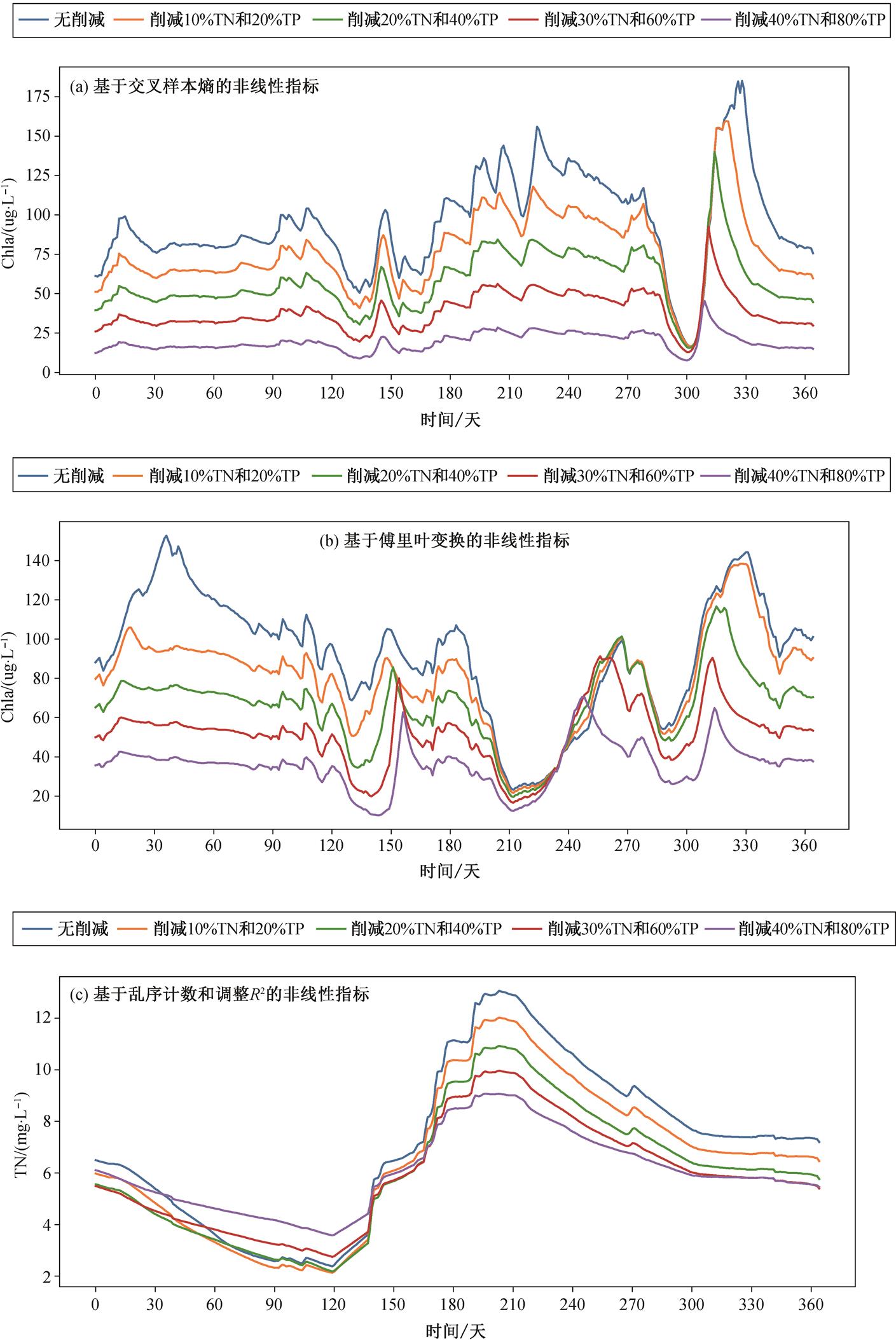
图1 4种非线性指标计算结果中最强非线性对应的样本情况
Fig. 1 Strongest nonlinear water quality responses indicated by the four indicators for nonlinearity strength

图2 基于交叉样本熵的非线性指标所指示的最强非线性的样本(对水质响应进行标准化处理)
Fig. 2 Strongest nonlinear water quality responses (scaled) indicated by the cross sample entropy based indicator
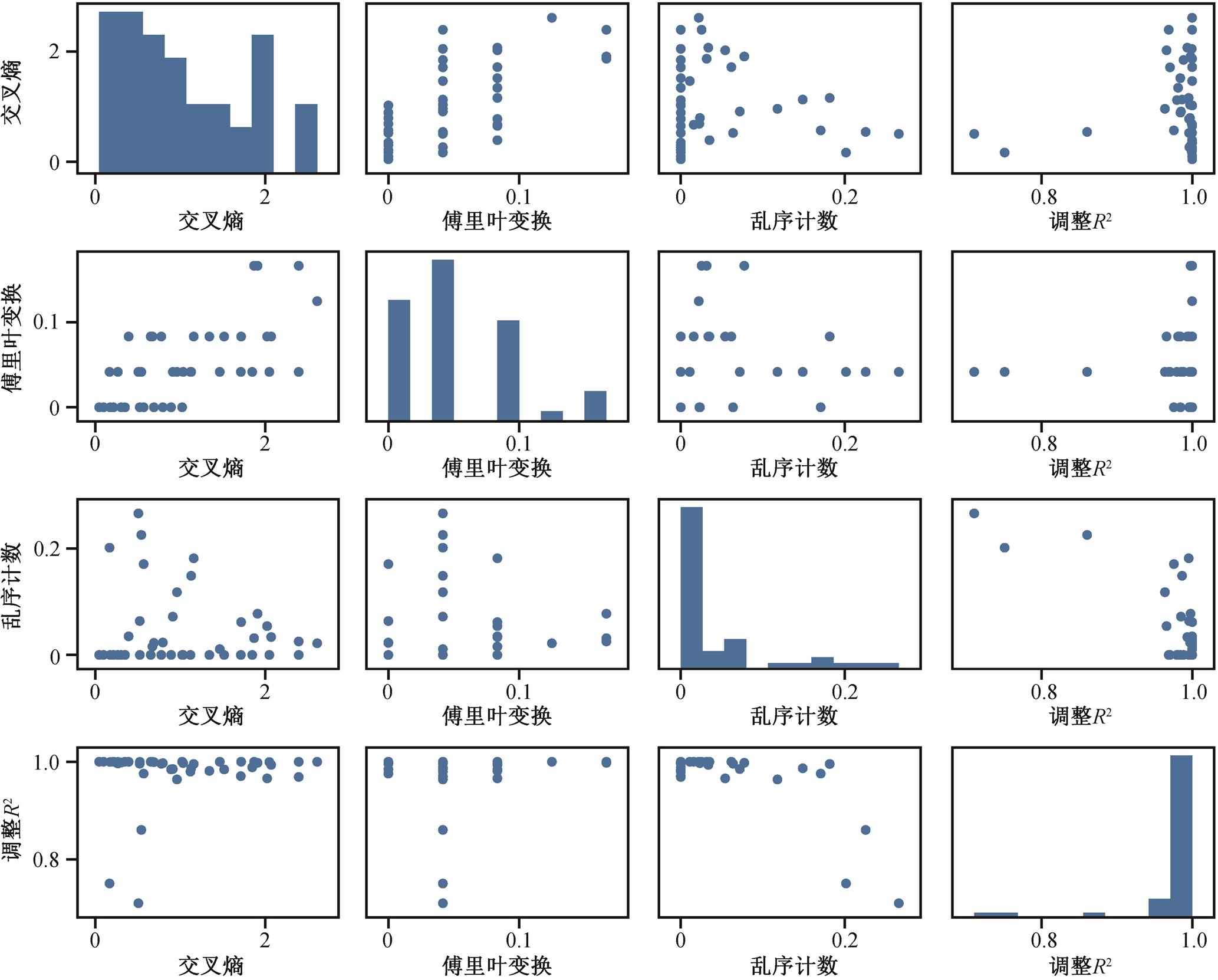
图3 4种非线性指标计算结果的分布和指标之间的相关性
Fig. 3 Distributions of the four nonlinearity strength indicators and the pair-wise correlations among them
综合共线性和区分度的分析结果, 我们认为 4个指标不能相互替代, 且区分度比较明显。根据 4个非线性指标指示的非线性特征及计算结果, 在实际使用中, 4 个非线性指标的选择和数值参考范围如表 2 所示。根据各指标分布的计算结果, 选择区分度明显的计算值作为显著非线性参考值, 并确保该计算结果的对应样本存在明显的非线性行为。
本研究中对水质响应非线性的关注主要局限在水质在某一负荷下的稳定响应, 而非负荷动态变化的情况下的水质响应。后者在时间维度上更复杂。并且, 由于湖泊物理化学生物过程中存在时滞效应, 水质响应的非线性程度更难衡量[23–24]。然而, 由于后者包含了本研究关注的非线性行为, 因此本研究结果对研究含时滞效应的非线性具有一定的借鉴意义。
从研究结果可以看出, 非线性的定义与管理需求有关。以基于交叉样本熵的非线性指标为例, 当某一季节内水质响应是线性的, 但季节之间存在差异时, 会识别出一定的非线性[25]。因此, 非线性的定义不仅取决于是否含有时滞效应, 也取决于所关注的时间尺度, 是季节内部还是年平均。
本文探讨的非线性不仅依赖于水体特征, 也依赖于情景设计(即实际管理关注的负荷削减程度)。想要更精细地衡量水体通过负荷削减从一种营养水平到另一种营养水平过程之中可能发生的非线性, 需要在两个水平之间设置更多的中间情景。因此, 本研究提出的非线性指标衡量的是情景限定下水体营养水平之间的非线性。
本研究提出的负荷削减–水质响应非线性指标在实际的水质管理中可有以下三方面的应用。
1)4 个水质响应非线性强度指标有助于进一步认识湖泊水质响应的非线性特征及其对水质管理的挑战。虽然水质响应的非线性被广泛提及, 但本研究结果表明, 非线性并不是一类明确的水质响应行为, 其包含不同类型的水质响应方式。虽然这些方式在某种程度上有重叠, 但区分度也非常明显。在实践中, 应当从水质管理的目的(是季节差异, 还是峰值; 是最不利的情况, 还是总体情况)出发, 采用不同的非线性指标来识别非线性水质响应的具体类型, 而不是仅仅停留在“非线性”这一指示不明的术语上。
2)采用 4 个水质响应非线性强度指标, 有助于进行针对性的水质监测。在基于数值模拟的水质响应基础上采用不同的非线性强度指标, 有助于认识不同水体水质响应的特点, 进而有针对性地对峰值或特定时段的水质进行监测, 强化对水质非线性响应的观测和动态规律的掌握, 进而支撑后续水质管理和污染控制决策。
3)采用不同的水质响应非线性强度指标, 有助于判断不同湖泊是否适用于模拟–优化的技术路线。水质管理优化通常建立在数值模拟和优化模型的基础之上, 由于直接的模拟–优化耦合方法受限于计算能力, 通常采用替代模型耦合优化模型的方法[26–27]。但是, 替代模型往往只关注水质响应的平均值。尽管水质响应的平均值也是非线性的[28], 但在模拟–优化的过程中, 可能会忽视其他动态过程的非线性。通过不同水质响应非线性强度指标的计算, 可以帮助判断某一水体是否存在其他类型的非线性水质响应, 以此揭示应用模拟–优化技术路线时, 应基于额外关注的时段, 有助于规避总体得到控制而局部未达预期的现象。
当然, 实际应用中的情景和模型特征可能与本研究采用的情景及模型特征不完全一致。因此, 使用本研究提出的指标来量化非线性, 需要对数据进行预处理。
表2 非线性指标的选择以及计算参考值
Table 2 Suggestions on the selection and nonlinearity threshold of the four nonlinearity strength indicator

指标名称指示非线性特征显著非线性参考值最强非线性参考值 基于交叉样本熵的非线性指标水质响应的季节性差异>0.5002.613 基于傅里叶变化的非线性指标水质响应峰值的提前、滞后、消失>0.0830.167 基于乱序计数的非线性指标负荷削减后水质的短暂恶化>0.0720.266 基于调整R2的非线性指标水质响应平均值的不成比例改变<0.9000.710
首先, 实际应用中的模型大多数为二维或三维的水动力水质水生态模型, 本研究在评估指标的过程中简化了空间复杂性, 仅为单点评估。在二维或三维模型中, 可以选择重要站点(如国家地表水水质自动监测站或省级监测站)进行非线性响应程度的评估, 也可以对空间进行平均来简化空间上的差异性。值得注意的是, 某些非线性响应行为可能源自空间差异性, 而空间差异性可能更多的是水动力原因造成的。因此在进行空间平均的情况下, 仍需对重要点位进行单独评估, 以便寻找非线性行为的主要来源。
部分非线性指标对情景的数量也有要求。计算基于交叉样本熵的非线性指标、基于傅里叶变化的非线性指标和基于乱序计数的非线性指标时, 要求情景的数量不少于 2 个; 计算基于调整 R2 的非线性指标时, 一般要求情景的数量不少于 3 个。值得注意的是, 对于任意两个情景之间非线性关系的衡量, 基于傅里叶变化的非线性指标和计算基于调整 R2 的非线性指标都是依赖于总情景个数的。
本研究首先依据负荷削减–水质响应非线性的特征, 定义 4 种水质响应非线性强度指标, 然后在典型负荷削减–水质响应时间序列样本的基础上, 对 4种指标进行计算及比较。结果表明, 4 种非线性指标不存在明显的共线性, 虽然对在非线性强度的指示有一定的重叠, 但具有明显的区分度。基于交叉样本熵、傅里叶变换、乱序计数和调整 R2 的非线性指标分别有助于识别有季节差异、峰值变化、短期内水质恶化和水质均值变化所产生的非线性行为, 可以满足不同的水质管理需求。本研究进一步结合计算结果给出 4 种指标达到显著非线性行为的参考值, 讨论了水质响应非线性定义的局限性以及所提指标的应用价值。本研究的结果有助于在水体水质数值模拟的基础上, 进一步区分水质响应非线性的不同种类及其对应的特点, 差异化地认识不同水质的行为特征, 帮助制定相应的水质监测方案和污染控制方案。
参考文献
[1] 中华人民共和国环境保护部, 中华人民共和国国家统计局, 中华人民共和国农业部. 第一次全国污染源普查公报[EB/OL]. (2010–02–11) [2021–12–28]. http://www.stats.gov.cn/sj/tjgb/qttjgb/qgqttjgb/202302/t20230218_1913282.html
[2] 中华人民共和国生态环境部, 国家统计局, 中华人民共和国农业农村部. 第二次全国污染源普查公报 [EB/OL]. (2020–06–10) [2021–12–28]. https://www. mee.gov.cn/xxgk2018/xxgk/xxgk01/202006/t20200610_783547.html
[3] 中华人民共和国环境保护部. 2007 年中国环境状况公报[EB/OL]. (2008–06–05) [2021–12–28]. https:// www.mee.gov.cn/gkml/sthjbgw/qt/200910/t20091031_180760.htm
[4] 中华人民共和国生态环境部. 2017 年中国生态环境状况公报 [EB/OL]. (2018–05–31) [2021–12–28]. https://www.mee.gov.cn/hjzl/sthjzk/zghjzkgb/201805/P020180531534645032372.pdf
[5] 蒋洪强, 吴文俊, 姚艳玲, 等. 耦合流域模型及在中国环境规划与管理中的应用进展. 生态环境学报, 2015, 24(3): 539–546
[6] 张文静, 王强, 吴悦颖, 等. 中国水污染物总量控制特色研究. 环境污染与防治, 2016, 38(7): 104–109
[7] 姚瑞华, 赵越, 徐敏, 等. 重点流域水污染防治的发展历程与展望//全国环境规划院(所)长联席会暨中国环境科学学会环境规划专业委员会 2013 年学术年会. 太原, 2013: 98–101
[8] 张晓玲, 梁中耀, 刘永, 等. 流域水质目标管理的风险识别与对策研究. 环境科学学报, 2014, 34(10): 2660–2667
[9] Liu W C, Chen W B, Kimura N. Impact of phosphorus load reduction on water quality in a stratified reservoir-eutrophication modeling study. Environ Monit Assess, 2009, 159: 393–406
[10] Chou W S, Lee T C, Lin J Y, et al. Phosphorus load reduction goals for Feitsui Reservoir Watershed, Tai-wan. Environ Monit Assess, 2007, 131: 395–408
[11] McCauley E, Downing J A, Watson S. Sigmoid rela-tionships between nutrients and chlorophyll among lakes. Canadian Journal of Fisheries and Aquatic Scie-nces, 1989, 46(7): 1171–1175
[12] Yuan L L, Jones J R. Rethinking phosphorus-chloro-phyll relationships in lakes. Limnol Oceanogr, 2020, 65(8): 1669–1960
[13] Kemp W M, Boynton W R, Adolf J E, et al. Eutro-phication of Chesapeake Bay: historical trends and ecological interactions. Marine Ecology Progress Se-ries, 2005, 303: 1–29
[14] 程庭莉. 基于支持向量机的三峡库区水质预测与评价方法研究[D]. 重庆: 重庆大学, 2013
[15] 梁勇. 基于支持向量回归的水质预测研究[D]. 武汉: 武汉理工大学, 2012
[16] 于王乐. 淮河蚌埠段水环境非线性特征分析与水质预测研究[D]. 合肥: 合肥工业大学, 2012
[17] Su H, Zou R, Zhang X, et al. Exploring the type and strength of nonlinearity in water quality responses to nutrient loading reduction in shallow eutrophic water bodies: Insights from a large number of numerical simulations. Journal of Environmental Management, 2022, 313: 115000
[18] Janssen A B G, De Jager V C L, Janse J H, et al. Spatial identification of critical nutrient loads of large shallow lakes: implications for Lake Taihu (China). Water Res, 2017, 119: 276–287
[19] Kroese D P. Cross-Entropy method. Encyclopedia of Operations Research Management Science, 2010, 2 (12): 1–12
[20] 伏潜, 朱跃龙, 万定生. 交叉熵相似性度量在水文时间序列匹配中的应用. 计算机与数字工程, 2015, 43(2): 164–167
[21] Zheng A, Casari A. Feature engineering for machine learning: principles and techniques for data scientists. Sebastopol, CA: O’Reilly Media, 2018: ix
[22] 蔡富, 孙付平, 戴海亮, 等. 小波和傅里叶变换在坐标时间序列分析中的应用. 全球定位系统, 2019, 44(4): 40–46
[23] Meals D W, Dressing S A, Davenport T E. Lag time in water quality response to best management practices: a review. J Environ Qual, 2010, 39(1): 85–96
[24] Vero S E, Basu N B, Van Meter K, et al. The environ-mental status and implications of the nitrate time lag in Europe and North America. Hydrogeology Journal, 2018, 26(1): 7–22
[25] Uchida T, Ukita M, Sekine M, et al. The study on the nonlinear characteristics of water quality in eutrophic sea areas and their modeling. Doboku Gakkai Ronbunshu, 1994, 503: 187–195
[26] 盛虎, 向男, 郭怀成, 等. 流域水质管理优化决策模型研究. 环境科学学报, 2013, 33(1): 1–8
[27] 刘永, 蒋青松, 梁中耀, 等. 湖泊富营养化响应 与流域优化调控决策的模型研究进展. 湖泊科学, 2021, 33(1): 49–63
[28] 周斌, 钱新, 王勤耕, 等. 高非线性水质模型参数最优化估值的改进遗传算法实现. 南京大学学报(自然科学版), 2007, 43(4): 377–388
Nonlinearity Strength Indicators for Numerical Simulation Based Load Reduction-Water Quality Responses
Abstract This study developed four nonlinearity strength indicators for water quality responses based on cross sample entropy, Fourier transformation, non-sequence counting, and adjusted R2 according to typical nonlinear load reduction-water quality responses suggested by previous studies. All the indicators were applied on typical numerical water quality simulation samples. Based on the calculation, the four indicators were compared with each other to provide suggestions on how to use them to detect the nonlinearity and measure the nonlinearity strength. Results show some overlaps among the four indicators, however, they are not interchangeable. The four indicators suggest seasonal differences, peak changes, short-term water quality deterioration, and averaged water quality changes respectively. After providing suggestions on how to use the four indicators to detect nonlinearity of water quality responses, this study further discusses the limitations on the nonlinearity definition and potential applications of the four indicators. This study will contribute to understanding, distinguishing, and analyzing the type of nonlinear water quality responses.
Key words nonlinearity; water quality response; load reduction; numerical simulation