2019年, 莱芜市并入济南市
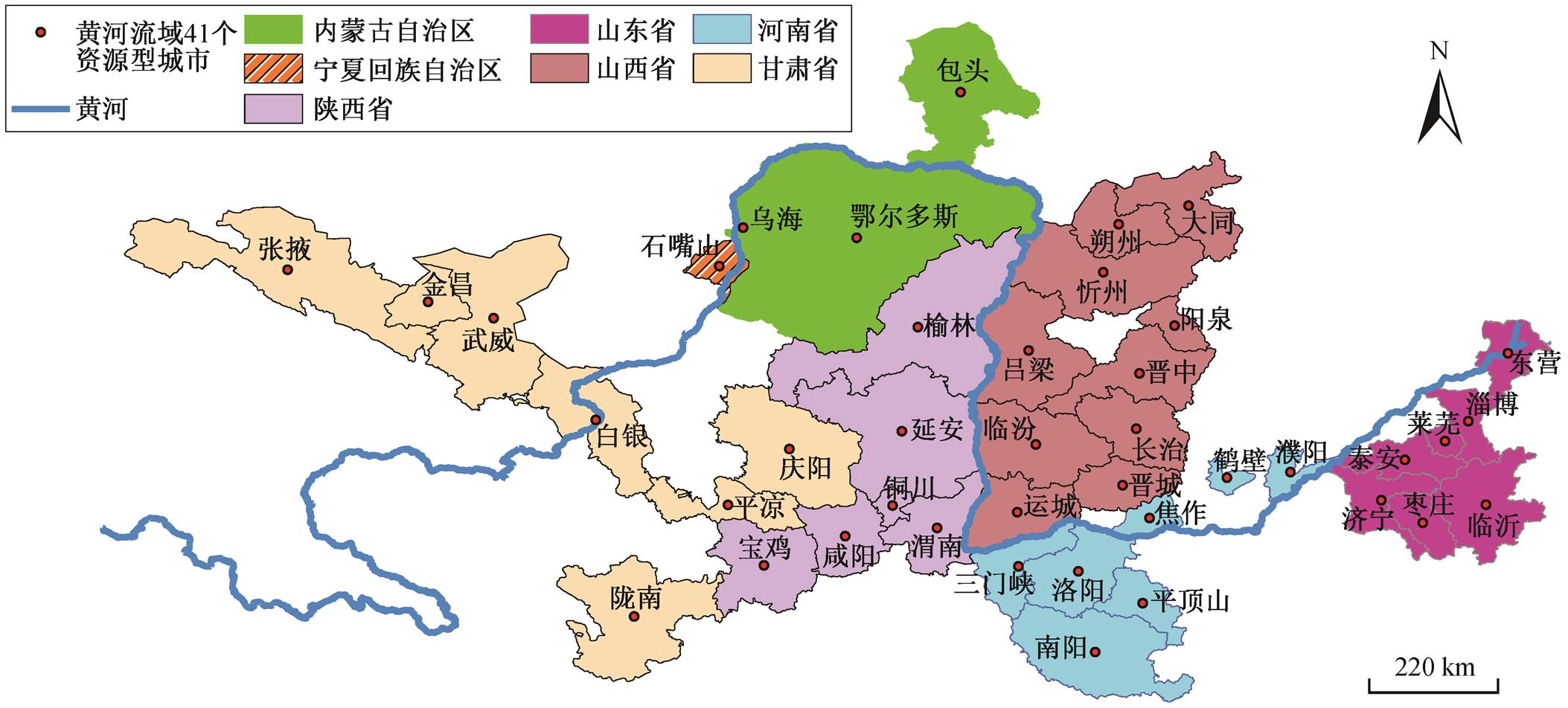
图1 黄河流域 41 个资源型城市分布
Fig. 1 Distribution of 41 resource-based cities in the Yellow River Basin
doi: 10.13209/j.0479-8023.2023.009
山西省自然科学基金(20210302124437, 201901D111074)资助
收稿日期: 2022–08–10;
修回日期: 2022–10–12
北京大学学报(自然科学版) 第59卷 第4期 2023年7月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 4 (July 2023)
摘要 针对黄河流域沿岸资源型城市城镇化和产业协同集聚对土地利用效率的影响, 基于 2000—2019 年黄河流域 41 个地区级资源型城市的面板数据, 采用空间自相关分析方法和空间杜宾模型, 解析城镇化和产业协同集聚对土地利用效率影响的空间溢出效应, 基于门槛回归模型, 讨论资源型城市产业协同集聚的门槛特征, 并构建拥挤效应矩阵表, 得到如下结果。1)黄河流域资源型城市之间的土地利用效率在空间上呈现以同高集聚或同低集聚为主的地理相关分布格局, 且城镇化的空间溢出抑制效应占总抑制效应的 70%, 表现出抑制作用; 产业协同集聚的空间溢出增长效应占总增长效应的 70%, 空间溢出抑制效应占总抑制效应的 20%, 表现出快速促进和逐渐抑制的作用。2)2014 年后, 部分黄河流域资源型城市的集聚效应向门槛聚集的程度加快, 其中洛阳、石嘴山、朔州、乌海和金昌表现优秀, 集聚效应最佳; 包头和鄂尔多斯形成城市间协同关系。3)资源型城市产业集聚总体上表现出集聚不足或拥挤的特征, 未来发展中应结合城市自身的特点, 发挥相邻城市间的协同带动作用。
关键词 资源型城市; 土地利用效率; 城镇化; 产业协同集聚; 空间杜宾模型; 门槛效应
黄河流域富含煤炭、石油和天然气, 沿岸分布大批资源型城市, 占流域城市总数的 50%左右, 占全国资源型城市总数的 30%[1]。然而, 资源型的城市密集分布导致生态环境脆弱和高质量发展不充分等问题[2]。随着资源型产业的集聚和城镇化发展, 城市土地的利用效率不足, 没有表现出与发展相协同的社会、经济和生态效益, 同时在经济发展的过程中还对生态和环境产生负面影响。2021 年 10 月印发的《黄河流域生态保护和高质量发展规划纲要》提出, 要“促进资源开发与新型城镇化建设和生态保护协调发展”[2]。在黄河流域, 亟待实现资源型城市产业和生态发展的转型升级, 增强区域的可持续发展能力[3]。
资源型城市兼具资源和城市两种特性, 在长期发展中呈现“资源主导、高速低质、发展脆弱、生态风险”的特征[4], 对资源的高度依赖使得土地利用效率受城镇化推动和产业协同集聚的影响更加突出。现有的研究集中于城镇化、产业协同集聚和土地利用效率之间的两两关系。针对城市与产业集聚的关系, 研究者通过面板数据进行两者关系的实证研究[5], 建立回归模型[6–7], 研究耦合关系[8–10]及耦合系统对区域经济发展[11]和创新承载能力[12]等方面的影响, 探讨两者交互作用机理[13]。针对城镇化与城市土地利用方面的关系, 研究者测算城市土地利用效率[14–15], 并分析其影响因素[16]和时空特 征[17], 研究城镇化过程中人口与土地之间的协 调[18]、耦合[19]和两者关系的滞后性[20], 以及在特定城市类别中城市土地利用效率的驱动因素[21]、机制[22]和制度影响[23]。针对产业协同集聚与土地利用的关系, 由于现实环境中产业的协同集聚更多地表现为相互关联产业空间上的集聚[24], 因此相关研究不可避免地涉及产业协同集聚与土地集约利用之间的数学统计相关性[25]和地理空间相关性[26], 以及不同维度[27]和结构[28]的协同集聚对土地利用效率的影响(包括倒“U”型曲线关系[29]等)。
现有研究集中于资源型城市的空间格局[30]、空间演变规律[31]、转型策略[32]和土地生态[33]等, 对资源型城市的研究深度不足, 缺乏以资源型城镇化发展为背景的产业集聚与土地利用关系研究。产业协同集聚和城镇化发展的最终落脚点在于如何在时间和空间上合理配置土地资源, 提高土地利用效率; 同时, 产业集聚与城镇化的发展进程相辅相成, 是经济发展和劳动力聚集在不同领域的同时期表现。因此, 产业协同聚集、城镇化和土地利用效率三者之间相互影响, 不应将其割裂开, 单纯地谈论两两关系。
黄河流域沿岸资源型城市的历史特征和时代地位愈来愈重要, 正确地认识和把握城镇化和产业协同集聚对土地利用效率的影响, 协调好城镇化发展过程中产业协同集聚对土地利用效率的影响, 是推动黄河流域资源型城市可持续发展的关键。因此, 本研究以 1999—2018 年黄河流域 41 个资源型城市为研究对象, 基于统计资料, 分析该区域资源型城市城镇化和产业协同集聚与土地利用效率之间的关系, 以期为资源型城市转型发展期间的城镇化推进、产业协同发展和土地利用优化提供决策支持, 促进黄河流域资源型城市的可持续发展, 推动国家重大战略的实施。
黄河流域有 42 个资源型城市[34], 分布在青海、甘肃、宁夏、内蒙古、山西、陕西、河南、山东 8个省(自治区)。由于缺乏青海省海西蒙古族藏族自治州的数据, 将其余 7 省 41 个地区级资源型城市列为研究对象(图 1)。按照资源类型划分, 约 54%为煤炭型城市; 按照发育程度划分, 49%为成熟型城市; 按照地理区位划分, 51%集中在中游区域。
本文研究数据包括 1999—2018 年黄河流域 41个资源型城市土地利用效率、产业协同集聚以及城镇化综合水平测算所需要的各指标值。数据来自2000—2019 年《中国城市统计年鉴》《中国环境统计年鉴》《中国城市建设统计年鉴》《中国能源统计年鉴》及相关省(自治区)市的统计年鉴、城市国民经济和社会发展公报等。个别缺失数据通过插值法补全。
2019年, 莱芜市并入济南市
图1 黄河流域 41 个资源型城市分布
Fig. 1 Distribution of 41 resource-based cities in the Yellow River Basin
本文的研究目标是在城镇化和产业集聚过程中合理地配置各要素, 使得土地利用保持高效性和可持续性。因此, 选择城市土地利用效率作为被解释变量, 产业协同集聚和城镇化作为核心解释变量, 将外资投入、政府干预、科研投入和环境规制作为控制变量来构指标体系(图 2)。
资源型城市土地利用效率受资源产业布置、社会经济发展和生态环境保护多重系统交互作用的影响[27,32], 对土地利用的最佳目标是最大化社会经济环境的期望产出和最小化环境与生态负面效应的非期望产出, 因此本研究叠加期望和非期望产出后的综合效率作为土地利用效率。基于新型城镇化的发展, 更加注重在人口城镇化过程中产业结构、生态环境和城市的公共服务水平, 以及城镇化布局和形态的优化等内容, 故本研究基于人口城镇化, 叠加经济、社会、生态 3 个维度[16], 构建城镇化指标体系。针对资源型城市, 采矿业与制造业共同形成城市的重要产业类型, 所以把采矿业、制造业和生产性服务业三者结合起来, 形成产业协同集聚指标体系[24], 更符合资源型城市的特征。
2.1.1被解释变量——城市土地利用效率
从资源型城市要素投入、期望与非期望产出 3个方面构建土地利用效率指标体系(表 1)。结合期望和非期望两方面的效益考虑, 采用改进的 SBM-DEA 模型[35]测算土地利用效率。对于黄河流域资源型城市, 有 n=41 个城市土地决策单元, 每个城市土地决策单元中有 m=3 种投入要素 X,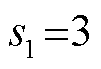 
种期望产出 Yg, 
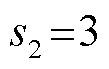种非期望产出 Yb, 其中 x∈Rm, yg∈
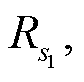yb∈
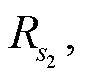通过矩阵计算形成生产可能集: P= {(x, yg, yb)| x≥Xλ, yg≤Ygλ, yb≥Ybλ, λ≥0}。包含期望和非期望产出的SBM-DEA模型的数学表达式为
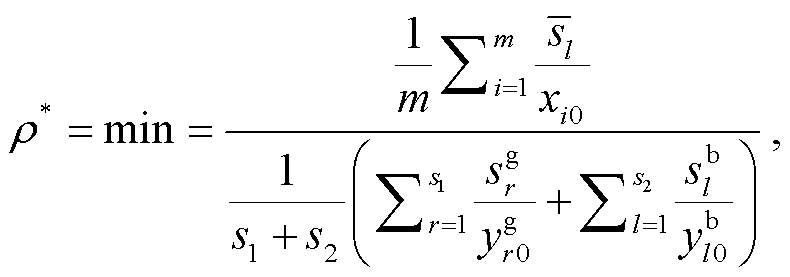(1)
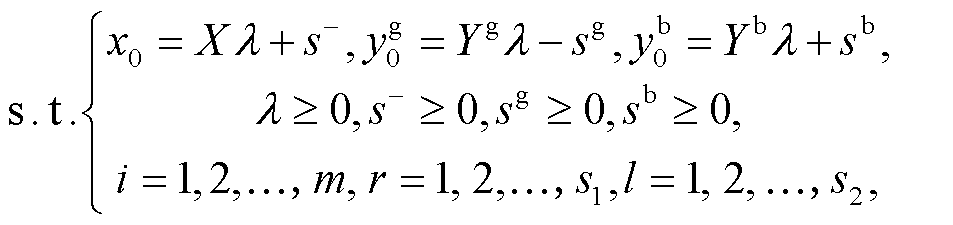(2)
其中, ρ*为效率数值, λ 为权重, x 为投入, s−为投入的松弛变量; yg 为期望产出, sg 为期望产出的松弛变量; yb 为非期望产出, sb 为非期望产出的松弛变量。
2.1.2核心解释变量Ⅰ——城镇化
城市的综合发展状况通常由城镇化水平衡量, 现有的研究多从人口、土地、经济、社会和生态等单个或多维度入手, 构建指标体系来测度城镇化水平[15–16,19]。为避免被解释变量(土地利用效率)与解释变量(城镇化)的共线性以及指标重复选取等问题, 本研究剔除土地维度, 构建人口、经济、社会和生态 4 个维度的城镇化综合指标体系(表 2)。就人口维度而言, 人口数量和质量都是关键, 故资源型相关产业及其延伸产业的劳动人员和技术人员, 以及以大学生为代表的高素质人才, 可以共同反映人口对城镇化的影响。从经济维度来看, GDP 的增长在一定程度上反映经济的向好趋势, 人均 GDP 更具公平性, 单纯地考虑经济增长而忽视经济增长背后的粗放问题, 是不合理的, 因此增加工业产值在 GDP中的占比和万元 GDP 能耗这两个指标更合理。就社会维度来说, 公共事业和公共基础设施均是其典型指标, 科技、教育、文化、卫生医疗和公共交通等多个方面皆代表社会维度的公共性。就环境维度而言, 资源型产业的发展存在工业“三废”的排放和污染问题, 城市生活垃圾的合理处置和工业固体废弃物的综合利用可以减少生产生活对环境的污染及负担, 同时林、草、花、藤等建成区绿化覆盖, 也可以为生态维度增加正向影响。因此, 选择常住人口、产业人口和大学生人数组成人口维度, 产值和能耗指标组成经济维度, 公共配套和基础设施投入组成社会维度, 城市污染和绿化组成生态维度, 运用熵值法客观赋予指标权重, 测算城镇化综合水平。
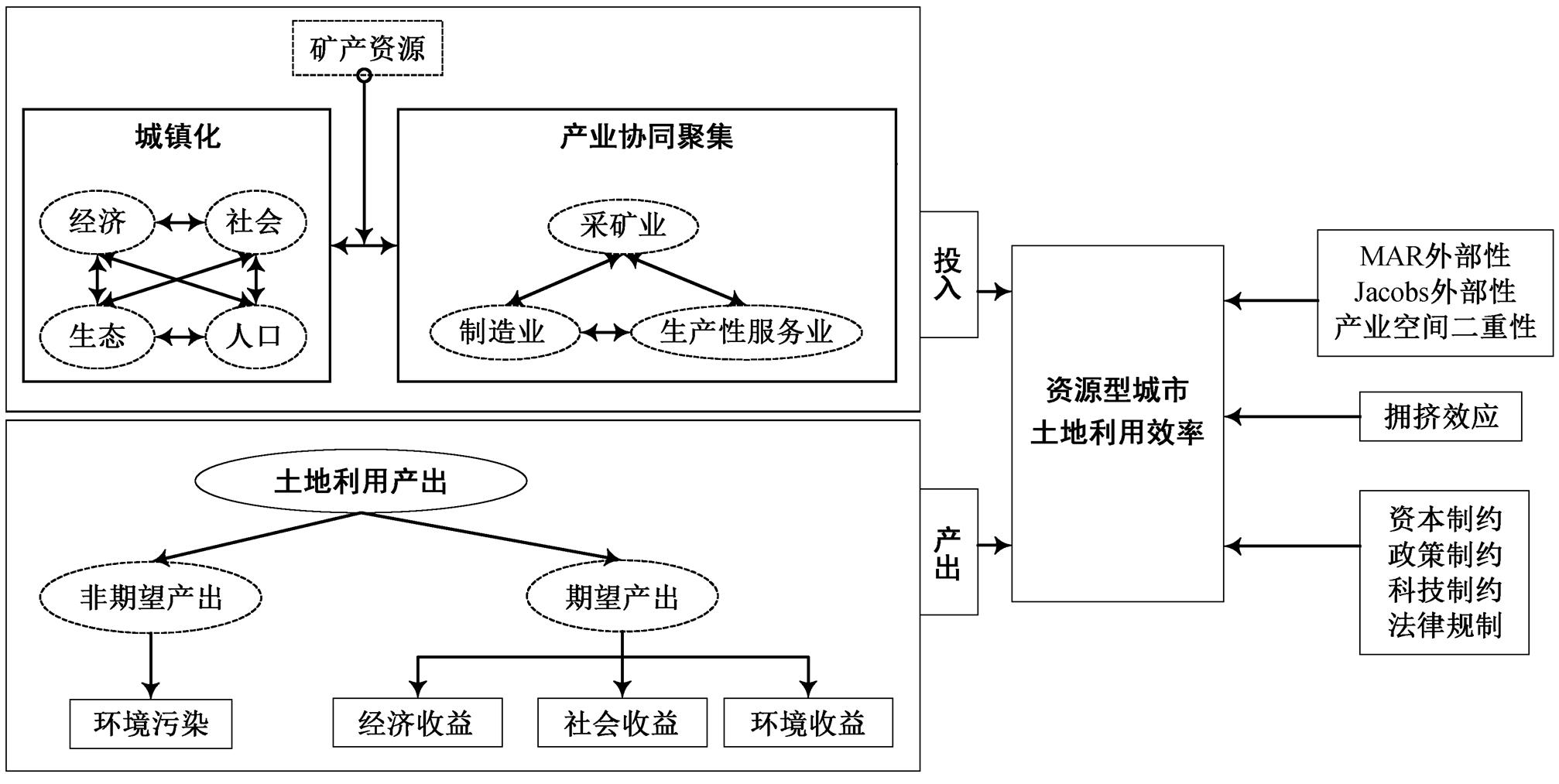
图2 资源型城市城镇化、产业协同集聚及城市土地利用效率关系
Fig. 2 Relationship between urbanization, industrial collaborative agglomeration and urban land use efficiency in resource-based cities
表1 土地利用效率的指标体系
Table 1 Indicator system of land use efficiency
准则层要素层指标层 投入指标资本全社会固定资产投资(万元) 劳动第二、三产业从业人数(人) 土地建成区面积(平方公里) 期望产出指标经济收益第二、三产业产值(万元) 社会收益城镇在岗职工平均工资(元) 环境收益公园绿地面积(公顷) 非期望产出指标对环境的负面影响(工业三废)工业废水排放量(万吨) 工业废气(SO2)排放量(吨) 工业固体废弃物产生量(万吨)
表2 城镇化综合测度指标体系
Table 2 Comprehensive measurement index system of urbanization
城镇化维度指标单位作用方向 人口常住人口城镇化率%+ 采矿业从业人员比重%+ 第三产业从业人员比重%+ 每万人拥有大学生人数人+ 经济人均 GDP元+ 第二产业产值占总产值比重%+ 万元 GDP 能耗吨标准煤/万元− 社会科技教育支出占财政支出比重%+ 每百人公共图书馆藏书册+ 每万人医院与卫生院床位数张+ 每万人拥有公共汽车台+ 生态建成区绿化覆盖率%+ 工业废水排放量万吨− 工业废气(SO2)排放量吨− 工业固体废弃物综合利用率%+ 城市生活垃圾无害化处理率%+
2.1.3核心解释变量Ⅱ——产业协同集聚
借鉴陈建军等[36]提出的修正 E-G 指数法, 将采矿业和制造业和生产性服务业从业人数作为基础数据, 计算产业协同集聚指数。生产性服务业包括交通、信息、科技服务、金融和租赁等 5 个行业。计算公式为
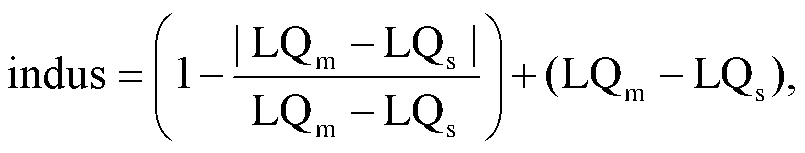(3)
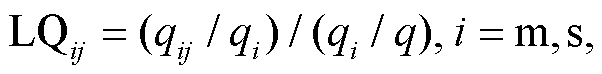(4)
其中, indus 为产业协同集聚指数; m 代表采矿业和制造业, s 代表生产性服务业; LQm 为采矿和制造业的集聚指数, LQs 为生产性服务业的集聚指数; LQij为 j 市 i 产业的熵值, 用来计算 LQm 和 LQs; q 为就业人数。
2.1.4控制变量
由外资投入、政府干预、科研投入和环境规制4 个方面组成控制变量, 其中外资投入变量=外商投资额/GDP, 政府干预变量=地方财政支出/GDP, 科研投入变量=科技支出/公共财政支出, 环境规制变量为污染治理综合指数。污染治理综合指数是由熵值法测算的综合指数, 包括污水处理厂集中处理率、工业 SO2 去除率、生活垃圾无害化处理率、一般工业固体废物综合利用率以及工业烟(粉)尘去除率 5 个指标。
为纠正传统模型因忽略空间溢出项而造成的设定偏差, 首先采用 Moran’s I 指数和莫兰散点图, 对土地利用效率进行空间自相关性检验, 确定其是否存在空间溢出效应。然后, 构建包含城镇化综合水平、产业协同集聚和土地利用效率 3 个核心变量的空间杜宾模型(spatial Dubin model, SDM), 并进行LM, LR 和 Wald 检验, 确保 SDM 具有最优的拟合效果。最后, 根据产业集聚理论和已有相关实证研究[29,36–37]显示的产业集聚与土地利用效率的倒“U”型关系, 运用门槛回归模型来检验这一非线性影响。
2.2.1空间自相关性检验
空间样本之间可能存在相互关联的地理属性, 因此利用 Moran’s I 指数衡量黄河流域资源型城市的空间自相关性, 描述资源型城市之间的平均关联程度、空间分布模式及显著性[38], 反映流域内资源型城市在空间上的总体相似程度。同时, 采用莫兰散点图分析资源型城市土地利用效率的空间差异程度。Moran’s I 指数的计算公式为
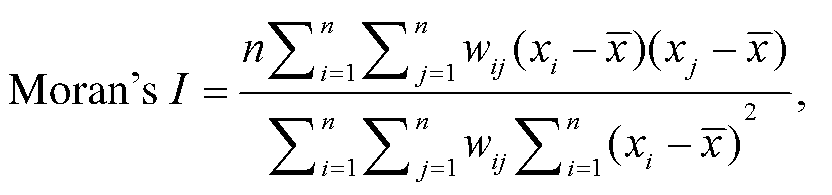(5)
其中, Moran’s I 为全局莫兰指数, 数值介于−1～1 之间, −1～0 表示负相关, 0～1 表示正相关, 0 为不相关, 绝对值越接近 1, 则相关性越强; n 为样本总数; i和 j 代表样本个体; wij 为空间反距离权重; x 为样本 变量。
采用莫兰散点图, 进一步考察城市土地利用效率的空间关联形式, 分析市域间的空间差异程度。莫兰散点图中, 第一、三象限分别表示“高–高”和“低–低”正相关, 代表黄河流域地域相邻资源型城市间的正向空间相关性; 第二、四象限分别表示“低–高”和“高–低”负相关, 代表黄河流域地域相邻资源型城市间的负向空间相关性。
2.2.2空间杜宾模型(SDM)
一个城市土地利用效率可能受到其他城市城镇化与产业协同集聚影响。因此, 忽略城镇化与产业协同集聚所伴随的空间相关性, 可能造成模型的错误设定。因此, 本文选用在空间效应评价中具有优势的空间杜宾模型来分析城镇化、产业协同集聚对土地利用效率的影响, 并采用偏导矩阵方法[39]测度分解的直接效应、间接效应(即空间溢出效应)和总效应。考虑到一般空间矩阵无法充分地反映黄河流域资源型城市之间的关联, 选用反距离权重矩阵来表征城市之间的空间效应。由城市之间距离的倒数构成矩阵, 主对角线元素为 0, 非主对角线上的元素为两个城市地理中心位置间距离的倒数。
首先, 将 SDM 一般模型构建为
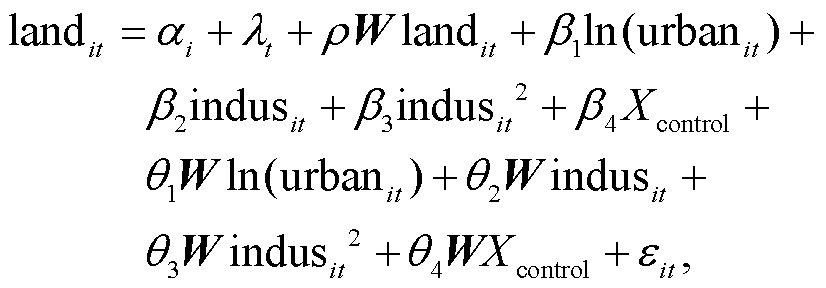(6)
其中, 下角标 i 和 t 分别表示城市和时间, landit为各地级市的土地利用效率, urbanit 为各地级市的城镇化水平, indusit 为各地级市的产业协同集聚指数, Xcontrol 为控制变量, βm(m=1, 2, 3, 4)为解释变量对本市的影响系数, θm 为解释变量的空间滞后项系数, ρ 为被解释变量的空间滞后项系数, ε 为随机变量, αi 为个体固定效应, λt 为时点固定效应, W 为反距离空间权重矩阵。
然后, 分解产业协同集聚对土地利用效率的影响, 计算直接效应(反映解释变量对本区域被解释变量的平均作用)、间接效应(即空间溢出效应, 反映解释变量对其他区域被解释变量的平均作用)和总效应(反映解释变量对全部区域被解释变量的平均作用), 计算公式为
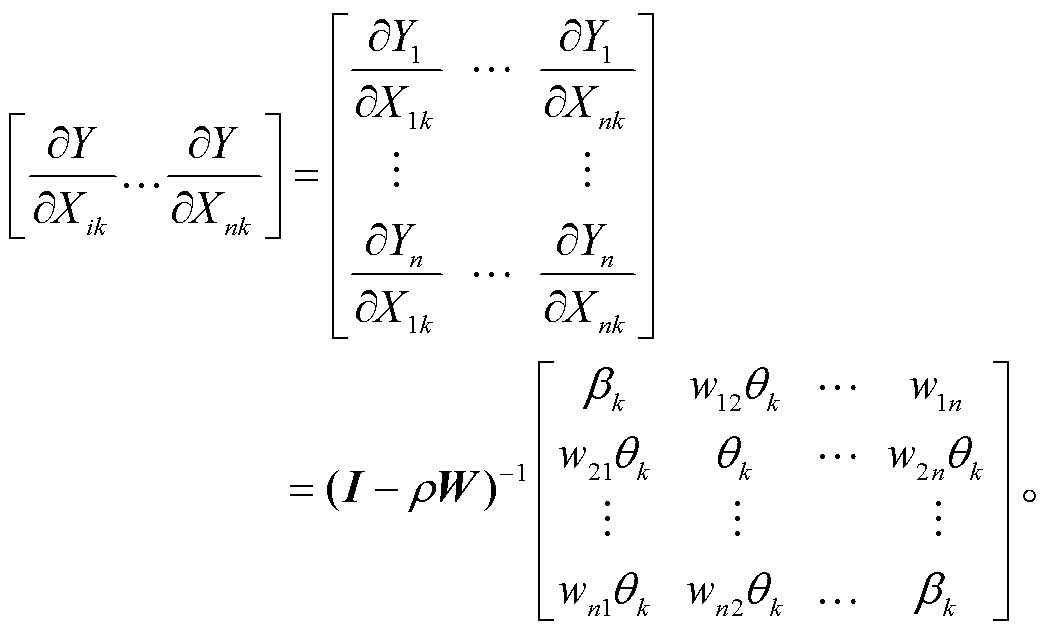(7)
式(7)第二个等号右侧矩阵中, 对角线元素的平均值为直接效应, 非对角线元素的均值为间接效应, 两者之和为总效应。
2.2.3门槛回归模型及检验
门槛效应指当某一变量达到临界值后引发其他变量发生突变, 向其他形式变化的现象, 该临界值即门槛值。集聚经济的外部性会对要素利用效率产生正反两方面的作用[24–26], 因此资源型城市主导产业的协同集聚对土地利用效率的提升存在积极和消极两方面影响以及发生突变的门槛值。本研究采用Hansen[40]提出的门槛回归模型检验产业协同集聚对土地利用效率的非线性影响。设定产业协同集聚为门槛变量, 模型表达式为
landit=μi+(β1ln(urbanit)+β2indusit+β3Xcontrol)I(indusit≤γ)+ (β1′ln(urbanit)+β2′indusit+β3′Xcontrol)I(indusit>γ)+εit, (8)
式中, I(×)为示性函数, 取值为 1 或 0, 当括号内条件满足时, I(×)=1, 否则为 0; γ 为门槛值。
采用全局 Moran’s I 指数度量资源型城市间土地利用效率的空间自相关性, 结果如图 3 所示。除2010 和 2011 年外, 其他年份土地利用效率的全局Moran’s I指数均显著为正, 说明黄河流域资源型城市的土地利用效率为空间正相关, 即以“高–高”和“低–低”两种类型为主导。对比 2004 和 2015 年的莫兰散点图(图 4), 2004 年位于“高–高”、“低–高”、“低–低”和“高–低” 4 种类型的城市数分别为 14, 6, 13 和 8, 而 2015 年分别变化为 14, 6, 18 和 3, 大部分城市土地利用效率表现出同高或同低的趋势, 并且随着时间的变化, “高–低”型空间集聚趋势处于下降趋势, “低–低”型空间聚集处于上升趋势。
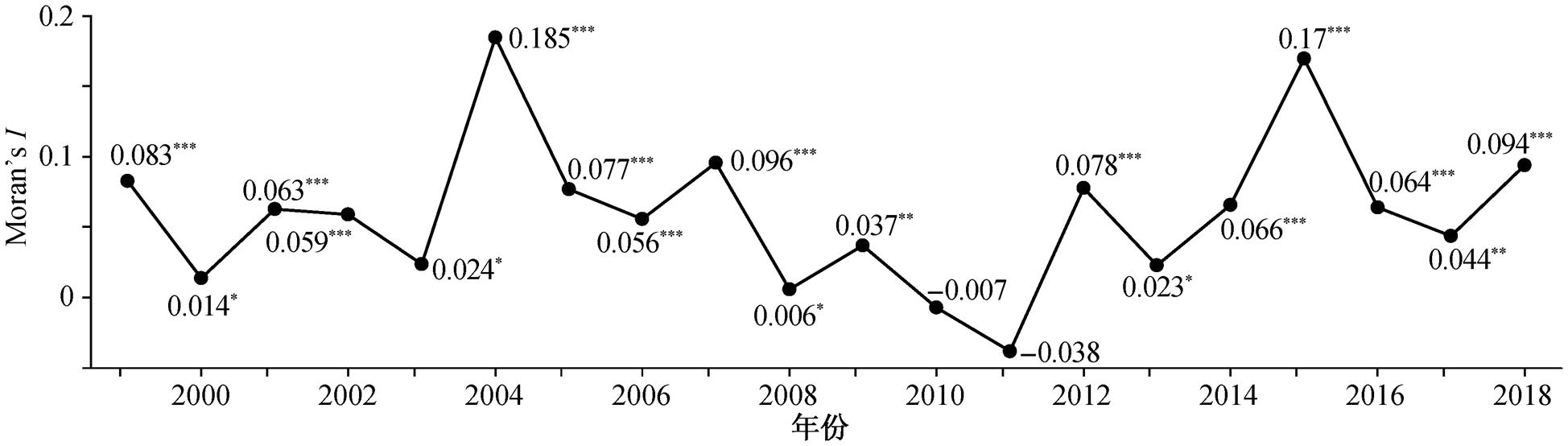
图3 Moran’s I指数及其显著性水平
Fig. 3 Moran’s I index and its level of visibility
图4 2004年(a)和2015年(b)资源型城市土地利用效率莫兰散点图
Fig. 4 Moran scatter plot of land use efficiency of resource-based cities in 2004 (a) and 2015 (b)
3.2.1模型比选与计算
产业集聚与土地利用效率之间具有倒“U”型关系[23–25], 因此引入产业协同集聚的二次项作为解释变量, 将部分绝对量取对数, 以便缓解异方差带来的影响。
为了提高回归统计的准确性, 分别运用空间自回归模型(SAR, 仅考虑空间被解释变量滞后)、空间误差模型(SEM, 仅考虑空间误差项自相关)和空间杜宾模型(SDM, 综合考虑二者的空间传导机制)进行回归分析。统计结果显示, 与 SAR 和 SEM 相比, SDM 的回归系数显著性更强(表 3), 说明 SDM在空间回归模型中表现最优; 另外, 从表 3 看出, SDM 模型的 Wland 参数估计值为 0.677, 且在 1%置信水平下显著, 由此可得流域内资源型城市自身的土地利用效率每增长 1%, 将引起与它相邻城市的效率值平均增长 0.677%。城镇化水平的系数显著为负, 表明资源型城市土地利用效率提升会受到城镇化进程中资源主导和生态环境风险制约, 导致提升速度变慢。产业协同集聚的系数在 1%的显著性水平下大于 0, 其二次项系数在 5%的显著性水平下小于 0, 证明存在倒“U”型关系, 城镇化初期产业协同集聚率先对土地利用效率发挥集聚效应, 到达峰值后会突变, 受到拥挤效应的支配。
进一步做统计检验(表 4), Hausman 检验结果显示 SDM 模型固定效应下的效果更优, LM 检验结果显示使用 SAR 或 SEM 模型考察城镇化和产业协同集聚对土地利用效率的空间效应存在产生误差的风险, LR 检验和 Wald 检验结果显示本研究中 SDM 不能退化为 SAR 或 SEM 的任何一种。因此, 将 SDM (固定效应)确定为本研究的核心模型。
3.2.2 SDM的效应分解
由表 3 可知, SDM 中城镇化和产业协同集聚的水平项系数和空间交互项系数对土地利用效率影响的显著性都很强, 但 SDM 的回归系数在反映解释变量对被解释变量的影响程度和空间溢出特征时表现欠佳, 需进一步测度直接效应、空间溢出效应以及总效应(表 5)。结果显示, 城镇化的直接和空间溢出效应均显著小于 0, 产业协同集聚的直接和空间溢出效应都显著大于 0, 产业协同集聚二次项的直接和空间溢出效应均显著小于 0; 城镇化与产业协同集聚不仅直接效应明显, 其空间溢出效应对土地利用效率的影响亦表现显著。观察城镇化的空间溢出抑制效应和总抑制效应可以发现, 城镇化所带动的空间溢出抑制效应占总抑制效应的 70%, 产业协同集聚所带动的空间溢出增长效应在总增长效应中的占比亦接近 70%, 产业协同集聚二次项所带动的空间溢出抑制效应在总抑制效应中的占比接近20%, 由此印证受资源主导、伴随生态风险的城镇化的空间溢出效应制约了土地利用效率的提升, 并且产业协同集聚带来的空间溢出效应对资源型城市土地利用效率具有快速促进和逐渐抑制作用。将分解的直接效应与传统的 OLS 回归结果做比较可以发现, SDM 的城镇化和产业协同集聚的直接效应更小, 说明在传统回归中存在因忽略空间效应导致的估计结果偏差。
基于产业协同集聚对土地利用效率具有倒“U” 型影响[24–26], 可以通过门槛回归模型来检验产业协同集聚对土地利用效率的非线性影响, 并寻找引起这种非线性关系的关键节点。将产业协同集聚作为门槛变量, 通过门槛效应检验、门槛值估计和门槛回归模型的参数估计 3 个步骤来检验产业协同集聚对土地利用效率的非线性关系, 由此识别产业协同集聚作用于土地利用效率使之发生变化的阈值(表6)。结果显示, 产业协同集聚的 F 统计量在显著性为 5%时仅通过单一门槛检验, 表明产业协同集聚作用于土地利用效率的门槛效应是单一门槛效应, 产业协同集聚的单一门槛值为 2.624; 产业协同集聚在≤2.624 和>2.624 的门槛区间内对土地利用效率的弹性系数分别为 0.069 和−0.045, 且显著性水平为 1%, 所以, 当产业协同集聚处于≤2.624 的门槛区间内时会发挥集聚效应, 一旦跨越门槛值 2.624, 拥挤效应占据上风。黄河流域资源型城市中, 产业协同集聚达到门槛值的有 10 个, 分别为金昌、包头、乌海、鄂尔多斯、咸阳、榆林、朔州、淄博、东营和济宁, 主要为煤炭型城市, 集中于黄河中下段。这些城市需注意适度集聚产业, 避免拥挤效应的负作用。其他城市目前没有达到巅峰状态, 可以采取措施, 使不同产业进一步适度集聚。
表3 SAR, SEM和SDM空间面板计量回归统计结果
Table 3 SAR, SEM, and SDM spatial panel regression statistical results
模型lnurbanindusindus2WlandWlnurbanWindusWindus2R2log-likelihood SAR−0.0441***[0.0170]0.0364**[0.0157]−0.00308**[0.0018]0.895403.167 SEM−0.0359***[0.0157]0.0374**[0.0149]−0.00281**[0.0017]0.983447.05 SDM−0.0369***[0.0134]0.0386**[0.0143]−0.00331**[0.0017]0.677***[0.0526]−0.0400**[0.0134]0.0460**[0.0167]−0.0031*[0.0019]0.995458.197
说明: log-likelihood 为对数似然估计函数值(也称最大似然估计值), 方括号内数字表示对应参数估计的标准误差。
表4 SDM的检验结果
Table 4 Results of SDM
检验方法统计量数值结论 Hausman57.97***拒绝 LMLM_error93.049***拒绝 Robust LM_error18.753不拒绝 LM_lag74.432***拒绝 Robust LM_lag0.137不拒绝 LRSDM-SAR58.15***拒绝 SDM-SEM61.61***拒绝 WaldSDM-SAR29.33***拒绝 SDM-SEM24.96***拒绝
表5 SDM的直接效应、间接效应和总效应
Table 5 Direct effect, indirect effect and total effect of SDM
效应类别变量系数tp 直接效应lnurban−0.031***−3.100.002 indus0.058***3.960 indus2−0.052***−3.000.003 间接效应(空间溢出效应)lnurban−0.070**−2.500.012 indus0.132***3.130.002 indus2−0.012**−2.530.011 总效应lnurban−0.100***−2.760.006 indus0.190***3.540 indus2−0.064***−2.760.006
为保证研究结果的准确性, 避免内生性和测度误差等影响实证结果, 本文采用重构空间权重矩阵、内生性检验和异质性分析等 3 种方式检验研究结果的稳健性。
3.4.1重新构建空间权重矩阵
通过反距离矩阵、邻接矩阵(如果两城市相邻, 则权重矩阵中所对应元素取 1, 否则取 0)和反距离平方矩阵(也称空间距离权重矩阵, 主对角线上的元素均等于 0, 非主对角线上的元素等于两个城市地理中心位置之间距离的平方的倒数), 分别进行稳健性检验。结果(表 7)表明, 与反距离矩阵相比, 邻接矩阵和反距离平方矩阵的城镇化和产业协同集聚的影响系数符号和显著性均未出现明显的变化, 说明研究结果是稳健的。
表6 产业协同集聚对土地利用效率的门槛效应检测结果及其特征
Table 6 Threshold effect results and characteristics of industrial collaborative agglomeration on land use efficiency
检验Fp结论估计值95%置信区间变量值域系数 单一门槛检验19.21**0.038接受2.624(2.5879, 2.6986)≤2.6240.0687*** >2.624−0.0454*** 双重门槛检验11.970.310拒绝 三重门槛检验9.730.493拒绝
表7 稳健性检验——重建空间权重矩阵
Table 7 Robustness test: reconstruction of spatial weight matrix
矩阵lnurbanindusindus2W lnurbanW indusW indus2R2log-likelihood SDM (反距离矩阵)−0.0369***0.0386**−0.00331**−0.0400**0.0460**−0.0031*0.995458.197 SDM (邻接矩阵)−0.0381**0.0457**−0.00387*−1.147**1.771**−0.187**0.896568.27 SDM (反距离平方矩阵)−0.0354**0.0405**−0.00350*−0.0430**0.0450**−0.0041*0.895557.09
3.4.2内生性检验
考虑到土地利用效率和产业协同集聚之间可能存在互为因果的关系, 选择合适的工具变量, 利用2SLS(两阶段最小二乘法)[3]进行估计。本研究将城市海拔的倒数与城市交通设施滞后一期(每万人拥有公共汽车台数)的交互项作为产业协同集聚的工具变量来检验内生性[41]。根据回归结果(表 8), Wald F 统计量为 48.77(大于经验标准 10.00), 说明选取的工具变量是有效的, 且城镇化和产业协同集聚的影响系数符号和显著性水平均未出现明显的变化, 证明研究结果是可靠的。
3.4.3异质性分析
根据 SDM 和门槛回归的分析, 影响土地利用效率的两个要素——城镇化及产业协同集聚程度可能在城市的不同发育程度、不同资源类型和不同地理区位等表现出不同的特点, 因此, 分别依据城市发育程度、资源类型和地理区位 3 种进行异质性分析(表 9)。
1)发育程度异质性: 资源开采利用进程不同, 资源型城市发育成熟程度也会有所差异。分不同程度探究资源型城市城镇化和产业协同集聚对土地利用效率影响, 可以看出, 仅成熟型城市的城镇化对土地利用效率的负面影响显著, 成熟型和衰退型城市产业协同集聚对土地利用效率的影响具有倒“U”型特征。成熟型城市数量占比近 50%, 成熟型和衰退型城市总数占到近 70%, 具有代表性, 回归分析结果与全样本结果一致。
2)资源类型异质性: 主导资源类型的不同也会导致城镇化和产业协同集聚对土地利用效率作用效果的差异。可以看出, 煤炭型和石油型城市的城镇化对土地利用效率的负面影响显著, 仅煤炭型城市产业协同集聚对土地利用效率的影响具有倒“U”型特征。煤炭型城市数量占到 54%, 具有代表性, 回归分析结果与全流域资源型城市结果一致。
3)地理区位异质性: 黄河流域上游和中游的划分以河口镇为界线, 中游和下游以桃花峪为界。资源型城市所处区段的不同也会导致城镇化和产业协同集聚对土地利用效率作用效果的差异。可以看出, 中游区域的资源型城市土地利用效率的影响不仅在城镇化方面显著, 而且受产业协同集聚的倒“U”型影响也显著。中游区城市数量占到 51%, 具有代表性, 回归分析结果符合全样本的检验结果。
综上所述, 通过重新构建权重矩阵、选择工具变量进行内生性检验以及按照不同标准对城市分类(发育程度、资源类型和地理区位)进行异质性分析, 并用 3 种方式进行稳健性检验, 发现城镇化和产业协同集聚对土地利用效率的影响系数大小有所差异, 但是符号和显著性水平均未出现明显的变化, 证明研究结果是稳健可靠的。
表8 稳健性检验——内生性检验(2SLS)
Table 8 Robustness test: endogeneity test (2SLS)
lnurbanindusindus2常数项N调整R2F −0.237**0.388**−0.0428**1.819***7790.90848.77
表9 稳健性检验——异质性检验
Table 9 Robustness test: heterogeneity test
划分类型类别lnurbanindusindus2N调整R2 发育程度成长0.0190.0609−0.005841600.2471 成熟−0.0449*0.0652*−0.00484*4000.1327 衰退−0.1930.335**−0.0477**1400.4107 资源类型再生−0.00222−0.07970.01381200.3016 煤炭−0.0745*0.130***−0.0136**4400.2252 石油−0.0558*−0.01360.00151000.2002 金属0.00616−0.002880.005152600.2354 非金属0.265−1.5260.599200.3673 地理区位上游−0.00898−0.01190.002872200.3911 中游−0.0586*0.146**−0.0169**4200.1854 下游0.0398−0.005270.000721800.2139
说明: 加粗数字表示位于黄河流域“中游”、发育程度为“成熟”的“煤炭”资源型城市的城镇化和产业协同集聚对土地利用效率的影响比其他类别样本更具有代表性, 回归结果与全样本结果一致。
1)资源型城市在不同发育程度、资源类型、地理区位的分样本与全样本之间存在一定的差异。尽管通过 Moran’s I 指数和 SDM 分析, 可知黄河流域资源型城市土地利用效率会受到其他城市城镇化与产业协同集聚影响, 相邻城市土地利用效率存在同高或同低现象, 且资源型城市的城镇化、产业协同集聚和土地利用效率之间有明显的空间溢出效应, 并通过了内生性检验和异质性分析, 然而, 异质性检验的结果同时表现出资源型城市在不同发育程度、资源类型和地理区位的分类中与全样本之间存在一定的差异。以资源型城市土地利用效率为例, 分别按照黄河流域资源型城市的发育程度、资源类型和地理区位进行分类对比(图 5)。可以看出, 发育程度的成长型和再生型城市土地利用效率曲线、资源类型的金属型和非金属型城市土地利用效率曲线、地理区位的上游区和下游区城市土地利用效率曲线与全样本之间存在一定的偏移。在产业集聚和城镇化情景中也存在同样的情况, 证明黄河流域资源型城市在整体上变化一致的情况下, 因发育程度、资源类型和地理区位不同而存在空间差异。
2)数据分析显示, 资源型城市的城镇化和产业协同集聚对土地利用效率存在线性和非线性的直接效应和空间效应, 其中黄河流域资源型城市城镇化对土地利用效率的线性关系表现为负向, 而产业协同集聚表现出快速促进和逐渐抑制的倒“U”型关系, 比较流域内各资源型城市的产业协同集聚值与门槛值, 41 个城市中超过门槛值的有 10 个(表 10)。各城市的产业协同集聚集中在 2011—2013 期间出现最高值拐点, 其中 2011 年仅鄂尔多斯到达产业协同集聚最高值拐点, 2013 年包头和乌海出现产业协同集聚最高值拐点, 其余城市均在 2012 年出现产业协同集聚最高值拐点。这与“十二五”期间国家发布一系列新兴产业转型和资源型城市可持续发展的政策文件和国家相关规划相吻合, 各资源型城市顺应政策导向, 基于个体特征进行了相应的资源转型研究和工作。其中, 朔州在发展煤炭产业的同时支持“右玉羊肉”等特色农业和发展陶瓷等地方产业; 鄂尔多斯和包头在产业协同集聚中表现为同进同退, 与“呼包鄂”城市经济圈对 3 个城市的战略协同政策相关, 体现“呼包鄂”城市群的一体化与辐射带动作用; 榆林和济宁两个城市在出现产业协同集聚拥挤时, 及时进行产业调整, 使得 2012 年之后拥挤程度逐渐减缓, 并靠近门槛值。2014—2018 年期间, 金昌和乌海产业调整为集聚正效应; 其余大于门槛值的城市中, 除东营因拥挤现象凸显, 导致产业集聚拥挤效应居高不下外, 其他城市都有回调, 朔州的回调幅度最大, 为 3.28, 回调至门槛值附近; 鄂尔多斯、包头回调幅度居中, 为 1.5 左右; 榆林和济宁变动不大, 稳定在略大于门槛值的范围内。产业集聚水平处于最优状态, 集中于门槛附近的城市主要有洛阳、石嘴山、朔州、乌海和金昌, 其中洛阳和石嘴山为小于门槛值的城市中通过促进发展向门槛靠近, 朔州、乌海和金昌为大于门槛值的城市中通过调整产业结构向门槛靠近。未曾达到门槛值的31 个城市, 大部分处于随时间缓慢上升的产业协同集聚正效应阶段, 目前产业政策基本上合理, 但需要提高产业集聚水平。
图5 黄河流域资源型城市土地资源利用效率变化
Fig. 5 Variations of land use efficiency of resource-based cities in the Yellow River Basin
表10 黄河流域资源型城市产业协同集聚拥挤效应的矩阵
Table 10 Matrix of industrial collaborative agglomeration crowding effect of resource-based cities in the Yellow River Basin
城市年份 200420052006200720082009201020112012201320142015201620172018 金昌2.63 2.71 2.79 2.84 3.022 3.02 2.86 包头2.99 3.05 3.63 3.99 4.55 4.97 5.4205.40 5.34 5.27 5.26 3.90 乌海2.82 3.29 3.56 3.74 3.7483.67 3.58 3.56 3.03 鄂尔多斯3.11 3.76 4.46 5.00 5.591 5.56 5.37 5.26 5.05 5.01 4.83 4.09 咸阳2.90 3.46 4.200 4.18 4.16 4.14 4.11 4.09 4.07 榆林3.2243.19 3.14 3.11 3.07 3.11 3.11 朔州3.40 4.39 5.22 5.68 5.9165.90 4.34 4.23 3.56 2.89 2.62 淄博2.70 2.81 3.11 3.77 4.3004.25 4.21 4.16 4.04 4.03 4.01 东营3.16 4.07 4.07 4.41 5.24 5.76 6.30 6.95 7.7007.39 6.85 6.75 6.72 6.39 6.39 济宁3.3983.14 3.08 3.08 3.08 3.01 2.94
说明: 表中仅保留产业协同集聚效应大于门槛值(2.624)的城市和效应值; 粗体数字表示产业协同集聚拐点。
3)大部分城市产业协同处于集聚正效应阶段, 但部分城市也表现出拥挤。对此, 我们提出如下建议。第一, 发挥相邻城市间的协同带动作用。在产业发展过程中, 资源型城市既要发挥资源优势, 更要注重产业的协同集聚, 加强上下游产业的关联与互通, 分享集聚效应的资源红利。在发展基础优势产业的同时, 应互相借鉴有益经验, 引进高端生产性服务业; 加强信息交流与要事沟通, 避开错路歧路, 转变城镇化持续发展的驱动要素; 发挥人才、技术和资金的相互帮扶与共享, 由依赖不可再生资源的消耗转向重视创新技术和高素质人才以及充足资金的联动作用, 缓解黄河流域的生态环境风险, 实现流域的高质量发展。第二, 在保持协调的同时, 城市的发展更要结合自身特点。正如产业协同集聚效应中所反映的, 除东营外, 部分城市需注意适度调整集聚程度, 避免拥挤效应的负作用。大部分城市目前并没有达到巅峰状态, 可以采取措施, 使不同产业进一步集聚, 但集聚的过程需摒弃原有方式, 提前考虑好矿产资源的不可再生性、城镇化的脆弱性、生态环境风险的威胁以及产业集聚的低端单一化等要素, 有效地组织配置资源禀赋、产业优势和土地要素, 促进黄河流域资源型城市绿色、健康和持续发展。
本文通过构建土地利用效率、城镇化、产业协同集聚的指标体系及测算方式, 采用空间自相关分析、空间杜宾模型以及门槛回归模型, 对 1999—2018 年黄河流域 41 个地区级资源型城市的面板数据进行实证研究, 解析城镇化和产业协同集聚对土地利用效率影响的空间效应, 验证产业协同集聚的门槛特征, 讨论资源型城市空间异质性, 构建产业协同集聚拥挤效应矩阵表, 提出政策建议。本研究得出以下结论。
1)黄河流域资源型城市之间的土地利用效率具有明显的空间自相关, 空间分布上以同高集聚或同低集聚为主, 共同享受富足资源禀赋的红利, 也共同受制于资源枯竭和环境生态破坏造成的困境。城镇化和产业协同集聚不仅直接效应明显, 其空间溢出效应在土地利用效率影响中的表现更显著。城镇化总效应中, 空间溢出抑制效应占比较大, 占总抑制效应的 70%; 产业协同集聚总效应中, 空间溢出增长效应占比较大, 占总增长效应的 70%; 产业协同集聚二次项总效应中, 空间溢出抑制效应占比相对较少, 占总抑制效应的 20%, 产业协同集聚对土地利用效率的空间溢出效应具有快速促进和逐渐抑制的作用。
2)黄河流域资源型城市产业协同集聚的门槛值为 2.624, 基于 2011—2013 年国家产业政策的调整, 除大型油田聚集的石油城市东营外, 大部分资源型城市向门槛聚集的速度加快, 表现优秀的几个城市为金属矿再生型中游城市洛阳、煤矿衰退型上游城市石嘴山、煤矿成长型中游城市朔州、煤矿衰退型上游城市乌海和金属矿成熟型上游城市金昌, 这些城市的协同聚集程度在门槛值左右浮动, 集聚效应最好; 金属矿再生型上游城市包头和煤矿成长型上游城市鄂尔多斯因城市群一体化发展, 形成协同状况。从总体上看, 无论发育阶段、资源类型和地理区位, 黄河流域各城市的产业结构调整政策成效明显, 大部分城市尚未达到门槛值, 具有较大的上升空间。
3)资源型城市的城镇化和产业协同集聚对土地利用效率存在线性和非线性的数据关系。本研究能较准确地识别引起空间溢出效应的变量, 并且有针对性地把握当前资源型城市的发展困境和转型方向。各个城市在空间上存在自相关和空间溢出的影响作用, 其中 75%的城市产业协同向集聚正效应方向发展, 25%的城市产业协同表现为聚集效应拥挤, 需要制定相应的政策引导城市间的协同和创新 作用。
参考文献
[1] 阎晓, 涂建军. 黄河流域资源型城市生态效率时空演变及驱动因素. 自然资源学报, 2021, 36(1): 223–239
[2] 中共中央国务院印发《黄河流域生态保护和高质量发展规划纲要》2021 年第 30 号国务院公报[EB/OL]. (2021–10–08)[2022–01–05]. https://www.gov.cn/gong bao/content/2021/content_5647346.htm
[3] 杨桐彬, 朱英明. 产业协同集聚对资源型城市可持续发展的影响. 北京理工大学学报(社会科学版), 2021, 23(4): 60–71
[4] 白中科. 资源型城市城镇化进程及生态整治路径研究. 中国土地, 2017(7): 17–19
[5] 严翔, 成长春, 贾亦真. 中国城镇化进程中产业、空间、人口对能源消费的影响分解. 资源科学, 2018, 40(1): 216–225
[6] 马志东, 俞会新. 产业集聚与城镇化关系的实证分析——基于我国东中西部差异的视角. 河北大学学报(哲学社会科学版), 2016, 41(6): 80–87
[7] 龙奋杰, 王雪芹, 王爵, 等. 产业发展与城镇化互动关系分析. 城市问题, 2015(7): 19–25
[8] 丛海彬, 邹德玲, 刘程军. 新型城镇化背景下产城融合的时空格局分析——来自中国 285 个地级市的实际考察. 经济地理, 2017, 37(7): 46–55
[9] 孙叶飞, 周敏. 中国城镇化、产业结构高级化对CO2 排放的影响——基于独立效应和联动效应双重视角. 资源科学, 2016, 38(10): 1846–1860
[10] 张勇, 蒲勇健, 陈立泰. 城镇化与服务业集聚——基于系统耦合互动的观点. 中国工业经济, 2013, 30(6): 57–69
[11] 刘肖, 金浩. 产业协同集聚与城镇化耦合的经济增长效应. 西北人口, 2021, 42(5): 16–29
[12] 陈斌. 长三角城镇化、产业集聚与区域创新承载力的耦合关系. 南通大学学报(社会科学版), 2020, 36(1): 42–49
[13] 马国勇, 蔡玲松. 城镇化与产业集聚交互作用机理研究. 哈尔滨工业大学学报(社会科学版), 2019, 21(5): 127–134
[14] 岳立, 李文波. 环境约束下的中国典型城市土地利用效率——基于DDF-Global Malmquist-Luenberger指数方法的分析. 资源科学, 2017, 39(4): 597–607
[15] 李佳佳, 罗能生. 城镇化进程对城市土地利用效率影响的双门槛效应分析. 经济地理, 2015, 35(7): 156–162
[16] 岳立, 薛丹. 新型城镇化对中国城市土地利用效率的影响研究. 经济问题探索, 2020, 41(9): 110–120
[17] 金贵, 邓祥征, 赵晓东, 等. 2005—2014 年长江经济带城市土地利用效率时空格局特征. 地理学报, 2018, 73(7): 1242–1252
[18] 刘欢, 邓宏兵, 李小帆. 长江经济带人口城镇化与土地城镇化协调发展时空差异研究. 中国人口·资源与环境, 2016, 26(5): 160–166
[19] 刘萌, 冯长春, 曹广忠. 中国城市土地投入产出效率与城镇化水平的耦合关系——对 286 个地级及以上城市行政单元的分析. 中国土地科学, 2014, 28 (5): 50–57
[20] 李子联. 人口城镇化滞后于土地城镇化之谜——来自中国省际面板数据的解释. 中国人口·资源与环境, 2013, 23(11): 94–101
[21] 樊鹏飞, 冯淑怡, 苏敏, 等. 基于非期望产出的不同职能城市土地利用效率分异及驱动因素探究. 资源科学, 2018, 40(5): 946–957
[22] 张荣天, 焦华富. 长江经济带城市土地利用效率格局演变及驱动机制研究. 长江流域资源与环境, 2015, 24(3): 387–394
[23] Yang Y T, Jiang G H, Zheng Q Y, et al. Does the land use structure change conform to the evolution law of industrial structure? An empirical study of Anhui province, China. Land Use Policy, 2019, 81: 657–667
[24] 刘月, 邹苗苗, 陈建军. 空间经济学视角下的产业协同集聚: 一个文献综述. 江淮论坛, 2017, 283(3): 47–53, 193
[25] 韩峰, 王琢卓, 杨海余. 产业结构对城镇土地集约利用的影响研究. 资源科学, 2013, 35(2): 388–395
[26] 黄和平, 彭小琳. 脱钩视角下城市土地利用效率变化与提升策略. 资源科学, 2016, 38(3): 493–500
[27] 张雯熹, 吴群, 王博, 等. 产业专业化、多样化集聚对城市土地利用效率影响的多维研究. 中国人口·资源与环境, 2019, 29(11): 100–110
[28] 符海月, 王昭雅. 区域产业结构调整与土地利用效率关系——基于城镇化水平视阈的考察. 中国土地科学, 2020, 34(10): 69–78+107
[29] 苗建军, 徐愫. 空间视角下产业协同集聚对城市土地利用效率的影响——以长三角城市群为例. 城市问题, 2020(1): 12–19
[30] 常江, 刘巷序. 煤炭资源型城市空间格局研究进展. 中国矿业, 2018, 27(7): 64–69
[31] 宋飏, 王士君, 王雪微, 等. 矿业城市生命周期与空间结构演进规律研究. 人文地理, 2012, 27(5): 54–61
[32] 朱琳, 卞正富, 朱环, 等. 资源枯竭型城市转型期土地利用与城市发展耦合关系分析——以徐州市贾汪区为例. 城市发展研究, 2013, 20(1): 54–59
[33] 杨清可, 段学军, 王磊, 等. 长三角区域一体化与城市土地利用效率的协同测度及交互响应. 资源科学, 2021, 43(10): 2093–2104
[34] 国务院办公厅: 国务院关于印发全国资源型城市可持续发展规划(2013—2020 年)的通知[EB/OL]. (2013– 11–12)[2022–01–05]. https://www.gov.cn/gongbao/con tent/2013/content_2547140.htm
[35] Tone K. A slacks-based measure of super-efficiency in data envelopment analysis. European Journal of Opera-tional Research, 2002, 143(1): 32–41
[36] 陈建军, 刘月, 邹苗苗. 产业协同集聚下的城市生产效率增进——基于融合创新与发展动力转换背景. 浙江大学学报(人文社会科学版), 2016, 46(3): 150–163
[37] 原毅军, 高康. 产业协同集聚、空间知识溢出与区域创新效率. 科学学研究, 2020, 38(11): 1966–1975
[38] 徐冬, 黄震方, 黄睿. 基于空间面板计量模型的雾霾对中国城市旅游流影响的空间效应. 地理学报, 2019, 74(4): 814–830
[39] Lesage J, PACE R K. Introduction to spatial econo-metrics. Boca Ration: CRC Press, 2009: 11–85
[40] Hansen B E. Threshold effects in non-dynamic panels: estimation, testing and inference. Journal of Economet-rics, 1999, 93(2): 345–368
[41] 宣烨, 余泳泽. 生产性服务业集聚对制造业企业全要素生产率提升研究——来自 230 个城市微观企业的证据. 数量经济技术经济研究, 2017, 34(2): 89–104
Impact of Urbanization and Industrial Collaborative Agglomeration on Land Use Efficiency of Resource-Based Cities in the Yellow River Basin, China
Abstract Based on the panel data of 41 prefecture-level resource-based cities in the Yellow River Basin from 2000 to 2019 and the relationship between urbanization and industrial collaborative agglomeration on land use efficiency, this paper uses spatial autocorrelation analysis and spatial Durbin model to analyze the spatial spillover effect of urbanization and industrial collaborative agglomeration on land use efficiency. The threshold regression model is used to discuss the threshold characteristics of industrial collaborative agglomeration in resource-based cities, and the crowding effect matrix table is innovatively constructed. The results show that the land use efficiency among resource-based cities in the Yellow River Basin is geographically correlated with the same high agglomeration or the same low agglomeration in space, and the spatial spillover inhibitory effect of urbanization accounts for 70% of the total inhibitory effect, showing an inhibitory effect. The spatial spillover growth effect of industrial collaborative agglomeration accounts for 70% of the total growth effect, and the spatial spillover inhibitory effect accounts for 20% of the total inhibitory effect, which shows the role of rapid promotion and gradual inhibition. After 2014, the agglomeration effect of some resource-based cities in the Yellow River Basin has accelerated to the threshold, among which Luoyang, Shizuishan, Shuozhou, Wuhai and Jinchang perform well and have the best agglomeration. Baotou and Ordos form a collaborative relationship between cities. The industrial agglomeration of most resource-based cities is still insufficient or crowded, and the future development should combine the characteristics of the city itself to play a synergistic role between adjacent cities.
Key words resource-based cities; land use efficiency; urbanization; industrial collaborative agglomeration; spatial Durbin model; threshold effect