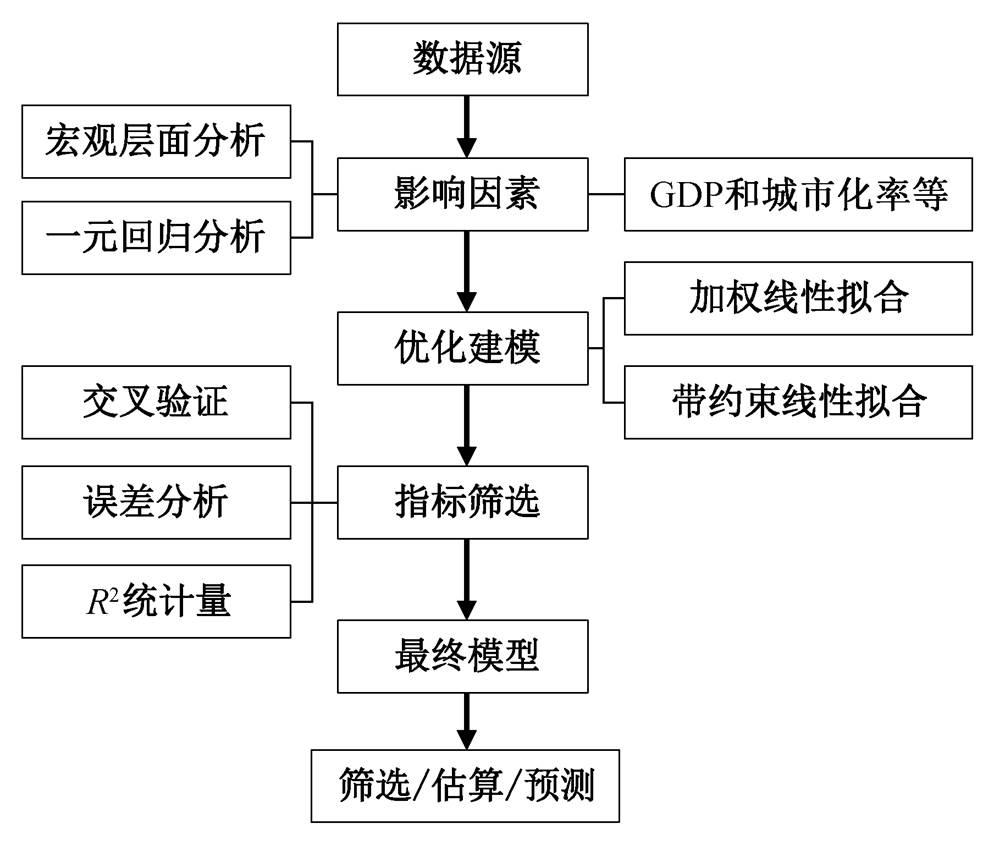
图1 基于统计年鉴的多元线性回归分析方法计算流程
Fig. 1 Workflow of the multiple linear regression analysis on statistical yearbooks
收稿日期: 2022–06–24;
修回日期: 2022–09–20
北京大学学报(自然科学版) 第59卷 第4期 2023年7月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 4 (July 2023)
doi: 10.13209/j.0479-8023.2023.043
国家重点研发计划(2018YFC0704300)和国家自然科学基金数学天元基金项目(12126348, 12126370)资助
摘要 针对不同统计年鉴中竣工面积统计数据差异较大的问题, 结合统计年鉴中关于城市用地需求和社会发展水平等相关数据, 运用加权回归分析模型, 分析不同数据源民用建筑的竣工面积统计值, 并对数据源进行分析与确认。针对全国及分省只有累积拆除面积数据以及缺失逐年拆除面积统计值的问题, 利用全国人口普查、城市用地需求和社会发展水平等相关数据, 建立约束回归分析模型, 提出分省逐年拆除面积计算方法, 估算拆除面积和拆除率。研究结果可为确定我国近 20 年建筑规模的实际情况和相关节能减排政策的制定提供科学参考。
关键词 建筑规模数据; 竣工面积; 拆除面积; 拆除率; 回归分析
随着建筑领域节能减排工作的推进, 现有的相关统计制度暴露出统计数据存在标准不统一、缺失严重等问题, 导致数据的准确性存疑, 可用性不足, 阻碍了节能减排政策的制定, 影响了我国建筑领域的优化与高质量发展。作为建筑业的重要指标, 民用建筑竣工面积和拆除面积的计算对于确认我国民用建筑规模和推进节能减排工作具有重要意义。
针对我国民用建筑面积的计算已开展多年的研究, 并取得一些成果。匡文慧等[1]以长春市为研究对象, 结合基于知识规则的遥感影像分类方法及空间网格技术, 提出城市不同类型用地面积的估算方法。刘菁等[2]通过分析不同统计年鉴指标的内涵, 选择固定资产投资住宅竣工面积作为数据源, 进行实有建筑面积的计算。王君等[3]用房地产开发企业住宅竣工面积减去《中国城乡建设统计年鉴》提供的镇年末住宅竣工面积, 得到市、县年末竣工面积, 进而得到城镇实有建筑面积。原雯等[4]基于年鉴统计数据的实际情况, 通过构建关于经济社会因子体系的多种回归模型, 预测 2017 和 2018 年北京市房屋竣工面积, 同时利用爬虫技术获取的高质量数据, 估算 2019 年北京市房屋竣工面积。
统计年鉴的数据具有权威性和简洁性等特点, 用于计算地区的建筑面积非常快速高效。目前主要有 3 种统计年鉴涉及民用建筑竣工面积: 《中国建筑业统计年鉴》《中国房地产统计年鉴》和《中国固定资产投资统计年鉴》。由于统计口径和方法等因素的影响, 3 种统计年鉴的统计值差异很大。统计年鉴的数据源选择对后续的研究非常重要, 本研究拟采用加权回归分析方法来确定合适的数据源。
拆除面积对计算地区建筑面积同样非常重要。由于自身经济发展的需要、城市规划的调整以及人口情况的变动等, 不同地区的拆除率不尽相同。现有统计年鉴中尚无民用建筑拆除面积的统计数据, 大部分学者以实有建筑面积为基数, 采用比例估算法进行估计, 但没有统一的标准。董迎春[5]通过专家咨询的方式, 将居住建筑拆除面积占上年末实有居住建筑面积的比例设为 0.5%, 公共建筑拆除面积占上年末实有公共建筑面积的比例设为 1%。黄禹等[6]利用 2001—2013 年各年住房减少面积和年末住房实有建筑面积计算城镇住房拆除率, 并利用固定效应模型和混合回归模型分析拆除率的影响因素。黄敬婷等[7]基于人口普查数据, 对 2001—2010 年 10年间的城镇地区住房拆除规模进行定量测算, 并分析影响城镇拆除规模的关键因素。刘存[8]基于人口普查和人口抽样调查数据, 运用轮换模型, 对我国不同建成年代的城镇居住建筑存量和拆除量进行测算, 并在此基础上对现有城镇居住建筑中节能建筑占比进行定量研究。唐守娟等[9]以北京市为例, 基于 Stella 建模平台, 构建城市居民住宅建筑系统流量–存量的动态模拟模型, 定量地模拟不同管理情景下钢材需求量和建筑拆除垃圾产生量的变化区间。Wu 等[10]按人口规模, 对城市住户采取分层三级随机抽样, 获得 2002—2009 年 9 个省份的微观数据, 计算省级民用建筑整体拆除面积。上述关于拆除面积估算的研究中, 测算结果年份较早, 无法反映近几年的变化, 且仅针对全国整体或部分省市进进行测算, 研究粒度太粗覆盖面不足。
多元线性回归模型可解释性强, 理论完善, 是计算建筑规模数据的有效方法。多元线性回归分析是处理多个连续变量之间相互依赖关系的机器学习方法[11], 针对不同的需求, 已经发展出岭回归[12]和LASSO[13]等多种变式。加权回归分析模型是针对误差具有不相同的方差情形提出的一种改进方法, 通过对不同的样本数据设定不同的权重, 使得误差的方差处于同一水平, 以便提高拟合精度[14]。针对具体问题, 回归模型会出现带约束的形式, 这类问题可通过罚函数法等多种约束优化算法来求解[15]。多元线性回归模型可基于决定系数等统计量来分析变量之间的相关性, 从而为变量筛选提供参考指标。与神经网络等模型相比, 多元线性回归分析模型的线性假设空间 VC 维度(Vanpik-Chervonenkis dimension)有限, 泛化能力较强, 不易受噪声干扰。此外, 多元回归分析模型的计算复杂度低, 适用于大数据处理和分析。
本文提出一种基于统计年鉴数据的多元回归分析方法, 用来解决民用建筑竣工面积数据源选择和拆除面积逐年拆分与预测两个问题。一方面, 通过分析民用建筑竣工面积相关统计现状, 指出不同来源统计结果不一致的问题, 并利用加权回归分析方法建立竣工面积与城市用地需求、社会发展水平等指标的回归模型, 进而确定民用建筑竣工面积的最优数据源。另一方面, 针对民用建筑领域分省逐年拆除面积统计值空白的问题, 基于全国第五次人口普查数据、全国第六次人口普查数据和其他统计年鉴数据, 计算得到 2001—2010 年累积 10 年各省拆除面积, 建立分省逐年拆除面积关于城市用地需求和社会发展水平等指标的约束回归分析模型, 计算2001—2019 年全国及 31 个省市自治区(除港澳台)民用建筑的逐年拆除面积和拆除率。
从宏观层面看, 房屋竣工面积的影响因素包括城市用地需求和社会发展水平等。拆除面积直接与竣工面积和实有建筑面积的增量相关, 从而也与城市用地需求和社会发展水平等因素相关。首先获取相关影响因子, 通过一元回归分析验证目标变量与影响因子之间是否存在线性关系。然后, 建立自变量与目标变量之间的加权或约束线性回归模型, 并通过交叉验证和拟合误差进行影响因子筛选, 获得最终模型。最后, 基于最终模型确认竣工面积的数据源, 来估算拆除面积。图 1 给出基于统计年鉴数据的多元线性回归分析计算流程。
竣工面积与城市用地需求、房产建筑行业发展水平以及社会发展水平等因素相关, 其中社会发展水平包括经济发展水平和人民生活水平。本文结合这些影响因素, 给出与竣工面积相关的影响因子 (表 1)。
房屋拆除面积受实有建筑面积和建筑竣工面积等因素的影响, 关系式为
本年实有面积 - 去年实有面积
=竣工面积 - 拆除面积。 (1)
引入与房屋拆除面积相关的一级指标(影响因子), 即城镇实有建筑面积增量和房屋竣工面积。根据式(1), 拆除面积也与表 1 中的指标存在线性关系。表 2 给出与拆除面积相关的影响因子(指标)。
本文从国家统计年鉴中收集 2001—2019 年与竣工面积和拆除面积影响因素相关的指标, 作为多元回归模型的自变量。所获取数据为各省(市、自治区)以年度为频次的时间序列。因变量 Y 为分省年度房屋竣工面积或分省年度房屋拆除面积。
图1 基于统计年鉴的多元线性回归分析方法计算流程
Fig. 1 Workflow of the multiple linear regression analysis on statistical yearbooks
表1 竣工面积影响因子及符号表示
Table 1 Influence factors of completed area and symbols
影响因素影响因子(指标)符号 城市用地需求常住人口(人)A1 城市化率(%)A2 房产建筑行业发展水平房地产生产值(亿元)A3 建筑业生产值(亿元)A4 社会发展水平GDP (亿元)A5 出生率(%)A6 第三产业生产值(亿元)A7 人均收入(元/人)A8 农村人均收入(元/人)A9 城镇人均收入(元/人)A10
表2 拆除面积影响因子及符号表示
Table 2 Influence factors of demolition area and symbols
指标类别影响因子(指标)符号 二级指标常住人口(人) 城市化率(%) 房地产生产值(亿元) 建筑业生产值(亿元) GDP (亿元) 出生率(%) 第三产业生产值(亿元) 人均收入(元/人) 农村人均收入(元/人) 城镇人均收入(元/人) 一级指标实有居住建筑面积增量(万 m2) 竣工面积(万 m2)
为确定线性模型的合理性, 首先对因变量和各自变量之间的关系进行初步回归分析。根据不同省份的数据, 建立各省因变量与各影响因子的一元回归拟合模型。根据 P 值和决定系数 R2, 判断自变量的显著性和模型的有效性[16]。
然后, 建立因变量与所有影响因子的多元线性回归模型。假设因变量与城市化率、常住人口、房地产生产值、建筑业生产值、GDP、出生率、第三产业生产值、人均收入、农村人均消费和城镇人均消费等指标线性相关, 构建如下线性回归模型:
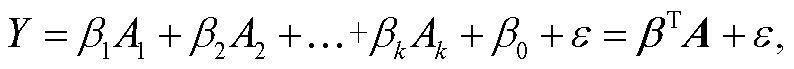(2)
其中,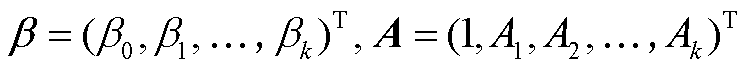
,ε 为随机误差。
由于不同省份不同年份的人口规模和经济发展水平等因素存在差异, 所以随机误差
应具有不同的方差。为统一地给全国各省市选出最显著相关的指标, 对每个样本数据引入权重
, 得到以下加权线性回归模型的广义最小二乘问题:
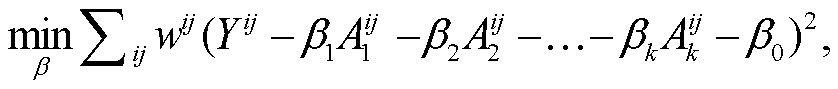(3)
其中, 上角标 i 表示省份, 上角标 j 表示年份。通过广义最小二乘法, 求出相应的 β 值, 给出模型的拟合或预测值
βTAij。为度量自变量对因变量的解释程度, 引入决定系数R2:
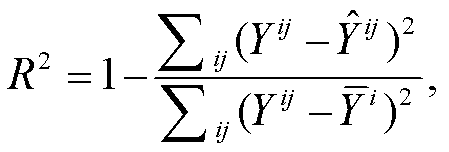(4)
其中,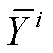
为某省份各年的均值。R2越趋近 1, 拟合效果越好。预测值
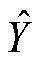越趋近 Y, 因变量受自变量的影响越大。
对于因变量 Y 没有观测值而只有约束条件的情形, 将因变量也作为优化变量, 与参数在约束条件下一同求解, 得到如下约束回归模型:
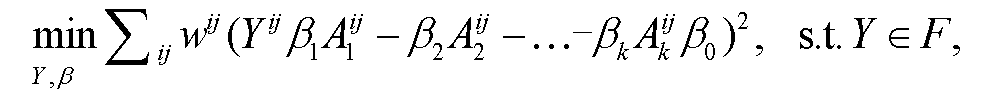(5)
其中, F 为可行域。
冗余或噪声较大的自变量会给模型带来较高的计算复杂度以及预测的不稳定性。为了选取合适的指标, 本文使用交叉验证方法[17]和基于误差的全子集法[18]进行变量筛选。首先按 7:3 的比例, 将数据集 D 随机地分为训练集 U 和校验集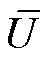
两部分,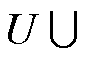
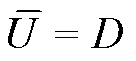。在训练集上进行线性回归, 在校验集上计算误差。对于式(3), 求解如下优化问题:
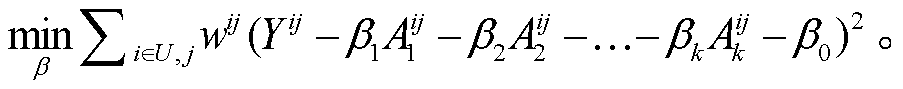(6)
对于式(5), 求解如下优化问题:
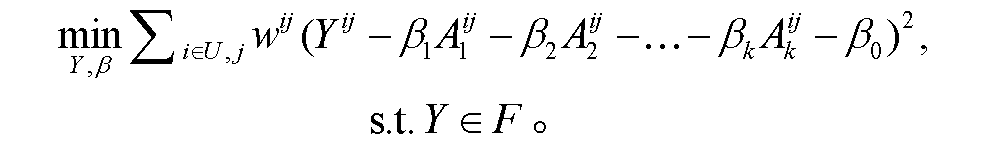(7)
得到参数值 β 后, 将其带入校验集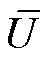中计算误差。对于式(3), 定义误差为
є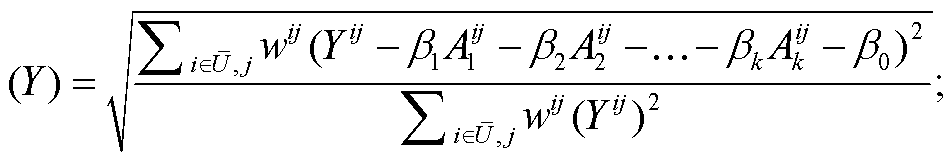
(8)
对于式(5)定义误差为
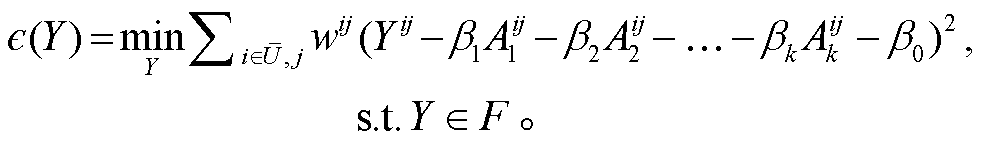(9)
然后, 利用相应的统计年鉴数据, 列出所有可能的自变量组合, 分别计算拟合后在校验集上的误差。选择最小误差对应的自变量组合和拟合系数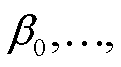
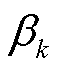作为最终模型的变量和系数。
利用式(3), 对每一种来源的竣工面积数据按照上述流程进行线性拟合, 选择最终模型误差最小的一种作为最优的数据源。对于拆除面积, 由于没有目标变量的直接观测值, 仅有累积 10 年之和, 因此利用式(5)按照上述流程拟合求解, 并由最终模型得到分省分年拆除面积和拆除率的估计值和预测值。
房屋竣工面积指在报告期内房屋建筑按照设计要求全部完工, 达到居住和使用条件, 经验收鉴定合格, 并正式移交使用的各栋房屋建筑面积的总和[19]。计算房屋竣工面积, 必须严格执行房屋竣工验收标准。
竣工面积数据来源于《中国建筑业统计年鉴》《中国房地产统计年鉴》和《中国固定资产投资统计年鉴》3 种统计年鉴。数据结构包括居住建筑竣工面积和公共建筑竣工面积, 所获取数据为各省(市、自治区)以年度为频次的时间序列。各年鉴对建筑类型有不同的划分方式。
1)《中国建筑业统计年鉴》划分为 8 类, 分别为住宅房屋, 商业及服务用房屋, 办公用房屋, 科研、教育和医疗用房屋, 文化、体育和娱乐用房屋, 厂房及建筑物, 仓库, 其他。
2)《中国房地产统计年鉴》划分为 4 类, 分别为住宅房屋、办公楼、商业营业用房及其他。
3)《中国固定资产投资统计年鉴》划分为两类: 住宅房屋及其他。
表 3 为 2005—2012 年 3 种统计年鉴的全国居住建筑竣工面积数据的对比。可以看出, 《中国固定资产投资统计年鉴》与《中国建筑业统计年鉴》数据差异较小, 在一定程度上说明这两种数据源的可靠性。《中国房地产统计年鉴》的竣工面积只有《中国固定资产投资统计年鉴》(或《中国建筑业统计年鉴》)的 1/3～1/2, 数据差异巨大。可认为《中国房地产统计年鉴》的数据最不合理, 下面不考虑该年鉴的数据。
表3 不同数据源竣工总面积对比
Table 3 Comparison of total completed area from different data sources
数据源面积/108m2 2005年2006年2007年2008年2009年2010年2011年2012年 《中国固定资产投资统计年鉴》13.2813.1414.6315.9418.4218.3219.7519.51 《中国建筑业统计年鉴》8.9510.2911.9313.3915.1917.2520.0723.42 《中国房地产统计年鉴》4.374.554.985.435.966.347.437.90
表 4 和图 2 展示江苏省和上海市的拟合效果。表 4 中 P 值均小于 0.05, 说明这些变量在线性回归模型中是显著的; 决定系数 R2 均大于 0.4, 说明线性回归模型是有效、可解释的。从图 2 可以看出, 将《中国固定资产投资统计年鉴》作为数据源时, 各省的竣工面积与表 1 中各项影响因子(指标)存在较强的线性相关性, 进一步说明基于这些影响因子构建线性回归模型具备合理性。
取权重 wij 为第 i 省份在第 j 年的实有人口占该年全国实有人口的比例, 满足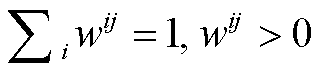
。基于回归模型(式(3))和校验误差(式(8))对变量进行筛选, 得出校验误差最小的自变量组合, 得到如下结论。
表4 《中国固定资产投资统计年鉴》单一指标拟合结果
Table 4 Fitting results with single factor for the “Statistical Yearbook of the Chinese Investment in Fixed Assets”
自变量因变量P值R2 常住人口(A1)上海市竣工面积[9.50×10–7, 2.88×10–5]0.779 GDP (A5)江苏省竣工面积[4.87×10–4, 4.93×10–3]0.481
1)《中国固定资产投资统计年鉴》的竣工面积与 GDP、第三产业生产值、人均收入、城市化率、农村人均消费和城镇人均消费相关。
2)《中国建筑业统计年鉴》的竣工面积与人口、GDP、人均收入、城市化率、农村人均消费和城镇人均消费相关。
利用式(4)和(8)计算决定系数 R2 和线性回归误差, 结果如表 5 所示。可以看出, 《中国固定资产投资统计年鉴》的决定系数更接近 1, 且误差更小, 说明选择《中国固定资产投资统计年鉴》作为数据源更加合理。
以上海市和江苏省为例, 用加权回归模型拟合《中国固定资产投资统计年鉴》的竣工面积和筛选出的最优变量, 拟合效果如图 3 所示。可以看到模型可以很好地展现数据的变化趋势。
通过分析 3 种统计年鉴中民用建筑竣工面积相关指标的数据特点和模型拟合结果, 最终确定《中国固定资产投资统计年鉴》的固定资产投资住宅竣工面积更准确可靠。
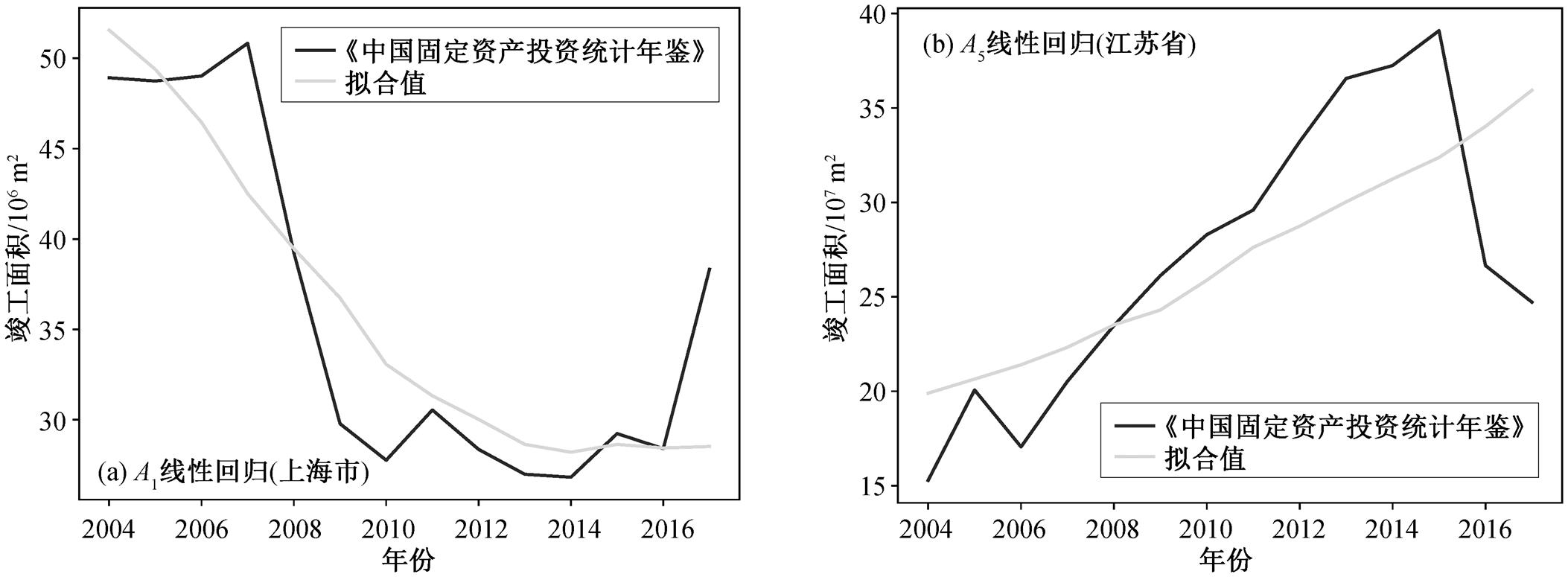
图2 《中国固定资产投资统计年鉴》中上海市和江苏省数据与单一指标拟合效果
Fig. 2 Fitting results with single factor of Shanghai and Jiangsu for the “Statistical Yearbook of the Chinese Investment in Fixed Assets”
表5 不同数据源竣工面积回归结果
Table 5 Regression results of completed areafrom different data sources
对比指标《中国固定资产投资统计年鉴》《中国建筑业统计年鉴》 є (Y)0.2380.443 R20.7870.635
根据第五次全国人口普查[20]和第六次全国人口普查[21]的长表数据, 获取 2001—2010 年累积十年的拆除率。将累计拆除率与各省的城镇住房存量相乘, 得到 2001—2010 年累积 10 年各省城镇居住建筑拆除面积。
由于所获取的数据只有各省 2001—2010 年累积 10 年的拆除面积, 因此需要对累积拆除面积数据按年份进行拆分。将拆分后获取的参数应用到之后的 10 年中, 据此预测 2010 年之后各省的拆除面积和拆除率。
记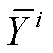为省份 i 居住建筑的 10 年累积拆除面积, 省份 i 年份 j 的真实拆除面积为
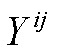, 则有约束集合
,其中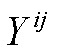未知。取加权系数
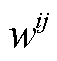为 1, 利用式(5)进行求解和变量筛选。得到最优自变量组合后, 对于 2010 年及之前的数据, 直接使用
作为拟合得到的各年居住建筑拆除面积; 对于2010 年之后的数据, 对拆除面积进行回归分析, 利用影响因子预测指定年份的拆除面积。为提高模型的鲁棒性, 用式(10)预测 2010 年之后的拆除面积:
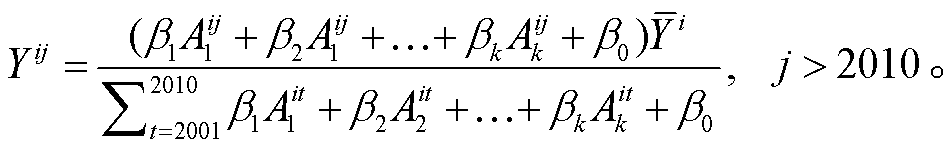(10)
得到拆除面积后, 结合竣工面积和实有居住建筑面积, 可以得到拆除率:
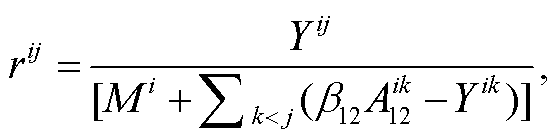(11)
其中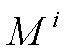
为初始的实有建筑面积, 
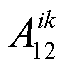为竣工面积。
由模型求解结果可知, 与拆除面积最相关的 4个指标为实有居住建筑面积增量、竣工面积、GDP和城市化率。通过计算, 得到全国及 31 省市自治区(不含港澳台) 2001—2019 年的民用建筑拆除面积。部分省市的拆除面积如图 4 所示。可以看出, 4 个城市在 2001—2019 年间的拆除规模整体呈增长趋势, 其中重庆市的建筑拆除规模显著大于其他 3 个城市。增速方面, 除天津市在 2015 年之后放缓外, 其他 3 个城市都有所提高。
利用式(11), 进一步得到 2001—2019 年的居住建筑拆除率。部分省市的结果如图 5 所示。北京和上海两座城市的拆除率整体上呈缓慢上升趋势, 天津和重庆两所城市则呈下降趋势, 尤其是重庆市在2002—2005 年之间明显下降。由于重庆市 2001—2019 年之间每年竣工面积的增长使得实有建筑面积增加, 导致在拆除规模逐年递增的情况下, 拆除率呈现明显下降趋势。
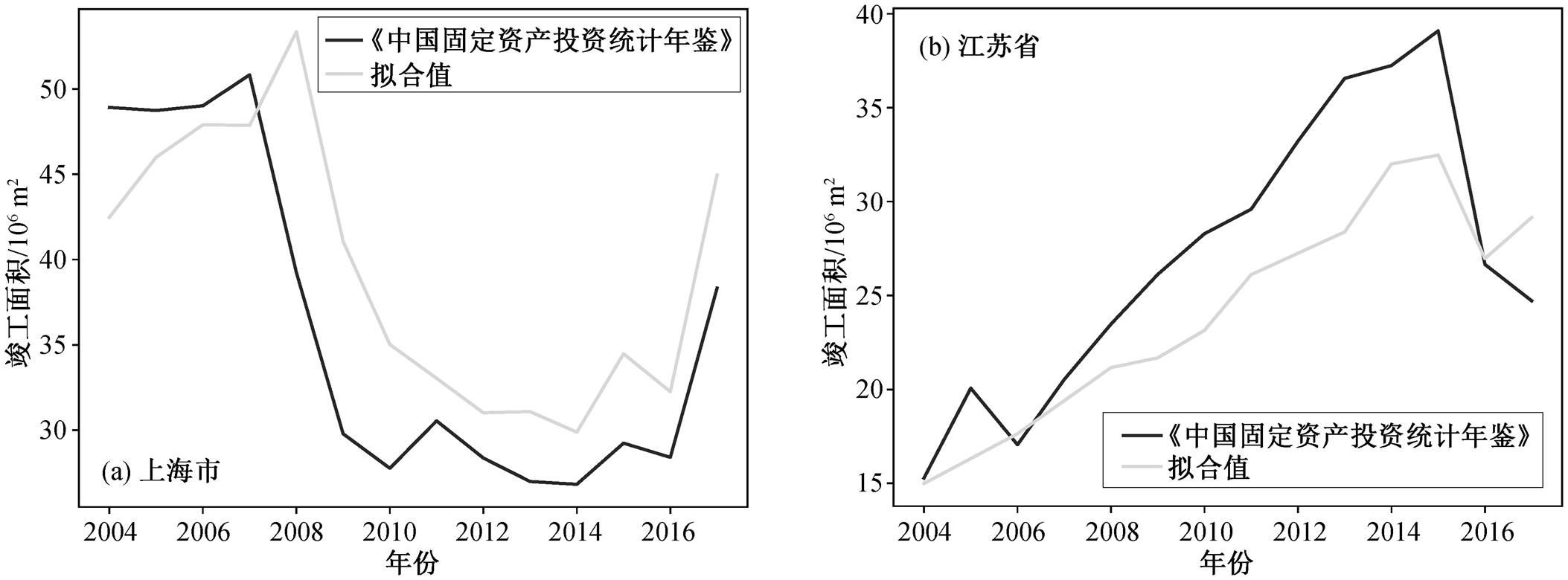
图3 《中国固定资产投资统计年鉴》的竣工面积和筛选的最优变量的拟合效果
Fig. 3 Fitting results of completed area and selected optimal variables of the “Statistical Yearbook of the Chinese Investment in Fixed Assets”
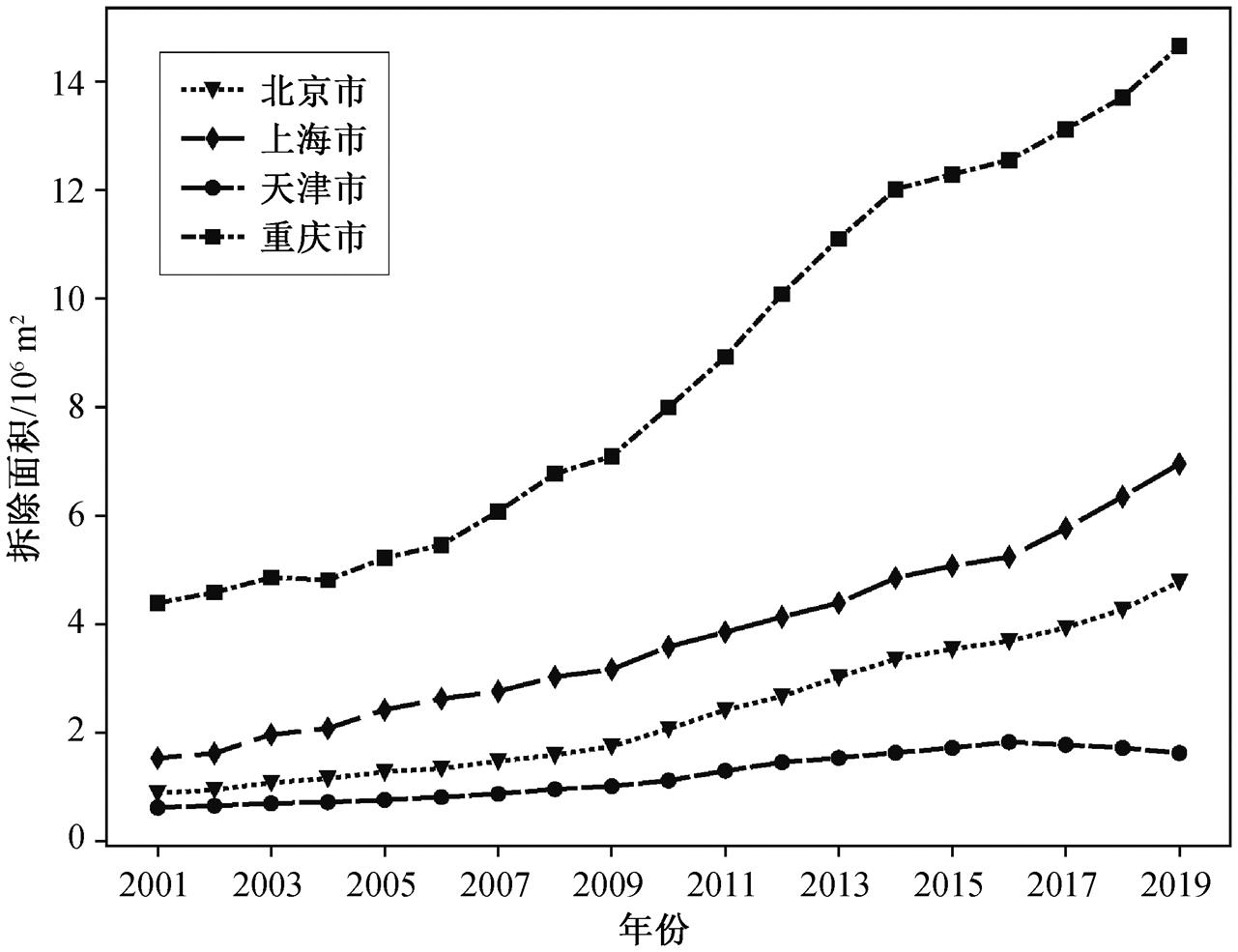
图4 部分省市城镇住宅拆除规模
Fig. 4 Demolition areas of urban residential buildings in some provinces and cities
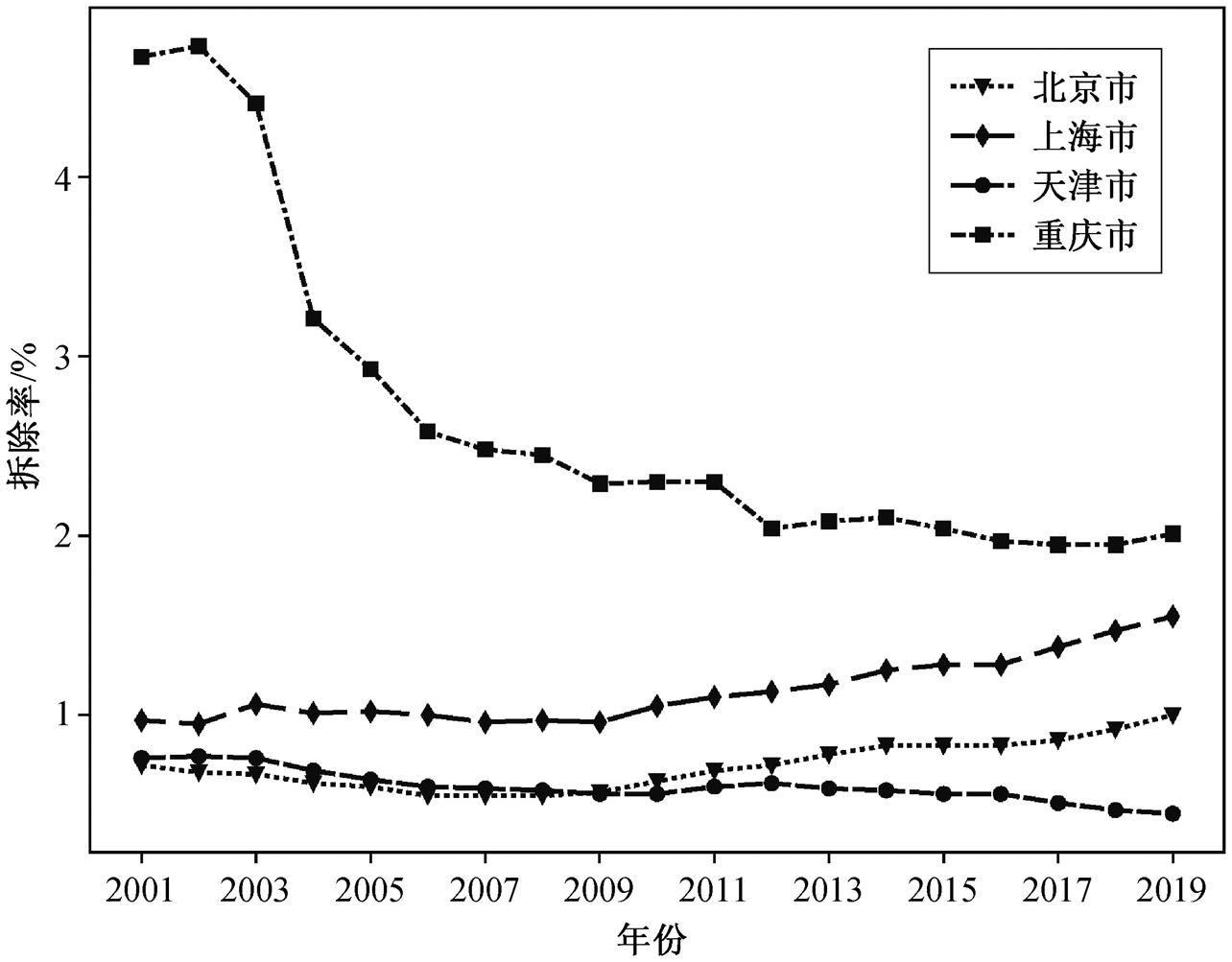
图5 部分省市城镇住宅拆除率
Fig. 5 Demolition rates of urban residential buildings in some provinces and cities
本文利用加权回归分析模型和约束回归分析模型, 分别对民用建筑竣工面积和拆除面积进行分析和预测。针对 3 种统计年鉴中民用建筑竣工面积统计数据不一致的问题, 考虑城市化率、GDP 和人均收入等社会经济发展等因素的影响, 选择合适的影响因子建立加权回归分析模型。通过对比拟合效果和相关系数, 确定《中国固定资产投资统计年鉴》的统计结果最具可靠性。针对人口普查数据仅能得到民用建筑累积 10 年拆除面积的问题, 加入城市化率和 GDP 等社会经济发展指标作为影响因子, 建立约束回归分析模型进行求解, 从而得到各省 2000—2010 年间逐年的拆除面积以及 2010 年之后的预测拆除面积, 补充了当前统计体系中建筑拆除面积的缺失。本文的研究结果可为确定我国近 20 年建筑规模的实际情况和相关节能减排政策的制定提供科学参考。
参考文献
[1] 匡文慧, 张树文, 张养贞. 基于遥感影像的长春城市用地建筑面积估算. 重庆大学学报, 2007, 29(1): 18–21
[2] 刘菁, 赵冬蕾, 刘珊珊. 民用建筑实有建筑面积数据获取方法研究. 建筑科学, 2020, 36(增刊2): 352–359
[3] 王君, 申鸿怡, 原雯, 等. 民用建筑面积及能耗强度计算方法研究. 建筑科学, 2020, 36(增刊2): 390–401
[4] 原雯, 王君, 申鸿怡, 等. 基于统计年鉴和网络大数据的房屋竣工面积估算. 北京大学学报(自然科学版), 2021, 57(5): 804–814
[5] 董迎春. 城镇居住建筑能耗影响因素的区域差异研究[D]. 北京: 北京交通大学, 2019: 17–18
[6] 黄禹, 刘洪玉, 徐跃进. 我国城镇住房拆除率及其影响因素研究. 中国房地产, 2016(21): 51–61
[7] 黄敬婷, 吴璟. 中国城镇住房拆除规模及其影响因素研究. 统计研究, 2016, 33(9): 30–35
[8] 刘存. 我国城镇居住建筑测算研究——基于轮换模型. 建筑设计管理, 2020(1): 40–46
[9] 唐守娟, 张力小, 郝岩, 等. 城市住宅建筑系统流量–存量动态模拟——以北京市为例. 生态学报, 2019, 39(4): 1240–1247
[10] Wu Jing, Gyourko J, Deng Yongfeng. Evaluating the risk of Chinese housing markets: what we know and what we need to know. China Economic Review, 2016, 39: 91–114
[11] 欧高炎, 朱占星, 董彬, 等. 数据科学导引. 北京: 高等教育出版社, 2017: 53–66
[12] Zou Hui. The adaptive lasso and its oracle properties. Journal of the American Statistical Association, 2006, 101: 1418–1429
[13] Hoerl A E, Kennard R W. Ridge regression: biased estimation for nonorthogonal problems. Technomet-rics, 1970, 12(1): 55–67
[14] Ruppert D, Wand M P. Multivariate weighted least squares regression. The Annals of Statistics, 1994, 22 (3): 1346–1370
[15] 刘浩洋, 户将, 李勇峰, 等. 最优化: 建模、算法与理论. 北京: 高等教育出版社, 2020: 283–286
[16] Betensky R A. The p-value requires context, not a threshold. The American Statistician, 2019, 73(1): 115–117
[17] Shao Jun. Linear model selection by cross-validation. Journal of the American Statistical Association, 1993, 88: 486–494
[18] Miller A J. Selection of subsets of regression variables. Journal of the Royal Statistical Society: Series A (Ge-neral), 1984, 147: 389–410
[19] 国家统计局. 房地产开发统计报表制度(公开版) [EB/OL]. (2021–03–16)[2021–05–18]. http://www. stats.gov.cn/tjsj/tjzd/gjtjzd/202103/t20210316_18149 39.html
[20] 国务院人口普查办公室, 国家统计局人口和社会科技统计司. 2000 年第五次全国人口普查主要数据. 北京: 中国统计出版社, 2001
[21] 国家统计局人口就业统计司, 国务院第六次人口普查办公室. 2010 年第六次全国人口普查主要数据. 北京: 中国统计出版社, 2011
Regression Analysis of Building Scale Data and Estimation of Demolition Rate
Abstract Since the statistical data of the completed area in different statistical yearbooks are quite different, this paper proposes a weighted regression model to analyze the statistical values of the completed area in order to analyze and confirm the data sources by combining the relevant data in the statistical yearbooks, such as urban land demand, social development level, etc. On the other hand, there are only the cumulative demolition area in the statistical yearbooks, and the annual statistical data of demolition area is missing. To estimate the demolition rate, a constrained regression model is established to calculate the annual demolition area of each province based on the national population census data, urban land demand, social development level, and other relevant data. The numerical results can provide a reference for understanding the actual situation of building scale in China over the last two decades, as well as making policies of energy conservation and emission reduction.
Key words building scale data; completed area; demolition area; demolition rate; regression analysis