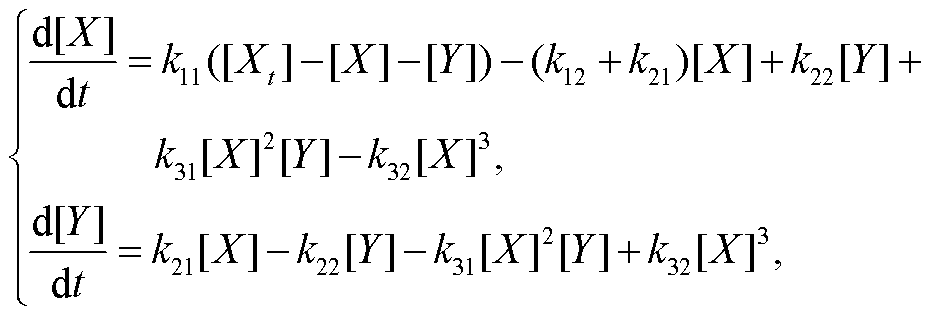 (1)
(1)
doi: 10.13209/j.0479-8023.2023.029
国家重点研发计划项目(2018YFA0900200)资助
收稿日期: 2022–05–31;
修回日期: 2022–06–07
北京大学学报(自然科学版) 第59卷 第4期 2023年7月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 4 (July 2023)
摘要 以简单生化振子模型为对象, 运用数值计算和理论分析, 研究负载对自激振子的影响。对振子动力学性质的分析结果表明, 振子经由绝缘模块以间接耦合的方式驱动负载的方案有利于维持振子动力学性质的稳定。负载与其上游模块的结合亲和力以及绝缘模块物质总量是影响负载相对振幅的两个关键因素。绝缘模块的引入能够打破负载振荡与回溯性在直接耦合方式下的权衡。对自由能耗散的计算结果表明, 振荡自由能耗散增加不一定意味着回溯性减小或负载振荡的增强。
关键词 负载; 自激振子; 回溯性; 绝缘模块
生物网络具有“模块性”, 每个模块的相对功能可以与其他模块隔离开, 相互连接的模块可以产生更高水平的功能[1], 从而简化对复杂网络功能的理解。然而, 当一个功能模块与其他功能模块相连时, 模块的动力学性质将发生改变。这种因模块耦合而影响模块动力学行为的现象称为回溯性(retroacti-vity)[2]。回溯性减弱了网络的模块化特性, 是模块化网络设计中的不利因素。目前有很多关于回溯性的研究, 如上下游模块结合机制对回溯性的影响[3], 回溯性强度对具有开关性、适应性等功能网络的响应时间[2,4]或网络鲁棒性[5]的影响, 回溯性诱发网络在信号转导、超敏等功能之间的转换[6], 在具有周期性输出信号的网络中减弱回溯性的机制[7–9], 等等。以昼夜节律为代表的内源自主节律在生物系统中广泛存在[10]。由于生物钟是一个有复杂负载的自激振子, 在负载的回溯性效应作用下, 生物系统如何维持生物节律的鲁棒性, 是一个值得研究的问题。此外, 对回溯性与自由能耗散之间是否存在权衡的问题存在争议[11–12]。在生物系统中, 生物节律, 尤其是正常的昼夜节律对维持生物系统正常生理功能十分重要[13–15], 针对自激振子模型的回溯性研究对于理解生物钟的鲁棒性具有启发意义。
本文针对布鲁塞尔振子和激活子–抑制子两种经典的自激振荡模型, 研究自激振子通过缓冲模块驱动下游负载振荡的动力学系统, 探求回溯性、下游模块振荡、振荡自由能耗散及其之间的关系。通过数值模拟研究, 发现下游负载模块经由缓冲绝缘模块与振子间接耦合的方式可以减弱回溯性。计算结果表明, 可以通过调节与缓冲模块结合的亲和力以及缓冲层的物质总量, 实现自激振子驱动下游负载显著的振荡。当负载与振子直接耦合时, 改变结合亲和力, 使得负载振荡与回溯性之间存在权衡; 当两者之间有适当的缓冲时, 自由能耗散增加不一定意味着回溯性减弱或负载振荡增强, 系统存在最佳振荡自由能耗散, 使得负载振荡与回溯性同时达到局部最优。
本文采用两个经典的简单生化振子, 即布鲁塞尔子(图 1(a))和激活子–抑制子(图 1(b)), 探究自激振子在负载作用下的回溯性。根据文献[7], 我们的模型采用两种模块耦合方式: 负载与振子直接耦合(图 1(c)); 负载经由缓冲绝缘模块与振子间接耦合(图 1(d))。上游的 C-B 模块代表上游振子。
对于无负载可逆布鲁塞尔子[16], 基于质量作用定律, 可得到其化学反应动力学方程:
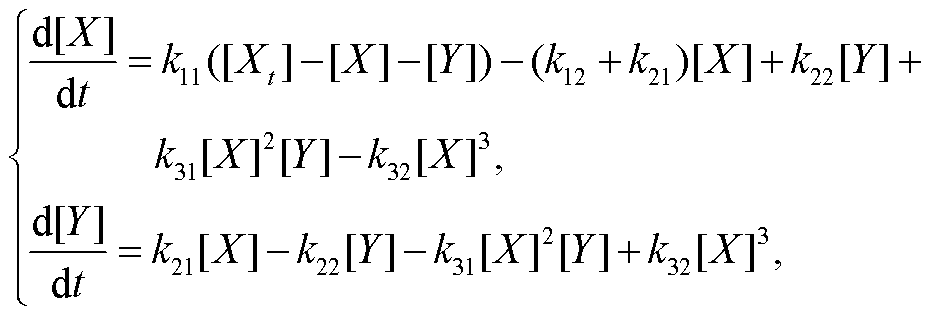 (1)
(1)
其中, 假定物质总浓度守恒, 即[A]+[X]+[Y]=[Xt]。本文将振荡参数固定为 k11=0.07, k12=0.5, k21=1.2, k22=0.02, k31=1, k32=0.001, [Xt]=6。
激活子–抑制子模型由一个负反馈和耦联的正反馈构成, 这种网络结构在生物振荡系统中十分常见[17], 且三节点网络中包含该拓扑结构的振子具有很强的鲁棒性[18]。本文用米氏方程的形式来描述该模型中节点的相互作用, 反应动力学方程为
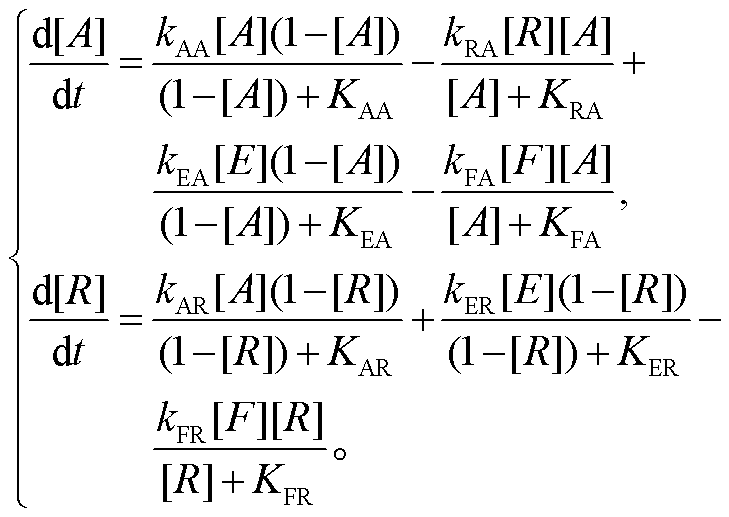 (2)
(2)
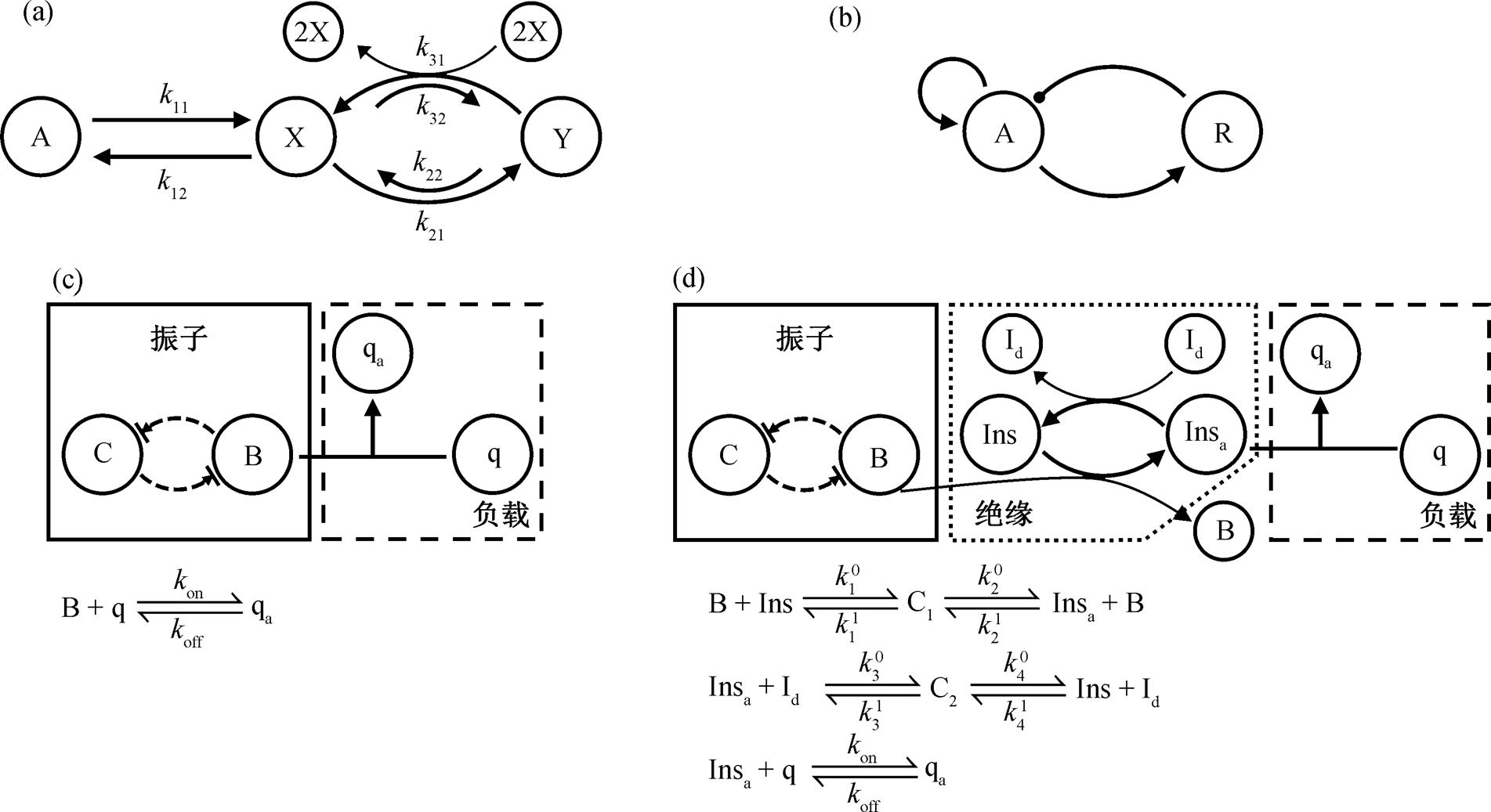
(a)布鲁塞尔子模型的网络结构, 其中 A, X 和 Y 为反应分子, A 的浓度不随时间变化, X 和 Y 为动力学变量, 箭头表示反应分子之间的转化; (b)激活子–抑制子模型的网络结构, 其中 A 和 R 表示不同的酶, 箭头表示对酶的激活, 圆点表示对酶的抑制; (c)振子通过直接耦合驱动负载示意图, 其中上游振子由酶 B 和酶 C 之间的酶促抑制表示, q 为在 B 的酶促作用下被活化的酶, 即负载; (d)上游振子经由绝缘模块间接驱动负载示意图, B 和 Id 分别使 Ins 活化和去活化。kon, koff 和 kij 为反应速率常数, 下角标 a 表示活化状态, C1 和 C2 表示酶促反应的中间复合物, Id 表示促进 Insa 失活的酶
图1 自激振子模型和模块耦合方式
Fig. 1 Models of self-sustained oscillators and coupling modes between modules
在该网络中, A 和 R 是两种酶, 具有活化和非活化两种状态, [A]或[R]表示活化的酶的浓度。在模型中, 我们假定激活子和抑制子的物质总浓度均恒为 1。kij表示其最大反应速率常数, Kij为解离常数, 下角标 ij表示 i对 j的作用, 每个方程中的后两项是基础生成项和基础降解项。本文中, 将振荡参数固定为 kAA=2.05116, KAA=0.227452, kRA=12.3656, KRA=2.6, kAR=1.01515, KAR=14.8093, kEA=0.3207,KEA=0.00264025, kFA=0.645237, KFA=0.00370536,kER=0.464292, KER=0.0766885, kFR=10.31, KFR=0.00543751, [E]=[F]=0.001。
直接耦合指负载通过与振子某一变量 B间的一个可逆的结合–解离反应来建立连接。在这种连接中, 振子的变量 B 既参与振子本身的动力学, 又参与同负载的结合而形成扣留, 从而对上游振子产生回溯性效应。经由绝缘模块的间接耦合指振子变量B作为酶, 使得缓冲物质 Ins 活化为 Insa, 继而活性的 Insa又通过结合–解离反应来连接负载, 同时 Insa可在酶 Id作用下失活, 且存在物质浓度守恒[Ins]+ [Insa]+[C1]+[C2]+[qa]=[Inst], [Id]+[C2]=[Idt], [q]+[qa]=[qt]。在这种间接驱动中, 缓冲模块是一个上推下拉环, 负载通过中间的缓冲, 对上游模块产生的回溯性可大幅度减弱。
首先, 我们针对有负载和无负载两种情况, 对比计算布鲁塞尔子(图 2(a), (c)和(e))和激活子–抑制子模型(图 2(b), (d)和(f))在有(无)缓冲模块时的动力学性质, 包括上游振子的振荡(图 2(a)和(b)), 参数空间中的振荡区域(图 2(c)和(d))以及上游振子的相位响应曲线(图 2(e)和(f))。计算相位响应曲线时, 首先给系统施加一个微扰, 如使振子的某一参数在0.05 个周期内增大 30%, 然后计算振子在不同耦合方式下的相位响应。考虑到振子周期在施加负载后会发生改变, 为方便比较各条相位响应曲线, 对振荡周期做归一化处理。图 2 显示, 相较于直接耦合方式, 负载经由绝缘模块的间接耦合方式能够减弱负载对振子的动力学性质的影响。图 2(a)和(b)展示两个上游振子中 X 和 R 变量的振荡行为。对比可见, 间接耦合情形都更接近无负载时振子的振荡曲线, 通过缓冲模块驱动负载, 在一定程度上消除了回溯性, 尤其是在图 2(b)中, 蓝色和红色曲线几乎与黄色线重合。图 2(c)和(d)显示, 通过绝缘模块驱动负载, 可以较好地恢复无驱动自由振子的振荡区间。图 2(e)和(f)对比无驱动、直接驱动和间接驱动3 种情形相位响应曲线。经由绝缘模块的间接耦合显著地减弱回溯性, 尤其是通过 X 和 A 驱动的情形。生物实验结果表明, 哺乳动物昼夜节律钟核心网络中的蛋白可激活 DBP 蛋白[19]和 KLF10 家族蛋白[20]等的转录, 其作为转录因子, 又可继续激活基因组中其他基因的转录, 这与经由绝缘模块的间接耦合方式相一致。
图 2 中关于回溯性的分析, 局限于负载对振子的影响。为考察不同负载方式下负载本身的动力学表现, 我们进一步探究显著影响负载振荡的因素。在振子与下游的连接中, 结合反应速率常数 kon (或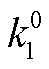 )和解离反应速率常数 koff (或
)和解离反应速率常数 koff (或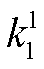 )是负载与振子(或绝缘模块)耦合的关键参数。首先检验它们对负载振荡的影响。负载振荡用负载相对振幅 RAq=Aq/qt表征, RAq 越大表明负载振荡越明显, 振子能更有效地驱动负载产生振荡行为。图 3(a)和(b)给出当布鲁塞尔子中的变量 X 直接连接负载和通过缓冲模块间接连接负载两种方式下, 负载相对振幅随反应速率常数的变化(负载的相对振幅 RAq 存在上限)。在两种负载耦合方式下, 当给定负载总量时, 负载相对振幅在 logkoff 与 logkon (或 log
)是负载与振子(或绝缘模块)耦合的关键参数。首先检验它们对负载振荡的影响。负载振荡用负载相对振幅 RAq=Aq/qt表征, RAq 越大表明负载振荡越明显, 振子能更有效地驱动负载产生振荡行为。图 3(a)和(b)给出当布鲁塞尔子中的变量 X 直接连接负载和通过缓冲模块间接连接负载两种方式下, 负载相对振幅随反应速率常数的变化(负载的相对振幅 RAq 存在上限)。在两种负载耦合方式下, 当给定负载总量时, 负载相对振幅在 logkoff 与 logkon (或 log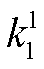 与 log
与 log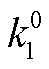 )呈线性分布的区域中表现最好, 结合和解离均为快过程, 满足绝热近似, 并且, 负载相对振幅与解离常数 Kd= koff/kon或
)呈线性分布的区域中表现最好, 结合和解离均为快过程, 满足绝热近似, 并且, 负载相对振幅与解离常数 Kd= koff/kon或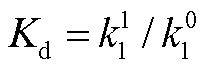 相关, 而与结合或解离反应速率常数的绝对值无关。
相关, 而与结合或解离反应速率常数的绝对值无关。
我们进一步考察两种振子在直接连接负载和通过缓冲模块驱动负载两种情形下, 解离常数 Kd 对下游负载的相对振幅和上游振子的相对振幅的影响。振幅和周期是振子的两个基本特性, 负载的回溯性可用振子加负载前后振幅或周期的相对变化来表征, 该值越趋近于 1, 则回溯性越小。图 3(c)和(d)展示布鲁塞尔子中的变量 X 和 Y 分别直接驱动以及通过缓冲模块间接驱动负载时, 负载相对振幅和上游振子相对振幅随解离常数的变化。可以看出, 无论负载是否经由绝缘模块与振子耦合, 负载相对振幅和振子相对振幅均随解离常数非单调变化, 均存在最佳 Kd 值, 使得负载相对振幅最大。当负载与振子直接耦合时, 产生较大的负载相对振幅常常伴随振子振幅的急剧变化, 表明此时负载相对振幅与回溯性之间存在权衡, 且回溯性随解离常数的变化与文献[21]相符。当负载经由绝缘模块间接地耦合于振子时, 回溯性相对较小, 且仅随解离常数发生微小的变化。这表明, 此时可实现在有效地带动负载振荡的同时, 维持对上游振子的原振荡, 间接耦合方式打破了负载振荡与回溯性之间的权衡。对激活子–抑制子模型的计算得到类似的结果, 如图 3(e)和(f)所示。在图 3(d)和(f)中, 尽管就负载相对振幅而言, 经绝缘模块耦合的表现略逊于直接耦合, 但前者的回溯性显著减小, 且几乎维持相对振幅不变。绝缘模块使得系统在带动负载产生显著振荡的同时, 可以实现较小的回溯性。

左列为布鲁塞尔子模型, 右列为激活子–抑制子模型。(a)和(b)为在不同耦合方式下的时间曲线; (c)和(d)为不同耦合方式下的振荡区域, 每条曲线与纵轴所围成的闭合区域为对应情况下的振荡区域, 其他部分为无振荡的稳定态; (e)和(f)为相位响应曲线, 扰动参数分别为k31和KAR
图2 回溯性及负载对振子动力学性质的影响
Fig. 2 Retroactivity and the effect of loads on the dynamical properties of oscillators
负载相对振幅随解离常数的变化及负载振荡与回溯性之间的权衡可以在理论上得到解释。我们以负载直接连于布鲁塞尔子 X 上为例进行分析。此时, 系统动力学方程为

实线表示直接连于 X (或 Y, A, R), 虚线表示经绝缘模块连于 X (或Y, A, R)。(a)和(c)负载直接连接布鲁塞尔子; (b)和(d)负载经绝缘模块连接布鲁塞尔子; (e)负载直接连接活化子–抑制子中的 A; (f)负载直接连接于活化子–抑制子中的 R
图3 负载及振子的相对振荡随结合解离参数的变化
Fig. 3 Oscillation of the load and retroactivity as a function of the reaction rate constant
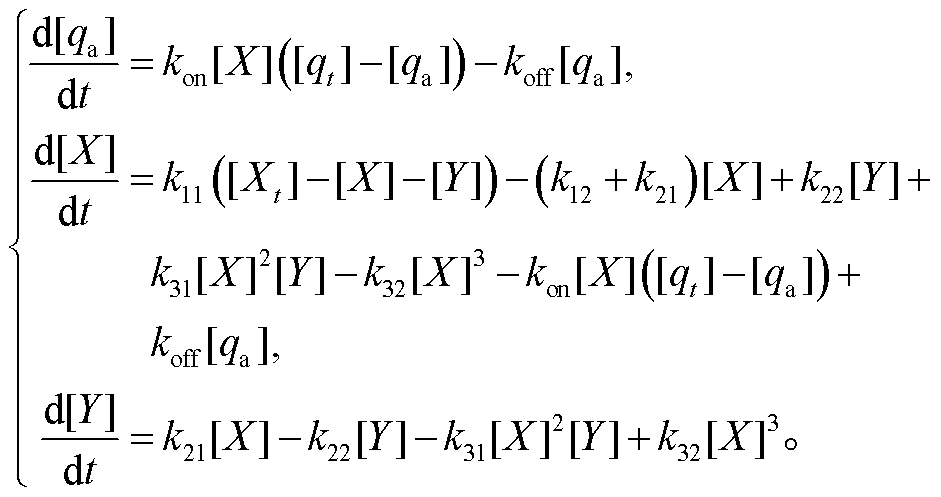 (3)
(3)
由于负载与振子之间的结合–解离反应相对于振子反应而言是快过程, 即 kon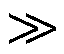 kij, koff
kij, koff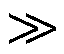 kij, i=1, 2, 3, j=1, 2, 因此, 可得慢流形 qr=[qa]/[qt]=[Xm]/(Kd+ [Xm])。负载相对振幅可近似为
kij, i=1, 2, 3, j=1, 2, 因此, 可得慢流形 qr=[qa]/[qt]=[Xm]/(Kd+ [Xm])。负载相对振幅可近似为
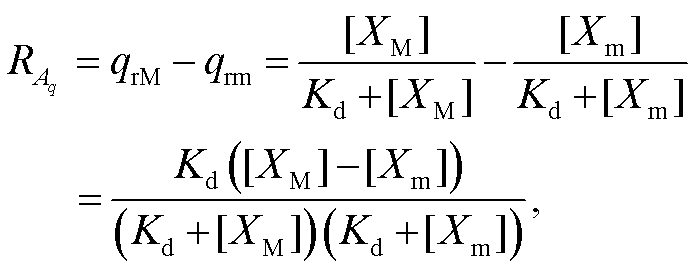 (4)
(4)
其中, 下角标 M 和 m 分别表示极大值和极小值。若假定回溯性很小, 即 X 振荡接近无负载情况, 则可将[XM]和[Xm]视为与负载无关的常数。此时, 负载相对振幅只是解离常数的函数。容易求得, 当 Kd=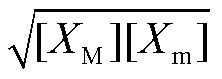 时, 负载相对振幅取得极大值:
时, 负载相对振幅取得极大值:
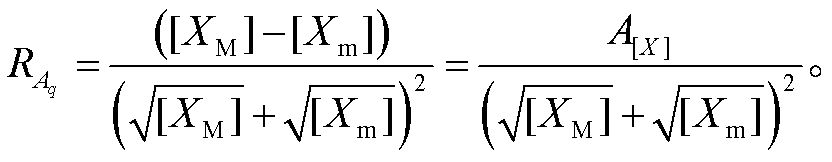 (5)
(5)
当负载直接与振子耦合时, 负载相对振幅存在上限, 且该上限与所连接的振子变量的振幅相关。当负载与振子间接耦合时, 尽管[qa]和[Insa]均为快变量, 但两者之间仍满足[Insa](1 - qr)/Kd - qr=0, 所以负载相对振幅随解离常数的变化趋势仍与直接耦合相同。另一方面, 利用绝热近似及隐函数定理[7],可得慢变量 X近似满足动力学方程:
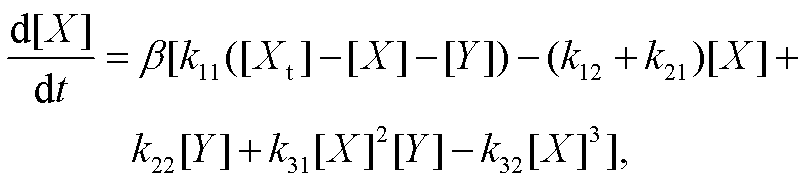 (6)
(6)
其中, 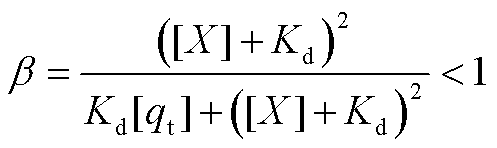 , 是体现回溯性的因子。由于 β 在 Kd=[X]时取极小值, 而在 Kd→0 或 Kd→∞时趋近 1, 故当负载与振子之间的结合亲和力过强或过弱时, 回溯性较小, 振子可较好地维持原有振荡, 负载振荡并不显著; 当负载获得较强的振荡时, 要求解离常数与[X]在同一量级, 致使回溯性较大。
, 是体现回溯性的因子。由于 β 在 Kd=[X]时取极小值, 而在 Kd→0 或 Kd→∞时趋近 1, 故当负载与振子之间的结合亲和力过强或过弱时, 回溯性较小, 振子可较好地维持原有振荡, 负载振荡并不显著; 当负载获得较强的振荡时, 要求解离常数与[X]在同一量级, 致使回溯性较大。
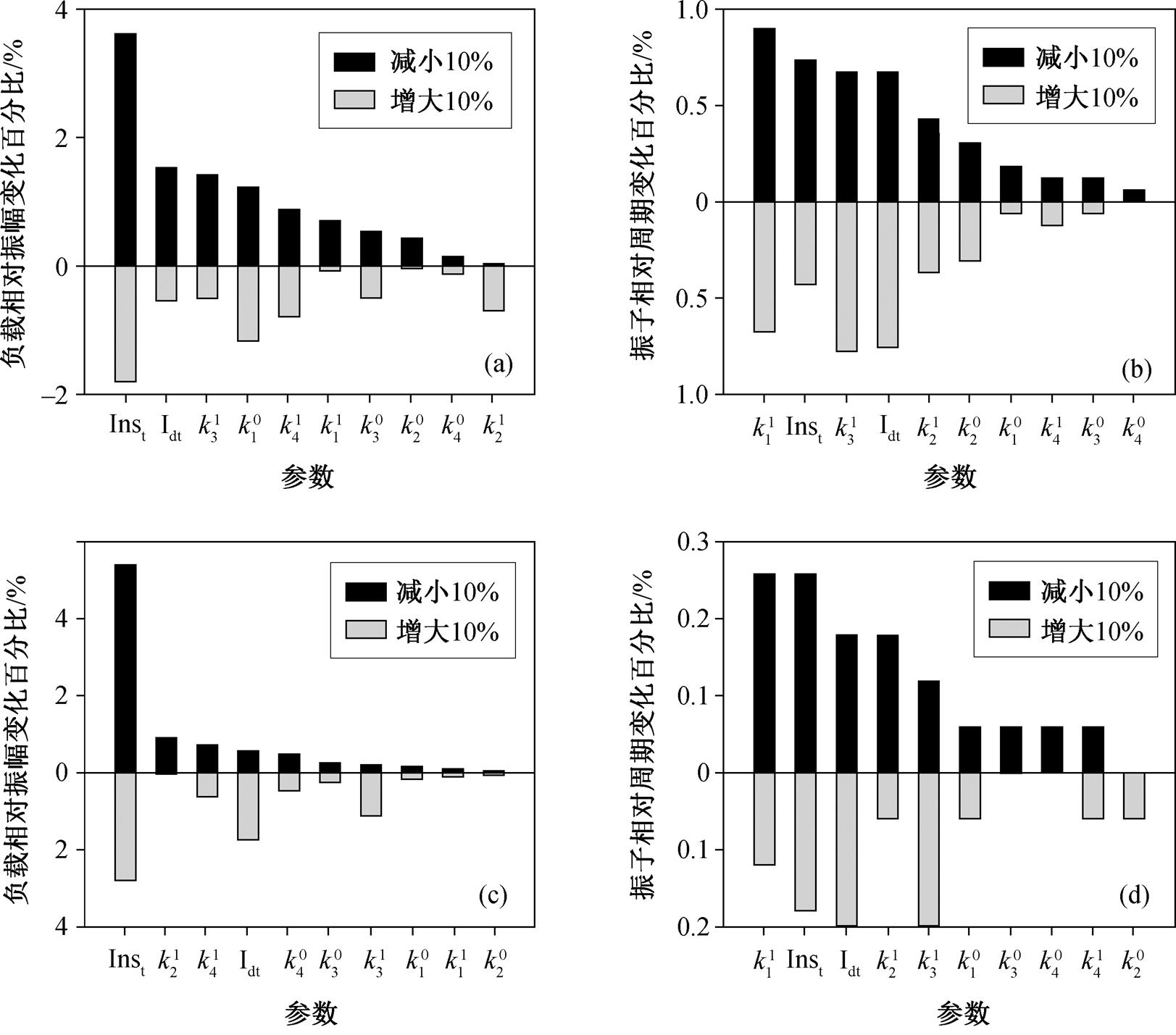
在间接通过缓冲模块驱动负载的耦合方式下, 负载的振荡与负载本身有关, 也受到绝缘模块相关参数的影响。为了确定缓冲模块中对负载振荡和回溯性产生显著影响的参数, 我们针对负载相对振幅和上游振子的相对周期进行参数敏感性分析。我们选择的基准参数能够使振子产生相对较大的振幅, 并且负载总量较大, 负载相对振荡较显著。图 4 展示布鲁塞尔子((a)和(b))和激活子–抑制子模型((c)和(d))中缓冲模块中参数的敏感性分析结果。图中显示各参数减小或增加 10%后对负载((a)和(c))以及上游振子((b)和(d))相对振幅影响的百分比, 并将参数按从大到小的次序进行排列。可以看出, 上推下拉环缓冲模块中起上推作用的酶 Ins 的总量[Inst]最为敏感, 对上推下拉环中起着酶促下拉作用的酶 Id 的总量[Idt]也较为敏感。对以振子相对周期为代表的振子振荡而言, [Inst]和[Idt]是排位靠前的敏感参数, 但敏感性弱于负载振荡。这表明, 可以通过增大[Inst]或[Idt], 使得负载产生更加强有力的振荡, 从而对上游振子产生较小的回溯性影响。
我们以布鲁塞尔子为例, 探究不同耦合方式下, 能量耗散在减弱回溯性或增强负载振荡中所起的作用。振荡自由能耗散指整个系统在一个振荡周期内消耗的自由能:
(a)和(b)负载通过布鲁塞尔子 X 间接与振子耦合, 无微扰时负载相对振幅为 0.3, 负载总量 qt=10; (c)和(d)负载通过激活子–抑制子 A 间接与振子耦合, 无微扰时负载相对振幅为 0.25, 负载总量 qt=10
图4 缓冲模块参数敏感性分析
Fig. 4 Parameter sensitivity analysis for insulator
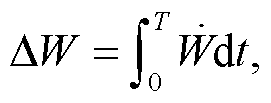 (7)
(7)
其中, T为振荡周期; 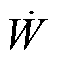 为自由能耗散速率。
为自由能耗散速率。
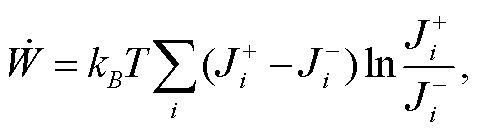 (8)
(8)
其中, 求和号遍历所有可逆反应, 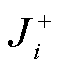 为正反应流,
为正反应流, 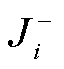 为逆反应流。根据式(7)和(8), 可计算系统振荡自由能耗散在振子、绝缘和负载 3 个模块中的分配。振子模块的振荡自由能耗散可通过振子的 3 个反应计算得到; 绝缘模块的振荡自由能耗散指的是图 1(d)中两个酶促反应的自由能耗散, 由负载参加的反应确定负载模块的自由能耗散。分别计算了振荡自由能耗散随解离常数 Kd 以及缓冲绝缘模块中 Ins 物质总量[Inst]的变化, 结果如图 5 所示。可以看出, 在直接耦合驱动负载下, 绝大多数的系统自由能用于上游振子模块的振荡。当增大解离常数时, 系统的自由能耗散先增大后减小; 当系统振荡自由能耗散随解离常数单调增多时, 以振子相对振幅表示的回溯性增大, 与之权衡的负载振荡增强, 说明自由能耗散增加不一定意味着回溯性减弱。对于间接耦合方式(图 5(b)和(c)), 系统的自由能耗散主要来自绝缘模块,当增大负载的解离常数时, 系统的振荡自由能耗散有些许增大。解离常数增大意味着负载与绝缘模块之间的结合亲和力下降, 参与绝缘模块中活化与失活的物质量将增多, 从而使得绝缘模块自由能耗散增大, 因而其在系统的振荡自由能耗散中占比增大。当增大[Inst]时, 振荡自由能耗散不断增大, 而以振子相对振幅和相对周期为指标的回溯性则随之非单调变化, 负载相对振幅不一定随之单调递增。当在图 5(d)黄色方块区间内增大[Inst]时, 系统振荡自由能耗散增大, 回溯性减弱, 负载振荡增强; 当[Inst]水平较低时, 增大[Inst]会带动负载振荡, 但同时会对振子产生较强的回溯性; 当[Inst]水平较高时, 增大[Inst]同样会增强回溯性, 但在增强负载振荡方面的作用并不显著。因此, 只有当绝缘模块物质总量[Inst]在合适范围内时, 系统振荡自由能耗散增加才会同时减弱回溯性并增强负载振荡。此外, 通过计算各模块的自由能耗散, 可知系统自由能耗散增多的部分主要来自绝缘模块, 这是因为[Inst]增多会使得参与振荡的绝缘物质增多, 从而使自由能耗散增多。
为逆反应流。根据式(7)和(8), 可计算系统振荡自由能耗散在振子、绝缘和负载 3 个模块中的分配。振子模块的振荡自由能耗散可通过振子的 3 个反应计算得到; 绝缘模块的振荡自由能耗散指的是图 1(d)中两个酶促反应的自由能耗散, 由负载参加的反应确定负载模块的自由能耗散。分别计算了振荡自由能耗散随解离常数 Kd 以及缓冲绝缘模块中 Ins 物质总量[Inst]的变化, 结果如图 5 所示。可以看出, 在直接耦合驱动负载下, 绝大多数的系统自由能用于上游振子模块的振荡。当增大解离常数时, 系统的自由能耗散先增大后减小; 当系统振荡自由能耗散随解离常数单调增多时, 以振子相对振幅表示的回溯性增大, 与之权衡的负载振荡增强, 说明自由能耗散增加不一定意味着回溯性减弱。对于间接耦合方式(图 5(b)和(c)), 系统的自由能耗散主要来自绝缘模块,当增大负载的解离常数时, 系统的振荡自由能耗散有些许增大。解离常数增大意味着负载与绝缘模块之间的结合亲和力下降, 参与绝缘模块中活化与失活的物质量将增多, 从而使得绝缘模块自由能耗散增大, 因而其在系统的振荡自由能耗散中占比增大。当增大[Inst]时, 振荡自由能耗散不断增大, 而以振子相对振幅和相对周期为指标的回溯性则随之非单调变化, 负载相对振幅不一定随之单调递增。当在图 5(d)黄色方块区间内增大[Inst]时, 系统振荡自由能耗散增大, 回溯性减弱, 负载振荡增强; 当[Inst]水平较低时, 增大[Inst]会带动负载振荡, 但同时会对振子产生较强的回溯性; 当[Inst]水平较高时, 增大[Inst]同样会增强回溯性, 但在增强负载振荡方面的作用并不显著。因此, 只有当绝缘模块物质总量[Inst]在合适范围内时, 系统振荡自由能耗散增加才会同时减弱回溯性并增强负载振荡。此外, 通过计算各模块的自由能耗散, 可知系统自由能耗散增多的部分主要来自绝缘模块, 这是因为[Inst]增多会使得参与振荡的绝缘物质增多, 从而使自由能耗散增多。
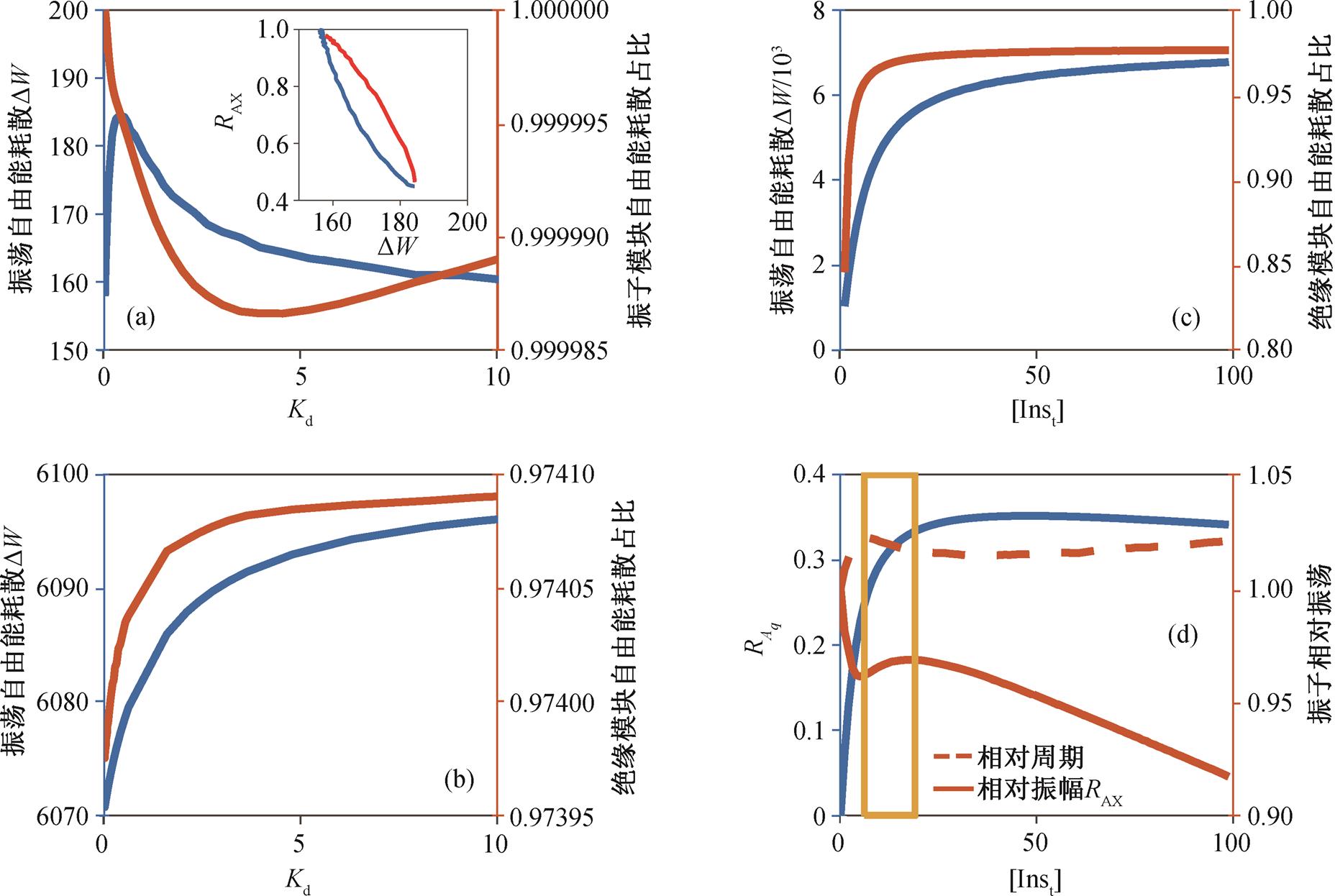
(a)负载直接连于 X, 右上小图显示振子相对振幅与系统振荡自由能耗散的关系; (b)负载经绝缘模块连于 X; (c)负载经绝缘模块连于 X 时振荡自由能耗散及其在绝缘模块占比随[Inst]的变化; (d)负载经绝缘模块连于 X 时负载相对振幅和回溯性随[Inst]的变化
图5 振荡自由能耗散及其分配
Fig. 5 Free energy dissipation and distribution
本文从动力学角度研究负载对自激生化振子的影响。从简单振子模型出发, 在负载与振子的直接耦合与经由绝缘模块的间接耦合两种方式下, 计算振子动力学性质的变化, 发现绝缘模块在维持振子动力学性质方面的优越性。通过调节参数, 使负载实现明显振荡, 获知负载与其上游模块的结合亲和力及绝缘模块物质总量是影响负载振荡的关键参数。在直接耦合方式下, 负载振荡与回溯性之间存在权衡。通过改变系统参数, 计算系统振荡自由能耗散及其在各模块之间分配的变化, 显示系统振荡自由能耗散增加不一定意味着回溯性减小或负载振荡增强, 系统或许存在最佳振荡自由能耗散, 使得负载振荡与回溯性同时达到局部最优。
参考文献
[1]Hartwell L H, Hopfield J J, Leibler S, et al. From molecular to modular cell biology. Nature, 1999, 402: C47–C52
[2]Jayanthi S, Nilgiriwala K S, Del Vecchio D. Retroac-tivity controls the temporal dynamics of gene transc-ription. ACS Synthetic Biology, 2013, 2(8): 431–441
[3]Pantoja-Hernández L, Álvarez-Buylla E, Aguilar-Ibáñez C F, et al. Retroactivity effects dependency on the transcription factors binding mechanisms. Journal of Theoretical Biology, 2016, 410: 77–106
[4]Wang J, Belta C, Isaacson S A. How retroactivity affects the behavior of incoherent feedforward loops. Iscience, 2020, 23(12): 101779
[5]Wang J, Belta C. Retroactivity affects the adaptive robustness of transcriptional regulatory networks // 2019 American Control Conference (ACC). Philadel-phia, 2019: 5396–5401
[6]Parundekar A, Viswanathan G A. Retroactivity indu-ced operating regime transition in an enzymatic futile cycle.PLOS ONE, 2021, 16(4): e0250830
[7]Del Vecchio D, Ninfa A J, Sontag E D. Modular cell biology: retroactivity and insulation. Molecular Syste-ms Biology, 2008, 4(1): 161
[8]Franco E, Friedrichs E, Kim J, et al. Timing molecu-lar motion and production with a synthetic transcrip-tional clock. Proceedings of the National Academy of Sciences, 2011, 108(40): E784–E793
[9]Mishra D, Rivera P M, Lin A, et al. A load driver device for engineering modularity in biological net-works. Nature Biotechnology, 2014, 32(12): 1268–1275
[10]Zhang E E, Kay S A. Clocks not winding down: un-ravelling circadian networks. Nature Reviews Molecu-lar Cell Biology, 2010, 11(11): 764–776
[11]Barton J P, Sontag E D. The energy costs of insulators in biochemical networks. Biophysical Journal, 2013, 104(6): 1380–1390
[12]Deshpande A, Ouldridge T E. High rates of fuel con-sumption are not required by insulating motifs to suppress retroactivity in biochemical circuits. Enginee-ring Biology, 2017, 1(2): 86–99
[13]Verlande A, Masri S. Circadian clocks and cancer: timekeeping governs cellular metabolism. Trends in Endocrinology and Metabolism, 2019, 30(7): 445–458
[14]Reinke H, Asher G. Crosstalk between metabolism and circadian clocks. Nature Reviews Molecular Cell Biology, 2019, 20(4): 227–241
[15]Li S, Wang Y, Wang F, et al. A new perspective for Parkinson’s disease: circadian rhythm. Neuroscience Bulletin, 2017, 33(1): 62–72
[16]Fei C, Cao Y, Ouyang Q, et al. Design principles for enhancing phase sensitivity and suppressing phase fluctuations simultaneously in biochemical oscillatory systems. Nature Communications, 2018, 9: 1434
[17]Cao Y, Wang H, Ouyang Q, et al. The free-energy cost of accurate biochemical oscillations. Nature Physics, 2015, 11(9): 772–778
[18]Castillo-Hair S M, Villota E R, Coronado A M. De-sign principles for robust oscillatory behavior. Sys-tems and Synthetic Biology, 2015, 9(3): 125–133
[19]Ripperger J A, Schibler U. Rhythmic CLOCK-BMAL1 binding to multiple E-box motifs drives circadian Dbp transcription and chromatin transitions. Nature Genetics, 2006, 38(3): 369–374
[20]Guillaumond F, Gréchez-Cassiau A, Subramaniam M, et al. Krüppel-like factor KLF10 is a link between the circadian clock and metabolism in liver. Molecular and Cellular Biology, 2010, 30(12): 3059–3070
[21]Prescott T P, Gyorgy A. Bounding the effect of retro-activity in the presence of parameter uncertainty // 2015 American Control Conference (ACC). Chicago, 2015: 3120–3125
Dynamical Effects of the Load on Self-sustained Oscillators
Abstract The effect of loads on self-sustained oscillators was studied by using numerical simulations and theoretical analysis with simple biological and chemical oscillators. Analyses of dynamical properties of the oscillators revealed that, the scheme in which the oscillators driving the load through indirect coupling via an insulator helped keeping the robustness of dynamical properties of the oscillators. The binding affinity between the load and its upstream module and the total amount of functional insulator were two key parameters that affected the relative amplitude of the load. The introduction of insulator module to the system can break the trade-off between the oscillations of the load and the retroactivity in the direct coupling scheme. Calculations of the free energy dissipation suggested that an increase in the free energy dissipation did not necessarily mean a decrease in the retroactivity or enhanced oscillations in the load.
Key words loads; self-sustained oscillators; retroactivity; insulator