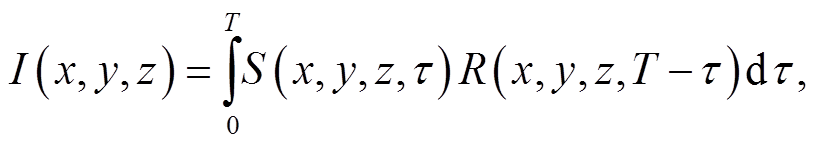
其中, T 为模拟中波场传播的总时间, τ 为波场传播的某一时刻。
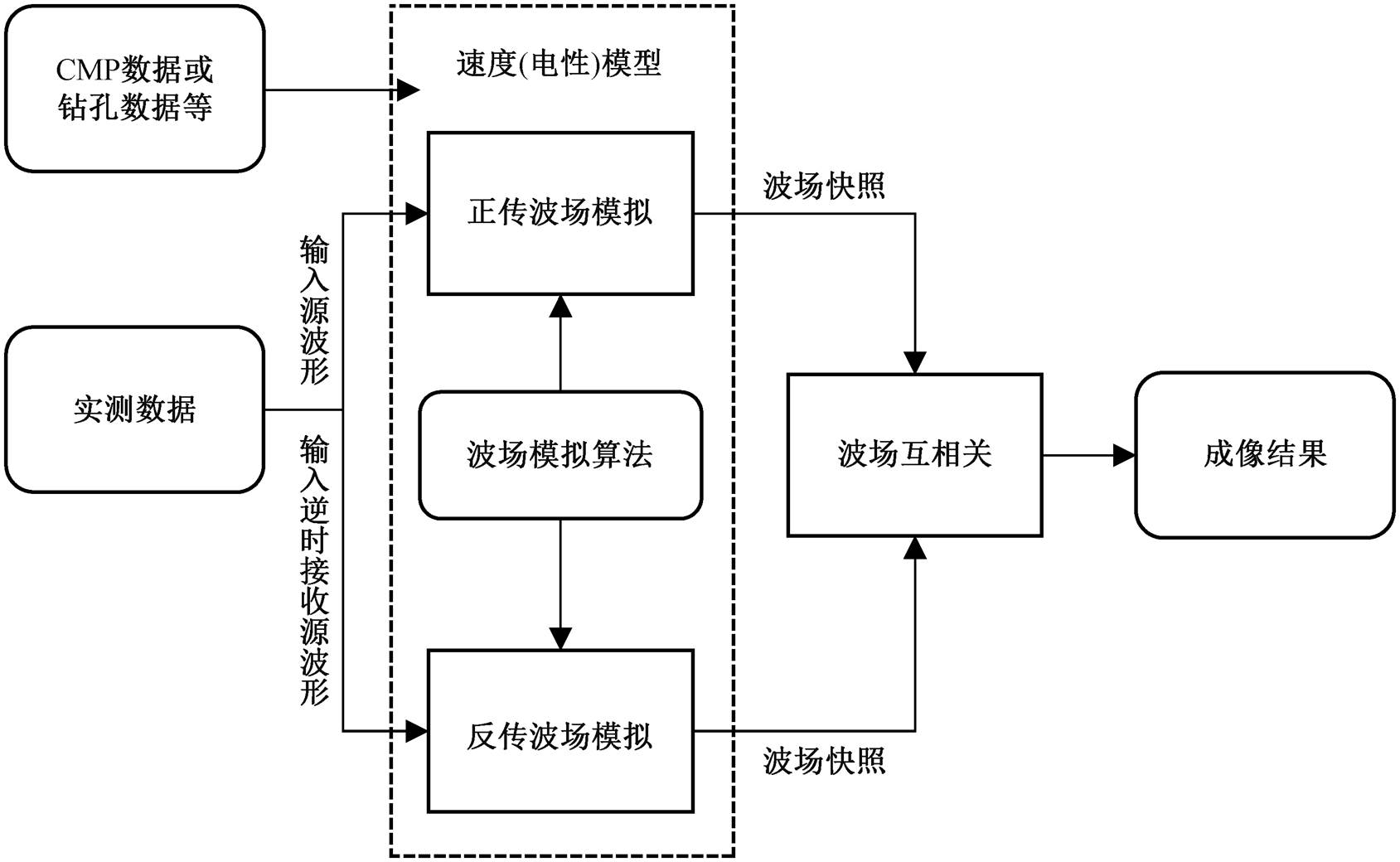
图1 RTM算法流程示意图
Fig. 1 Sketch of the RTM algorithm
北京大学学报(自然科学版) 第59卷 第3期 2023年5月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 3 (May 2023)
doi: 10.13209/j.0479-8023.2023.015
国家自然科学基金(42021003)资助
收稿日期: 2022–04–30;
修回日期: 2022–05–27
摘要 为了分析探地雷达数据处理过程中各种可能的误差对逆时偏移算法成像效果的影响, 通过数值模拟测试, 对模型存在速度误差和数据存在噪声的情况进行分析。对于模型存在速度误差的情况, 选用不同模型速度、不同异常体深度以及简化速度模型的情况进行成像效果测试。结果表明, 随着速度误差加大, 异常体位置偏离也变大, 且异常体深度越大, 位置偏离越大。对于各层速度相差不大的层状结构, 使用简化的均匀半空间模型进行成像, 依然可以较好地分辨地下的异常体。对于存在噪声的情况, 选用加入不同噪声水平的数据进行成像测试, 结果表明逆时偏移(RTM)算法对噪声有较好的压制效果, 即使接收的数据中有效信号的信噪比在−15dB 左右, 该算法仍然能将对应的结构成像出来。
关键词 探地雷达; 三维逆时偏移; 模型速度误差; 数据噪声
探地雷达(ground penetrating radar, GPR)使用天线向地下发出高频电磁波(0.01~1GHz), 通过接受电性异常体的反射波来推断地下结构, 是探测地下浅层结构的重要手段[1], 具有简单快捷、无损探测和分辨率高等优势[2], 应用领域非常广泛[3], 已在地质勘探[4]、沉积学研究[5]、考古[6]、地质灾害评估[7]、城市工程[8]以及地下水监测等多个领域发挥重要作用。
GPR 采集的原始数据是时间记录, 反映出来的是一个假的未聚焦图像[9], 相对于真实情况, 异常体的结构和位置可能存在较大的偏差。偏移处理可以将原始图像从时间域转换到深度域, 并将图像中的异常体还原为原本的形状和位置。考虑到 GPR使用的电磁波工作频率高, 与弹性波遵循相同形式的波动方程, 因此勘探地震中的许多偏移处理方法也被引入 GPR 的数据处理过程[10], 逆时偏移(rever-se time migration, RTM)便是其中一种处理方法。多数偏移方法对波场的模拟计算, 求解的是波动方程的近似形式——单程波动方程, RTM 则是通过直接求解原始波动方程来模拟波场传播, 其原理比较直观, 并且能够应用于处理具有大倾角反射体或多次波的复杂结构, 与其他偏移方法相比, 具有很高的精度[11−12]。
Baysal 等[13]和 McMechan[14]分别提出弹性波的叠前和叠后 RTM 成像算法。之后, Fisher 等[9]将二维 RTM 成像算法引入 GPR 数据处理中, 并指出二维 RTM 在大角度的反射体、产生衍射的结构界面和空间不均匀结构等情况下可以带来显著的改善。朱尉强[15]发展了 GPR 的并行三维 RTM 算法, 张崇民[16]利用 GPR 三维 RTM 成像方法研究工程隐蔽病害, 焦翠翠[17]将 RTM 应用在矿井富水区的 GPR 三维成像研究中。
对于实际数据, RTM 成像质量可能受数据质量和波场模拟电性模型的影响。杨仁虎等[18−20]对地震波 RTM 算法中震源子波形态、直达波、速度结构和噪声等因素对成像精度的影响进行过一系列研究, 对 RTM 在地震成像实践中的应用起到一定的参考作用。本文针对 GPR 三维 RTM 成像算法进行研究, 探讨各个影响因素对 GPR 的 RTM 成像效果的影响。
RTM 成像方法通过直接求解双向波动方程实现波场外推, 比其他偏移算法精度更高。图 1 为叠前 RTM 算法流程示意图。对于共发射点的 GPR 数据, 首先根据实际情况建立电性结构模型, 在发射点位置激发实际发射波形, 计算介质中的正传波场S(x, y, z, t); 然后在接收点将接收波形进行反向时间轴上的激发, 计算介质中的反传波场 R(x, y, z, t); 最后对模拟得到的正传波场 S 和反传波场 R 应用互相关成像条件, 得到成像结果 I(x, y, z, t)[21]:
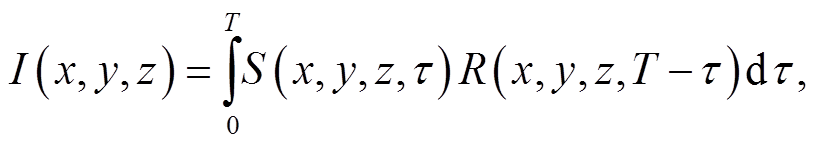
其中, T 为模拟中波场传播的总时间, τ 为波场传播的某一时刻。

图1 RTM算法流程示意图
Fig. 1 Sketch of the RTM algorithm
对于一个区域的 RTM 成像, 需要将发射源布置在不同的位置来得到反射数据, 然后对每个位置的共发射点数据分别进行叠前 RTM 成像, 最后将成像结果叠加, 得到最终的地下结构信息。
在对波场 S 和 R 的模拟中, 采用空间 4 阶时间 2阶的时域有限差分法[22]求解波动方程。算法的稳定性条件[23]要求库朗数小于 6/7, 即波在一个时间步长内走过的距离小于约 0.85 个空间步长; 算法的频散关系要求一个波长包含至少 10 个空间网格[24]。
模拟数据与实际数据存在很大的差别。数值模拟试验中, 速度结构为准确已知, 通过共中心点剖面(common midpoint profile, CMP)或钻孔等方法得到的地下速度模型, 可能与实际情况存在一定程度的偏差, 不能准确地反映地下实际速度。另外, 实际数据中可能出现背景噪音和杂波等不需要的信号, 对成像造成干扰。针对这些情况, 我们通过数值模拟实验, 讨论速度模型差异以及噪声对 RTM成像效果的影响。
数值模拟采用的模型设置如下: 模型长度为 5m, 宽度为 2m, 深度为 4m, 背景相对介电常数为5, 相对磁导率为 1, 电导率为零。如图 2 所示, 在 y轴中间深度为 2m 处, 沿 x 轴依次放置 3 个半径为0.1m 的点状空腔。发射源采用主频为 400MHz 的雷克子波。进行数值计算时, 空间网格间距取为0.02m×0.025m×0.02m, 模型区域共 250×80×200 个网格点, 一个波长范围内包含大约 16 个网格, 避免空间频散。时间步长为 0.0158ns, 库朗数为 0.4, 满足稳定性条件。
图 3 给出理想状态下 RTM 成像结果 y 方向的竖直切片。经过逆时偏移成像, 3 个异常体的位置都得到很好的还原。
对于实际数据, 需要通过各种方法(如 CMP 和钻孔等)获得介质速度, 建立 RTM 初始模型。但是, 获得的速度可能存在一定的偏差, 不能准确地代表实际的地下介质速度结构。本文通过模拟实验, 测试模型速度结构差异对成像结果的影响。
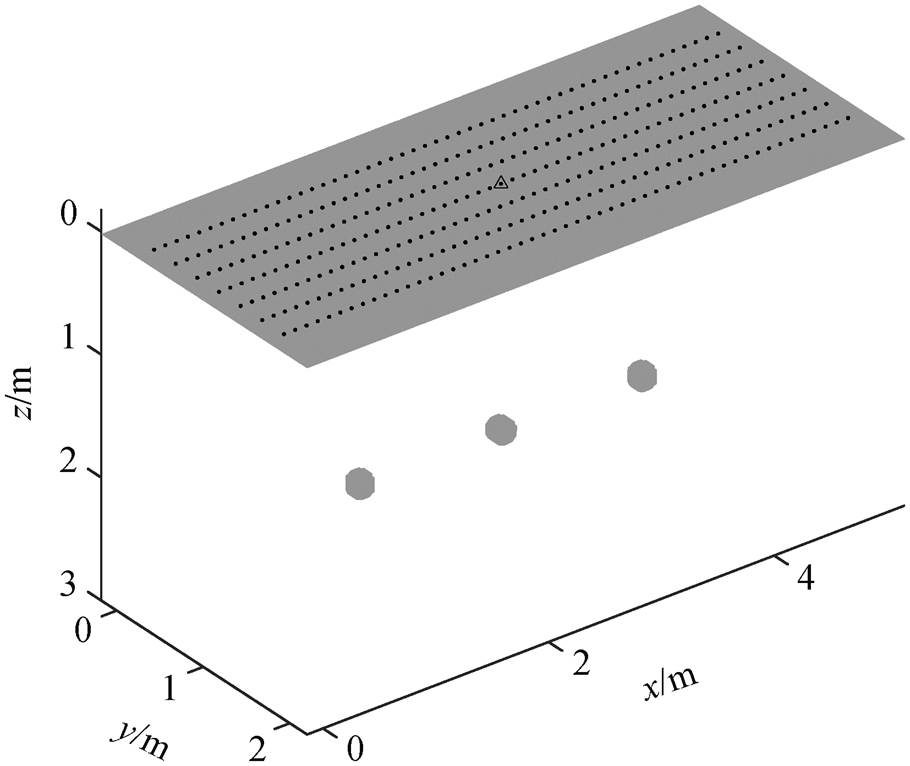
大圆点示意 3 个点状空腔的尺度和位置; 三角形示意发射源位置, 其坐标为(2.5m, 1m, 0); 点线示意接收点的 7 条测线, 从y=0.25m到 y=1.75m, 每隔 0.25m 布置一条测线, 每条测线上的测点(点线上的小圆点)间距为 0.1 m
图2 数值模拟测试模型
Fig. 2 Model for numeric simulation
设置 RTM 初始模型的介质速度分别比实际情况快或慢 2%, 5%和 10%, 分别在这些初始模型上进行 RTM 成像。取各个结果的 y 方向竖直切片进行对比观察, 结果如图 4 所示。当介质速度误差为 2%时, 异常体的形态与理想状态差别不大, 介质速度的误差几乎没有影响(图 4(a))。当介质速度误差达到 5%时, 对异常体的聚焦效果减弱, 导致异常体的成像形态有所展宽, 成像位置也有所偏差(图 4(b))。当介质速度误差达到 10%时, 异常体的波形已无法聚焦到一点, 呈现类似球形波阵面的形状(图 4(c)和(d)); 成像位置的偏离也非常大, 介质速度比实际情况小的时候成像位置偏上(图 4(c)), 介质速度比实际情况大的时候成像位置偏下(图 4(d))。
在介质速度误差相同的情况下, 如果异常体的深度不同, 对成像结果的影响也不同。图 5 给出介质速度误差为 5%的情况下, 分别在异常体深度为 1m 和 3m 的成像结果。结合图 4(b)可以看到, 对于相同的速度误差, 异常体深度越大, 成像结果的误差越大。
对于水平层状结构, 使用均一介质模型测试RTM 的成像效果。如图 6(a)所示, 在原始模型的基础上, 分别在深度 0.8~1.2m 和 1.2~1.6m 之间加入速度与背景相差 10%的高速层和低速层, 对应的相对介电常数为 4.1 和 6.2, RTM 成像所用的介质模型不变, 仍然为均一速度模型。从成像结果(图 6(b)) 可以看到, 界面和异常体的位置均能成像出来。虽然由于界面反射信号太强而使得异常体的信号较弱, 但是其位置没有很大的偏差, 说明对于水平层状结构, 可以取各层速度的大致平均值作为均一速度结构进行 RTM 成像, 也能较好地恢复地下异常体的位置。
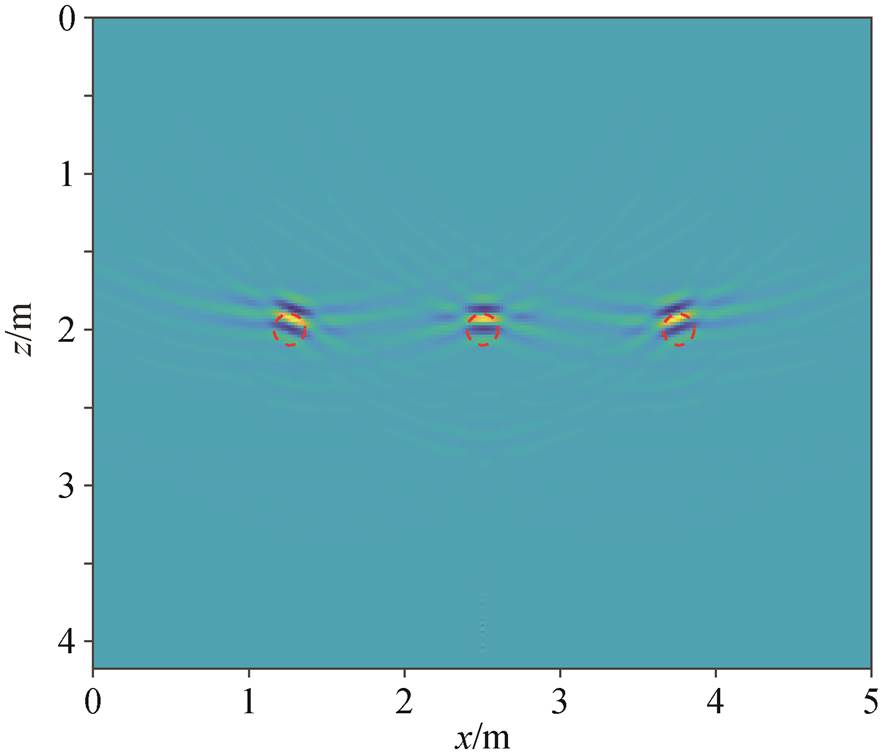
红色虚线表示异常体的实际位置。成像结果为波场互相关的值, 表明地下结构信息, 该数值本身没有实际意义, 故未给出色标, 下同
图3 理想状态下 RTM 成像结果在 y=1 m 处的竖直切片
Fig. 3 Vertical slice at y=1 m of the RTM imaging results under ideal conditions
对于实际的 GPR 数据, 噪声往往是一个不可忽略的问题, 各种成像算法也需要对数据中的噪声有一定的鲁棒性。本研究的数值模拟测试中, 对接收数据分别加入相对于有效信号具有不同噪声水平的高斯白噪声, 然后进行 RTM 成像, 检测噪声干扰对RTM 成像效果的影响。
图 7(a1)~(a3)展示部分加入不同噪声之后的接收数据。噪声水平与有效信号相当(信噪比为 0dB) 时, 有效信号较为清晰(图 7(a1)); 信噪比为−15dB时, 有效信号勉强可见(图 7(a2)); 信噪比为−30dB时, 有效信号肉眼不可见(图 7(a3))。
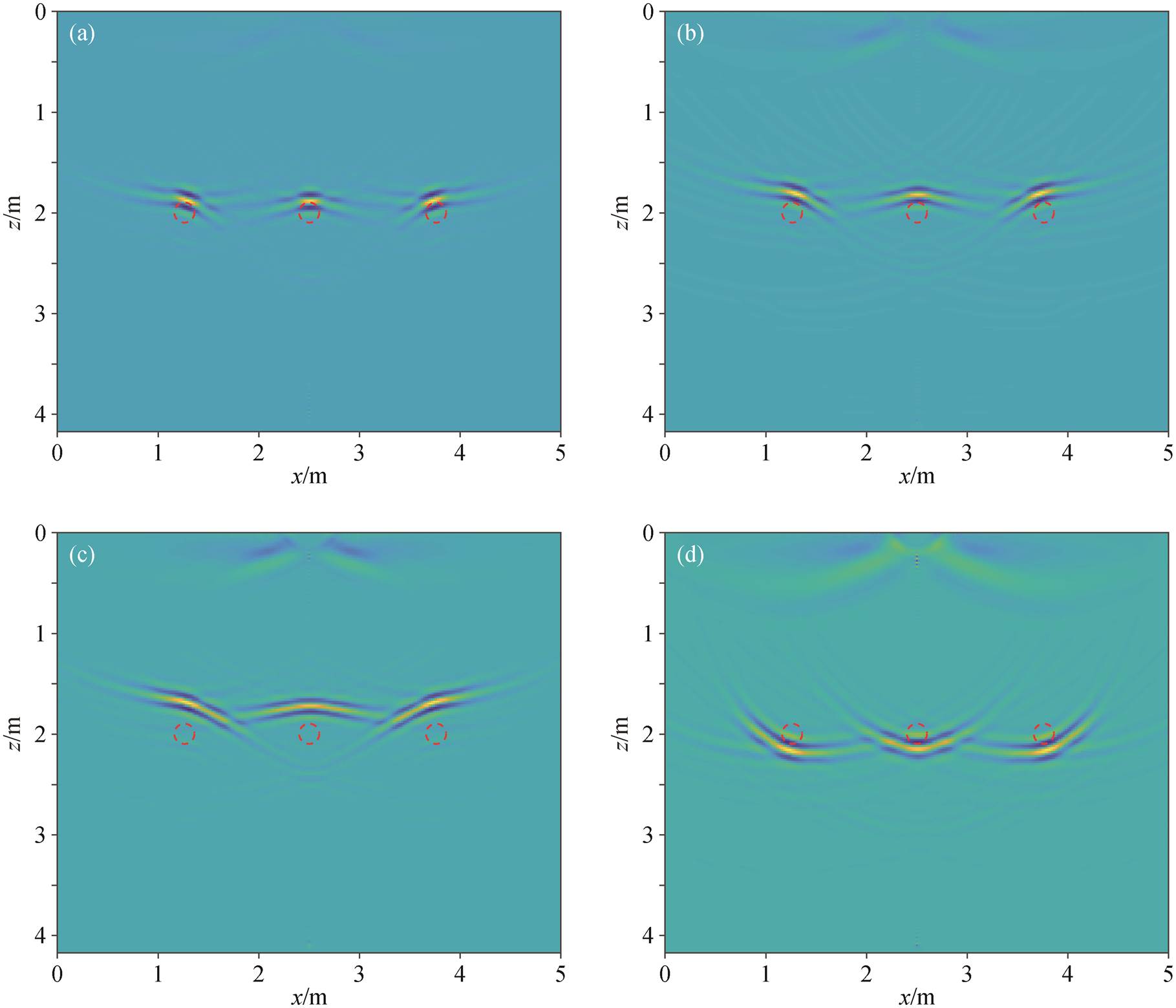
(a)速度比实际情况小 2%; (b)速度比实际情况小 5%; (c)速度比实际情况小 10%; (d)速度比实际情况大 10%
图4 不同介质速度误差下RTM成像结果的竖直切片
Fig. 4 Vertical slices of RTM imaging results at different velocity errors
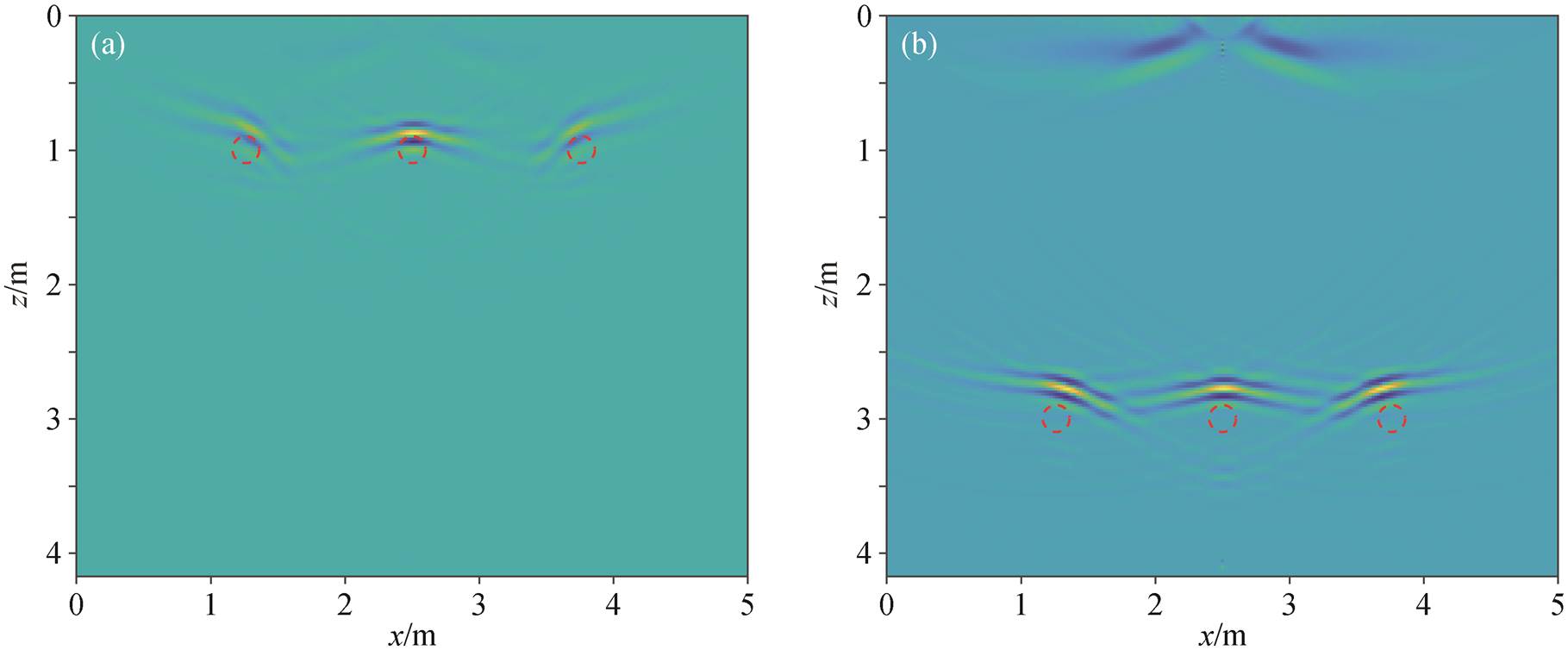
异常体深度: (a)为1 m; (b)为3 m
图5 相同速度误差下不同异常体深度RTM成像结果的竖直切片
Fig. 5 Vertical slices of RTM imaging result at different anomalous body depths with the same velocity error

(a)水平层状结构下生成数据的相对介电常数模型; (b)均一介质初始模型的RTM成像结果。虚线示意分层界面和异常体的实际位置
图6 y=1 m处的竖直切片
Fig. 6 Vertical slice at y=1 m
图 7(b1)~(b3)给出对应噪声水平下的 RTM 成像结果。在 0dB 信噪比的情况下, 噪声对成像结果基本上没有影响(图 7(b1)); 在−15dB 信噪比的情况下, 噪声对成像结果有较明显的影响, 背景出现很多杂乱的条纹, 但依然能够较好地识别异常体(图 7(b2)); 在−30dB 信噪比的情况下, 只能勉强分辨出异常体(图 7(b3)); 当信噪比低于−30dB 时, 异常体则完全无法成像。结合前面对含噪声原始信号的分析可以得出, 只要原始数据信噪比大于−15dB 左右, RTM成像也能较好地给出异常体信息(图 7(c)和(d))。该数值测试结果表明, RTM 算法对噪声有较好的压制效果。
本文通过对 GPR 的 RTM 成像算法各种影响因素的研究, 分析 GPR 三维 RTM 算法在速度结构误差和噪声影响下的鲁棒性, 研究结果可为实际数据采集中数据质量的控制提供参考。
对速度结构的分析表明, 在模型介质速度与实际速度结构相差不大的情况下, 成像结果几乎没有偏差; 随着速度误差增大, 成像结果中异常体位置的偏离也变大, 并且对于相同的速度误差, 异常体深度越大, 成像结果偏离越大。所以, 进行 RTM成像要尽可能获得准确的速度结构。另外, 对于速度误差不是特别大的层状结构, 使用简化的均匀半空间速度模型进行 RTM 成像, 可以较好地分辨地下的异常体和层状结构。
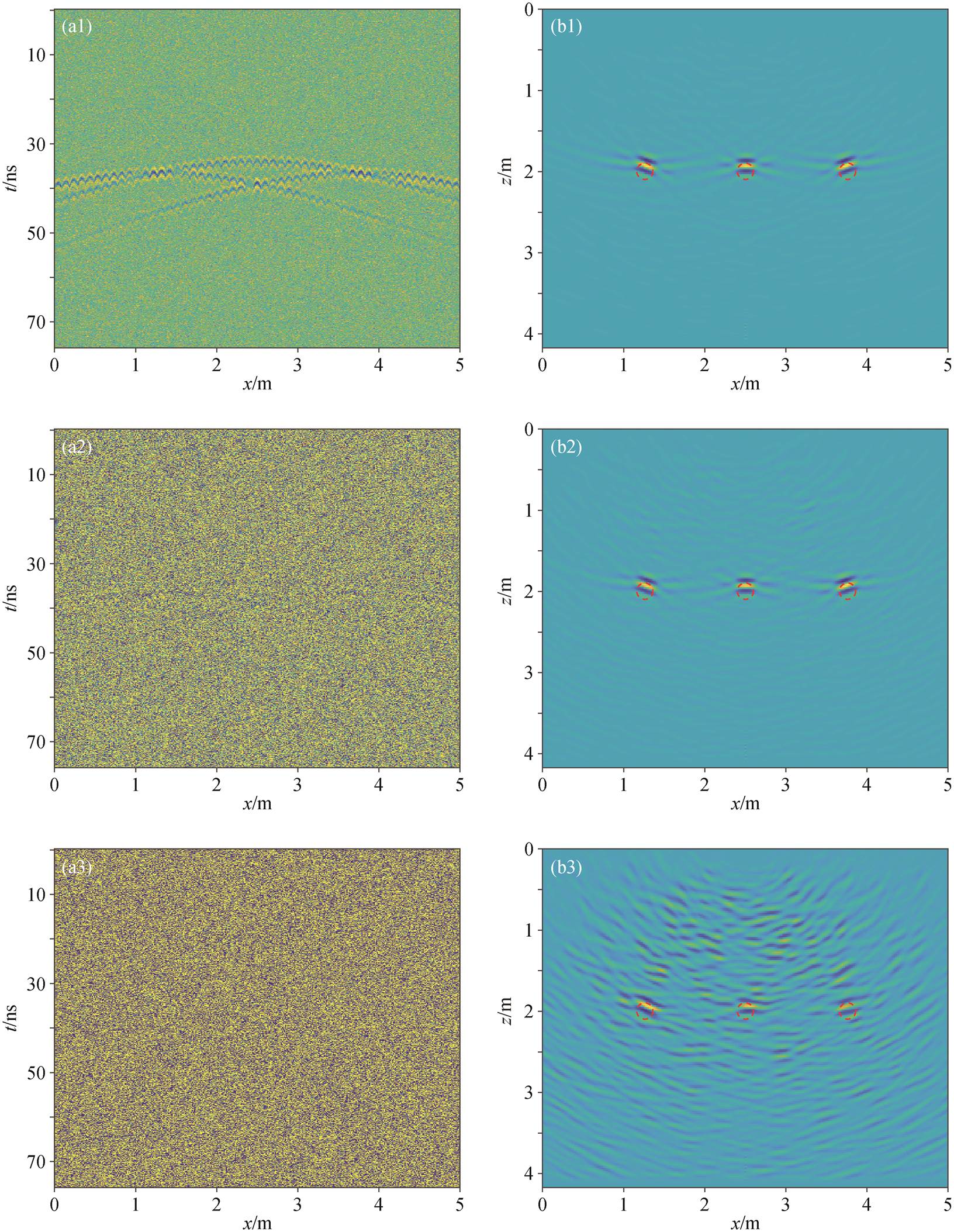
加入高斯白噪声的信噪比: (a1)和(b1)为 0dB; (a2)和(b2)为−15dB; (a3)和(b3)为−30 dB
图7 加入高斯白噪声后的模拟接收数据((a1)~(a3))以及对应的RTM成像结果竖直切片((b1)~(b3))
Fig. 7 Simulated received data after adding white Gaussian noise ((a1)~(a3)) and the corresponding vertical slices of RTM imaging results ((b1)~(b3))
对含噪声数据的分析结果表明, RTM 算法对噪声有较好的压制效果, 即使接收数据中的有效信号仅能勉强分辨(例如信噪比大于−15dB 时), RTM 算法依然能较有效地压制噪声, 并将对应的结构成像出来。
参考文献
[1] 曾昭发. 探地雷达方法原理及应用. 北京: 科学出版社, 2006
[2] Mellett J S. Ground penetrating radar applications in engineering, environmental management, and geo-logy. Journal of Applied Geophysics, 1995, 33: 157– 166
[3] 赵卫平, 潘和平, 李清松, 等. 井中雷达应用进展. 工程地球物理学报, 2005, 2(4): 297–303
[4] Zhang Di, Li Jiacun, Liu Shaotang, et al. Multi-frequencies GPR measurements for delineating the shallow subsurface features of the Yushu strike slip fault. Acta Geophys, 2019, 67(2): 501–515
[5] Bakker M A J, Van Der Meer J J M. Structure of a pleistocene push moraine revealed by GPR: the eas-tern Veluwe Ridge, The Netherlands. Geological So-ciety London Special Publications, 2003, 211(1): 143– 151
[6] Trinks I, Johansson B, Gustafsson J, et al. Efficient, large-scale archaeological prospection using a true three-dimensional ground-penetrating radar array sys-tem. Archaeological Prospection, 2010, 17(3): 175–186
[7] Benson A K. Applications of ground penetrating radar in assessing some geological hazards: examples of groundwater contamination, faults, cavities. Journal of Applied Geophysics, 1995, 33: 177–193
[8] Busetti A, Calligaris C, Forte E, et al. Non-invasive methodological approach to detect and characterize high-risk sinkholes in urban cover evaporite karst: integrated reflection seismics, PS-InSAR, Leveling, 3D-GPR and ancillary data. A NE Italian case study. Remote Sensing, 2020, 12(22): 3814
[9] Fisher E, McMechan G A, Annan A P, et al. Examples of reverse-time migration of single-channel, ground- penetrating radar profiles. Geophysics, 1992, 57(4): 577–586
[10] Berkhout A J. Wavefield extrapolation techniques in seismic migration, a tutorial. Geophysics, 1981, 46 (12): 1638–1656
[11] Zhu Jinming, Lines L R. Comparison of Kirchhoff and reverse-time migration methods with applications to prestack depth imaging of complex structures. Geo-physics, 1998, 63(4): 1166–1176
[12] Yoon K, Shin C, Sangyong S U H, et al. 3D reverse-time migration using the acoustic wave equation: an experience with the SEG/EAGE data set. Leading Edge, 2003, 22(1): 38–41
[13] Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration. Geophysics, 1983, 48(11): 1514–1524
[14] McMechan G A. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 1983, 31(3): 413–420
[15] 朱尉强. 逆时偏移成像技术在探地雷达数据处理中的应用[D]. 北京: 北京大学, 2016
[16] 张崇民. 工程隐蔽病害地质雷达三维逆时偏移成像方法[D]. 济南: 山东大学, 2019
[17] 焦翠翠. 基于RTM的矿井富水区成像研究[D]. 西安: 西安科技大学, 2020
[18] 杨仁虎, 常旭, 刘伊克. 叠前逆时偏移影响因素分析. 地球物理学报, 2010, 53(8): 1902–1913
[19] 杨仁虎. 逆时偏移随机噪声影响分析. 地球物理学进展, 2021, 36(6): 2618–2627
[20] 杨仁虎. 逆时偏移速度误差影响分析. 地球物理学进展, 2021, 36(4): 1630–1639
[21] Claerbout J F. Toward a unified theory of reflector mapping. Geophysics, 1971, 36(3): 467–481
[22] Georgakopoulos S V, Birtcher C R, Balanis C A, et al. Higher-order finite-difference schemes for electro-magnetic radiation, scattering, and penetration, part I: theory. IEEE Antennas Propag Mag, 2002, 44(1): 134–142
[23] Fang Jiayuan. Time domain finite difference computa-tion for Maxwell’s equations [D]. Berkeley: Univer-sity of California, 1989
[24] Liu Qinghuo. The PSTD algorithm: a time-domain method requiring only two cells per wavelength. Mic-rowave and Optical Technology Letters, 1997, 15(3): 158–165
Study on Influencing Factors of Pre-Stack Reverse Time Migration Imaging of Ground Penetrating Radar
Abstract To analyze the influence of various possible errors in the actual ground-penetrating radar data processing on the imaging effect of the reverse time migration algorithm, numerical simulation tests are used to analyze the effect of the velocity errors in model and noises in data. For velocity error, models with different velocities and abnormal body depths, and simplified velocity models are used to test the subsequent imaging effect. Results show that with the increase of the velocity error and the depth of the abnormal body, the deviation of the position of the abnormal body also increases. For the layered structure with slight differences in velocity between each layer, imaging using a simplified uniform half-space model can still effectively distinguish the anomalies. Imaging tests are also performed on data with different noise levels. The results show that the reverse time migration (RTM) algorithm is effective on noise suppression. Even if the signal-to-noise ratio of the valid signal in the received data is around −15 dB, the RTM algorithm can still image the corresponding structure.
Key words ground penetrating radar; 3D reverse time migration; velocity errors; data noise