北京大学学报(自然科学版) 第59卷 第2期 2023年3月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 2 (Mar. 2023)
doi: 10.13209/j.0479-8023.2022.125
教育部人文社会科学基金(18YJA760015)和国家自然科学基金(41971331)资助
收稿日期: 2022‒04‒13;
修回日期: 2022‒07‒13
述评
公共服务设施可达性度量方法研究综述
公共服务设施可达性度量方法研究综述
高巍1 欧阳玉歆2 赵玫3,† 高勇4 孟浩瀚4
1.北京交通大学建筑与艺术学院, 北京 100044; 2.北京城建设计发展集团股份有限公司, 北京 100034; 3.北京理工大学设计与艺术学院, 北京 100081; 4.北京大学地球与空间科学学院, 北京 100871;†通信作者, E-mail: zhaomei@bit.edu.cn
摘要 对既有研究中采用的公共服务设施可达性度量方法进行梳理和总结, 从数理统计、拓扑网络和几何网络3个方面对比不同方法的基本原理、度量指标、优缺点和适用范围, 指出当前的方法学任务是在理论和经验方面合理的指标与简单指标之间寻找适度的平衡, 而新数据技术的涌现为可达性度量方法提供新的发展方向。
关键词 公共服务设施; 可达性; 度量方法
可达性指从一个地方到达另一个地方的容易程度[1]。Hansen[2]于 20 世纪 50 年代首次提出“可达性”概念后, 西方学者开始关注这一问题。随着应用领域的不断扩展和度量方法的日益改进, 形成对可达性的多种解释, 如距离成本、出行时间和旅行费用等, 但多衍生自以下 3 种经典定义[3]: 1)地点可达性, 即汉森(Hansen)定义; 2)效果可达性, 即本阿基瓦和莱尔曼(Ben Akiva & Lerman)定义; 3)时空间可达性, 即伦特普(Lenntorp)定义。在城市规划与交通出行领域, 普遍应用的理论依据主要是Hansen[2]提出的可达性概念, 即“交通网络中节点间相互作用机会的大小”, 该定义强调可达性的空间属性, 即出发地、目的地(机会)和空间阻抗。20 世纪 60—70年代, 可达性逐渐成为西方学者研究的热点[4]。国内从 20 世纪 80 年代开始通过计算机辅助评价出行可达性的研究[5], 至 2019 年可达性研究成果数量已经位居世界前列[6]。随着可达性应用范围逐渐广泛, 相关研究着重在以下 4 个方面: 1)交通网络的空间格局演变对区域发展影响的研究; 2)新建交通基础设施的区域经济效应评价; 3)选址分析与区位评价; 4)园林与建筑设计、景观规划研究[7]。
作为公众生存和发展必不可少的资源和服务内容, 公共服务设施是实现城市可持续发展的前提[8], 其选址与区位分析是可达性应用研究的一个重要领域。国际上 1980 年已开展将可达性应用于公共服务设施空间布局的研究[9], 近年来越来越多的学者通过对公共服务设施可达性的分析评价, 辨别设施分布的均衡情况, 进而助力城市空间规划, 协调公平与效率。21 世纪以来, 国内的相关研究日益活跃, 但在城市科学领域, 对公共服务设施可达性及其度量方法的系统性认知还有所不足[10], 部分原因是有关可达性的多种空间、时间维度和多模式性质, 在定义、测度和建模方面过去 30 年里经历了各种变化[11‒12], 衍生出许多模型来衡量不同目标的可达性。另一方面, 公共服务设施类别和需求的多样性也使可达性的度量方法难以统一, 多采取单一类别对应单一度量方法的研究方案, 从而给相关规划者和研究人员带来挑战。
本文对既有研究中的公共服务设施可达性度量方法进行梳理, 对比分析不同方法的适用范围, 希望为相关研究方法的认知与选择提供帮助。
1 空间可达性度量方法分类
随着空间可达性研究的逐渐深入, 可达性的度量方法也不断改进。1959 年, Hansen[2]首次使用潜能模型对可达性进行度量, 其后发展出多种多样的度量方法来适应不同需求的研究。陈洁等[7]从网络特性差异的角度对空间可达性度量方法进行梳理, 并指出由于选取的可达性度量指标不同以及度量方式不同, 最终结果将各具特色(表 1)。彭科[3]基于定义和构成要素的不同, 对度量方法进行归类和总结, 指出由于在要素构成上的差别, 不同定义下的度量方法会导致计算结果的显著差异(表 2)。
可达性主要受交通系统、土地利用、时间条件和个体特性 4 个因素影响[13], 不同的可达性度量方法涉及的影响因素类型及其制约程度各不相同, 通常根据设施的特点和研究的需求决定, 故常常需要针对设施的类型选用其适宜的度量方法。从既有文献来看, 在区域和城市科学领域, 可达性度量方法可以分为 3 个应用层次(表 3)。其中, 基础应用层次仅涉及交通系统因素, 较高应用层次同时考虑交通系统和土地利用因素, 最高层次则综合考虑交通系统、土地利用、时间条件和个体特性 4 种因素[7]。目前, 公共服务设施可达性的度量方法多属于基础应用层次和较高应用层次。近年来, 随着大数据技术的发展, 相关度量方法不断更新和完善, 针对公共服务设施可达性的研究方法逐渐成熟, 可达性度量模型结合 GIS 进行可达性评价的分析方法也逐步普及, 且因其计算结果精确、便于数据管理和图示表达等优点, 被众多研究者采用。
表1 基于网络特性的可达性度量方法分类[7]
Table 1 Classification of accessibility measurement methods based on network characteristics[7]

网络特性衡量方式度量模型 几何网络将空间距离、时间距离(跨越空间距离所需的时间)和经济距离(跨越空间距离所支付的费用)作为基本因子来度量可达性距离法、累计机会法、等值线法、潜能模型法、时空法和效用法等 拓扑网络通过整体可达性矩阵与最短距离矩阵运算来获取节点和网络的可达性水平拓扑法(如矩阵方法和空间句法)
表2 基于定义与构成要素的可达性度量方法分类[3]
Table 2 Classification of accessibility measures based on definitions and components[3]
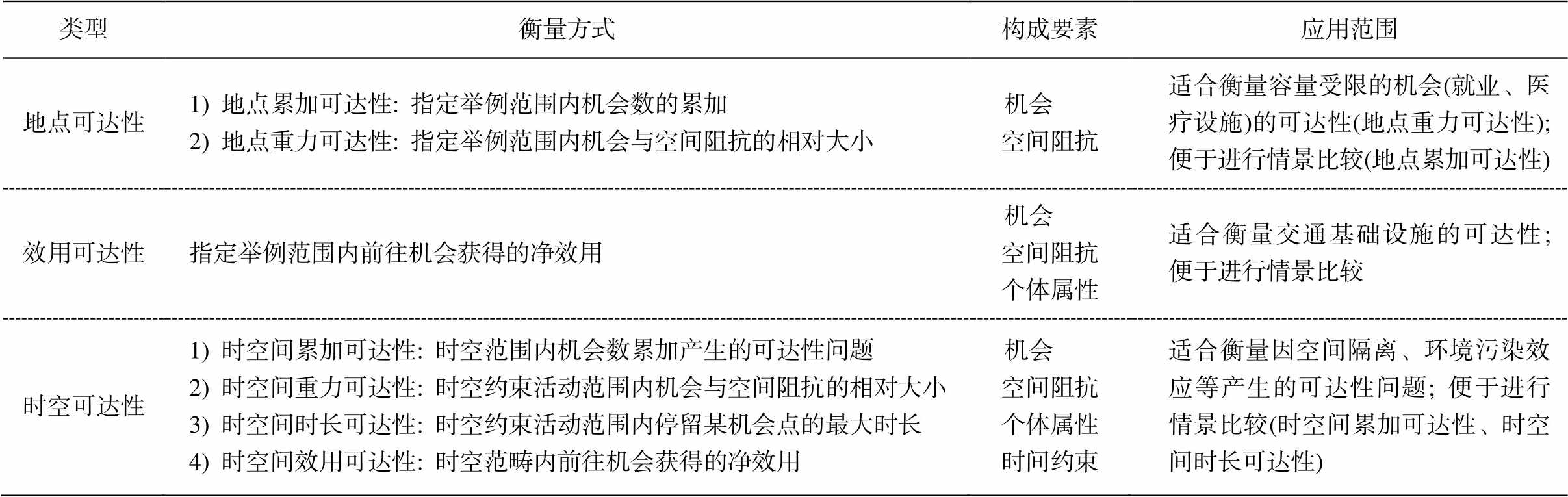
类型衡量方式构成要素应用范围 地点可达性1) 地点累加可达性: 指定举例范围内机会数的累加2) 地点重力可达性: 指定举例范围内机会与空间阻抗的相对大小机会 空间阻抗适合衡量容量受限的机会(就业、医疗设施)的可达性(地点重力可达性); 便于进行情景比较(地点累加可达性) 效用可达性指定举例范围内前往机会获得的净效用机会 空间阻抗个体属性适合衡量交通基础设施的可达性; 便于进行情景比较 时空可达性1) 时空间累加可达性: 时空范围内机会数累加产生的可达性问题2) 时空间重力可达性: 时空约束活动范围内机会与空间阻抗的相对大小3) 时空间时长可达性: 时空约束活动范围内停留某机会点的最大时长4) 时空间效用可达性: 时空范畴内前往机会获得的净效用机会 空间阻抗个体属性时间约束适合衡量因空间隔离、环境污染效应等产生的可达性问题; 便于进行情景比较(时空间累加可达性、时空间时长可达性)
表3 不同应用层次下的可达性度量方法
Table 3 Reachability measurement at different application levels

应用层次考虑因素度量方法特点 基础应用交通系统距离法仅考虑交通因素, 解释性强, 操作简便 较高应用交通系统土地利用潜能模型法、累计机会法和等值线法等同时考虑交通系统和土地利用两个因素, 模型更符合真实情况, 是目前可达性研究中应用最广泛的层次 最高应用交通系统土地利用时间条件个体特性时空法和效用法综合考虑4种主要影响因素, 但相对更复杂, 难以理想化实现
2 公共服务设施的可达性度量方法
公共服务设施空间布局是空间可达性的主要应用领域之一, 在针对公共服务设施可达性的研究中采用的可达性度量方法有多种, 如统计指标法、比例法、空间句法、距离法、旅行成本或费用法、累计机会法、等值线法、两步移动搜索法及其改进形式、潜能模型及其改进形式、胡弗模型、核密度法以及最小行进成本法等。不同的度量方法可以通过不同的方式实现, 如建立在 GIS 等平台下的核密度法和距离法、建立在 Depthmap 等平台下的空间句法以及直接通过数学方法计算实现的比例法和统计指标法等, 这些方法可以归纳为基于数理统计、基于拓扑网络和基于几何网络 3 类。
2.1 基于数理统计的方法
基于数理统计的方法是通过问卷调查、访谈和现场观察等手段获取数据, 并运用统计原理和回归技术, 分析和梳理可达性的阻力因素和评价标准, 得到可达性的衡量指数。根据数据的性质和研究目的, 统计模型已经从简单的线性回归模型转变为离散选择和结构方程模型, 在这些研究中, 可达性指标主要基于距离或机会累积[14]。
基于数理统计的方法应用领域较为广泛, 对于较大或较小的研究单元均能适用, 其优点是对可达性的影响因素考虑比较全面, 将建筑环境的其他因素和社会经济指标也作为统计模型中的解释变量, 也常常用于主观层面的可达性研究[15]。这种方法具有稳健的校准和验证技术, 结果简明清晰。但是, 由于缺乏量纲, 参数和变量众多, 不易形成能在规划设计中推广的统一的计算方法[16], 对可达性单个侧面的度量效果不理想[17]。
2.2 基于拓扑网络的方法
基于拓扑网络的方法强调要素之间的连通关系, 多用于对航空、地铁和公路等网络的分析, 包括矩阵方法和空间句法(space syntax)。
矩阵方法将交通网络抽象成拓扑网络, 通过网络邻接矩阵构建整体可达性矩阵, 通过网络连通性矩阵构建最短距离矩阵, 再基于这两个矩阵计算节点的可达性水平[18‒19]。如果用 A(aij)表示 n 阶邻接矩阵(aij表示点 i 与 j 间的路径数目, n 表示交通网络中站点数量), 用于计算点 i 到 j 之间的路径问题, 对邻接矩阵 A 的各级幂求和, 矩阵 D 即可表示可达性: D=A+A2+A3+…+Am, 其中 m 是网络直径, 表示交通网络中两站点之间的最大值路径, 则交通网络中不同地点的可达性的计算公式[20]如下:
Di = di / (∑di / n) ,(1)
其中, Di 用于衡量交通网中站点 i的相对可达性, di 表示地点 i 在 m 步阈值内能够到达其他站点的路径数总和, di = ∑dij, j= 1, …, n。
空间句法是一种基于拓扑距离的网络可达性模型, 由 Hillier 等[21]于 1984 年提出。这是一种以二维街道网络系统为对象, 分析拓扑系统中心轴和节点可达性的方法, 侧重以图形可视化来表达街道连通性、关联性以及空间拓扑关系, 其常用的可达性指标包括深度、平均深度和整合度等。深度指空间节点之间的最短拓扑距离, 常用一个节点到其他任意节点的深度值之和(即总深度)表达, 计算公式[22]如下:
平均深度为节点 i 到其他任意节点总深度的均值, 计算公式[22]如下:
MDi=Di/(n−1)。 (3)
整合度是可达性分析的关键指标之一, 反映一个节点与系统中其他节点的聚集或离散程度, 由深度值推导而来, 通过相对不对称值 RAi 和实际相对不对称值 RRAi 表达, 计算公式[23]如下:
RAi=2(MDi−1)/(n−2), (4)
RRAi=RAi/Dn, (5)
其中, Dn=2{n[log2((n+2)/3−1) +1]}/[(n−1)(n−2)]。空间句法的相关指标可以通过 Dethmap 等对应的软件工具计算获得, 近期的研究中常使用空间句法方法来描述基于街道网络的可达性[24‒26]。
2.3 基于几何网络的方法
几何网络是交通网络的几何表现, 与拓扑网络相比, 其内部规律与真实道路交通网络更相似。目前, 针对公共服务设施可达性的研究大多采用基于几何网络的数学模型。这类方法受空间尺度的局限性较小, 可适用于宏观、中观和中微观等多尺度的研究(如度量县域中学和城市医院等公共服务设施的可达性), 但不适用微观尺度的可达性研究。基于可达性的定义和影响因素等方面, 可以将基于几何网络的方法大致分为空间阻隔、机会累积和空间相互作用 3 类模型。
2.3.1空间阻隔模型
空间阻隔模型是从空间阻隔的角度定义公共服务设施可达性, 即需求点(人)到达供给点(公共服务设施)获取服务过程中花费的成本(时间、距离或费用等)。这一类度量方法属于基础应用层次, 仅考虑交通系统因素, 以距离法为代表。
距离法是通过评价某点交通出行的便捷程度来衡量可达性水平, 度量模型中的“距离”可以指空间距离、时间或费用等, 是最直观简洁的可达性度量方法。其中, 空间距离法在路网空间格局研究中应用较多, 也常用于公共服务设施的可达性测度。关于距离的测量, 有欧式距离、曼哈顿距离和网络最短路径距离, 其中欧式距离和网络最短路径距离的使用更广泛[27], 计算公式[28]如下:
其中, Ai 表示区域 i 的可达性, tij 是从区域 i 到 j的出行成本, J 为区域集合。
距离法考虑了距离因素, 涵义直观, 计算简便, 适于宏观层面的可达性评价, 但缺少对供需点规模等其他因素的考虑, 尤其是采用欧氏距离时, 甚至忽视实际的路网空间形态, 因此使用范围受限。在实际应用中, 常用两种改进的评价方法: 最小邻近距离法和费用加权距离法。
1)最小邻近距离法: 通过计算需求点到最邻近设施点的距离来衡量可达性。虽然计算结果有误差, 只能做到近似准确, 但计算简便, 数据要求低, 是目前应用最广泛的方法之一。例如, 曾文等[27]采用最小邻近距离法, 使用欧氏距离代替实际路网距离, 将居住用地作为空间单元, 分析 4 类城市社区服务设施(教育、商业、医疗和公园绿地)的可达性, 并研究低收入群体的服务设施空间剥夺问题, 取得较好的效果。
2)费用加权距离法: 采用网络距离来表征起始点到最邻近目的点的距离, 与人的实际行进距离较为接近, 计算方式比最小邻近距离法复杂, 但避免了最小邻近距离法采用欧氏距离度量可达性可能带来的精度不高问题。例如, 陈秋晓等[29]采用旅行费用法(即费用加权距离法), 利用网络距离表征实际出行距离, 从机会公平的视角对城市公园绿地的可达性进行精细的评价, 并指出模型存在忽略供需关系的缺陷, 引入公园吸引力指数来修正评价结果。
2.3.2机会累积模型
机会累积模型是从机会累积的角度来定义公共服务设施可达性, 是一种总体度量, 即居民在一定的出行范围(时间、距离)内可获得服务机会的数量。机会数量越多, 可达性越高。基于机会累积的度量方法属于较高应用层次, 同时考虑了交通系统和土地利用因素。该方法包括累计机会法和等值线法, 均于 20 世纪 70 年代提出, 是在距离法的基础上发展而来。这两种方法的原理较为相似, 由于其简单性和易解释性, 成为常用的可达性度量方法之一。
1)累计机会法: 通过设定一个出行成本, 将这一成本范围内从某点出发可获得的机会数量作为可达性指标。例如, 在研究区域栅格化的基础上, 综合考虑设施等级和特征, 对公共服务设施的可达性进行评价, 计算公式[28]如下:
Ai 表示区域 i 的可达性, t 表示可获得服务范围的出行成本, Ojt 表示范围 t 内区域 j 的居民可获得的机会数量, j 是区域 i 内出行成本小于 t 的区域。累计机会法在距离法的基础上考虑了供给点规模, 即不同类型公共服务设施的服务半径存在差异, 也就是承认居民对不同公共服务设施的出行意愿存在差异[30]。
2)等值线法: 对出行成本进行进一步分级, 按照分级后的成本, 分别累计可获得的机会数量, 数量越多, 可达性越好。在实际研究中, 可以根据需要选取不同的等值线(如扩散等时线等)作为研究对象来观察可达性情况[31]。
累计机会法和等值线法这两种机会累积模型本质上还是通过需求点的交通出行便捷程度来衡量可达性, 虽然将供给点规模纳入考虑范畴, 但对空间边界的选择带有主观性, 计算结果可能存在较大的误差; 同时, 该类模型未考虑距离衰减和需求点规模, 且默认所有机会点的吸引力相同, 忽略了需求的多样性[32]。
2.3.3空间相互作用模型
空间相互作用模型从空间相互作用角度定义公共服务设施可达性, 即需求点(人)与供给点(公共服务设施)之间的相互影响或作用潜力, 两点之间的相互作用力越大, 可达性越高。这一类度量方法与基于机会累积的方法同属较高应用层次, 但进一步考虑了供需点间的相互作用力和距离衰减因素, 更符合实际情况, 在可达性的度量评价中应用最广泛, 发展出潜能模型、两步移动搜索法和胡弗(Huff) 模型等。
1)潜能模型, 又称势能模型、重力模型, 最初是法国学者拉格朗日在牛顿力和能的基础上提出的, 后来被引入地理学中, 逐步发展成潜能模型。Hansen[2]首次采用该模型来度量工作地的可达性。潜能模型结合供需点间的相互作用力与空间效应随距离而衰减的特征来衡量可达性, 两点间的力越大, 距离越小, 可达性越高。因此, 潜能模型中距离衰减函数的确定是衡量可达性的关键。同时, 由于潜能模型的适应性较好, 距离衰减函数的可变性较强, 在实际应用中需根据具体研究需求, 进一步确定模型、参数和研究尺度[7]。潜能模型的计算公式[28] 如下:
其中, Ai 表示 n 个地点对点 i 产生的总潜力值, Dj 表示区域 j 的机会, tij 表示点 i 与 j 间的出行阻抗, α 为摩擦系数。
与距离法和累计机会法等模型相比, 潜能模型考虑的因素较为全面, 模型的适应性强, 目前已有诸多学者对其进行不同侧面的改进。例如, 汤鹏飞等[33]在判别农村居民点和乡村小学空间布局合理性的研究中, 通过引入学校服务能力因子, 综合考虑设施规模、居民行为选择和极限出行时间, 对潜能模型进行针对性的改进, 使模型更适用于度量县域范围的基础教育设施可达性。目前, 潜能模型及其扩展形式已广泛应用于公共服务设施的可达性评价, 但存在计算繁琐、距离衰减函数适用性差异大以及容易夸大可达性较低地区的可达性等缺陷, 这是该模型需要重点改进的方面。
2)两步移动搜索法。移动搜索法是潜能模型的重要扩展, 该方法由 Radke 等[34]于 2000 年提出, Luo 等[35]于 2003 年进行改进, 并将其命名为两步移动搜索法(two-step floating catchment area method, 2SFCA)。2SFCA 的实现方式如下: 对供给点与需求点预先设定极限出行成本(距离或时间), 分别以供需两点为基础, 以各自的极限出行成本为搜索半径(即搜索阈值), 完成两次搜索, 计算半径范围内可获得的设施数量, 数量越多, 可达性越高[36]。
经典的 2SFCA 方法由两个步骤组成: 第一步, 如式(9)[37]所示, 通过将设施 i 的容量 Si 除以特定区域内每个需求点的总人口数 d0, 计算得到设施 i 的供需比 Ri; 第二步, 如式(10)[37]所示, 将第一步导出的同一区域 d0 内的供需比 Ri 相加, 测度需求点 j的可达性 Aj。两步均通过衰减函数 f(dij)引入距离衰减效应, 其中 dij 为点 i 与 j 之间的距离。
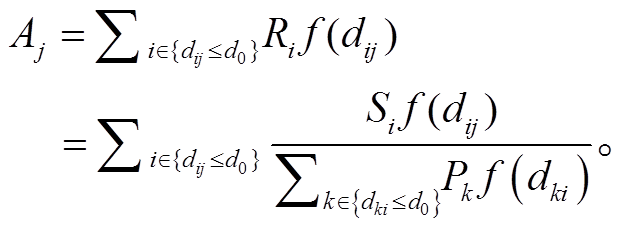 (10)
(10)
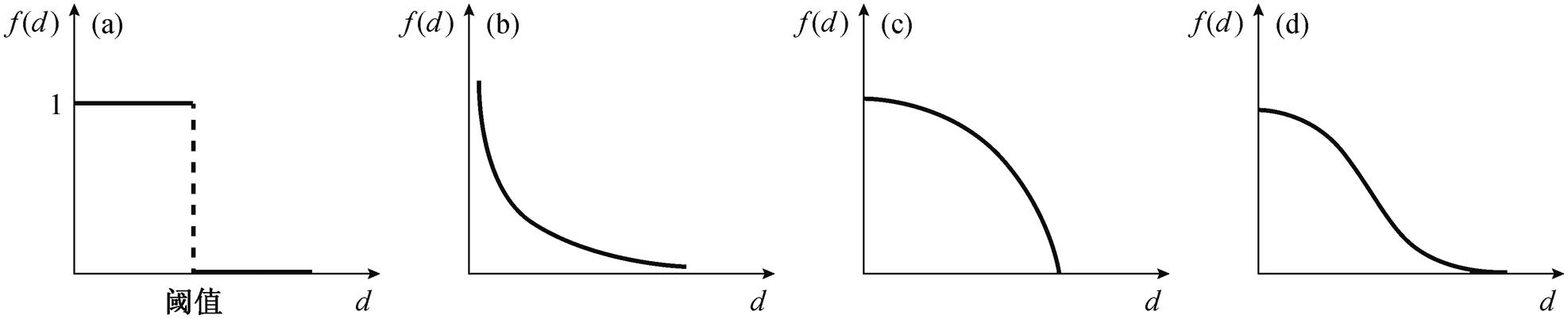
2SFCA 和潜能模型同属一个理论框架, 均考虑了供需点规模和供需两点间的空间作用力, 不同之处在于对距离的处理: 2SFCA 最初采用两分法, 即阈值范围内可达性相同, 阈值范围外可达性为零(图 1(a)); 潜能模型采用连续型距离衰减函数(图1(b)), 考虑供给点吸引力随距离而衰减的特征, 但是未设定出行极限[39]。由于考虑的因素相对全面, 2SFCA 在近期的公共服务设施可达性研究中应用愈加广泛, 陶卓霖等[38]将近年来国内外两步移动搜索法的扩展形式归纳为 4 种类型 14 种方式, 包括针对距离衰减函数(图 1(c)和(d))、搜索阈值、供需关系以及出行方式等方面的扩展。Gong 等[37]同时从距离衰减和设施规模分级半径这两个角度对两步移动搜索法进行改进, 以便对比单一有效服务半径与按规模分级的服务半径两种情形下公共服务设施的可达性。近年来,Alford-Teaster 等[40]进一步扩展两步移动搜索法, 提出宽带网络环境下远程医疗可达性度量的 2SVCA 模型以及基于度量供给点潜在拥挤度的 i2SFCA 模型[41], 并基于扩展的胡弗模型, 将 2SFCA 和 i2SFCA 集成到同一个概念框架中。与潜能模型相比, 2SFCA 的优点在于计算相对简便, 且更易于理解。Luo 等[42]针对早期的二进制结构限制和没有考虑距离衰减的问题, 提出增强的 2SFCA (E2SFCA), 在可达性计算中添加距离衰减权重, 通过采用不同形式的连续或分段函数(如负线性形式、指数形式、高斯形式和核密度形式等[37]), 解决了距离摩擦效应不足的问题, 获得更好的结果。
3)胡弗模型。潜能模型是通过供需点间的空间作用力来描述设施规模的竞争效应, 但忽略了居民行为选择的影响。Huff [43]在潜能模型的基础上提出能综合反映供给点规模、行为选择和距离因子的概率模型。最初的胡弗模型仅以设施面积作为供给点的规模因子, 然而, 设施的吸引力还可能来自服务质量和服务特色等方面, 于是 Nakanishi 等[44]提出适用范围更广的模型改进式。胡弗模型认为“任何一个设施对所有的空间区域都有服务功能, 只是访问一个服务设施的概率有大有小”[45], 其计算公式[43]如下:
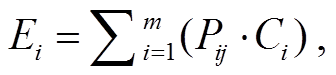 (12)
(12)
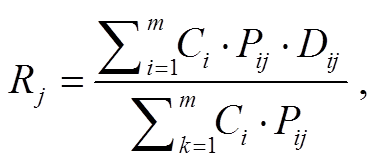 (13)
(13)
其中, Pij 为需求点 i 访问服务设施 j 的概率, Ej 为服务设施 j 的预期访问量, Ci 为需求点 i 的人口数, m 为需求点总数, Rj 为设施服务半径。
胡弗模型的实现步骤如下: 首先利用潜能模型计算供需点相互作用力影响下的空间可达性, 然后计算需求点到供给点的概率和供给点的潜在服务人数[46]。潜在服务人数越多, 供给点的供给压力越大, 可达性越低。胡弗模型最早应用于商业领域, 常用于计算商场集中区域居民选择某一商场的概率, 由此可以计算出商业设施的潜在服务人数, 为设施的空间布局提供依据。改进后的模型应用范围增大, 如 Lin 等[47]在空间相互作用模型基础上提出引力空间边界框架, 通过在 GIS 平台建立以胡弗模型为基础的引力多边形服务域算法, 将其应用于火车站停车换乘的空间布局研究。最终的胡弗模型综合考虑供给点规模、空间行为选择因素和距离因素, 但未考虑需求点规模[48]。
3 可达性度量方法比较
综上所述, 基于数理统计、基于拓扑网络和基于几何网络的三类常用公共服务设施可达性度量方法, 其原理、方法与适用情况各不相同(表 4)。基于数理统计的统计分析法在近年研究中的应用频率逐步降低; 基于拓扑网络的方法中以空间句法的应用居多, 但由于适用的空间尺度不同, 在城市尺度的公共服务设施可达性研究中应用较少[49]; 基于几何网络的方法则更多地应用于城市公共服务设施的可达性研究。同时, 潜能模型和两步移动搜索法等基于空间相互作用的方法考虑因素更全面, 能更准确地模拟现实环境, 其模型所需数据问题也因大数据的发展得到更好的解决。
表4 常用的公共服务设施可达性评价方法比较
Table 4 Comparison of commonly used evaluation methods for the accessibility of public service facilities
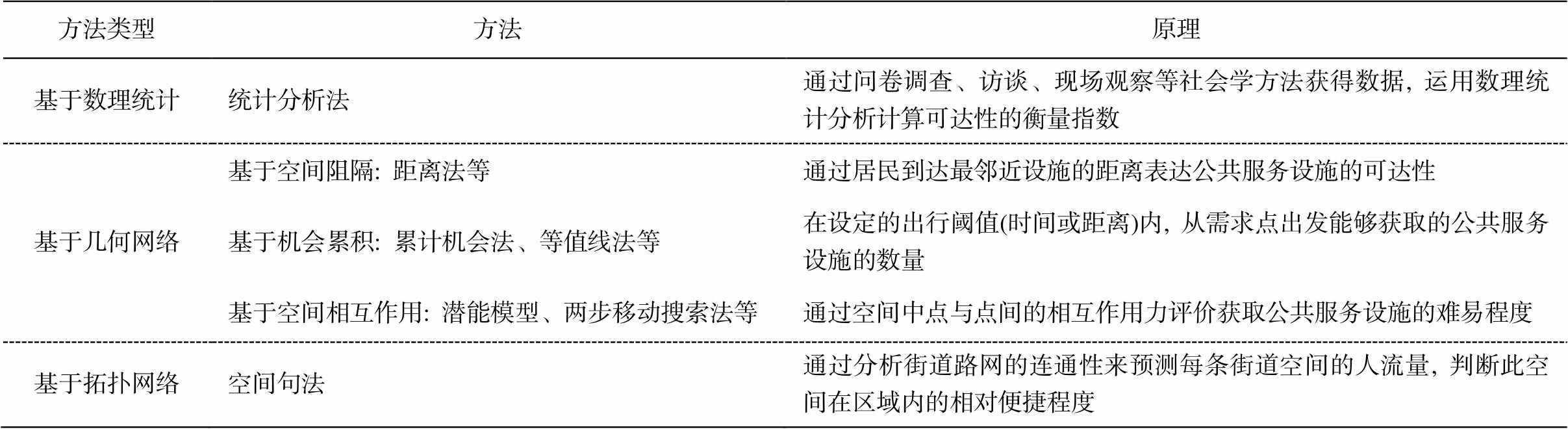
方法类型方法原理 基于数理统计统计分析法通过问卷调查、访谈、现场观察等社会学方法获得数据, 运用数理统计分析计算可达性的衡量指数 基于几何网络基于空间阻隔: 距离法等通过居民到达最邻近设施的距离表达公共服务设施的可达性 基于机会累积: 累计机会法、等值线法等在设定的出行阈值(时间或距离)内, 从需求点出发能够获取的公共服务设施的数量 基于空间相互作用: 潜能模型、两步移动搜索法等通过空间中点与点间的相互作用力评价获取公共服务设施的难易程度 基于拓扑网络空间句法通过分析街道路网的连通性来预测每条街道空间的人流量, 判断此空间在区域内的相对便捷程度
由于研究者对可达性定义的不同以及研究对象的差异, 影响可达性的因素相应地不同, 因此需要有针对性地选择可达性度量方法。从前面对常用公共服务设施可达性度量方法的分析可以看出, 不同的度量模型有其自身的适用性(表 5), 研究者在选择模型时, 需综合考虑所采用的方法能否反应可达性影响因素的变化和差异以及模型所需数据是否易于获取等条件。
1)基于空间阻隔的方法: 通过居民到达最邻近设施的距离表达公共服务设施的可达性。这种方法计算简便, 易于实现, 是其他模型发展的基础。但是, 随着城市的发展, 交通出行愈加便捷, 距离对居民出行的影响减弱, 其他因素对可达性的影响权重相应地提升, 导致此类方法的应用领域不断 缩小[16]。
2)基于机会累积的方法: 在设定的出行阈值(时间或距离)内, 从需求点出发能够获取的公共服务设施的数量。这种方法强调某点在一定范围内所能获得的机会累积量, 在距离法的基础上考虑供给点的位置和规模, 但忽略距离衰减、需求点规模和供需双方间相互作用力的影响, 使得其应用范围较为有限, 模型阈值的确定是这类方法的难点。
表5 常用的公共服务设施可达性度量模型比较
Table 5 Comparison of commonly used common service facility accessibility measurement models

方法类型方法度量指标优缺点文献 基于空间阻隔最小邻近距离法节点之间的出行障碍或阻力, 包括: 物理(欧式)/网络距离、出行时间/成本、服务质量数据易获得, 计算简便, 直观易懂, 适合宏观层面的可达性评价; 距离测量方式的选择对结果有影响, 缺少对供需点规模等其他因素的考虑[27‒50] 费用加权距离法[29] 基于机会累积累计机会法在节点周围绘制一个或多个出行成本等值线定义分区, 测量每个等值线内机会数计算简便, 数据要求低, 在距离法的基础上考虑了不同类型设施的服务半径差异; 不能区分活动和行程目的, 忽略了距离衰减和需求点规模等因素[51‒52] 等值线法[31] 基于空间相互作用潜能模型通过测量连续尺度上的出行阻抗来定义可达性区域综合考虑了距离衰减以及供需点规模等多种因素; 计算繁琐, 衰减函数的确定有较强的主观性, 可达性较低区域的可达性值容易被夸大, 且未对临界时间/距离进行界定[5,33] 两步移动搜索法分别以供给和需求点为基础进行两次搜索, 计算半径范围内可获得设施数量计算相对简便, 综合考虑了供需点规模等多种因素; 忽略了距离衰减, 且未对临界时间/距离进行界定[40,53] 胡弗模型通过设施引力和距离阻力两个要素计算居住地去往特定设施的出行概率在潜能模型的基础上综合考虑了设施规模、空间选择行为和距离衰减, 可以计算出需求点选择特定供给点的概率; 计算复杂, 可解释性低, 且未考虑需求点规模[54]
3)基于空间相互作用的方法: 通过空间中点与点间的相互作用力来评价获取公共服务设施的难易程度, 在近年来的可达性评价研究中应用最广泛。由于考虑的因素较为全面(同时考虑了交通因素、距离衰减、供需点规模及两者之间的相互作用力等因素), 能较好地体现居民选择公共服务设施的一般行为规律, 更全面地度量居民获取公共服务的难易程度。但是, 此类方法的计算较为繁琐, 较难理解, 同时模型中一些参数(如潜能模型中的距离衰减系数)的确定具有较强的主观性, 可能对可达性的度量结果造成不良影响。
总体而言, 针对可达性度量问题, 简单模型容易分析和理解, 但由于无法捕捉可达性的不同方面, 有时不准确。考虑因素较全面的模型中纳入可达性的不同变量和测度, 不仅增加模型的复杂性, 也影响其实用性(对很多研究者来说, 清晰易读的方法至关重要[55])。方法学当前的主要任务之一是在理论与经验合理的指标与简单指标之间找到适当的平衡[56], 以便更有效地使用。在未来一段时期, 开发一个统一的可达性理论和测量方法仍然是研究人员和公共服务设施规划者的一项艰巨任务[57]。从近 5年的研究成果来看, 数学模型结合 GIS 进行可达性评价的方法越来越受到重视, 其中两步移动搜索法和潜能模型两种方法及其改进形式逐渐成为公共服务设施可达性研究的常用方法。
在传统的测度方法之外, 近期的研究通过引入辅助概念(如时空可达性、虚拟可达性、积极和规范的可达性以及公平的可达性[6]), 为可达性定义增加了更多的维度。传统的可达性模型通常只关注到达目的地的单一路径(即假设所有出行者都有相似的目标, 并做出到达目的地的最佳选择), 不反映出行者对设施及路线选择的偏好或随机性。然而, 情况并非总是如此。近期的研究表明, 个体出行行为在决定设施可达性和可用性方面起着至关重要的作用, 越来越多的研究者使用将人员流动模式(如老龄化人口、通勤者以及低收入群体等[58‒60])纳入特定个人特征来改善传统的可达性方法, 从而有助于理解不同的公共服务设施用户群体对交通出行的看法, 帮助研究人员和从业者找到改善不同人群可达性的最佳政策。研究结果显示, 应用效用模型来捕捉出行者行为的随机性和交通网络的负数用, 可以从出行者的角度更好地理解出行阻抗[61]。
此外, 随着信息和通信技术的不断发展, 大数据时代下海量数据的获取也为可达性度量方法指明新的发展方向, 各类开放地图网站、导航公司、共享出行公司、通信公司以及交通管理部门提供的移动定位和社交网络等多种类型大数据, 内含信息丰富, 不仅为各种模型的应用提供了更大的平台, 也可以弥补度量方法的某些缺陷, 为建立具有越来越高时空分辨率的可达性定义、方法和模型提供了可能性。例如, 为潜能模型等空间相互作用模型提供了以前较难获得的供需点规模数据, 从而实现更精确的可达性度量。同时, 可大规模获取的城市流量数据也实现了空间句法从城市微观层面到中微观层面的应用转型。随着遥感技术和机器学习工具的进步, 卷积神经网络等方法开始使用开放式街道图像平台(如谷歌、百度街景图像)来测量基于街道网络和设计的可达性问题。
Aviral 等[14]认为, 可达性度量方法最新的 3 个显著进步是使用机器学习工具度量街道形态、使用基于网络的地图软件和基于位置的数据精确度量出行和活动位置以及计算基于活动测度的时间变化。
4 结束语
可达性是城市公共服务设施选址布局的重要参考原则。随着近年来学术领域的广泛关注, 公共服务设施的可达性度量方法已经逐渐形成较为完整的体系。由于可达性是一个多维度概念, 找到能够准确地捕捉所有公共服务设施可达性组成部分的测度方法相对困难。因适用范围不同, 既有的方法在实际应用中存在一些不足, 即使应用频率最高的空间相互作用模型, 也由于忽略影响可达性的个体差异和时间因素而具有一定的局限性。此外, 笼统地将某单一公共服务设施规模信息作为吸引力指标, 也会导致结果出现误差。因此, 根据研究需求规避模型的缺陷而采用合适的方法, 依然是可达性研究的重点之一。
随着数据时代的到来, 城市研究与社会生活面临变革。一方面, 新数据技术的涌现为可达性度量方法的进一步发展和完善提供了可能性; 另一方面, 互联网生活深入社会各个方面, 物理环境对人的约束性逐渐消减, 进而影响着居民对公共服务设施的选择。当前, 全球对公共服务设施可达性的研究仍处在不断发展的过程中, 仅仅针对路网等因素进行相关评价已经不能满足研究需求, 结合新数据技术、社会心理和人类行为等因素的可达性度量方法的改进与探索值得期待。
参考文献
[1] 约翰斯顿R J. 人文地理学词典. 柴彦威, 译. 北京:商务印书馆, 2004
[2] Hansen W G. How accessibility shapes land use. Jour-nal of the American Planning Association, 1959, 25 (2): 73‒76
[3] 彭科. 空间可达性衡量方法评述. 城市规划, 2017, 41(11): 72‒79
[4] Geurs K T, Ritsema J R. Accessibility measures: re-view and applications. Evaluation of accessibility im-pacts of land-use transportation scenarios, and related social and economic impact [R]. Utrecht: Utrecht University, 2001
[5] 宋正娜, 陈雯, 张桂香, 等. 公共服务设施空间可达性及其度量方法. 地理科学进展, 2010, 29(10): 1217‒1224
[6] Shi Y, Blainey S, Sun C, et al. A literature review on accessibility using bibliometric analysis techniques. Journal of Transport Geography, 2020, 87: 102810
[7] 陈洁, 陆锋, 程昌秀. 可达性度量方法及应用研究进展评述. 地理科学进展, 2007, 26(5): 100‒110
[8] Zhao Y, Zhang G, Lin T, et al. Towards sustainable urban communities: a composite spatial accessibility assessment for residential suitability based on net-work big data. Sustainability, 2018, 10(12): 1‒18
[9] Guy C M. The assessment of access to local shopping opportunities: a comparison of accessibility measures. Environment and Planning B: Urban Analytics and City Science, 1983, 10(2): 219‒238
[10] Geneviève B, El-Geneidy A M. The insider: a plan-ners’ perspective on accessibility. Journal of Trans-port Geography, 2017, 64(10): 33‒43
[11] Lee H Y. Accessibility and location choice: innova-tions in measurement and modeling [D]. Seattle: Uni-versity of Washington, 2009
[12] Mavoa S, Witten K, McCreanor T, et al. GIS based destination accessibility via public transit and wal-king in Auckland, New Zealand. Journal of Transport Geography, 2012, 20(1): 15–22
[13] Geurs K T, van Wee B. Accessibility evaluation of land-use and transport strategies: review and research directions. Journal of Transport Geography, 2004, 12 (2): 127‒140
[14] Aviral M, Elisabete S. Literature review of acces-sibility measures and models used in land use and transportation planning in last 5 years. Journal of Geographical Science, 2022, 32(3): 560‒584
[15] Delmellea E C, Casas I. Evaluating the spatial equi- ty of bus rapid transit-based accessibility patternsin a developing country: the case of Cali, Colombia. Transpot Policy, 2012, 20: 36‒46
[16] 王丽娟. 城市公共服务设施的空间公平研究——以重庆市主城区为例. 昆明: 云南大学出版社, 2016
[17] Hunter E, MacNamee B, Kelleher J D. A comparison of agent-based models and equation based models for infectious disease epidemiology // AICS. Dublin, 2018: 33–44
[18] Wheeler D C, O’Kelly M E. Network topology and city accessibility of the commercial internet. Profe-ssional Geographer, 1999, 51(3): 327‒339
[19] Xu W T, Zhang W, Li L. Measuring the expected locational accessibility of urban transit network for commuting trips. Transportation Research Part D, 2017, 51(3): 62‒81
[20] 汪明峰, 宁越敏. 城市的网络优势——中国互联网骨干网络结构与节点可达性分析. 地理研究, 2006, 25(2): 193‒203
[21] Hillier B, Hanson J. The social logic of space. Cam-bridge: Cambridge University Press, 1984
[22] Khalesian M, Pahlavani P, Delavar M R. A GIS-based traffic control strategy planning at urban intersec-tions. International Journal of Computer Science & Network Security, 2009, 9(1): 166‒174
[23] Alitajer S, Nojoumi G M. Privacy at home: analysis of behavioral patterns in the spatial configuration of traditional and modern houses in the city of Hamedan based on the notion of space syntax. Frontiers of Architectural Research, 2016, 5(3): 341‒352
[24] Alkamali N, Alhadhrami N, Alalouch C. Muscat city expansion and accessibility to the historical core: space syntax analysis. Energy Procedia, 2017, 115: 480–486
[25] Badhan I M. Space syntax analysis: tracing the rationale for accessibility of recreational/movement economy growth along Hatirjheel Lake Park through integration and connectivity. International Journal of Scientific & Engineering Research, 2019, 10(10): 1197–1206
[26] Lee S, Yoo C, Seo K W. Determinant factors of pedestrian volume in different land-use zones: com-bining space syntax metrics with gis-based buil-tenvironment measures. Sustainability, 2020, 12(20): 8647
[27] 曾文, 向梨丽, 张小林. 南京市社区服务设施可达性的空间格局与低收入社区空间剥夺研究. 人文地理, 2017, 32(1): 73‒81
[28] 陆化普, 王继峰, 张永波. 城市交通规划中交通可达性模型及其应用. 清华大学学报(自然科学版), 2009, 49(6): 781‒785
[29] 陈秋晓, 侯焱, 吴霜. 机会公平视角下绍兴城市公园绿地可达性评价. 地理科学, 2016, 36(3): 375‒383
[30] 李然好, 龚世泽, 高勇. 北京市公共服务设施可达性及其对住房价格的影响. 北京大学学报(自然科学版), 2021, 57(5): 875‒884
[31] 张鲜鲜, 李久生, 赵媛, 等. 南京市高级中学可达性及空间分布特征研究. 测绘科学, 2015, 40(11): 111‒114
[32] Yoshida N, Deichmann U. Measurement of accessibi-lity and its applications. Journal of Infrastructure De-velopment, 2009, 1(1): 1‒16
[33] 汤鹏飞, 向京京, 罗静, 等. 基于改进潜能模型的县域小学空间可达性研究——以湖北省仙桃市为例. 地理科学进展, 2017, 36(6): 697‒708
[34] Radke J, Mu L. Spatial decompositions, modeling and mapping service regions to predict access to social programs. Geographic Information Sciences, 2000, 6 (2): 105‒112
[35] Luo W, Wang F. Measures of spatial accessibility to health care in a GIS environment: synthesis and a case study in the chicago region. Environment & Plan-ning B, 2003, 30(6): 865‒884
[36] Wang F. Measurement, optimization, and impact of health care accessibility: a methodological review. Annals of the Association of American Geographers, 2012, 102(5): 1104‒1112
[37] Gong S, Gao Y, Zhang F, et al. Evaluating healthcare resource inequality in Beijing, China based on an improved spatial accessibility measurement. Transac-tions in GIS, 2021, 25(3): 1504‒1521
[38] 陶卓霖, 程杨. 两步移动搜寻法及其扩展形式研究进展. 地理科学进展, 2016, 35(5): 589‒599
[39] Liu M, Jiang Y. Measuring accessibility of urban scales: a trip-based interaction potential model. Ad-vanced Engineering Informatics, 2021, 48(4): 101293
[40] Alford-Teaster J, Wang F, Tosteson A, et al. Incor-porating broadband durability in measuring geogra-phic access to health care in the era of telehealth: a case example of the 2-step virtual catchment area (2SVCA) method. Journal of the American Medical Informatics Association, 2021, 28(11): 2526‒2530
[41] Wang F. From 2SFCA to i2SFCA: integration, deriva-tion and validation. International Journal of Geogra-phical Information Science, 2021, 35(3): 1‒11
[42] Luo W, Qi Y. An enhanced two-step floating catch-ment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health & Place, 2009, 15(4): 1100‒1107
[43] Huff D L. A probabilistic analysis of shopping center trading area. Land Economics, 1963, 39(1): 81‒89
[44] Nakanishi M, Cooper L G. Parameter estimate for multiplicative interactive choice model: least squares approach. Journal of Marketing Research, 1974, 11: 303‒311
[45] 王远飞, 张超. GIS和引力多边形方法在公共设施服务域研究中的应用——以上海浦东新区综合医院为例. 经济地理, 2005, 25(6): 800‒803
[46] Huff D, Mccallum B M. Calibrating the Huff model using ArcGIS business analyst. ESRI White Paper. Redlands: ESRI Inc, 2008
[47] Lin T G, Xia J C, Robinson T P, et al. Enhanced huff model for estimating park and ride (PnR) catchment areas in Perth, WA. Journal of Transport Geography, 2016, 54(6): 336‒348
[48] Nir K, David B, Itzhak O. The spatial organization of accessibility and functional hierarchy: the case of Israel. Computers, Environment and Urban Systems, 2020, 80(3): 101429
[49] 杨滔. 基于空间句法的多尺度空间结构. 城市设计, 2018(2): 22‒31.
[50] Farber S, Bartholomew K, Xiao L, et al. Assessing social equity in distance based transit fares using a model of travel behavior. Transportation Research Part A Policy and Practice, 2014, 67: 291–303
[51] El-Geneidy A, Levinson D, Diab E, et al. The cost of equity: assessing transit accessibility and social disparity using total travel cost. Transportation Re-search Part A Policy & Practice, 2016, 91: 302‒316
[52] 湛东升, 谢春鑫, 张文忠, 等. 基于累计机会可达性的北京城市公共服务设施复合功能识别. 地球信息科学学报, 2020, 22(6): 1320‒1329
[53] 柳泽, 杨宏宇, 熊维康, 等. 基于改进两步移动搜索法的县域医疗卫生服务空间可达性研究. 地理科学, 2017, 37(5): 728‒737
[54] 王远飞, 张超. GIS和引力多边形方法在公共设施服务域研究中的应用——以上海浦东新区综合医院为例. 经济地理, 2005(6): 800‒803
[55] Scheurer J, Curtis C. Accessibility measures: over-view and practical applications [R]. Working Paper No. 4, Impacts of Transit Led Development in a New Rail Corridor. Perth: Curtin University, 2007
[56] Bertolini L. Sustainable urban mobility, an evolution-nary approach. European Spatial Research and Policy, 2005, 12(1): 109‒125
[57] Handy S. Is accessibility an idea whose time has fi-nally come?. Transportation Research Part D: Tran-sport and Environment, 2020, 83: 102319
[58] Horner M W, Duncan M D, Wood B S, et al. Do aging populations have differential accessibility to active-ties? analyzing the spatial structure of social, profess-sional, and business opportunities. Travel Behav Soc, 2015, 2(3): 182–191
[59] Wang D, Chai Y. The jobs-housing relationship and commuting in Beijing, China: the legacy of Danwei. J Transp Geogr, 2009, 17: 30–38
[60] Morency C, Páez A, Roorda M J, et al. Distance traveled in three canadian cities: spatial analysis from the perspective of vulnerable population segments. J Transp Geogr, 2011, 19(1): 39–50
[61] Malekzadeh A, Chung E. A review of transit accessi-bility models: challenges in developing transit acces-sibility models. International Journal of Sustainable Transportation, 2020, 24(9): 238–250
A Review on Accessibility Measurements of Public Service Facilities
GAO Wei1, OUYANG Yuxin2, ZHAO Mei3,†, GAO Yong4, MENG Haohan4
1. School of Architecture and Design, Beijing Jiaotong University, Beijing 100044; 2. Beijing Urban Construction Design & Development Group co. Limited, Beijing 100034; 3. School of Design and Art, Beijing Institute of Technology, Beijing 100081; 4. School of Earth and Space Sciences, Peking University, Beijing 100871; † Corresponding author, E-mail: zhaomei@bit.edu.cn
Abstract Based on the three levels of mathematical statistics, topological network and geometric network, the accessibility measurements on public service facilities in existing studies are teased, and the fundamental principles, metrics, range of applicability, the advantage and disadvantage of these different measurements are reviewed. It is pointed out that current methodological task is to find the right balance between a measure that is theoretically and empirically sound and one that is sufficiently plain, and emergence of new data technologies provides a new direction for accessibility measurements.
Key words public service facilities; accessibility; measurements



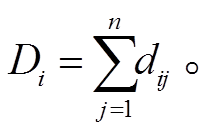 (2)
(2)
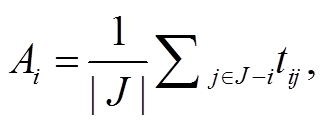 (6)
(6)
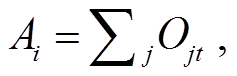 (7)
(7)
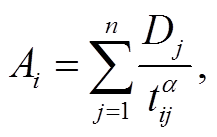 (8)
(8)
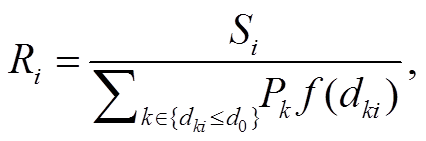 (9)
(9)
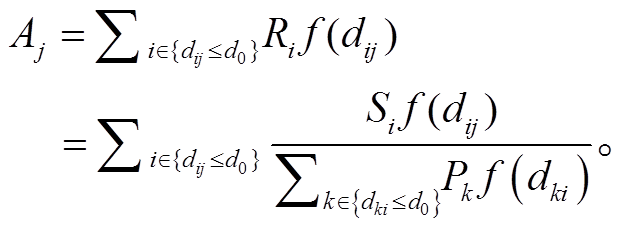 (10)
(10)
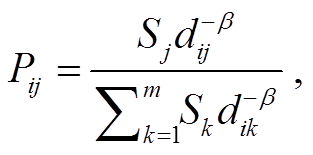 (11)
(11)
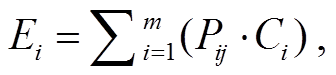 (12)
(12)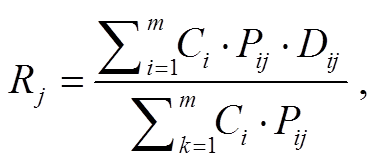 (13)
(13)
