(1)
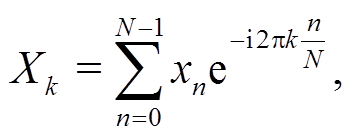
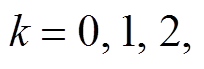
北京大学学报(自然科学版) 第59卷 第2期 2023年3月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 2 (Mar. 2023)
doi: 10.13209/j.0479-8023.2022.098
国家重点研发计划(2020YFB1314000)资助
收稿日期: 2022–03–13;
修回日期: 2022–04–06
摘要 在工业领域, 设备运行过程中采集的原始故障信号具有强噪声以及多工况的特点, 现有的基于数据的轴承故障诊断模型的抗噪能力与泛化能力相对较弱。针对以上问题, 提出一种基于频域降采样(down-sampling)和卷积神经网络(CNN)的轴承故障诊断方法 Ds-CNN。频域降采样包含最大偏移降采样和噪声横截断两个部分, 可以实现样本增强, 降低样本在频域的差异性, 同时减弱噪声对频域信号的影响。基于频域信号建立的CNN模型能够自动提取降采样后频域信号的故障特征, 并完成对轴承故障的识别分类。实验结果表明, 在强噪声环境和多工况条件下, 与目前常用模型相比, Ds-CNN 具有更高的识别准确率。
关键词 轴承故障诊断; 深度学习; 卷积神经网络(CNN); 强噪声; 多工况
随着现代工业和传感器监测技术的迅速发展, 工业生产过程中可以获得大量的设备传感器数据。挖掘这些数据包含的有价值的信息是智能故障诊断的重要任务, 也是当前研究的热点内容[1]。旋转机械设备广泛应用于工业领域, 作为其关键部件, 轴承是最容易损坏的部件之一[2]。轴承故障会导致大型旋转机械设备停机, 造成巨大的经济损失, 甚至危及工作人员的生命安全。精准有效的轴承故障诊断对实现旋转机械设备的智能化、提高设备运行的可靠性具有重要意义。
大数据时代, 采用基于数据的智能故障诊断方法实现设备故障的自诊断、自识别是大势所趋[3]。对于轴承的故障诊断, 常采用传感器采集的振动信号作为信号源, 对采集的信号进行特征提取和状态识别。常用的信号特征提取方法有小波分析[4–5]、傅里叶变换(Fast Fourier Transform, FFT)[6]和经验模态分解(empirical mode decomposition, EMD)[7]等。状态识别过程中, 一般采用人工智能方法识别提取特征中的故障信息, 实现故障自动诊断, 常用的方法有人工神经网络(artificial neural networks, ANN)[8]以及支持向量机(support vector machine, SVM)[9]等。
近年来, 人工智能渗入各个研究领域, 与传统浅层机器学习方法相对应的深度学习方法也在轴承故障诊断方面取得广泛的应用, 如卷积神经网络(convolutional neural network, CNN)[10]、深度信念网络(deep belief network, DBN)[11]、堆栈自编码器(stacked auto encoder, SAE)[12]和长短期记忆(long short term memory, LSTM)[13]等。这些基于深度学习的轴承故障诊断方法都取得很好的成果, 但在环境复杂的工业生产中, 仍需要考虑以下问题。1)强噪声环境: 由于生产环境恶劣, 不可避免地使传感器采集的数据包含噪声, 有必要研究模型的抗噪性能。2)多工况条件: 设备作业环境多变, 导致设备运转工况变化大, 目前轴承故障诊断中采用数据驱动的算法大多数仅适用于单一工况下的故障识别分类, 模型的泛化能力弱, 需要考虑变负载对故障诊断模型的影响。
现有研究采用的故障信号输入类型有时域、频域和图像[14–15]等, 诊断模型从不同类型信号中获取的故障信息不同[16]。相对于大多数基于时域信号的诊断分类模型, 本文根据振动信号在频域的变化规律, 考虑频域受噪声影响更小的特点, 提出一种基于频域降采样(Down-sampling)和 CNN 的故障诊断方法(Ds-CNN)。频域降采样方法包括最大偏移降采样和噪声横截断两个部分, 能够降低不同环境下样本之间的差异性。在此基础上搭建的基于频域信号的 CNN 模型可以实现对轴承故障的自动识别和分类, 在强噪声环境和多工况条件下依然保持高识别率。
快速傅里叶变换(FFT)是一种高效快速计算的离散傅里叶变换(DFT)算法, 可以将信号从时域变换到频域。有限长度离散信号 X(n) (n=0, 1, 2, …, N-1)的 DFT 可以定义为
(1)
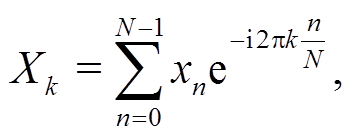
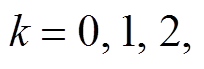
采用 FFT 算法时, 需要满足采样定理, 要求采样频率 fs.max必须大于信号中最高频率 fmax的两倍(fs.max > 2fmax), 从而防止频谱混叠。此外, 当时域信号进行 FFT 变换时, 无论取几个点(
值), 用于分析的频率范围都由采样频率 fs.max决定。如果取N 个点进行 FFT, 变换后相邻两个点之间的频率间隔为f s.max/N。第 
个点的频率为 k(fs.max/N), k=0, 1, 2, …, N-1。这N个点的值是对称的, 所以实际上只使用N/2个点。在采样频率不变时, 为了提高频谱分辨率, 需要延长采样数据的长度, 间接地降低频谱泄漏的影响。
作为深度学习的一种重要方法, 卷积神经网络(CNN)在语音和图像处理方面都得到重要的应用。一般而言, CNN 由卷积层、池化层和全连接层构成, 输入数据的特征提取由卷积层和池化层实现, 全连接层主要负责分类。
在卷积层, 用一组的卷积核对输入信号进行卷积运算, 每个卷积核用于提取局部输入信号的特征。通过以固定的步长滑动卷积核, 并对新的感受区域重复卷积运算, 得到由单个卷积核提取的输入信号特征, 此过程中卷积核的权值是共享的。每个卷积核对应的特征图可以通过激活函数得到。卷积运算的过程描述如下:
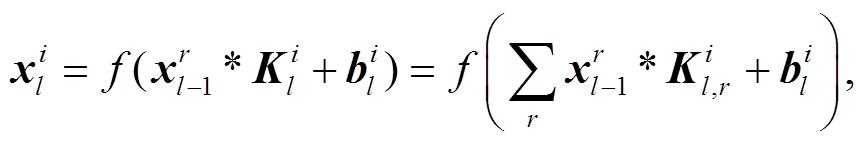(2)
其中,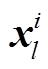 
是卷积层 l 第 i 个输出的特征图, f(·)是非线性激活函数, 
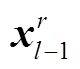是卷积层 l-1 生成的特征图的第 r个卷积区域, 
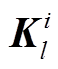是卷积层 l第 i 个卷积核的权重矩阵, 
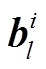是偏置值。在CNN中, 修正线性单元(ReLu)常用于激活单元增加表达能力, ReLu 函数表达式 如下:
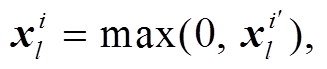(3)
其中,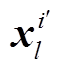 
是卷积层 l第 i 个卷积核未经过非线性激活的输出。通常, 每个卷积层后会增加一个池化层, 用于生成更低维度特征图, 最大池化层(max-pooling layer)可以取一定区域内特征的最大值作为输出。最大池化的表达式如下:
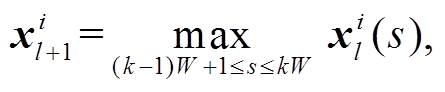(4)
其中,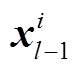 
是最大池化层的输出, 
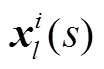代表池化区域中的第s个值, 
是池化区域的宽度。最后采用全连接层对之前提取的特征进行整合和分类, 并用 Softmax 函数将全连接层最后神经元的输出转化为概率:
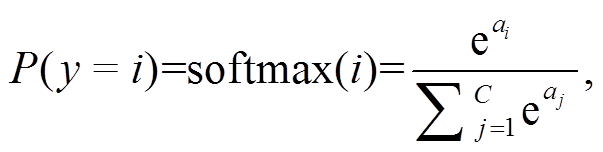(5)
其中,P(y=i)是第 i 个类别的概率(1≤i≤C), C 是类别数, ai是全连接层最后神经元输出的第 i 个值。
基于频域降采样和 CNN 的故障诊断方法(Ds-CNN)框架如图 1 所示。在训练阶段, 首先将训练集的原始振动信号通过 FFT 转换至频域, 采用最大偏移降采样的方式对频域信号进行降维处理和样本增强, 随后输入 CNN 中对模型进行训练。在测试阶段, 对于有噪声或变工况的测试样本, 将其转换至频域后进行最大降采样和噪声横截断处理, 最后将其输入已训练好的 CNN 模型中, 识别测试样本的故障类别。
FFT 可以将信号从时域转换到频域, 能够更清楚地观察信号的特性。与时域信号相比, 频域信号受噪声的影响较小, 并且频谱中的峰值能更好地表征故障特征。我们在 20201 年的研究中指出频谱的变化规律, 即当工况条件发生改变时, 频谱会发生横向偏移, 当信号受到噪声影响时, 频谱幅值会纵向改变[17]。为了突出频谱中峰值的重要, Zou 等[18]提出移动最大值(moving maximum)的方法, 受此启发, 本文提出一种最大偏移频域降采样的方法, 使其更适用于多工况条件下的识别。
假设原始频域信号 xsignal = {x1,x2,…,xn}, FFT 变换后有 n 个点, 第 i 个点的幅值表示为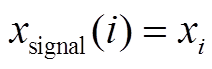
, 本文提出的最大偏移频域降采样方法表示如下:
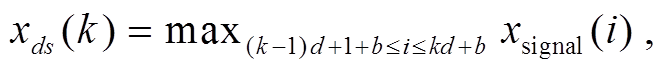(6)
其中,
为经过最大偏移降采样后得到频域信号, 
, d 为降采样系数, 若 n/d不为整数, 则 n/d向上取整, 运算时, 超过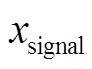
范围以外的值自动补零。b 为降采样的偏置值, 当 b=0 时, 该算法为最大降采样, 相当于滤波器大小为 d×1, 步长为 d 的一维最大池化操作; b<0 时, 该算法为最大左偏降采样; b>0 时, 该算法为最大右偏降采样。最大左偏和最大右偏降采样会分别出现 i<1 和 i>n 的情况, 此时自动补零, 使
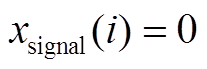。以一个简单的时序输入为例, 当 n=12, d=4 时, 在不同偏置值的情况下, 最大偏移降采样获取的结果如图 2 所示。
为了更直观地表现最大偏移降采样的作用, 以实验轴承数据集中的内圈故障样本为例, 展示训练样本的预处理流程。如图 3 所示, 原始时域信号共有 4096 个点, 经过 FFT 转换到频域, 得到点数为2048 的频谱图, 最后通过降采样系数为 4 的最大降采样(b=0)获取点数为 512 的频谱。通过调整降采样系数 d 值, 可以生成不同分辨率的频谱; 通过调整
值控制样本降采样过程的左右偏移, 实现对训练样本的数据增强, 提高训练样本的多样性。
当信号受到噪声的影响时, 频谱幅值会纵向改变。为了减少频谱中噪声的影响, 在降采样后, 提出一种噪声横截断的方法:
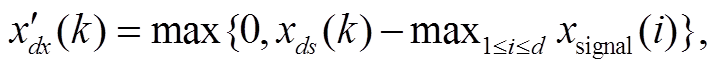(7)
其中,
是噪声横截断后的信号。该方法表达的含义为最大偏移降采样的频域信号
统一减去最大降采样后第一项的值, 如果减后的值为负数则置零。由于频谱中靠近原点的超低频往往不会有故障信号的特征, 因此采用最大降采样后第一项的数值来衡量噪声的强度。减法运算类似数字信号的滤波。噪声横截断的作用是减少噪声对频谱纵向幅值的影响, 同时使降采样后频谱原点的信号幅值为 0, 更贴合频谱的实际情况。本研究中, 将噪声横截断用于对含有噪声的测试集进行处理, 流程如图 4 所示。图 4(a)中的噪声频域信号经过最大降采样, 对噪声信号进行第一次处理, 降低了频谱维度, 保留了峰值特征。但是, 由于噪声的影响, 图 4(b)中的频谱出现浮空的状态。经过噪声横截断后, 图4(c)中截断下层噪声, 频谱整体向下移动, 降低了噪声对频谱幅值的影响。
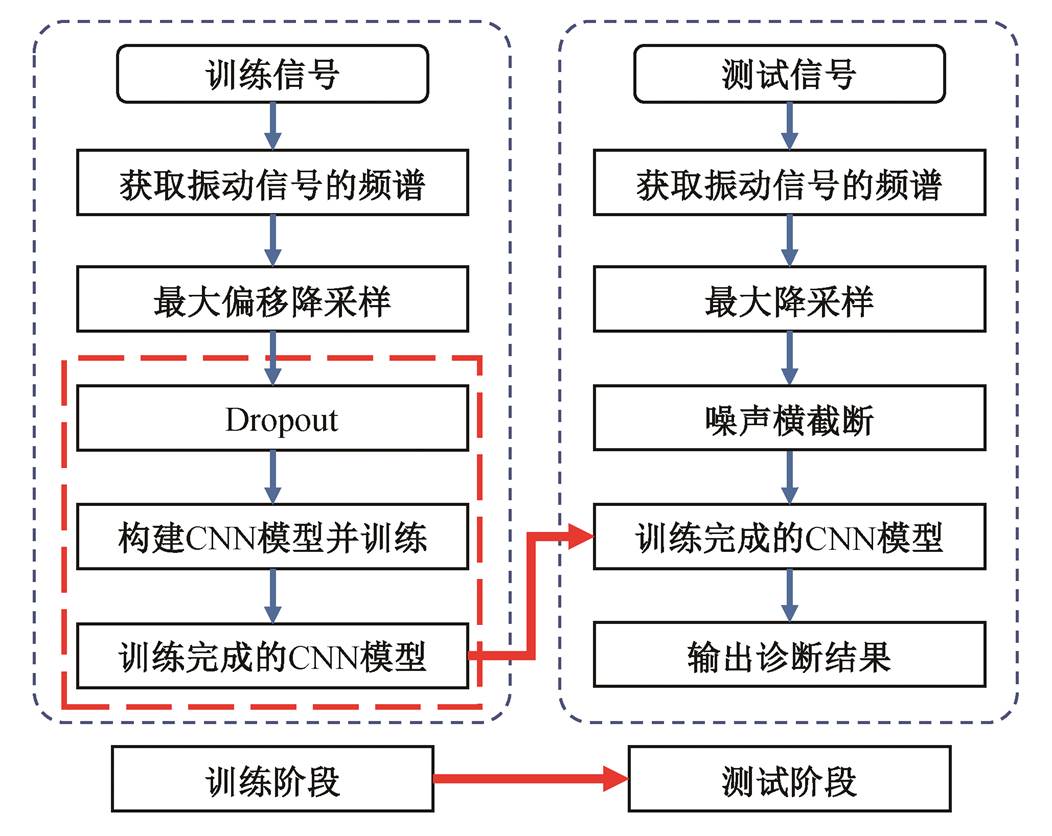
图1 Ds-CNN故障诊断方法框架
Fig. 1 Structure of fault diagnosis method of Ds-CNN
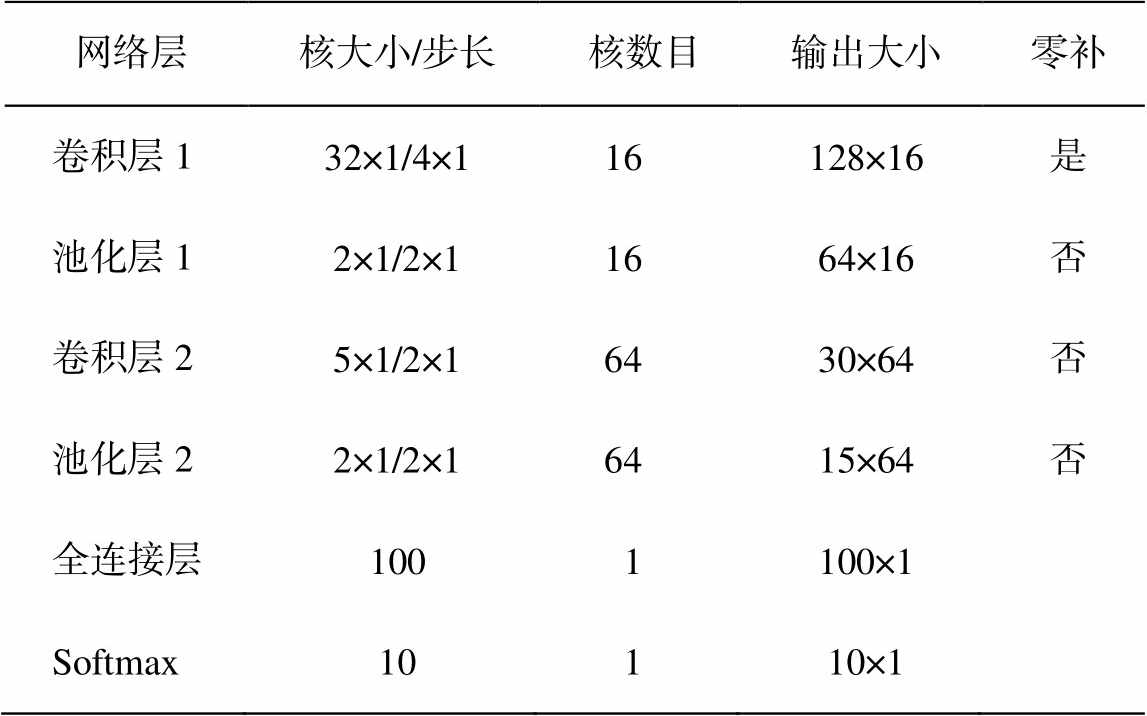
现有研究大多以时域振动信号为输入, 建立一维卷积神经网络(1D-CNN)的故障诊断模型[19]。在相同噪声强度下, 频域信号受噪声的影响更小, 并且频谱更能直观地反映噪声和工况的影响。因此, 对数据进行预处理后, 本文提出一种基于频域信号的 1D-CNN 模型, 其结构如图 5 所示。在信号输入环节中, 对时域信号滑窗获取样本, 通过 FFT 将其转换到频域, 采用最大偏移降采样的方法对频域样本处理并降维, 对同一个样本选用不同的偏置值扩充样本的多样性, 最终得到网络模型的输入信号。随后采用 Dropout[20]的方式对输入信号随机置零, 增强模型的抗干扰能力。采用两层的卷积神经网络提取频域信号的特征, 最后用全连接层和 Softmax完成故障的分类。基于频域信号的 1D-CNN 模型结构参数如表 1 所示。
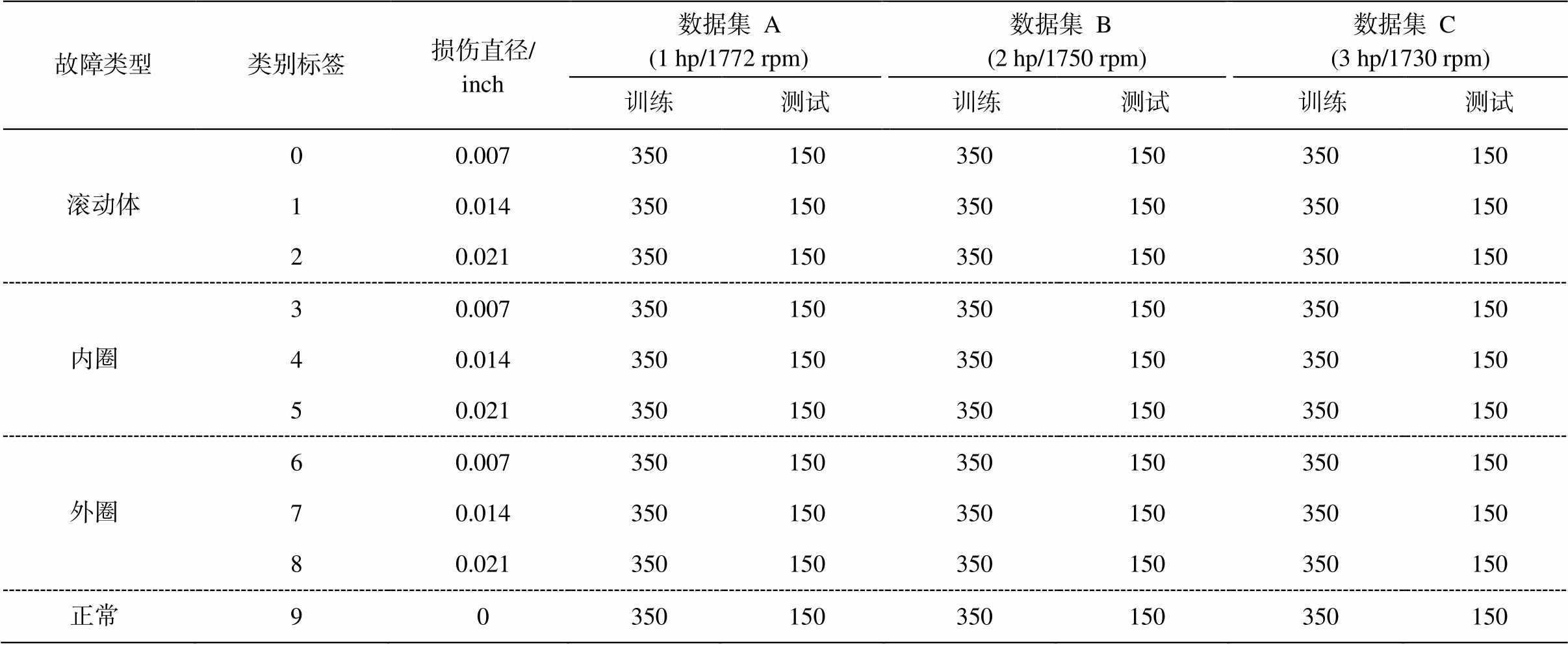
本文选用 Case Western Reserve University (CW-RU)的轴承实验数据库[21], 数据集采样频率为 12kHz。实验中采用电火花加工(EDM)方法对滚动轴承进行加工, 模拟不同的故障类型, 通过安装在驱动端的加速器采集振动信号数据。选取轴承在不同转速下的滚动体故障(BF)、内圈故障(IRF)、外圈故障(ORF)和正常(Normal) 4 种状态。除正常状态外, 每一种故障类型包含 0.007, 0.014和 0.021inch不同的故障直径, 代表不同的损伤程度, 所以共有10 种故障类型。通过交叉重叠的滑动窗口对原始振动信号进行切分获取训练样本和测试样本, 每个样本取 4096 个点。数据集 A, B 和 C 代表来自不同工况条件下的故障样本。3 个数据集在 1, 2 和 3 马力(hp)不同负载(对应转速 1772, 1750 和 1730rpm)条件下, 分别包含 3500 个训练样本和 1500 个测试样本, 即每一种故障类型包含 350 个训练样本和 150个测试样本。实验数据集的具体情况如表 2 所示。
为了研究模型在噪声环境下的鲁棒性, 在测试样本中加入高斯白噪声, 生成不同信噪比的噪声样本。信噪比的定义如下:
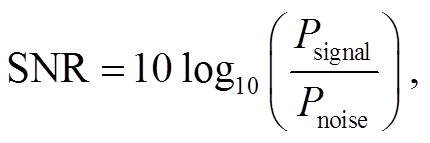(8)
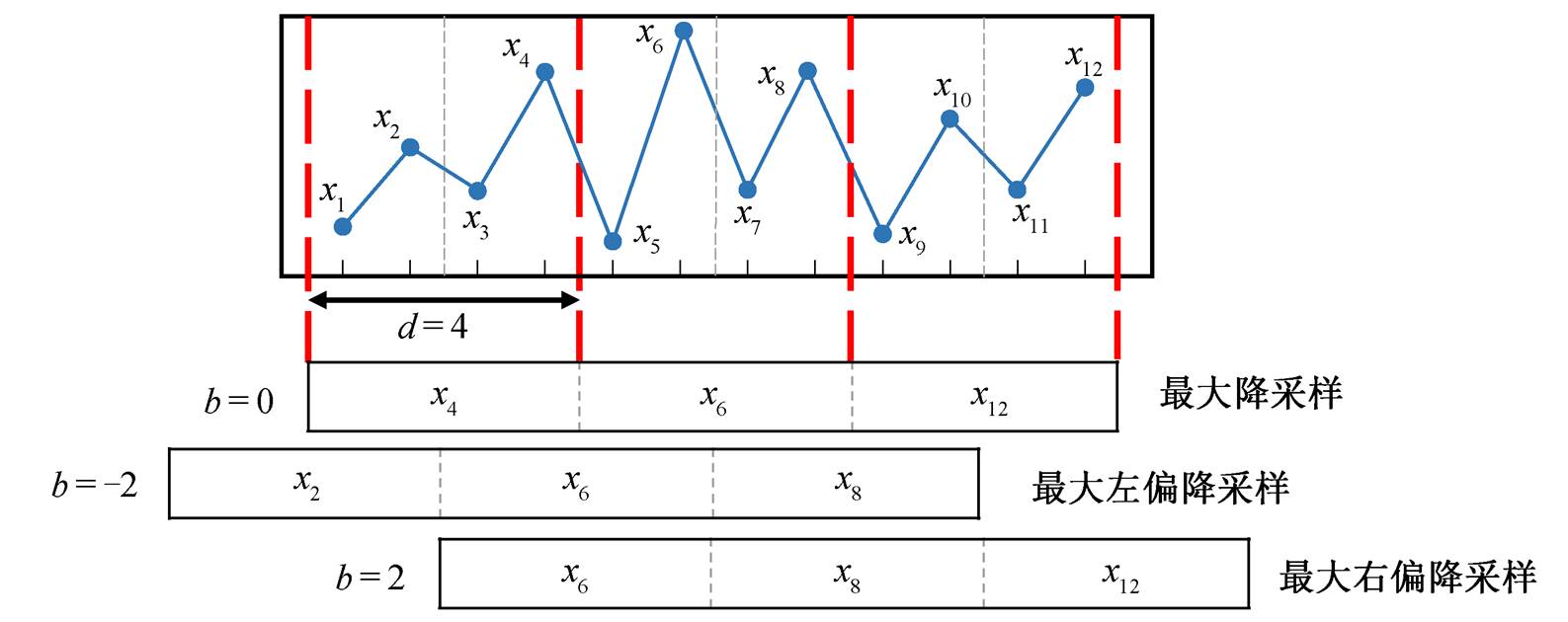
图2 最大偏移降采样算法示例
Fig. 2 Demonstration of maximum down-sampling with bias
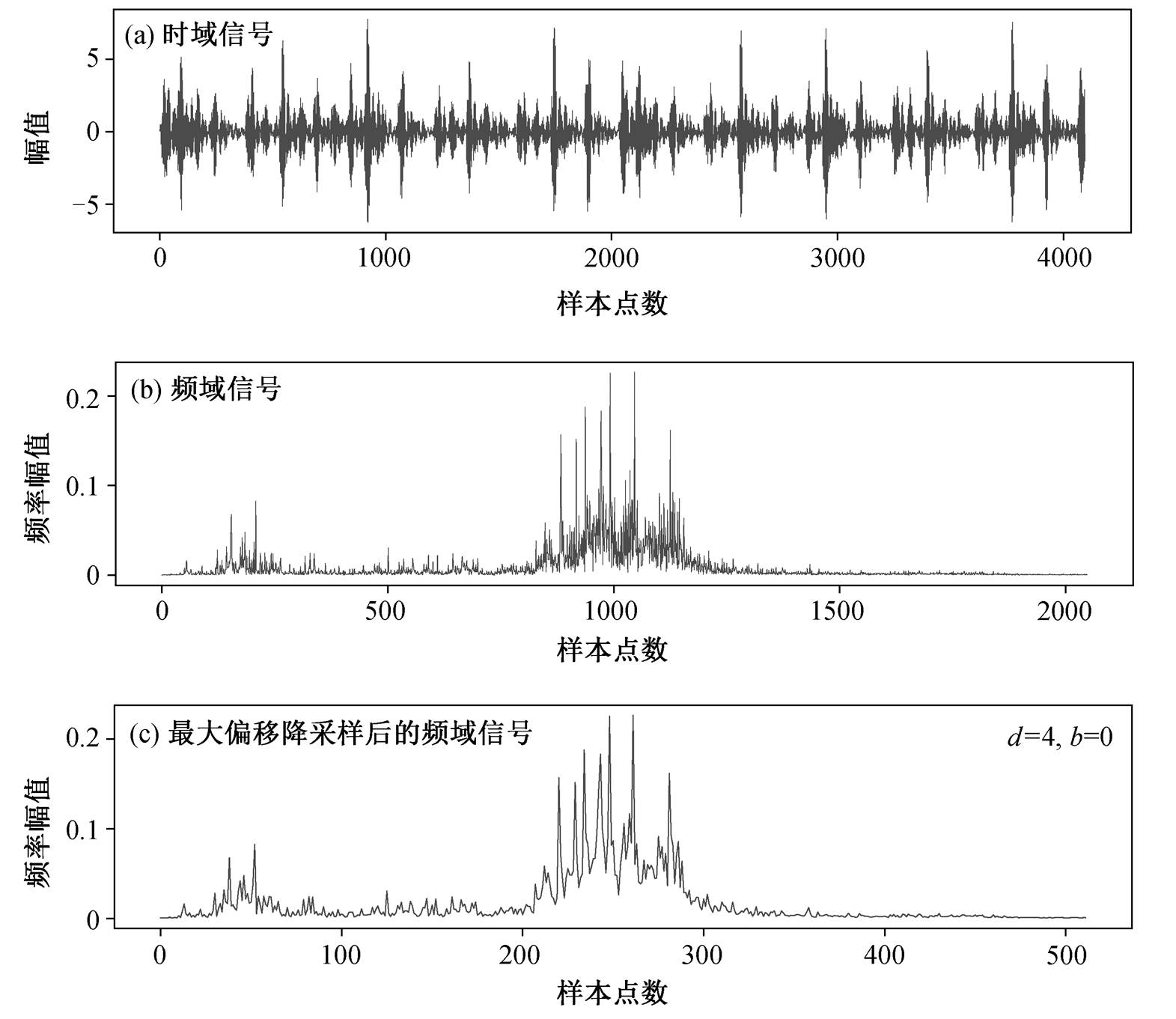
图3 训练样本预处理
Fig. 3 Preprocessing of training sample
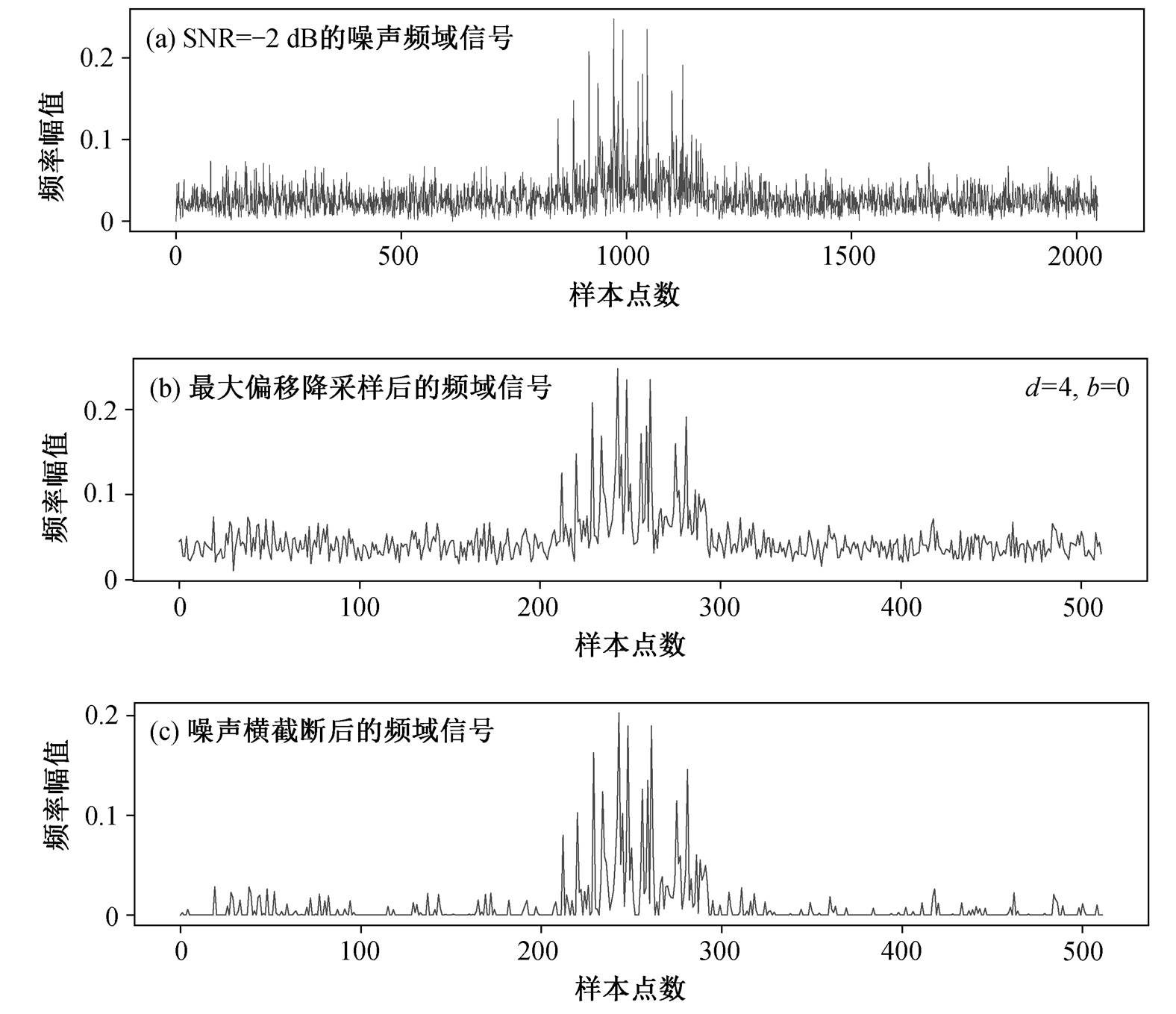
图4 噪声样本处理流程
Fig. 4 Processing of noise sample
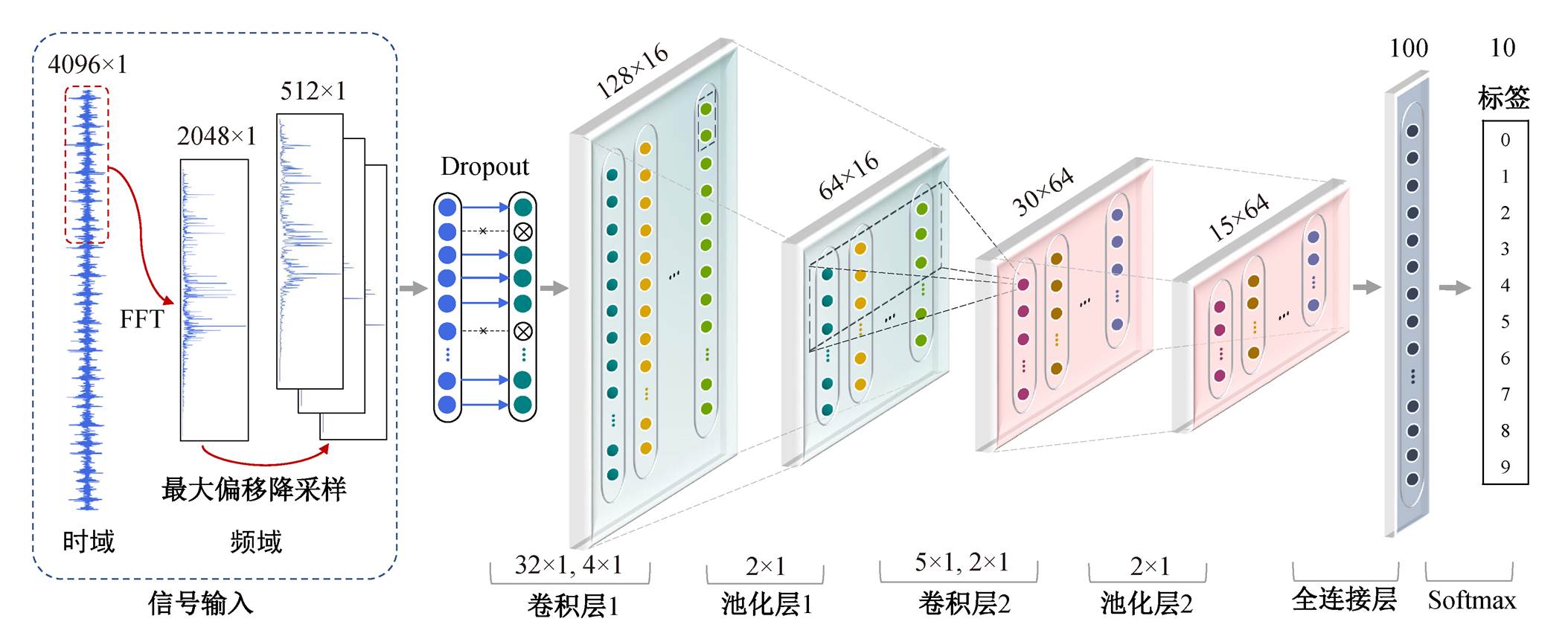
图5 一维卷积神经网络的结构
Fig. 5 Architecture of one-dimensional convolutional neural network
表1 CNN网络结构参数
Table 1 Structures and parameters of CNN
网络层核大小/步长核数目输出大小零补 卷积层132×1/4×116128×16是 池化层12×1/2×11664×16否 卷积层25×1/2×16430×64否 池化层22×1/2×16415×64否 全连接层1001100×1 Softmax10110×1
其中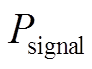
和
分别代表信号和噪声的能量。信噪比越小, 噪声对信号的干扰越大。图 6 展示 1hp 条件下信噪比为 0 时, 对 0.021inch 故障直径的内圈故障(IRF-0.021)原始信号添加高斯白噪声的过程。图 7 展示 1hp 条件下信噪比为 0 时, 10 种故障类型的频域原始波形和噪声波形。
为了评估模型的抗噪性能和跨领域性能, 分别在强噪声和多工况条件下对训练的模型进行测试, 经过实验结果分析和对比, 最终确定以下 Ds-CNN参数。
表2 滚动轴承数据集描述
Table 2 Description of rolling element bearing datasets
故障类型类别标签损伤直径/inch数据集 A (1 hp/1772 rpm)数据集 B (2 hp/1750 rpm)数据集 C (3 hp/1730 rpm) 训练测试训练测试训练测试 滚动体00.007350150350150350150 10.014350150350150350150 20.021350150350150350150 内圈 30.007350150350150350150 40.014350150350150350150 50.021350150350150350150 外圈 60.007350150350150350150 70.014350150350150350150 80.021350150350150350150 正常 90350150350150350150
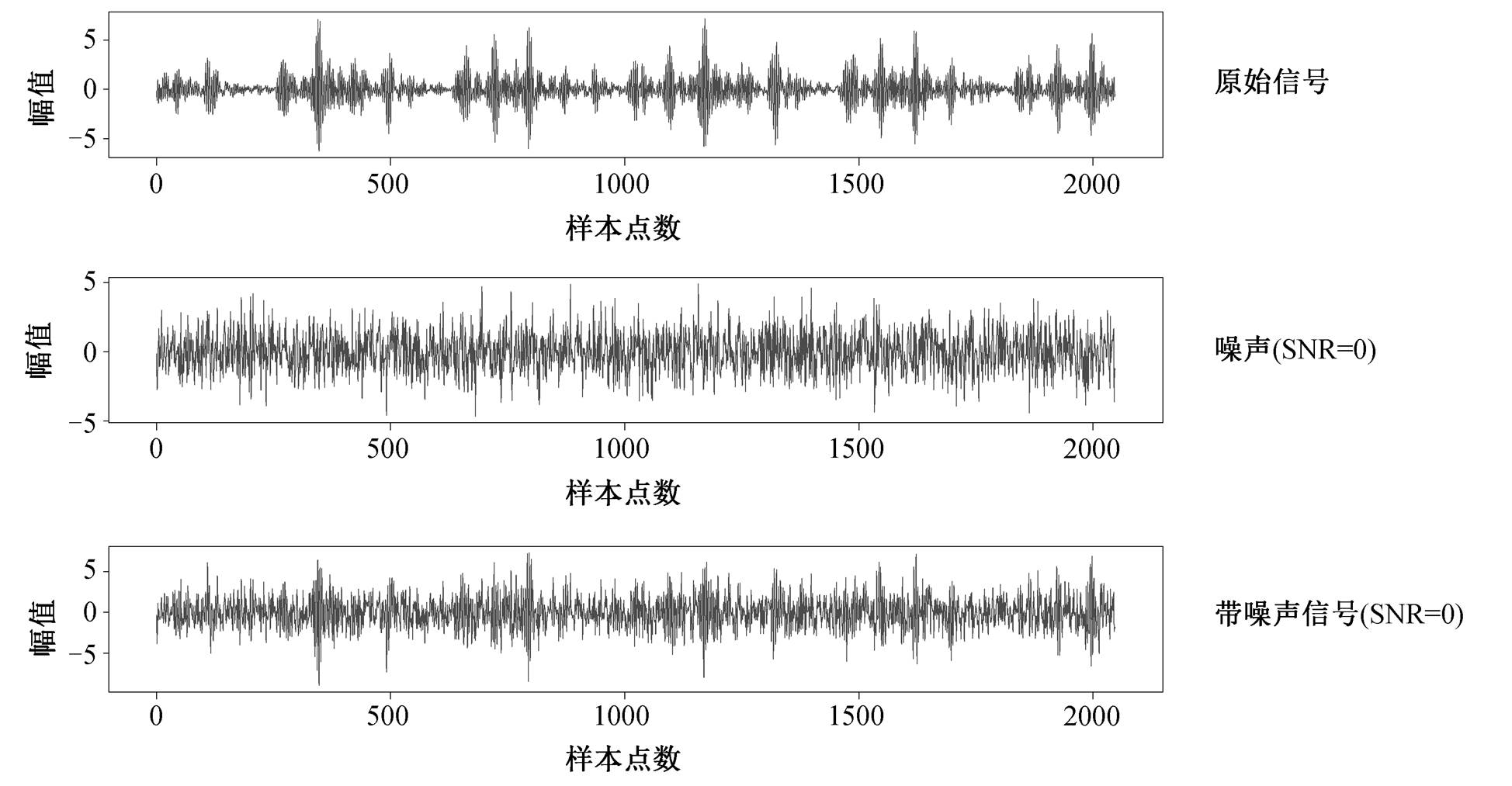
图6 内圈故障原始信号(IRF-0.021)、高斯白噪声和SNR=0的复合噪声信号
Fig. 6 Figures for original signal of inner race fault (IRF-0.021), the additive white Gaussian noise, and the composite noisy signal with SNR = 0
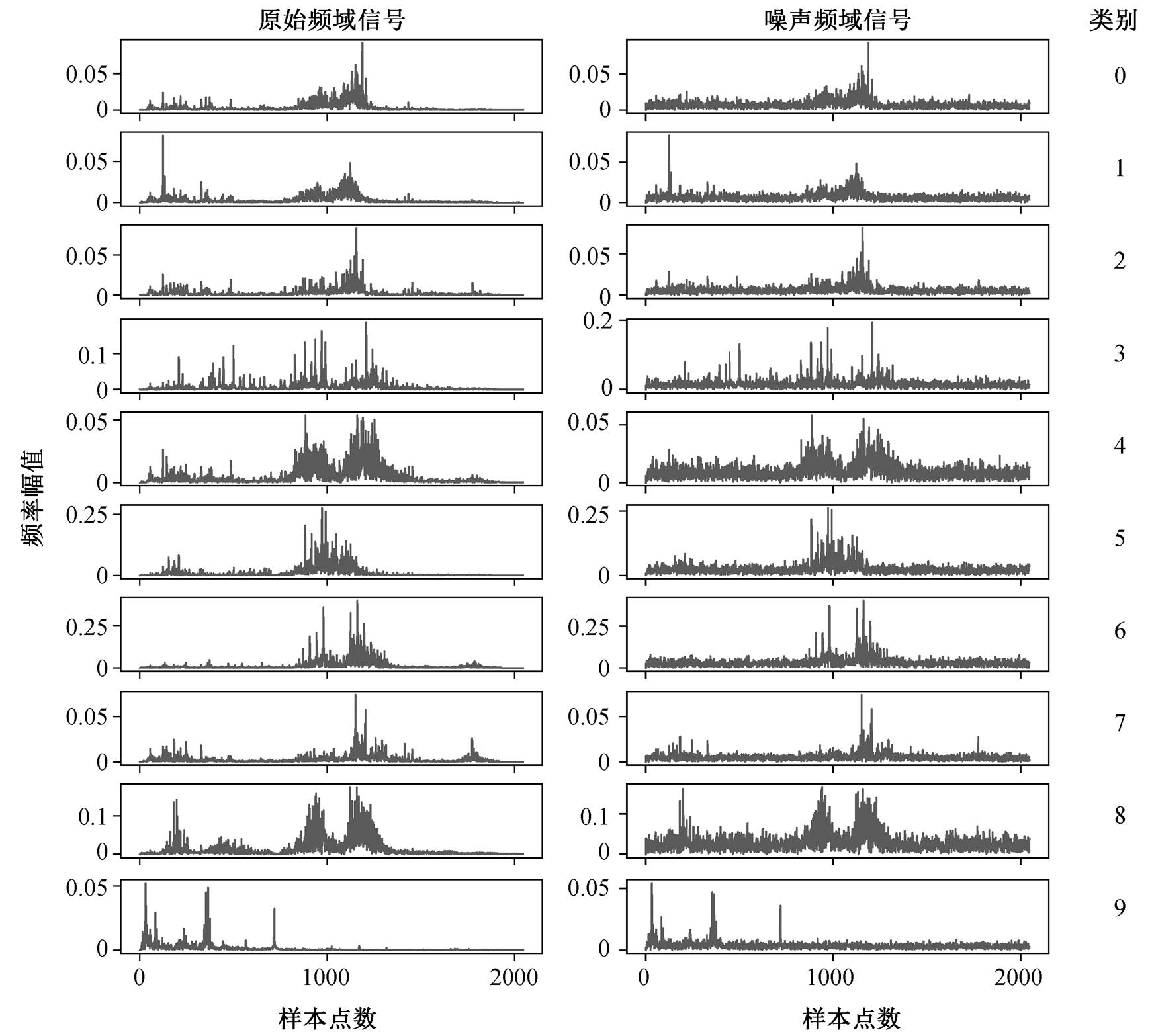
图7 10种故障类型在频域的原始波形和噪声波形(1 hp, SNR=0)
Fig. 7 Original and noisy waveforms of the ten fault types in frequency domain (1 hp, SNR=0)
1)数据预处理。原始时域信号共 4096 个点, 经过 FFT 转换到频域, 得到点数为 2048 的频谱图, 最后通过降采样系数 d = 4 的最大降采样, 获取点数为 512 的频谱。降采样的偏置值分别选取−2, 0 和 2, 将训练样本数量扩展为 3 倍, 共获取 10500个训练样本。
2)网络参数设置。输入维度为 512×1 的一维信号; 输入层采用 Dropout 操作, 置零率 Dropout rate设为 0.1; 每个卷积层后采用批量归一化处理(batch normalization)来提高网络训练效率; 激活函数选用ReLu; 损失函数选用交叉熵函数; 采用 Adam 优化算法更新网络权值; 批大小(Batch Size)为 64; 训练轮次(Epoch)为 100。
为了验证本文提出的 Ds-CNN 方法的优越性, 选取以下模型进行对比实验。
1) SVM: 2048 个点的频域信号经过最大降采样后, 利用支持向量机(SVM)训练并完成分类, SVM的核函数为径向基核函数。
2) DNN: 2048 个点的频域信号经过最大降采样后, 搭建深度神经网络(DNN)训练并完成分类, DNN为 512-256-100-10 的 4 层网络结构。
3) CNN-512: 2048 个点的频域信号经过最大降采样后, 训练得到 CNN 模型, 训练样本数量没有发生改变, 没有采用偏移最大降采样和噪声横截断, 但网络参数设置与 Ds-CNN一致。
4) CNN-2048: 通过FFT将 4096 个点的原始时域信号转换至频域, CNN 的输入为未经过降采样的频域信号, 长度为 2048 个点。第一层卷积核大小为128, 步长为 8, 卷积核数量为 16; 第二层卷积核大小为 16, 步长为 4, 卷积核数量为 64。
研究模型在强噪声环境下的抗噪性能, 即同一工况下, 利用不含噪声的训练样本训练得到的模型对含有噪声的测试样本的识别准确率。选取工况条件为 1hp 的轴承振动信号进行实验, 训练集为原始数据, 对测试集的样本分别增加信噪比 SNR 从−6dB 到 6dB 的噪声信号。每个模型均以 10 次实验的平均结果作为评价标准, 实验结果如图 8 所示。
研究模型在多工况条件下对非同一工况样本的识别率, 即某一种负载下的训练样本训练得到的模型对另一负载下的测试样本的识别率。当选用数据集 A 作为训练集, 数据集 B 作为测试集时, 表示为A→B。每个模型均以 10 次实验的平均结果作为评价标准, 实验结果如图 9 所示。
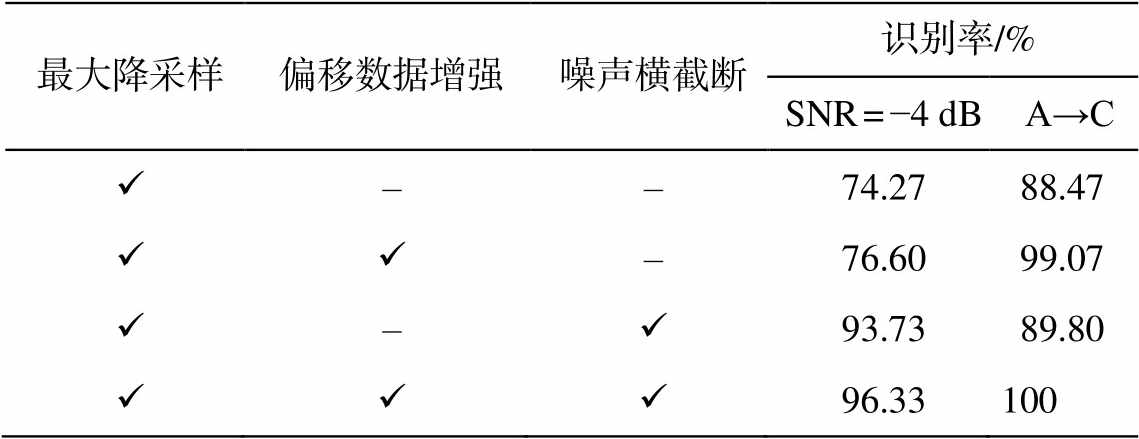
为了清楚地证明 Ds-CNN 中最大偏移降采样和噪声横截断两个算法的有效性, 在 CNN 网络结构不变的情况下, 采用消融实验的方式, 将 Ds-CNN中数据预处理的部分拆解, 以强噪声 SNR=−4 dB 和多工况 A→C 两种情况为例, 明确最大偏移降采样和噪声横截断的作用, 验证预处理算法的有效性。消融实验的结果如表 3 所示。
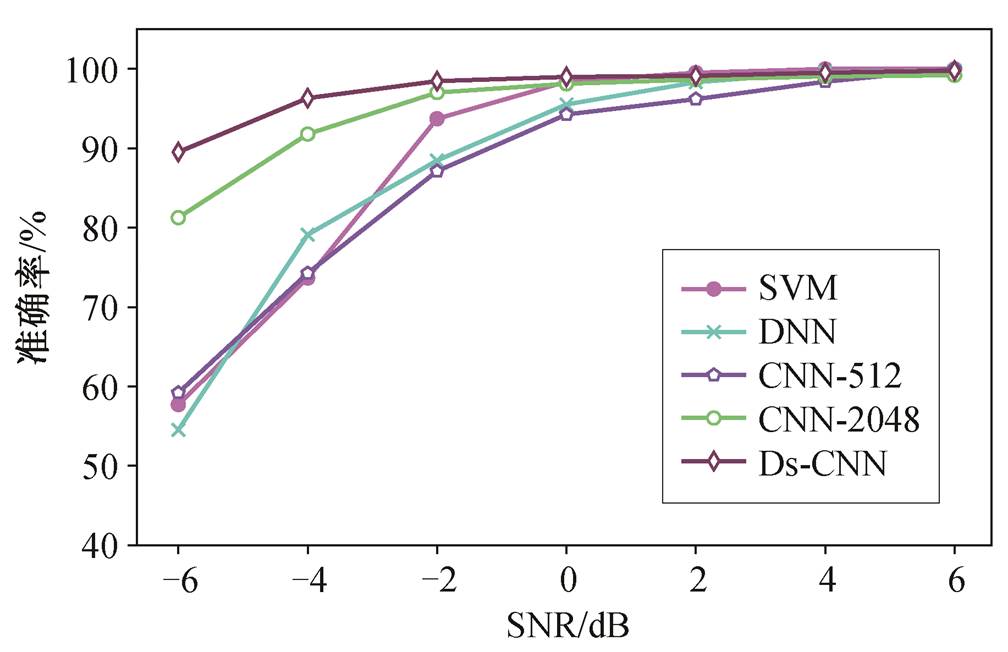
图8 不同模型在不同信噪比下的诊断结果
Fig. 8 Diagnosis results of different models under different SNRs
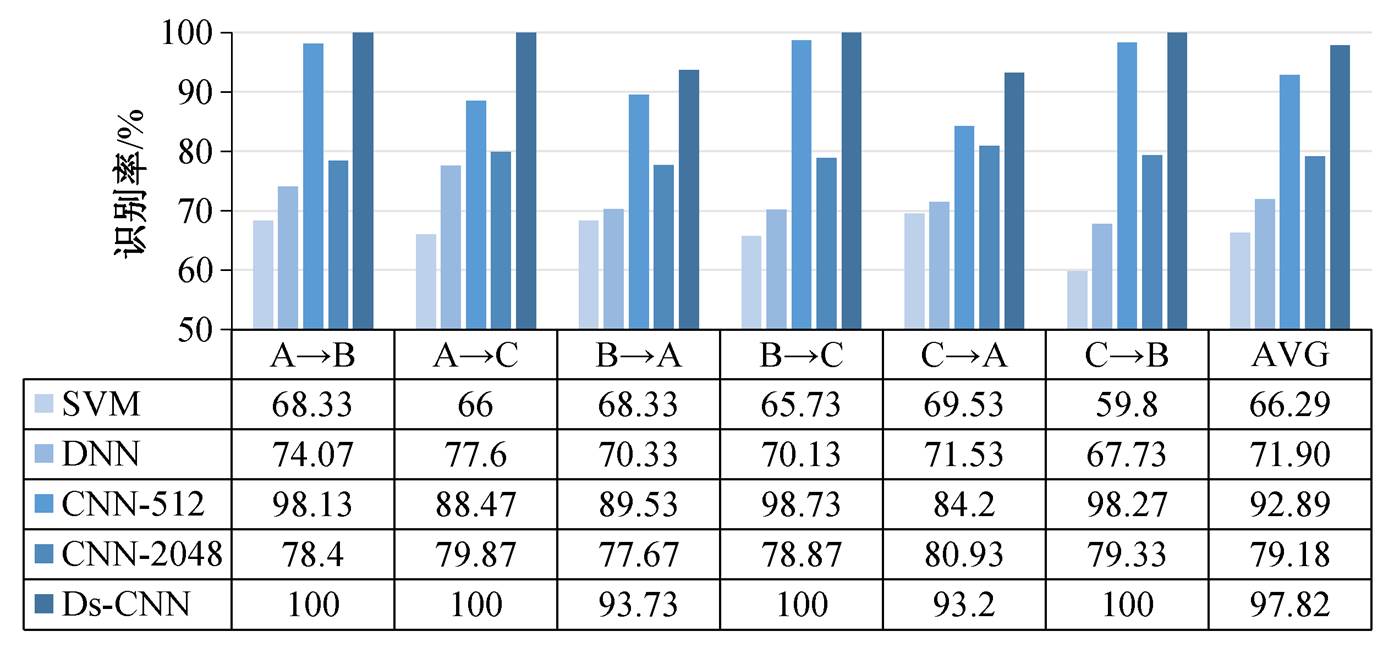
图9 不同模型在多工况条件下的诊断结果
Fig. 9 Diagnosis results of different models under multiple working conditions
为了更好地验证 Ds-CNN 同时在噪声环境、不同工况条件下的鲁棒性, 选取测试集为非同一工况下的噪声数据集。以图 9 中 A→B 为例, 进一步在测试集 B 中增加噪声(SNR=0)。实验中, 由训练集 A 训练得到的 Ds-CNN 模型对另一工况条件下的噪声测试集的识别精度为 99.27%。利用生成的混淆矩阵展现具体的分类结果, 如图 10 所示。
由图 8 可以看出, Ds-CNN 识别 SNR 为−6dB 的强噪声环境下的测试样本, 依然有接近 90%的准确率。与其他模型相比, Ds-CNN 在强噪声环境下的抗噪能力优于常用的 CNN, SVM 和 DNN。对比CNN-512 与 CNN-2048 识别噪声测试样本的精度可知, 采用降采样后频谱分辨率降低, 模型的抗噪能力减弱。相对于 CNN-512, Ds-CNN 采用噪声横截断的方法, 可以减少噪声对频谱的影响, 提高了模型抗噪能力。
表3 Ds-CNN消融实验
Table 3 Ablation experiment of Ds-CNN
最大降采样偏移数据增强噪声横截断识别率/%SNR = −4 dBA→C ü––74.27 88.47 üü–76.60 99.07 ü–ü93.73 89.80 üüü96.33100
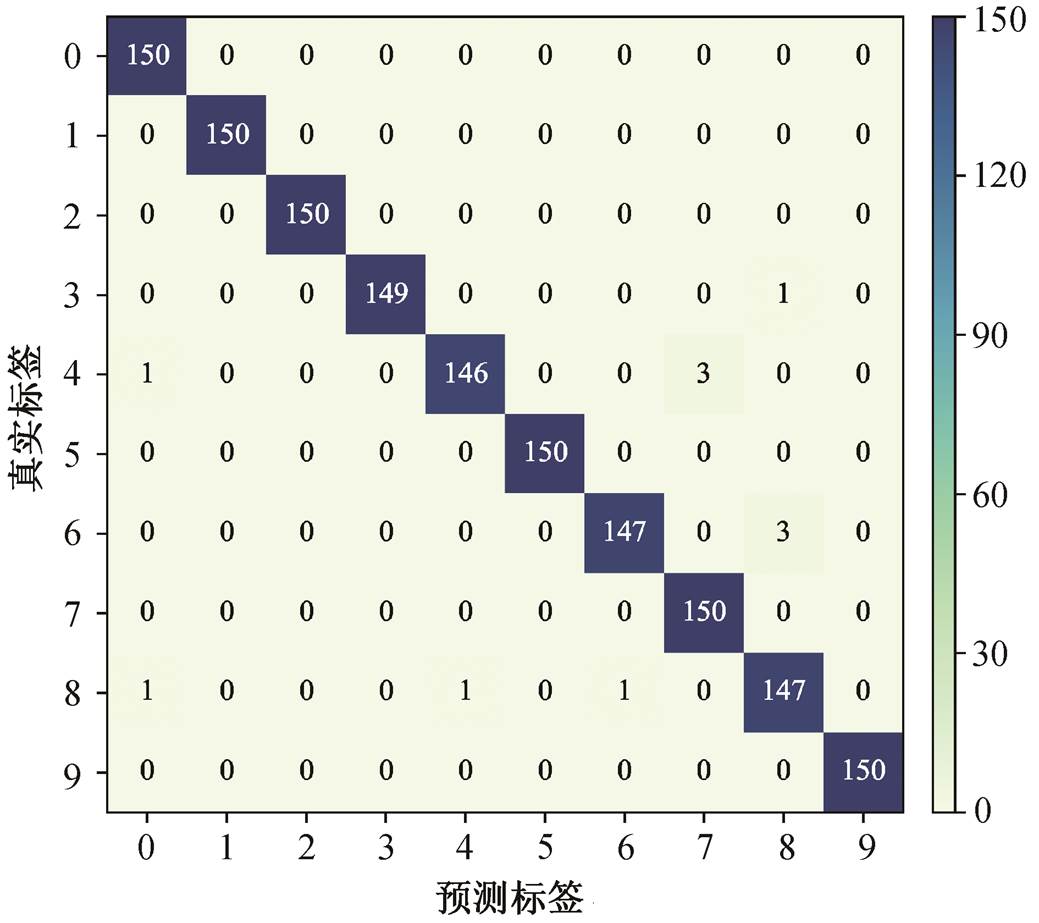
图10 由原始数据集 A 训练获得的 Ds-CNN 模型识别噪声测试集 B (SNR = 0)的分类混淆矩阵
Fig. 10 Classification confusion matrix of Ds-CNN trained by original dataset A when testing on noisy dataset B (SNR = 0)
由图 9 可以发现, 在多工况的实验中, Ds-CNN平均识别准确率达到 97.82%, 部分多工况实验的识别准确率高达 100%。Ds-CNN 在多工况条件下的适应能力优于其他模型。采用降采样的方式可以使不同工况样本频谱之间的差异性减小, 因此 CNN-512 在多工况条件下的识别率远超 CNN-2048。Ds-CNN 通过偏移降采样, 进一步扩充了样本的多样性, 使得多工况条件下的识别率高于CNN-512。
由表 3 可知, 在 Ds-CNN 的频域降采样预处理中, 最大偏移频域降采样的方法主要用于提高不同负载工况条件下故障样本的识别率, 由于训练样本的数据增强, 提升了模型的鲁棒性; 噪声横截断的方法使模型适用于强噪声干扰条件下的故障识别, 模型的抗噪能力显著提升, 对于不同负载工况条件下模型故障识别能力的改善不明显。
由图 10 可知, Ds-CNN 能够同时适用于多工况条件和强噪声背景下的故障识别。由单一工况原始训练集得到的模型, 在工况改变和噪声干扰两个因素的共同影响下, 依然保持着高识别率。
本文针对强噪声环境和多工况条件下的轴承故障诊断问题, 提出基于频域降采样和 CNN 的故障诊断方法 Ds-CNN。该方法一方面通过偏移最大降采样实现样本增强, 减少样本的差异性; 另一方面通过噪声横截断, 提高降采样后模型的抗噪能力, 并且可以同时保证强噪声环境和多工况条件下的轴承故障诊断的识别准确率。
本文研究结果表明, 降低样本的采样点数获取更低分辨率的频谱, 会使不同工况之间的频谱差异性减小, 提升多工况条件下模型的适应能力, 但频谱分辨率的降低会导致模型的抗噪能力减弱。相对于已有的轴承故障诊断方法, 该方法能够适用于由于噪声干扰、负载变化和转速变化导致的训练样本与实际样本分布不一致的情况, 对实际现场的设备轴承故障诊断有一定的参考价值。
本文实验数据采用的振动信号属于稳态信号, 对于实际现场非稳态振动信号的故障诊断仍需要进一步研究。
参考文献
[1] Sun Jiedi, Yan Changhong, Wen Jiangtao. Intelligent bearing fault diagnosis method combining compressed data acquisition and deep Learning. IEEE Transac-tions on Instrumentation and Measurement, 2018, 67 (1): 185–195
[2] Li Jie, Wang Yu, Zi Yanyang, et al. A local weighted multi-instance multilabel network for fault diagnosis of rolling bearings using encoder signal. IEEE Tran-sactions on Instrumentation and Measurement, 2020, 69(10): 8580–8589
[3] 雷亚国, 贾峰, 孔德同, 等. 大数据下机械智能故障诊断的机遇与挑战. 机械工程学报, 2018, 54(5): 94–104
[4] Shen Changqing, Wang Dong, Kong Fanrang, et al. Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier. Measure-ment, 2013, 46(4): 1551–1564
[5] Fei Shengwei. Fault diagnosis of bearing based on wavelet packet transform-phase space reconstruction-singular value decomposition and SVM classifier. Arabian Journal for Science and Engineering, 2017, 42(5): 1967–1975
[6] Rai V K, Mohanty A R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform. Mechanical Systems and Signal Proce-ssing, 2007, 21(6): 2607–2615
[7] Wang Jun, Du Guifu, Zhu Zhongkui, et al. Fault diagnosis of rotating machines based on the EMD manifold. Mechanical Systems and Signal Processing, 2020, 135: 106443
[8] Samanta B, Nataraj C. Use of particle swarm optima-zation for machinery fault detection. Engineering Applications of Artificial Intelligence, 2009, 22(2): 308–316
[9] Goyal D, Choudhary A, Pabla B S, et al. Support vector machines based non-contact fault diagnosis system for bearings. Journal of Intelligent Manufac-turing, 2020, 31(5): 1275–1289
[10] 曲建岭, 余路, 袁涛, 等. 基于一维卷积神经网络的滚动轴承自适应故障诊断算法. 仪器仪表学报, 2018, 39(7): 134–143
[11] Gan Meng, Wang Cong, Zhu Chang'an. Construction of hierarchical diagnosis network based on deep lear-ning and its application in the fault pattern recogni-tion of rolling element bearings. Mechanical Systems and Signal Processing, 2016, 72/73: 92–104
[12] Li Chuanhao, Zhang Wei, Peng Gaoliang, et al. Bearing fault diagnosis using fully-connected winner-take-all autoencoder. IEEE Access, 2018, 6: 6103–6115
[13] Zhao Rui, Yan Ruqiang, Wang Jinjiang, et al. Lear-ning to monitor machine health with convolutional bi-directional LSTM networks. Sensors, 2017, 17(2): 273
[14] 曹现刚, 张国祯, 张鑫媛, 等. 基于振动图像和DCNN的采煤机滚动轴承故障诊断. 煤矿机械, 2020, 41(7): 149–152
[15] Wang Huaqing, Li Shi, Song Liuyang, et al. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Computers in Industry, 2019, 105: 182–190
[16] Pang Shan, Yang Xinyi, Zhang Xiaofeng, et al. Fault diagnosis of rotating machinery with ensemble kernel extreme learning machine based on fused multi-domain features. ISA Transactions, 2020, 98: 320–337
[17] Zhou Xiangyu, Mao Shanjun, Li Mei. A novel anti-noise fault diagnosis approach for rolling bearings based on convolutional neural network fusing fre-quency domain feature matching algorithm. Sensors, 2021, 21(16): 5532
[18] Zou Lei, Li Yang, Xu Feiyun. An adversarial denoi-sing convolutional neural network for fault diagnosis of rotating machinery under noisy environ-ment and limited sample size case. Neurocomputing, 2020, 407: 105–120
[19] Zhang Wei, Peng Gaoliang, Li Chuanhao, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors, 2017, 17(2): 425
[20] Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from over-fitting. The Journal of Machine Learning Research, 2014, 15(1): 1929–1958
[21] CWRU. The case western reserve university bearing data center [EB/OL]. (2021–08–10) [2022–03–10]. https://engineering.case.edu/bearingdatacenter/download-data-file
Bearing Fault Diagnosis Method Based on Down-Sampling in Frequency Domain and CNN
Abstract In the industrial field, the original fault signals collected during the operation of the equipment have the characteristics of strong noise and multiple working conditions. Most of previous data-driven fault diagnosis methods for bearings have relatively weak anti-noise ability and generalization ability. To solve these problems, a novel bearing fault diagnosis method based on down-sampling in frequency domain and convolutional neural network (CNN), called Ds-CNN, is proposed. Down-sampling in frequency domain consists of maximum down-sampling with bias and noise transverse truncation, which can realize data augmentation, reduce the difference between samples in frequency domain, and reduce the influence of noise on signals in frequency domain. The CNN model based on frequency domain signals can automatically extract fault features from signals after down-sampling and complete the identification and classification of bearing faults. The results of the experiment show that Ds-CNN has higher recognition accuracy than common models under strong noise environment and multiple working conditions.
Key words bearing fault diagnosis; deep learning; convolutional neural network (CNN); strong noise; multiple working conditions