北京大学学报(自然科学版) 第59卷 第2期 2023年3月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 2 (Mar. 2023)
doi: 10.13209/j.0479-8023.2022.106
中国地质调查局地质调查项目(DD20211364)和国家重点研发计划(2021YFC3000504-02)资助
收稿日期: 2022‒03‒11;
修回日期: 2022‒04‒21
摘要 通过将时序卷积网络(TCN)与 Transformer 解码器进行组合, 提出一种基于 Transformer 的滑坡短期位移预测模型。将预处理过的位移与降雨序列作为模型的输入, 以时序自回归方式输出未来 3 日的位移预测结果。实验结果表明, 与支持向量机(SVM)和长短期记忆(LSTM)等传统模型相比, 该模型精度较高, 在快速变形期的预测优势尤为突出。对模型注意力机制的分析结果表明, 模型关注的重点在位移峰值和大降雨附近, 具有较高的可信度。
关键词 边坡工程; 滑坡位移; 短期预测; Transformer; 注意力机制
滑坡是斜坡上的土体或岩体受自然或人为因素的影响, 在重力作用下, 沿着一定的软弱面或软弱带, 顺斜坡向下滑移的自然现象, 在我国具有分布范围广、发生频率高和灾害损失严重等特点[1]。近年来, 我国对地质灾害防治工作的投入不断加大。2019 年, 自然资源部实施普适型监测设备研发和示范应用工作以来, 中国地质监测院负责的地质灾害监测预警管理系统已经上线近 2.5 万个监测点, 分布在西藏、四川、重庆、广东和陕西等地区。基于监测数据, 进行及时有效的滑坡短期位移预测, 可以为预警预报工作提供支持, 对降低滑坡灾害带来的生命财产损失具有重要意义。
对于布设监测设备的单体滑坡, 传统方法一般根据水文地质和工程地质条件建立机理模型, 位移、形变和降水等是其重要输入参数。在普适型滑坡监测工作中, 短期内对 2.5 万个坡面全部建立机理模型既不可能, 也不可行。因此, 探索一种基于机器学习方法的滑坡短期位移预测模型, 对开展普适型滑坡的预警预报工作具有重要意义。
在既有的研究中, 基于机器学习的滑坡位移预测模型大多从时间序列分析出发, 采用滑动平均、HP 滤波(Hodrick-Prescott filter)以及经验模式分解(empirical mode decomposition, EMD)等方法, 将滑坡位移分解为趋势项和周期项, 应用三次多项式、三角函数和 ARIMA 等统计模型以及支持向量机(support vector machine, SVM)、长短期记忆(long short-term memory, LSTM)和极限学习机(extreme learning machine, ELM)等机器学习模型, 对分解后的两个时间序列分别进行训练和预测, 然后将两个序列叠加, 得到最终的位移预测值[2‒8]。Liu 等[9]借鉴滑坡危险性判断的研究方法, 通过粒子群优化算法(particle swarm optimization, PSO)和 SVM 方法, 将滑坡位移分解为趋势项和周期项, 并得到滑坡危险性因子, 用于后续周期项预测。李麟玮等[10]利用聚类方法, 将滑坡的变形状态划分为变形稳定状态和变形突变状态两类, 构建考虑滑坡变形状态动态转换的位移区间预测框架, 而非对滑坡位移进行 分解。
上述研究多针对三峡库区滑坡或类似大型的有长期监测数据的坡面, 采用库水位、降水和气温等监测数据, 以月为单位开展中期位移预测工作, 针对滑坡短期位移预测的研究相对较少[6,11]。然而, 在普适型滑坡监测工作中, 大多数滑坡的监测时长不足一年, 难以体现滑坡的长期位移趋势, 基于时间序列分析的位移分解方法并不适用。同时, 普适型滑坡监测工作的目标是开展以日乃至小时为单位的短期预测, 高时间分辨率使得滑坡位移规律变得更加复杂。受限于普适型滑坡监测工作的硬件规模, 降雨之外的其他诱发因子监测数据总体上缺失, 进一步加大滑坡位移预测的难度, 也对模型的表达能力提出更高的要求。为了满足普适型监测工作中滑坡短期位移预测需求, 需要建立表达能力更强的, 能够更好地表征滑坡位移变化过程的预测模型。
研究表明, 递归神经网络(recurrent neural net-work, RNN)和 LSTM 等动态预测模型在中期位移预测中具有独特的优势[7]。在滑坡短期位移预测中, 由于高时间分辨率的影响, 时间距离相同时的序列长度变得更长。以 6 小时为例, 一个月数据的序列长度高达 120, LSTM 在这种长输入序列应用场景中的表现并不理想[12]。
近年来, 谷歌研究团队提出的基于自注意力机制(self-attention)的 Transformer 模型[13]在序列生成相关任务(机器翻译、文本生成和音乐生成等)中取得良好的效果, 展现出非常优秀的特征表达能力。该模型不再依赖传统的卷积神经网络(convolutional neural network, CNN)和 RNN, 而是依靠自注意力机制来计算输入与输出表示, 对长期依赖有更强的表达能力, 能够应对滑坡短期位移预测任务中高时间分辨率带来的长距离依赖问题。同时, 注意力机制也具有良好的可解释性, 能在一定程度上帮助研究者理解模型做出特定输出的原因, 了解模型捕捉重点信息的能力[14], 使得研究者可以结合模型关注的滑坡变形特征, 对模型的可靠性进行深入的评估。
基于上述背景, 本文提出将 Transformer 模型应用到普适性滑坡监测工作中, 实现未来 3 日的滑坡位移预测, 以期提升滑坡短期位移预测的整体精度和可靠性。
普适型滑坡监测工作中, 从监测设备接收到监测数据的时间间隔不固定, 且由于仪器故障或传输网络故障等原因, 经常出现短时的数据缺失, 而时序分析与建模工作往往要求数据是等时距的。通过重采样和插值, 可以将原始监测数据处理为规则的等时距序列数据, 供后续建模时使用。其中, 重采样负责将数据重新采样为时间间隔相等的数据, 插值则是对监测中的缺失值进行补偿, 可采用样条插值等常用的方法。
在滑坡短期位移预测场景下, 监测数据的时间分辨率为日, 乃至小时级别, 单位时间内的位移变化量受仪器噪声的影响十分明显。在构建预测模型之前, 需要对包含大量噪声的非平稳时间序列进行降噪处理。本文使用基于变分模态分解的部分重构(partial reconstruction, PR)方法进行滑坡位移数据的降噪。
变分模态分解(variational mode decomposition, VMD)是 Dragomiretskiy 等[15] 2014 年提出的一种信号分解方法, 解决了不同频谱分量分离的最优化问题, 在非平稳信号分解方面有可靠的数学基础, 对噪声有很好的容忍度[16]。研究表明, VMD 方法在信号分解与降噪处理中比 EMD 更具优势[17]。VMD算法中, 本征模态函数(intrinsic mode function, IMF)被定义为一个有带宽限制的调幅–调频信号, 表达式如下:
uk(t) = Ak(t)cos(ϕk(t)),(1)
其中, Ak(t)为瞬时振幅, ϕk(t)为相位。VMD 的目标是将原始信号分解为包含多个不同频率尺度且相对平稳的子模态。
首先构造变分问题, 假设原始信号 f(t)被分解为 K个分量, 各个模态围绕中心频率大致紧凑, 且各模态估计带宽之和最小。通过调制信号的高斯平滑度, 即梯度的 L2 范数来估计带宽, 则该带约束的变分问题表示为
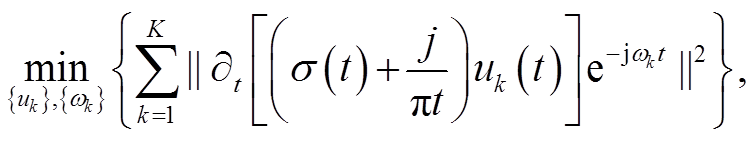
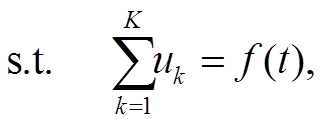(2)
式中, ωk为子模态的中心频率,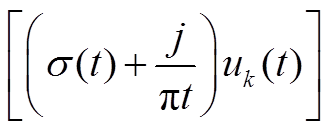 
为子模态通关 Hilbert 变换得到的解析信号, 指数项
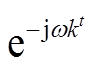将各模态的解析信号频谱转换到基带。使用拉格朗日乘数和交替方向乘子法求取上述变分问题的最优解, 可得{uk}:={u1, u2, …, uk}, 从而将原始信号分解为 K个 IMF 分量。其中, K的数值需要人工设置, 可以将 EEMD 方法分解得到的子序列个数作为 K值[18‒20]。
VMD 分解得到多个子模态后, 大多数重要信息集中在低频模态中, 信息量随着频率的增加而不断减少, 可以采用部分重构方法, 将高频模式设置为 0, 仅使用低频信号进行信号重构, 实现原始信号的降噪[21]。与 EMD 方法相反, VMD 分解结果中子模态频率按序号递增, 重构后的信号可表示为
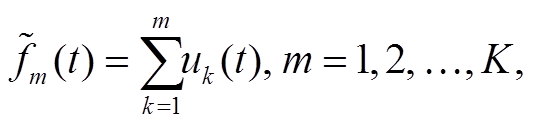(3)
其中, m为用于信号重构的子模态数量, 可依据子模态与原始信号的相关性来确定。
Transformer 完全基于自注意力机制(self-atten-tion)来提取内在特征, 可以学习长期依赖关系, 并且比 RNN 类模型更容易并行化。原始的 Transfor-mer 应用于分类问题, 通过 embedding 层得到单一时刻样本的高维特征, 并使用位置编码(positional encoding)来保留原始序列中的位置信息。随后, 基于 query-key-value 思想, 自注意力层将原始特征映射为 Q, K和 V三个特征, 使用 Q和 K计算不同时刻特征与当前时刻特征的相关性, 并通过对 V的加权求和得到下一时刻的特征[13]。其中, 时刻 t对时刻t−k特征的权重计算公式为
weightt−k= softmax(Qt × KT)t−k, k=0, 1, 2, …, t。 (4)
然而, 滑坡位移预测本质上是一个回归问题, embedding 层并不适用于回归问题的特征提取, 需要对原始模型进行改造。考虑到单一时刻的样本无法有效地描述当前时刻滑坡的运动状态, 本研究采用时序卷积网络(temporal convolutional network, TCN)替代 embedding 层。TCN 由因果卷积(causal convolution)和空洞卷积(dilated convolution)组成, 并引入残差连接来提升模型效果[22]。其中, 因果卷积可以保证当前时刻的特征仅与历史时刻的样本有关, 适用于时序自回归场景。使用 TCN 可以在保持输入形式不变的前提下, 将长度可控的历史信息引入当前时刻的特征中, 并保留 Transformer 模型训练的可并行性。考虑到预测模型中长期记忆部分由自注意力机制完成, TCN 不需要考虑过长时间的历史信息, 可以不引入空洞卷积。模型中使用的 TCN结构如图 1 所示。
本文使用的 Transformer 模型整体结构如图 2所示, 滑坡位移和雨量等序列数据分别经过 TCN后, 将对应时刻上的特征进行拼接, 经过全连接层进行特征混合, 附加位置编码后输入 Transformer的自注意力层, 输出当前时刻的隐层状态 ht, 最终通过全连接层输出下一时刻的滑坡位移量。
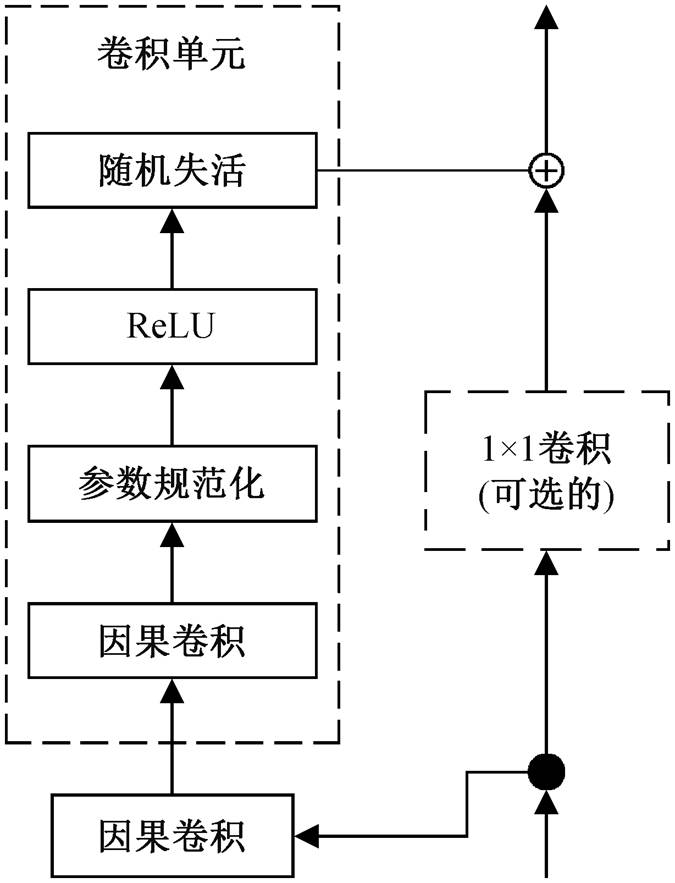
图1 TCN的结构
Fig. 1 Structure of TCN
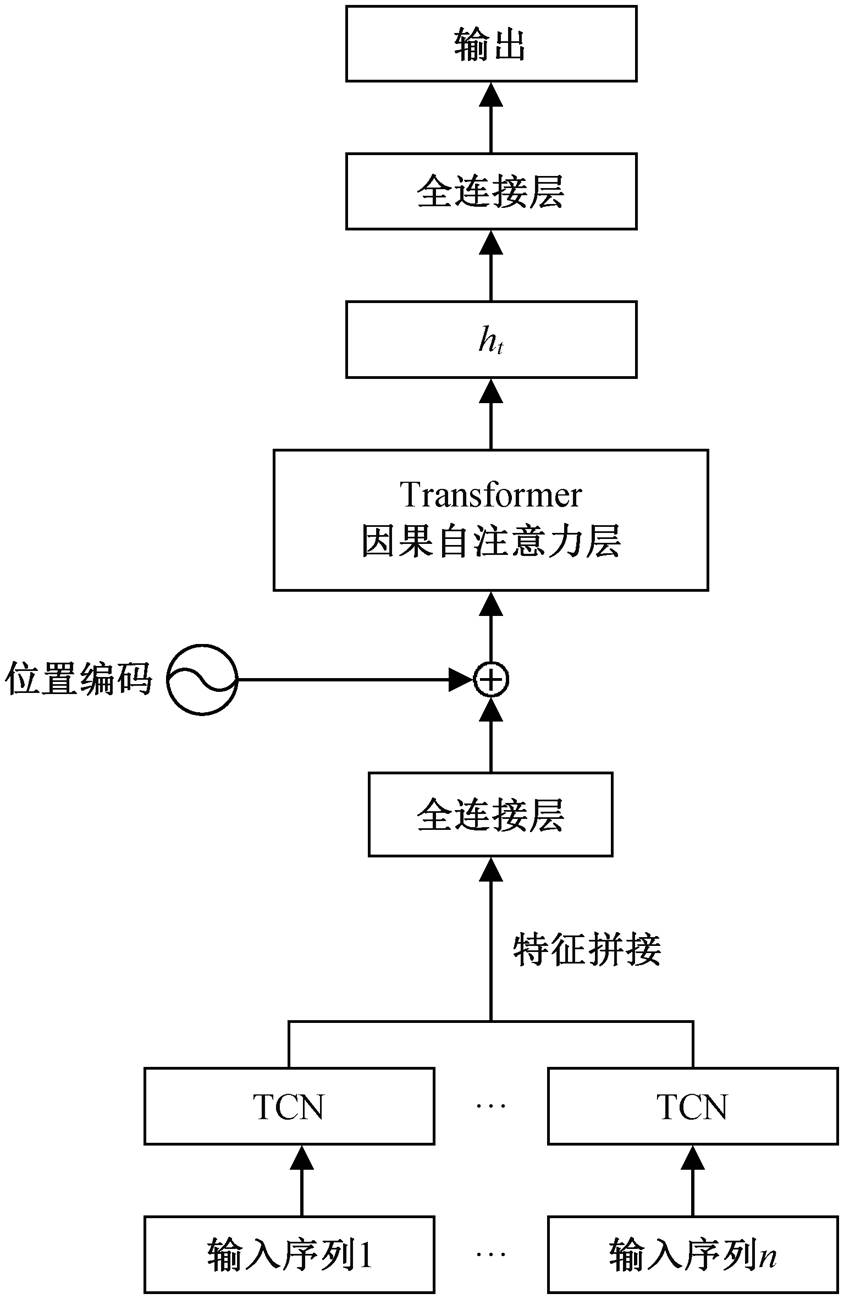
图2 面向滑坡短期位移预测的Transformer模型结构
Fig. 2 Modified Transformer for landslide short-term displacement predictions
基于 Transformer 的滑坡短期位移预测流程如图 3 所示, 具体步骤如下。
1)数据预处理: 使用重采样与插值方法对原始滑坡位移序列进行等间隔化处理后, 采用基于变分模态分解的部分重构方法进行降噪。
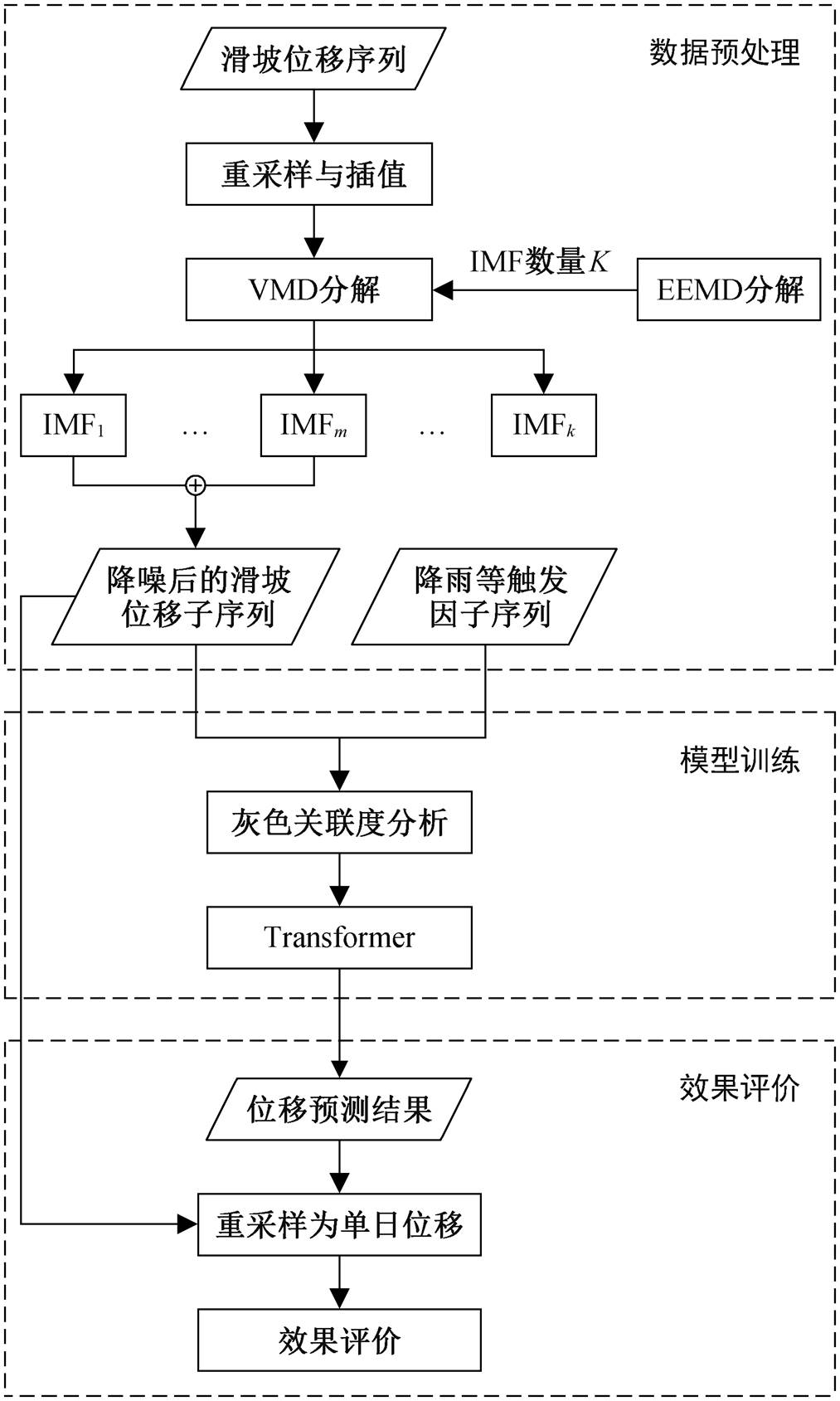
图3 滑坡位移预测流程
Fig. 3 Flowchart of landslide displacement prediction
2)因子遴选与模型训练: 首先采用灰色关联分析(grey relational analysis, GRA)方法[23]为模型确定合适的输入因子, 然后使用训练集进行模型训练与调优。
3)建模效果评价: 使用调优后的模型对滑坡位移序列进行预测, 并以日为单位对 3 日预测结果进行效果评价。
卡门子湾滑坡位于湖北省宜昌市秭归县泄滩乡的陈家湾村, 长江支流泄滩河左侧, 其地理坐标为31°01′27″N, 110°36′50″E。滑坡前缘高程约为 160m, 后缘高程约为 290m, 地形坡度为 35°～45°, 坡向为 315°。滑坡的整体纵长约为 192m, 横宽约为135m, 面积约为 2.7×104m2, 厚度为 10～25m, 总体积约为 5.0×105m3, 主滑方向为 350°[24]。露头地层主要为中侏罗统沙溪庙组, 夹层为黄绿色中厚长石粉砂岩和紫红色中薄粉砂质泥岩, 层理姿态为 30°～ 45°。该滑坡体于 2019 年 11 月 29 日呈现初期变形, 12 月 10 日滑坡体的中下部整体滑动, 部分滑入泄滩河, 造成长达 135m 的 005 乡道、供水管道和 280 伏高压线断裂, 近 36hm2的柑橘果园毁坏, 阻碍 13 个村庄共 12300 人出行[24]。
考虑到该滑坡仍有继续滑动的风险, 中国地质环境监测院(自然资源部地质灾害技术指导中心)与湖北省地质环境总站等单位安装了滑坡监测预警设备, 于 2019 年 12 月开始对卡门子湾滑坡进行专业监测。该监测点适应普适型监测工作, 通过物联网将监测预警设备连接到地质灾害预警管理系统, 滑坡体上的监测设备分布如图 4 所示。该滑坡体的坡面在监测期间持续滑动, 并在汛期呈现明显的加速位移趋势, 发生滑坡灾害的风险较高。因此, 对其开展变形预测具有显著的科研和实践价值。
监测设备中, 裂缝计可以指征滑坡的累计位移, 体现滑坡的整体变形特征。卡门子湾滑坡共布设 3个裂缝计(04LF, 05LF和07LF), 2020 年累计位移与降雨监测数据如图 5 所示。可以发现, 3 个裂缝计的变形趋势基本上一致, 呈上升趋势, 在 2020 年 4 月和 6 月发生过两次明显的变形。结合雨量数据, 发现两次变形均伴随大到暴雨。第一次变形前发生过日降雨量为 48.9mm 的大到暴雨, 第二次变形前存在连续降雨, 并在变形中发生日降雨量为 59.8mm的暴雨, 降雨结束后滑坡的变形逐渐恢复平稳, 据此推断卡门子湾滑坡变形与降雨有明显的关联。整体来看, 卡门子湾滑坡在 2020 年的变形曲线与阶跃型变形曲线[25]较为相似。
本研究选择累计位移量最大的 07LF 监测点开展位移预测工作。考虑到监测时段内共发生过两次快速变形, 我们以第二次快速变形的起始点(2020年 6 月 17 日)为界, 将前半段监测数据用于模型训练(以 8:2 的比例切分为训练集和验证集), 后半段监测数据作为测试集。
正常情况下, 裂缝计的数据记录间隔 5 分钟到1 小时不等。研究表明, 重采样的时间分辨率对预测精度有一定的影响[26]。图 6 显示, 时间分辨率越高, 保留的细节越多, 但过高的时间分辨率会导致单位时间内的位移量较小, 受噪声影响更明显。由于采样间隔为 1 小时的位移曲线无法直观地表达滑坡的形变趋势, 为了尽可能多地保留细节信息, 同时结合普适型滑坡监测、预报工作的实际需求, 本次实验选取 6 小时为重采样后的时间分辨率, 使用二次样条函数插值进行缺失值的补偿。为保持实验数据的一致性, 降雨量数据也以 6 小时为时间分辨率进行重采样。
将原始位移监测数据重采样为等时距时间序列后, 采用 VMD 方法对位移时间序列进行分解。其中, K值参考 EEMD 分解结果设置为 8, 惩罚因子设置为默认值 2000, 噪声容忍度设置为 0, 收敛准则容忍度设置为 1×10−7。图 7 中按频率升序排列展示分解得到的 8 个 IMF。可以发现, 低频率 IMF 体现了滑坡位移的整体趋势及周期性变化, 高频率 IMF则更接近于随机抖动。本文使用概率密度函数(pro-bability density function, PDF)距离来度量IMF 与原始信号之间的相似性[27‒28], 确定 m=5。图 8 展示最终的降噪结果, 可以发现基于 VMD 的部分, 重构方法对滑坡位移序列有较好的降噪效果。本文也尝试使用间隔阈值(interval thresholding, IT)与直接阈值(direct thresholding, DT)方法进行降噪[27‒29], 发现通过阈值保留下来的信号为极高频率的上下抖动, 故放弃此类方法。
基于降噪后的滑坡位移序列进行建模预测时, 首先需要确定模型的输入。在不同变形状态下, 滑坡对外界触发因素的响应存在差异[9], 降雨对滑坡变形的作用存在一定的滞后性[10]。对三峡库区滑坡的相关研究表明, 滑坡发生前 1～2 个月的有效降雨量与滑坡变形有明显的关系[2,8,11]。因此, 选择合适的输入序列长度对模型预测效果十分重要。
灰色关联分析(grey relational analysis, GRA)是一种定量描述因素间关联程度的方法, 能够反映两个因素变化趋势的一致性。为确定合适的输入序列长度, 本文采用 GRA 方法计算前两个月的累计降雨量、累计位移量与未来 3 日位移量的关联度, 取分辨系数 ρ=0.5, 计算结果如图 9 所示。随着时间增加, 滑坡位移量的自相关性持续下降, 30 天后下降速度减缓; 滑坡位移量与累计降雨量的相关性则在9～12 天出现峰值, 随后快速下降, 42 天后趋于稳定。输入序列应在覆盖降雨作用滞后时间的同时, 避免引入过长的历史信息, 因此选取前 30 天的滑坡位移量和累计降雨量序列作为模型的输入。
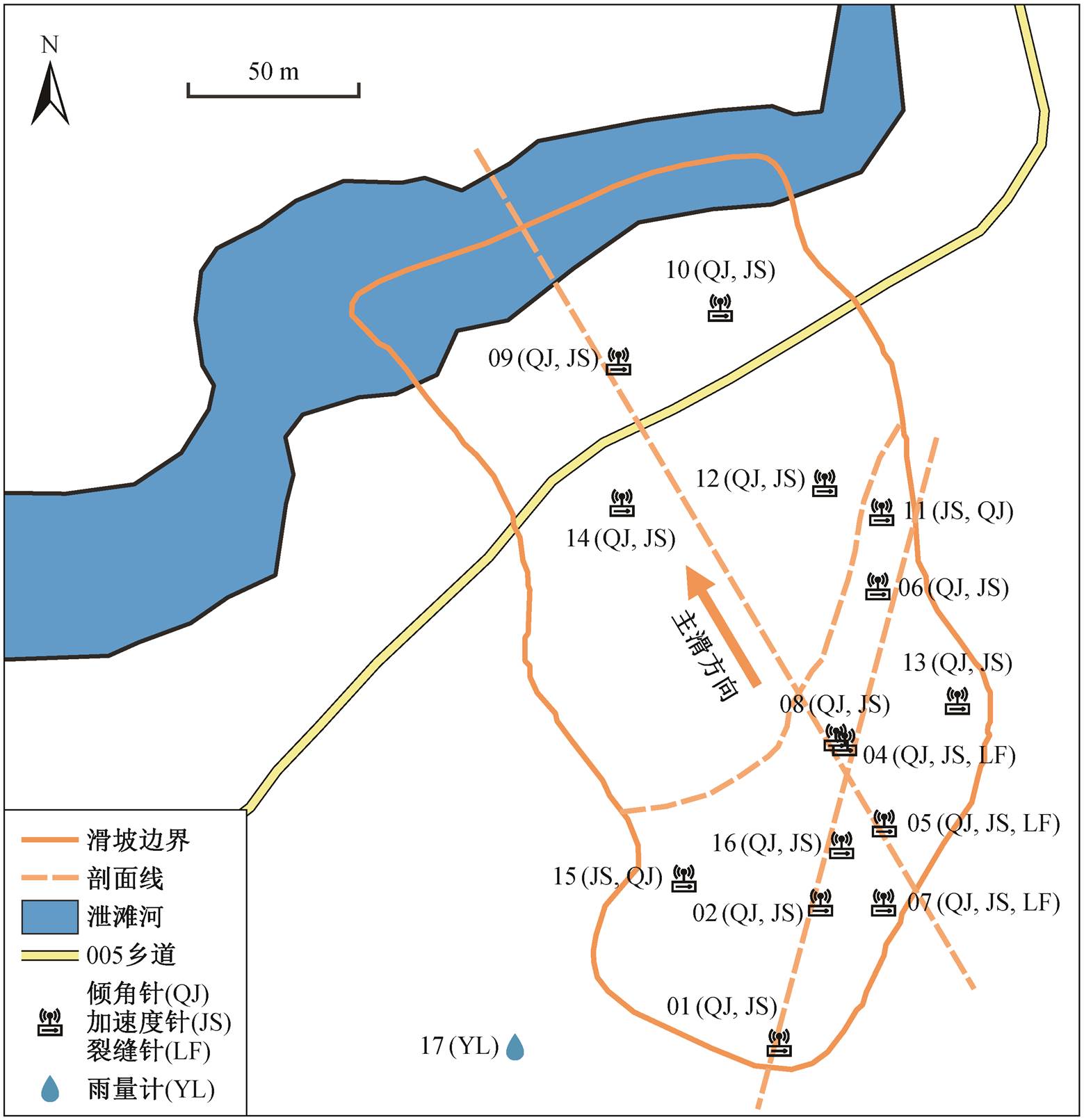
图4 卡门子湾滑坡监测点分布
Fig. 4 Distribution of monitoring points in Kamenziwan landslide
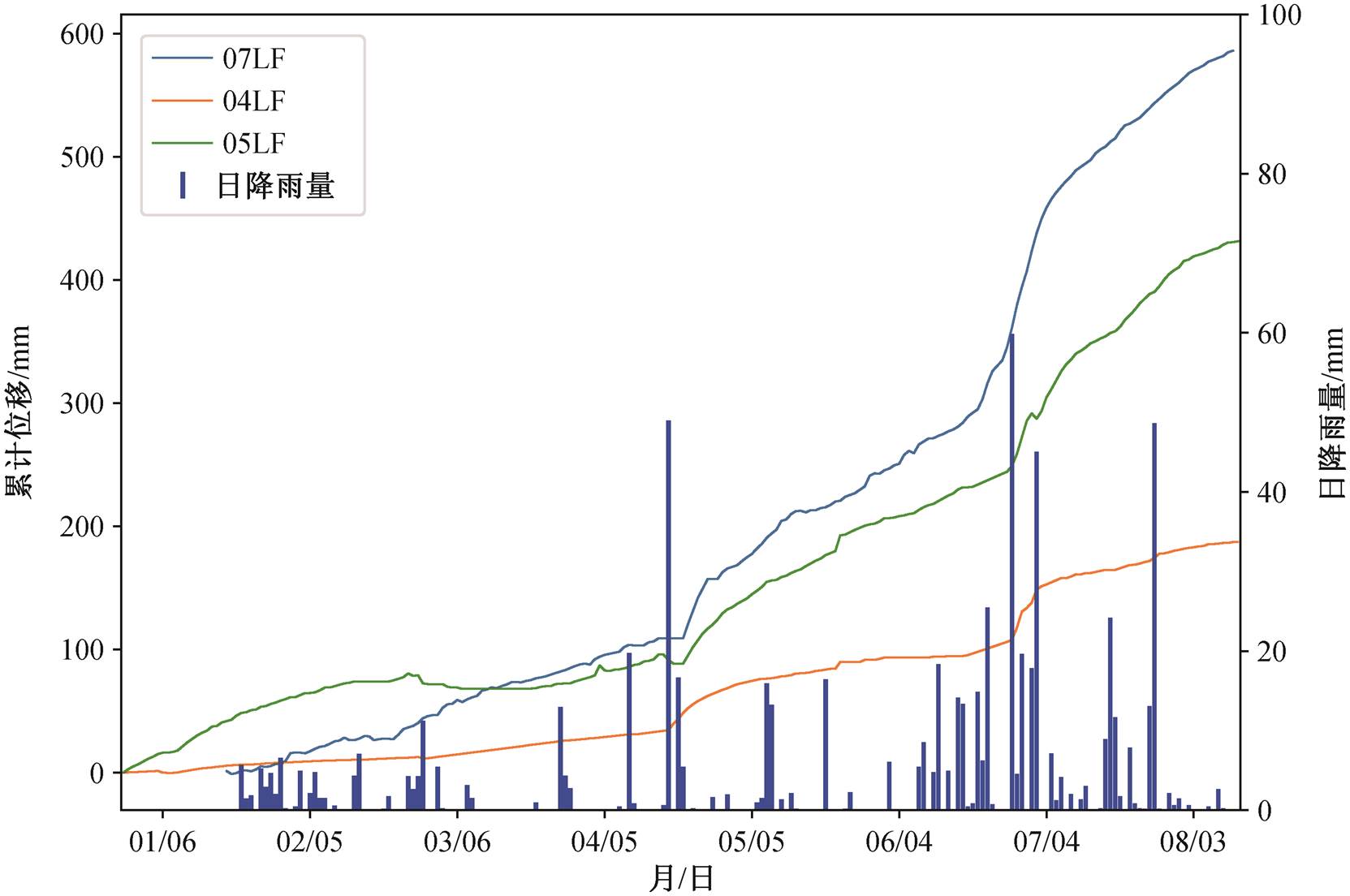
图5 滑坡累计位移和日降雨量监测数据
Fig. 5 Monitoring data of cumulative displacement and daily precipitation
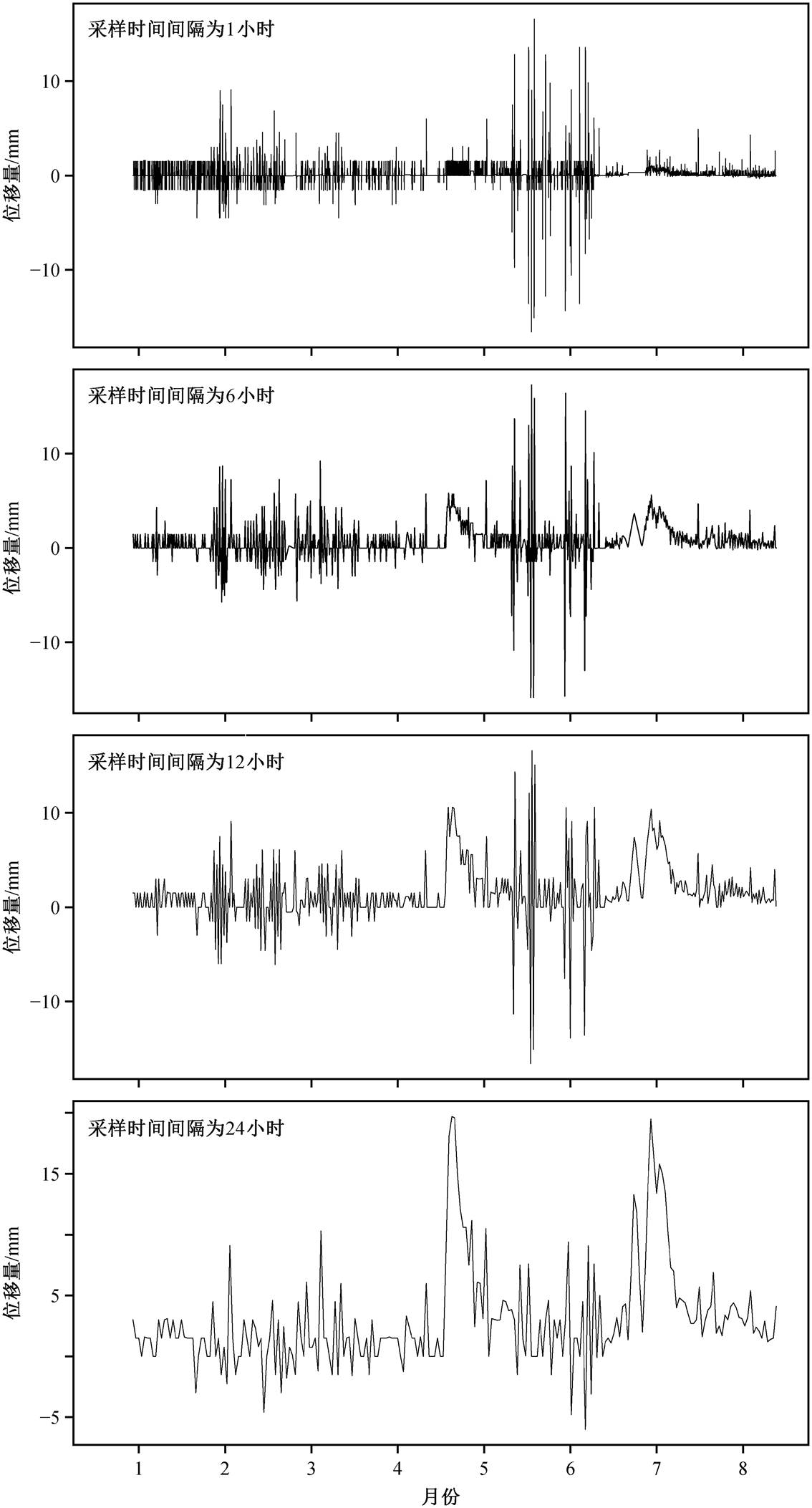
图6 不同时间分辨率下的位移曲线
Fig. 6 Displacement curve with different temporal resolutions
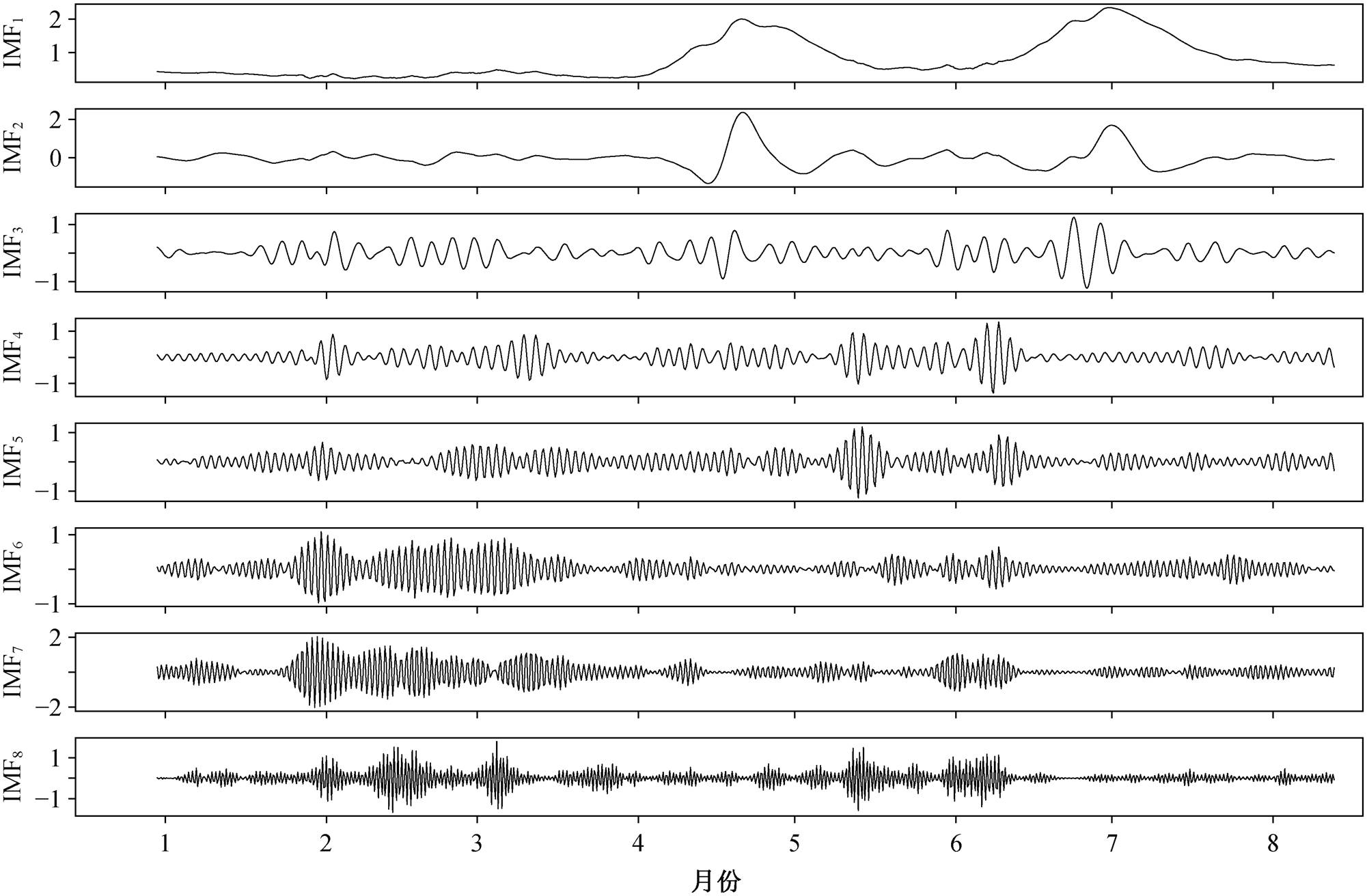
图7 裂隙计 07LF 位移序列分解结果
Fig. 7 Decomposed IMFs of crack meter 07LF
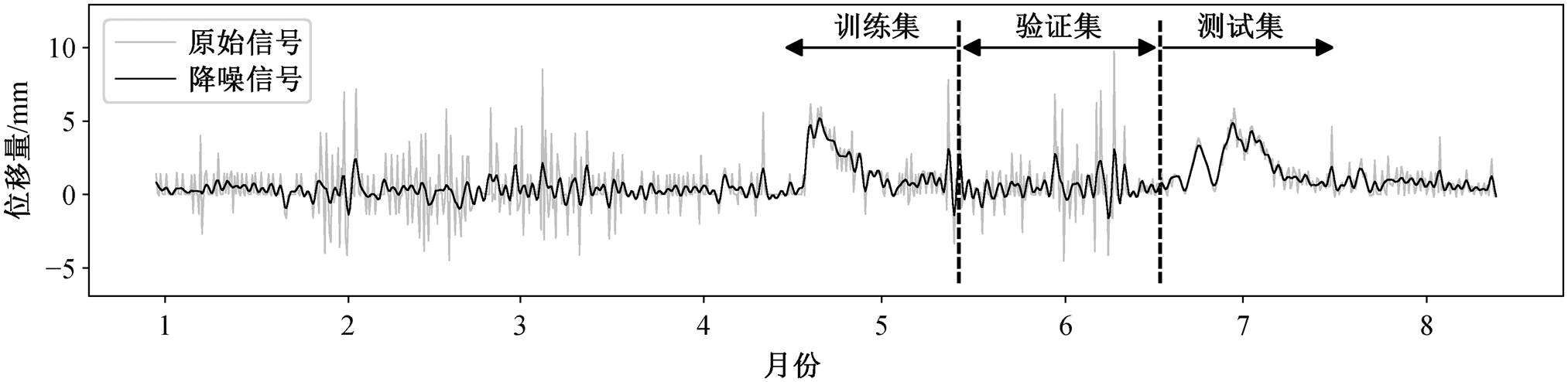
图8 采样间隔为 6 小时时基于 VMD-PR 的降噪结果
Fig. 8 Result of VMD-PR denoising when the sampling interval is six hours
采用自回归方式进行预测时, 也需要将预测时段内的降雨数据作为模型的输入。上述分析结果表明, 近期降雨量与滑坡位移量有较强的相关性。例如, 前一日降雨量与未来 3 日位移量的关联度高达0.77, 未来数日的降雨量对滑坡短期位移量的预测有重要参考价值。鉴于中国气象局和彩云天气等平台均提供较为可靠的短期气象预报数据, 因此可以将预测时段内的降雨数据也作为模型的输入, 提高模型的表达能力。
使用 Pytorch 框架搭建 Transformer 模型, atten-tion 部分使用 fast-transformer 软件包实现。模型的输入为前 30 天的位移和降雨序列以及未来 3 日的降雨数据, 模型的输出为未来 3 日的位移量, 位移量和雨降量被归一化到[0, 1]。模型参数设置如下: 1) TCN 部分, 设置卷积层数为 2, 卷积核大小为 7, 输出通道数为 8, 最终得到的特征会考虑前 12 个时刻,即前 3 日的样本信息; 2)attention层数为 1, 特征大小为 64, attention head 数为 4。模型的总参数量为27.6k。
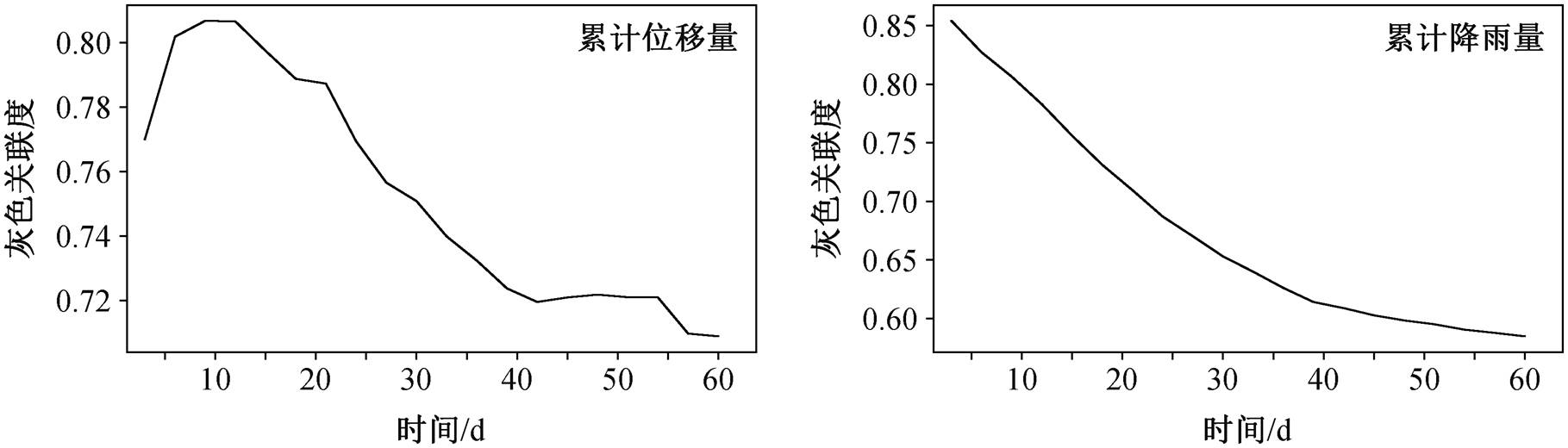
图9 3 日位移量与影响因子间的灰色关联度
Fig. 9 Degrees of gray correlation between 3-day displacement and the influence factors
序列生成任务中, 由于上一时刻的输出会作为样本输入到模型中, 存在误差累积问题。模型训练过程中, 为了降低 teacher forcing 带来的误差累积问题, 采用计划采样方法, 将模型输出与真实标签按一定的概率进行采样, 随着训练轮数的增加, 真实标签的采样率 p逐渐减少至最小值:
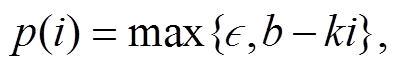(5)
其中, 0≤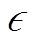
<1 为 p的最小值,0≤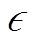<1 为训练开始时的 p, i为训练轮数, 0<k <1是 p随训练轮数的衰减速率。本文采用双解码器 Transformer 方法[30]进行计划采样, 设置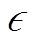= 0, b=1, k=0.005, 损失函数采用L1Loss, 使用 Adam 优化方法[31]完成模型训练。模型在训练集和验证集的收敛状况良好, 没有出现明显的过拟合现象(图 10)。
参照文献[6‒7,9,32‒35], 选用在滑坡位移预测中应用较多的 SVM 和 LSTM 作为比对模型, 对本文模型的预测效果进行对比评价。其中, SVM 模型的输入为近 3 日的降雨量、位移量和未来 3 日的降雨量, 考虑到降雨对滑坡变形影响的滞后性, 将前12 天的累计降雨量也作为模型的输入。采用 PSO算法对 SVM 模型进行参数寻优, 设置粒子种群数为 1000, 最大迭代步数为 300, 惯性权重 w=1, 学习因子 c1=1.5, c2=1.7。设定 SVM 核函数为 RBF核, PSO 寻优范围为 C:=[0,10], γ:=[0,10], 得到最优参数组合为 C = 0.78, γ = 0.22。LSTM 模型与 Trans-former 类似, 拥有对历史信息的记忆能力, 其输入和参数与 Transformer一致, 为近 3 日的降雨量、位移量和未来 3 日的降雨量, LSTM 层数为 1, 隐层状态数为 64。
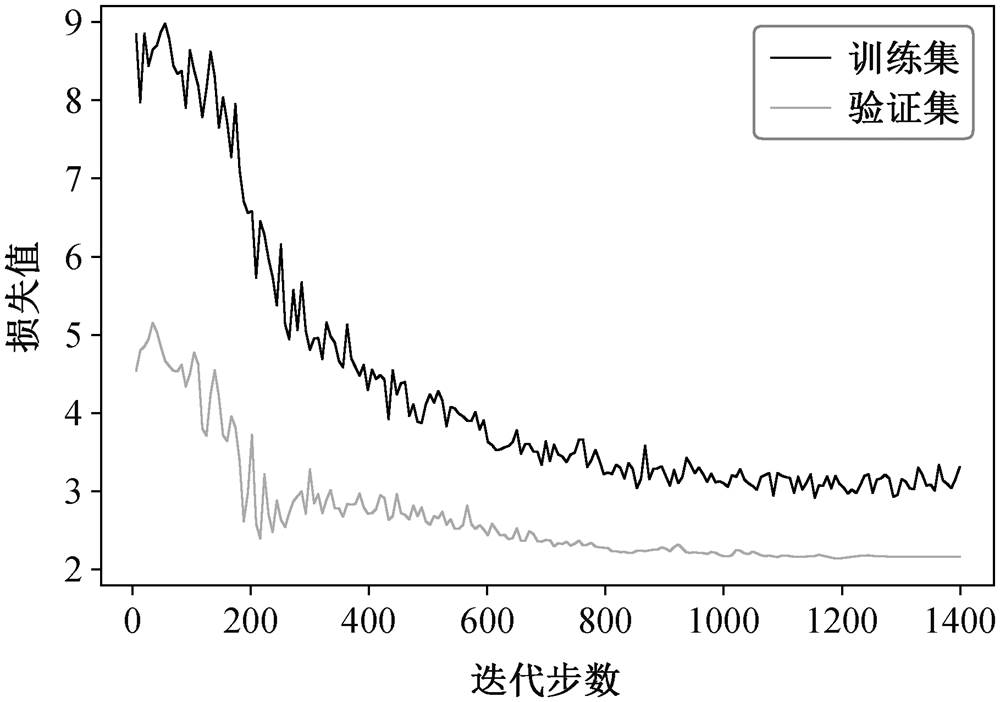
图10 Transformer模型损失曲线
Fig. 10 Loss curve of Transformer
各个模型在测试集的滑坡位移预测结果如图11 所示, 预测精度见表 1。Transformer 的 3 日预测结果 RMSE 分别为 1.708, 1.768 和 1.592, R2分别为0.847, 0.838 和 0.868, 整体预测精度最高。PSO-SVM 和 LSTM 的 1 日预测精度较高, 2 日和 3 日预测精度明显下降。Transformer 的 3 日预测结果较为稳定, 第 2 日和第 3 日预测结果的 RMSE 和 R2均明显优于 PSO-SVM 和 LSTM。
在实际预警工作中, 及时预知可能发生的快速变形是短期预测应用于灾害防治的关键所在。选取快速变形期(2020 年 6 月 17 日至 7 月 14 日, 见图 10中标示)做进一步的分析。表 2 给出各模型在快速变形期的预测精度, Transformer 的 3 日预测精度具有明显的优势, LSTM 的预测精度相比表 1 有较大幅度的下降。图 11 显示, Transformer 的 3 日预测结果在快速变形期与实际监测值曲线贴合较好, PSO-SVM 和 LSTM 的预测结果对实际监测值第一个峰值的预测较差, 且存在一定的滞后现象。模型预测的滞后可能直接导致应急措施不能及时实施, 从而增加滑坡事故带来的生命财产损失。可以通过对预测序列进行平移, 将使得误差值最小的平移值作为滑坡预测的时效性评价指标:
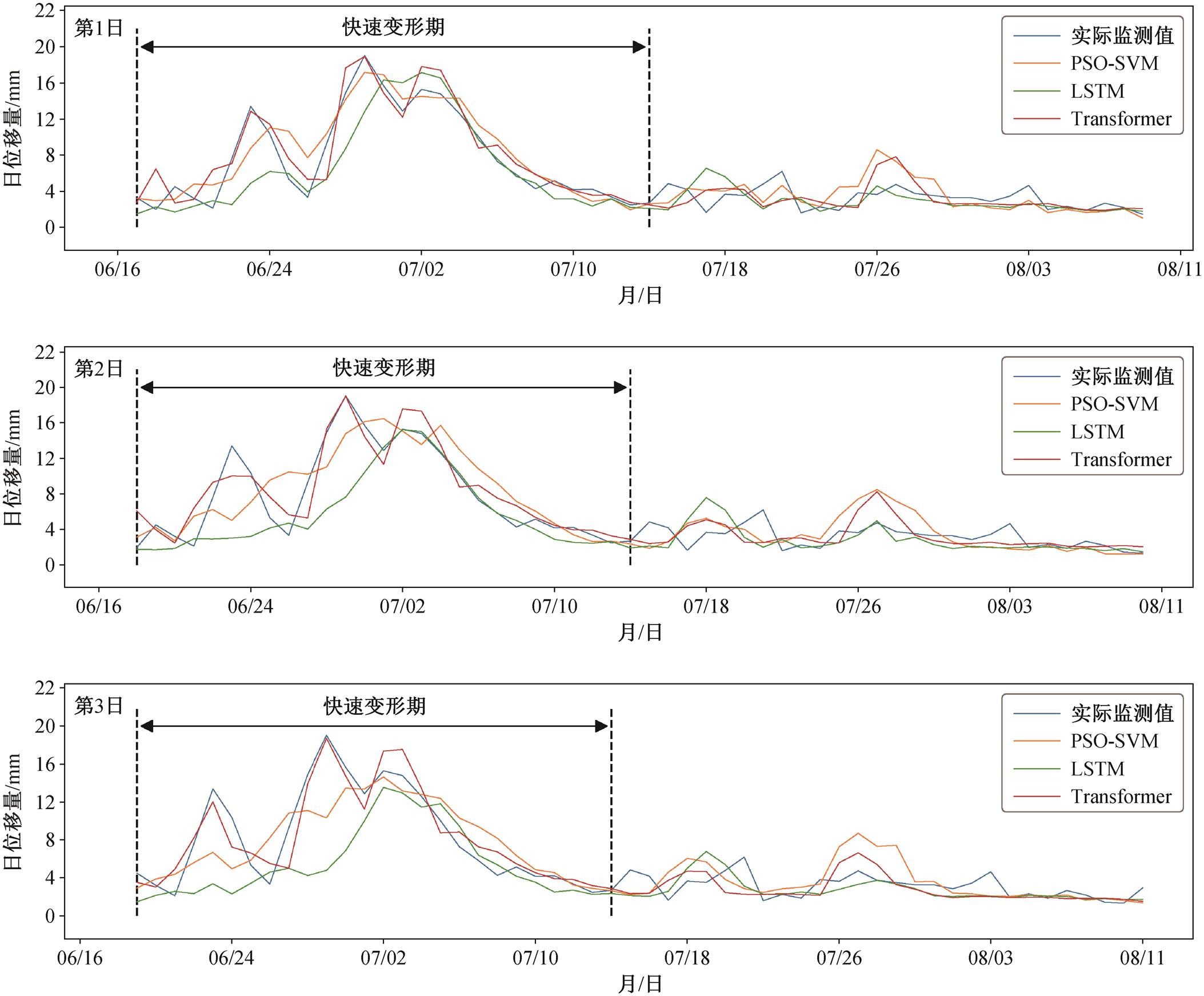
图11 滑坡位移预测结果
Fig. 11 Predict values of landslide displacement
表1 滑坡位移预测精度
Table 1 Accuracy evaluation of landslide displacement predictions
模型第1日第2日第3日RMSER2RMSER2RMSER2 PSO-SVM1.8650.8182.6200.6452.6170.643 LSTM 2.4990.6723.0310.5243.5910.328 Transformer1.7080.8471.7680.8381.5920.868
说明: 粗体数字表示最优结果, 下同。
表2 快速变形期位移预测精度
Table 2 Accuracy evaluation of landslide displacement predictions during the period of accelerating deformation
模型第1日第2日第3日 RMSER2RMSER2RMSER2 PSO-SVM2.1600.8153.3280.5543.2700.557 LSTM2.9860.6464.0130.3525.066−0.063 Transformer1.9800.8452.0460.8311.7840.868
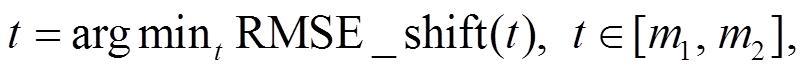(6)
其中, t表示预测序列的滞后天数, t<0 则表示预测序列超前于监测序列; m1和 m2为 t的取值范围, 此处取 m1=−5, m2=5; RMSE_shift(t)为平移后预测序列与真值的 RMSE:
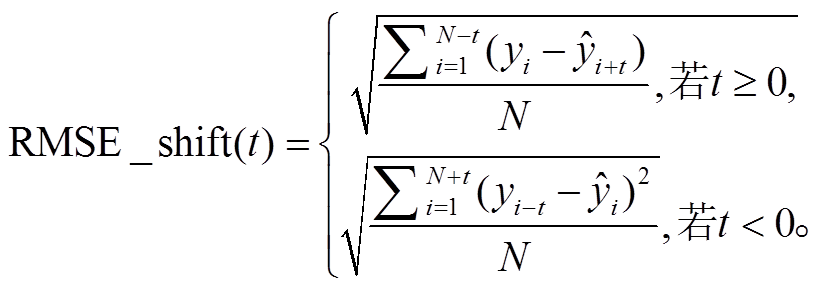(7)
表 3 给出各个模型 3 日预测的滞后天数 t及对应的 RMSE_shift, 可以发现 LSTM 的滞后天数与预测距离正相关, PSO-SVM 第 2 日预测结果的滞后天数为 2, 对预测结果进行平移后误差显著减小。Tr-ansformer 模型的 3 日预测滞后天数均为 0, 比 PSO-SVM 和 LSTM 具有显著优势, 拥有较好的时效性。
由于 Transformer 模型具有输出自注意力的能力, 因此当前时刻注意力构成中, 不同时刻因子的权重反映模型当前时刻对历史信息的注意力分布, 可以辅助研究者判断模型的可信程度[14]。对 fast-transformer 软件包进行修改, 将 Q和 K 添加到模型的输出中, 根据式(4)即可以计算模型的注意力分布。本文模型在快速变形期的注意力分布如图 12 所示, 对其中的注意力强度进行了归一化处理, 4 个head 的注意力总和为 1。可以发现, head1～head3 的注意力集中分布在日位移量的峰值以及集中降雨时段, head4 的注意力则分散地分布在快速变形期之前。卡门子湾的滑坡变形受降雨的影响较明显, 加速变形往往发生在大规模降雨之后, 模型对降雨事件的关注符合滑坡变形规律。模型对位移峰值的关注, 一方面可能因为滑坡位移呈阶跃型, 位移峰值往往出现在降雨之后数日, 两类事件的注意力有所重叠; 另一方面, 在降雨导致的快速变形结束后, 变形将逐渐恢复平稳, 位移峰值的出现标志着短期内位移速率将快速下降, 模型对位移峰值的关注有助于对整体位移趋势的把控。
图 13 进一步展示 4 个 attention head 的注意力随时间远近的变化情况。可以发现, head1～head3 的注意力分布集中在近期信息上, 并随着时间的增加而衰减, 第 11 日明显下降, 基本上不关注 15 日以后的信息。这一结果与 3.2 节中的相关性分析结果基本上吻合。head4 则重点关注远距离信息, 注意力主要分布在 17～30 日。总体而言, 从注意力分布来看, 该模型能够有效地结合长期信息与短期信息, 重点关注位移峰值和集中降雨等重点事件, 对滑坡位移规律的把握较为准确, 模型的关注点与地质规律基本上一致, 具有较高的可信度。
本文以普适型滑坡监测工作为背景, 结合滑坡短期位移预测的应用场景及需求, 使用时序卷积网络(TCN)对 Transformer 模型进行改造, 提出一种基于 Transformer 的滑坡短期位移预测模型, 并在卡门子湾滑坡体上开展实例验证, 应用效果良好, 说明模型具有可行性和有效性。
本研究的滑坡位移短期预测建模中, 所用数据的时间分辨率较高, 原始数据的信噪比较低, 采用VMD-PR 方法能够有效去除原始信号中的高频噪声。针对位移预测的时序自回归问题, 本研究采用TCN 替代原始 Transformer 中的 embedding 层, 对Transformer 模型进行改造, 所提模型可以成功地应用于滑坡位移预测, 在实例检验中具有较高的预测精度, 输出的 3 日位移预测值 RMSE 均在 1.8 mm 以内, 在快速变形期的预测优势尤为明显, 总体上优于 SVM 和 LSTM 两种常见模型。与传统模型相比, 本文模型在位移预测中能够准确地把握位移突变点, 较好地克服突变点滞后问题。实例研究中, 通过分析 Transformer 的注意力分布, 发现所提模型能够有效地结合长期信息与短期信息, 并重点关注位移峰值和集中降雨等关键事件, 模型架构具有较高的可信度。
表3 快速变形期位移预测时效性评价
Table 3 Timeliness evaluation of landslide displacement predictions during the period of accelerating deformation
模型 第1日第2日第3日tRMSE_shifttRMSE_shifttRMSE_shift PSO-SVM02.16022.75903.270 LSTM12.81223.57524.155 Transformer01.98002.04601.784
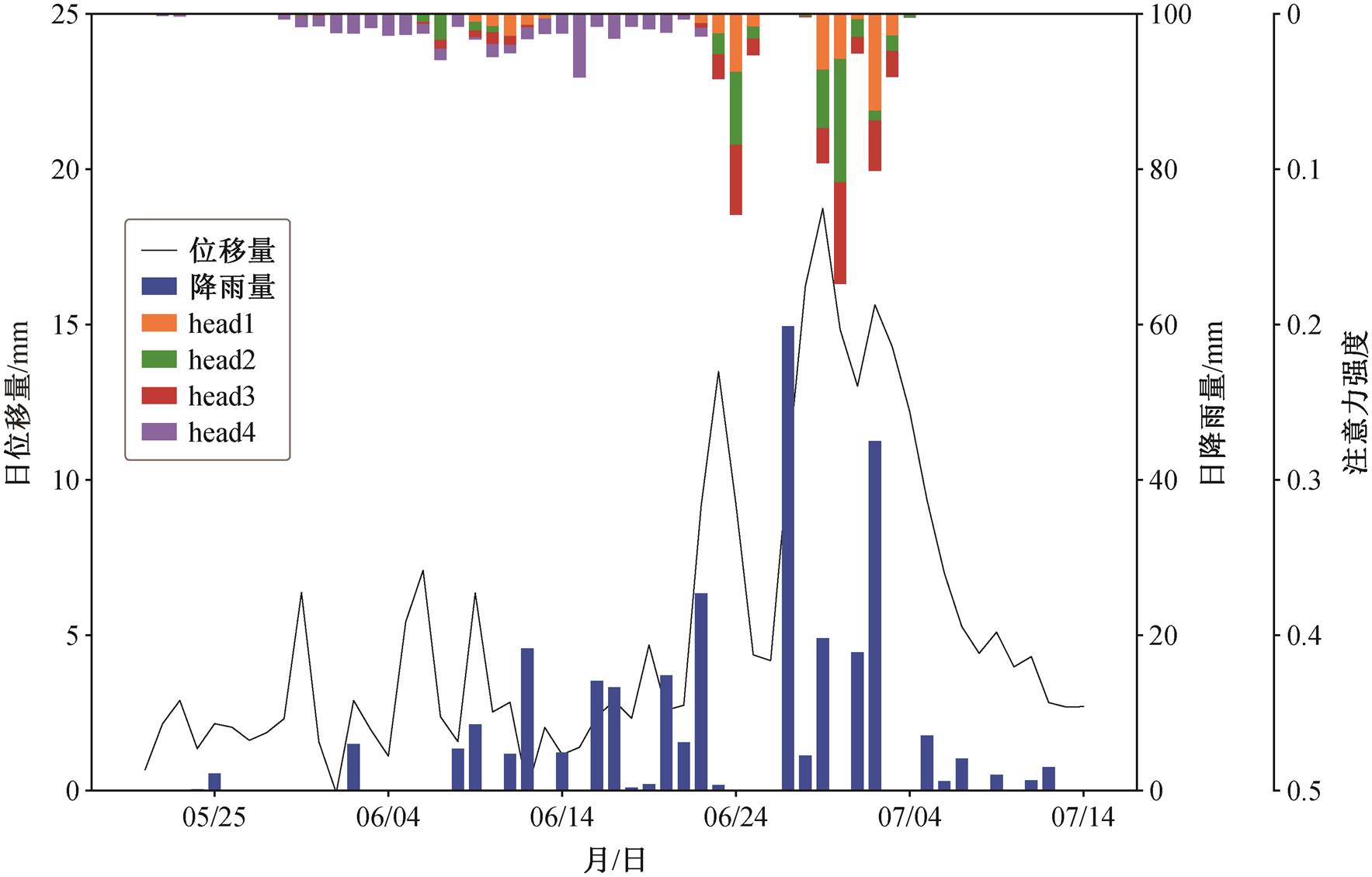
图12 Transformer 注意力分布
Fig. 12 Attention distribution of Transformer
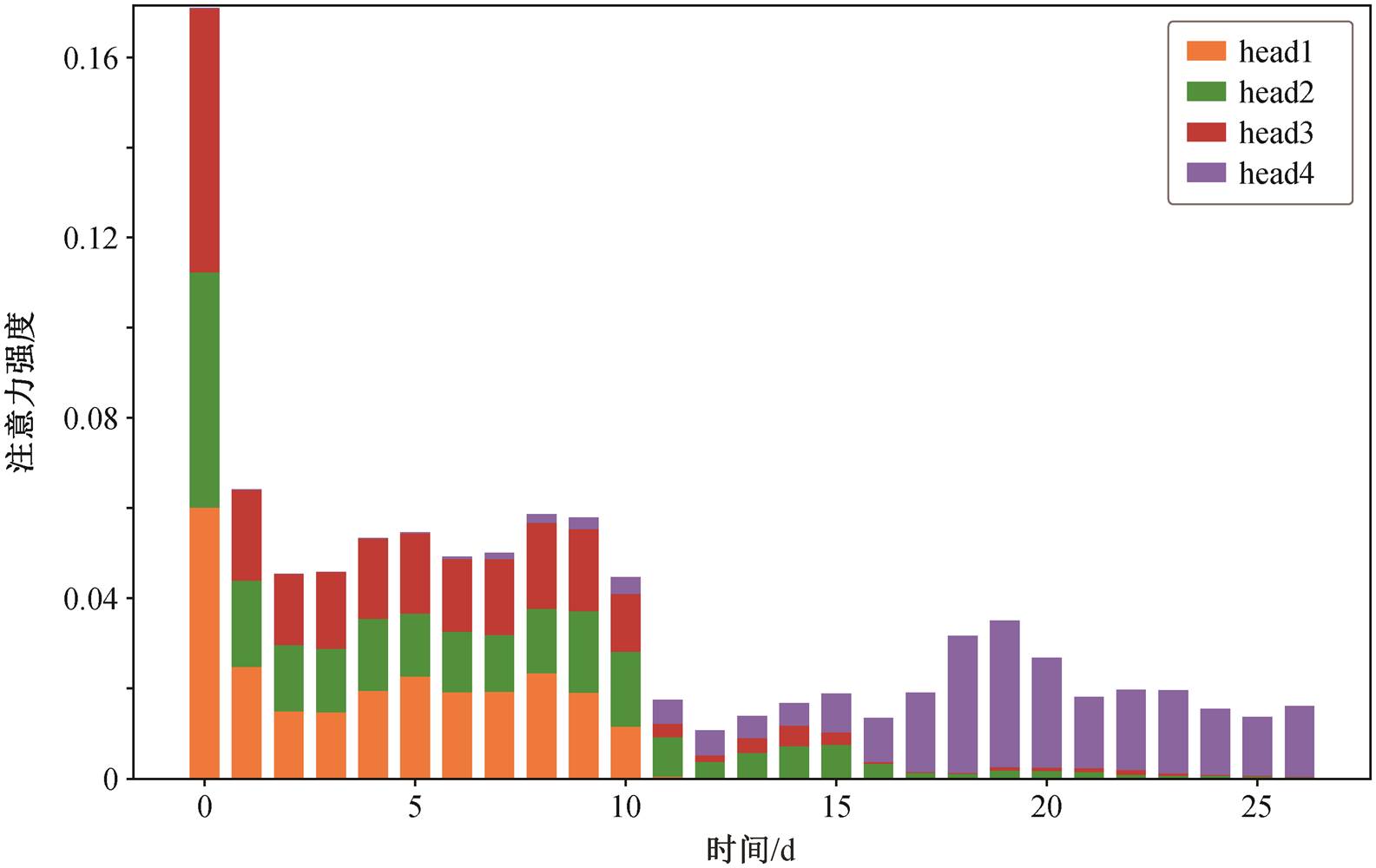
图13 注意力随时间距离的分布
Fig. 13 Attention distribution over time span
得益于 Transformer 的并行化优势, 本文模型的训练速度优于同为深度学习方法的 LSTM, 但训练和预测耗时明显高于 SVM 等传统机器学习模型,高训练成本也使得自动在线调优存在很大的困难。如何提升模型的训练和预测效率, 将模型快速应用到大量滑坡监测点, 是未来研究中应当关注的问题。同时, 不同类型的滑坡(土质坡、岩质坡、黄土型滑坡、第四系与基岩混合边坡等)往往呈现不同的变形规律, 本文模型投入大规模实际应用前, 还应补充针对不同类型滑坡的建模实验, 进一步明确模型的适用范围。
参考文献
[1] 许强, 黄润秋, 李秀珍. 滑坡时间预测预报研究进展. 地球科学进展, 2004, 19(3): 478–483
[2] 杜娟, 殷坤龙, 柴波. 基于诱发因素响应分析的滑坡位移预测模型研究. 岩石力学与工程学报, 2009, 28(9): 1783–1789
[3] 张俊, 殷坤龙, 王佳佳, 等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究. 岩石力学与工程学报, 2015, 32(2): 382–391
[4] Meng M, Chen Z Q, Huang D, et al. Displacement prediction of landslide in Three Gorges Reservoir area based on H-P filter, ARIMA and VAR models. Yantu Lixue/Rock and Soil Mechanics, 2016, 37: 552–560
[5] Huang F, Huang J, Jiang S, et al. Landslide displace-ment prediction based on multivariate chaotic model and extreme learning machine. Engineering Geology, 2017, 218: 173–186
[6] Zhu X, Xu Q, Tang M, et al. Comparison of two optimized machine learning models for predicting dis-placement of rainfall-induced landslide: a case study in Sichuan Province, China. Engineering Geology, 2017, 218: 213–222
[7] 杨背背, 殷坤龙, 杜娟. 基于时间序列与长短时记忆网络的滑坡位移动态预测模型. 岩石力学与工程学报, 2018, 37(10): 2334–2343
[8] Sun M, Xu W, Wang H, et al. A novel hybrid intelligent prediction model for valley deformation: a case study in Xiluodu Reservoir Region, China. Com-puters, Materials and Continua, 2020, 66(1): 1057–1074
[9] Liu Y, Xu C, Huang B, et al. Landslide displacement prediction based on multi-source data fusion and sensitivity states. Engineering Geology, 2020, 271: 105608
[10] 李麟玮, 吴益平, 苗发盛, 等. 考虑变形状态动态切换的阶跃型滑坡位移区间预测方法. 岩石力学与工程学报, 2019, 38(11): 2272–2287
[11] Zhang L, Shi B, Zhu H, et al. PSO-SVM-based deep displacement prediction of Majiagou landslide consi-dering the deformation hysteresis effect. Landslides, 2021, 18(1): 179–193
[12] Zhou H, Zhang S, Peng J, et al. Informer: Beyond efficient transformer for long sequence time-series forecasting // Proceedings of the AAAI Conference on Artificial Intelligence, Online Meeting, 2021: 11106–11115
[13] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Advances in Neural Information Proces-sing Systems, 2017, 8(1): 8–15
[14] Yanagimto H, Hashimoto K, Okada M. Attention visualization of gated convolutional neural networks with self attention in sentiment analysis // Procee-dings of ICMLDE 2018. Sydney: IEEE, 2019: 83–90
[15] Dragomiretskiy K, Zosso D. Variational mode decom-position. IEEE Transactions on Signal Processing, 2014, 62(3): 531–544
[16] Liu W, Cao S, Chen Y. Applications of variational mode decomposition in seismic time-frequency analy-sis. Geophysics, 2016, 81(5): V365–V378
[17] Li F, Zhang B, Verma S, et al. Seismic signal denoi-sing using thresholded variational mode decompose-tion. Exploration Geophysics, 2017, 49(4): 450–461
[18] Liu H, Mi X, Li Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LS-TM network and ELM. Energy Conversion and Mana-gement, 2018, 159: 54–64
[19] Niu H, Xu K. A hybrid model combining variational mode decomposition and an attention-GRU network for stock price index forecasting. Mathematical Bio-sciences and Engineering: Applied Intelligence, 2020, 17(6): 7151–7166
[20] Bisoi R, Dash P K, Parida A K. Hybrid Variational Mode Decomposition and evolutionary robust kernel extreme learning machine for stock price and move-ment prediction on daily basis. Applied Soft Compu-ting Journal, 2019, 74: 652–678
[21] Komaty A, Boudraa A, Dare D. EMD-based filtering using the hausdorff distance // 2012 IEEE Internatio-nal Symposium on Signal Processing and Information Technology. Ho Chi Minh City: IEEE, 2012: 292–297
[22] Bai S, Kolter J Z, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling [EB/OL]. (2018–04–19)[2021–11–09]. https://arxiv.org/abs/1803.01271
[23] Liu S, Lin Y. Introduction to grey systems theory. Understanding Complex Systems, 2010, 68: 1–18
[24] Yin Y, Huang B, Zhang Q, et al. Research on recently occurred reservoir-induced Kamenziwan rockslide in Three Gorges Reservoir, China. Landslides, 2020, 17 (8): 1935–1949
[25] 许强, 汤明高, 徐开祥, 等. 滑坡时空演化规律及预警预报研究. 岩石力学与工程学报, 2008, 27(6): 1104–1112
[26] Wenyi Z, Juan M, Mingzhi Z, et al. Effects of sampl-ing frequency on short-term prediction of landslide displacement: a case study of Kamenziwan landslide. PervasiveHealth: Pervasive Computing Technologies for Healthcare, 2020: 144–148
[27] Komaty A, Boudraa A O, Augier B, et al. EMD-based filtering using similarity measure between probability density functions of IMFs. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27–34
[28] Yang G, Liu Y, Wang Y, et al. EMD interval threshol-ding denoising based on similarity measure to select relevant modes. Signal Processing, 2015, 109: 95–109
[29] Kopsinis Y, McLaughlin S. Development of EMD-based denoising methods inspired by wavelet thre-sholding. IEEE Transactions on Signal Processing, 2009, 57(4): 1351–1362
[30] Mihaylova T, Martins A F T. Scheduled sampling for transformers // ACL 2019 — 57th Annual Meeting of the Association for Computational Linguistics, Proce-edings of the Student Research Workshop. Florence, 2019: 351–356
[31] Kingma D P, Ba J L. Adam: a method for stochastic optimization // 3rd International Conference on Lear-ning Representations, ICLR 2015 — Conference Track Proceedings. San Diego, 2015: 1–15
[32] Ren F, Wu X, Zhang K, et al. Application of wave- let analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping landslide in the Three Gorges, China. En-vironmental Earth Sciences, 2015, 73(8): 4791–4804
[33] Li L W, Wu Y P, Miao F S. Prediction of non-equidistant landslide displacement time series based on grey wolf support vector machine. Journal of Zhejiang University (Engineering Science), 2018, 52 (10): 1998–2006
[34] Jiang H, Li Y, Zhou C, et al. Landslide displacement prediction combining LSTM and SVR algorithms: a case study of shengjibao landslide from the three gorges reservoir area. Applied Sciences, 2020, 10(21): 1–21
[35] Xing Y, Yue J, Chen C, et al. A hybrid prediction model of landslide displacement with risk-averse adaptation. Computers and Geosciences, 2020, 141: 104527
A Transformer-Based Model for Short-Term Landslide Displacement Prediction
Abstract A Transformer-based short-term landslide displacement prediction model is proposed by combining temporal convolutional network (TCN) with a Transformer decoder. This model takes the preprocessed displace-ment and rainfall sequences as input and outputs the displacement predictions for the next three days in a time-series autoregressive manner. The experimental results show that the model achieves higher prediction accuracy than support vector machine (SVM) and long short-term memory (LSTM), and performs particularly well during predicting rapid deformation periods. At the same time, through the analysis of the attention mechanism of the model, it is found that the model focuses on the peak of displacements and heavy rainfalls, indicatingthat the model is reasonably reliable.
Key words slope engineering; landslide displacement; short-term prediction; Transformer; attention mechanism