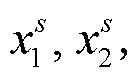
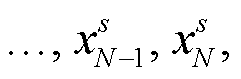 上角标s代表震源。如果忽略爆破时刻的不同, 每个震源都是相同的爆炸源, 即震源机制是相同的。所以, 在频率域中, 可以用F(ω)表示单个爆炸源。N个爆炸震源组成的混合震源Fall(ω)[14]在频率域中表示为
上角标s代表震源。如果忽略爆破时刻的不同, 每个震源都是相同的爆炸源, 即震源机制是相同的。所以, 在频率域中, 可以用F(ω)表示单个爆炸源。N个爆炸震源组成的混合震源Fall(ω)[14]在频率域中表示为doi: 10.13209/j.0479-8023.2022.047
河北省地震科技星火计划(DZ20200827054)和国家自然科学基金(41874071)资助
北京大学学报(自然科学版) 第58卷 第5期 2022年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 58, No. 5 (Sept. 2022)
收稿日期: 2021–06–01;
修回日期: 2022–05–22
摘要 根据稳相点分析的叠加方法原理, 提出一种波形叠加方法, 消除台站记录中高铁波场的串扰噪声, 生成虚拟道集, 并用合成的高铁数据进行验证。通过建立高铁桥梁振动方程, 获得精细的高铁震源时间函数, 然后使用有限元方法,在分层介质模型中进行高速铁路波场正演模拟计算, 并对不同速度的高铁列车正演模拟记录进行时移叠加, 获得虚拟道集, 从而验证叠加方法的正确性。
关键词 高铁; 干涉场; 震源时间函数; 虚拟道集
高铁列车经过高架桥时会引起桥体振动, 并通过桥墩传导到地下。关于高铁列车经过桥体的振动模型和高铁通过时引起周围地表振动的响应及频率, 已有大量的研究[1‒9]。然而, 高铁振动信号复杂, 非常难以处理。温景充等[10]基于新的密集观测资料, 指出高铁震源激发的波场是稳定的、重复性强的地震干涉波场。高铁相邻桥墩的震源之间存在串扰噪声[11], 如果采用传统地震勘探中常用的互相关等混响分离方法, 无法得到正确的虚拟道集。最近, 石永祥等[12]通过分析高铁波场的特征, 得到其相干振幅和相干相位的解析表达式, 发现高铁波场有干涉波场的特性, 存在主瓣, 可以利用这个特征进行地下介质成像。通过稳相点分析, 不同速度的列车记录叠加可以消除源与源之间的串扰噪声, 也可以生成高铁的虚拟道集[13]。
为了验证生成虚拟道集的原理, 需要正演出高速铁路通过高架桥的波场数据。本文参照 Wu 等[5]模拟列车通过桥梁时引发周围地表位移的振动模型, 对高架桥采用欧拉‒伯努利桥梁模型, 对桩体和土体采用开尔文体模型, 以便得到更贴近真实情况的高铁震源时间函数。利用得到的震源时间函数, 通过谱元法正演弹性条件下的高速铁路波场, 得到波场合成数据。基于对合成数据的处理, 合成虚拟道集, 并用合成的高铁数据验证该方法的正确性。
地震勘探中有由N个震源组成的测线, 设测线上震源排布沿 x轴方向, 震源的位置依次为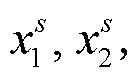
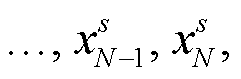 上角标s代表震源。如果忽略爆破时刻的不同, 每个震源都是相同的爆炸源, 即震源机制是相同的。所以, 在频率域中, 可以用F(ω)表示单个爆炸源。N个爆炸震源组成的混合震源Fall(ω)[14]在频率域中表示为
上角标s代表震源。如果忽略爆破时刻的不同, 每个震源都是相同的爆炸源, 即震源机制是相同的。所以, 在频率域中, 可以用F(ω)表示单个爆炸源。N个爆炸震源组成的混合震源Fall(ω)[14]在频率域中表示为
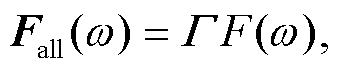 (1)
(1)
其中, ![]() 表示震源编码矩阵[14‒16]:
表示震源编码矩阵[14‒16]:
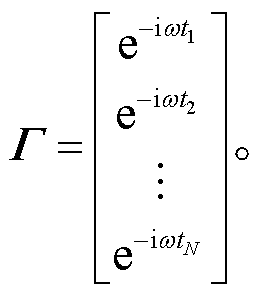 (2)
(2)
声波方程建立了压强与速度之间的关系, 地震勘探中用声波方程进行数据的正演及处理。频率域中, 声波方程的格林函数可以表示为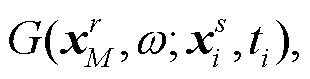 位置
位置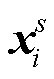 处ti时刻激发的震源在位置
处ti时刻激发的震源在位置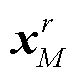 处的格林函数简写为标量
处的格林函数简写为标量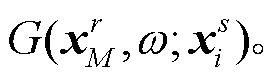
震源激发的波场被台站接收。设有M个台站, 台站的位置坐标依次为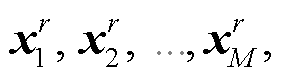 上角标r代表台站。由混合震源Fall(ω)在
上角标r代表台站。由混合震源Fall(ω)在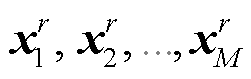 处形成的波场
处形成的波场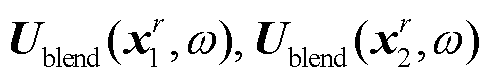 和
和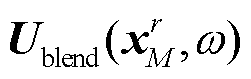 可表示为
可表示为
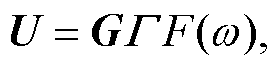 (3)
(3)
其中,
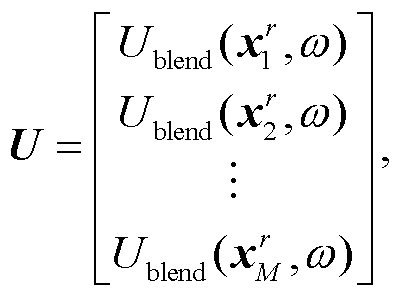 (4)
(4)
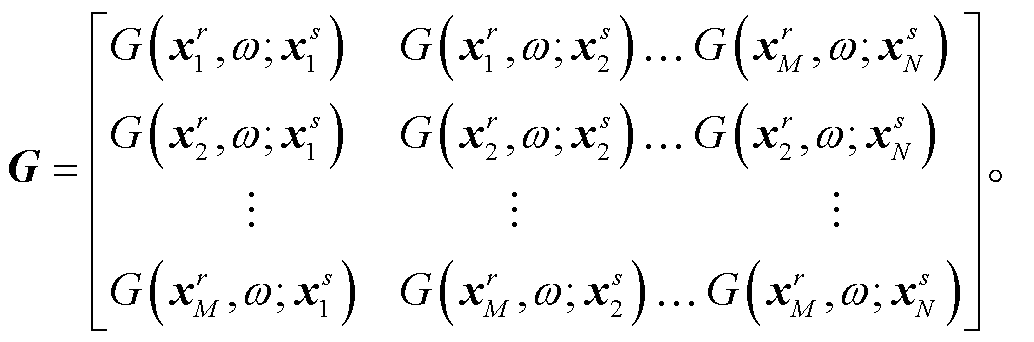 (5)
(5)
在进行混合震源采集分离时, 分离出式(5)右边的格林函数, 即需要在式(3)两边同时右乘![]() 的伪逆算子
的伪逆算子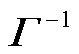 [14‒16]:
[14‒16]:
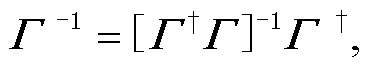 (6)
(6)
其中,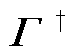 表示Γ的转置共轭。式(3)两边同时右乘伪逆算子
表示Γ的转置共轭。式(3)两边同时右乘伪逆算子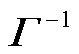 , 则有
, 则有
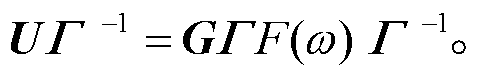 (7)
(7)
将式(6)代入式(7):
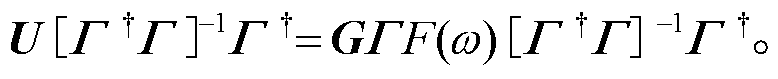 (8)
(8)
式(8)的两边同时出现 [Γ†Γ]-1, 是一个调节所有频率下振幅的因子[16]。将式(8)的右边 ΓΓ†一项展开:
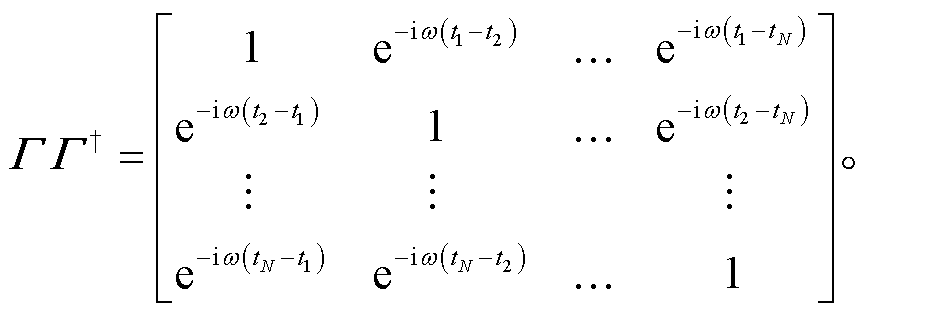 (9)
(9)
如果震源编码矩阵 Γ 中的震源激发时间t1, t2, …, tN是随机的, 即满足下式[17]:
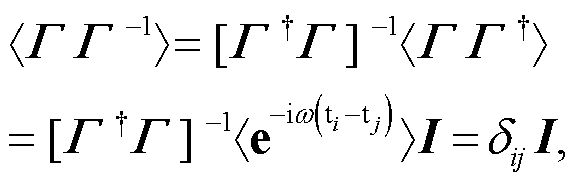 (10)
(10)
其中, 〈∙〉表示集平均(ensemble average), I表示单位 矩阵。
若震源激发时间t1, t2, …, tN是随机的, 那么式(9)是对角线为1, 非对角线为0的单位矩阵, 即满足式(10), 那么式(10)就能保证串扰噪声的压制。因此, 震源激发时间的随机性保证了地震勘探中多震源数据的分离, 能够压制串扰噪声, 这是地震勘探中混合震源数据分离的关键[14‒18]。
实际上, 高速铁路波场的震源激发时间延迟不是随机的, 而是依次等间距线性延迟激发, 不满足式(10)。所以, 串扰噪声不能通过传统地震勘探方法压制, 而是要基于高速铁路波场的特点提取虚拟格林函数, 并合成虚拟道集。
假设列车以恒定的速度v在高架桥上移动, 每个桥墩之间的间距都为L, 高速铁路波场的震源激发间隔时间不是随机的, 都是t=L/v。列车经过每个桥墩都会产生垂向振动, 可以将每个桥墩视为震源。台站的位置坐标是xg, 第l号桥墩震源的位置坐标是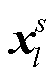 , 上角标s代表震源, 下角标l代表桥墩编号。忽略震源激发时刻的差别, 由
, 上角标s代表震源, 下角标l代表桥墩编号。忽略震源激发时刻的差别, 由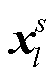 处桥墩产生的震源时间函数在频率域F(ω)中是相同的。
处桥墩产生的震源时间函数在频率域F(ω)中是相同的。
高速列车行驶方向的单位向量是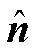 。取第n号桥墩震源的激发时刻为0时刻, 那么高速列车在高架桥上激发的移动组合源Fall(ω)可以在频率域中表示为
。取第n号桥墩震源的激发时刻为0时刻, 那么高速列车在高架桥上激发的移动组合源Fall(ω)可以在频率域中表示为
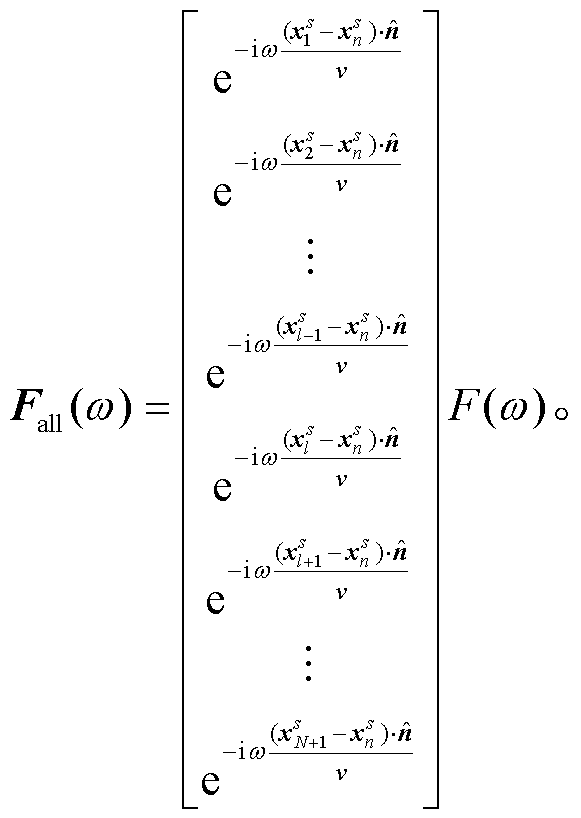 (11)
(11)
对比式(1)、(2)和(11) 可以看出, 式(1)和(2)中的震源激发时间 t1, t2, …, tN 是随机的, 需要满足 式(10); 式(11)中高铁震源的激发时间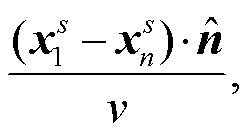
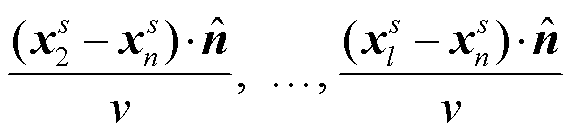 不是随机的, 而是有规律地依次线性叠加, 不满足式(10)。
不是随机的, 而是有规律地依次线性叠加, 不满足式(10)。
桥墩震源的弹性动力学方程的格林函数在时间域中可以表示为二阶张量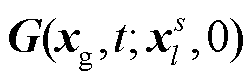 , 即为列车以速度v行驶, 在0时刻到达
, 即为列车以速度v行驶, 在0时刻到达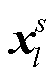 处桥墩后激发的震源, 在台站位置xg处t时刻的格林函数。当认为垂直向下的Z方向是桥墩施加力的主要方向, 同时理论分析中只讨论竖直方向的位移分量时, 则只有分量
处桥墩后激发的震源, 在台站位置xg处t时刻的格林函数。当认为垂直向下的Z方向是桥墩施加力的主要方向, 同时理论分析中只讨论竖直方向的位移分量时, 则只有分量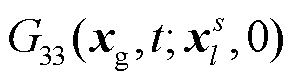 (简写为
(简写为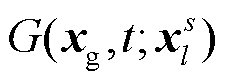 , 在频率域中记为
, 在频率域中记为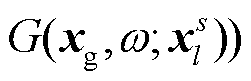 。
。
在频率域中, 所有桥墩产生的震源时间函数Fall(ω)激发的波场被台站记录到的垂向数据信号d(xg, ω)为
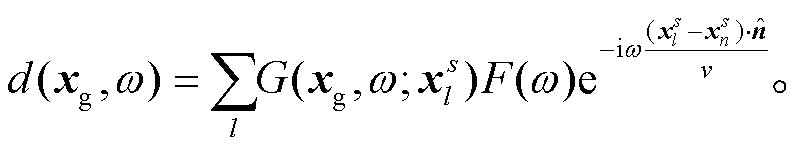 (12)
(12)
石永祥等[12]把方程(12)右端进行如下变换:

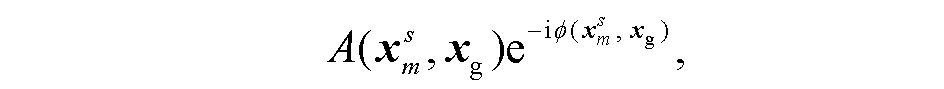 (13)
(13)
其中, 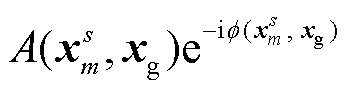 包含其他桥墩震源对
包含其他桥墩震源对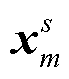 处桥墩震源引起的波场的干扰,
处桥墩震源引起的波场的干扰, 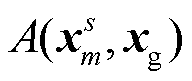 为相干振幅,
为相干振幅, 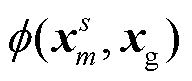 为相干相位。当介质横向变化不大时, 相干相位只与
为相干相位。当介质横向变化不大时, 相干相位只与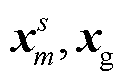 之间的角度θ相关[12]。可以认为
之间的角度θ相关[12]。可以认为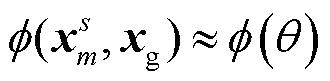 , 从而有
, 从而有
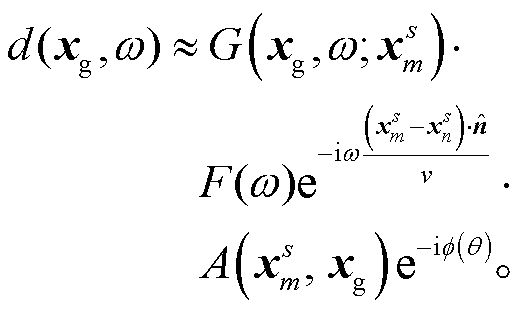 (14)
(14)
石永祥等[12]在详细地分析相干相位的性质后, 定义了特征时间变量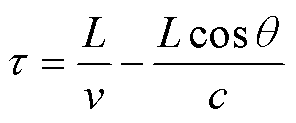 , 其中c为介质的速度, τ的物理含义是同一辆高速列车在两个相邻桥墩处分别激发波场的波前在接收点的到时差。当频率 ω与特征时间 τ满足
, 其中c为介质的速度, τ的物理含义是同一辆高速列车在两个相邻桥墩处分别激发波场的波前在接收点的到时差。当频率 ω与特征时间 τ满足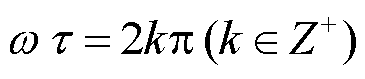 时, ϕ(θ)可以取得对 θ 的极大值。ϕ(θ)稳定点的极大值在炮检距远大于列车长度时为0, 在炮检距远大于桥墩间距的区域,相位 ϕ(θ)从 0 过渡到
时, ϕ(θ)可以取得对 θ 的极大值。ϕ(θ)稳定点的极大值在炮检距远大于列车长度时为0, 在炮检距远大于桥墩间距的区域,相位 ϕ(θ)从 0 过渡到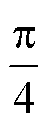 。定义 ϕ(θ)取得极大值时对应的 θ为高铁的主瓣方向, k = 1 对应着基阶主瓣。图1显示不同频率( f )、列车速度和介质速度下相干相位(ϕ)的分布及主瓣的方向(θ)(图中黑线所示)。
。定义 ϕ(θ)取得极大值时对应的 θ为高铁的主瓣方向, k = 1 对应着基阶主瓣。图1显示不同频率( f )、列车速度和介质速度下相干相位(ϕ)的分布及主瓣的方向(θ)(图中黑线所示)。
殷常阳等[13]基于稳相点性质, 提出对不同的速度v进行叠加:
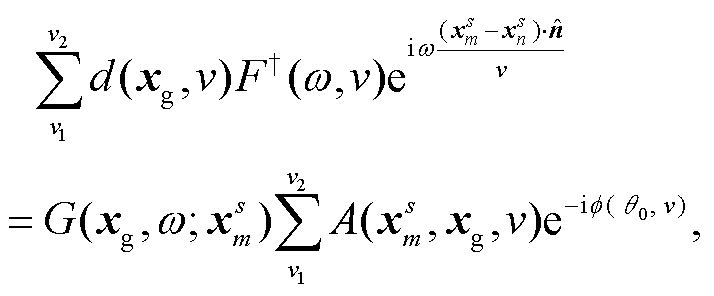 (15)
(15)
其中, 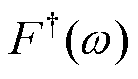 表示震源时间函数的共轭除以震源时间函数模的平方
表示震源时间函数的共轭除以震源时间函数模的平方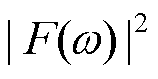 , 则
, 则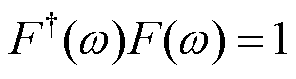 。当 v1< v0< v2时, 叠加项覆盖了相干相位 ϕ 的极大值点, 根据稳相点原理,
。当 v1< v0< v2时, 叠加项覆盖了相干相位 ϕ 的极大值点, 根据稳相点原理, 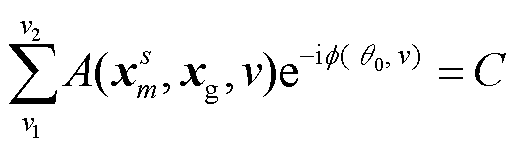 。C是积分过程带来的振幅项, 其相位是固定的, 则式(15)变为
。C是积分过程带来的振幅项, 其相位是固定的, 则式(15)变为
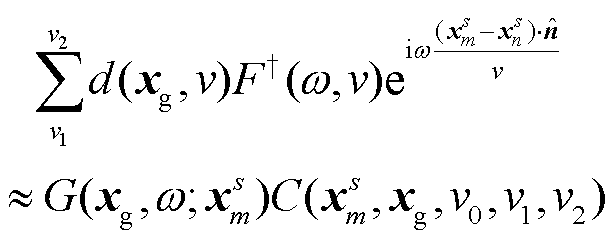
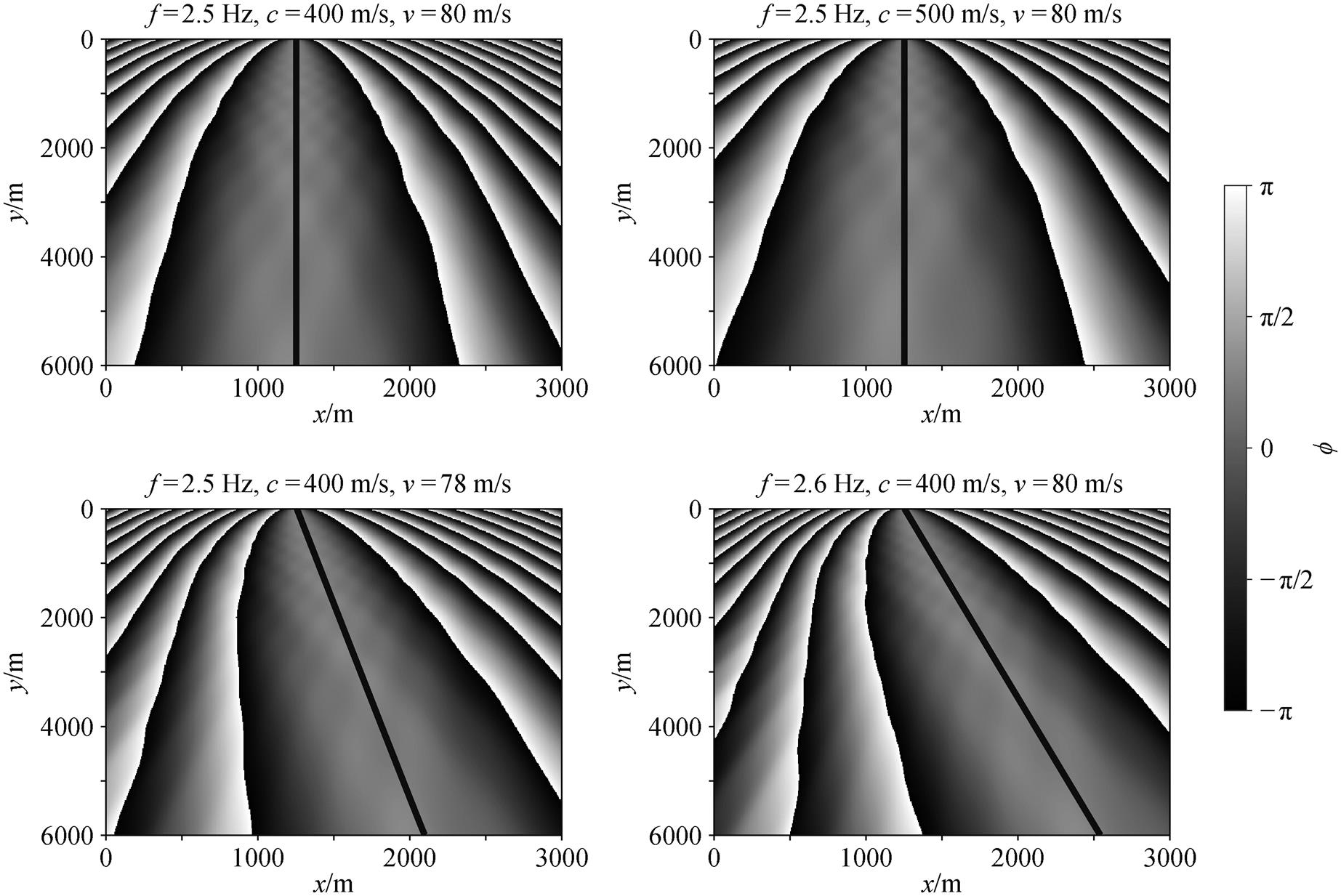
图1 相干相位在不同频率、介质速度和列车速度下的分布
Fig. 1 Distribution of coherent phase at different frequencies , medium velocity and train speed
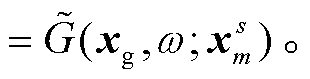 (16)
(16)
与真实的格林函数 G 相比, 虽然叠加得到的虚拟格林函数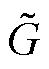 的振幅中串扰噪声没有完全去除, 但相位是正确的, 意味着时间域中虚拟格林函数的走时与真实的格林函数相同。
的振幅中串扰噪声没有完全去除, 但相位是正确的, 意味着时间域中虚拟格林函数的走时与真实的格林函数相同。
为了验证上述方法, 需要模拟行驶在高架桥上高铁的地震波场。首先, 需要得到一个贴近真实的震源时间函数。
为了方便推导, 取桥梁的微元段 dx, 使用如图2所示的欧拉‒伯努利桥梁模型。其中, f(x, t)是单位长度上外力, u(x, t)为垂直挠度, I为桥梁转动惯量, E为桥梁弹性模量, m为桥梁单位长度的质量。欧拉‒伯努利桥梁方程[5]为
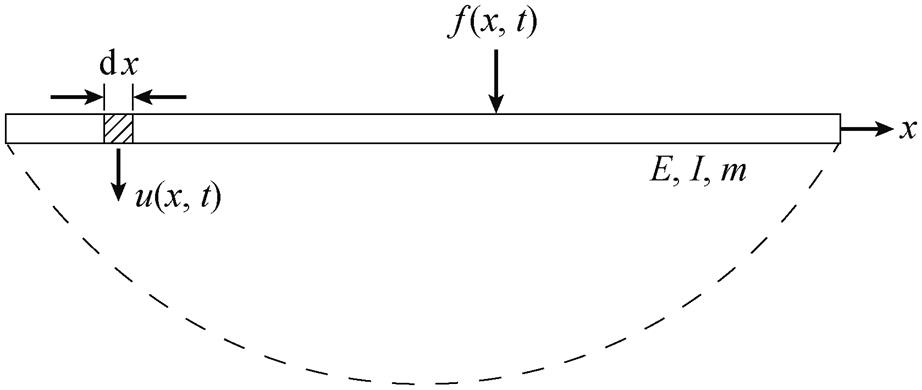
图2 欧拉‒伯努利桥梁模型[5]
Fig. 2 Euler-Bernoulli bridge model[5]
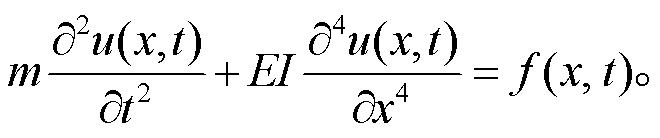 (17)
(17)
高铁由多节车厢组成, 每节车厢都可以视为负载, 且每节车厢都有前后两组车轮, 由于列车的速度恒定, 所以每节车厢到达桥墩的时间间隔可以视为恒定[5‒6], 则外力f(x, t)表示为
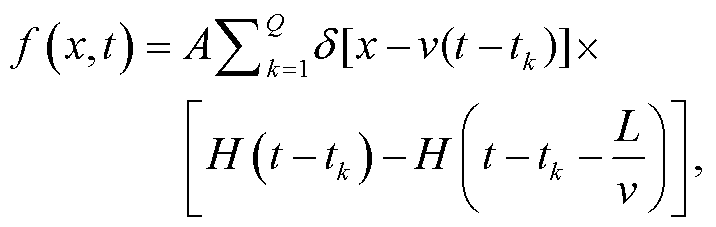 (18)
(18)
其中, L为桥墩之间的间距, Q为高铁车厢节数, v为高铁运行速度, A为高铁移动负载, 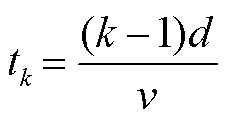 (d为每节车厢的长度)为第k节车厢到达的时间, δ(x)是Delta函数, H(t)是Heaviside函数。
(d为每节车厢的长度)为第k节车厢到达的时间, δ(x)是Delta函数, H(t)是Heaviside函数。
桥梁振动方程的初始条件和边界条件[5‒7]为
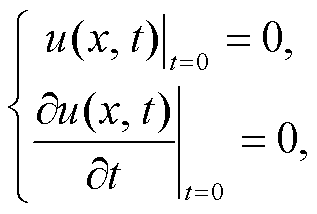 (19)
(19)
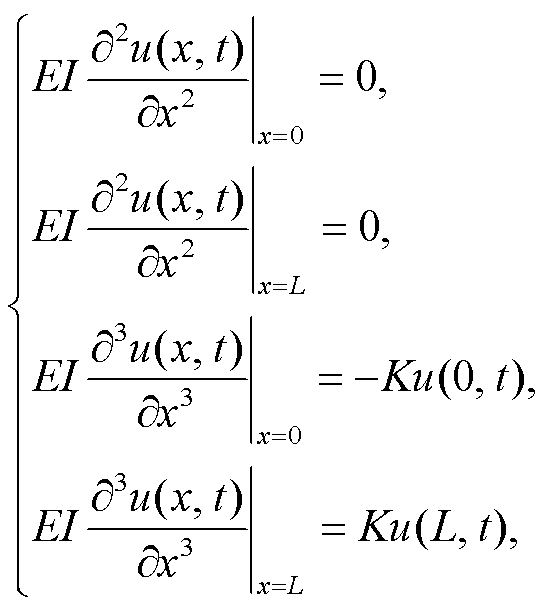 (20)
(20)
式(20)中, K表示桥墩支撑座的等效弹性系数, I表示桥梁的转动惯量, E表示桥梁的杨氏模量。
求解式(17)~(20), 可以得到桥梁在外力作用下的垂直挠度u(x, t)。
每一节车厢都有前后两组轮子, 前轮和后轮都导致桥墩处产生垂直挠度 u(x, t)[5‒6]。以前轮为例, 高铁的前轮t时刻会在x=0 处受支座作用力。桥墩的间距是L, 前轮会在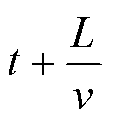 时刻, 在 x=L处受支座作用力。所以, 支座受前轮的作用力为
时刻, 在 x=L处受支座作用力。所以, 支座受前轮的作用力为
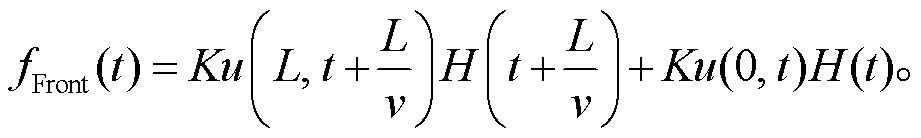 (21)
(21)
前轮与后轮相距d0, 所以后轮总比前轮有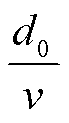 的时间延迟, 则支座受后轮的作用力为
的时间延迟, 则支座受后轮的作用力为
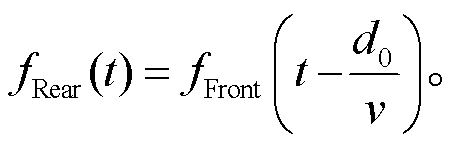 (22)
(22)
前后轮一起对桥墩弹性支座施加的力为
 (23)
(23)
求得ftotal(t)后, 还需要求解高铁移动对桥墩的影响, 从而计算桥墩与土体之间的相互作用, 最后求出激发波场的震源时间函数fs (t)。
根据文献[5‒8]的研究结果, 列车在高架桥引起的地面振动模型如图3所示。弹性系数为K的弹簧支座下方, 连接着质量为 M 的桥梁支柱(可以视为刚体)。为了保证支柱稳定, 底部有桩帽托住。桩帽有5个桩体支撑, 每个桩体可以视为开尔文体模型。同时, 土壤地基也可视为开尔文体模型。所以在频率域中, 图3所示模型的定解方程[5‒8]为
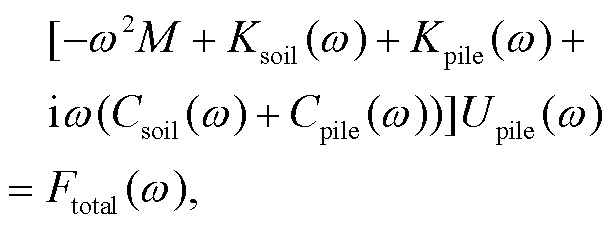 (24)
(24)
其中, 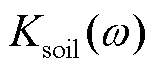 表示频率域中土体的开尔文体模型的等效弹性系数,
表示频率域中土体的开尔文体模型的等效弹性系数, 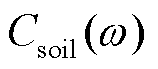 表示频率域中土体的开尔文体模型的等效阻尼系数;
表示频率域中土体的开尔文体模型的等效阻尼系数; 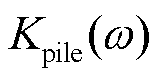 表示频率域中桩体的开尔文体模型的等效弹性系数,
表示频率域中桩体的开尔文体模型的等效弹性系数, 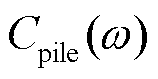 表示频率域中桩体的开尔文体模型的等效阻尼系数;
表示频率域中桩体的开尔文体模型的等效阻尼系数; 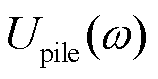 表示频率域中桩体的位移,
表示频率域中桩体的位移, 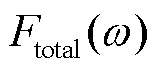 是震源时间函数ftotal (t)的频率域表示。
是震源时间函数ftotal (t)的频率域表示。
由式(24)可以得到桩体的位移:
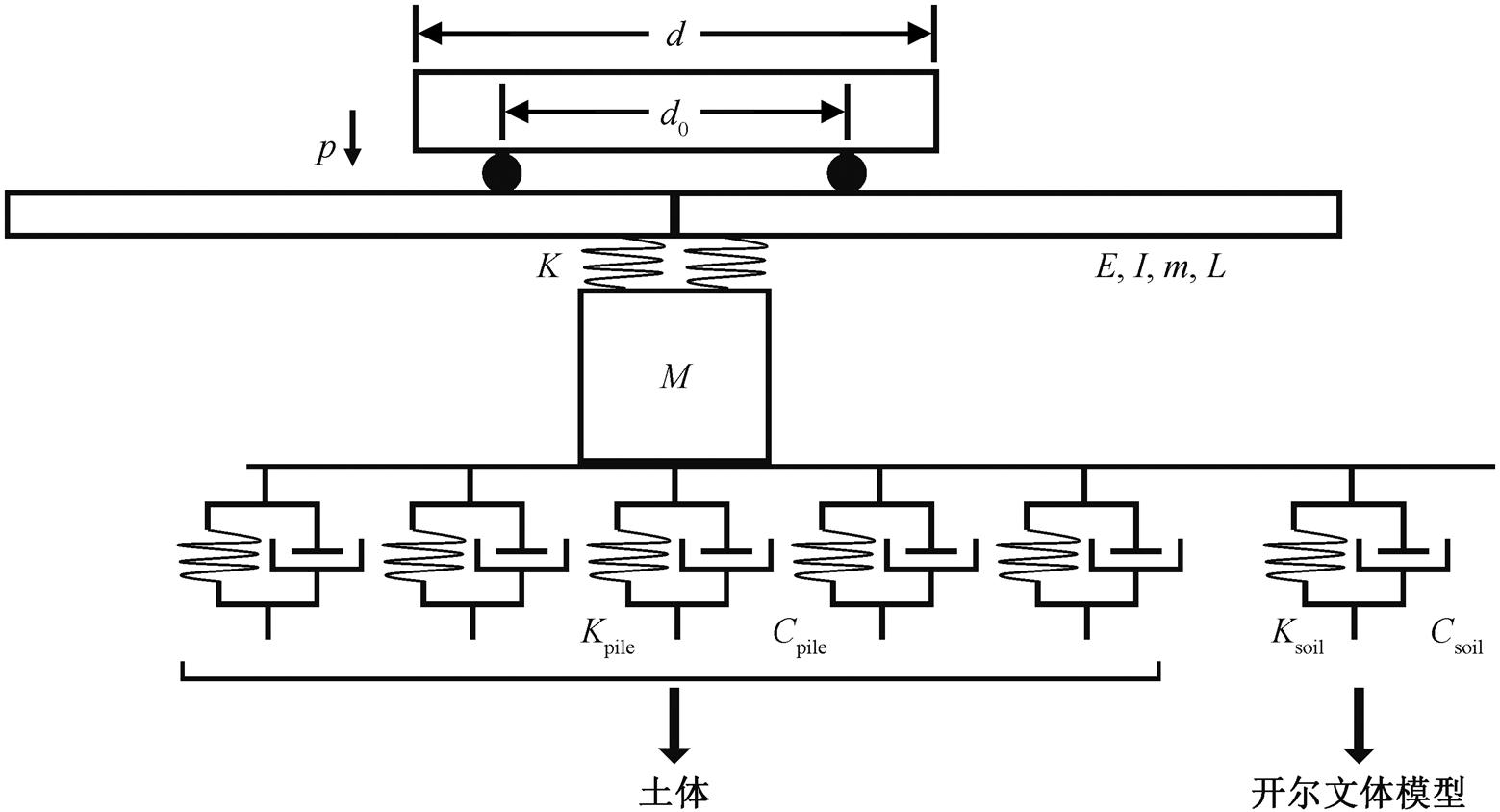
图3 高铁‒桥梁‒支撑住‒桩体‒土体模型[5‒8]
Fig. 3 High-speed rail-bridge-support pile-soil model[5‒8]
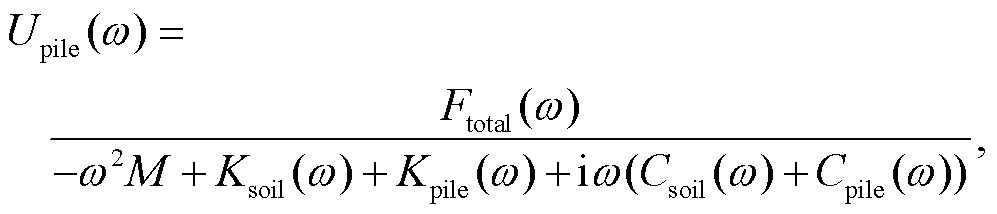 (25)
(25)
其中,
 (26)
(26)
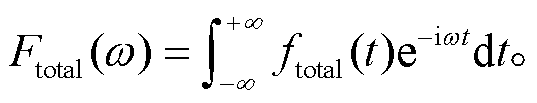 (27)
(27)
得到频率域的震源时间函数Fs (ω):
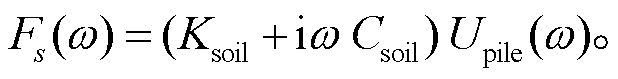 (28)
(28)
把式(28)从频率域转换到时间域:
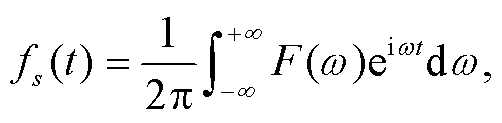 (29)
(29)
fs(t)即为时间域的震源时间函数, 也是由高铁移动引起的震源作用于桥墩时, 激发波场的震源时间函数。不同车速时桥梁长度L=32m 的震源时间函数如图4所示, 其中高铁、桥梁、桩体和土体的参数来自文献[5]。
高铁列车的速度为v, 桥墩的间距为L, 第j+1个桥墩震源的震源时间函数在时间上会有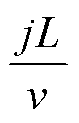 的延迟。设高铁线路沿x轴正方向行驶, 则在空间上沿x轴正方向会有jL的延迟, 总的震源时间函数为
的延迟。设高铁线路沿x轴正方向行驶, 则在空间上沿x轴正方向会有jL的延迟, 总的震源时间函数为
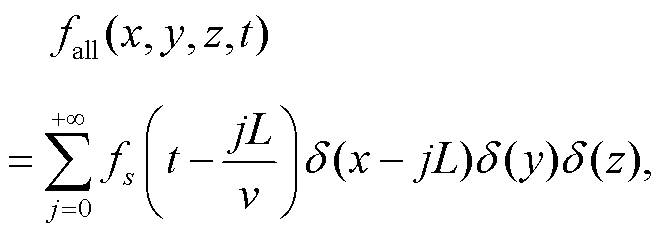 (30)
(30)
fall (x, y, z, t)的加载方向竖直向下。
利用谱元法, 由震源时间函数fall (x, y, z, t), 可以进行高速铁路波场正演: 顶层是自由表面, 其余是 Clayton-Engquist 吸收边界[19]。本文采用图5所示的介质速度模型: 第一层密度 ρ1=2.2kg/m3, P波速度 α1=1600m/s, S 波速度 β1=400m/s, 厚度 h1=150m; 第二层密度 ρ2=2.4kg/m3, P 波速度 α2=2400m/s, S波速度β2=750m/s, 厚度h2=250m。
图6是高速铁路平面分布图, 行驶在铁路高架桥(黑色实线)上高铁的速度为 v, 桥墩间距 L=32m, 共有63个桥墩。
根据式(15)和(16), 合成虚拟道集的步骤如下。
1)消除震源影响。高速列车速度变化造成震源时间函数变化, 所以需要反卷积震源时间函数, 要注意保留震源时间函数时间延迟的信息。
2)确定目标震源位置。从63个桥墩中选定目标桥墩的位置, 即求解第 n号桥墩到台站的格林函数, 其中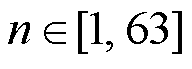 。
。
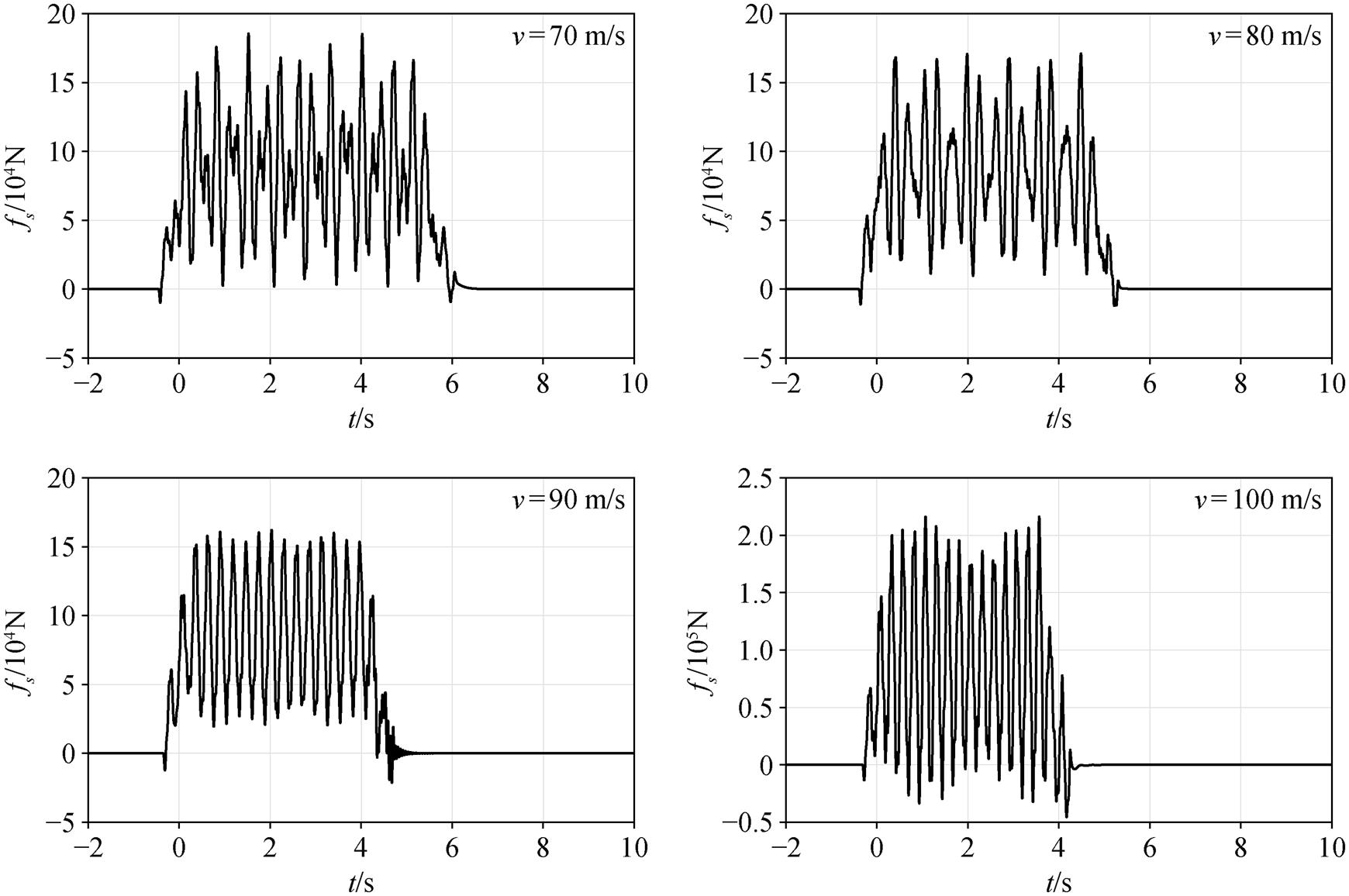
图4 桥梁长度L=32 m时不同车速下的震源时间函数
Fig. 4 Source time function of L=32 m bridge at different train speeds
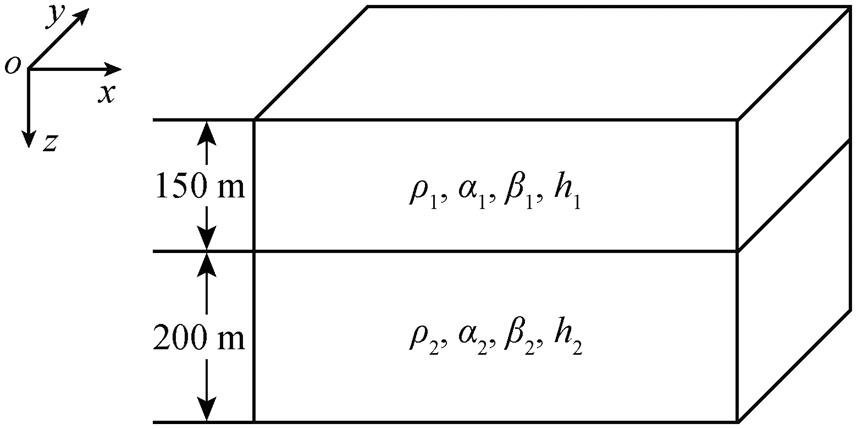
图5 介质的速度模型示意图
Fig. 5 Schematic diagram of velocity model of the medium
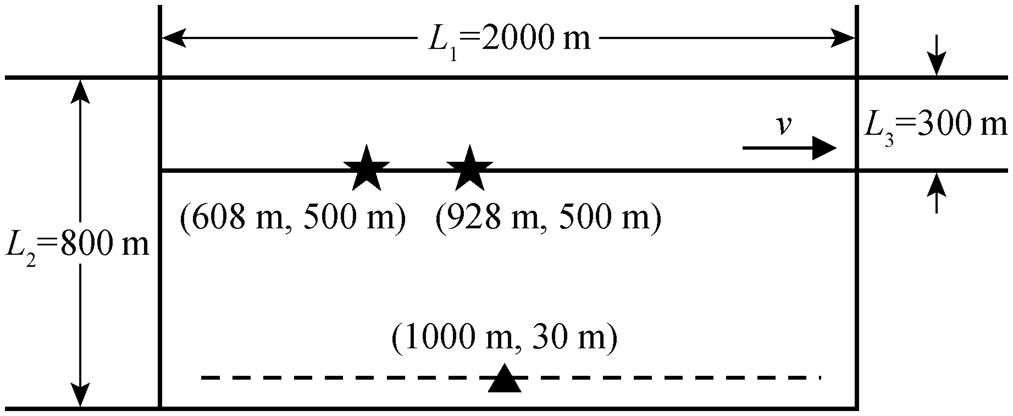
实线表示高速铁路, 由高架桥支撑; 五角星表示其中两个桥墩, 三角形表示布设在地表的台站; 虚线表示 x 轴从 100 m 至1900 m, y轴30 m处, 台间距为100 m的测线
图6 高速铁路及台站平面分布示意图
Fig. 6 Schematic diagram of high-speed rail and station distribution
3)对齐不同速度的波形。取列车速度v=70~ 100m/s, 速度间隔为2m/s, 16个速度取值, 做16 次正演, 每个台站都可以记录到16个不同高速列车速度产生的波形。桥墩之间的时间延迟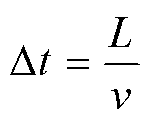 , 如果计算第n号桥墩到台站的格林函数, 那么第n号桥墩激发的起始时间为
, 如果计算第n号桥墩到台站的格林函数, 那么第n号桥墩激发的起始时间为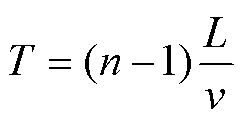 , 所以16个不同高速列车速度造成的波形的起始时间为 T1=0,
, 所以16个不同高速列车速度造成的波形的起始时间为 T1=0,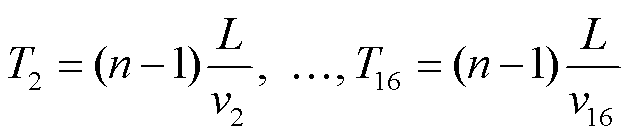 。以T1, T2, …, T16 为起始时间, 对齐不同速度的波形。
。以T1, T2, …, T16 为起始时间, 对齐不同速度的波形。
4)叠加不同速度的波形。上述每个台站获得16 个不同高速列车速度产生的波形, 每个速度对应的波形起始时间为 T1, T2, …, T16。首先需要对齐波形, 即把不同速度波形的起始时间 T1, T2, …, T16 平移到零时刻, 然后进行叠加, 即获得第 n 号桥墩到台站的格林函数。
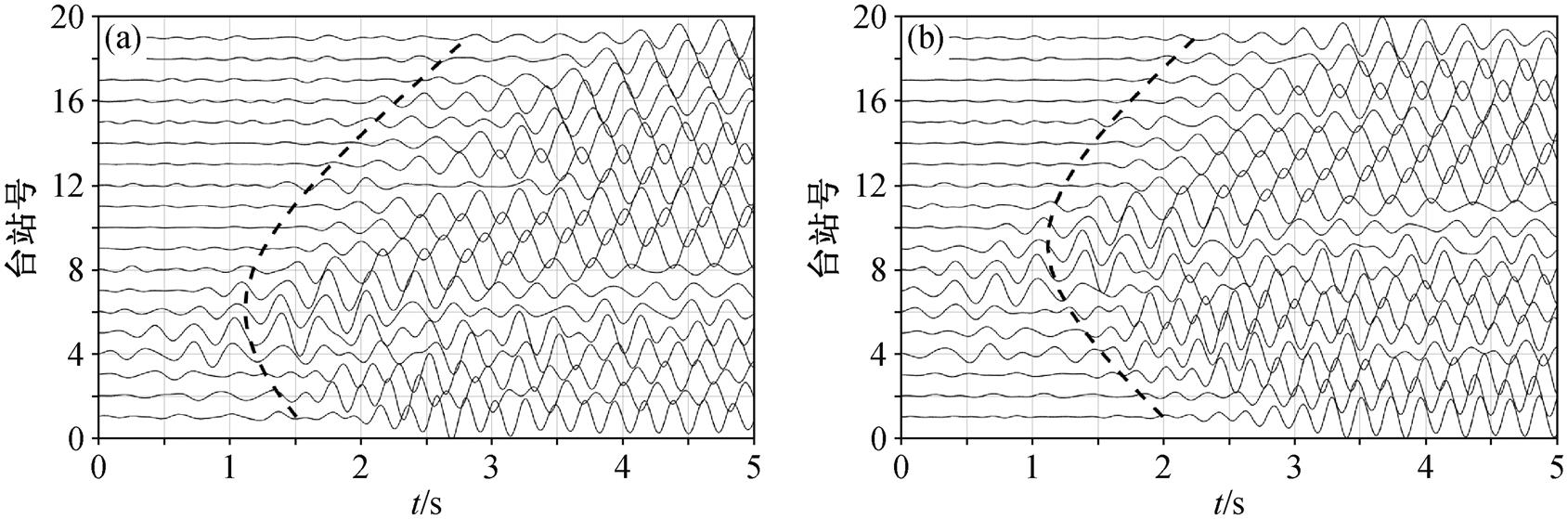
选取第20号桥墩(608m, 500m)和第30号(928m, 500m)桥墩, 求取这两个桥墩到台阵的格林函数。图7显示两个桥墩分别到坐标为(1000m, 30m)的台站(图6中三角形所示) X 分量虚拟道集中的单道, 反射S波的理论到时满足
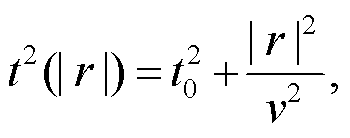 (31)
(31)
其中,  是桥墩到台站的距离, v是反射界面之上的介质速度,
是桥墩到台站的距离, v是反射界面之上的介质速度,  是在台站
是在台站 处桥墩到台站的到时, t0是|r|=0时桥墩沿垂直向下路径的双程走时。
处桥墩到台站的到时, t0是|r|=0时桥墩沿垂直向下路径的双程走时。
图8是第20号桥墩和第30号桥墩分别到x轴从100m至1900m, y轴30m处, 台间距为100m的测线台站(图6中虚线所示)的虚拟道集, 反射S波的理论到时仍然满足式(31)。
从图7和8可以看出, 在反射S波震相到时合成数据的X分量中, 弹性波存在多个震相的相互干扰。与声波方程的模拟计算相比, 弹性波方程的计算更加复杂[13]。同时, 反射波能量强, 首波和直达波能量弱, 叠加后仍然存在部分串扰噪音, 相对来说, 反射波的到时能更好地体现出来。
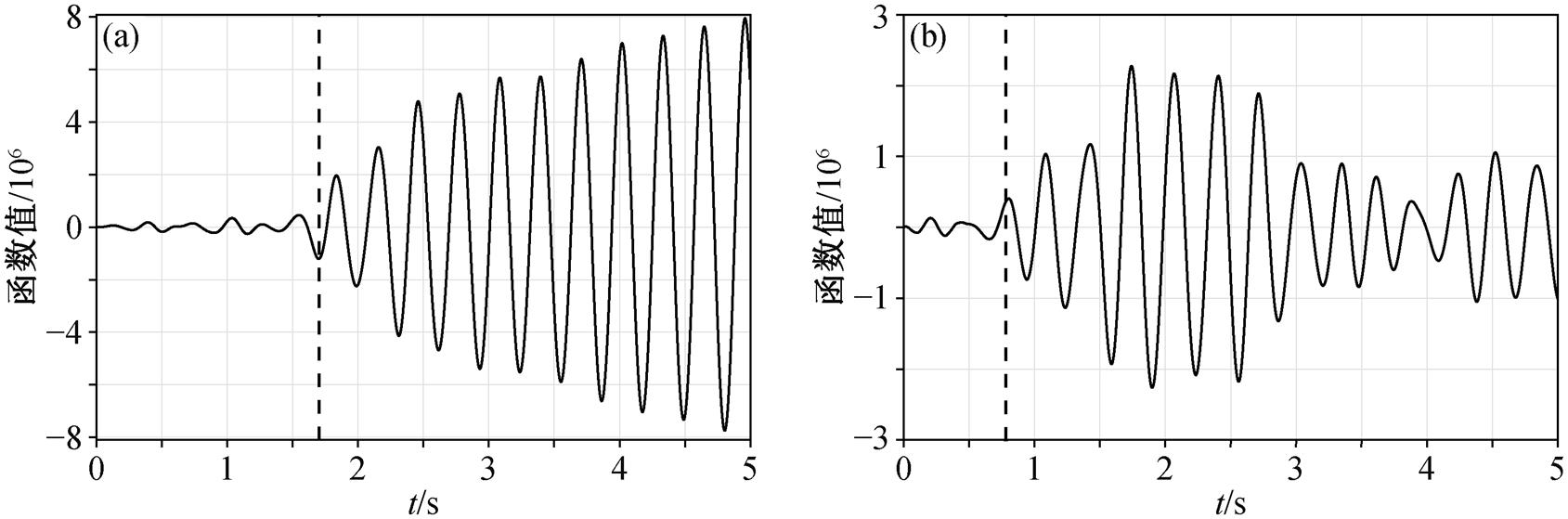
(a)第 20 号桥墩; (b)第 30 号桥墩; 黑色虚线示意反射S波的理论到时
图7 不同桥墩到坐标为(1000 m, 30 m)的台站X分量虚拟道集中的单道
Fig. 7 X-component single gather from different piers to (1000 m, 30 m) station
(a)第 20 号桥墩; (b)第 30 号桥墩; 黑色虚线示意反射 S 波的理论到时
图8 不同桥墩到测线台站 X 分量的虚拟道集
Fig. 8 Virtual gathers of X-components from different piers to stations
本文只考虑震源时间函数向下时的合成记录情况。真实的震源时间函数不仅有垂直向下的, 也有平行于铁路方向的。在进行虚拟道集合成时, 叠加速度范围的选取至关重要, 必须保证叠加速度项覆盖相干相位 ϕ的极大值点。本文采取的是70~100m/s的速度范围叠加, ϕ的极大值点在此速度范围内是可以取到的。如果叠加速度没有覆盖 ϕ的极大值, 则会造成虚拟道集的生成失败, 因此需要确定 ϕ的极大值点的对应速度后再进行叠加。
高铁列车速度在大范围的变化可以保证有效地消除串扰噪声。实际上, ±5m/s 的变化范围已经能够满足稳相点求和的需求(如图1所示, 主瓣区以外相位变化剧烈)。观测结果显示, 车速的实际变化幅度为±5 m/s [20], 可以满足计算需求。
虚拟道集中, 有时桥墩附近台站的反射S波到时不清晰(图8)。原因是如果接收台站过于接近桥墩, 桥墩震源振动的近场项会对波场特征产生较大的影响, 导致到时特征不显著。因此, 在叠加不同高铁列车的速度时, 台站与桥墩震源应当保持一定的距离, 避免桥墩震源振动的近场项对虚拟道集的生成造成影响。
本文提出一种基于稳相点分析的波形叠加方法, 可以消除高铁列车通过高架桥时引起的多桥墩震源的串扰噪声, 生成特定频率高铁波场的虚拟道集。高架桥的桥梁采用欧拉‒伯努利模型, 土体和桩体采用开尔文体模型, 通过正演模拟得到高铁列车通过高架桥时的震源时间函数, 并使用有限元方法给出分层介质模型中高铁波场的正演模拟结果。在此基础上, 对不同速度的高铁列车正演模拟记录进行叠加, 获得虚拟道集。通过对比, 发现结果与反射S波的理论走时相符, 验证了本文高铁震源虚拟道集生成方法的正确性。
参考文献
[1]高广运, 谢伟, 陈娟, 等. 高铁运行引起的高架桥群桩基础地面振动衰减分析. 岩土力学, 2019, 40 (8): 3197‒3206
[2]Chen Feng. Prediction and mitigation analyses of ground vibrations induced by high speed train with 3-dimensional finite element method and substructure method. Journal of Vibration and Control, 2011, 17 (11): 1703‒1720
[3]Krylov V V. Generation of ground vibrations by su-perfast trains. Applied Acoustics, 1995, 44(2): 149‒ 164
[4]Wu W H, Smith H A. Efficient modal analysis for structures with soil-structure interaction. Earthquake Engineering & Structural Dynamics, 1995, 24(2): 283–299
[5]Wu Y S, Yang Y B. A semi-analytical approach for analyzing ground vibrations caused by trains moving over elevated bridges. Soil Dynamics and Earthquake Engineering, 2004, 24(12): 949–962
[6]Yang Y B, Hung H, Chang D W. Train-induced wave propagation in layered soils using finite/infinite element simulation. Soil Dynamics and Earthquake Engineering, 2003, 23(4): 263–278
[7]Yang Y B, Lin C L, Yau J D, et al. Mechanism of resonance and cancellation for train-induced vib-rations on bridges with elastic bearings. Journal of Sound and Vibration, 2004, 269(1/2): 345–360
[8]Yang Y B, Yau J D, Hsu L C. Vibration of simple beams due to trains moving at high speeds. Enginee-ring Structures, 1997, 19(11): 936–944
[9]陈棋福, 李丽, 李纲, 等. 列车振动的地震记录信号特征. 地震学报, 2004, 26(6): 651–659
[10]温景充, 宁杰远, 张献兵. 高铁地震波场特点的理论分析. 北京大学学报(自然科学版), 2019, 55(5): 813–822
[11]张唤兰, 王保利, 宁杰远, 等. 高铁地震数据干涉成像技术初探. 地球物理学报, 2019, 62(6): 2321–2327
[12]石永祥, 温景充, 宁杰远. 高铁震源地下介质成像的理论分析. 中国科学: 地球科学, 2022, 52(5): 893‒902
[13]殷常阳, 石永祥, 伍晗, 等. 利用高铁震源生成虚拟道集的理论分析. 地球物理学报, 出版中
[14]Mahdad A, Doulgeris P, Blacquiere G. Separation of blended data by iterative estimation and subtraction of blending interference noise. Geophysics, 2011, 76(3): Q9–Q17
[15]Wapenaar K, Neut J, Van der Thorbecke J. Deblen-ding by direct inversion. Geophysics, 2012, 77(3): A9–A12
[16]Wu S, Blacquière G, van Groenestijn G-J A. Shot repetition: an alternative seismic blending code in marine acquisition. Geophysics, 2018, 83(6): P29–P37
[17]Schuster G T, Wang X, Huang Y, et al. Theory of multisource crosstalk reduction by phase-encoded sta-tics: theory of multisource crosstalk reduction. Geo-physical Journal International, 2011, 184(3): 1289–1303
[18]Moore I, Dragoset B, Ommundsen T, et al. Simulta-neous source separation using dithered sources // SEG Technical Program Expanded Abstracts. Las Vegas, 2008: 2806–2810
[19]Clayton R, Engquist B. Absorbing boundary condi-tions for acoustic and elastic wave equations. Bulletin of the Seismological Society of America, 1977, 67(6): 1529–1540
[20]蒋一然, 鲍铁钊, 宁杰远, 等. 高架桥下方高铁地震信号频谱特征研究. 北京大学学报(自然科学版), 2019, 55(5): 829‒838
Validation of the Virtual Gather Generation Method from Synthetic Data for High-Speed Rail Seismic Source
Abstract Based on the principle of superposition method which can eliminate the crosstalk noise of the high-speed rail seismic wavefield recorded by the stations and generate virtual gathers, the operation ways of the superposition method are given and the method is verified on the synthetic high-speed rail data. The precise source time function of the high-speed rail is obtained by establishing the vibration equation of the high-speed rail viaduct, and the forward modeling of the high-speed rail wavefield in layered medium is calculated by using the finite element methodand time-shift superposition of forward modeling of the high-speed rail wavefield with different speeds is carried out. The virtual gathers are obtained, which verifies the correctness of the stacking method.
Key words high-speed rail; interference field; source time function; virtual gather