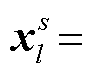
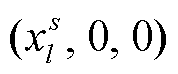 , 其中上角标 s代表震源。假设桥墩的结构相同, 相邻桥墩产生的震源时间函数在时间域仅存在时间延迟 L/v (这一相邻桥墩的时间延迟对应的频率称为高铁的桥频f b)。
, 其中上角标 s代表震源。假设桥墩的结构相同, 相邻桥墩产生的震源时间函数在时间域仅存在时间延迟 L/v (这一相邻桥墩的时间延迟对应的频率称为高铁的桥频f b)。doi: 10.13209/j.0479-8023.2022.046
河北省地震科技星火计划(DZ20200827054)和国家自然科学基金(41874071)资助
北京大学学报(自然科学版) 第58卷 第5期 2022年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 58, No. 5 (Sept. 2022)
收稿日期: 2021–05–30;
修回日期: 2022–05–22
摘要 针对运行于高架桥上高铁引发的震源, 基于对移动组合源形成的波场传播的理论分析, 提出一种利用多台互相关测量高铁波场视速度的方法。然后, 生成分层介质条件下的高铁波场合成数据, 计算信号视速度, 并通过与理论结果的对比, 验证方法的正确性。
关键词 高铁; 移动组合源; 干涉场; 视速度
随着中国东部经济的发展, 对地下空间的利用需求越来越迫切。因此, 自动监测路基病害, 实现地震预测和预警尤为重要。然而, 中国东部地震震源相对缺乏, 地震观测资料信噪比低, 严重地制约了地震学手段对该区域地下结构的探测与监测。
高铁产生的振动是一种全新的优质地震震源, 能够激发稳定的、重复性强的地震波场。探索利用高铁这类移动组合震源进行地下结构探测与监测相关的新理论、新方法和新技术, 既能提供满足覆盖要求的进行地下结构探测与监测的优质绿色震源, 也能解决观测资料信噪比低的问题。
观测结果表明, 高铁震源不同于地震震源和爆炸源, 具有明显的分立谱特征[1–4]。与此相呼应的是, 高铁波场有干涉场特点, 甚至远台信号先于近台信号到达台站[5], 这与传统震源的波场明显不同。要正确地进行地下结构探测, 必须针对高铁地震波场特征, 改进已有方法或寻找新方法。
虽然高铁震源反演方面的研究已取得重要进展[6–8], 但是利用高铁地震波场观测资料正确地反演地下结构仍然面临考验[9–10], 其中的关键问题是如何正确地进行信号提取和应用。王晓凯等[13">[11–12] 利用信号分析方法, 从高铁地震记录中实现信号提取。但是, 单台法提取的地震信号容易受到噪声的干扰。温景充等[13]基于模拟记录, 讨论高铁地震面波相速度频散曲线的提取和修正方法, 为利用高铁振动的面波信号研究地下结构奠定了基础, 但是其所用方法为双台法, 仍然容易受到噪声的干扰。
基于台阵资料的视速度测量是传统地震学的经典方法[14–16]。该方法测量地震波在地表的传播速度, 在信噪比高的情况下, 可以得到确定性结果。对于面波, 得到的是面波相速度和群速度, 避免了地震波传播路径偏离大圆弧对计算结果的影响。对于体波, 可以得到相应的视速度, 为进一步的分析和计算提供高质量的基础资料。
对于在高架桥上匀速行驶的高铁, 如果把固定的等间隔桥墩视为点源, 则每个桥墩点源的震源时间函数大致相同, 依次等间隔延迟激发, 那么将在特定的频率形成稳定干涉场。石永祥等[17]基于理论分析发现, 在特定的频率, 高铁波场在特定角度以球面波方式传播。在台站间距较小时, 可以将高铁波场的传播视为平面波传播来处理。
针对上述特点, 本文设计基于多台法测量不同频率下视速度的方法。当震相为面波时, 测量结果即为面波的相速度。最后, 基于合成数据, 利用本文提出的方法计算视速度。通过与已知速度结果的对比, 验证方法的正确性。
为了分析台间距较小时高铁波场的平面波特征, 本文首先建立右手直角坐标系, 设定高铁行进方向为 x 轴的正方向, 竖直向下为 z 轴的正方向, 并根据右手定则确定 y 轴的正方向。设高铁行驶在高架桥上时, 桥墩震源对地面的力主要沿垂直方向。以竖直方向位移为例, 涉及的格林函数为 z 方向作用力产生的 z 方向位移, 即 G33 分量(下面用 G表示)。假设桥墩等间距分布, 间距为 L, 且高铁的速度 v恒定不变。第 l号桥墩震源位置的坐标是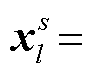
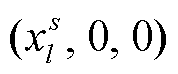 , 其中上角标 s代表震源。假设桥墩的结构相同, 相邻桥墩产生的震源时间函数在时间域仅存在时间延迟 L/v (这一相邻桥墩的时间延迟对应的频率称为高铁的桥频f b)。
, 其中上角标 s代表震源。假设桥墩的结构相同, 相邻桥墩产生的震源时间函数在时间域仅存在时间延迟 L/v (这一相邻桥墩的时间延迟对应的频率称为高铁的桥频f b)。
将原点桥墩处的震源时间函数的傅里叶变换记为 F(ω), 则坐标为 xg 的接收点的竖直方向频域地震记录 d(xg, ω)表示为各个桥墩产生波场的叠加:
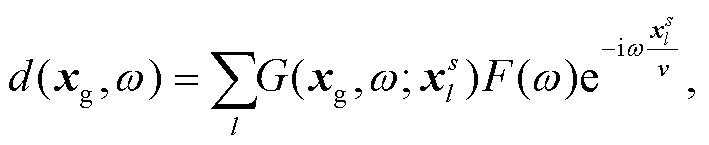 (1)
(1)
其中,  是第 l 个桥墩点源到接收点的格林函数分量。式(1)可写为如下形式:
是第 l 个桥墩点源到接收点的格林函数分量。式(1)可写为如下形式:
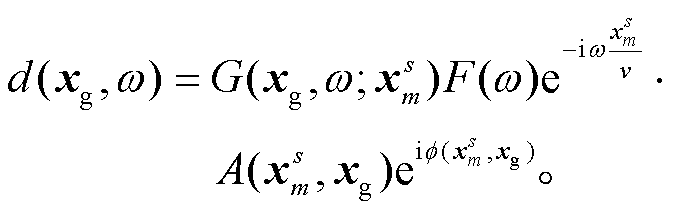 (2)
(2)
这样, 将记录分解为第 m 个桥墩发出的波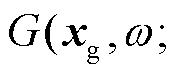
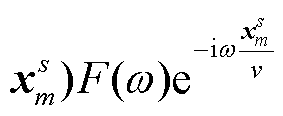 以及其他桥墩形成的相干场 Aeiϕ 两部分。A 和 ϕ 分别表达高铁相干场的幅值特征和相位影响。考虑高铁地震波场在介质横向均匀情况下的平移对称性,
以及其他桥墩形成的相干场 Aeiϕ 两部分。A 和 ϕ 分别表达高铁相干场的幅值特征和相位影响。考虑高铁地震波场在介质横向均匀情况下的平移对称性, 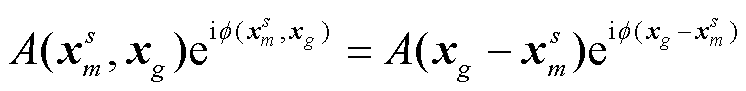 , 其中
, 其中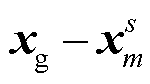 即为第 m 个桥墩指向接收点的位置矢量。如图 1 所示, 可以用桥墩‒台站连线方向与 y 轴的夹角 θ 来描述该矢量的方向。
即为第 m 个桥墩指向接收点的位置矢量。如图 1 所示, 可以用桥墩‒台站连线方向与 y 轴的夹角 θ 来描述该矢量的方向。
定义特征时间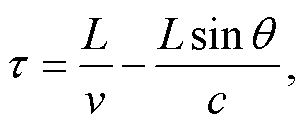 其物理含义是同一辆高速列车在两个相邻桥墩处分别激发的波场的波前在台站 xg 处的到时差。对于给定的频率ω, 当 θ 满足
其物理含义是同一辆高速列车在两个相邻桥墩处分别激发的波场的波前在台站 xg 处的到时差。对于给定的频率ω, 当 θ 满足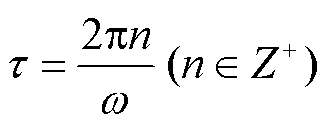 时, A 取得最大值, ϕ 取得极值, 此时对应的就是高铁地震波场的主瓣[17]。
时, A 取得最大值, ϕ 取得极值, 此时对应的就是高铁地震波场的主瓣[17]。
由于高铁相干场的影响, 难以从数据中直观地看出桥墩的格林函数, 因此让接收点发生一个小的偏移, 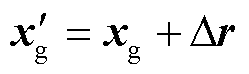 , 从而有
, 从而有
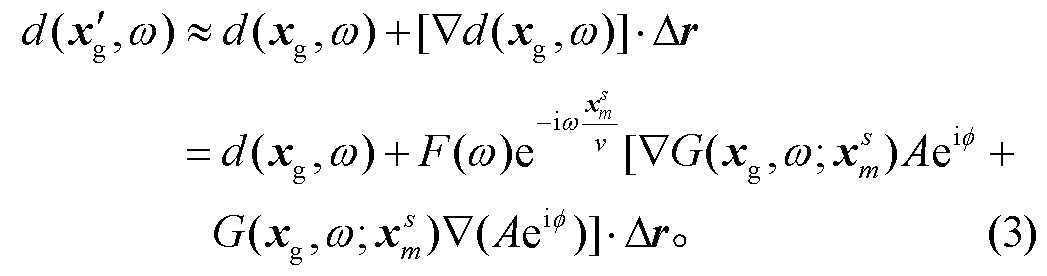
式(3)对任一个桥墩 m 成立, 所以对于给定的频率ω, 存在某个桥墩 m0, 该桥墩‒台站连线方向与 y 轴的夹角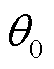 满足关系
满足关系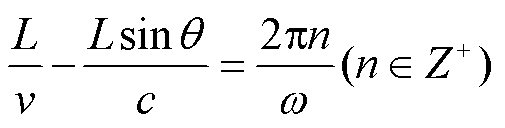 时,
时, 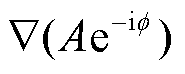
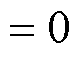 , 从而有
, 从而有
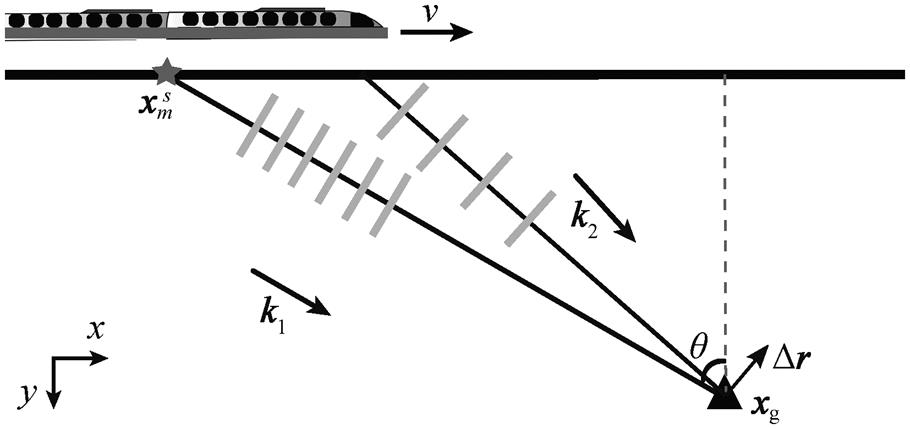
高速列车以速度v行驶, 在位置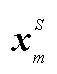 处的桥墩激发震源;行驶一段距离后, 在下一个桥墩继续激发震源, 所产生平面波的波矢分别为k1和k2; 灰色直线表示波阵面
处的桥墩激发震源;行驶一段距离后, 在下一个桥墩继续激发震源, 所产生平面波的波矢分别为k1和k2; 灰色直线表示波阵面
图1 高铁波场示意图
Fig. 1 Schematic diagram of high-speed rail wavefield

其中, 波矢 k的方向与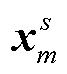 到 xg的位置矢量方向一致。这样, 在特定频率下, 可以用平面波表达高铁远场地震信号。不同频率对应的角度 θ和波矢 k不同, 因此高铁地震波场中不同的频率对应不同方向的平面波。
到 xg的位置矢量方向一致。这样, 在特定频率下, 可以用平面波表达高铁远场地震信号。不同频率对应的角度 θ和波矢 k不同, 因此高铁地震波场中不同的频率对应不同方向的平面波。
从 1.1 节得到结论: 在特定的频率, 可以认为等间距桥墩高铁地震波场是主要能量沿某一特定方向传播的平面波, 描述其传播行为的表达式为
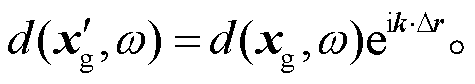
对在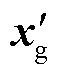 和
和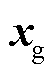 处的台站做互相关, 即对式(4)两边同时左乘
处的台站做互相关, 即对式(4)两边同时左乘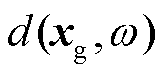 的共轭
的共轭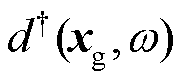 , 得
, 得
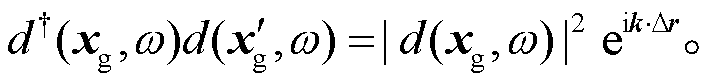 (5)
(5)
式(5)表示两个台站的互相关结果, 相位差为
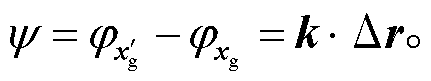 (6)
(6)
利用式(6)可以求取波数, 其中
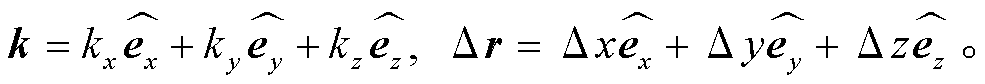
这里有 3 个未知数 kx, ky 和 kz, 所以需要 3 个以上台站对进行求解, 即有
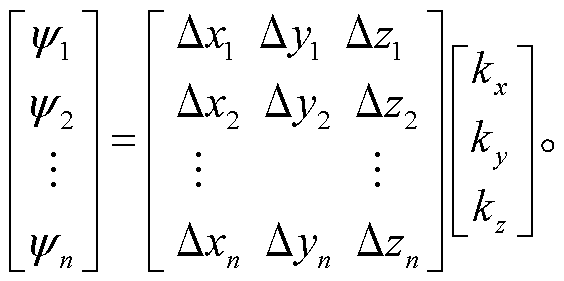 (7)
(7)
求解式(7)就可以得到 kx, ky 和 kz。然后, 求出 k 的模:
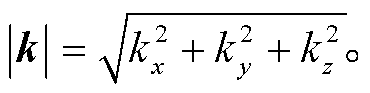 (8)
(8)
利用式(8)的结果, 即可得到波速:
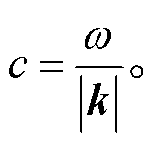 (9)
(9)
在实际场景中, 考虑到台站分布在地表, 所以在垂直方向始终有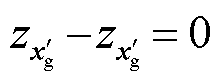 , 所以始终无法求出kz。所以, 我们可以利用 kx 和 ky 求出面波相速度或者体波视速度:
, 所以始终无法求出kz。所以, 我们可以利用 kx 和 ky 求出面波相速度或者体波视速度:
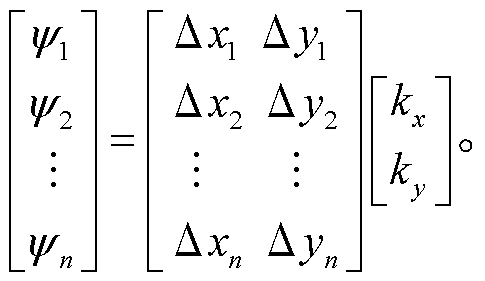 (10)
(10)
求解式(10), 得到 kx 和 ky, 求出 k 的模:
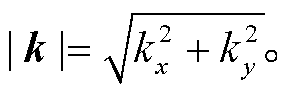 (11)
(11)
类似式(9), 利用波数和频率, 可以求出面波相速度或者体波视速度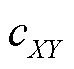 :
:
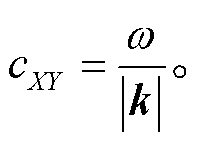 (12)
(12)
只有当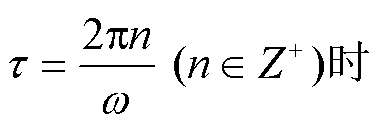 , 以上假设才成立。此时
, 以上假设才成立。此时
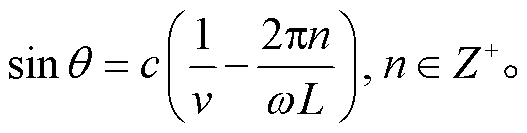 (13)
(13)
可以发现, 当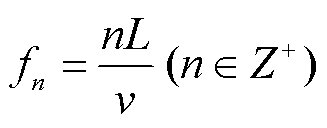 时, sin θ = 0。这个频率是高铁的桥频及其倍频。受限于正弦函数的取值范围, 只有在频率 fn 附近的一段频率范围内, 上述方法才有效。这一段有效的频率范围与波的视速度 c 有关。
时, sin θ = 0。这个频率是高铁的桥频及其倍频。受限于正弦函数的取值范围, 只有在频率 fn 附近的一段频率范围内, 上述方法才有效。这一段有效的频率范围与波的视速度 c 有关。
利用式(10)~(12)求解视速度, 至少需要 3 个台站的地震记录。分别将台站 1 和台站 2 的地震面波记录与台站 3 的记录做互相关, 得到相位差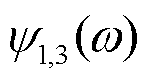 和
和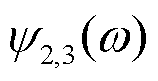 :
:
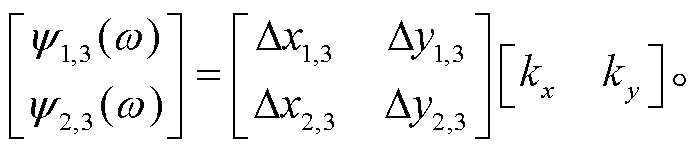 (14)
(14)
式(14)有唯一解的条件是 3 个台站不在同一直线上。台站 1 与台站 2 之间也可以计算相位差, 得到一个与式(14)线性相关的方程。实际上, 也可以利用更多台站对的结果, 形成一个超定方程, 但这样做不一定有利于方程的正确求解, 因为相位ψ具有非唯一性。
相位的非唯一性是利用互相关方法求取两个台站间面波相位差的时候遇到的共性问题。例如, 用传统的双台法提取频散曲线时, 就会得到多条相位相差 2π 的频散曲线, 且频率越高, 相邻频散曲线的相速度差就越小, 仅通过单一频率的结果无法分辨哪个是正确的相速度值。在提取天然远震面波或背景噪声相速度时, 频段是比较完整的, 可以通过低频长周期的相速度值确定选取哪一条频散曲线。但是, 对于高铁地震记录, 只能得到桥频及其倍频附近一段频率范围的结果, 因此难以通过低频结果进行约束。针对这一问题, 可以考虑的解决方法有以下两种。
第一种方法是尽量减小台间距, 基于密集台阵进行观测, 使得台间距小于最小波长。这就相当于将相位差限制在 2π 以内。但是, 这样做会使低频部分的误差变大, 因为面波方法一般要求台间距不小于波长的一半[16]。
第二种方法是对相位进行整数个 2π 的校正, 将每组台站对计算出的相位差加上 2kπ。比如, 整数k取值为−4~5, 则共有 10 组不同的相位, 如果考虑式(10), 方程组中包含 n个台站对, 则需要计算的方程数量为 10n, 计算量极大, 且筛选困难。因此, 本文考虑使用式(14), 每次解方程只包含两个台站对, 利用不同的台站对解出两个结果, 对两个结果进行比较后筛选正确值。作为测试, 设置 4 个台站, 位置坐标分别为(0m, 0m)、(80m, 150m)、(120m, −120m)和(200m, 30m)。模拟沿 x 方向传播的平面瑞利波, 给定的相速度在 300~600m/s 范围内, 则能够直接计算出台站间的相位差。图 2(a)和(b)分别展示用前 3 个台站计算出来的相速度结果及用后 3个台站算出来的相速度结果, 二者仅在模型值(虚线)处重合。利用这一特点, 就可以筛选出正确的相速度值。想要得到误差更小的测量结果, 可以考虑利用更多的台站组合, 每个台站组合包括 3 个台站。对于不同台站组合的筛选结果, 利用不同台站正确重合的特点取交集。
本文基于接近实际情况的桥墩间距和高铁速度设计合成数据, 高铁运行和台站位置模型如图 3 所示。高铁速度 v=80m/s, 桥墩间距 L=30m。考虑合成数据在特定时窗内的完整性, 将铁路长度设为9000m, 共 301 个桥墩。台站 1 的位置坐标为(4500m,2000m), 台站 2 的位置坐标为(4550m, 2000m), 台站 3 的位置坐标为(4500m, 2050m), 台站 4 的位置坐标为(4550m, 2050m)。
高铁线路的桥梁段主要分布在我国东部平原地区。因此, 本文针对近地表为松散沉积的情况给出介质结构模型(图 4(a)): 第一层密度 ρ1=2.6kg/m3, P波速度 α1=800m/s, S 波速度 β1=350m/s, 厚度 h1=20 m; 第二层密度 ρ2=3.0kg/m3, P 波速度 α2=1000m/s, S 波速度 β2=450m/s, 厚度 h2=50m; 第三层密度 ρ3 =3.3kg/m3, P 波速度 α3=1200m/s, S 波速度 β3=750m/s, 向下无限延伸。由于台站布设在地表, 求取视速度时, 可以利用面波的相速度结果, 根据上述模型计算得到瑞利波理论频散曲线(图 4(b))。
在生成模拟数据时, 本文沿用 Yao 等[16]给出的震源时间函数以及格林函数计算方法。本文只关注格林函数中的 G33 分量, 因此只计算瑞利波的格林函数, 即
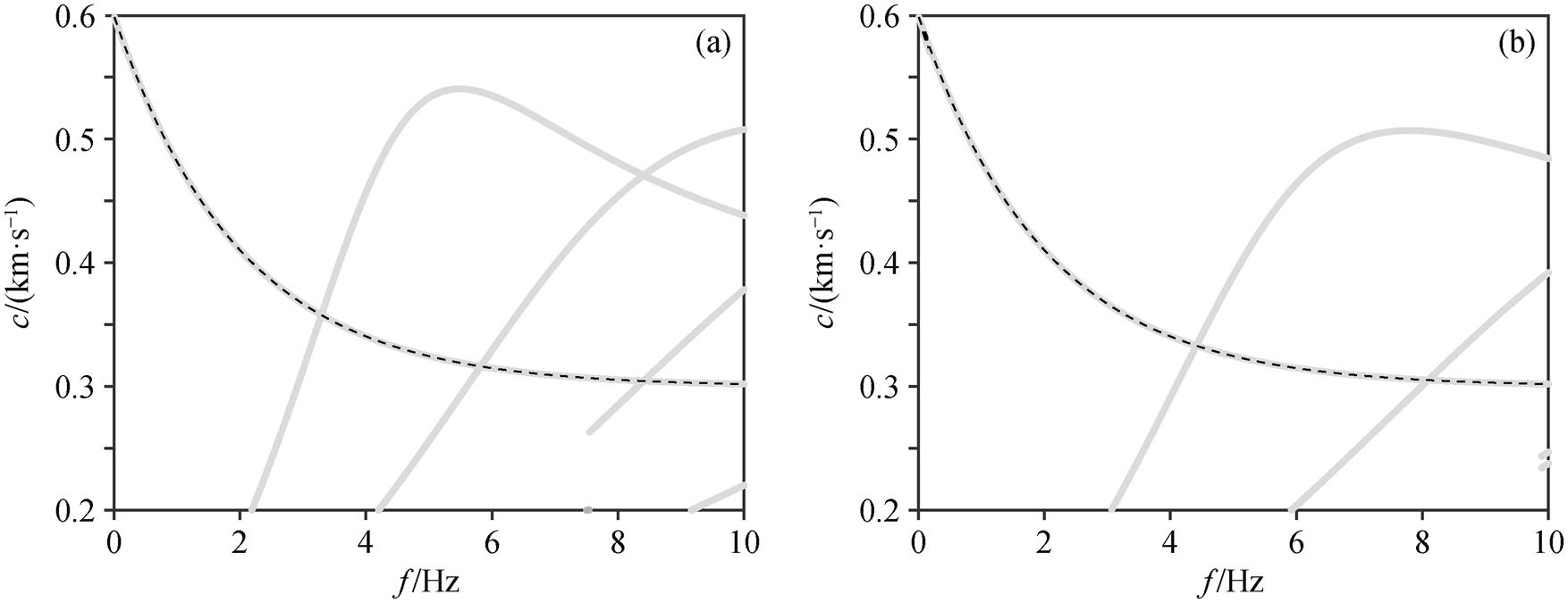
(a)前3个台站计算结果的频散曲线; (b)后3个台站计算结果的频散曲线。灰色实线为计算的相速度值, 黑色虚线为参考值
图2 不同台站组合相速度计算结果
Fig. 2 Calculated results of phase velocity from different station combinations
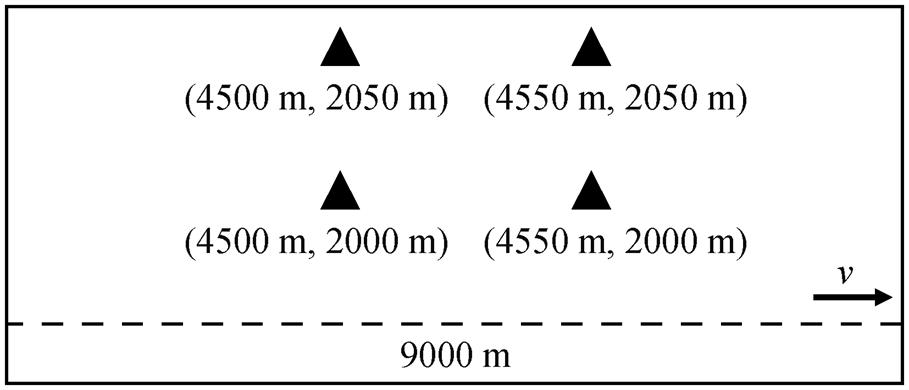
虚线表示高速铁路, 由桥墩架起, 桥墩的间距为30m, 共有 301 个桥墩; 三角形为布设在地表的 4 个台站
图3 高铁运行及台站位置示意图
Fig. 3 Schematic diagram of the high-speed rail and station locations
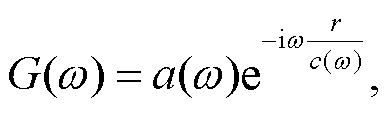
其中, a(ω)为振幅项, r 为场源距离, c(ω)为瑞利波相速度。计算得到 4 个台站的垂向地震记录如图 5 所示。
基于上述 4 个台站的模拟地震记录, 计算得到瑞利波相速度, 经过筛选后的结果见图 6。由于本文选取的桥墩间距为 30m, 列车行驶速度为 80m/s,对应的桥频约为 2.67Hz, 两倍和三倍桥频分别为5.33Hz 和 8Hz。如图 6(a)所示, 我们在桥频附近的2.36~3.16Hz 范围内筛选出的相速度值与模型值一致。如图 6(b)和(c)所示, 在两倍桥频附近, 相速度值在 5.15Hz 左右出现跳变, 分别在 4.28~5.08Hz 和5.19~6.11Hz 范围内得到正确的相速度值。图 6(d)中, 在三倍桥频附近的 7.39~8.51Hz 范围内能够得到正确的相速度值。
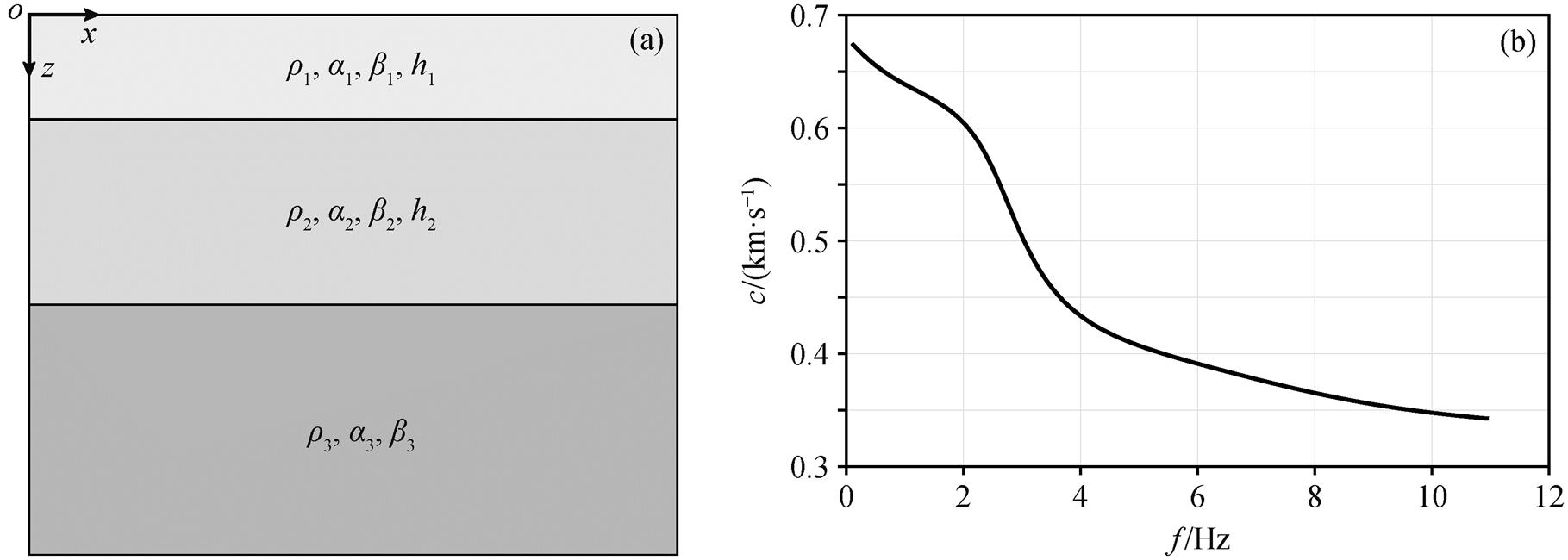
图4 速度模型(a)和参考频散曲线(b)
Fig. 4 Velocity model (a) and reference dispersion curve (b)
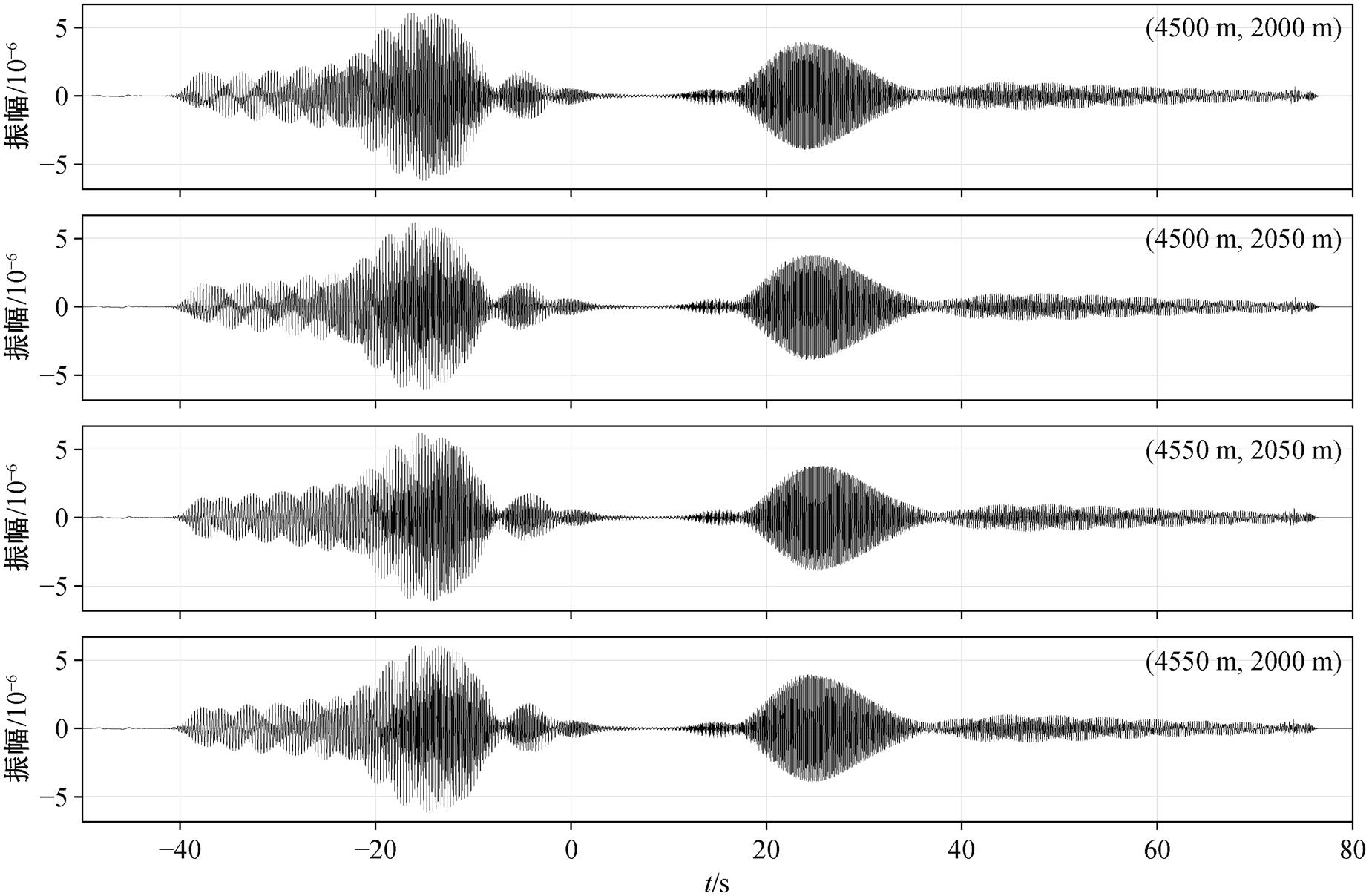
图5 4个台站的 z 方向模拟地震记录
Fig. 5 Synthetic seismic records of four stations in z direction
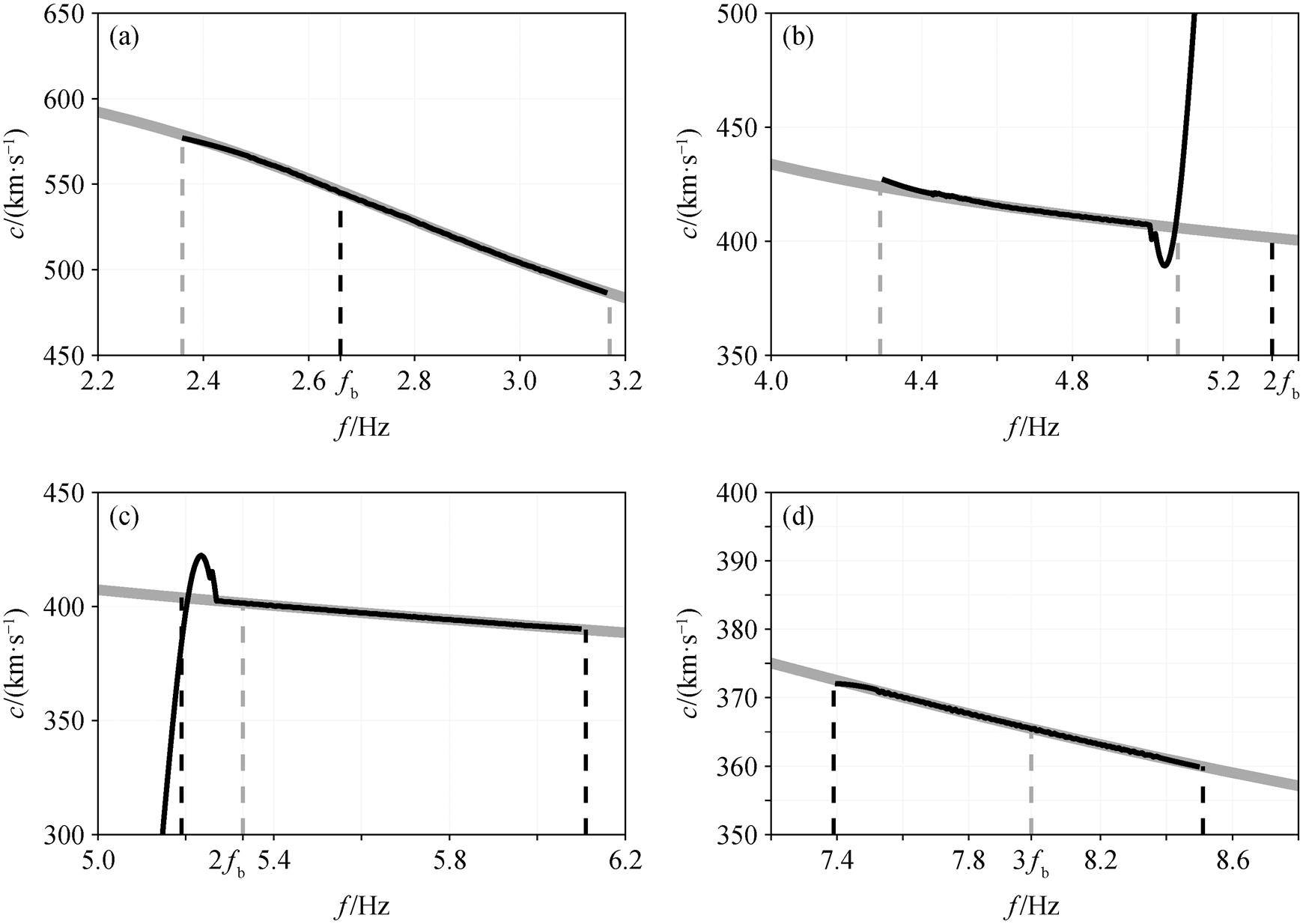
(a)一倍桥频; (b)和(c)两倍桥频; (d)三倍桥频。灰色曲线是参考频散曲线, 黑色曲线是基于台阵法得出的频散曲线, 灰色虚线是桥频及其倍频, 黑色虚线是频率范围的端点值
图6 瑞利波频散曲线计算结果
Fig. 6 Calculated results of Rayleigh wave dispersion curve
我们知道, 相速度本身在 5.15Hz 附近并没有跳变, 所以这个跳变是由计算方法引起的。主要原因是计算两倍桥频附近的频散曲线时相位跳跃了2π, 计算过程中忽略周期跳跃导致数值不稳定。
上述结果显示, 多台法能够较有效地获取高铁振动产生波场的面波相速度值。但是, 出现一个明显的问题: 相速度结果在两倍桥频附近出现跳变, 导致一小段频率范围内的结果不可用。结合测试过程中台站分布和高铁地震波场传播的规律, 我们认为这一误差是由以下原因造成的。由于每一组计算涉及 3 个台站和两个台站对, 若其中一对台站的连线与某个频率的面波主要传播方向垂直, 从理论上讲, 这两个台站间的相位差趋于零。在模拟数据中, 会因为数据的截断产生误差; 应用到真实数据中时, 数据本身的噪声带来的相位测量误差也不容忽视。对于理论上相位相等的这两个台站, 产生的相对误差就比较大, 从而使得相速度的测量结果不准确。解决这一的方法是利用更多的台站数据, 基于最小二乘法, 降低不确定性因素的影响。
本研究的数值实验是在已知视速度的情况下估计频率的范围, 进行视速度的提取。如果视速度是未知的, 由式(14)可以知道, 当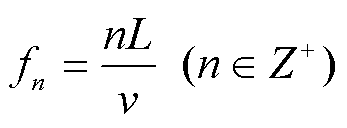 , sinθ=0 时, 台站垂直于某个桥墩, 计算得到的频率是高铁的桥频及其倍频。在桥频 fn及其倍频处, 视速度是准确值。对于不同的列车速度, 桥频 fn及其倍频是变化的, 可以形成一段频率范围的视速度值。同时, 用前 3 个台站计算得到的相速度结果与用后 3 个台站计算得到的相速度结果仅在相速度的正确值处有重合(图 2)。利用这一特点, 就可以筛选出正确的相速度值。
, sinθ=0 时, 台站垂直于某个桥墩, 计算得到的频率是高铁的桥频及其倍频。在桥频 fn及其倍频处, 视速度是准确值。对于不同的列车速度, 桥频 fn及其倍频是变化的, 可以形成一段频率范围的视速度值。同时, 用前 3 个台站计算得到的相速度结果与用后 3 个台站计算得到的相速度结果仅在相速度的正确值处有重合(图 2)。利用这一特点, 就可以筛选出正确的相速度值。
本文分析了以等间距桥墩为震源的高铁地震信号的叠加干涉特征, 提出利用多台站相位差提取波场视速度的方法。针对相位计算结果存在多值性的问题, 本文提出通过比较不同台站组合计算结果的方法来获得正确的相速度值。与双台法相比, 本文提出的利用多台提取相速度的方法无需对计算值进行校正, 能够适应更复杂的情况。基于模拟的瑞利波记录进行测试的结果表明, 所得相速度在一定频率范围内与参考模型值接近, 从而证明了本文方法的有效性。
参考文献
[1]徐善辉, 郭建, 李培培, 等. 京津高铁列车运行引起的地表振动观测与分析. 地球物理学进展, 2017, 32(1): 421‒425
[2]蒋一然, 鲍铁钊, 宁杰远, 等. 高架桥下方高铁地震信号频谱特征研究. 北京大学学报(自然科学版), 2019, 55(5): 829‒838
[3]蒋一然, 梁萱, 宁杰远, 等. 高铁地震 4D地频图及其可用性研究. 北京大学学报(自然科学版), 2019, 55(5): 850‒858
[4]包乾宗, 许杰, 许明瑞. 高铁地震信号时频特征对比分析. 北京大学学报(自然科学版), 2019, 55(5): 805‒812
[5]温景充, 宁杰远, 张献兵. 高铁地震波场特点的理论分析. 北京大学学报(自然科学版), 2019, 55(5): 813–822
[6]温景充, 宁杰远. 高铁波场等效震源时间函数反演方法研究. 北京大学学报(自然科学版), 2019, 55(5): 823‒828
[7]张固澜, 何承杰, 李勇, 等. 高铁地震震源子波时 间函数及验证. 地球物理学报, 2019, 62(6): 2344‒ 2354
[8]胡光辉, 张固澜, 孙思宇, 等. 高铁地震信号直达波波形反演建模. 地球物理学报, 2019, 62(12): 4817‒4824
[9]Quiros D A, Brown L D, Kim D. Seismic interfero-metry of railroad induced ground motions: body and surface wave imaging. Geophysical Journal Interna-tional, 2016, 205(1): 301–313
[10]Brenguier F, Boué P, Ben-Zion Y, et al. Train traffic as a powerful noise source for monitoring active faults with seismic interferometry. Geophysical Re-search Letters, 2019, 46(16): 9529‒9536
[11]王晓凯, 陈文超, 温景充, 等. 高铁震源地震信号的挤压时频分析应用. 地球物理学报, 2019, 62(6): 2328‒2335
[12]王晓凯, 陈建友, 陈文超, 等. 高铁震源地震信号的稀疏化建模. 地球物理学报, 2019, 62(6): 2336‒ 2343
[13]温景充, 石永祥, 宁杰远. 高铁地震面波相速度频散曲线提取. 地球物理学报, 2021, 64(9): 3246‒3256
[14]Forsyth D W, Webb S, Dorman L M, et al. Phase velocities of Rayleigh waves in the MELT experiment on the East Pacfic Rise. Science, 1998, 280: 1235–1238
[15]Ritzwoller M H, Lin F C, Shen W. Ambient noise tomography with a large seismic array. Comptes Ren-dus Geosciences, 2011, 343(8): 558‒570
[16]Yao H, Van der Hilst R D, De Hoop M V. Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis —I. phase velocity maps. Geophysical Journal International, 2006, 166: 732‒744
[17]石永祥, 温景充, 宁杰远. 高铁震源地下介质成像的理论分析. 中国科学: 地球科学, 2022, 52(5): 893‒902
An Array-Based Method for Measuring Apparent Velocity of the High-Speed Rail Seismic Wavefield
Abstract For the seismic source generated by the high-speed rail with viaduct, a theoretical method is proposed to measure the apparent velocity of the high-speed rail wavefield generated by a moving source set by using cross-correlation of the waves recorded by multiple stations. Furthermore, synthetic data of the high-speed rail wave-fields in layered media is generated, and the apparent velocity of a phase in it is calculated. The correctness of the method is verified compared with the theoretical results.
Key words high-speed rail; moving source combination; interference field; apparent velocity