doi: 10.13209/j.0479-8023.2022.081
国家重点研发计划(2018YFE0203801)资助
北京大学学报(自然科学版) 第58卷 第5期 2022年9月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 58, No. 5 (Sept. 2022)
收稿日期: 2021–09–30;
修回日期: 2021–12–04
摘要 针对当前主流的剪枝方法所获得的压缩模型推理时间较长和效果较差的问题, 提出一种易用且性能优异的层剪枝方法。该方法将原始卷积层转化为可融合残差卷积块, 然后通过稀疏化训练的方法实现层剪枝, 得到一种具有工程易用性的层剪枝方法, 兼具推理时间短和剪枝效果好的优点。实验结果表明, 在图像分类任务和目标检测任务中, 该方法可使模型在精度损失较小的情况下获得极高的压缩率, 优于先进的卷积核剪枝方法。
关键词 卷积神经网络; 层剪枝; 可融合残差卷积块; 稀疏化训练; 图像分类
卷积神经网络在图像分类、目标检测和实例分割等计算机视觉任务中都表现出优异的性能。由于工业界对精度的需求越来越高, 网络规模愈发庞大, 但在资源受限的端侧, 硬件平台无法部署过大的模型。为解决这种矛盾, 研究者提出各种各样的模型压缩方法, 如模型剪枝[1–5]、权重量化[6–9]和神经网络结构搜索[10–12]等。其中, 模型剪枝由于其优异的压缩性能而成为模型压缩的主流方法, 可分为非结构化剪枝与结构化剪枝。
非结构化剪枝方法由 Han 等[13]2015 年提出, 认为卷积神经网络中越小的权重对网络越不重要, 因此可将其减掉。此类方法的模型压缩效果较好, 但需要特殊的硬件结构或软件加速库才能实现提速,实用性较差。
结构化剪枝的主流方法是对整个卷积核进行剪枝, 因此易于部署。Li 等[14] 2016 年提出基于 L1范数对卷积核进行剪枝的方法, 认为 L1 范数小的卷积核可以被剪裁。He 等[15]将靠近每层卷积核几何中心点的卷积核裁减掉, 实现模型压缩。Liu 等[16]提出基于批归一化层的剪枝方法, 通过稀疏化批归一化层的缩放因子筛选不重要的卷积核。
可以将层剪枝方法视为一种结构化剪枝方法, 它将整个卷积层视为一个整体进行剪枝, 剪枝粒度更大。通常, 粒度越大的剪枝方法越不容易得到优异的剪枝性能, 因此很少有人研究层剪枝方法。然而, 网络在硬件中推理时, 层数越多意味着耗时越多, 而耗时问题实际上是工程应用中最应该关注的, 因此对层剪枝的研究极具工程意义。Chen 等[17] 2018 年提出一种基于特征表示的层剪枝方法, 对每个卷积层训练一个线性分类器, 然后基于分类器对卷积层进行排名和剪裁, 但这种方法极其复杂且耗时。本文使用特殊的可融合残差卷积块及简单的稀疏化训练, 实现一种简单易用的层剪枝方法, 其压缩性能不仅可以超过之前的层剪枝方法, 甚至超越目前先进的卷积核剪枝方法。
本文层剪枝方法的基本框架如图 1 所示, 分为4 个步骤: 第一步, 将初始网络中的卷积、批归一化和激活结构转化为包含层重要性因子 mi 的可融合残差卷积块; 第二步, 通过稀疏化训练, 使重要性因子更趋于零; 第三步, 将训练好的稀疏网络中不重要的层剪裁掉; 第四步, 将未减掉的可融合残差卷积块融合为原本的普通卷积结构, 最终得到压缩后的模型。
如图 2 所示, 本文使用的可融合残差卷积块由ResNet[18]中普通残差块变形而成。图 2(a)为ResNet中的残差块, 图 2(b)为普通可融合残差卷积块, 二者最大的不同在于可融合残差卷积块仅包含一组卷积结构, 使其可以通过融合去除捷径分支, 变为普通卷积层。此外, 在可融合残差卷积块中添加了重要性因子 mi 来表示该层的重要性程度, 添加可训练参数 gi 来自适应地控制捷径分支信息的流动。当可融合残差卷积块的输入输出特征图通道数或尺寸不一致时, 不能直接使用捷径分支进行连接。本文采用添加 1×1 卷积和平均卷积的方式分别处理这两种情况, 如图 2(c)和(d)所示。
可融合残差卷积块的特点是可在训练后融合为普通卷积层, 使得使用它并不会更改推理模型结构, 这是层剪枝方法实现的最关键因素。图 3 展示具体的融合过程, 其中, ![]() 表示在捷径分支上的平均池化或卷积操作(普通情况下表示无操作)。
表示在捷径分支上的平均池化或卷积操作(普通情况下表示无操作)。
在训练结束后, 批归一化层和重要性参数 mi 可简单地通过线性关系融合到其前面的卷积层中。因此, 可融合残差卷积块可以由下式表示:
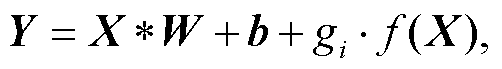 (1)
(1)
式中, ![]() 表示卷积操作, X和Y分别表示输入和输出的特征图, W和b表示卷积的权重和偏置, 表示线性乘法。离散卷积具有分配律, 因此, 式(1)可以被融合成一个卷积操作:
表示卷积操作, X和Y分别表示输入和输出的特征图, W和b表示卷积的权重和偏置, 表示线性乘法。离散卷积具有分配律, 因此, 式(1)可以被融合成一个卷积操作:
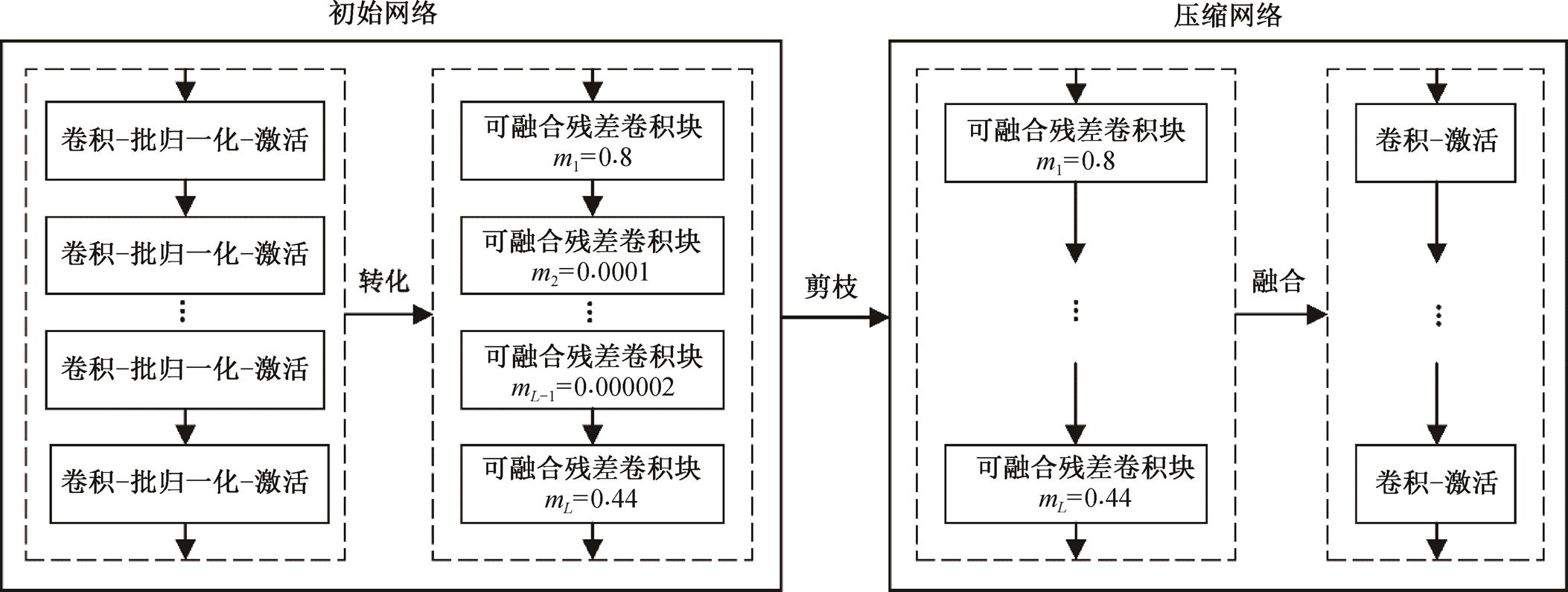
图1 层剪枝框架
Fig. 1 Framework of layer pruning
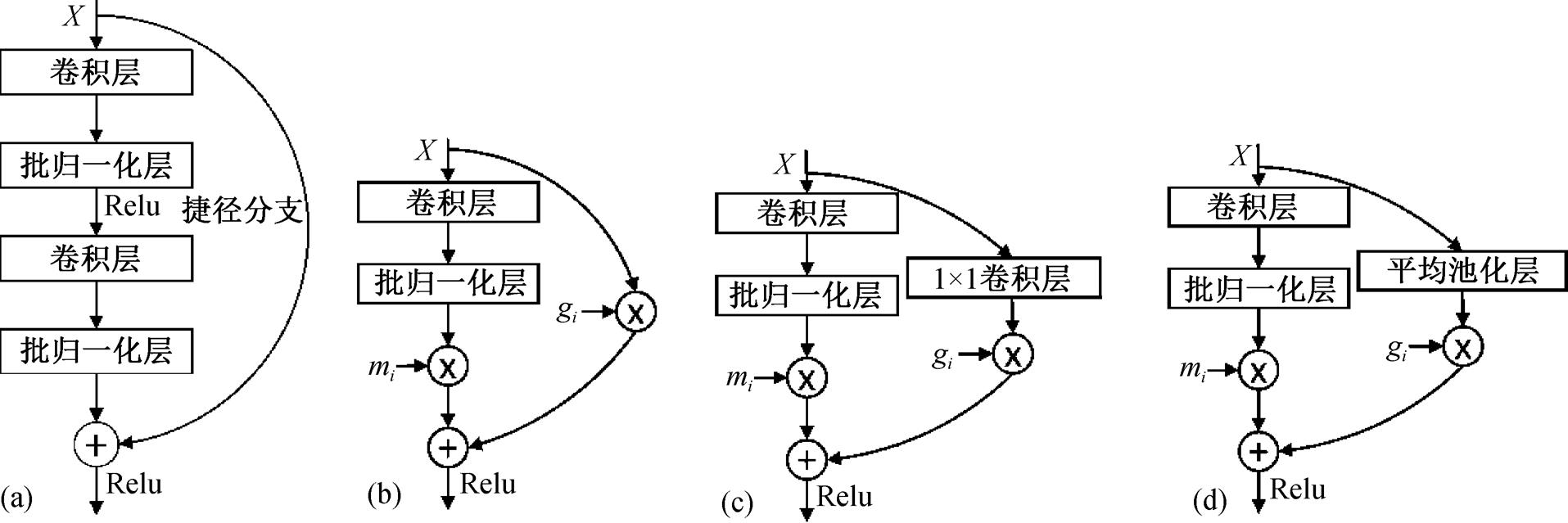
图2 ResNet残差块和3种可融合残差卷积块
Fig. 2 Residual block of ResNet and three fusible residual convolutional blocks
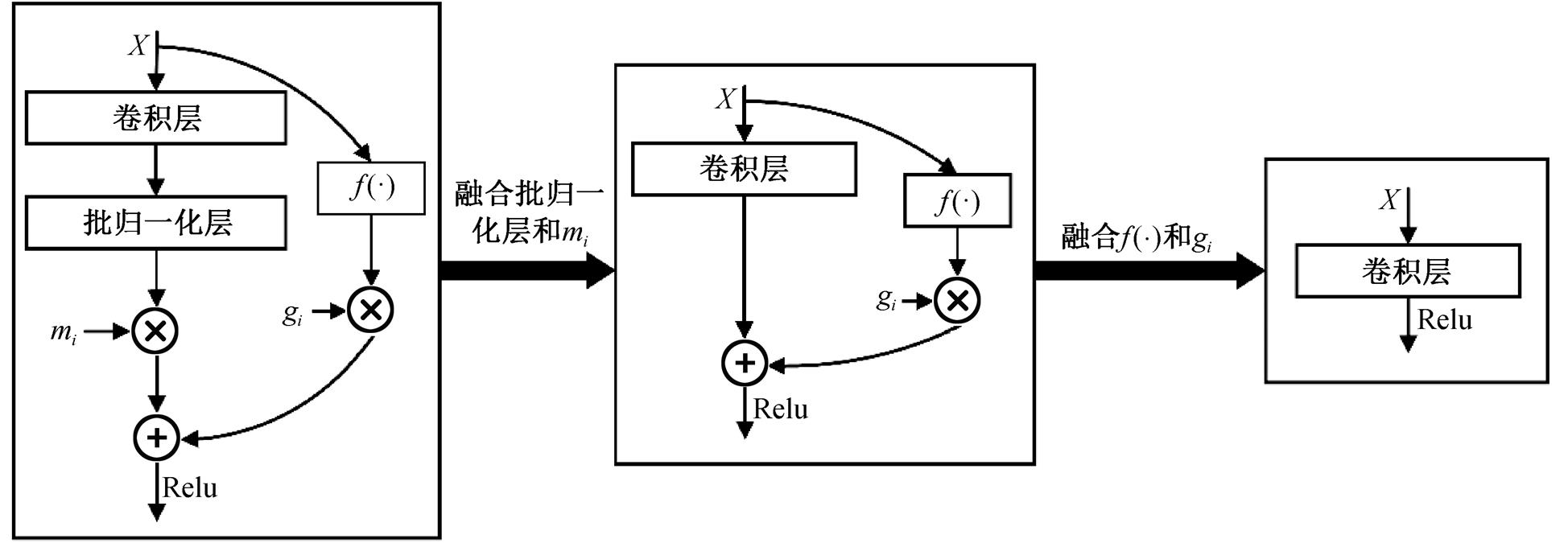
图3 可融合残差卷积块融合过程
Fig. 3 Fusion process of fusible residual convolutional blocks
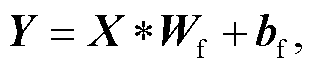 (2)
(2)
式中, Wf和bf是融合卷积的权重和偏置。无论是无操作、卷积或平均池化, 式(1)中 f()都可由一个权重为 Ws 和偏置为 bs 的卷积表示。因此, 可以通过下面的运算求得 Wf和 bf:
 (3)
(3)
 (4)
(4)
式中, j和q表示第j个输出通道和第 q 个输入通道对应的卷积, 例如, 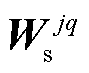 表示
表示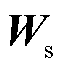 第 j 个输出通道和第 q 个输入通道所对应的卷积核权重值; t 和 u 分别表示输出和输入通道的总数。
第 j 个输出通道和第 q 个输入通道所对应的卷积核权重值; t 和 u 分别表示输出和输入通道的总数。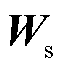 可以通过下式求得:
可以通过下式求得:
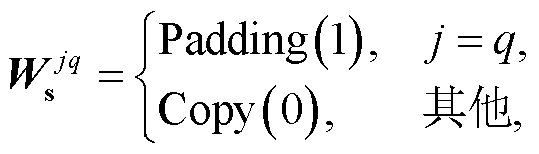 (5)
(5)
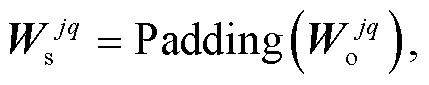 (6)
(6)
 (7)
(7)
式中, 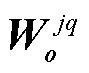 表示捷径分支上 1×1 卷积的权重, v 表示卷积层的卷积核大小, Padding 表示通过在四周补 0 来得到一个 v×v 的卷积核; Copy 表示通过复制来得到一个 v×v 的卷积核。式(5)~(7)分别对应捷径分支上无操作、1×1 卷积操作以及平均池化操作的情况。此外, 当捷径分支上进行 1×1 卷积时, 式(4)中的
表示捷径分支上 1×1 卷积的权重, v 表示卷积层的卷积核大小, Padding 表示通过在四周补 0 来得到一个 v×v 的卷积核; Copy 表示通过复制来得到一个 v×v 的卷积核。式(5)~(7)分别对应捷径分支上无操作、1×1 卷积操作以及平均池化操作的情况。此外, 当捷径分支上进行 1×1 卷积时, 式(4)中的 等于对应 1×1 卷积的偏置值, 其他情况时
等于对应 1×1 卷积的偏置值, 其他情况时 均为 0。至此, 可融合残差卷积块结构便通过数学运算融合为一个普通卷积层。
均为 0。至此, 可融合残差卷积块结构便通过数学运算融合为一个普通卷积层。
在训练中, 需要对重要性因子进行稀疏化, 使其值更趋于零, 从而获得更大的剪枝率。本文采用经典的 L1 正则化进行稀疏化训练, 并定义 γ为稀疏因子, 稀疏因子越大, 稀疏程度越高。
稀疏化训练后, 便可将模型中重要性因子较小的层减掉。图 4 展示剪枝的过程, 首先将重要性因子前的卷积层和批归一化层裁减掉, 然后将可训练参数 gi 线性地叠加到前层或后层的卷积层中。多数情况下, 捷径分支上无操作, 因此整个可融合残差卷积块被裁减掉; 对于捷径分支上有卷积或平均池化的情况, 该操作将保留, 但 1×1 卷积和平均池化的计算量和耗时可忽略。
将本文层剪枝方法在不同数据集和不同网络结构上进行实验, 并与目前先进的卷积核剪枝方法和层剪枝方法进行对比。
本文采用规模不同的图像分类数据集 CIFAR-10 和 ImageNet 在不同网络结构进行实验, 验证本文方法的有效性。此外, 在牛津大学视觉团队整理的 Oxford Hand 数据集上对本文方法在目标检测上的有效性进行测试, 性能评价指标使用非极大值抑制(NMS)阈值为 0.5 情况下的平均精度均值(mAP)。所用数据集概况如表 1 所示。
首先, 在 CIFAR-10 上对 VGG-16 网络进行实验。表 2 中实验结果表明, 与当前先进的剪枝方法相比, 本文提出的层剪枝方法在保证精度损失更低的情况下, 计算量和参数量的裁减比例更高。
VGG-16 属于不包含残差结构的网络, 为体现方法的普适性, 本研究还在包含残差结构的网络ResNet-56 上进行实验。表 3 中实验结果表明, 本文的层剪枝方法依然适用于包含残差结构的网络。
由于轻量级网络冗余度较低, 剪枝难度较大, 研究者通常不在轻量级网络上进行实验。为展示所提方法的优异性, 本文在 MobileNet 上进行实验。表 4 中实验结果表明, 本文方法在轻量级网络上依然可以有效地剪枝。
本研究在 ImageNet 上对 ResNet-50 网络进行实验, 来证明本文方法在大型数据集上的适用性。表 5 中实验结果表明, 本文方法在大型数据集上依然具有优势。
目标检测是比图像识别难度更高的一种基础性计算机视觉任务。为展示本文方法在目标检测上的有效性, 本研究以 SSD 模型为例进行实验。表 6 中实验结果表明, 本文方法对目标检测依然有效。
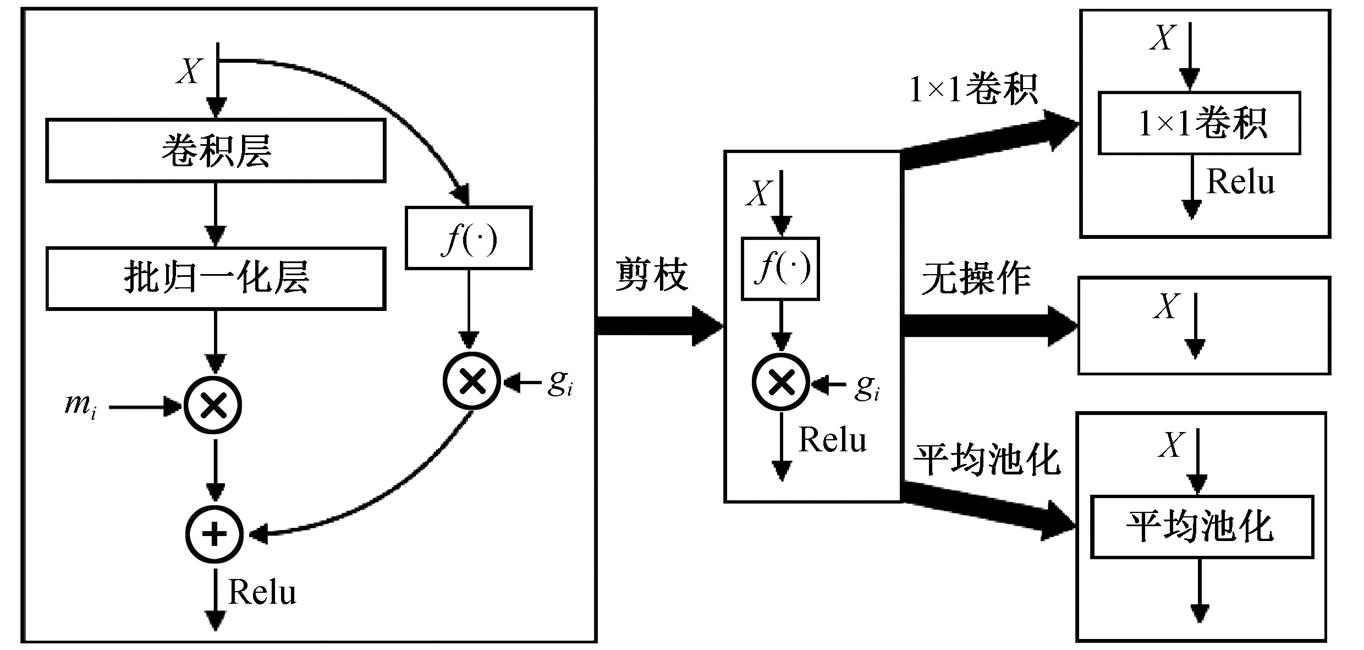
图4 可融合残差卷积块剪枝过程
Fig. 4 Prune process of fusible residual convolutional blocks
表1 本文所用数据集概况
Table 1 Overview of the datasets used in the article

数据集类别数训练数量/测试数量实验所用网络结构CIFAR-101050000/10000VGG-16, ResNet-56, MobileNetImageNet10001200000/50000ResNet-50 Oxford Hand19163/1856SSD
表2 CIFAR-10数据集上VGG-16模型应用各剪枝方法的效果
Table 2 Effects of various pruning methods applied to VGG-16 on CIFAR10

剪枝方法Top-1准确率/% 计算量/M 参数量/M 未剪枝94.15314.29 (0.0%)14.99 (0.0%)SSS[19]93.21183.69 (41.6%)3.94 (73.7%)Zhao等[20]93.37190.56 (39.3%)3.93 (73.8%)本文方法(γ=0.01)93.45138.53 (55.9%)3.61 (75.9%)GAL[21]92.22190.05 (39.5%)3.37 (77.5%)Chen等[17]92.40171.90 (45.3%)1.44 (90.4%)HRank[22]92.53109.17 (65.3%)2.65 (82.3%)本文方法(γ =0.1)92.7184.00 (73.3%)1.18 (92.1%)
说明: 括号中数据为裁减比例, 下同。
表3 CIFAR-10数据集上ResNet-56模型应用各剪枝方法的效果
Table 3 Effects of various pruning methods applied to ResNet-56 on CIFAR10

剪枝方法Top-1准确率/% 计算量/M 参数量/M 未剪枝93.69126.55 (0.0%)0.85 (0.0%) L1[14]93.4991.96 (27.3%)0.73 (14.1%) 本文方法(γ=0.001)93.7581.00 (36.0%)0.61 (28.2%) Chen等[17]92.1975.7 (40.2%)0.42 (50.6%) NISP[23]92.7056.00 (55.7%)0.41 (51.8%) 本文方法(γ=0.01)92.7246.37 (63.4%)0.35 (58.5%) GAL[21]90.7951.05 (59.7%)0.29 (65.9%) HRank[22]91.1533.58 (73.5%)0.27 (68.2%) 本文方法(γ=0.1)91.5933.49 (73.5%)0.26 (68.3%)
表4 CIFAR-10数据集上MobileNet模型应用层剪枝方法的效果
Table 4 Effects of layer pruning method applied to MobileNet on CIFAR10

剪枝方法Top-1准确率/% 计算量/M 参数量/M 未剪枝92.1547.18 (0.0%)3.22 (0.0%) 本文方法(γ =0.001)93.0329.77 (36.9%)2.14 (33.5%) 本文方法(γ =0.01)92.2824.52 (48.0%)2.11 (34.5%) 本文方法(γ =0.1)90.4616.23 (65.6%)1.78 (44.7%)
表5 ImageNet数据集上ResNet-50模型应用各剪枝方法的效果
Table 5 Effects of various pruning methods applied to ResNet-50 on ImageNet

剪枝方法Top-1 准确率/%Top-5 准确率/%计算量/B参数量/M 未剪枝76.1592.874.1125.56 GAL-1[21]71.9590.942.3521.26 本文方法(γ=0.001)73.8891.302.1713.63 SSS[19]74.1891.912.8418.66 HRank[22]74.9892.332.3216.21 本文方法(γ=0.01)75.0192.352.1713.63 GAL-0.5[21]69.8889.751.8614.73 本文方法(γ=0.05)69.9590.031.62 11.25
从表 2~6 中实验结果可以看到, 稀疏因子 γ 与模型的性能及剪枝比例有强相关性。稀疏因子越大, 模型性能越差, 但剪枝比例越高。原因是, 稀疏因子的增加会导致模型的参数分布更趋于零, 致使模型的表达能力降低, 同时参数的趋零化导致可以剪裁更多的层。为了直观地看到稀疏因子对模型参数分布和模型性能的影响, 本研究在 CIFAR-10数据集上对 ResNet-110 进行稀疏化实验。从图 5 展示的实验结果可以看到, 大稀疏因子值对应了更趋零的参数分布和更低的准确率。
表6 Oxford Hand数据集上SSD模型应用各剪枝方法的效果
Table 6 Effects of various pruning methods applied to SSD on Oxford Hand
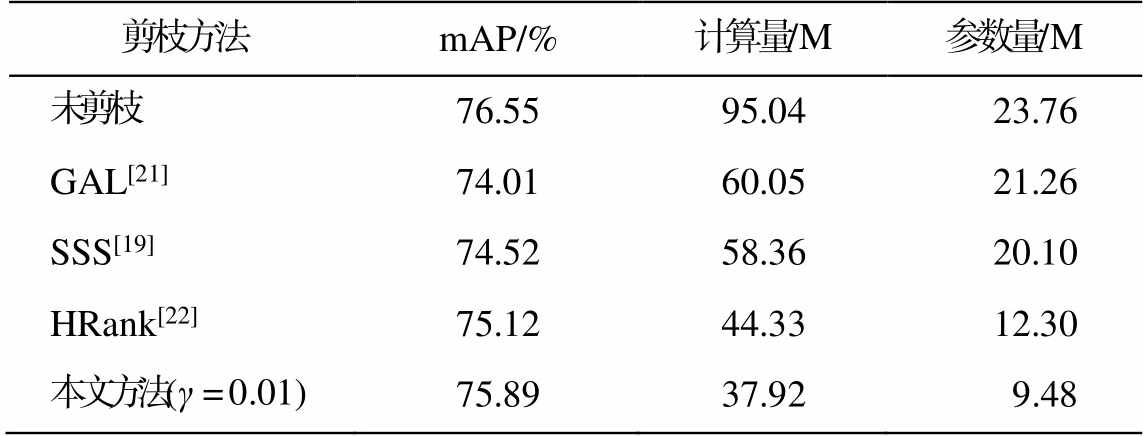
剪枝方法mAP/%计算量/M参数量/M 未剪枝76.5595.0423.76 GAL[21]74.0160.0521.26 SSS[19]74.5258.3620.10 HRank[22]75.1244.3312.30 本文方法(γ =0.01)75.8937.929.48
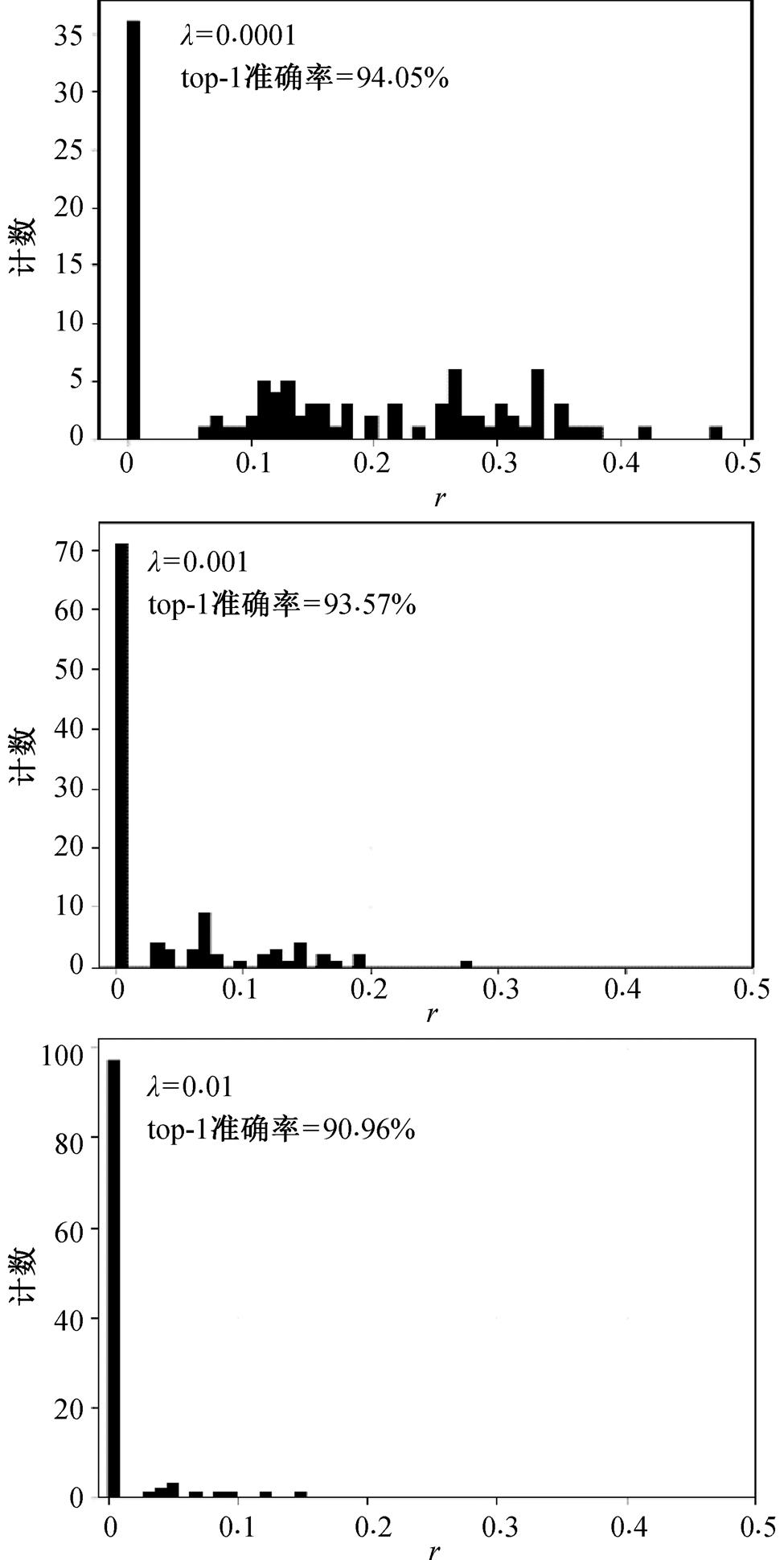
图5 稀疏因子实验
Fig. 5 Experiment of sparse factor
推理耗时是展示模型剪枝方法优劣性的重要工程标准。本文设置一个简单的补充实验, 证明层剪枝在减少推理耗时方面比卷积核剪枝更有优势。实验中针对 VGG-16 网络, 随机生成参数量和运算量均相同的层剪枝网络和卷积核剪枝网络, 在CIFAR-10 数据集上统计二者在 GPU 上推理测试集中所有图片的耗时。表 7 展示 100 次实验的平均结果, 可以看到层剪枝方法耗时更少。
表7 层剪枝和卷积核剪枝推理耗时对比
Table 7 Comparison of inference time between layer pruning and convolutional kernel pruning

剪枝方法计算量/M参数量/M耗时/s 卷积核剪枝68.54.22.01 层剪枝68.54.21.65
本文针对现有卷积核剪枝方法在减少推理耗时不足和现有层剪枝方法复杂且性能差的问题, 提出基于可融合残差卷积块的层剪枝方法, 并利用可融合残差卷积块和稀疏化训练的方式实现。实验结果表明, 该方法在保证精度损失较低的前提下, 有优异的压缩性能。
在未来的工作中, 我们将探索如何将层剪枝方法和卷积核剪枝方法共同使用, 以求更高的压缩率, 便于在端侧智能设备上部署和加速。
参考文献
[1]Wen W, Wu C, Wang Y, et al. Learning structured sparsity in deep neural networks // Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelno, 2016: 2082–2090
[2]Zhou H, Alvarez J M, Porikli F. Less is more: towards compact CNNS // European Conference on Computer Vision. Cham: Springer, 2016: 662–677
[3]Han S, Mao H, Dally W J. Deep compression: compres-sing deep neural network with pruning, trained quantize-ation and Huffman coding [EB/OL]. (2015–11–20)[2021–05–20]. https://arxiv.org/abs/1510.00149v3
[4]Liu Z, Sun M, Zhou T, et al. Rethinking the value of network pruning [EB/OL]. (2019–03–05)[2021–05–20]. https://arxiv.org/abs/1810.05270
[5]Changpinyo S, Sandler M, Zhmoginov A. The power of sparsity in convolutional neural networks [EB/OL]. (2017 –02–21)[2021–05–20]. https://arxiv.org/abs/1702.06257
[6]Rastegari M, Ordonez V, Redmon J, et al. XNORNet: imagenet classification using binary convolutional neural networks // European Conference on Computer Vision. Cham: Springer, 2016: 525–542
[7]Zhou Shuchang, Wu Yuxin, Ni Zekun, et al. DoReFaNet: training low bitwidth convolutional neural networks with low bitwidth gradients [EB/OL].(2018–02–02)[2021–05–20]. https://arxiv.org/abs/1606.06160
[8]Jacob B, Kligys S, Chen B, et al. Quantization and training of neural networks for efficient integer-arithmetic-only inference [EB/OL]. (2017–12–15) [2021–05–20]. https://arxiv.org/abs/1712.05877
[9]Courbariaux M, Bengio Y. Binarynet: training deep neural networks with weights and activations constra-ined to +1 or –1 [EB/OL]. (2016–04–18)[2021–05–20]. https://arxiv.org/abs/1511.00363
[10]Jin J, Yan Z, Fu K, et al. Neural network architecture optimization through submodularity and supermodu-larity [EB/OL].(2018–02–21)[2021–05–20]. https://ar xiv.org/abs/1609.00074
[11]Baker B, Gupta O, Naik N, et al. Designing neural network architectures using reinforcement learning [EB/OL]. (2016–11–07)[2021–05–20]. https://arxiv.o rg/abs/1611.02167v1
[12]Zhang L L, Yang Y, Jiang Y, et al. Fast hardware-aware neural architecture search [EB/OL]. (2020–04– 20)[2021–05–20]. https://arxiv.org/abs/1910.11609
[13]Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural network // Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, 2015: 1135–1143
[14]Li H, Kadav A, Durdanovic I, et al. Pruning filters for efficient convnets [EB/OL]. (2017–03–10)[2021–05–20]. https://arxiv.org/abs/1608.08710
[15]He Y, Liu P, Wang Z, et al. Pruning filter via geometric median for deep convolutional neural networks accelera-tion // IEEE Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 4340–4349
[16]Liu Zhuang, Li Jianguo, Shen Zhiqiang, et al. Lear-ning efficient convolutional networks through network slimming // IEEE International Conference on Com-puter Vision. Venice, 2017: 2736–2744
[17]Chen S, Zhao Q. Shallowing deep networks: layer-wise pruning based on feature representations. IEEE Transactions on Pattern Analysis and Machine Intelli-gence. 2018, 41(12): 3048–3056
[18]He K, Zhang X, Ren S, et al. Deep residual learning for image recognition // IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, 2016: 770–778
[19]Huang Z, Wang N. Data-driven sparse structure selection for deep neural networks // Proceedings of the European Conference on Computer Vision (ECCV). Munich, 2018: 304–320
[20]Zhao C, Ni B, Zhang J, et al. Variational convolutional neural network pruning // Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 2780–2789
[21]Lin S, Ji R, Yan C, et al. Towards optimal structured cnn pruning via generative adversarial learning // Pro-ceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 2790–2799
[22]Lin M, Ji R, Wang Y, et al. HRank: filter pruning using high-rank feature map // Proceedings of the IEEE/CVF Conference on Computer Vision and Pat-tern Recognition. Seattle, 2020: 1529–1538
[23]Yu R, Li A, Chen C F, et al. NISP: pruning networks using neuron importance score propagation // Procee-dings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City, 2018: 9194–9203
Layer Pruning via Fusible Residual Convolutional Block for Deep Neural Networks
Abstract Aiming at the problems of long inference time and poor effect of the compression model obtained by the current mainstream pruning methods, an easy-to-use and excellent layer pruning method is proposed. The original convolution layers in the model are transformed into fusible residual convolutional blocks, and then layer pruning is realized by sparse training, therefore a layer pruning method with engineering ease is obtained, which has the advantages of short inference time and good pruning effect. The experimental results show that the proposed layer pruning method can achieve a very high compression rate with less accuracy loss in image classification tasks and object detection tasks, and the compression performance is better than the advanced convolutional kernel pruning methods.
Key words convolutional neural network; layer pruning; fusible residual convolutional block; sparse training; image classification