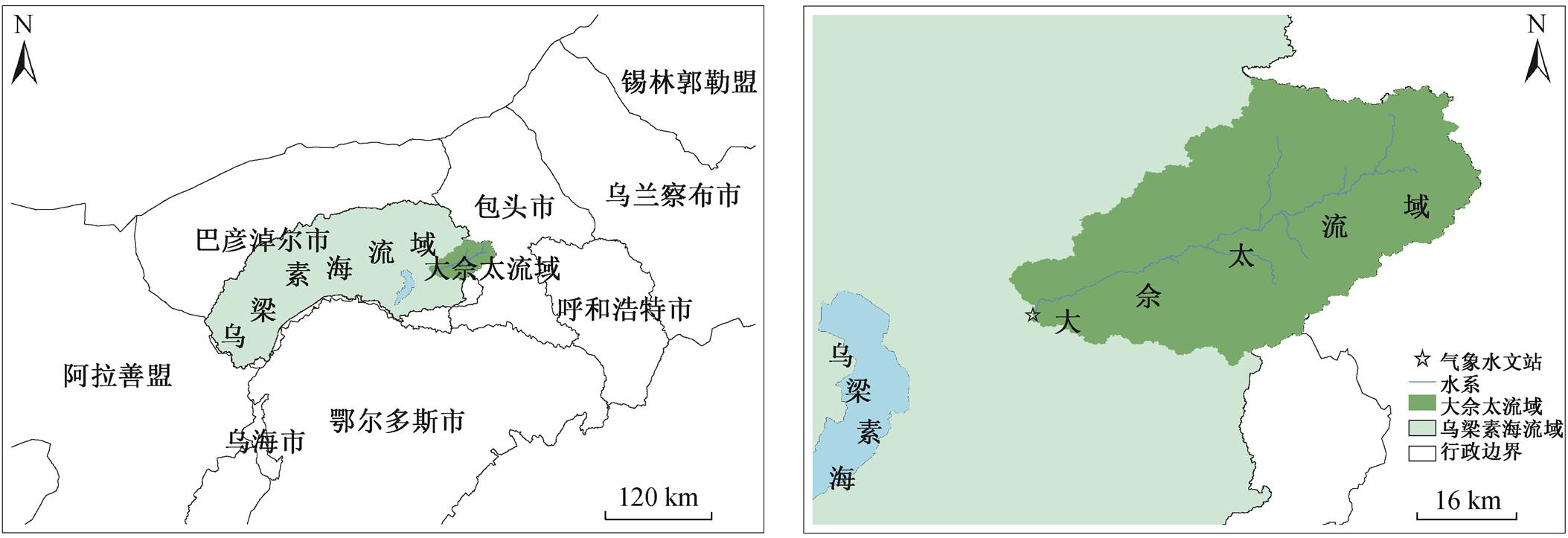
图1 内蒙大佘太流域地理位置
Fig. 1 Location of the Dashetai watershed
摘要 基于 LSPC 构建内蒙大佘太流域水文模拟模型, 利用 Morris 和 Sobol 两种全局敏感性分析方法, 识别水文敏感参数及敏感下垫面类型, 评估不同敏感性分析方法和模型输出度量方法对敏感性分析结果的影响。主要结论如下: 1)模型对日、月两尺度的径流模拟效果好, 模拟值与观测值的决定系数 R2>0.6, 纳什系数NSE>0.5, 说明 LSPC 模型适用于对内陆干旱半干旱地区的流域水文模拟; 2)两种敏感性分析方法对参数敏感指数排序和敏感参数识别均有影响, 而 MAE 和 MSE 两种度量方法的影响主要体现在敏感参数识别方面; 3)敏感水文参数为下层土壤含水量(LZSN)和地下水蒸发系数(AGWETP), 敏感下垫面类型为草地、耕地、林地和水域, 与大佘太流域的降水和土地利用类型有关。
关键词 全局敏感性分析; 水文参数; LSPC模型; 大佘太流域
面源污染是当前我国水环境治理中的突出难点[1], 可根据水文过程将其产生过程分为两种: 在水文产流过程中产污与在汇流过程中汇入河道。流域模型可以精准地模拟产流和汇流过程, 是研究面源污染的有效手段, 其中 LSPC (Loading Simulation Program in C++)是应用较为广泛的模型之一。Estes等[2]利用 LSPC 模型, 模拟墨西哥湾两种降雨模式、4 种土地利用类型下的水文–水质过程, Sahoo 等[3]探究气候变化对 Tahoe 湖流域湖库的影响。在最大日负荷总量(TMDL)计划中, 美国 EPA 将其运用于 Helena 湖流域[4], Flynn 等[5]运用于 Flathead湖流域, 制定出最佳管理措施(BMPs)。
流域模型的参数众多, 不同参数对模型输出的影响程度不同。同时率定所有参数的成本过高, 借助全局敏感性分析方法识别关键参数是模型构建和应用中不可或缺的环节[6–8], 常用的敏感性分析方法有 Morris 法和 Sobol 法等[9]。其中, Morris 法能以较小的计算成本, 快速地求出参数的敏感指数, 实现参数敏感性排序[10–11], 已广泛应用于水文水质模拟中, 如新安江模型[12]和 SWMM 模型[13–15]。Sobol法不易受模型结构影响, 可遍历所有样本空间, 具有适用性强和敏感性分析结果更加稳健等优点[9,16], 在水文水质模型中也得到较广泛的运用。例如, Leimgruber 等[17]、常晓栋等[18]和陈建等[19]利用Sobol 法评估 SWMM 模型参数敏感性, Zadeh 等[20]、Yan 等[21]和 Zhang 等[22]将 Sobol 法运用于 SWAT 模型, 刘松等[12]将其运用于新安江模型。虽然对流域模型进行参数敏感性分析的研究较多, 但关于敏感性分析方法对参数敏感性结果的影响却鲜有关注。同时, 流域模型的输出结果和观测数据都为时间序列, 比较和评估两个时间序列的方法很多, 方法的不同对敏感性分析结果可能产生影响。
目前, 流域模型研究集中于水资源充足的区域, 对蒸散发强、河流主要由地下水补给的干旱半干旱地区的适用性研究较少。本研究以内蒙大佘太流域为研究对象, 基于 LSPC模型构建流域模型, 利用全局敏感性分析方法识别水文敏感参数和敏感下垫面, 评估不同敏感性分析方法和模型输出的不同度量方法对参数敏感性结果的影响, 以期测试 LSPC模型在我国干旱半干旱地区的适用性, 为水文模型参数率定、模型校准和不确定性分析提供借鉴。
大佘太流域位于内蒙乌梁素海东部(图 1), 流域地势东北高西南低, 海拔 1170～2005m (图 2(b)), 坡度 0.20°～51.89° (图 2(c)), 流域面积为 3459km2, 流域出口为大佘太水库。流域内主要有大佘太和小佘太两乡镇, 是典型的农牧区。流域中草地面积为2103.83km2, 占 60.82%; 耕地面积为 1231.00km2, 占 35.59%; 建筑用地、林地、水域和其他 4 种土地利用类型面积占 3.59%。流域降水少而蒸散发强, 年降水量为 172mm, 年蒸发量高达 2365mm。年均温 3.5ºC, 年平均风速为 1.6m/s。流域水资源具有时空分配不均和年际变化大等特点, 乌苏图勒河为主要河流, 全长116.5 km[23]。
土地利用数据来自 GlobeLand30 (2020 版), 空间分辨率为 30m, 包括耕地、林地和草地等共 10 个一级类型数据, 本研究将其合并为林地、草地、耕地、水域、建筑用地和其他 6 类(图 2(a))。DEM数据为 ASTER GDEM 数字高程数据, 空间分辨率为 30m, 来源于地理空间数据云, 利用其提取水系、确定流域边界和划分子流域等。气象数据来源于中国气象局官网, 包括降雨量、气温和风速等。潜在蒸散发采用 Hamon PET 法[24]计算得到, 露点计算采用 Bosen[25]和 Jensen 等[26]总结的经验公式得到。水文数据来源于水文年鉴, 主要指标有流量和水位等。
基于 LSPC 构建大佘太流域水文模型, 包括以下 3 个步骤。
1)划分子流域。根据流域的地形特征对流域进行空间离散, 是分布式水文模型的重要步骤, 直接影响模拟结果[27]。首先利用 DEM数据确定水系, 将大佘太水库作为流域出口, 并借助 ArcGIS, 将研究区域划分为 17 个子流域(图 2 (d))。为了便于计算机识别, 对子流域进行编码。
2)确定水文响应单元(hydrologic response unit, HRU)。HRU 指按照土地利用类型和降雨等将流域空间离散后的计算单元[28], 可降低土地利用方式和降雨等的空间差异对模型的影响。本研究主要考虑土地利用类型的空间异质性, 根据土地利用类型, 将流域划分为 6 类 HRU。
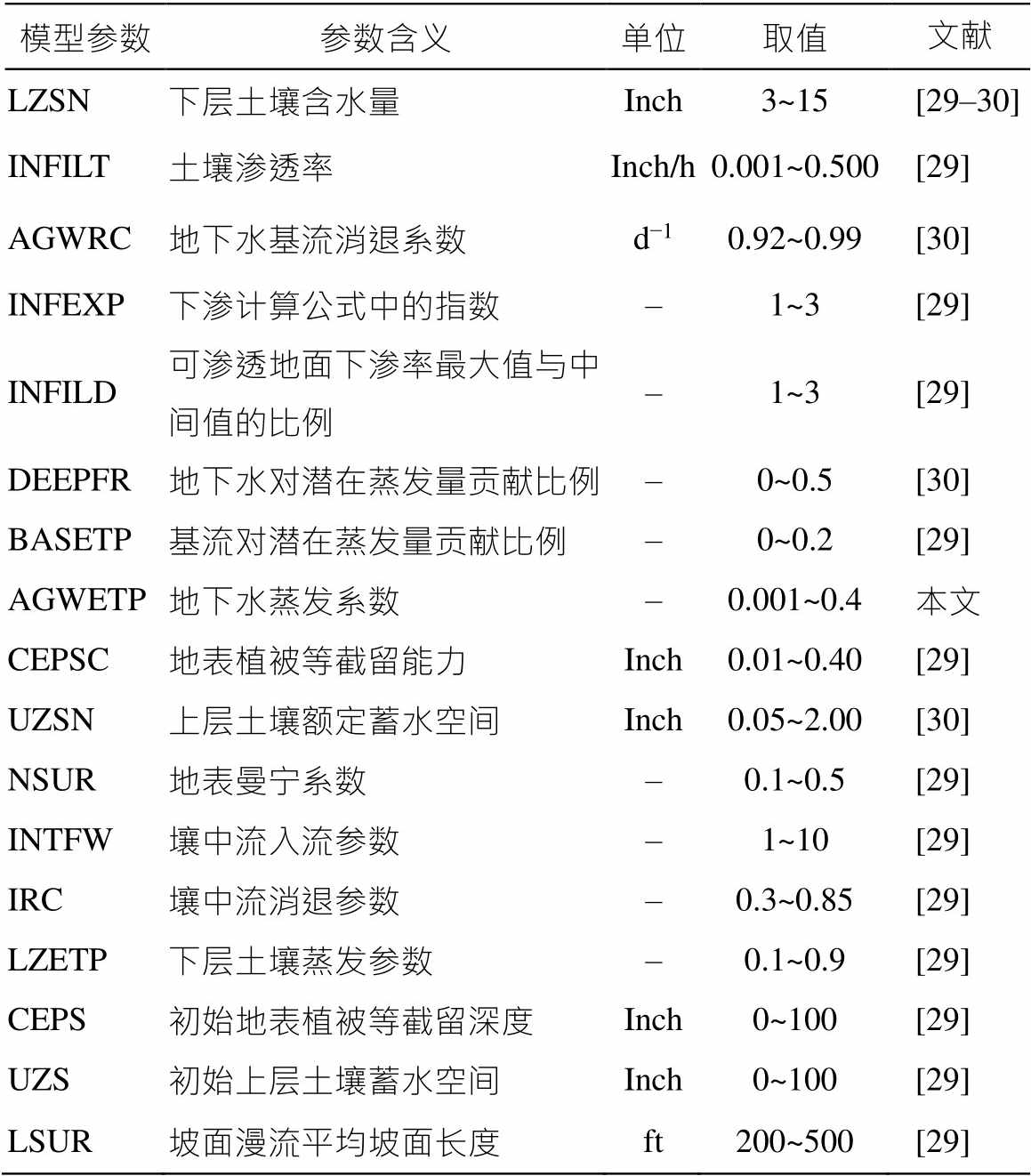
3)流域建模。首先制作输入文件。气象数据是逐小时数据, 存储在.WDM 文件内, 可直接读取; 基础地理数据利用 ArcGIS 编辑为.WSD 和.RCH 等文件格式。其中, .WSD 文件包含土地利用方式和透水地块占比等流域特征信息, .RCH 文件包含水系编号等河道特征数据。在此基础上, 生成主程序文件。根据流域水文过程, 将基础地理数据和气象水文数据制成模型的主控文件, 文件中包含模型结构和参数等内容。其中, 模型参数取值范围主要参考文献[29‒30](表 1)。
图1 内蒙大佘太流域地理位置
Fig. 1 Location of the Dashetai watershed
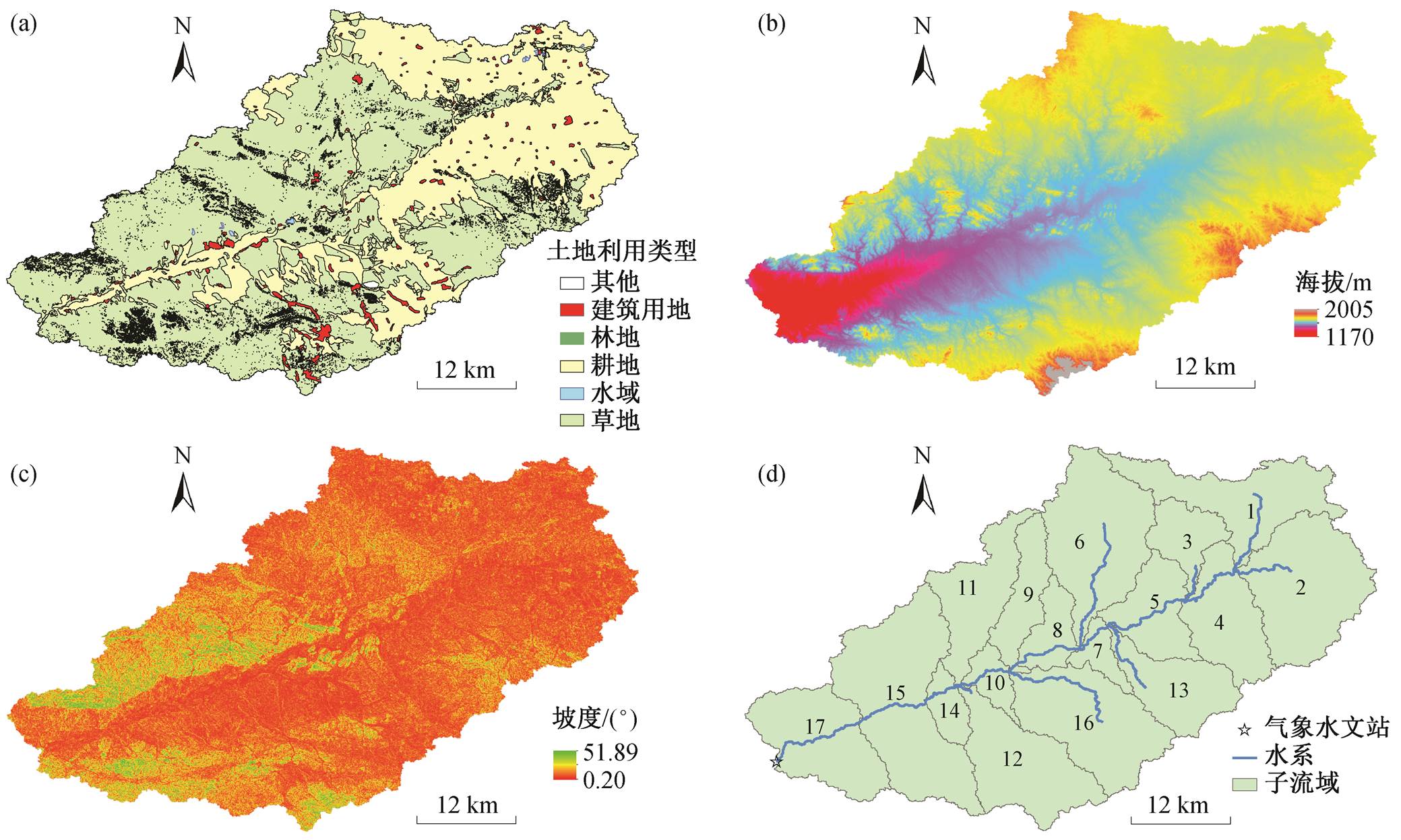
图2 大佘太流域基础地理数据((a)～(c))、水系和子流域(d)
Fig. 2 Basic geographic data ((a)–(c)), water system and sub-basin (d) of the Dashetai watershed
Morris 法的原理与局部敏感性分析方法中“一次变化一个因子”方法(one-factor-at-a-time, OAT)相近, 即以基效应(elementary effect, EE)为指标[11], 如式(1)所示, 对初始状态进行多次反复采样, 求各次采样的基效应, 并用式(2)求其均值 μi, 衡量每个参数对模型输出的全序影响。
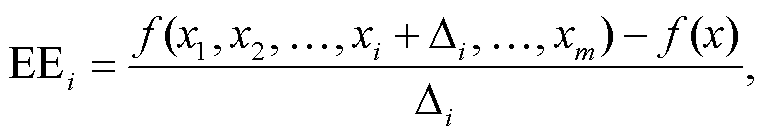(1)
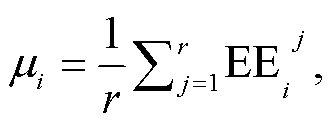(2)
式中, EEi 为第 i 个参数的基效应, f (x1, x2, …, xi+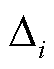
, …, xm)为参数 xi 受扰动后的状态, f (x)为初始状态, m 为参数个数, 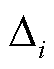为 xi 的变化量, EEi j为第 i 个参数第 j 次采样的基效应。
表1 大佘太流域模型主要水文参数及取值范围
Table 1 Main hydrological parameters and value ranges of the Dashetai watershed model
模型参数参数含义单位取值文献 LZSN下层土壤含水量Inch3～15[29–30] INFILT土壤渗透率Inch/h0.001～0.500[29] AGWRC地下水基流消退系数d−10.92～0.99[30] INFEXP下渗计算公式中的指数‒1～3[29] INFILD可渗透地面下渗率最大值与中间值的比例‒1～3[29] DEEPFR地下水对潜在蒸发量贡献比例‒0～0.5[30] BASETP基流对潜在蒸发量贡献比例‒0～0.2[29] AGWETP地下水蒸发系数‒0.001～0.4本文 CEPSC地表植被等截留能力Inch0.01～0.40[29] UZSN上层土壤额定蓄水空间Inch0.05～2.00[30] NSUR地表曼宁系数‒0.1～0.5[29] INTFW壤中流入流参数‒1～10[29] IRC壤中流消退参数‒0.3～0.85[29] LZETP下层土壤蒸发参数‒0.1～0.9[29] CEPS初始地表植被等截留深度Inch0～100[29] UZS初始上层土壤蓄水空间Inch0～100[29] LSUR坡面漫流平均坡面长度ft200～500[29]
Sobol 法的核心是方差分解[12], 计算公式如下:
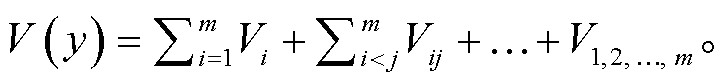(3)
各阶敏感度为各阶方差除于总方差。其中, 一阶敏感度刻画单一模型参数对模型输出的影响, 计算公式为
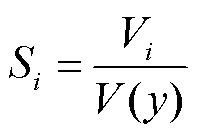。(4)
式(3)和(4)中, V(y)为总方差, Vi 为参数 xi 的一阶方差, Vij 为 xi 和 xj 的二阶方差, …, V1,2,…, m表示 m 个参数的m阶方差。
敏感性分析利用 Python 的 SALib 模块实现, 采样方法设定至关重要。Sobol 法大多采用蒙特卡洛随机采样法生成样本[31]。Morris 方法则因计算敏感性指数时需保证输入样本与模型输出值一一对应, 对采样方法的要求更严格, 大多采用可实现多维分层抽样的拉丁超立方采样法[32]。此外, 为获得可靠的结果, 本研究利用蒙特卡洛随机采样法重采样2000 次, 获得 Sobol 法的样本; 利用拉丁超立方采样法重采样 2000 次, 获得 Morris 法的样本。
有研究表明, 流域模型的水文参数中 LZSN 和INFILT 为敏感水文参数[29–30], 在手动校准模型时, 发现模型输出结果对 AGWETP 的变化比较敏感。LSPC 模型是一个复杂的非线性流域模型, 水文模块涉及的参数众多。本研究设置 6 种 HRU, 由于每种 HRU 的参数取值不同, 待率定的参数增加 6 倍。同时模型输入仅对极少数参数敏感, 对所有参数进行敏感性分析的时间成本过高且没必要。因此, 本研究选取 LZSN, INFILT 和 AGWETP 这 3 类水文参数和 6 种 HRU, 共 18 个参数(表 2)进行全局敏感性分析。
本研究采用均方误差(MSE)、纳什效率系数(NSE)、平方绝对误差(MAE)、Q-Q 图(Quantile-Quantile Plot)、时间序列图和碎石图等指标评估模型稳健性和参数敏感性。各指标的计算公式为
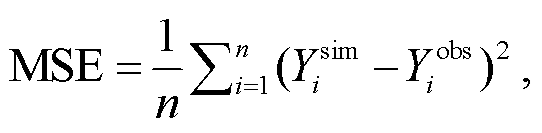(5)
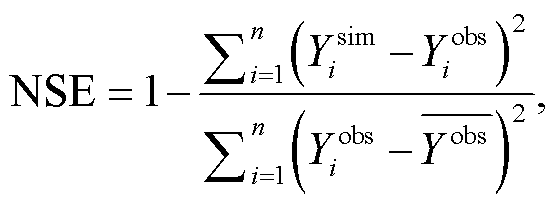(6)
表2 用于大佘太流域模型敏感性分析的18个参数
Table 2 18 parameters used in the sensitivity analysis of the Dashetai watershed model
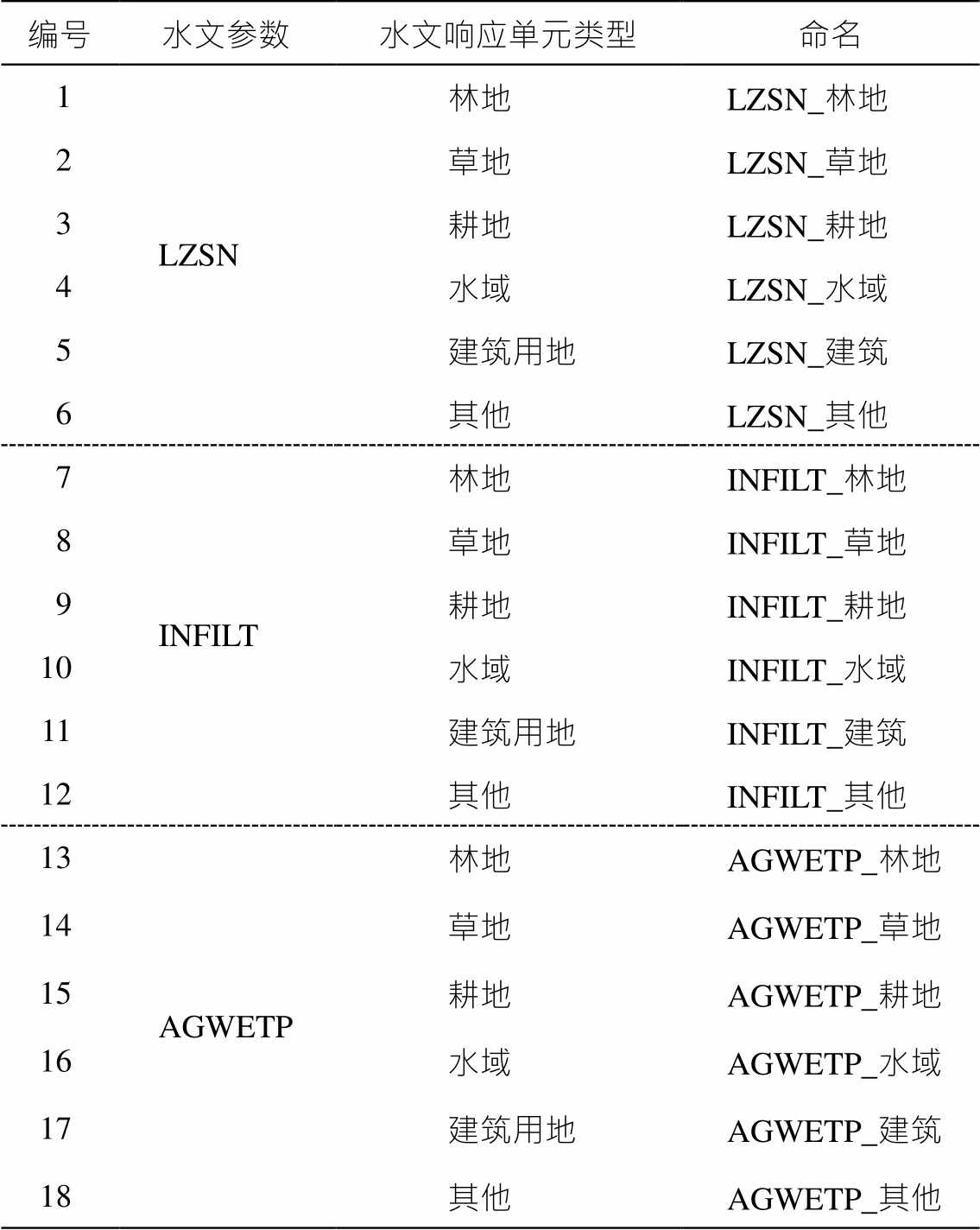
编号水文参数水文响应单元类型命名 1LZSN林地LZSN_林地 2草地LZSN_草地 3耕地LZSN_耕地 4水域LZSN_水域 5建筑用地LZSN_建筑 6其他LZSN_其他 7INFILT林地INFILT_林地 8草地INFILT_草地 9耕地INFILT_耕地 10水域INFILT_水域 11建筑用地INFILT_建筑 12其他INFILT_其他 13AGWETP林地AGWETP_林地 14草地AGWETP_草地 15耕地AGWETP_耕地 16水域AGWETP_水域 17建筑用地AGWETP_建筑 18其他AGWETP_其他
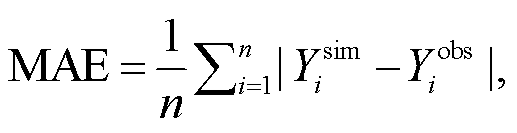(7)
式中,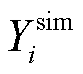 
为模型模拟值,
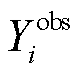为观测值,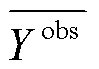 
为观测值的均值。
从日流量模拟时间序列(图 3)可以看出, 模拟值与观测值的变化趋势整体上一致, 但模拟值曲线波动较大。两者断流时间相近, 出现在 12 月至次年 3 月。峰值出现时间也相近, 但模拟值与观测值的差异较大, 未出现峰值时模拟效果更理想。R2 = 0.6482>0.6 (图 4(a)), 结合日径流量 Q-Q 图(图 4(b)), 可知模拟值与观测值的相关关系较强。同时, NSE = 0.5316, 根据《水文情报预报规范》(GB/T 22482－2008)对水量模拟方面的规定, 校准后的模型对日径流量的模拟结果介于可接受(NSE>0.5)与较好(NSE>0.7)之间。
月径流量模拟时间序列(图 5)显示, 模拟值与观测值的变化趋势整体上一致, 波峰和波谷出现时间相近。R2 = 0.8197>0.6 (图 6(a)), 结合月径流量 Q-Q 图(图 6(b)), 可知模拟值与观测值月尺度的相关性强于日尺度。同时, NSE = 0.7794, 根据《水文情报预报规范》(GB/T 22482－2008)在水量模拟方面的规定, 校准后的模型对日径流量的模拟结果介于较好(NSE>0.7)与好(NSE>0.9)之间。
总之, 校准后的模型对日和月两个尺度的径流量模拟效果较理想, 模型较稳健, 说明 LSPC 模型适用于位于干旱半干旱地区的大佘太流域。
为确定敏感性参数选取标准, 根据各敏感性指标大小的排序绘制碎石图(图 7 和 8)。
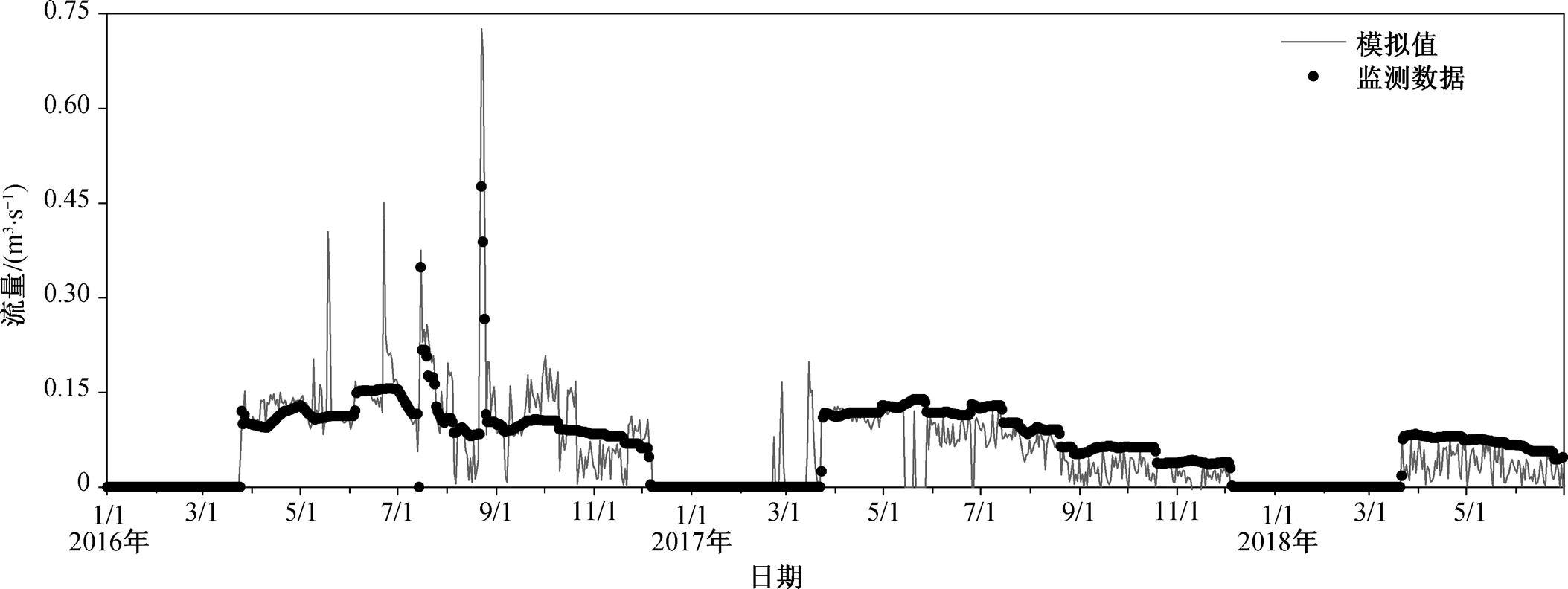
图3 日径流量模拟值与观测值时间序列对比
Fig. 3 Comparison of the time series of simulated and observed daily runoff values
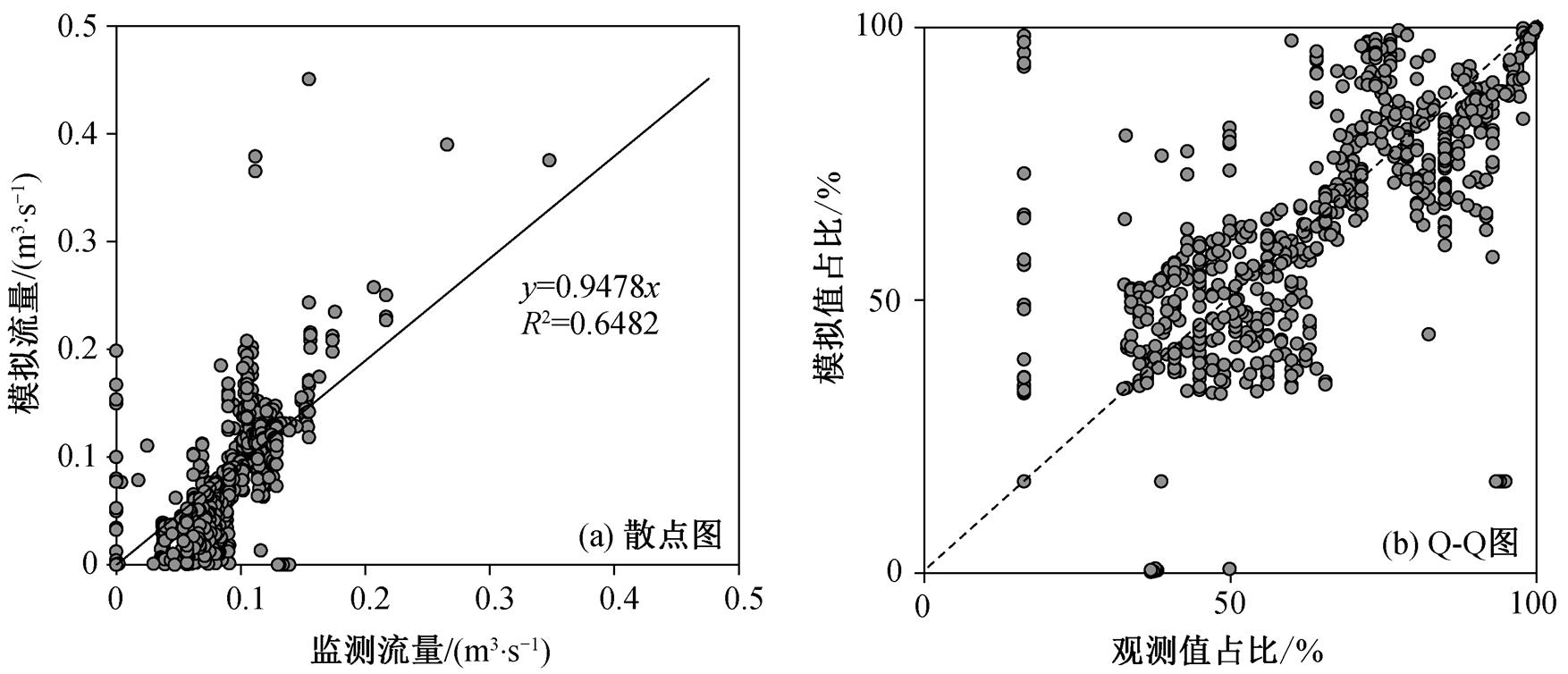
图4 日尺度径流模拟值与观测值对比
Fig. 4 Comparison of simulated and observed daily runoff values
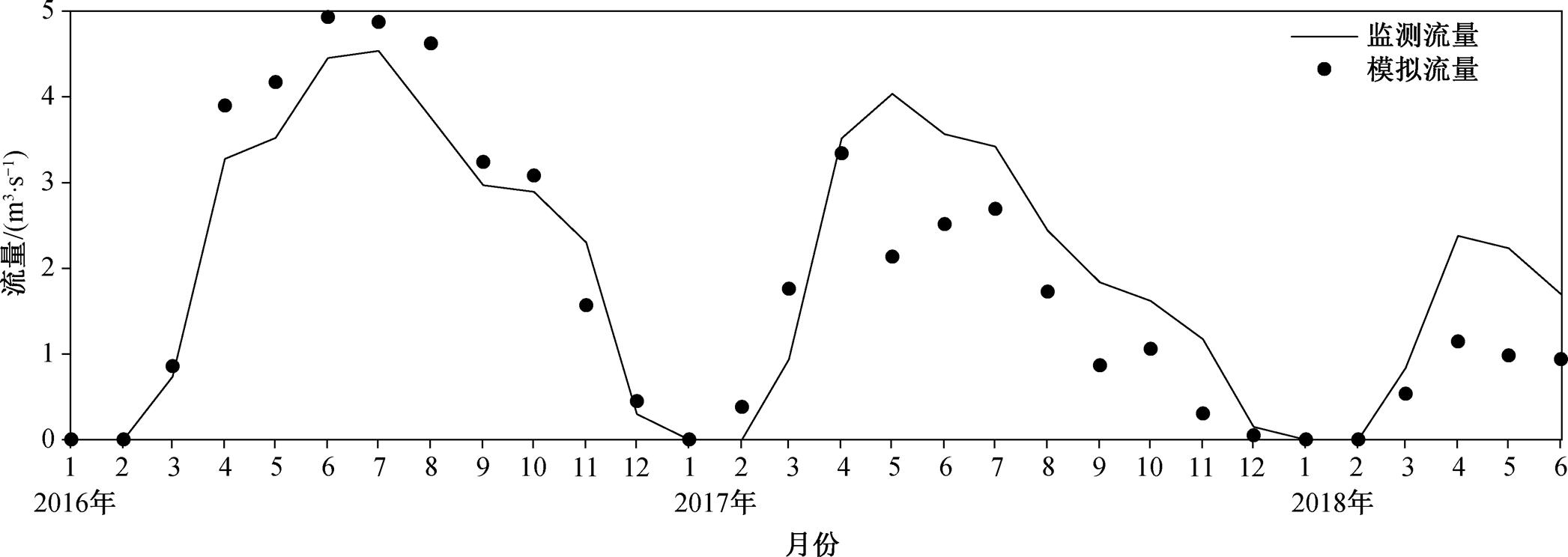
图5 月径流量模拟值与观测值时间序列对比
Fig. 5 Comparison of the time series of simulated and observed monthly runoff values
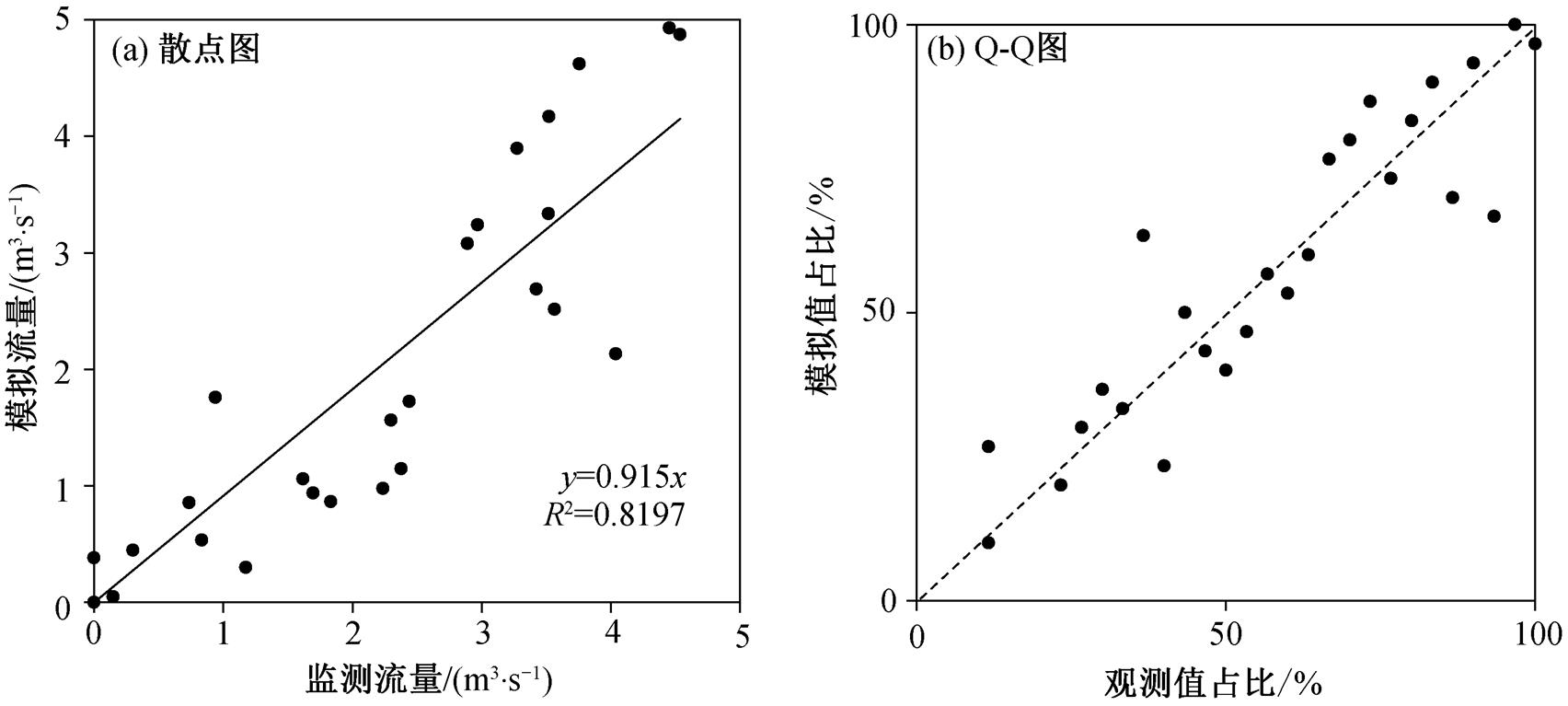
图6 月尺度径流模拟值与观测值对比
Fig. 6 Comparison of simulated and observed monthly runoff values
3.2.1 Morris法
根据 Morris 指数排序结果(图 7), 当模型输出度量方法为 MAE 时, LZSN_草地、LZSN_水域, AGWETP_草地、AGWETP_水域和 LZSN_林地这5 个参数的敏感性最突出, 能够解释 62.36%的输出变化, 敏感水文参数主要为 LZSN 和 AGWETP, 敏感 HRU 主要为草地、水域、林地 3 类。当模型输出度量方法为 MSE 时, LZSN_草地、AGWETP_草地、LZSN_水域和 AGWETP_水域这 4 个参数的敏感性最突出, 能够解释 68.59%的输出变化, 敏感水文参数主要为 LZSN 和 AGWETP, 敏感 HRU 主要为草地和水域两类。
度量方法对敏感参数的影响主要体现在两个方面。1)LZSN_水域和 AGWETP_草地两个参数的敏感指数排列顺序不同。比较两种度量方法的敏感指数排序结果, 除 LZSN_水域和 AGWETP_草地两个参数外, 其余 16 个参数排列顺序一致, 当度量方法为 MAE 时, LZSN_水域排名第二, AGWETP_草地排名第三, 当度量方法为 MSE 时, 两参数排列顺序相反。2)根据碎石图确定的敏感参数不同。度量方法为 MSE 时, 筛选出 4 个敏感参数, 而度量方法为MAE 时多筛选出 LZSN_林地一类, 敏感 HRU 也多出林地一类。
为避免度量方法对敏感参数排序结果的影响, 取两种度量方法下敏感参数的并集作为敏感参数集合, 即敏感水文参数主要为 LZSN 和 AGWETP, 敏感下垫面主要为草地、水域和林地。
3.2.2 Sobol法
根据 Sobol 指数排序结果(图 8), 当模型输出度量方法为 MAE 时, LZSN_草地、AGWETP_草地、LZSN_耕地和 AGWETP_耕地这 4 个参数的敏感性最为突出, 能够解释 85.5%的输出变化, 敏感水文参数主要为 LZSN 和 AGWETP, 敏感 HRU 主要为草地和耕地两类; 当模型输出度量方法为 MSE 时, LZSN_草地、LZSN_耕地, AGWETP_草地以及AGWETP_水域这 4 个参数的敏感性最为突出, 能够解释 87.5%的输出变化, 敏感水文参数主要为LZSN 和 AGWETP, 敏感 HRU 主要为草地、耕地和水域。
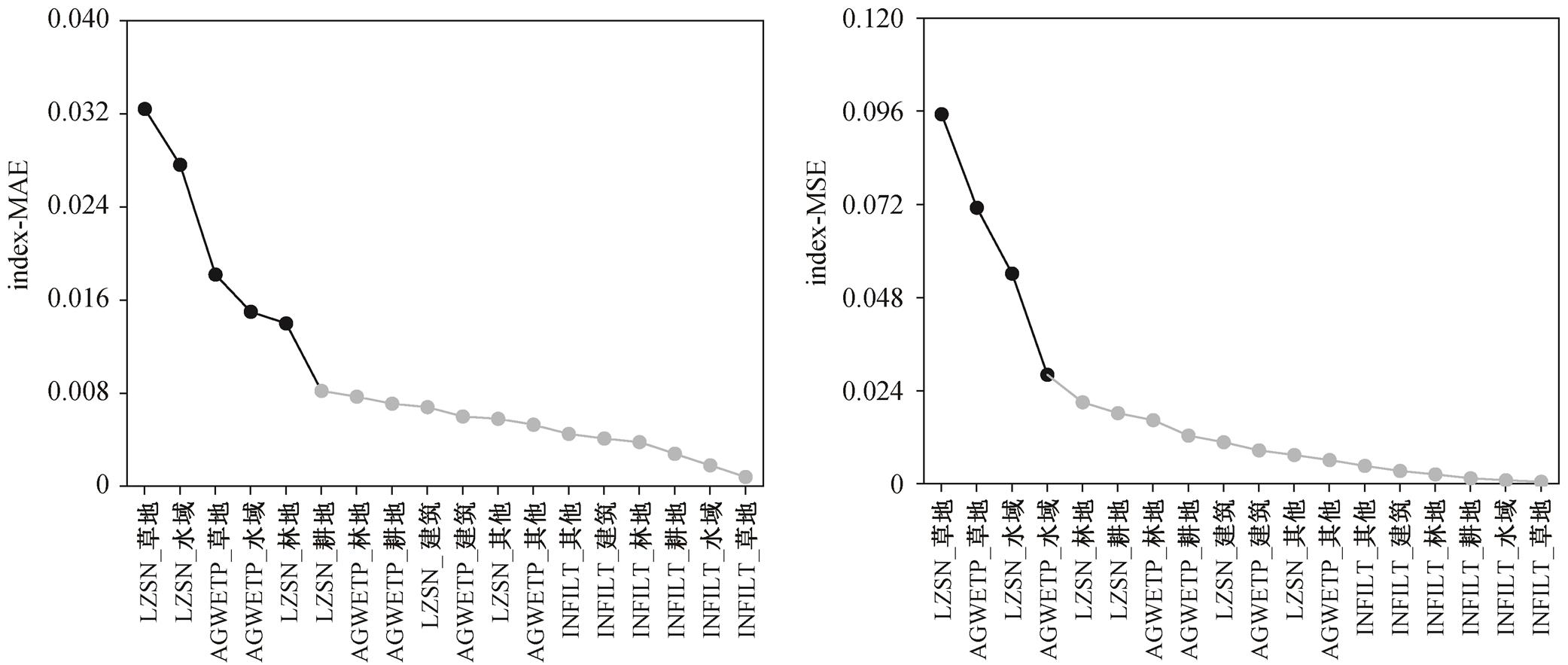
图7 Morris敏感指数排序结果
Fig.7 Morris sensitivity index sorting results
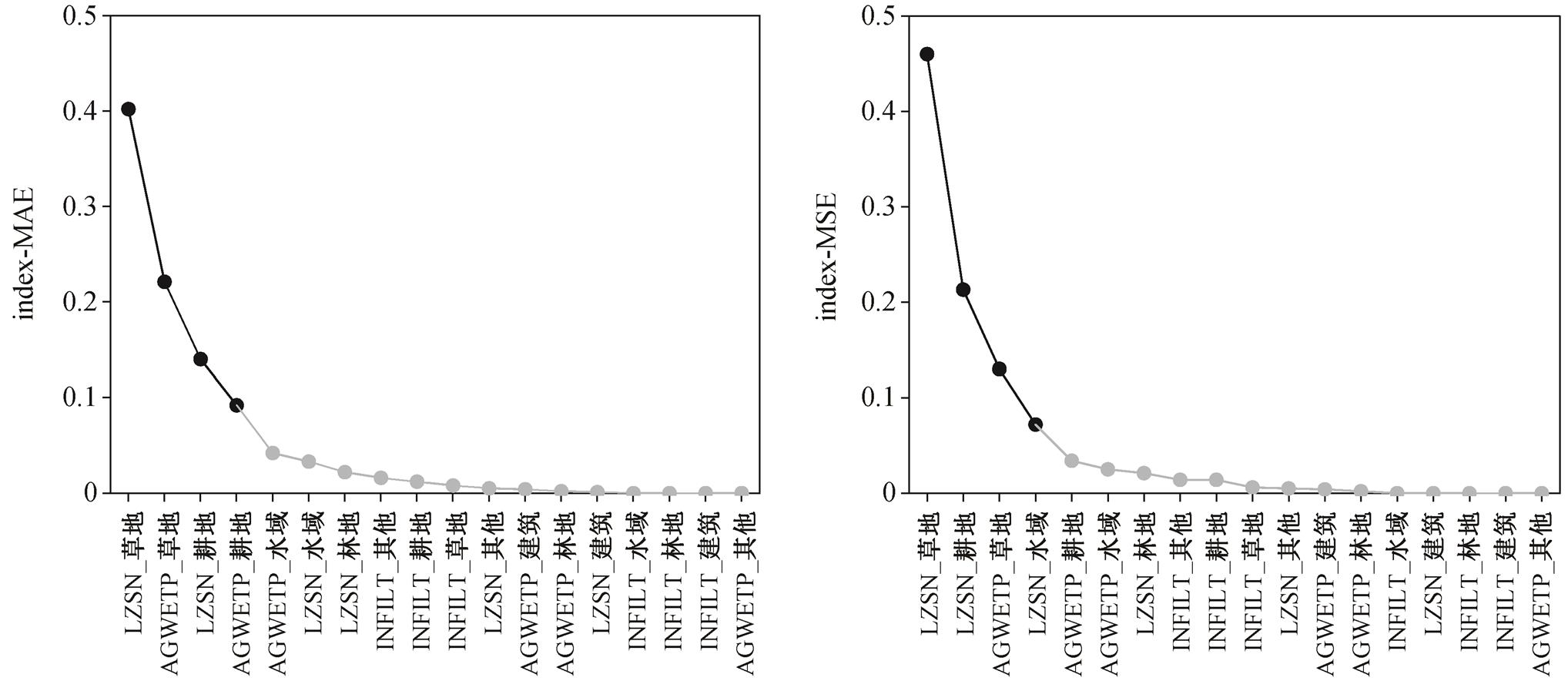
图8 Sobol敏感指数排序结果
Fig. 8 Sobol sensitivity index sorting results
度量方法对敏感参数的影响主要体现在两方面。1)敏感指数排列顺序存在差异, 主要体现在排名 2～6 位的参数, 排名在第 7 位之后的参数除LZSN_建筑和 INFILT_水域的相对位置不同外, 其余参数排名一致。排名差异较大的参数为 INFILT_水域, 当度量方法为MAE时此参数排第 4 位, 当度量方法为 MSE 时排第 6 位。2)根据碎石图确定的敏感参数不同。度量方法为 MSE 时多筛选出参数AGWETP_水域, 度量方法为 MSE 时多筛选出参数AGWETP_耕地, 因此度量方法为 MSE 时确定的敏感HRU 也多出水域这一类。
为避免度量方法对敏感性分析结果的影响, 取两种度量方法下敏感参数的并集作为敏感参数集合。此时, 敏感水文参数主要为 LZSN 和 AGWETP,敏感下垫面主要为草地、耕地和水域。
3.2.3 Morris 法与 Sobol 法的对比
度量方法相同时, 两类敏感指数中参数 LZSN_草地都是最敏感的, 其余 17 个参数的敏感指数排列顺序有较大的差异。当度量方法为 MAE 时(图 9), 排名差异较大的是 INFILT_草地、INFILT_耕地和AGWETP_林地, 在 Morris 指数中其排名分别是第18, 16 和 7 位, 在 Sobol 指数中其排名分别是第 10, 9和 13 位; 当度量方法为 MAE 时(图 10), 排名差异较大的也是 INFILT_草地、INFILT_耕地和 AGWETP_林地。
两种敏感分析方法筛选出的敏感水文参数都为LZSN 和 AGWETP, 而敏感 HRU 有差异。对于Morris 法, 敏感 HRU 主要为草地、水域和林地; 对于 Sobol 法, 敏感 HRU 主要为草地、耕地和水域。为避免分析方法产生的影响, 取其并集作为敏感HRU 集合, 即为草地、耕地、林地和水域。
大佘太流域位于 400mm 等降水线附近, 蒸发量远大于年降水量, 年内断流时间长, 上层土壤干燥, 径流主要由下层土壤和地下径流补充, 在模型中直接与下层土壤含水量(LZSN)和地下水蒸发系数(AGWETP)相关, 因此 LZSN 和 AGWETP 为模型的敏感参数。大佘太流域地表主要被草地(占比60.85%)、农作物(35.55%)和林地(1.53%)覆盖, 草地、耕地和林地成为影响模型的敏感下垫面, 水域可能是因为影响水循环过程而成为敏感下垫面。
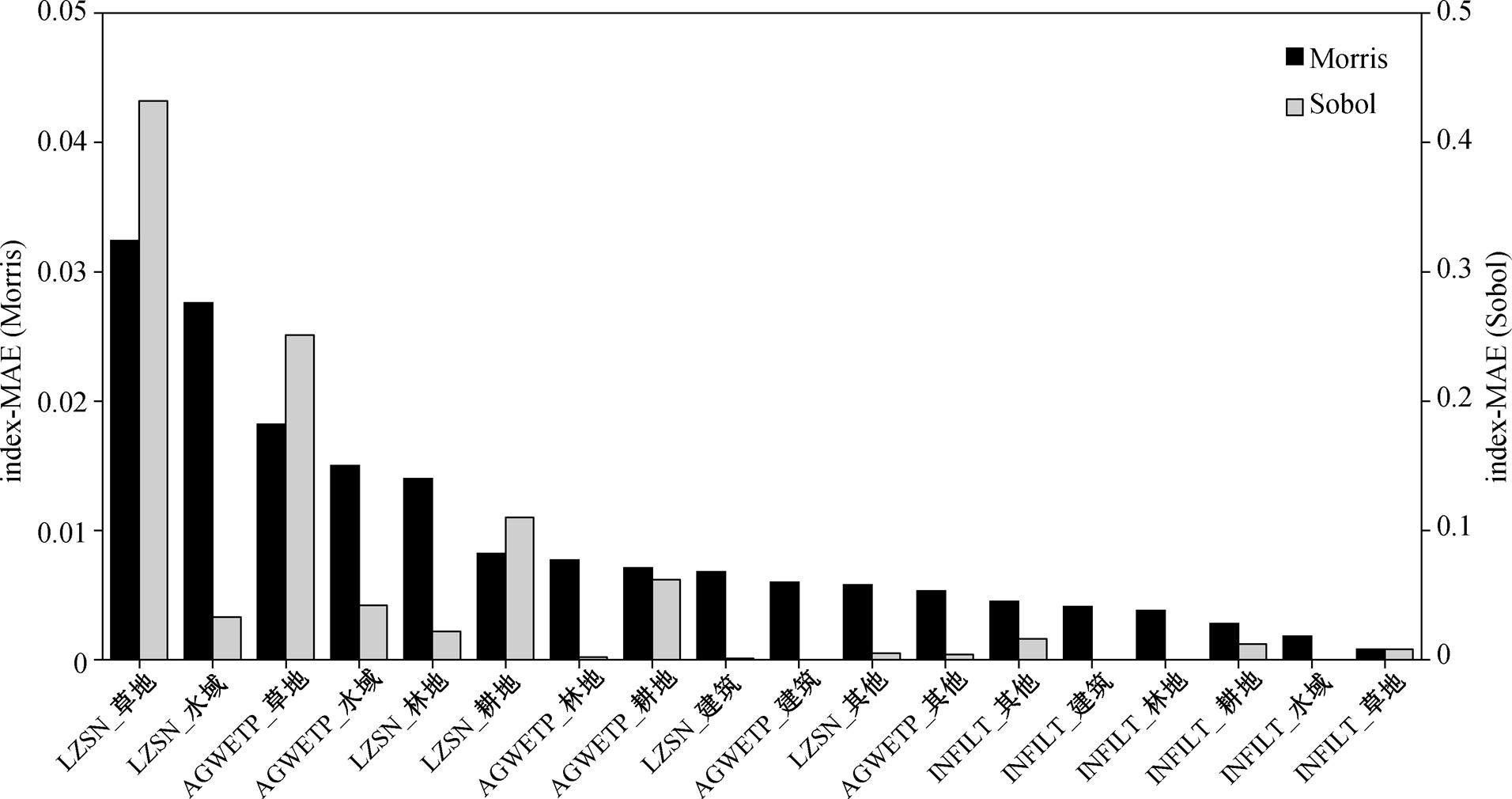
图9 度量方法MAE下Morris和Sobol的敏感指数排序比较
Fig. 9 Morris and Sobol sensitivity index ranking comparison when the measurement method is MAE
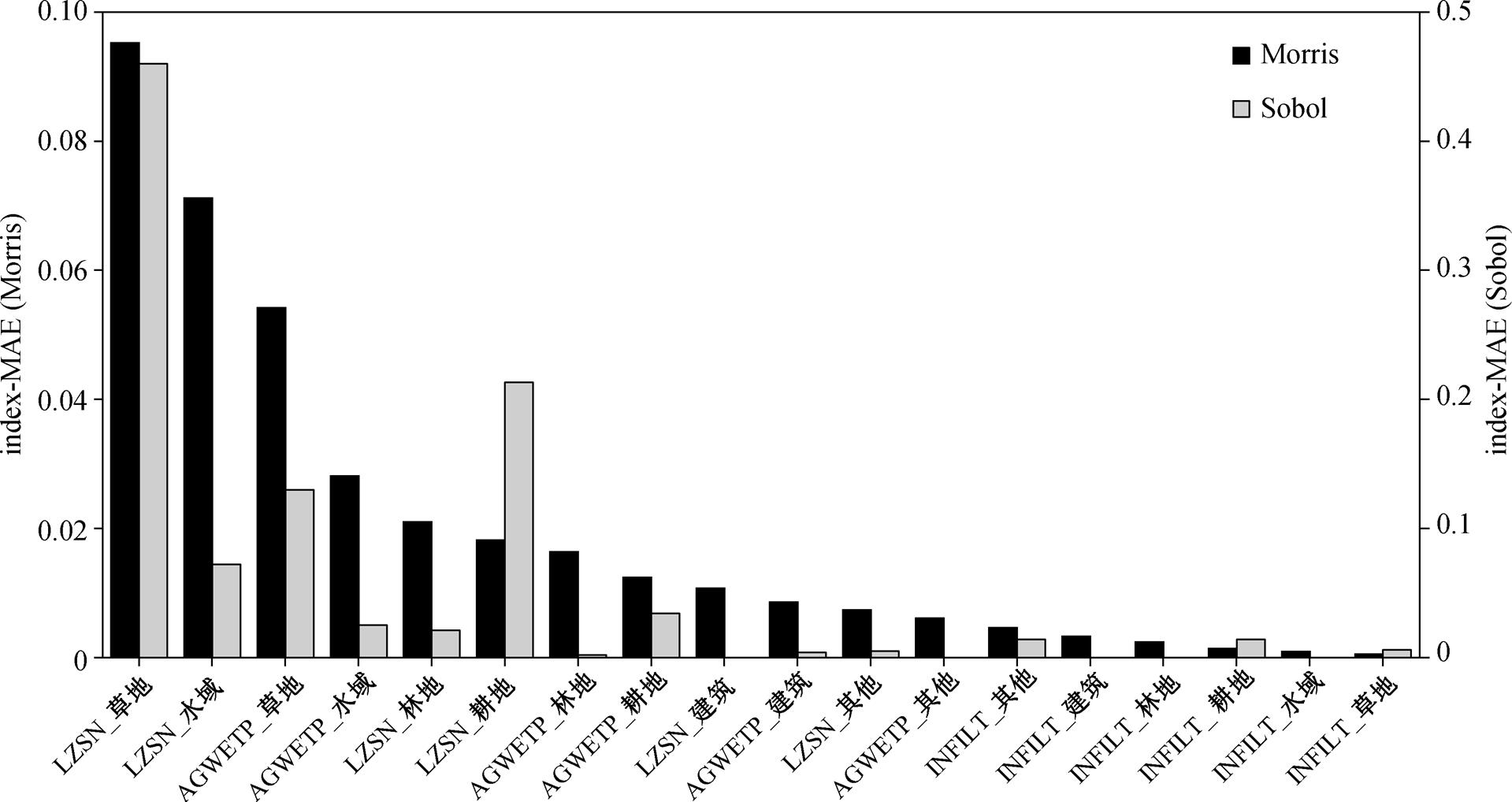
图10 度量方法MSE下Morris和Sobol敏感指数排序比较
Fig. 10 Morris and Sobol sensitivity index ranking comparison when the measurement method is MSE
本研究基于 LSPC 模型构建内蒙大佘太流域模型, 利用全局敏感性分析方法识别水文敏感参数和敏感下垫面, 并评估敏感性分析方法和模型输出的度量方法对参数敏感性结果的影响, 得到如下主要结论。
1)大佘太流域模型对日和月两个尺度的径流模型效果好, 模拟值与观测值的决定系数 R2>0.6, 纳什系数 NSE>0.5, 满足模型适用性要求, LSPC 模型适用于位于内陆干旱半干旱地区的大佘太流域。
2)Morris 和 Sobol 两种敏感性分析方法对敏感参数识别和敏感指数排序都有较大的影响, 体现在两个方面: 第一, 对于同一度量方法, 两类敏感指数的相对排名差异较大; 第二, 筛选出的敏感参数有互不包含的, 当度量方法为 MSE 时多筛选出AGWETP_水域这一参数, 当度量方法为 MSE 时多筛选出 AGWETP_耕地这一参数, 直接影响敏感下垫面识别。
3)MAE 和 MSE 两种度量方法对参数敏感性结果的影响主要体现在敏感参数识别方面, 对敏感指数排序影响不大。但是, 这也影响敏感下垫面类型的识别, 即当度量方法为 MAE 时, 林地可能被误识别为敏感下垫面。
4)为降低度量方法和敏感性分析方法对结果的影响, 取其各自的并集作为敏感水文参数和下垫面的集合。此时, 敏感水文参数为下层土壤含水量(LZSN)和地下水蒸发系数(AGWETP), 敏感下垫面类型为草地、耕地、林地和水域。这是因为大佘太流域位于干旱半干旱区, 蒸散发量远大于降水量, 河流水量主要由地下水和下层土壤含水补充, 且地表主要被草地、农作物和林地覆盖。
参考文献
[1]奚磊, 侯明明, 张胜伟. 水环境中磷的农业非点源污染研究. 安徽农学通报, 2007, 13(10): 42–44
[2]Estes M G, Al-Hamdan M, Thom R, et al. Watershed and hydrodynamic modeling for evaluating the impact of land use change on submerged aquatic vegetation and seagrasses in Mobile Bay [C] // OCEANS. Biloxi, MS, 2009: M10-0044
[3]Sahoo G B, Schladow S G, Reuter J E, et al. Effects of climate change on thermal properties of lakes and reservoirs, and possible implications. Stochastic En-vironmental Research & Risk Assessment, 2011, 25 (4): 445–456
[4]EPA. Water quality restoration plan and total maximum daily loads (TMDLs) for the Lake Helena watershed planning area [EB/OL] (2004) [2021–06–01]. https:// www.researchgate.net/publication/335681862_Water_ Quality_Restoration_Plan_and_Total_Maximum_Daily_Loads_TMDLs_for_the_Lake_Helena_Watershed_Planning_Area_Volume_I_-Watershed_Char acterization_ and_Water_Quality_Status_Review
[5]Flynn K F, Steg R F, Bond J I, et al. Identification of a management framework for TMDL source alloca-tions in the Flathead Lake Basin, Montana // Water-shed Management to Meet Water Quality Standards and TMDLS (Total Maximum Daily Load). San Antonio, TX: American Society of Agricultural and Biological Engineers, 2007: 701P0207
[6]周云峰, 周永潮, 郑春华, 等. 采用Sobol方法的暴雨径流管理模型参数灵敏度分析. 浙江大学学报(工学版), 2019, 53(2): 146–153
[7]Ascough II J C. Green T R, Ma L, et al. Key criteria and selection of sensitivity analysis methods applied to natural resource models [EB/OL]. (2005) [2021–06–01]. https://www.mssanz.org.au/modsim05/papers/ ascough_2.pdf
[8]Herman J D, Kollat J B, Reed P M, et al. Technical note: method of Morris effectively reduces the com-putational demands of global sensitivity analysis for distributed watershed models. Hydrology and Earth System Sciences, 2013, 17(7): 2893–2903
[9]陈卫平, 涂宏志, 彭驰, 等. 环境模型中敏感性分析方法评述. 环境科学, 2017, 38(11): 4889–4896
[10]Morris M D. Factorial sampling plans for preliminary computational. Technometrics, 1991, 33(2): 161–174
[11]Campolongoa F, Saltelli A. Sensitivity analysis of an environmental model: an application of different ana-lysis methods. Reliability Engineering & System Safety, 1997, 57(1): 49–69
[12]刘松, 佘敦先, 张利平, 等. 基于 Morris 和 Sobol的水文模型参数敏感性分析. 长江流域资源与环境, 2019, 28(6): 46–53
[13]谭明豪, 姚娟娟, 张智, 等. 基于 Morris 的 SWMM水质参数灵敏度分析与应用. 水资源与水工程学报, 2015, 26(6): 117–122
[14]张伟, 张江, 张曼. 基于 Morris 筛选法的 SWMM参数敏感性分析. 江苏水利, 2021(3): 35–39
[15]黄金良, 杜鹏飞, 何万谦, 等. 城市降雨径流模型的参数局部灵敏度分析. 中国环境科学, 2007, 27 (4): 549–553
[16]Tang Y, Reed P, Wagener T, et al. Comparing sensi-tivity analysis methods to advance lumped watershed model identification and evaluation. Hydrology and Earth System Sciences, 2007, 11(2): 793–817
[17]Leimgruber J, Krebs G, Camhy D, et al. Sensitivity of model-based water balance to low impact develop-ment parameters. Water, 2018, 10(12): 1838
[18]常晓栋, 徐宗学, 赵刚, 等. 基于 Sobol 方法的SWMM模型参数敏感性分析. 水力发电学报, 2018, 37(3): 59–68
[19]陈建, 梁川, 陈梁. SWAT 模型的参数灵敏度分析 ——以贡嘎山海螺沟不同植被类型流域为例. 南水北调与水利科技, 2011, 9(2): 41–45
[20]Zadeh F K, Nossent J, Sarrazin F, et al. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model. Environmental Modelling and Soft-ware, 2017, 91: 210–222
[21]Yan X, Lu W, An Y, et al. Uncertainty analysis of parameters in non-point source pollution simulation: case study of the application of the Soil and Water Assessment Tool model to Yitong River watershed in northeast China. Water and Environment Journal, 2019, 33(3): 390–400
[22]Zhang C, Chu J, Fu G. Sobol’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China. Journal of Hydrology, 2013, 480: 58–68
[23]石岚, 徐丽娜, 郝玉珠. 一种水动力与统计模型相结合的动态临界面雨量方法研究及应用. 内蒙古气象, 2016(5): 31–34
[24]Hamon W R. Estimating potential evapotranspiration. Transactions of the American Society of Civil Engi-neers, 1963, 128(1): doi:10.1061/TACEAT.0008673
[25]Bosen J F. An approximation formula to compute relative humidity from dry bulb and dew point tem-peratures. Monthly Weather Review, 1958, 86(12): 486
[26]Jensen D T, Hargreaves G H, Temesgen B, et al. Computation of ETo under nonideal conditions. Jour-nal of Irrigation and Drainage Engineering, 1997, 123 (5): 394–400
[27]张峰, 廖卫红, 雷晓辉, 等. 分布式水文模型子流域划分方法. 南水北调与水利科技, 2011(3): 101–105
[28]邹强, 唐建喜, 李淑松, 等. 基于水文响应单元的泥石流灾害易发性分区方法. 山地学报, 2017(4): 496–505
[29]罗川, 李兆富, 席庆, 等. HSPF 模型水文水质参数敏感性分析. 农业环境科学学报, 2014, 33(10): 1995–2002
[30]李燕, 李兆富, 席庆. HSPF 径流模拟参数敏感性分析与模型适用性研究. 环境科学, 2013, 34(6): 2139–2145
[31]刘欢, 吴琼莉, Cournède P H. 不同抽样算法对Sobol 敏感性分析影响的研究. 数学物理学报, 2018, 38(2): 372–384
[32]McKay M D, Beckman R J, Conover W J. A compari-son of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, 1979, 21(2): 239–245
Global Sensitivity Analysis of Hydrological Parameters of the Watershed Simualtion Model
Abstract A hydrological simulation model was developed for the Dashetai watershed in the Inner Mongolia Autonomous Region with LSPC (Loading Simulation Program in C++). Two global sensitivity analysis (GSA) methods, Morris and Sobol, were applied to identify hydrological sensitive parameters and sensitive surface landuse types. The impacts of two GSA methods and model output measures on sensitivity analysis results were also evaluated. The main conclusions are as follows. 1) The model has a good fit for daily and monthly runoff simulation. The R2 of the simulated value and the observed value is greater than 0.6, and NSE between them is greater than 0.5, which indicates that LSPC model is suitable for hydrological simulation of inland arid and semi-arid areas. 2) The two GSA methods have impacts on the identification of sensitive parameters and the ranking of sensitive indexes; while the impact of the two measurement methods of MAE and MSE is mainly reflected in the identification of sensitive parameters. 3) The sensitive hydrological parameters are lower zone nominal storage (LZSN) and active groundwater evapotranspiration (AGWETP), and the sensitive underlying landuse types are grassland, farmland, forest and water. All have close relationships with precipitation and landuse types in the study area.
Key words global sensitivity analysis; hydrological parameters; LSPC model; Dashetai watershed
doi: 10.13209/j.0479-8023.2022.052
国家自然科学基金(51721006)资助
收稿日期: 2021-08-16;
修回日期: 2021-09-15