面向侧信道防御的安全除法器设计
马兵文1 燕雪松2 刘豪1 刘朋远3 易江芳1,†
1.北京大学信息科学技术学院系统结构研究所, 北京 100871; 2.北京智芯微电子科技有限公司, 北京 100192; 3.国网宁夏电力有限公司营销服务中心(国网宁夏电力有限公司计量中心), 银川 750001 ; †通信作者, E-mail: yijiangfang@mprc.pku.edu.cn
摘要 在利用运算部件的侧信道计时攻击及防御方法基础上, 针对密码系统中常用的除法部件, 基于固定延迟和可变延迟除法算法, 进行面向侧信道防御的安全除法器设计。该设计兼顾性能和安全, 适用于不同需求的工作环境。实验结果证明了该方法的有效性, 尤其适合面向 IoT 应用的低功耗嵌入式处理器使用。
关键词 微体系结构; 侧信道; 计时攻击; 除法器;
由于较强的隐蔽性, 侧信道攻击逐渐成为密码系统的严重威胁。特别是在针对微体系结构的侧信道攻击出现以后, 微处理器的设计不仅要考虑性能、成本和功耗, 还需要考虑安全问题。作为微处理器不可或缺的部分, 运算部件在追求高性能的同时, 也可能带来安全隐患, 成为侧信道攻击的渠道。因此, 研究面向侧信道防御的运算部件成为微处理器结构设计的重要课题。
侧信道攻击是通过测量密码算法的运行时间、功耗和电磁辐射等信息变化来推测密钥, 从而破解密码系统[1]。早期的侧信道攻击主要针对智能卡, 后来, Brumley 等[2]通过远程方式对服务器进行侧信道计时攻击(timing attack)。与针对智能卡测量功耗和电磁辐射的方法不同, 这种方式可以通过测量和分析算法运行时间变化来完成攻击。这种利用程序运行时间或周期数等微体系结构信息作为信道的攻击方式, 被称为微体系结构攻击[3], 主要分析系统中各组件的结构特征, 进而获取敏感信息。
Grossschadl 等[4]提出在某些嵌入式处理器中采用提前终止的方法来提高运算单元性能, 使得运算时间随着输入数据的不同发生改变。攻击者正是通过挖掘两者的对应关系来获得敏感信息。该工作引起嵌入式处理厂商的普遍重视。ARM 9E 之前的处理器在硬件上都未支持常数时间的乘法器设计, 但此后的处理器都在硬件上支持了常数时间的32 位乘法器(表 1)。不过, 大多数的 64 位乘法器还是采用软件支持的方式来达到常数执行时间的效果, 主要通过编译器选项和库函数来实现。传统的除法器都采用固定延迟算法, 比如广泛使用的 MicroBlaze, NIOSII 和 LEON3 处理器中都采用固定延迟除法器。
表1 ARM处理器对常数时间乘法器的支持
Table 1 Multipliers in ARM microprocessors

特性ARM处理器型号 硬件不支持常数时间ARM7T (32位), ARM9T (32位) 硬件支持常数时间ARM9E, ARM10E, ARM11, Cortex-A (A32), Cortex-R (A32), Cortex-M0/M1/M3/M4 无硬件支持, 软件支持常数时间ARM各系列中部分的64位乘法 无硬件支持, 软件不支持常数时间ARM各系列中部分的64位乘法
对于现有的侧信道计时攻击, 防御方式主要有3 种。第一种是引入随机性, 使得统计出来的时间信息不可用[2]。该类方法中, 原始信息以随机方式进行更改, 防止攻击者向关键操作部件输入已知数据, 并利用计时信息来获得密钥。这样的方式通常会引入一定的性能损失, 并且需要提供随机数产生源, 这在嵌入式系统中是很高的要求。第二种防御方式的主要思想是, 使所有的敏感信息操作与输入无关[5]。该方法需要对每一步的敏感信息操作结果都进行约简(reduction), 这需要软件配合, 并保证约简操作不会被编译器优化。第三种防御方式是运行时间常数化, 通过预设运算时间, 并将其设置为某个固定值的倍数, 保证不泄漏敏感信息。该方法虽然安全性好, 但整个运算按照最长时间进行统计, 性能损失过大。兼顾安全和性能是安全运算部件设计的关键问题。
为解决该问题, 本文设计一款面向侧信道防御的安全除法器, 利用同一套数据通路, 实现固定延迟和可变延迟两种算法。基于运行时间常数化设计思想, 通过配置固定延迟除法器的运算周期, 隐藏部分原始信息, 有效地防止敏感信息泄漏。同时, 结合除法算法的特点, 利用可变延迟算法来提高运算性能, 达到兼顾安全和性能的目的。
1 安全除法器设计
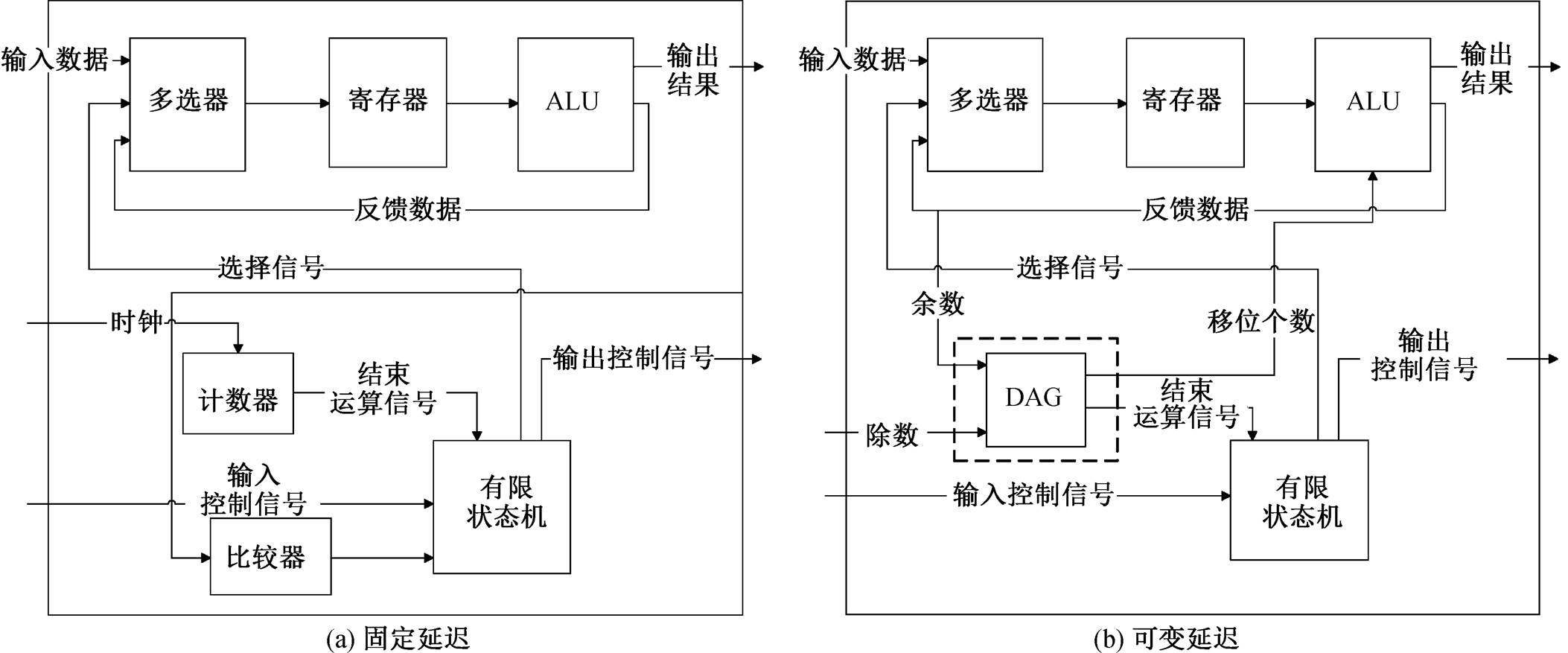
常见的除法算法可分为两类: 基于减法的数字迭代算法和基于乘法运算的函数迭代算法[6]。数字迭代算法原理简单, 易于实现, 又可分为恢复余数和非恢复余数两种算法。本文选择恢复余数的数字迭代算法来实现固定延迟除法器, 数据通路如图1(a)所示。基于该数据通路, 考虑可变延迟除法器的改造。
模拟除法手算, 固定延迟除法器每周期商左移一位, 除数右移一位, 操作数位数决定移位次数, 这样可以保证除法器的计算延迟是固定的。在实际操作中可以进行优化, 比如被除数中有 n 个连续的0, 则可以考虑在一周期内移动 n 位操作数, 无需一位一位的移动。Matthews 等[7]提出的可变延迟除法器的设计思想是, 在每次迭代中, 被除数和除数都自左至右找到当前的第一个 1。这种方法能够保证每个周期都产生一位非零的商, 因此整个算法需要的周期数就是商中 1 的个数。特别地, 如果操作数都是 2 的幂, 则除法器的计算延迟为 。当基数为 2时, 恢复余数的可变延迟除法器算法(伪代码)如下所示。
1 Y=Dividend, X=Divisor, Z=0
2 while(X≤Y){
3 msb∆←⌊log2Y⌋‒⌊log2X⌋
4 Estimatedivisor←divisor∙2msb∆
5 A←Y‒Estimatedivisor
6 B←Y‒Estimatedivosr/2
7 Z[(A<0)?msb∆‒1:msb∆]=1
8 Y←(A<0)?B:A}
在实现方面, 与固定延迟相比, 可变延迟除法器中需要新增加模块——地址差值生成器(Delta address generator, DAG)(图 1(b))。其中, DAG 的功能为, 在每次迭代中, 找到被除数和除数各自最高的 1 的位置, 并计算差值, 将其作为操作数的移位位数。直到部分余数小于除数, 整个计算结束。特别地, 操作数都为 2 的幂, 则移位完成后, 计算结束。
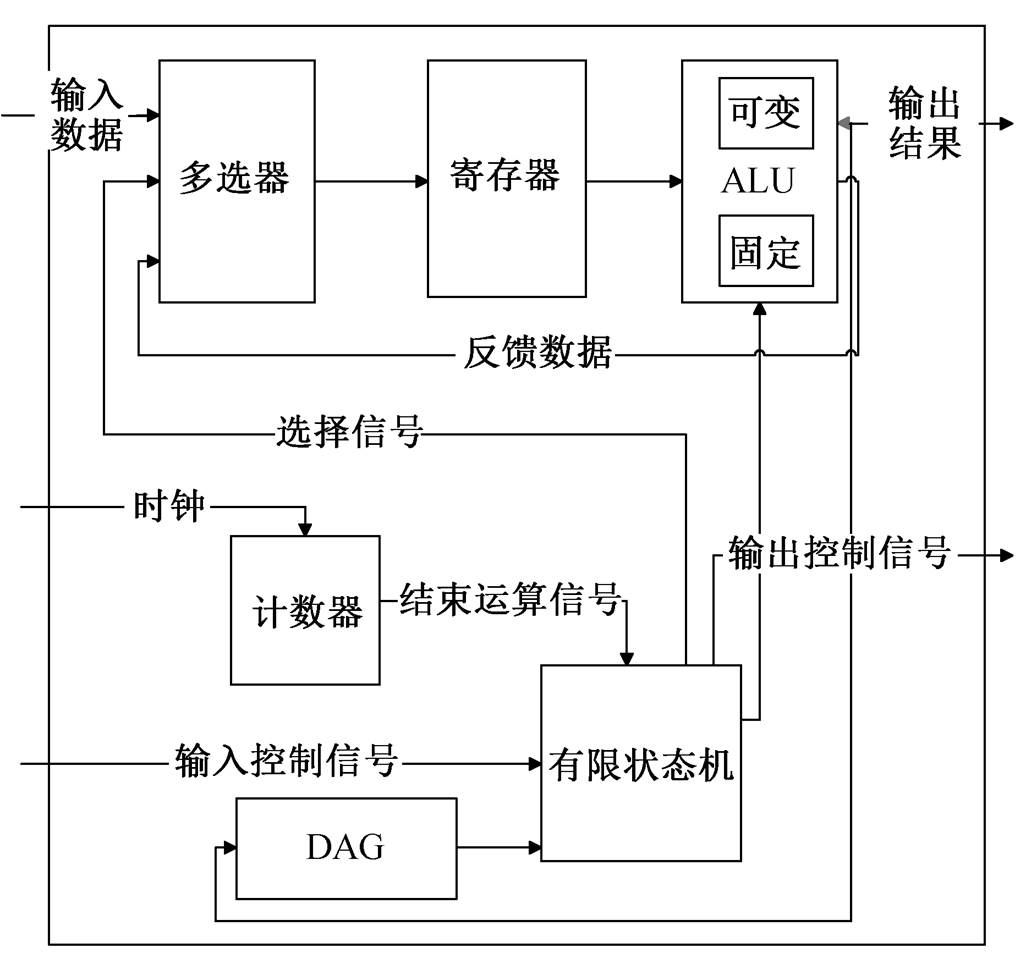
为了兼顾安全和性能, 把上述两套算法有机地结合起来的方法有以下几种。第一种方法是把固定延迟和可变延迟除法器同时集成到一个模块中, 但这样做面积会增大, 为接近原来的两倍。第二种方法是在固定延迟的数据通路基础上尽量复用功能部件, 通过配置寄存器在两套算法之间切换来减小面积。但是, 这种分时复用的工作方式无法同时做到安全和高效。第三种方案是在固定延迟数据通路中复用功能部件, 实现可变延迟除法器, 同时将除法运算过程分为两个串行阶段, 先按照固定延迟除法器进行计算, 再切换为可变延迟除法器完成后续操作。通过调节固定延迟除法器的运行周期, 可以隐藏原始输入的部分特征, 防止敏感信息泄漏。利用可变延迟除法器完成后续计算操作, 可以提高除法器的处理效率, 达到性能和安全兼顾的目的。本文采用第三种方案。安全除法器的算法(伪代码)如下所示。
1 Y=Dividend, X=Divisor, Z=0, index=0
2 while(index
3 X←X≪(N‒index)
4 if(Y≥X){
5 Y←Y‒X
6 Z[N‒index]=1}
7 else{ Z[N‒index]=0}
8 index←index+1}
9 while(X≤Y){
10 msb∆←⌊log2Y⌋‒⌊log2X⌋
11 Estimatedivisor←divisor∙2msb∆
12 A←Y‒Estimatedivisor
13 B←Y‒Estimatedivisor/2
14 Z[(A<0)?msb∆‒1:msb∆]=1
15 Y←(A<0)?B:A}
比如, 对于 32 位除法器, 调节固定延迟除法器的运行周期为 32, 可变延迟部分无需计算, 这样就相当于一个 32 位固定延迟除法器。同理, 调节固定延迟除法器的运行周期为 0, 则直接切换成可变延迟除法器完成运算。当然, 可以根据需要, 将固定延迟除法器的运行周期调节为某个中间值, 则整个除法器既能隐藏输入的部分信息, 又能获得较高的运算效率。
安全除法器的实现方案是添加一个计数器。该计数器根据配置参数, 控制固定延迟除法器的运行周期数, 并保存部分余数和商, 之后整个除法器切换为可变延迟算法进行计算。计算结束后, 将两部分商进行拼接, 获得最终的商和余数。数据通路如图 2 所示。
2 安全性分析
根据上述安全除法器的设计原理, 可知固定延迟除法器运行 f 个周期, 会计算出商的高 f 位。如果商的 MSB(最高非 0 位)大于(32−f ), 也就是说, 商的高 f 位不全为 0, 则固定延迟除法器对商会产生影响。反之, 则说明商的高 f 位全为 0, 固定延迟除法器对商无影响。因此, 固定延迟除法器的运行周期数与操作数据无关。对于可变延迟除法器, 其运行周期数则是由商中的 1 的个数决定, 与操作数据 有关。
在实际运算中, 安全除法器的总运行周期是由固定延迟除法器的延迟 f 和商中低(32−f )位中 1 的个数决定。即使攻击者知道 f , 并获得运行周期数, 也只能推测商的低位中 1 的个数, 而无法获得整个商, 也就无从推测操作数据。上述分析表明, 本文的安全除法器可以隐藏部分原始信息, 从而有效地防止敏感信息泄漏。
3 实验与评测
3.1 性能评测
由可变延迟除法算法可知, 其运算周期与商中1 的数量相等。为测试该除法器的计算性能, 需随机产生若干操作数据。本文采用以下策略产生随机数: 指定商的 MSB (最高非 0 位)分别为 0, 1, 2, …, 28 位, 为每种情况生成 3 万组随机操作数<q, d, r>, 分别作为商、除数和余数, 这样也就获得被除数。配置不同的固定延迟除法器运行周期, 测量并计算总运行周期数, 实验结果如表 2 所示。
表2中, 第一列是对固定延迟除法器运行周期的配置, 第二列是可变延迟部分的平均执行周期数, 总周期数就是固定延迟和可变延迟阶段的周期数总和。可以看出, 随着固定延迟运行周期数的增高, 可变延迟阶段的平均周期数逐渐减小。总体上看, 使用可变延迟除法器能够带来较大的运算性能提升, 改善除法器的处理效率。
表2 安全除法器总运行周期
Table 2 Total operation cycles of secure divider
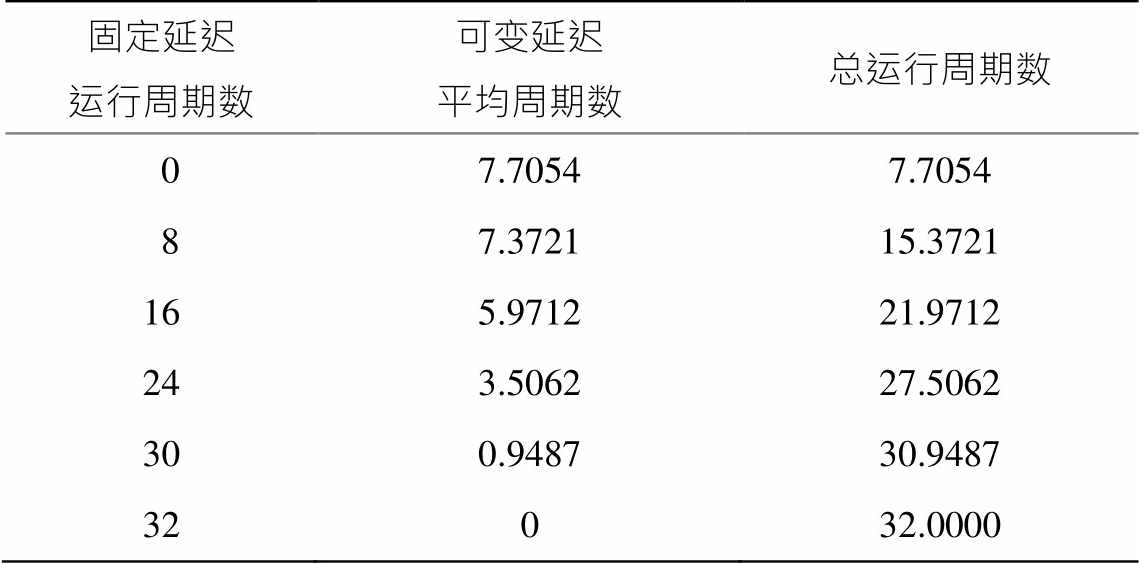
固定延迟运行周期数可变延迟平均周期数总运行周期数 07.70547.7054 87.372115.3721 165.971221.9712 243.506227.5062 300.948730.9487 32032.0000
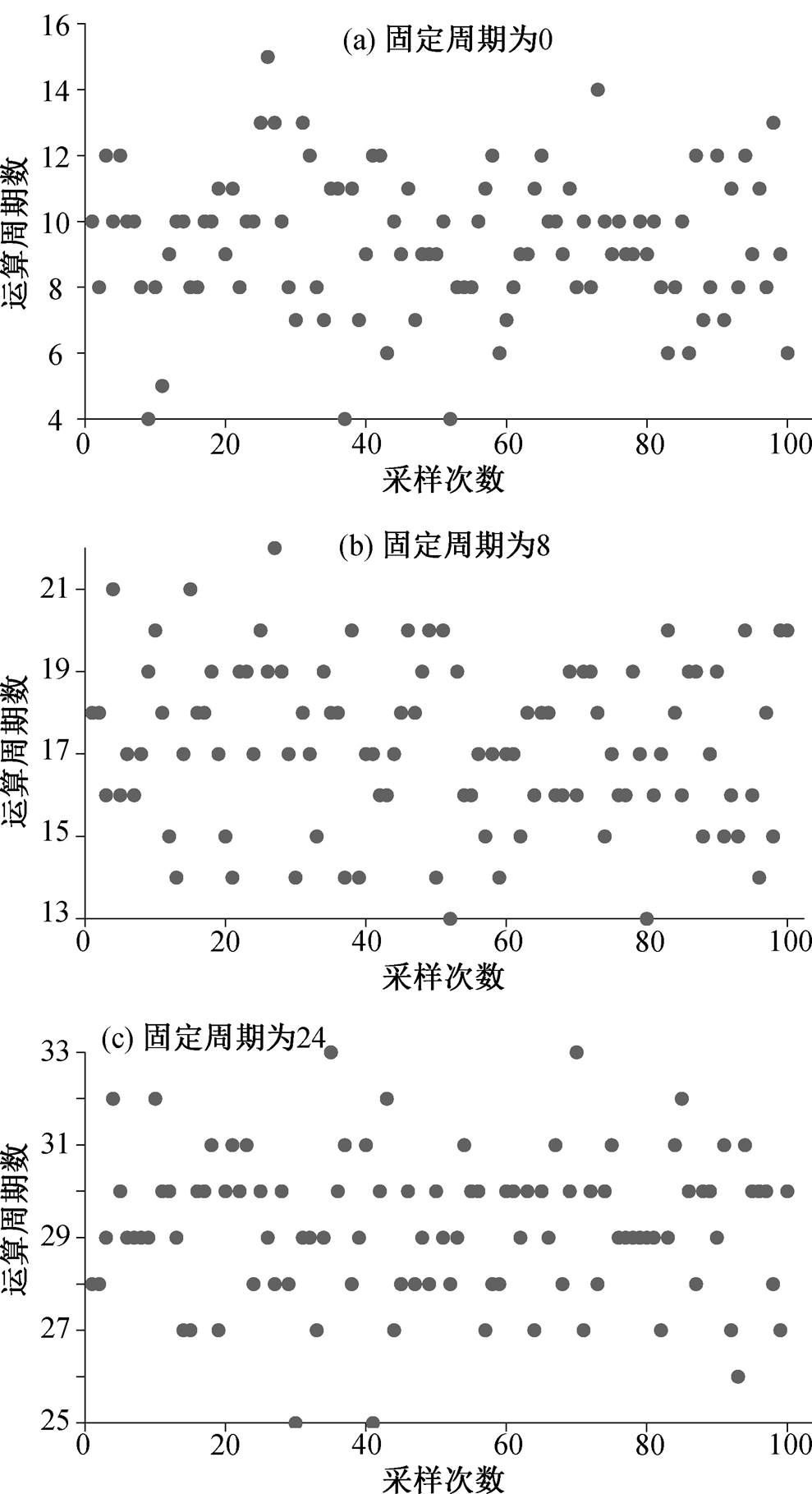
3.2 安全测试
为测试安全性能, 以可变延迟除法器(即固定延迟周期数为 0)作为比较对象, 随机产生 100 万对操作数(被除数和除数), 作为可变延迟除法器和安全除法器的输入, 对两种除法器的总运行周期数进行等间隔采样, 不同配置下的部分分布如图 3 所示。可以看出, 在相同输入下, 与可变延迟除法器运行周期数相比, 安全除法器的总运行周期分布发生较大的变化, 且数据波动幅度变小, 说明该方法可以隐藏原始输入的特征, 保证敏感信息安全。同时, 随着配置的固定周期数变大, 数据波动更为平缓, 逐渐向固定延迟靠拢。
3.3 时序与面积分析
选择 Xilinx Artix-7 FPGA 芯片对本文中的 3 种除法器进行实现, 并使用 Vivado2018 进行综合, 面积和时序评估结果如表 3 所示。可以看出, 固定延迟除法器逻辑简单, 占用硬件资源较少, 频率较高。由于增添了新模块 DAG, 可变延迟除法器占用资源增多, 频率下降。相比于可变延迟除法器, 安全除法器增加的硬件资源并不多, 频率接近可变延迟除法器。
表3 各除法器时序和面积评估
Table 3 Frequency and area of each divider
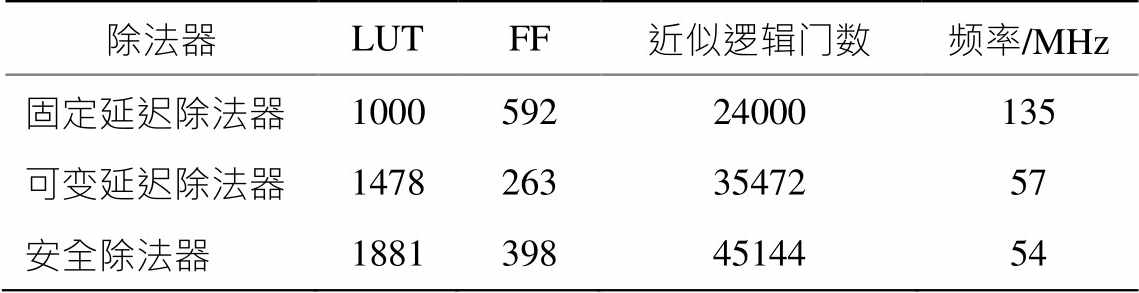
除法器LUTFF近似逻辑门数频率/MHz 固定延迟除法器100059224000135 可变延迟除法器14782633547257 安全除法器18813984514454
4 结论
针对利用运算部件的侧信道计时攻击, 本文提出一种安全除法器设计。采用恢复余数的数字迭代算法作为基础, 该除法器将除法运算过程分为两个串行阶段, 先按照固定延迟除法器进行计算, 再切换为可变延迟除法器完成后续操作。通过调节固定延迟除法器的运行周期, 可以隐藏原始数据的部分特征, 防止敏感信息泄漏。利用可变延迟除法器完成后续计算操作, 可以提高除法器的处理效率, 达到性能和安全兼顾的目的。本文的设计使用FPGA进行实现, 并开展性能测试和安全测试。结果表明, 本文设计硬件开销小, 能够兼顾安全和性能, 尤其适合面向IoT应用的嵌入式处理器使用。
参考文献
[1]Wright P. Spy catcher: the candid autobiography of a senior intelligence officer. New York: Viking Press, 1987
[2]Brumley D, Boneh D. Remote timing attacks are practical. Computer Networks, 2005, 48(5): 701–716
[3]Biham E, Shamir A. Differential fault analysis of secret key cryptosystems // Advances in Cryptology-CRYPTO’97. Berlin: Springer Berlin Heidelberg, 1997: 513–525
[4]Grossschadl J, Oswald E, Page D, et al. Side-channel analysis of cryptographic software via early-termi-nating multiplications // International Conference on Information Security and Cryptology (ICISC 2009). Berlin: Springer Berlin Heidelberg, 2010: 176–192
[5]Dhem J, Koeune F, Leroux P, et al. A practical implementation of the timing attack // Proceedings of the International Conference on Smart Card Research and Applications (CARDIS’98). Berlin: Springer-Verlag, 1998: 167–182
[6]Nikmehr H. Architectures for floating-point division [D]. Australia: University of Adelaide, 2005
[7]Matthews E, Lu A, Fang Z, et al. Rethinking integer divider design for FPGA-based soft-processors // IEEE 27th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM). San Diego, 2019: 289–297
Design of Secure Divider for Side Channel Defense
MA Bingwen1, YAN Xuesong2, LIU Hao1, LIU Pengyuan3, YI Jiangfang1,†
1. School of Electronics Engineering and Computer Science, Peking University, Beijing 100871; 2. Beijing Smart-Chip Microelectronics Technology Co, Ltd, Beijing 100192; 3. STAET GRID Ningxia Marketing Service Center (Metrology Center), Yinchuan 750001; † Corresponding author, E-mail: yijiangfang@mprc.pku.edu.cn
Abstract According to the common methods of side channel timing attack and defense using arithmetic unit, based on the division algorithms of fixed delay and variable delay, a secure divider was designed. The design considered both high performance and high security. It was suitable for different working environments. Experi-mental results showed that the proposed divider was effective, especially for low power embedded microprocessors for IoT applications.
Key words microarchitecture; side channel; timing attack; divider
doi: 10.13209/j.0479-8023.2021.128
国家电网总部科技项目(5700-201941313A-0-0-00)资助
收稿日期: 2021-07-09;
修回日期: 2021-12-24