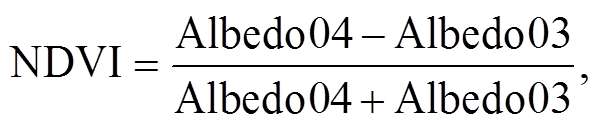
摘要 为了得到中国东部地区大范围的地面 PM2.5 浓度分布, 用机器学习方法建立一个模型, 用 2019 年葵花8 号静止卫星大气顶层反射率数据和欧洲中心气象资料作为输入数据, 地面 PM2.5 浓度作为输出数据。验证结果表明, 在不同时间尺度下, 该模型对中国东部地区均有较高的精度。对于小时 PM2.5 的浓度反演,该模型的十折交叉验证的相关系数为 0.82, 均方根误差为 20.11μg/m3。将 2019 全年卫星‒气象格点数据放入模型, 得到中国东部地区全年逐小时的 PM2.5 格点数据, 利用该格点数据分析中国东部地区 PM2.5 浓度的季节变化和空间分布, 取得良好的效果。
关键词 卫星遥感; 大气层顶反射率; PM2.5浓度; 机器学习
随着我国工业化进程的不断推进, 工业和机动车尾气等人为排放急剧增加, 导致我国中东部地区空气污染情况日益加剧, 极端污染现象频发, 京津冀地区尤为显著[1]。大气颗粒物(particulate matter, PM)是空气污染物的重要组成部分, 尤其是空气动力学粒径 ≤ 2.5 m 的细颗粒物(PM2.5)[2], 不仅对空气质量、能见度和人体健康有重大影响[3], 而且会影响成云和降雨过程, 对气候变化造成直接或间接的影响[4]。因此, 对 PM2.5 的分布, 尤其是近地面质量浓度的监测研究, 具有重要的理论和实际意义。
目前, PM2.5 的监测方法主要有地面监测和遥感监测两种。地面监测具有数据精确、时间连续的优点, 缺点是测站成本高, 站点分布不均匀, 监测尺度小, 无法获得连续的区域尺度的 PM2.5 浓度分布数据[5]。遥感监测是通过建立卫星数据与 PM2.5 浓度数据关系的模型来反演 PM2.5 浓度, 具有监测空间范围大、时序长、数据获取容易等特点, 可以获取大范围的 PM2.5 反演数据, 很好地弥补地面监测与模型拟合的不足[6]。
过去利用遥感数据反演 PM2.5 浓度的方法主要是用气溶胶光学厚度(aerosol optical depth, AOD)和气象数据与 PM2.5 浓度数据构建模型。使用 AOD 反演 PM2.5 主要有以下几种方法。1)比例因子法[7‒8], 优点是不需要地面 PM2.5 浓度的监测数据就可以进行模拟, 缺点是对其他输入数据的要求较高, 需要准确的地面污染物排放清单, 且易受气象初始场和化学机理影响[9]。2)基于 AOD 与 PM2.5 之间物理关系的方法[10], 利用站点数据, 构造一个 PM2.5 与AOD 关系的半经验公式。由于 PM2.5 与 AOD 之间是复杂的非线性关系, PM2.5 的反演效果不理想。3)基于数值统计模型的方法, 从早期的单一线性模型发展成引入越来越多变量的高级统计模型, 如线性混合效应模型[11]和时空权重回归模型[12]等。但是, 这些模型依然是将 AOD 与 PM2.5 的关系描述成线性关系, 模拟得到的 PM2.5 仍然存在较大的误差。近年来, 随着人工智能的发展, 人们开始尝试用机器学习的方法反演 PM2.5。Yao 等[13]建立 AOD 与地面PM2.5 关系模型, 同时考虑边界层高度、风速和温度等气象因素,PM2.5 反演值与观测值的相关系数可达 0.8。Li 等[14]加入时间和空间权重, 构造神经网络模型, 进一步提高 PM2.5 浓度值的反演效果。
虽然前人使用 AOD 产品反演 PM2.5 已经取得较多的成果, 但 AOD 产品存在许多不足, 如冬季因暗像元少导致 AOD 缺失[15], 卫星反演 AOD 过程中产生误差。为了解决这些问题, Shen 等[16]直接使用MODIS 的大气层顶反射率, 替代 AOD 输入深度神经网络中, 证明了使用大气层顶反射率的可行性, 但是效果不佳。Liu 等[15] 2019 年使用日本葵花 8 号静止卫星(Himawari-8)的大气层顶反射率数据反演PM2.5, 但他们在选取训练集和测试集时没有分站点进行选取, 自变量的选取也存在复共线性过高等问题。
本文在前人工作的基础上做如下改进: 分站点选取训练集和测试集; 对构建模型的自变量进行筛选和剔除; 在机器学习方法方面, 舍弃随机森林算法, 使用极限梯度增强算法(extreme gradient boos-ting, XGBoost)构建模型。将卫星‒气象格点数据放入模型, 获得中国东部地区 PM2.5 浓度格点数据, 并与观测数据进行对比。
选择 Himawari-8 卫星数据作为遥感输入变量, 用欧洲中期天气预报中心第五代大气再分析资料(the fifth generation atmospheric reanalysis data of the European center for medium range weather forecasts, ECMWF-ERA5)作为气象输入变量, 地面PM2.5 浓度作为输出变量。由于我国西部地区站点较少, 工业化程度不高, 污染程度较低, 所以本文选取我国东部地区(105°—135°E, 18°—53°N)作为研究区域。
1.1.1 PM2.5数据
逐小时地面 PM2.5 质量浓度监测数据来自中国环境监测中心(http://www.cnemc.cn)。数据时间为2019 年 1 月 1 日—12 月 31 日, 北京时 08:00—17:00, 时间分辨率为 1 小时。剔除全年数据少于 50 个、空间距离小于 0.05°以及 105°E 以西的站点后, 得到1011 个观测站点的地面 PM2.5 浓度数据, 以此作为模型的输出变量。
1.1.2 遥感数据
Himawari-8 卫星是日本于 2014 年发射的新一代静止气象卫星, 具有空间分辨率高、观测频率高、数据质量稳定的优点。本文使用 Himawari-8卫星的 L1 数据作为卫星遥感的输入数据, 数据的空间分辨率为 0.05°, 时间分辨率为 10 分钟, 覆盖范围是 80°—160°E, 60°S—60°N。为了与地面 PM2.5浓度数据相匹配, 选取的 L1 级数据的时间为 2019年 1 月 1 日—12 月 31 日, 北京时 08:00—17:00, 时间分辨率为 1 小时, 空间范围为 105°—135°E, 18°—53°N, 共计 3650 个时次的卫星数据。
本研究初始使用的遥感输入数据是 0.46, 0.51和 0.64μm 这 3 个可见光通道以及 0.86, 1.61 和 2.26 μm 这 3 个近红外通道(对应 L1 数据中 Albedo01~ Albedo06)的大气顶层反射率。为了排除有云条件下云格点对卫星反射率的影响, 使用 Himawari-8 卫星二级产品(CLP Data)中的云检测产品, 对 L1 级数据进行云格点的剔除。L1 级卫星数据还包含太阳天顶角(SOZ)、太阳方位角(SOA)、卫星天顶角(SAZ)和卫星方位角(SAA) 4 个角度信息。考虑到Himawari-8 卫星是地球静止卫星, 在相同地区 SAZ是保持不变的, 将 SAZ 数据舍弃后, 本文选择 SAA与 SOA 之差作为相对方位角(RA), 用 cos (SOZ)修正大气层顶反射率数据, 将它们作为角度变量放入模型。考虑到卫星的大气层顶反射率受地表植被影响很大, 本文利用 0.86μm 近红外通道(Albedo04)和0.64μm 可见光红通道(Albedo03)大气层顶反射率数据计算得到归一化植被指数(normalized difference vegetation index, NDVI):
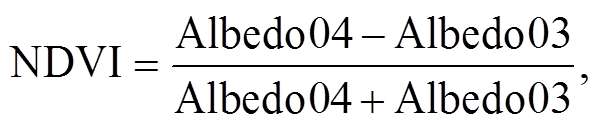
NDVI也作为输入变量[17]。
1.1.3 气象数据
考虑到地面气象条件对 PM2.5 扩散的影响, 本文选用 ECMWF-ERA5 再分析资料(http://apps.ecm wf.int/datasets/)。ERA5 是目前全球最强大的气象监测数据集, 比以前的 ERA-Interim 产品有更高的时空分辨率。本文选用的 ERA5 再分析资料空间范围为 105°—135°E, 18°—53°N, 空间分辨率为 0.25° ×0.25°; 时间范围为 2019 年 1 月 1 日—12 月 31 日, 北京时 08:00—17:00, 时间分辨率为 1 小时。
参考前人工作, 本文选择的气象变量为地面气压(SP, 单位为 hPa)、10m 经向风速(U10, 单位为m/s)和 10m 纬向风速(V10, 单位为 m/s)、2m 温度(T2M, 单位为 K)、大气水汽含量(TCWV, 单位为kg/m2)、总柱臭氧(TCO3, 单位为 kg/m2)、相对湿度(RH, 单位为%)和行星边界层高度(PBLH, 单位为 m)。Liu 等[15]的研究结果表明, 变量 SP, U10, V10, TCWV, TCO3 和 PBLH 对 PM2.5 有显著影响; PBLH, SP 和 T2M 与大气稳定度有关, 影响气溶胶的垂直分布; T2M 和 RH 影响气溶胶的物理化学过程, 如生成和吸湿增长[18]; U10 和 V10 会影响气溶胶的水平输送; TCO3 对气溶胶的光学性质有潜在的影响[19]。
1.2.1 研究思路与流程
本研究使用遥感数据反演中国东部地区地面PM2.5 浓度的整体思路如图 1 所示。本文的工作大致分为 3 个阶段。
第一阶段: 数据处理。将 Himawari-8 卫星数据和 ERA5 辅助气象数据作为自变量, 地面站点观测的 PM2.5 浓度值作为因变量。首先剔除卫星数据的有云格点和 SAZ > 80°的格点, 然后所有自变量经过方差扩大因子(variance inflation factor, VIF)检验[20]。VIF 可以衡量多元线性回归模型中复共线性的严重程度。复共线性指自变量之间存在线性相关关系, 即一个自变量可以是其他一个或几个自变量的线性组合。使用机器学习算法时, 如果没有去除具有显著线性关系的自变量, 就会造成模型性能降低[21]。通常将 10 作为判断边界, VIF < 10 时不存在复共线性, VIF ≥ 10 则存在强烈的复共线性。去除有强烈复共线性(VIF ≥ 10)的自变量(卫星 Albedo01, Albedo02, Albedo04 和 Albedo05 通道反射率数据)后, 剩余的自变量 VIF 均小于 10 (图 2)。将卫星数据与气象数据插值处理为相同时间分辨率(1 小时)和空间分辨率(0.25° × 0.25°)的卫星‒气象格点数据集, 并将其与地面 PM2.5 浓度按照站点经纬度进行匹配, 得到训练和测试模型需要的数据集。
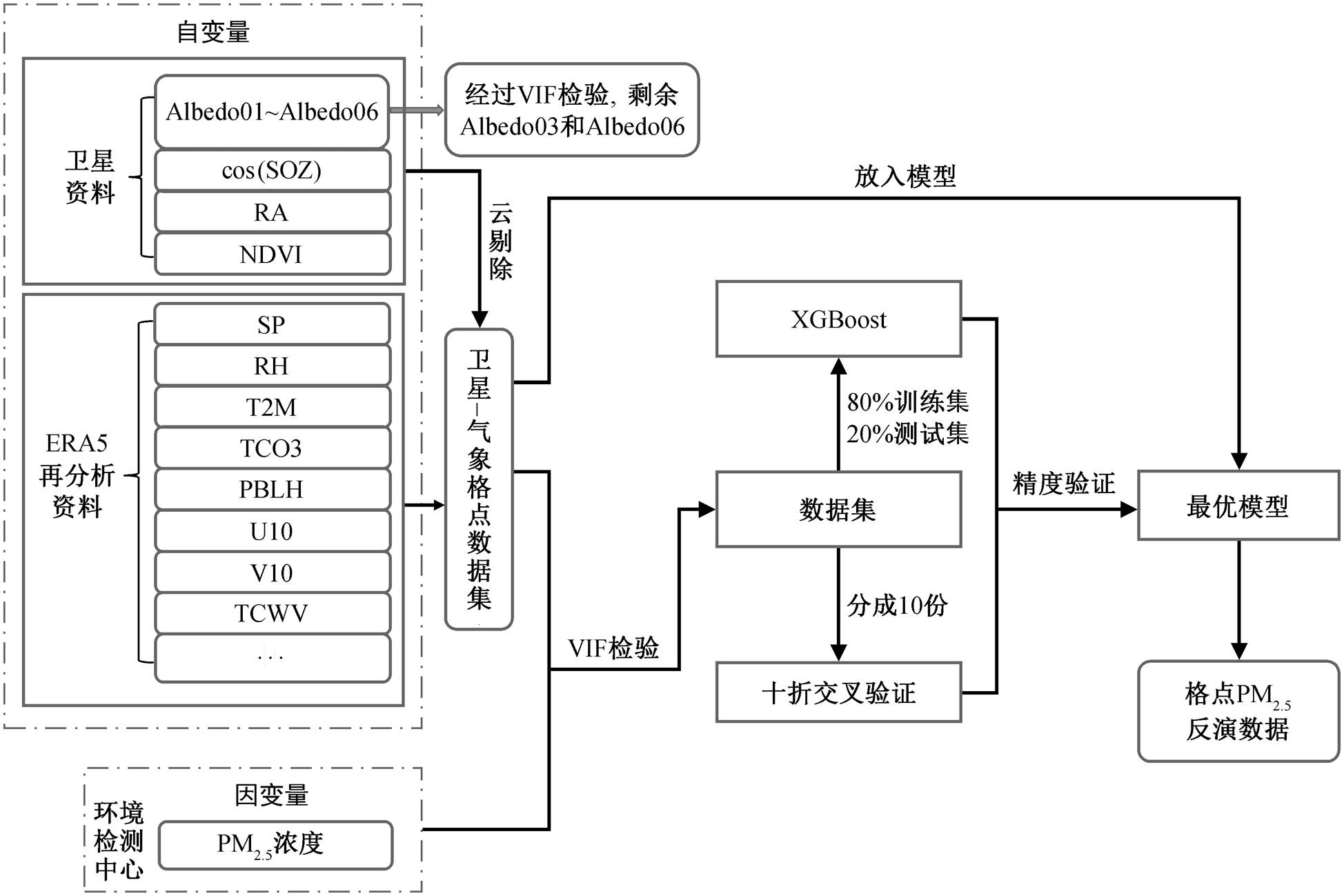
图1 本文反演PM2.5浓度的技术路线
Fig. 1 Flow chart for PM2.5 inversion in this study
第二阶段: 训练和验证模型。按照观测站点将数据集随机分成 10 份, 先用其中的 8 份作为训练集, 剩余两份作为测试集, 通过调整模型参数不断训练模型, 再进行十折交叉验证模型的综合表现。训练和验证是一个不断循环的过程。在每次训练模型的过程中, XGBoost 会自动输出所有自变量的重要性(图 2)。
第三阶段: 将卫星‒气象格点数据集放入模型, 得到中国东部地区 PM2.5 浓度格点数据。通过该格点数据, 得到中国东部地区没有地面观测站点处的地面 PM2.5 浓度值。
1.2.2 极限梯度增强(XGBoost)算法简介
前人在使用机器学习方法研究 PM2.5 问题时, 大多使用随机森林(random forest, RF)算法, 本文首次使用 XGBoost 算法(https://pypi.org/project/xgboo st/)构建模型。
随机森林[22]是一个典型的多个决策树的组合分类器, 属于集成学习算法。随机森林的随机性体现在数据的随机性选取以及待选特征的随机选取两个方面, 优点是可以解决决策树容易过拟合的问题, 模拟结果不会因训练数据的局部异常而剧烈变化, 缺点是由于采样的随机性, 不能保证训练到每一个数据格点, 因此可解释性不高, 无法明确放入的学习器(自变量)是否有效, 且由于其集成学习的特点, 对大样本数据的运算非常耗时。
XGBoost 是从决策树(decision tree, DT)、随机森林、梯度提升决策树(gradient boosting decision tree, GBDT)一步一步地进化而来, 其优势在于内置交叉验证, 允许在每一轮优化过程迭代中使用交叉验证, 可以方便地获得最优迭代次数[23]。此外, 由于优化了正则项, XGBoost 处理大数据的速度远大于其他算法。
由于本研究的总样本量接近 100 万, 使用随机森林计算会非常缓慢。本研究的意图是反演没有地面观测站点的 PM2.5 数据, 需要在构建模型的过程中更全面地使用训练数据。XGBoost 自带训练过程中的交叉验证, 排除了模型过拟合的问题。因此, 本文选用 XGBoost 算法构建模型。
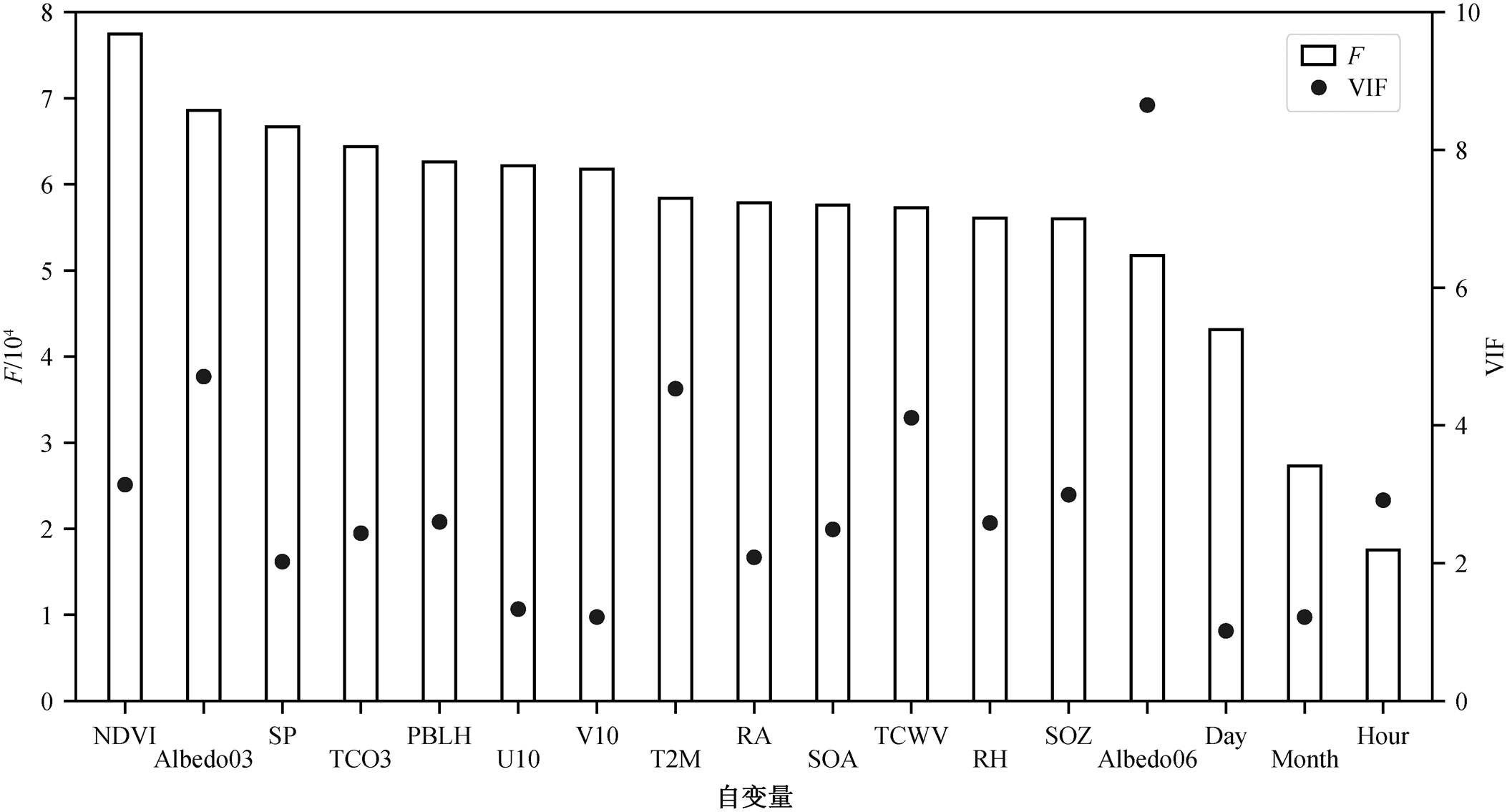
图2 模型各自变量的重要性因子(F)和方差扩大因子(VIF)
Fig. 2 Feature importance (F ) and variance inflation factor (VIF) of each input variable in the model
1.2.3 构建模型
本文选择 2019 年为研究对象。考虑到夜晚卫星无可见光波段的观测数据, 挑选北京时 08:00—17:00, 每天有 10 个时次的样本。1011 个站点, 365天共有 3690150 个样本。剔除所有变量中的缺省值和异常值后, 最终得到 973418 个样本。
每个站点随机抽取 20%的数据作为测试集, 剩余 80%作为训练集。这样做的意义在于, 对模型来说, 测试集的站点观测数据没有参与模型训练, 能更有效地检验模型的应用效果。XGBoost 模型有随机森林拟合(tree booster)和线性拟合(linear booster)两种方法, 本研究选择 tree booster 拟合方法, 将XGBoost 算法应用到训练集中。调整的参数主要有max_depth (树的最大深度)、eta (学习速率)、gamma(节点分裂所需的最小损失函数值)和 num_boost_ round (模型循环次数)。经过不断循环验证, 最终使用的参数为‘max_depth’: 8, ‘gamma’: 1, ‘eta’: 0.1 和‘num_boost_round’: 4350。
自变量放入模型后, XGBoost 算法可以输出各自变量的重要性(F), 表示算法在训练和构建模型时使用某个自变量的次数。如图 2 所示, 卫星数据和气象数据是反演 PM2.5 浓度模型中比较重要的参数, 虚拟变量时间(Month, Day 和 Hour)的重要程度较低, NDVI 和 Albedo03 是最重要的两个自变量, 说明用大气层顶反射率反演地面 PM2.5 是可行且有效的。NDVI 代表着地表的差异化信息, 重要性排第一位, 一方面是因为本文的 NDVI 包含 0.86μm 通道(Albedo04和)和 0.64μm 通道(Albedo03)反射率的信息, 另一方面是因为城市和乡村的地表类型呈现与PM2.5 相似的分布特征。Albedo03 代表红光的大气层顶反射率, 重要性排第二位, 是因为空气中的颗粒物浓度越高, 对应可见光波段的反射率越高。
为了避免因训练集的选取而造成模型偏差, 进行十折交叉验证(ten-fold cross-validation, 10CV)。首先将数据集按照站点随机分成 10 个子集, 每个子集中有 10%的训练数据。然后将 10 个子集中的 9份用来训练模型, 剩余的一份子集用于验证模型性能。该过程重复 10 次, 以便对每个子集进行测试。最后, 将模型预测的 10 个测试集的评估平均值作为该模型的准确性估计值。十折交叉验证的 10 个测试集涵盖所有观测站点, 用该测试集可以更好地验证模型在不同地理位置上的拟合效果。
本文使用多个指标, 进行模型调整以及评估模型的准确性。这些指标包括相关系数(R)、均方根误差(RMSE)、平均绝对误差(MAE)、线性回归斜率(Slope)和平均绝对百分比误差(MAPE)[24]。
R 和 Slope 直接表征反演值与观测值的相关性, 这两个指标越接近 1, 表示模型效果越好。RMSE和 MAE 表征反演值与观测值在数值上的绝对差异, MAPE 在比较差异的同时, 还与观测真值相比较, 这 3 个指标的数值越小, 表示模型效果越好。
图 3(a)显示测试集反演值与观测值的关系, 数据量总为 186158 个, 模型拟合结果的相关系数 R值为 0.831, Slope 为 0.978, RMSE 为 18.67μg/m3, 说明整体上略高估 2%~3%。图 3(b)中的 973418 个反演值是所有站点数据进行 10 次独立的训练和验证后得到的, 在与观测值逐一对比后, 可以看出 10CV的 R 值(0.821)小于本文所用模型, 拟合斜率与模型一致, RMSE 增加 1.44μg/m3。上述结果证明, 模型拟合结果优于 10CV 结果, 本研究训练出的模型是最优模型。
Yao 等[13] 2012 年利用人工神经网络算法, 结合AOD 数据中的气象要素, 反演得到中国地面 PM2.5浓度的 R = 0.80, Slope = 0.63。相比之下, 本文模型的效果更优。
Liu 等[15] 2019 年同样使用 Himawari-8 卫星大气层顶反射率数据反演中国地区 PM2.5 浓度, 10CV 验证结果的 R = 0.92, RMSE = 17.2μg/m3, Slope = 0.81。与之相比, 本文模型效果不够好。但是, Liu 等[15]没有分站点训练模型, 相当于模型对测试集的站点信息已经熟悉, 因此测试集的反演值更接近真值; 另外, 他们对自变量没有进行 VIF 剔除, 所以其模型结果的可信度有待商榷。
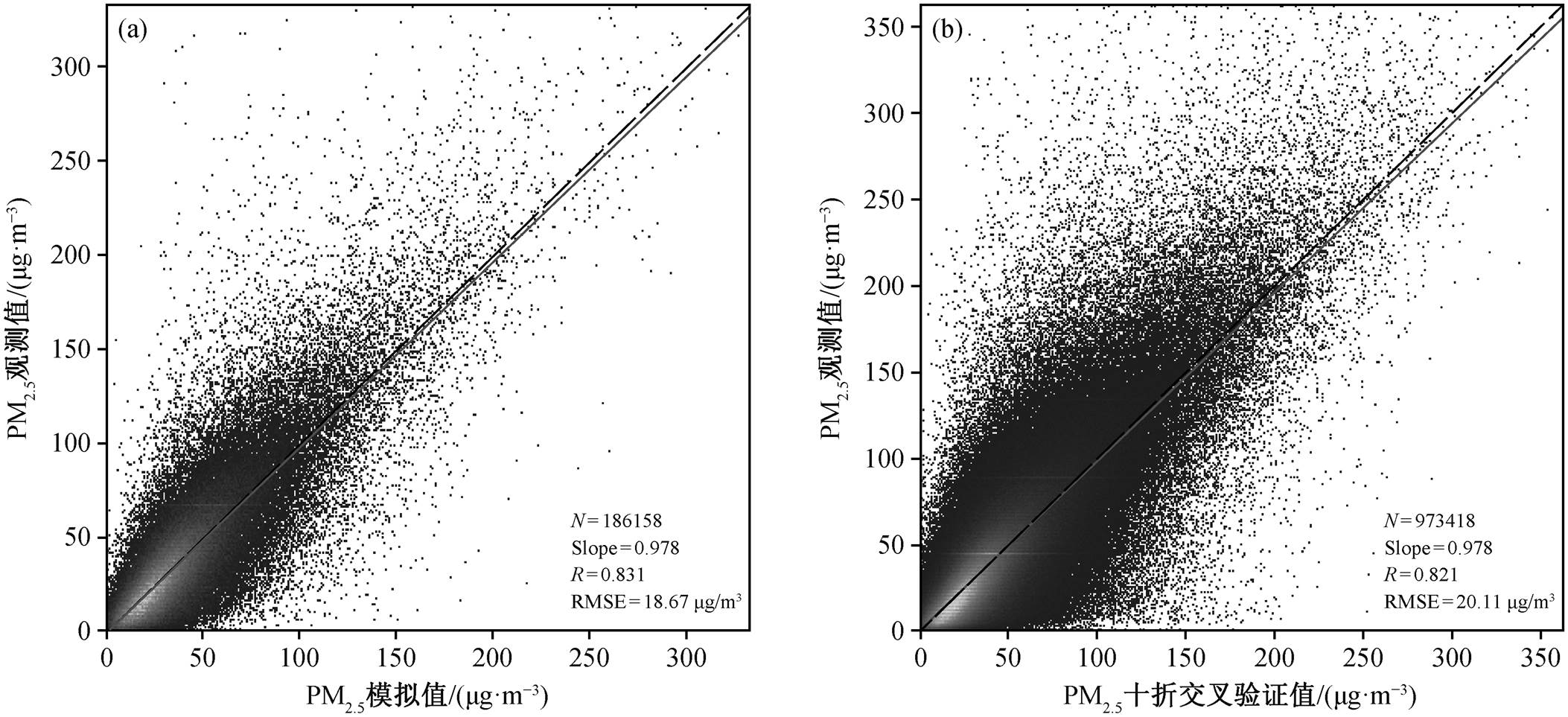
图3 模型拟合结果(a)与十折交叉验证结果(b)
Fig. 3 Results of XGBoost model (a) and ten-fold cross validation (b)
综上所述, 本文模型在拟合精度方面有所提升, 可信度更高。
对用十折交叉验证得到的我国东部地区所有站点的 PM2.5 浓度反演值和观测值进行统计分析, 结果见表1 和 2。
将 08:00—11:00 作为上午, 12:00—17:00 作为下午, 观察模型对一天当中不同时刻 PM2.5 浓度的反演效果。从表 1 看出, 上午的 PM2.5 浓度和波动幅度整体上高于下午, PM2.5 浓度平均最高值出现在上午 09:00, 平均最低值在下午 17:00, 上午和下午的 R 值分别是 0.79 和 0.84, RMSE 值分别是 21.58和 17.4μg/m3, MAE 值分别是 14.4 和 11.2μg/m3, 可见模型对午后(12:00) PM2.5 浓度的反演效果优于上午。每天的 10 个时次中, 反演效果最好的是下午15:00 (R = 0.87), 最差的是早上 08:00 (R = 0.78)。
表1 十折交叉验证结果在不同时刻的表现
Table 1 Results of the ten-fold cross-validation for different hours of a day
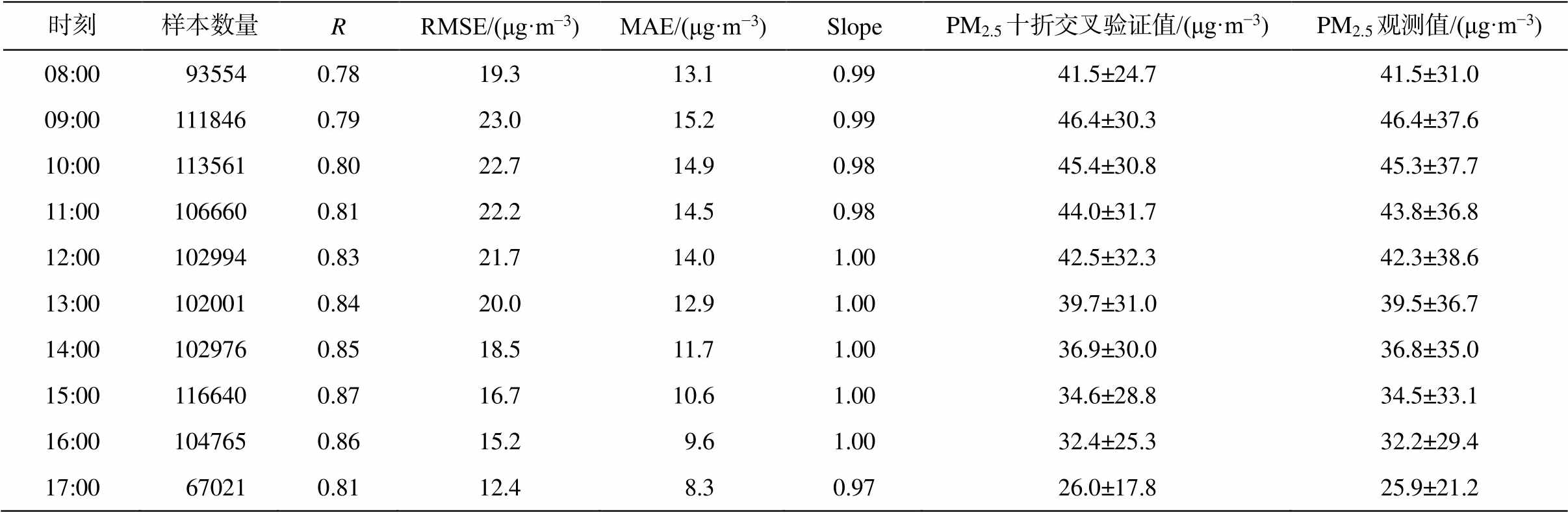
时刻样本数量RRMSE/(μg·m−3)MAE/(μg·m−3)SlopePM2.5十折交叉验证值/(μg·m−3)PM2.5观测值/(μg·m−3) 08:00 935540.7819.313.10.9941.5±24.741.5±31.0 09:001118460.7923.015.20.9946.4±30.346.4±37.6 10:001135610.8022.714.90.9845.4±30.845.3±37.7 11:001066600.8122.214.50.9844.0±31.743.8±36.8 12:001029940.8321.714.01.0042.5±32.342.3±38.6 13:001020010.8420.012.91.0039.7±31.039.5±36.7 14:001029760.8518.511.71.0036.9±30.036.8±35.0 15:001166400.8716.710.61.0034.6±28.834.5±33.1 16:001047650.8615.2 9.61.0032.4±25.332.2±29.4 17:00 670210.8112.4 8.30.9726.0±17.825.9±21.2
表2 十折交叉验证结果在不同季节的表现
Table 2 Results of the ten-fold cross-validation for different seasons

季节样本数量RRMSE/(μg·m−3)MAE/(μg·m−3)SlopePM2.5十折交叉验证值/(μg·m−3)PM2.5观测值/(μg·m−3) 春季2733430.8018.412.40.9837.1±24.637.1±30.3 夏季2110910.6511.5 8.20.9424.0±10.624.0±15.2 秋季3049310.7915.711.01.0036.5±20.436.4±25.7 冬季3100530.8126.718.91.0062.0±42.362.0±51.7
将十折交叉验证结果与观测平均值逐日进行对比, 结果见图 4。观测 PM2.5 浓度年平均值为 39.6 μg/m3, 反演所得 PM2.5 浓度年平均值为 39.7μg/m3, RMSE年平均值较小(1.28μg/m3)。将 2019 年的 3—5 月作为春季, 6—8 月作为夏季, 9—11 月作为秋季, 12—次年 2 月作为冬季, 四季 PM2.5 浓度的反演效果见表 2。从图 4(b)可以看出, 模型反演值与观测值的差值冬季最大, 但在可接受的范围内, 日平均绝对误差小于 6μg/m3。虽然冬季的 PM2.5 浓度最高(平均值为 62.0μg/m3), 波动也最大(方差为 51.7μg/m3), 但模型在冬季的表现是四季中最好的(R = 0.81, Slope = 1.00, RMSE = 26.7μg/m3), 其次是春季和秋季, 表现最差的是夏季。
从图 5(a)的统计结果可知, 所有站点的 R 值从0.41 到 0.97 不等, 绝大多数介于 0.8~0.95 之间。R > 0.8 的站点有 778 个, 占站点总数的 77.1%; R < 0.6的站点有 97 个, 占站点总数的 9.6%。从图 5(b)的统计结果可知, 所有站点 RMSE 值的分布存在南部较低、中部较高、东北地区也有高值的情况。RMSE > 20μg/m3 的站点有 49 个, 占站点总数的4.8%; RMSE < 10μg/m3的站点有 342 个, 占站点总数的 33.9%; RMSE < 15μg/m3 的站点有 774 个, 占总站点数的 76.5%。综合图 5(a)和(b)的统计结果来看, R > 0.8 且 RMSE < 15μg/m3 的站点占总站点数的 3/4以上, 反映模型对我国东部地区的反演效果整体上较好。
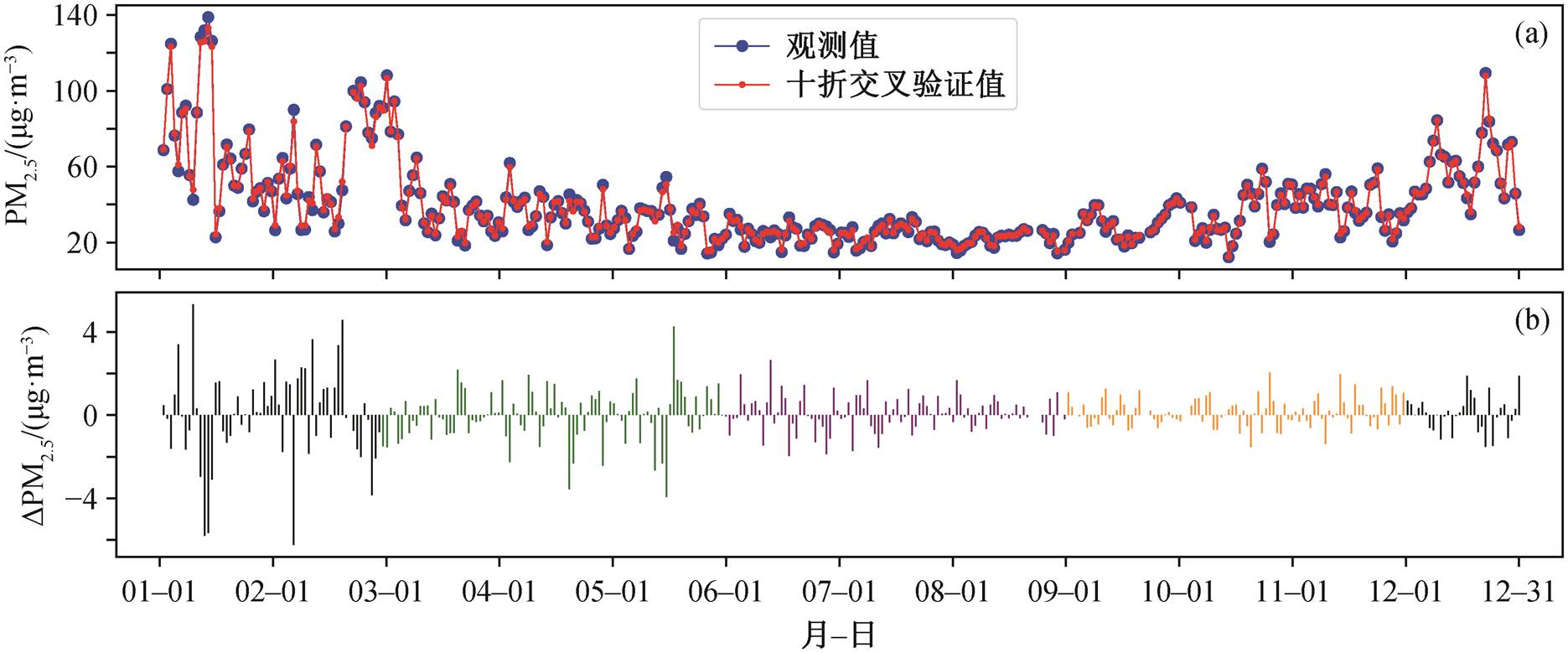
图4 全国所有站点PM2.5浓度逐日平均值(a)以及观测值与反演值的差值(b)
Fig. 4 Daily average of the observed and the retrieved data from all stations in China (a) and difference between daily observation and CV-fitted data (b)
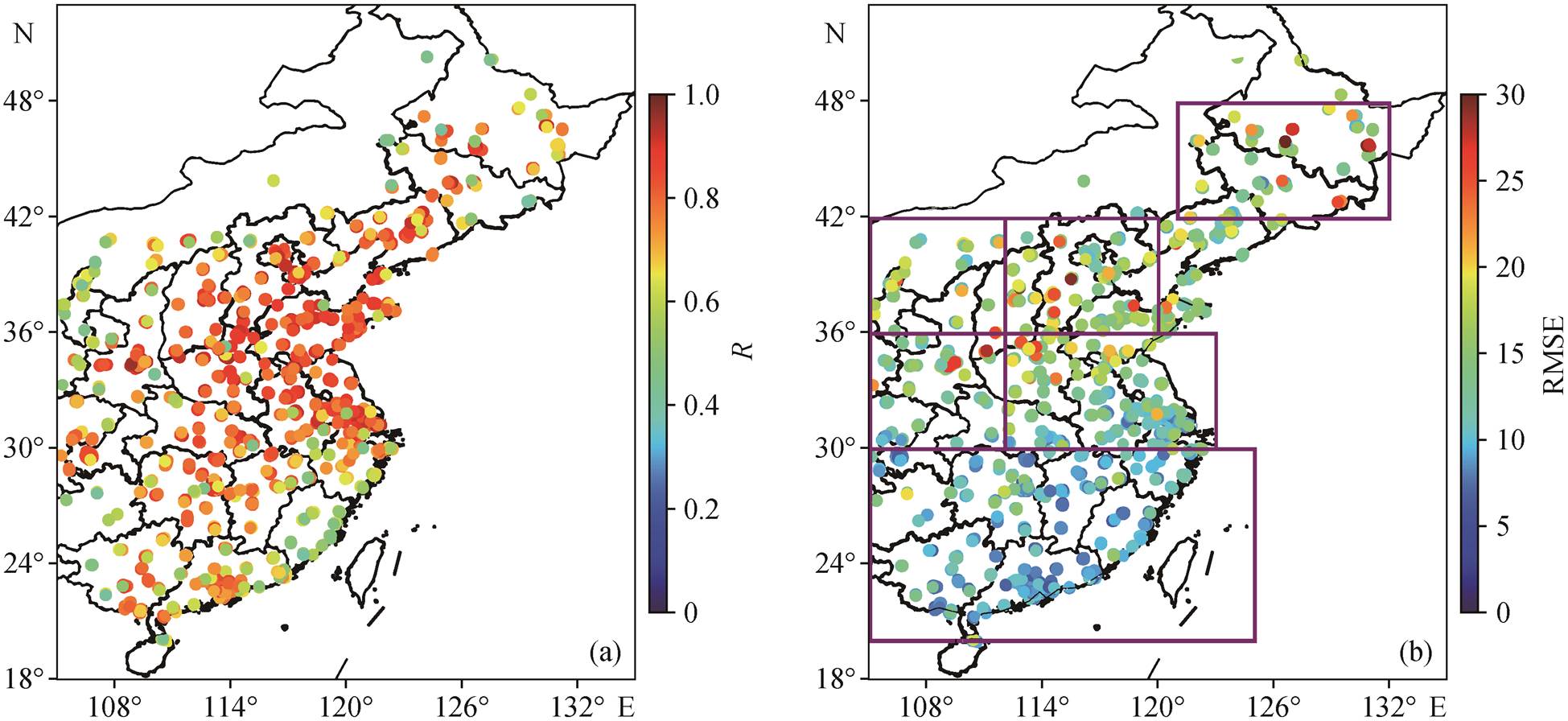
图5 十折交叉验证集中地面站点相关系数与均方根误差分布
Fig. 5 Distribution of R and RMSE from the ten-fold cross-validation for ground station
同时, 本文模型对不同区域的反演效果有差异。如图 5(b)中紫色方框所示, 将我国所有观测站点按照经纬度大致分为东北(121°—132°E, 42°—48°N)、华北(112°—120°E, 36°—42°N)、华东(112°—123°E, 30°—36°N)、中部(105°—112°E, 30°—36°N)、南部(105°—125°E, 20°—30°N)和西北(105°—112°E, 36°—42°N) 6 个区域, 各区域十折交叉验证结果见表 3。可以看出, 模型对华北和华东地区的反演效果最好, 其次是中部和南部地区, 东北和西北地区效果最差, 我们认为有以下原因。1)站点数量和数据质量问题: 东北和西北地区地理面积广阔, 但测站较少, 有观测站的地方也存在数据连续性不好和缺失较多的情况。2)地理特征不同: 东北地区冬季地面有积雪, 本文模型是依据大气层顶反射率判断晴空时近地面 PM2.5 浓度, 会出现高估; 西北地区存在近地面沙尘较大的情况, 反映在大气层顶反射率上也会出现异常高值, 使模型过高地估计近地面 PM2.5 浓度。另外, 虽然南部地区观测站点最多, 数据质量也较好, 但模型对南部地区的反演效果却不如华北和华东地区, 表明本文模型对重污染地区的反演效果优于低污染区域。
给模型输入 0.25° × 0.25°的 2019 年卫星‒气象格点数据, 去除水面格点后, 得到我国东部地区陆地的格点化 PM2.5 数据。由于云检测, 每个时次都存在大量缺值, 故选择年平均值和季节平均值来应用模型(图 6)。
将每个观测站点周围 0.12°内格点的数据作为与该观测站点对应的格点值, 分别计算 6 个区域反演值和观测值的年平均和季节平均值, 用RMSE和MAPE 衡量反演效果。从表 4 可以看出, 模型对华北、华东及南部地区的反演效果比较好,年平均和季节平均的 MAPE 都在 20 以下, 对东北和中部地区的反演效果次之, 西北地区最差, 原因仍然是模型将西北地区近地面的沙尘视为 PM2.5 高值区。从总体上看, 本文模型可以较好地表征中国东部地区地面 PM2.5 浓度的分布和变化情况。
本文建立一套有效的 PM2.5 浓度反演模型, 结合 Himawari-8 卫星数据和 ERA5 气象数据, 得到我国东部地区 2019 年 1 月 1 日至 2019 年 12 月 31 日大范围的逐小时地面 PM2.5 格点数据, 结论如下。
1)用卫星 L1 级大气顶层反射率数据构建地面PM2.5反演模型是可行的, 模型中最重要的因子是归一化植被指数(NDVI), 其次是 0.64μm 通道反射率(Albedo_03)。
2)十折交叉验证结果表明, 本文模型在华北和华东地区的表现最好, 模型对 PM2.5 高值区的反演效果好于低值区。
3)对我国东部地区的格点反演结果表明, 本文模型在大部分地区的表现都很好, 其中华北、华东和南部地区效果最好。
本文模型存在以下不足之处: 在反演格点PM2.5数据时, 西北地区出现异常高值, 说明本文模型对西北地区 PM2.5 浓度的反演不适用。未来的工作将从以下方面做出改进: 1)由于我国幅员辽阔, 地表类型差异较大, 用单一模型反演全国范围的PM2.5 浓度效果有限, 下一步将分区域训练模型; 2) 开发有云覆盖格点的 PM2.5 浓度反演方法, 以期得到更全面的逐小时 PM2.5 格点数据; 3)本文得到的全国格点PM2.5数据的分辨率上有待提高, 下一步拟将空间分辨率提升到0.05° × 0.05°。
表3 十折交叉验证结果在不同区域的表现
Table 3 Results from the ten-fold cross-validation for different regions
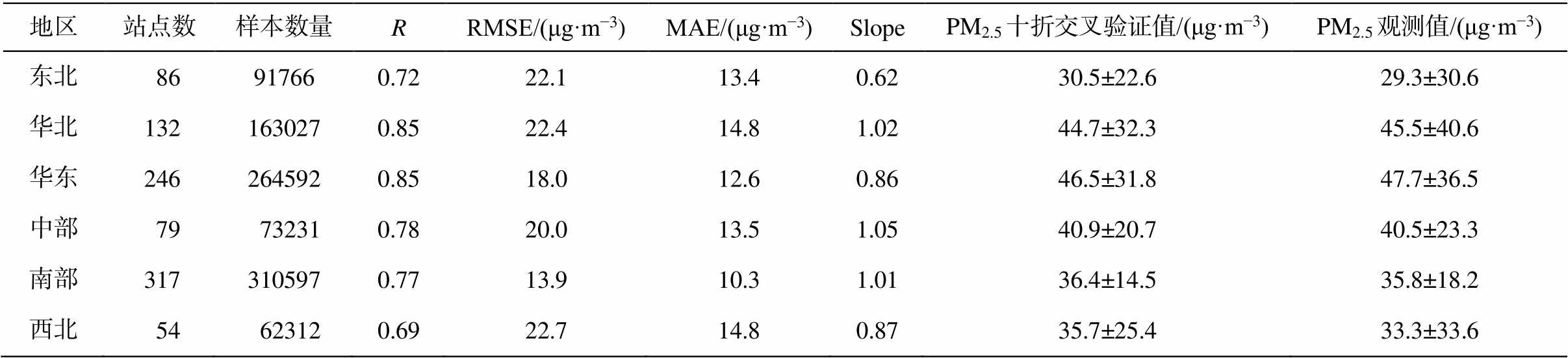
地区站点数样本数量RRMSE/(μg·m−3)MAE/(μg·m−3)SlopePM2.5十折交叉验证值/(μg·m−3)PM2.5观测值/(μg·m−3) 东北86917660.7222.113.40.6230.5±22.629.3±30.6 华北1321630270.8522.414.81.0244.7±32.345.5±40.6 华东2462645920.8518.012.60.8646.5±31.847.7±36.5 中部79 732310.7820.013.51.0540.9±20.740.5±23.3 南部3173105970.7713.910.31.0136.4±14.535.8±18.2 西北54 623120.6922.714.80.8735.7±25.433.3±33.6
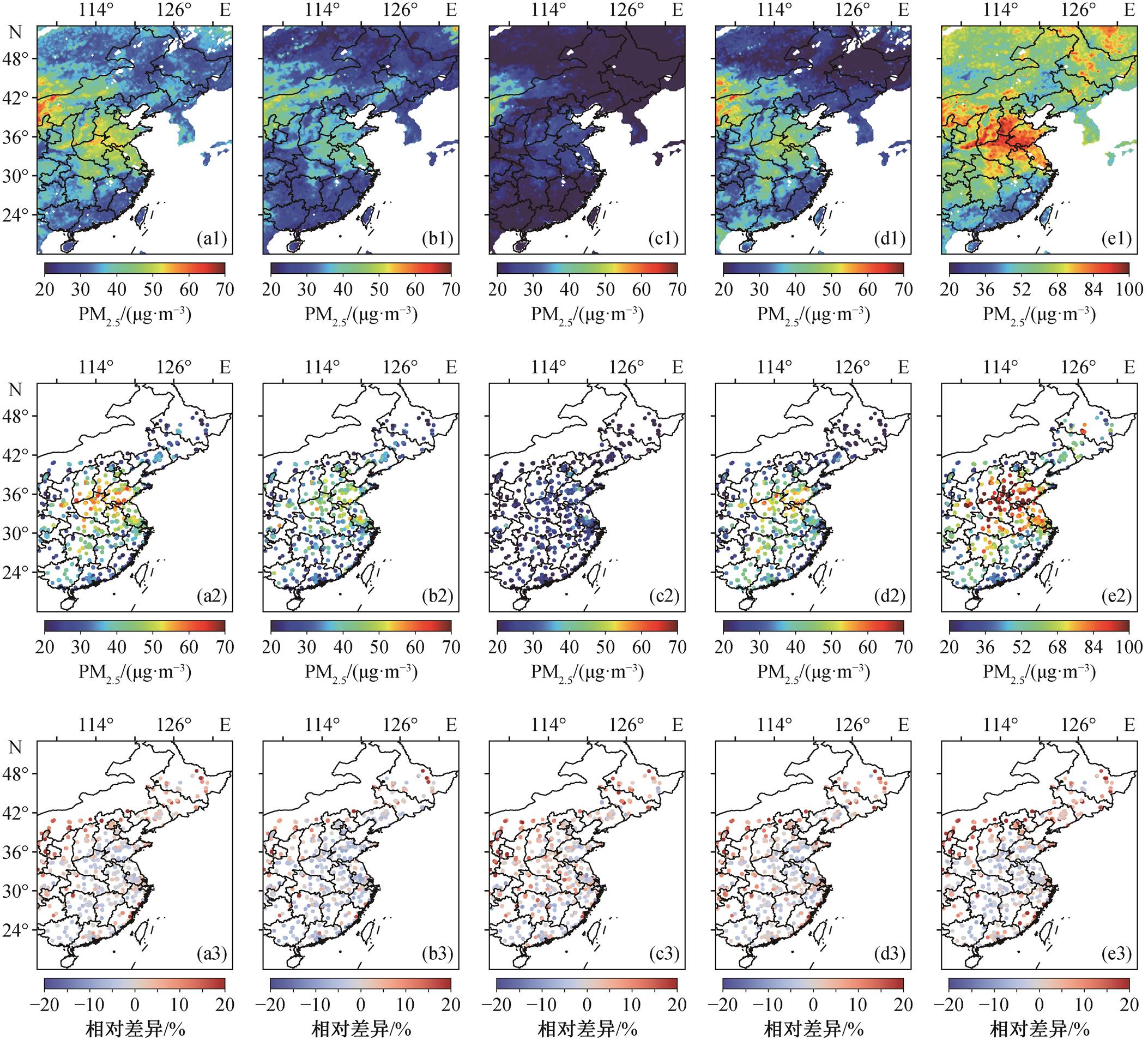
(a1)~(a3) 2019年全年平均值; (b1)~(b3) 2019年春季平均值; (c1)~(c3) 2019年夏季平均值; (d1)~(d3) 2019年秋季平均值; (e1)~(e3) 2019年冬季平均值。(a1)~(e1)模型反演得出的地面PM2.5浓度格点值; (a2)~(e2)观测站点实测PM2.5浓度值; (a3)~(e3)观测站点附近反演值与观测值之差除以观测值
图6 中国东部地区PM2.5模型反演与地面观测的年平均和季节平均值
Fig. 6 Annual and seasonal average PM2.5 concentrations between model estimation and surface measurement in eastern China
表4 不同区域的不同时间尺度PM2.5反演值与观测值对比
Table 4 Comparison between retrieval PM2.5 and observed PM2.5 in different regions at different time scales
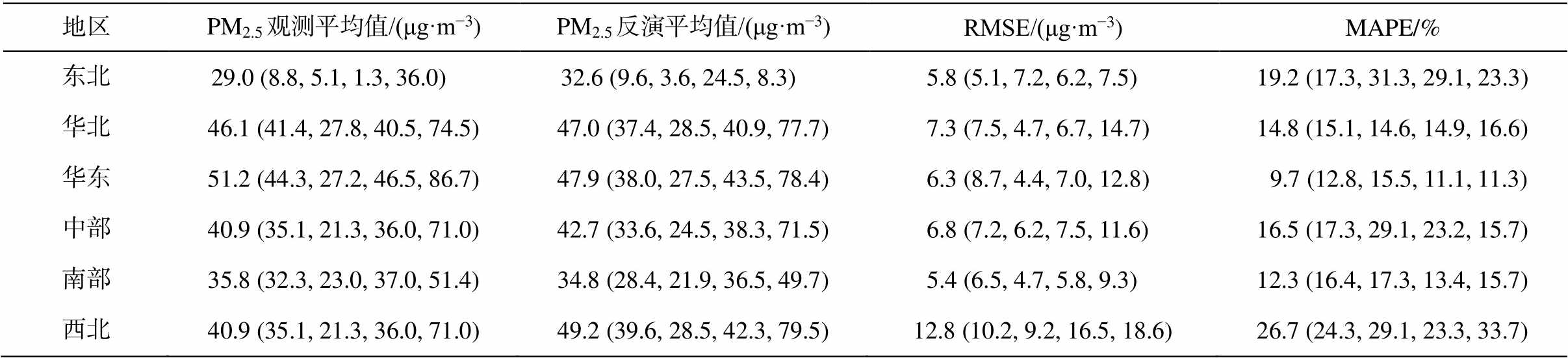
地区PM2.5观测平均值/(μg·m−3)PM2.5反演平均值/(μg·m−3)RMSE/(μg·m−3)MAPE/% 东北 29.0 (8.8, 5.1, 1.3, 36.0) 32.6 (9.6, 3.6, 24.5, 8.3)5.8 (5.1, 7.2, 6.2, 7.5)19.2 (17.3, 31.3, 29.1, 23.3) 华北46.1 (41.4, 27.8, 40.5, 74.5)47.0 (37.4, 28.5, 40.9, 77.7)7.3 (7.5, 4.7, 6.7, 14.7)14.8 (15.1, 14.6, 14.9, 16.6) 华东51.2 (44.3, 27.2, 46.5, 86.7)47.9 (38.0, 27.5, 43.5, 78.4)6.3 (8.7, 4.4, 7.0, 12.8) 9.7 (12.8, 15.5, 11.1, 11.3) 中部40.9 (35.1, 21.3, 36.0, 71.0)42.7 (33.6, 24.5, 38.3, 71.5)6.8 (7.2, 6.2, 7.5, 11.6)16.5 (17.3, 29.1, 23.2, 15.7) 南部35.8 (32.3, 23.0, 37.0, 51.4)34.8 (28.4, 21.9, 36.5, 49.7)5.4 (6.5, 4.7, 5.8, 9.3)12.3 (16.4, 17.3, 13.4, 15.7) 西北40.9 (35.1, 21.3, 36.0, 71.0)49.2 (39.6, 28.5, 42.3, 79.5)12.8 (10.2, 9.2, 16.5, 18.6)26.7 (24.3, 29.1, 23.3, 33.7)
说明: 数据格式为“全年(春季, 夏季, 秋季, 冬季)”。
参考文献
[1] 霍彦峰, 杨关盈, 白庆梅, 等. 基于 MODIS 气溶胶产品的安徽省颗粒物浓度反演研究. 环境科学与技术, 2017, 40(2): 59‒64
[2] 郭新彪, 魏红英. 大气 PM2.5 对健康影响的研究进展. 科学通报, 2013, 58(13): 1171‒1177
[3] 杨振宇. 浅谈PM2.5对环境与健康的影响. 科技风, 2013(13): 208
[4] 张小曳. 中国大气气溶胶及其气候效应的研究. 地球科学进展, 2007, 22(1): 12‒16
[5] 于雪, 赵文吉, 孙春媛, 等. 大气PM2.5遥感反演研究进展. 环境污染与防治, 2017, 39(10): 1153‒1158
[6] Lary D J, Remer L A, Macneill D, et al. Machine learning and bias correction of MODIS aerosol optical depth. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 694‒698
[7] Van Donkelaar A, Martin R V, Brauer M, et al. Global estimates of ambient fine particulate matter concen-trations from satellite-based aerosol optical depth: development and application. Environmental Health Perspectives, 2010, 118(10): 847‒855
[8] Van Donkelaar A, Martin R V, Spurr R J D, et al. Optimal estimation for global ground-level fine par-ticulate matter concentrations. Journal of Geophysi-cal Research —Atmospheres, 2013, 118(11): 5621‒ 5636
[9] Zhang Y, Li Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sensing of Environment, 2015, 160: 252‒262
[10] Zeng Q, Chen L, Zhu H, et al. Satellite-based esti-mation of hourly PM2.5 concentrations using a vertical-humidity correction method from Himawari-AOD in Hebei. Sensors, 2018, 18(10): 3456
[11] 郝静, 孙成, 郭兴宇, 等. 京津冀内陆平原区 PM2.5浓度时空变化定量模拟. 环境科学, 2018, 39(4): 1455‒1465
[12] He Q, Huang B. Satellite-based high-resolution PM2.5estimation over the Beijing-Tianjin-Hebei region of China using an improved geographically and tempor-ally weighted regression model. Environmental Pollu-tion, 2018, 236: 1027‒1037
[13] Yao L, Lu N, Jiang S. Artificial neural network (ANN) for multi-source PM2.5 estimation using sur-face, MODIS, and meteorological data // 2012 Inter-national Conference on Biomedical Engineering and Biotechnology. Macao: IEEE, 2012: 1228‒1231
[14] Li T, Shen H, Yuan Q, et al. Geographically and tem-porally weighted neural networks for satellite-based mapping of ground-level PM2.5. ISPRS Journal of Pho-togrammetry and Remote Sensing, 2020, 167: 178‒ 188
[15] Liu J, Weng F, Li Z. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm. Atmospheric En-vironment, 2019, 208: 113‒122
[16] Shen H, Li T, Yuan Q, et al. Estimating regional ground-level PM2.5 directly from satellite top-of-atmosphere reflectance using deep belief networks. Journal of Geophysical Research —Atmospheres, 2018, 123(24): 13875‒13886
[17] Gupta P, Levy R C, Mattoo S, et al. A surface reflec-tance scheme for retrieving aerosol optical depth over urban surfaces in MODIS Dark Target retrieval algo-rithm. Atmospheric Measurement Techniques, 2016, 9(7): 3293‒3308
[18] 李同文, 孙越乔, 杨晨雪, 等. 融合卫星遥感与地面测站的区域 PM2.5 反演. 测绘地理信息, 2015, 40(3): 6‒9
[19] 杜佳威, 汤田玉, 黄敏. 基于遥感影像的 PM2.5 浓度分布的探索. 电子世界, 2014, 3(15): 187
[20] Duc L, Saito K, Hotta D. Analysis and design of cov-ariance inflation methods using inflation functions. Part 1: theoretical framework. Quarterly Journal of the Royal Meteorological Society, 2020, 146: 3638‒ 3660
[21] 归庆明, 姚绍文, 顾勇为, 等. 诊断复共线性的条件指标‒方差分解比法. 测绘学报, 2006, 35(3): 210‒214
[22] 申原, 陈朝亮, 钱静, 等. 基于随机森林的高分辨率 PM2.5 遥感反演——以广东省为例. 集成技术, 2018, 7(3): 31‒41
[23] Chen Jiangping, Yin Jianhua, Zang Lin, et al. Sta-cking machine learning model for estimating hourly PM2.5 in China based on Himawari 8 aerosol optical depth data. Science of the Total Environment, 2019, 697: 134021
[24] 曹雨, 王峰, 黄沃, 等. 应用统计学. 北京: 人民邮电出版社, 2013
Retrieval of Ground PM2.5 Concentrations in Eastern China Using Data from Himawari-8 Satellite
Abstract In order to retrieve the large-scale ground PM2.5 concentration distribution in eastern China, a model was built using machine learning. The model used the top-of-atmosphere reflectance data of the Himawari-8 geostationary satellite in 2019 and the meteorological data of the European Center as the input data, and the ground PM2.5 concentration was the output data. Validation results showed that the model had high accuracy on different time scales in eastern China. The ten-fold cross-validation of the model had a correlation coefficient of 0.82 and a root-mean-square error of 20.11 μg/m3 for hourly PM2.5 concentration inversion. The hourly satellite-meteorologi-cal grid data throughout the year of 2019 were input to the model, and the corresponding PM2.5 grid data for the eastern China obtained. Good results were achieved for the PM2.5 grid data after analyzing the seasonal variation and spatial distribution of PM2.5 concentration over eastern China.
Key words satellite remote sensing; top-of-atmosphere reflectance; PM2.5 concentration; machine learning
doi: 10.13209/j.0479-8023.2022.032
国家重点研发计划(2016YFC0202004)和国家自然科学基金(42030607, 42075133)资助
收稿日期: 2021-04-11;
修回日期: 2021-05-12