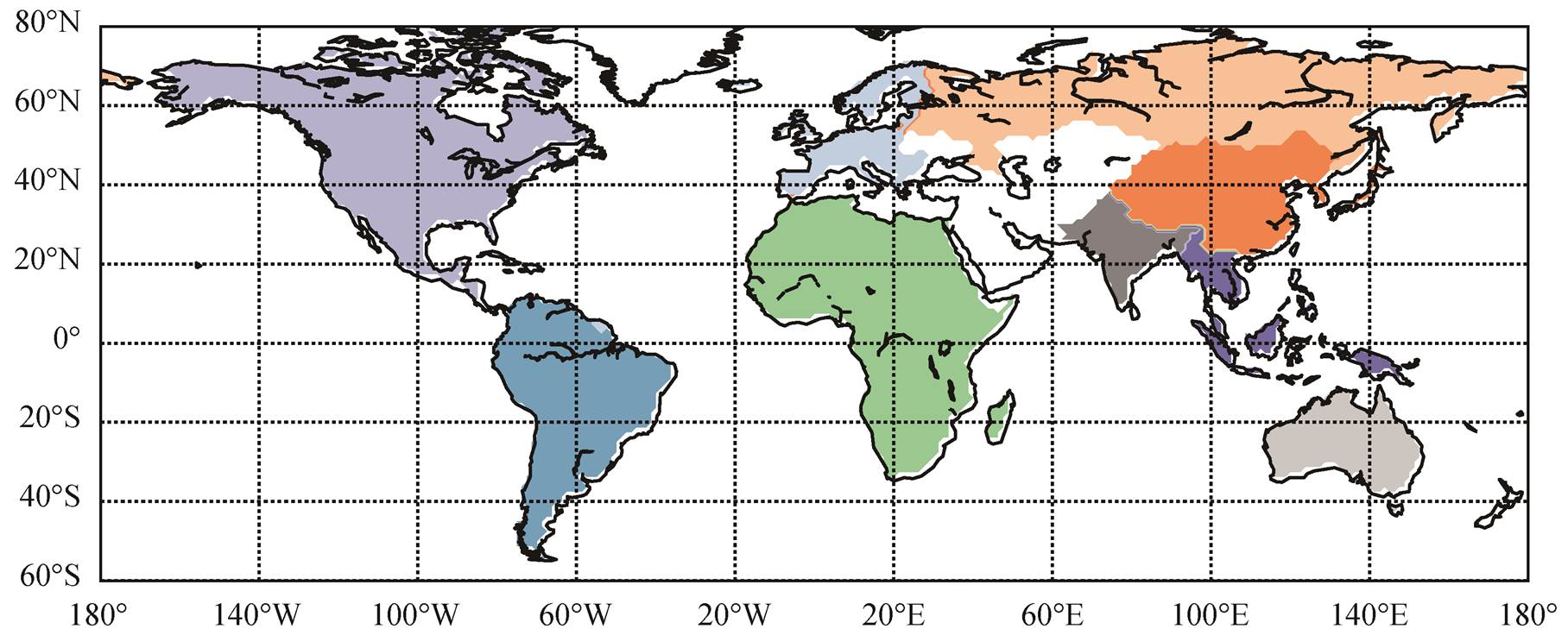
图1 RECCAP全球分区
Fig. 1 RECCAP regions
摘要 为探究全球及区域尺度总初级生产力(GPP)及其模型模拟的不确定性来源, 基于广泛使用的光能利用率模型的算法结构, 搭建多算法集成模型, 结合气象再分析数据和卫星遥感数据, 模拟全球及区域尺度总初级生产力, 并使用方差分析方法对模拟结果的不确定性来源进行量化研究。结果表明: 1)集成模型与基于通量观测升尺度(FLUXCOM)的 GPP 之间具有较强的一致性, 皮尔逊相关系数达 0.97, 均方根误差为 24.36 gC/(m2·月), 且集成模型的表现优于单一结构配置模型; 2)光合有效辐射、水分相关数据及水分限制因子为不确定性的主要来源, 相对贡献分别为 41.73%, 26.79%和 23.82%; 3)不确定性的构成具有明显的区域差异, 干旱区域水分限制因子的相对贡献超过 80%, 低温区域温度限制因子的相对贡献超过 40%。使用光能利用率模型估算 GPP 时, 控制光合有效辐射和水分相关数据的不确定性可以有效地提高模拟精度, 而在极端环境条件(干旱、低温)下, 优化环境条件限制因子至关重要。
关键词 总初级生产力; 光能利用率模型; 不确定性; 集成模型; 相对贡献
总初级生产力(gross primary productivity, GPP)是植被通过光合作用吸收 CO2 的整体效率, 是 CO2从大气圈进入生物圈的第一步, 也是碳循环中至关重要的一步[1]。GPP 是全球碳循环中重要的通量组分, 贡献约 20 倍于人为源的碳通量[2], 是诸如粮食、木材和纤维等生态系统功能的驱动因素, 也是陆地生态系统减缓全球变暖、抵消日益增加的 CO2 排放的核心表征[1,3]。因此, 区域乃至全球尺度下 GPP 的准确估算有助于更全面深入地理解生态系统功能和全球碳循环[4]。
具有代表性的 GPP 估算模型根据其原理可分为 4 类: 光合作用相关酶动力学过程模型、光能利用率模型、依赖通量塔数据的机器学习模型和经验统计模型[5]。其中, 光合作用相关酶动力学过程计算输入参数复杂, 计算资源消耗较大; 机器学习模型黑箱性强, 可理解性差; 统计模型模拟快速简便, 但缺失生物化学过程信息, 模拟结果可解释性低; 光能利用率模型在长时间序列数据可获得性、数据可靠性、计算效率、过程可解释性和结果准确性方面达到平衡, 常用于区域和全球尺度 GPP 时空动态模拟[6–10]。
光能利用率(LUE)模型的核心思想是, 光合作用吸收的 CO2 由植被吸收的光能与植被转化吸收光能的效率决定, 分别估算出植被吸收的光能及光能转化率, 即可估算出植被光合作用吸收 CO2 的量。影响植被吸收光能的因素主要是到达地表的短波辐射和植被的冠层结构, 影响光能转化率的主要因素则包括植被本身的特质以及温度、水分供给等环境因素。模型主要由三部分构成: 植被吸收的光合有效辐射(APAR)、最佳环境条件下的最大光能利用效率(εmax)和表征环境条件限制的环境因子[11–12]。在光能利用率模型的核心框架下, 发展出多种多样的模型结构来估算植被吸收光能的能力以及温度、水分等因素对植被光能转化效率的影响。现有的研究中多使用单一模型结构, 或简单地使用多个固定结构进行 GPP 模拟, 未充分利用已有的多元化模型结构。因此, 搭建一个充分耦合多种算法的多模型结构 GPP 集成模型, 对快速、准确地模拟区域及全球尺度 GPP 具有重要意义。
采用光能利用率模型模拟区域或全球 GPP 仍存在较大的不确定性。模型驱动数据、模型结构以及模型参数是 GPP 估算中不确定性的 3 个主要来源[13–14]。模型驱动数据主要是气象数据和遥感数据, 这些数据存在观测误差、传感器差异和空间异质性等不确定性来源[15–16]。使用不同的模型结构模拟 GPP 时, 相互间差异较大, 并且对于不同条件下不同模型结构的表现优劣至今没有明确的结论[17–19]。模型参数(如 εmax)会显著地影响模型结果[20–21], 并构成 GPP 模拟中不确定性的主要来源。对 GPP 模拟的不确定性进行多角度分析, 能够帮助我们深入地理解不确定性的来源, 对提高 GPP 模拟精度、获取准确的大尺度 GPP 碳通量具有重要意义。现有研究多倾向于探讨单个因素的定量影响, 或对多个因素的影响进行定性分析[18,22–24], 缺少对区域及全球尺度 GPP 模拟不确定性的系统性定量分析。
本研究基于广泛使用的光能利用率模型的结构算法, 搭建多算法集成模型, 并使用方差分析方法, 对 GPP 模拟的不确定性进行系统性的定量分析。本研究的目标包括: 1)搭建可靠、高效的 GPP多算法集成模型; 2)定量地评估 GPP 模拟中各模型结构和驱动数据的不确定性; 3)系统地分析不同地区、不同环境条件下模型结构和驱动数据对不确定性的相对贡献。
本研究以全球陆地为研究区域, 基于 1.25°× 1.25°的全球陆地栅格搭建模型。在进行区域分析时, 按 Regional Carbon Cycle Assessment and Pro-cesses (RECCAP)对全球陆地的区域划分方案进行。RECCAP 将全球划为九大区域(图 1), 包括北美洲、南美洲、非洲、欧洲、俄罗斯、东亚、南亚、东南亚和澳大利亚, 其中不包含格陵兰、南极洲、中东、乌克兰、新西兰和哈萨克斯坦这些冰川覆盖或生产力较低的区域[25]。
模型的输入数据主要是卫星遥感数据以及再分析气象数据。卫星遥感数据包括土地利用类型、植被指数和水分指数, 主要来自中分辨率成像光谱仪(MODIS)产品; 土地利用数据来自 MCD12C1①https://lpdaac.usgs.gov/products/mcd12c1v006;; 植被指数包括增强植被指数(EVI)、归一化植被指数(NDVI)和使用叶面积指数(LAI)计算而得的光合有效辐射吸收比(FPAR), 分别来自 MOD13C2②https://lpdaac.usgs.gov/products/mod13c2v006;、AVHRR NDVI3g [26]和 GLASS [27]。地表水分指数(LSWI)使用 MCD43C4③https://lpdaac.usgs.gov/products/mcd43c4v006, 通过短波(SW)、近红外(NIR)波段反射率来计算。所有数据均统一重采样至 1.25°×1.25°网格, NDVI 和 FPAR 通过最大值合成法(MVC)转换为月数据。

图1 RECCAP全球分区
Fig. 1 RECCAP regions
气象相关数据包括光合有效辐射(PAR)、温度(T)、热通量、蒸散发以及土壤湿度相关数据。光合有效辐射和温度数据来自 MERRA-2④https://disc.gsfc.nasa.gov/datasets/M2TUNXLND_5.12.4/summary?keywords=2d,diurnal,Time-Averaged,Single-Level,Assimilation,Land%20Surface%20Diagnostics;和 ERA5⑤https://www.ecmwf.int/en/era5-land;。热通量数据包括潜热(LH)和显热(SH), 来源于MERRA-2。用于计算饱和蒸气压亏缺(VPD)的露点温度(Tdew)和地表大气压(Psur)数据来自 ERA5。蒸散发数据包括潜在蒸散(PET)和实际蒸散发(ET), 来自 USGS FEWS NET [28]。土壤湿度相关数据包括土壤湿度(SM)、土壤持水量(FC)以及土壤萎蔫点(WP)。土壤持水量和土壤萎蔫点是土壤本身的性质, 在模拟中, 我们认为土壤这两种性质不随时间变化, 该数据来自 IGBP-DIS⑥https://daac.ornl.gov/SOILS/guides/igbp.html; 土壤湿度数据来自NOAA CPC Soil Moisture [29]。所有气象相关数据均统一重采样至 1.25°×1.25°网格, 6 小时分辨率温度数据用于求取月最低温和月均温, 天分辨率PET被加总为月 PET。
FLUXCOM GPP 是使用随机森林(RF)、神经网络(ANN)和多元自适应样条回归(MARS) 3 种机器学习方法, 将 FLUXNET 涡度协方差通量塔的碳通量测量值与遥感和气象数据相结合产出的全球 GPP数据[10]。FLUXCOM GPP 与 FLUXNET 站点观测和全球植被动态模型结果在时空动态上具有一致性[30], 在本研究中作为基准数据集(表 1), 用于模型参数率定以及模拟结果验证。
1.3.1光能利用率集成模型
在 LUE 模型中, 通过将 PAR、FPAR、水分限制因子(Ws)、温度限制因子(Ts)和 εmax 相乘, 估算得到 GPP。FPAR, Ts 和 Ws 这 3 个主要模型结构均已发展出多种计算方法。本研究中, 对 FPAR, Ws和 Ts 的核心模型结构, 分别引入多种已有算法, 搭建多算法集成 GPP 模型。进行 GPP 模拟时, 遍历 3种 FPAR、5 种 Ws 和 4 种 Ts 的模型结构组合(共 60种), 得到多种模型结构下的 GPP 模拟结果, 实现多算法集成快速模拟(图 2)。
表1 研究数据来源及相关信息
Table 1 Data source and information
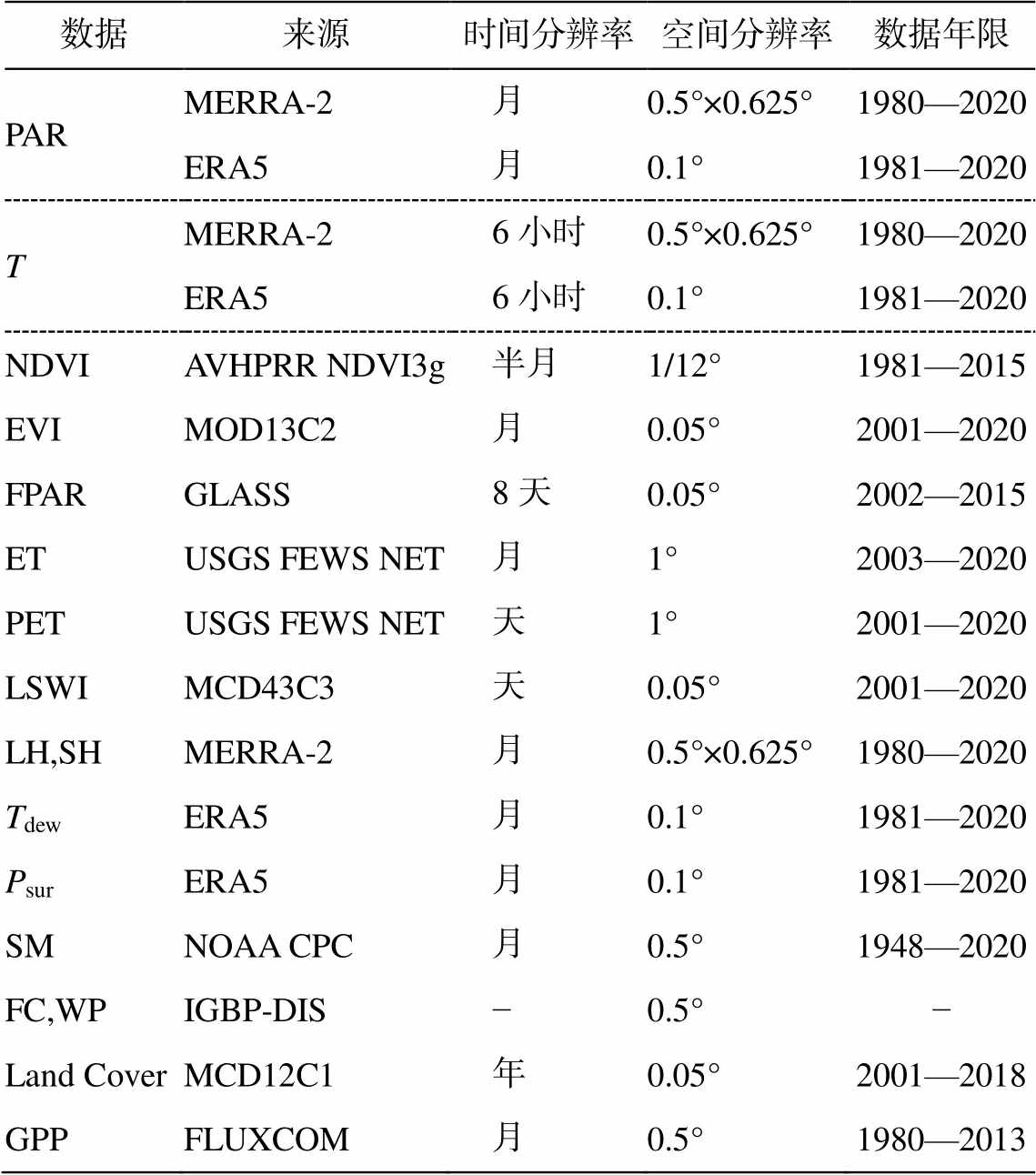
数据来源时间分辨率空间分辨率数据年限 PARMERRA-2月0.5°×0.625°1980—2020 ERA5月0.1°1981—2020 TMERRA-26小时0.5°×0.625°1980—2020 ERA56小时0.1°1981—2020 NDVIAVHPRR NDVI3g半月1/12°1981—2015 EVIMOD13C2月0.05°2001—2020 FPARGLASS8天0.05°2002—2015 ETUSGS FEWS NET月1°2003—2020 PETUSGS FEWS NET天1°2001—2020 LSWIMCD43C3天0.05°2001—2020 LH,SHMERRA-2月0.5°×0.625°1980—2020 TdewERA5月0.1°1981—2020 PsurERA5月0.1°1981—2020 SMNOAA CPC月0.5°1948—2020 FC,WPIGBP-DIS−0.5°− Land CoverMCD12C1年0.05°2001—2018 GPPFLUXCOM月0.5°1980—2013
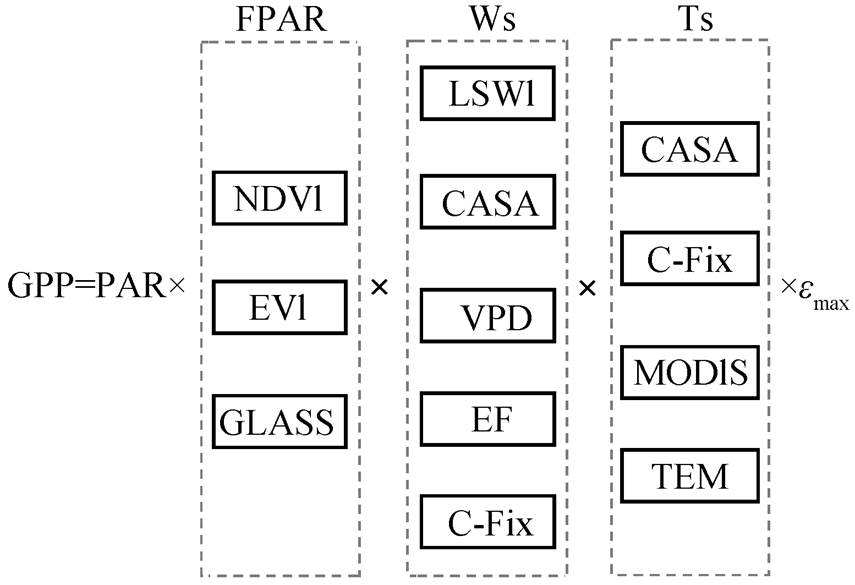
图2 GPP多算法集成模型框架
Fig. 2 Framework of GPP meta-model
FPAR 主要采用卫星遥感反演的植被指数, 通过经验公式计算得到, NDVI [31]、EVI [32] 和 LAI [27]均可用于 FPAR 的估算。NDVI 和 EVI 使用简单的线性经验公式估算 FPAR, 通过 LAI 估算 FPAR 需要使用冠层光学模型(表 2)。
Ws 衡量水分条件对植被光合作用能力的影响, 取值范围为[0, 1], 在较大的栅格尺度上对植被水分供给条件进行估算, 存在较大的不确定性, 也衍生出多种依据不同原理和使用不同数据进行估算的方法。CASA (Carnegie-Ames-stanford approach)模型中, 使用蒸散发数据来衡量环境水分条件[33]; 在 C-Fix (Carbon Fix)模型中, 结合土壤湿度以及潜热显热通量评估植被光合作用能力受水分因素的影响[34]; LSWI 也用于估算水分因素的影响, 通过实际 LSWI值与生长季最大 LSWI 的比值来衡量水分条件[5]; VPD 用于 MODIS GPP 算法中, 参数随植被类型改变[35] (表 3); 蒸发率(EF)也直接用于水分限制因子的估算[31] (表 2)。
表2 FPAR, Ws和Ts 3种主要模型结构的不同算法
Table 2 Algorithms for three main model structures (FPAR, Ws, Ts)

模型结构算法文献 FPARFPARNDVI =1.24×NDVI−0.168[31] FPAREVI =(EVI−0.1)×1.25[32] FPARGLASS =1−τPAR[27] WsWsCASA =0.5×ET/PET+0.5[33] WsC-Fix =0.5×Fs+0.5×Fa[34] WsLSWI =(1+LSWI)/(1+LSWImax)[5] WsVPD =(VPD−VPDmin)/( VPDmax −VPDmin)[35] WsEF =LH/(LH+SH)[31] TsTsCASA =Tscaled1×Tscaled2 , 其中Tscaled1 =0.8+0.02×Topt −0.005×Topt2,[33] [36] [35] [34]
Ts 衡量环境温度对植被光合作用转化 CO2 能力的影响, 取值范围为[0, 1], 常用的估算温度条件影响的方法有 4 种。在 CASA 模型中, Tscaled1 反映最适温度时植物内在的生化作用对光合作用的限制, Tscaled2 反映环境温度从最适温度向高温或低温变化时植物光能利用率的变化[33]。在 TEM (terrestrial ecosystem model)中, 同样基于植被生长的最高温(40ºC)、最低温(0ºC)和最适温度(21ºC)评估环境温度对植被的影响[36]; MODIS 使用最低温反映温度条件对植被生理过程的影响, 其参数随植被类型改变[35](表 3); C-Fix 模型中, 通过一系列参数及归一化方式来量化温度对植物光合作用的影响, 其中 Cl, ΔHa,p, ΔHd,p, Rg 和 ΔS 分别为 21.77, 52.75kJ/mol, 221kJ/mol 和 704.98J/(K∙mol)[34] (表2)。
1.3.2模型参数率定与验证
本文模型中, FPAR, Ws 和 Ts 不同算法中的参数均来自已有的研究。率定参数时, 以 2010 年的FLUXCOM 数据为基准训练集, 使用最小二乘法, 针对不同植被类型和纬度带(从 80°N 到 60°S, 每20°划分为一个纬度带)以及每一种模型结构组合对εmax 进行参数率定:
GPPi,c=a+![]() +e , (1)
+e , (1)
xi,c=Wsi,c×Tsi,c×APARi,c , (2)
表3 WsVPD和TsMODIS模型参数
Table 3 Parameters for WsVPD and TsMODIS
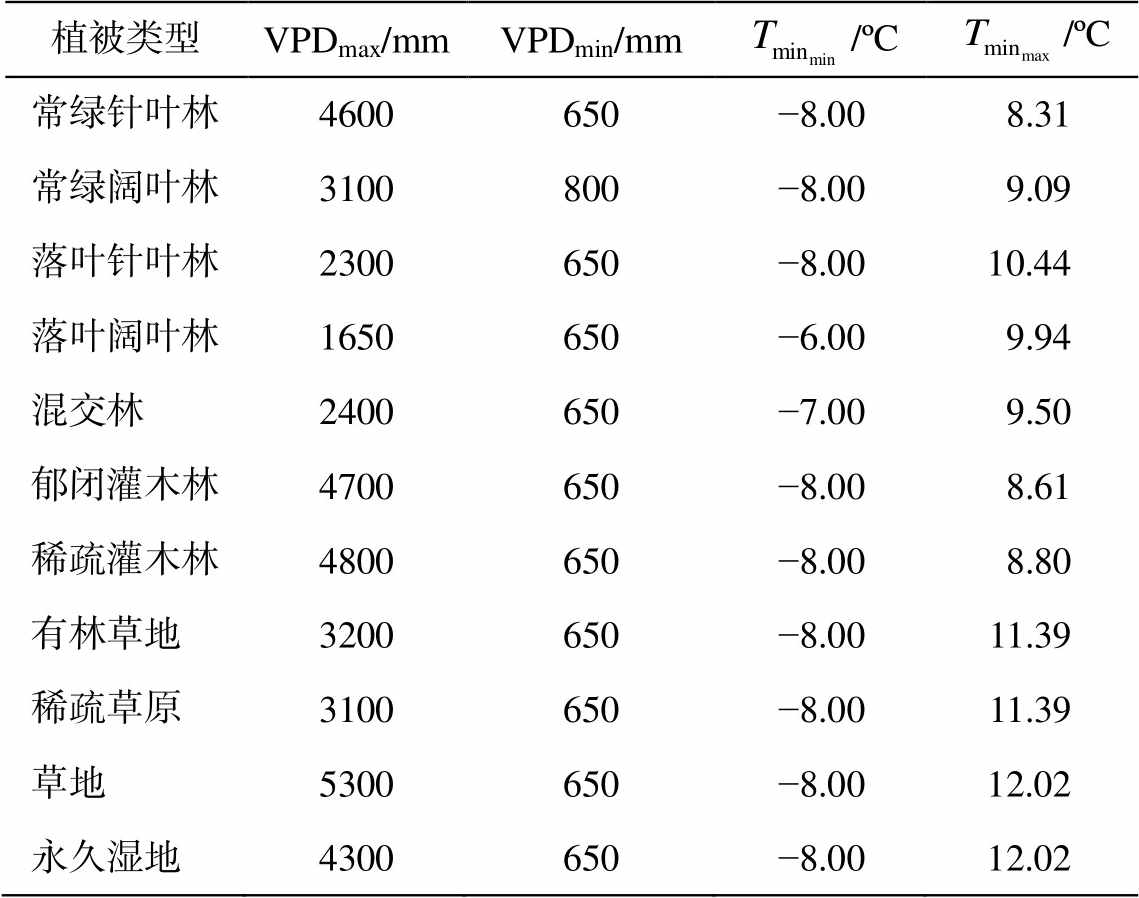
植被类型VPDmax/mmVPDmin/mm/ºC /ºC 常绿针叶林4600650−8.008.31 常绿阔叶林3100800−8.009.09 落叶针叶林2300650−8.0010.44 落叶阔叶林1650650−6.009.94 混交林2400650−7.009.50 郁闭灌木林4700650−8.008.61 稀疏灌木林4800650−8.008.80 有林草地3200650−8.0011.39 稀疏草原3100650−8.0011.39 草地5300650−8.0012.02 永久湿地4300650−8.0012.02
其中, i 表示每个网格, j 代表该网格的主要植被类型, k 代表该网格所属的纬度带, c代表模型结构, e是误差项。
我们使用均方根误差(RMSE)和皮尔逊相关系数(r2)评估模型结果与基准数据之间的一致性。此外, 在空间和时间维度上比较模型结果与基准数据, 验证其时空分布的一致性。
1.3.3不确定性模拟与分析
本研究将 GPP 模型模拟的不确定性分为两大类: 来源于模型结构的不确定性及来源于驱动数据的不确定性。前者通过多算法集成模型中所有模型结构的组合进行定量评估; 后者则根据不同驱动数据自身的不确定性(标准差 σ), 取±σ, ±0.5σ 及原值 5个梯度, 输入多种模型结构进行模拟运算来进行定量评估。共进行 7500 次模拟(3×4×5×5×5×5), 分别对应 3 种 FPAR 算法、4 种 Ts 算法、5 种 Ws 算法以及辐射数据、水分数据、温度数据的各 5 个梯度取值。
对于温度和辐射这类在再分析数据集中均有收录的指标, 结合 MERRA-2 和 ERA5 数据集获取其均值与标准差; 对于 ET, PET 和土壤湿度等仅在个别数据集中有收录或不同数据集中口径不一致的数据, 使用文献结果(表 4)。
GPP 结果的相对不确定性(relative uncertainty, RU)定义为标准差占均值的百分比[43–44]:
RU=![]() ×100%。 (3)
×100%。 (3)
根据不确定性模拟结果, 使用方差分析方法, 解析不同因子对模拟结果不确定性的贡献。将结果总方差拆分为各因子贡献、各因子交互作用贡献以及随机误差贡献, 其平方和分解公式如下:
ST=SA+SB+SA×B+Se 。 (4)
表4 驱动数据不确定性
Table 4 Relative uncertainties of model drivers
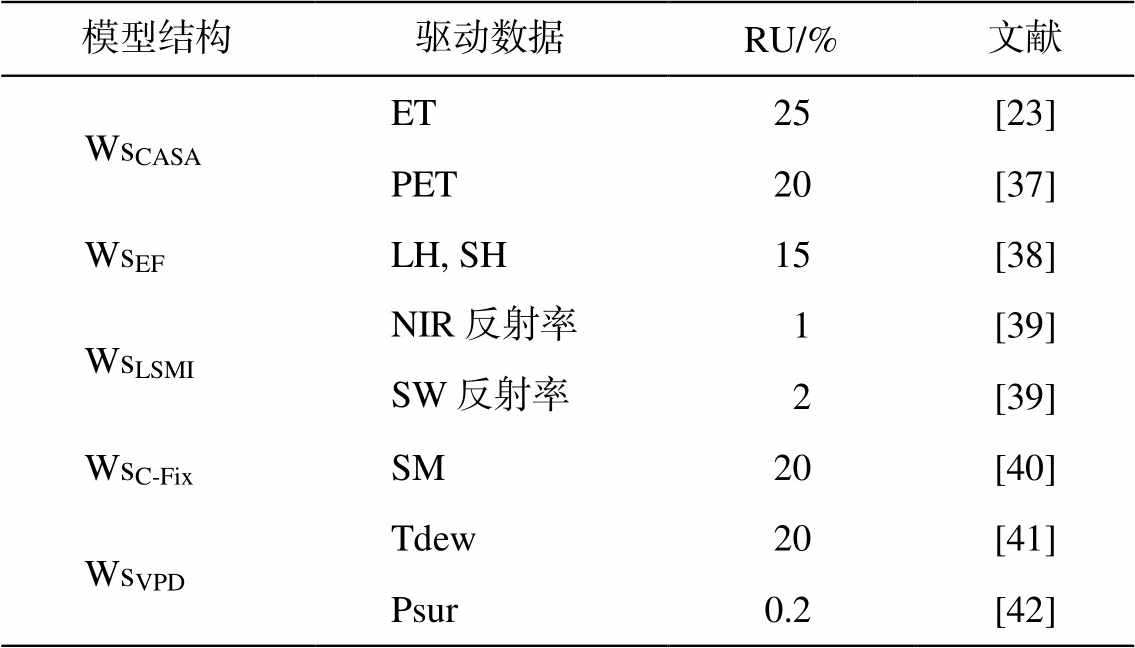
模型结构驱动数据RU/%文献 WsCASAET25[23] PET20[37] WsEFLH, SH15[38] WsLSMINIR反射率1[39] SW反射率2[39] WsC-FixSM20[40] WsVPDTdew20[41] Psur0.2[42]
在分析中, 引入相对贡献概念, A因子的相对贡献即该因子贡献的方差占总方差的比例(SA/ST)。
使用集成模型模拟 2010—2013 年全球 GPP, 结果与 FLUXCOM 的一致性较高。FPAREVI, WsVPD 和TsTEM 模型结构表现最优, r2 达到 0.95, RMSE 为26.18gC/(m2·月)。FPARNDVI, WsC-Fix 和 TsC-Fix 模型结构表现相对稍差, 但 r2 仍有 0.89, RMSE 为 38.25gC/(m2·月)。多模型模拟均值与 FLUXCOM 的相关系数达 0.97, RMSE 为 24.36 gC/(m2·月), 且与任一单个模型结构组合结果相比, GPP 均值与基准数据的一致性都更高, 误差更小。多模型平均的年总GPP 与 FLUXCOM 结果集中分布于 1:1 线, 一致性较好(图 3(a))。多模型平均全球 GPP 与 FLUXCOM的年内变化趋势表现一致, 仅在冬季月份略偏小(图 3(b))。按纬度和经度统计, 多模型平均年 GPP与 FLUXCOM 在纬度(图 3(c))和经度(图 3(d))上吻合度高。尤其在生产力最高的热带地区, 集成模型表现优异, 与 FLUXCOM 高度吻合(图 3(c))。总体来看, 本研究开发的 GPP 集成模型在模拟结果准确度和时空分布一致性方面有优秀的表现, 在全球 GPP模拟及不确定性研究中具有可靠性。
通过对比 2013 年全球 GPP 模拟结果及其不确定性的空间分布, 发现 GPP 高值区集中于赤道附近热带雨林集中的地区, 如亚马逊雨林、中美洲、非洲中西部和印度尼西亚, 全年累积 GPP 高达 2500 gC/m2, 最高超过 3000gC/m2(图 4(a)), 相对不确定性较小, 处于 10%水平(图 4(b)); 非洲中部、美国东部、南美洲中部、南亚、东南亚和中国东南部的生产力水平次之, 全年 GPP 达 1500~2000gC/m2, 其相对不确定性处于 10%~20%水平; 东北亚、西伯利亚以及欧洲全年 GPP 为 500~1000gC/m2, 相对不确定性约为 20%; 其他区域的初级生产力处于较低水平, 全年总生产力低于 500gC/m2, 其中澳大利亚中部及西海岸、青藏高原、中亚、南非、美国西部和南美洲西海岸 GPP 模拟结果的相对不确定性较高, 在30%以上。
全球年总 GPP 达到 118.11 (±7.37) PgC, RU 为6.24%, PAR、水分相关数据和 Ws 是全球 GPP 模拟不确定性的主要来源, 分别贡献 41.73%, 26.79%和23.82%, 合计超过 92% (图 5)。RECCAP 各区域中, 南美年总 GPP 最高, 达 29.97 (±1.97) PgC, 虽然绝对不确定性较高, 但其 RU 处于较低水平, 仅为6.58%。其中, PAR、水分相关数据以及 Ws 是不确定性的主要贡献者, 分别贡献 37.86%, 31.35%和22.77%。非洲年总 GPP 次于南美, 达 24.46 (±2.19) PgC, 其 RU 比南美高, 达 8.96%。其中, PAR 和水分数据是主导因素, 分别贡献 40.60%和 35.03%, Ws也有一定比例(18.25%)的贡献。北美年总 GPP 也处于较高水平, 仅次于上述两个区域, 达 12.65 (±1.07) PgC, RU 为 8.47%。其中, Ws、PAR、水分数据和温度数据均有可观的贡献, 分别为 23.39%, 22.21%, 21.75%和 17.31%。东南亚年总 GPP 达 10.92 (±0.62)PgC, RU 在所有区域中最低, 仅为 5.68%。其中, PAR是绝对主导因素, 贡献 63.00%, 水分数据和 FPAR分别贡献 19.93%和 8.00%。俄罗斯年总 GPP 达 8.14(±0.59) PgC, RU 为 7.22%, PAR、水分数据、Ts 和Ws 是其不确定性的主要来源, 分别贡献 33.20%, 17.60%, 15.56%和 10.89%。东亚、欧洲和南亚区域的 GPP 相对较低, 分别为 6.84 (±0.45), 4.42 (±0.29)和 3.92 (±0.35) PgC, 其 RU 为 6.52%, 6.47%和 9.12%, PAR、水分数据和 Ws 是不确定性主导因素, 其中PAR 最为重要, 在各区域的贡献均超过 30%。澳大利亚区域年总 GPP 仅为 3.61(±0.55) PgC, 相对不确定性却高达 15.2%, 居各区域之首, 其中 Ws 贡献达64.43%, 是导致该区域 GPP 模拟不确定性较高的主要原因。这是由于该区域水分条件较差, 在干旱区域, 不同 Ws 结果差异大, 导致 Ws 相对贡献高, GPP 模拟的不确定性较大[22,24,44]。
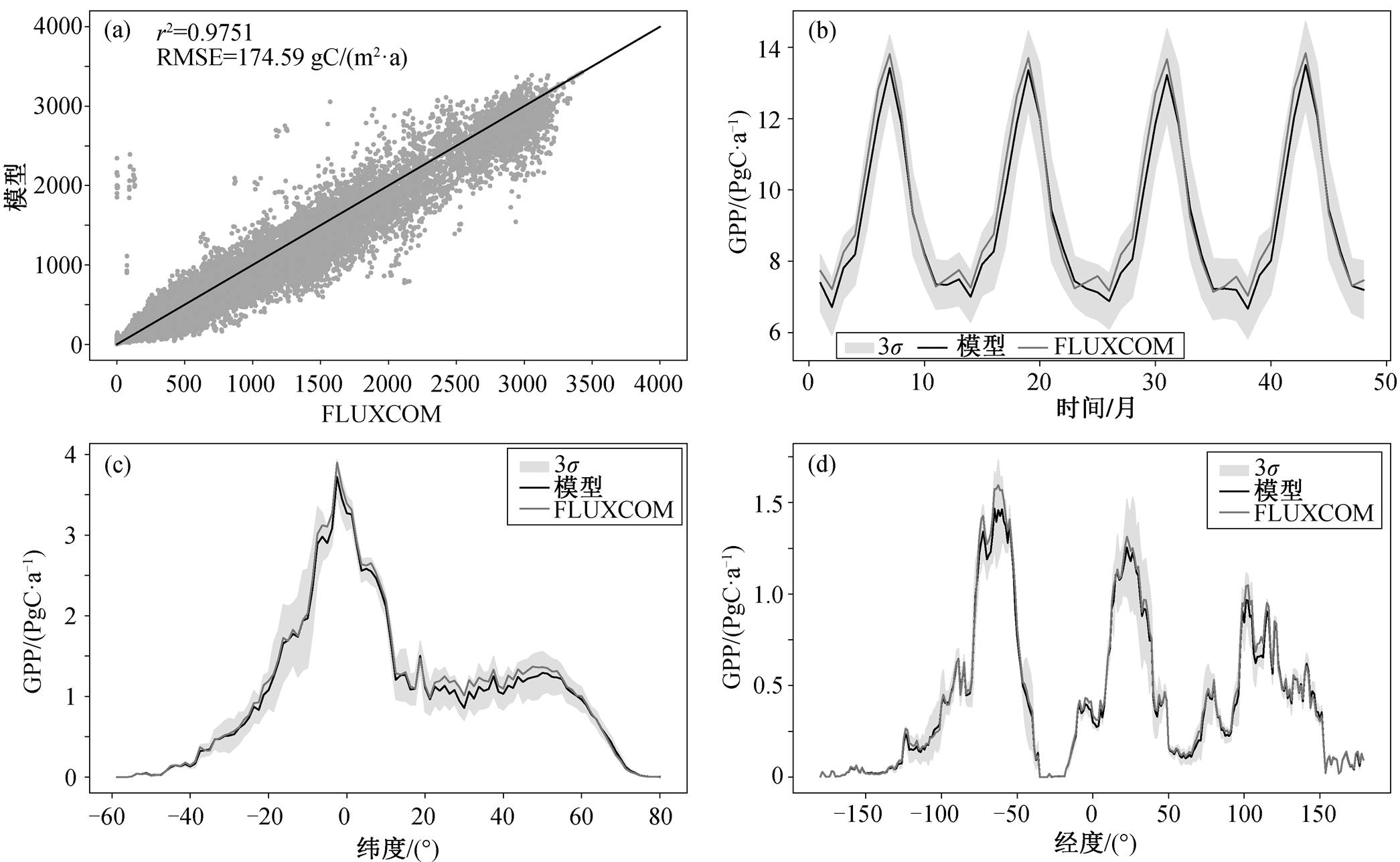
图3 2010—2013年模型结果与FLUXCOM验证对比
Fig. 3 Validation of model results against FLUXCOM in 2010–2013
GPP 模拟的不确定性随环境条件的不同而变化, 影响光合作用的关键环境条件是辐射、温度和水分。为深入理解其不确定性, 本研究进一步探讨不同土壤水分、温度和 PAR 条件下 GPP 模拟的情况及其不确定性来源, 结果如图 6 所示。
在年均土壤湿度较低的干旱条件(<220mm)下, RU 最高, 达 30%, 不同 Ws 结果的差异较大, 对不确定性的贡献超过 70%, FPAR 也有相当比例(10%)的贡献。这就解释了澳大利亚区域 RU 较高且由Ws 主导的现象。随着土壤湿度增加, GPP 增加, RU也降至最低水平(约 6%), Ws 和 FPAR 的贡献减少, PAR 和水分数据的贡献增加。在生产力最高的最佳水分(280~480mm)条件下, PAR 和水分数据是不确定性的主要来源, 贡献比例超过 70%。随着土壤含水量由最佳水平向更高水平变化, GPP 急剧下降, RU 也略有上升。Ws 贡献增加, 成为不确定性的主要贡献者, PAR 贡献略有减少, 但仍接近 30%。
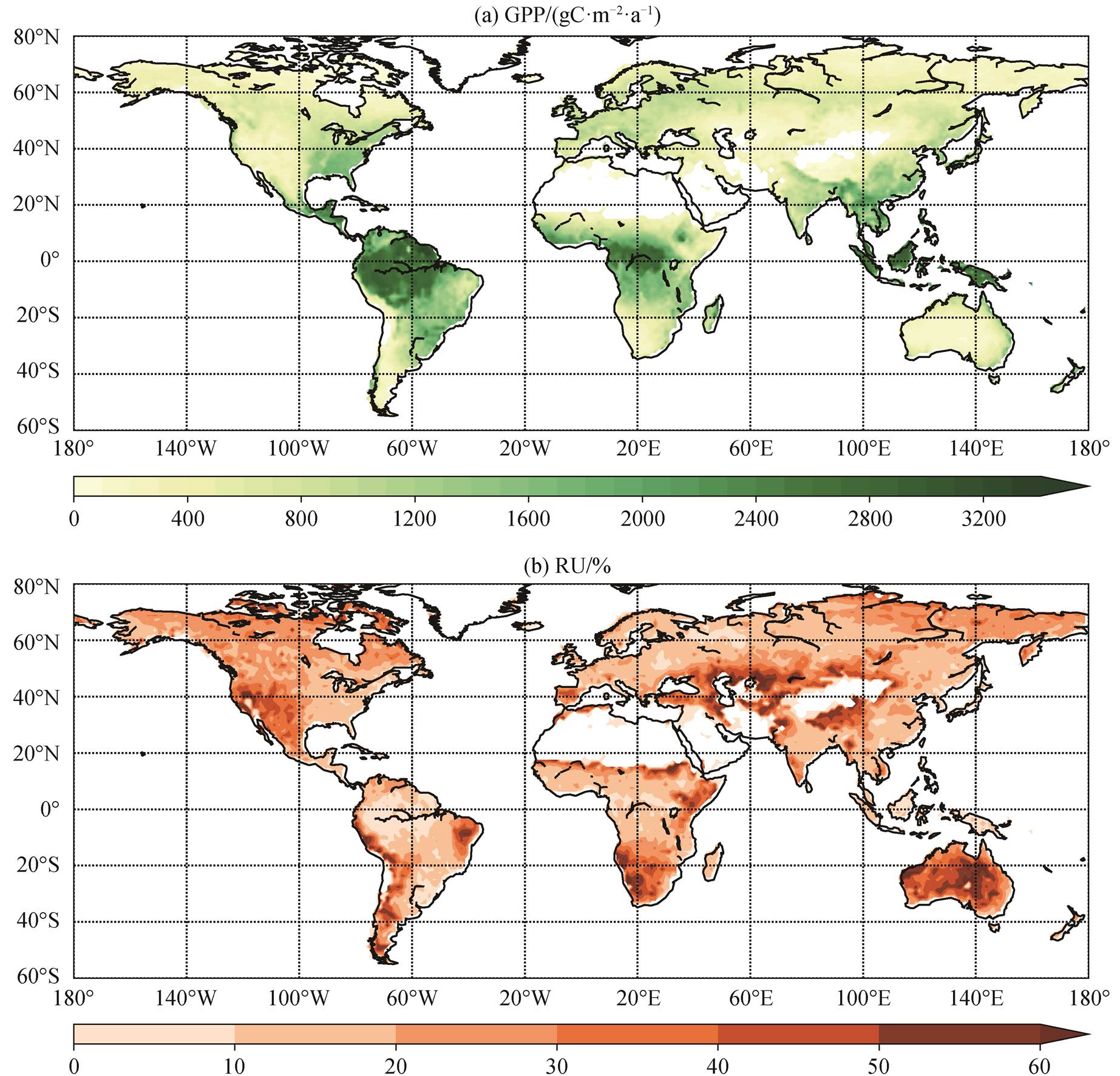
图4 全球GPP (2013年)及其不确定性分布
Fig. 4 Global distribution of GPP (2013) and its relative uncertainty
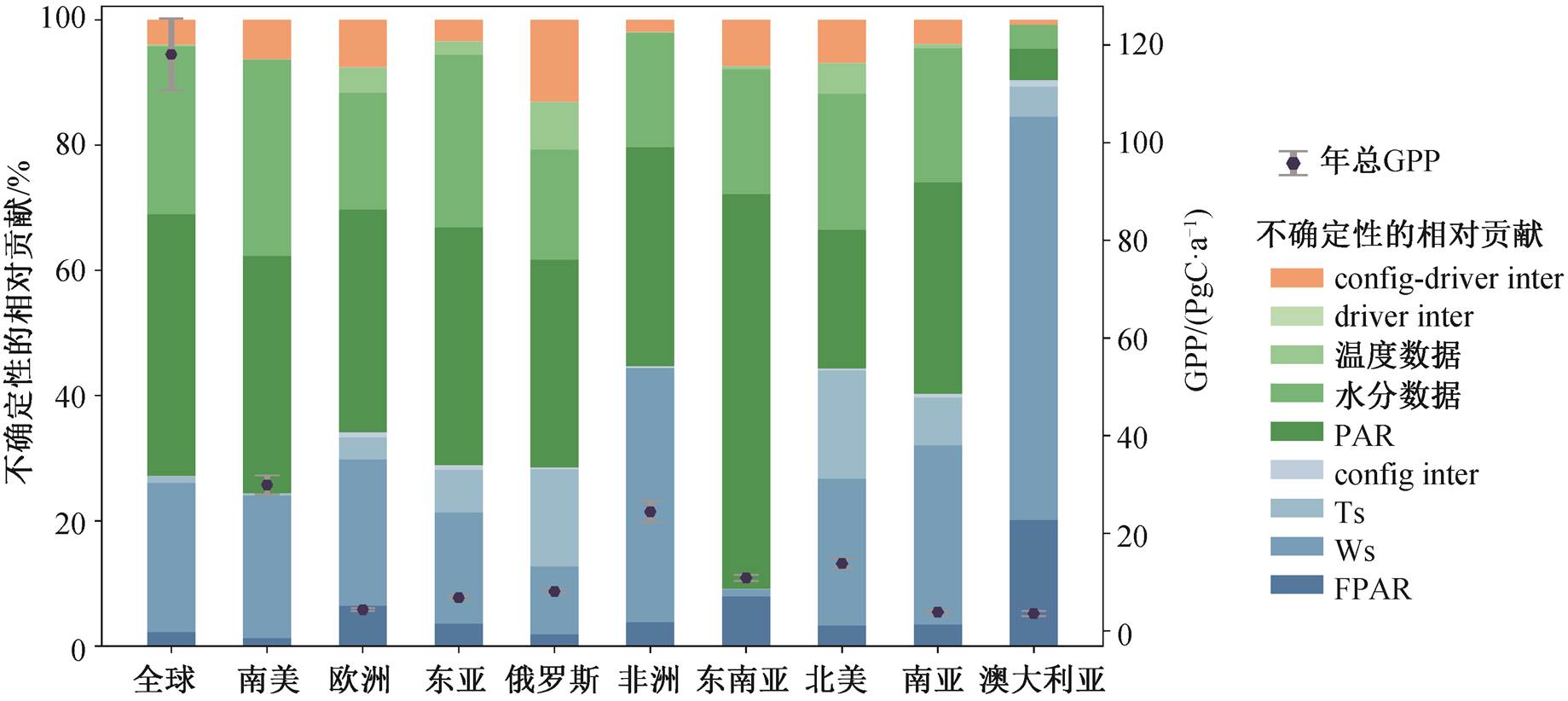
config inter为模型结构间交互作用, driver inter为驱动数据间交互作用, config-driver inter为模型结构–驱动数据交互作用, 下同
图5 全球及区域GPP模拟的不确定性来源
Fig. 5 Uncertainty sources of global and regional GPP estimates
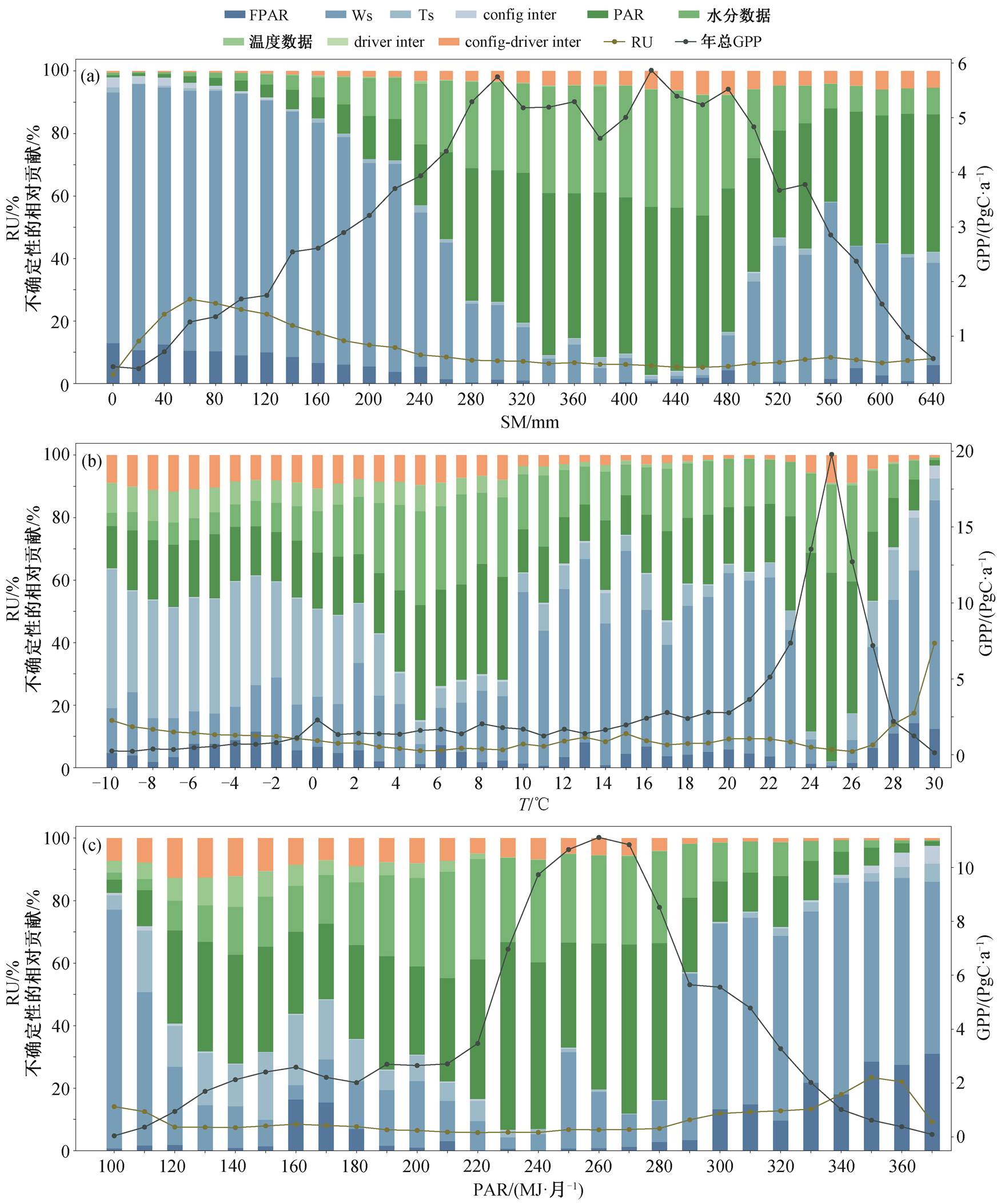
(a)年均土壤湿度, (b)年均温, (c)年均PAR
图6 不同环境条件下GPP,RU及不确定性来源
Fig. 6 GPP, RU and sources of uncertainties under different environmental conditions
在年均温极低(<0ºC)条件下, 生产力水平较低, RU 处于中等水平(10%左右)。不同 Ts 的结果差异较大, 对不确定性的贡献超过 40%, 解释了高纬度低温地区 Ts 的贡献相对较大的现象。在中等温度(0~20ºC)条件下, GPP 和 RU 都处于较低水平, Ws 是不确定性的主要来源, 其贡献超过 40%。在植被生长的最适温度(23~27ºC)下, 生产力水平较高, RU 处于最低水平(约 6%), PAR 是不确定性的主要来源, 贡献超过 50%。在高温条件下, 生产力极低, RU 处于最高水平(超过 30%), 不确定性主要由 Ws 贡献。
在辐射条件较差的地区, 生产力水平较低, RU相对较高(约 10%), Ws 和 Ts 是不确定性的主要来源。与有适宜水分和温度条件的情况类似, 在适宜植被生长的光照条件下, GPP 较高, RU 处于低水平(6%)。PAR 和水分数据是不确定性的主要来源, Ws也有近 20%的贡献。在光照极强的区域, 生产力水平随着 PAR 的增加而降低, RU 也随之上升, 最高达到 20%。FPAR 和 Ws 是不确定性的主要来源, 不确定性贡献超过 80%。
在大多数区域, 特别是生产力水平高的区域, PAR、水分数据和 Ws 是不确定性的主要来源。PAR是光合作用过程的主导因素, 也是最重要的模型驱动数据[45–46]。本研究的结果表明, PAR 是影响 GPP模拟不确定性的主导因素, 进一步显示 PAR 在 GPP模拟中的重要性。在诸如澳大利亚的干旱区域, Ws是不确定性的主要贡献者, 不同 Ws 算法的差异则导致较高的 RU。已有研究揭示了类似的现象, Cai等[17]在全球 GPP 研究中发现, 不同 Ws 算法的产出结果有较大的差异; Jiang 等[22]在站点尺度 GPP 模拟中发现, Ws 算法是 GPP 模拟重要的不确定性来源, 在干旱时期影响尤甚。在低温区域, 与已有的研究[17,22,47]结论相似, 不同 Ts 的产出结果差异较大, Ts 对不确定性的相对贡献也较为可观。
因此, 为减少 GPP 模拟的不确定性, PAR 和水分数据的优化极为重要。广泛使用的再分析 PAR 数据结合了站点测量数据、模型计算结果及全球大气条件的动态监测结果[48], 其不确定性主要来自数据同化过程中使用的辅助数据及动态模型过程[49]。多种水分数据用于衡量水分限制, 包括使用遥感数据计算的 LSWI 以及通过模型模拟的蒸散发和热通量等, 遥感数据的相对不确定性较小, 其他水分数据的不确定性普遍较高(表 4)。优化数据同化过程及水分相关指标模拟方法, 是降低 PAR 和水分相关数据不确定性, 继而降低 GPP 模拟不确定性的重要方向。此外, 开发新的基于可观测指标或遥感数据的水分限制因子算法, 也是控制 GPP 模拟不确定性的可行方法。
本研究整合已有的 FPAR、Ws 和 Ts 模型结构, 结合多个数据源, 构建基于光能利用率的 GPP 集成模型, 定量分析全球及各区域 GPP 模拟的不确定性, 解析模型结构和驱动数据的相对贡献, 并探讨不同环境条件对 GPP 模拟不确定性的影响, 得到如下结论。
1)集成模型与 FLUXCOM 结果具有较强的时空一致性, r2 达 0.97 , RMSE 为 24.36gC/(m2·月), 且集成模型的表现优于任何单一模型结构配置, 在 GPP研究中具有可靠性。
2)光合有效辐射、水分相关数据及 Ws 是 GPP模拟中不确定性的主要来源, 其相对贡献分别为41.73%, 26.79%和 23.82%。控制气象再分析辐射数据及水分相关数据的不确定性, 对 GPP 的准确模拟具有重要意义。
3)GPP 模拟的不确定性构成具有明显的区域差异, 干旱区域水分限制因子的相对贡献超过 80%, 低温区域温度限制因子的相对贡献超过 40%。因此, 在模拟区域 GPP 时, 优化极端环境条件(干旱、低温)下的环境限制因子至关重要。
参考文献
[1] Beer C, Reichstein M, Tomelleri E, et al. Terrestrial gross carbon dioxide uptake: global distribution and covariation with climate. Science, 2010, 329: 834–838
[2] Canadell J G, Kirschbaum M U F, Kurz W A, et al. Factoring out natural and indirect human effects on terrestrial carbon sources and sinks. Environmental Science & Policy, 2007, 10(4): 370–384
[3] Ballantyne A P, Alden C B, Miller J B, et al. Increase in observed net carbon dioxide uptake by land and oceans during the past 50 years. Nature, 2012, 488: 70–81
[4] Speckman H N, Frank J M, Bradford J B, et al. Forest ecosystem respiration estimated from eddy covariance and chamber measurements under high turbulence and substantial tree mortality from bark beetles. Global Change Biology, 2015, 21(2): 708–721
[5] Zhang Y, Xiao X M, Wu X C, et al. Data descriptor: a global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Scientific Data, 2017, 4: 170165
[6] Farquhar G D, Caemmerer S V, Berry J A. A biochemical-model of photosynthetic CO2 assimila-tion in leaves of C-3 species. Planta, 1980, 149(1): 78–90
[7] De Pury D G G, Farquhar G D. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell and Environ-ment, 1997, 20(5): 537–557
[8] Zhang Y L, Song C H, Sun G, et al. Development of a coupled carbon and water model for estimating global gross primary productivity and evapotranspiration based on eddy flux and remote sensing data. Agri-cultural and Forest Meteorology, 2016, 223: 116–131
[9] Running S W, Nemani R R, Heinsch F A, et al. A continuous satellite-derived measure of global terres-trial primary production. Bioscience, 2004, 54(6): 547–560
[10] Tramontana G, Jung M, Schwalm C R, et al. Predic-ting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeos-ciences, 2016, 13(14): 4291–4313
[11] Monteith J L. Solar-radiation and productivity in tro-pical ecosystems. Journal of Applied Ecology, 1972, 9(3): 747–766
[12] Monteith J L. Climate and the efficiency of crop production in Britain. Philosophical Transactions of the Royal Society of London Series B — Biological Sciences, 1977, 281: 277–294
[13] Xiao J F, Davis K J, Urban N M, et al. Uncertainty in model parameters and regional carbon fluxes: a model-data fusion approach. Agricultural and Forest Meteorology, 2014, 189: 175–186
[14] Keenan T F, Carbone M S, Reichstein M, et al. The model-data fusion pitfall: assuming certainty in an uncertain world. Oecologia, 2011, 167(3): 587–597
[15] Ruppert J C, Linstadter A. Convergence between ANPP estimation methods in grasslands — a practical solution to the comparability dilemma. Ecological In-dicators, 2014, 36: 524–531
[16] Fensholt R, Proud S R. Evaluation of earth obser-vation based global long term vegetation trends — comparing GIMMS and MODIS global NDVI time series. Remote Sensing of Environment, 2012, 119: 131–147
[17] Cai W W, Yuan W P, Liang S L, et al. Large dif-ferences in terrestrial vegetation production derived from satellite-based light use efficiency models. Re-mote Sensing, 2014, 6(9): 8945–8965
[18] Zhang L X, Zhou D C, Fan J W, et al. Comparison of four light use efficiency models for estimating ter-restrial gross primary production. Ecological Model-ling, 2015, 300: 30–39
[19] Yuan W P, Cai W W, Nguy-Robertson A L, et al. Uncertainty in simulating gross primary production of cropland ecosystem from satellite-based models. Ag-ricultural and Forest Meteorology, 2015, 207: 48–57
[20] He H L, Liu M, Xiao X M, et al. Large-scale estimation and uncertainty analysis of gross primary production in Tibetan alpine grasslands. Journal of Geophysical Research-Biogeosciences, 2014, 119(3): 466–486
[21] Wagle P, Gowda P H, Xiao X M, et al. Parameterizing ecosystem light use efficiency and water use effi-ciency to estimate maize gross primary production and evapotranspiration using MODIS EVI. Agricul-tural and Forest Meteorology, 2016, 222: 87–97
[22] Jiang S Z, Zhao L, Liang C, et al. Comparison of satellite-based models for estimating gross primary productivity in agroecosystems. Agricultural and Fo-rest Meteorology, 2021, 297: 108253
[23] Lian J J, Huang M B. Comparison of three remote sensing based models to estimate evapotranspiration in an oasis-desert region. Agricultural Water Manage-ment, 2016, 165: 153–162
[24] Yuan W P, Cai W W, Xia J Z, et al. Global comparison of light use efficiency models for simulating terres-trial vegetation gross primary production based on the La Thuile database. Agricultural and Forest Meteo-rology, 2014, 192: 108–120
[25] Ciais P, Yao Y, Gasser T, et al. Empirical estimates of regional carbon budgets imply reduced global soil heterotrophic respiration. National Science Review, 2020, 8(2): nwaa145
[26] Pinzon J E, Tucker C J. A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sensing, 2014, 6(8): 6929–6960
[27] Xiao Z Q, Liang S L, Sun R, et al. Estimating the fraction of absorbed photosynthetically active radia-tion from the MODIS data based GLASS leaf area index product. Remote Sensing of Environment, 2015, 171: 105–117
[28] Senay G B. Satellite psychrometric formulation of the operational simplified surface energy balance (SSEBop) model for quantifying and mapping evapotranspira-tion. Applied Engineering in Agriculture, 2018, 34(3): 555–566
[29] Van Den Dool H, Huang J, Fan Y. Performance and analydsis of the constructed analogue method applied to US soil moisture over 1981–2001. Journal of Geo-physical Research — Atmospheres, 2003, 108(D16): doi: 10.1029/2002JD003114
[30] Jung M, Schwalm C, Migliavacca M, et al. Scaling carbon fluxes from eddy covariance sites to globe: synthesis and evaluation of the FLUXCOM approach. Biogeosciences, 2020, 17(5): 1343–1365
[31] Yuan W P, Liu S, Zhou G S, et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agricultural and Forest Meteorology, 2007, 143(3/4): 189–207
[32] Xiao X M, Zhang Q Y, Braswell B, et al. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sensing of Environment, 2004, 91(2): 256–270
[33] Potter C S, Randerson J T, Field C B, et al. Terrestrial ecosystem production — a process model-based on global satellite and surface data. Global Biogeoche-mical Cycles, 1993, 7(4): 811–841
[34] Veroustraete F, Sabbe H, Eerens H. Estimation of carbon mass fluxes over Europe using the C-Fix mo-del and Euroflux data. Remote Sensing of Environ-ment, 2002, 83(3): 376–399
[35] Running S, Zhao M. User’s guide daily GPP and annual NPP (MOD17A2/A3) products NASA earth observing system MODIS land algorithm [EB/OL]. (2015–10–07) [2020–12–21]. https://lpdaac.usgs.gov/ documents/495/MOD17_User_Guide_V6.pdf
[36] Raich J W, Rastetter E B, Melillo J M, et al. Potential net primary productivity in South-America: applica-tion of a global-model. Ecological Applications, 1991, 1(4): 399–429
[37] Nikam B R, Kumar P, Garg V, et al. Comparative evaluation of different potential evapotranspiration estimation approaches. International Journal of Re-search in Engineering and Technology, 2014, 3(6): 544–552
[38] Draper C S, Reichle R H, Koster R D. Assessment of MERRA-2 land surface energy flux estimates. Journal of Climate, 2018, 31(2): 671–691
[39] Strahler A H, Muller J, Lucht W, et al. MODIS BRDF/albedo product: algorithm theoretical basis document version 5.0 [EB/OL]. (1999–04) [2020–01– 08]. https://lpdaac.usgs.gov/documents/97/MCD43_ ATBD.pdf
[40] Xia Y L, Ek M B, Wu Y H, et al. Comparison of NLDAS-2 simulated and NASMD observed daily soil moisture. Part I: comparison and analysis. Journal of Hydrometeorology, 2015, 16(5): 1962–1980
[41] Paredes P, Martins D S, Pereira L S, et al. Accuracy of daily estimation of grass reference evapotranspira-tion using ERA-Interim reanalysis products with as-sessment of alternative bias correction schemes. Ag-ricultural Water Management, 2018, 210: 340–353
[42] Ukhurebor K E, Azi S O, Aigbe U O, et al. Analyzing the uncertainties between reanalysis meteorological data and ground measured meteorological data. Mea-surement, 2020, 165: 108110
[43] Jia W X, Liu M, Wang D D, et al. Uncertainty in simulating regional gross primary productivity from satellite based models over northern China grassland. Ecological Indicators, 2018, 88: 134–143
[44] Jia W X, Liu M, Yang Y H, et al. Estimation and uncertainty analyses of grassland biomass in Northern China: comparison of multiple remote sensing data sources and modeling approaches. Ecological Indica-tors, 2016, 60: 1031–1040
[45] Cai W W, Yuan W P, Liang S L, et al. Improved es-timations of gross primary production using satellite-derived photosynthetically active radiation. Journal of Geophysical Research — Biogeosciences, 2014, 119 (1): 110–123
[46] Mercado L M, Bellouin N, Sitch S, et al. Impact of changes in diffuse radiation on the global land carbon sink. Nature, 2009, 458: 1014–1087
[47] Baldocchi D. Breathing of the terrestrial biosphere: lessons learned from a global network of carbon dioxide flux measurement systems. Australian Journal of Botany, 2008, 56(1): 1–26
[48] Betts A K, Zhao M, Dirmeyer P A, et al. Comparison of ERA40 and NCEP/DOE near-surface data sets with other ISLSCP-II data sets. Journal of Geophysical Research — Atmospheres, 2006, 111(D22): doi: 10. 1029/2006JD007174
[49] Zhang X T, Liang S L, Wang G X, et al. Evaluation of the reanalysis surface incident shortwave radiation products from NCEP, ECMWF, GSFC, and JMA using satellite and surface observations. Remote Sensing, 2016, 8(3): 225
Uncertainty Analysis of Gross Primary Productivity Estimates Based on a Light Use Efficiency Meta-Model
Abstract To investigate global and regional gross primary productivity (GPP) and its sources of uncertainties, widely used model structures of light use efficiency models are integrated to build a meta-model.Meteorological reanalysis data and remote sensing data are combined to estimate GPP, and a systematical and quantitative uncertainty analysis is conducted based on the ANOVA approach. Results show that: 1) the meta-model results correspond well with the upscaling of eddy-covariance measurements (FLUXCOM) GPP with a Pearson correlation coefficient of 0.97 and root mean square error of 24.36 gC/(m2·month) and outperforms any single combination of model structure. 2) Photosynthetically active radiation (PAR), water-related data and water regulation scalar (Ws) are the three main sources of uncertainties for global GPP estimates, contributing 41.73%, 26.79% and 23.82% respectively to total variance. 3) Sources of uncertainties of regional GPP depend on environmental conditions. For arid areas, Ws is the dominant contributor (over 80%). In cold areas, temperature regulation scalar (Ts) introduces over 40% of uncertainty. The findings not only highlight the necessity to reduce uncertainty of PAR and water-related data to reduce uncertainty in global and regional GPP estimates, but also point out the importance of improving performances of Ws and Ts algorithms under extreme environmental conditions.
Key words GPP; light use efficiency model; uncertainty; meta-model; relative contribution
doi: 10.13209/j.0479-8023.2022.003
国家自然科学基金(41771495)资助
收稿日期: 2021-03-31;
修回日期: 2021-04-23