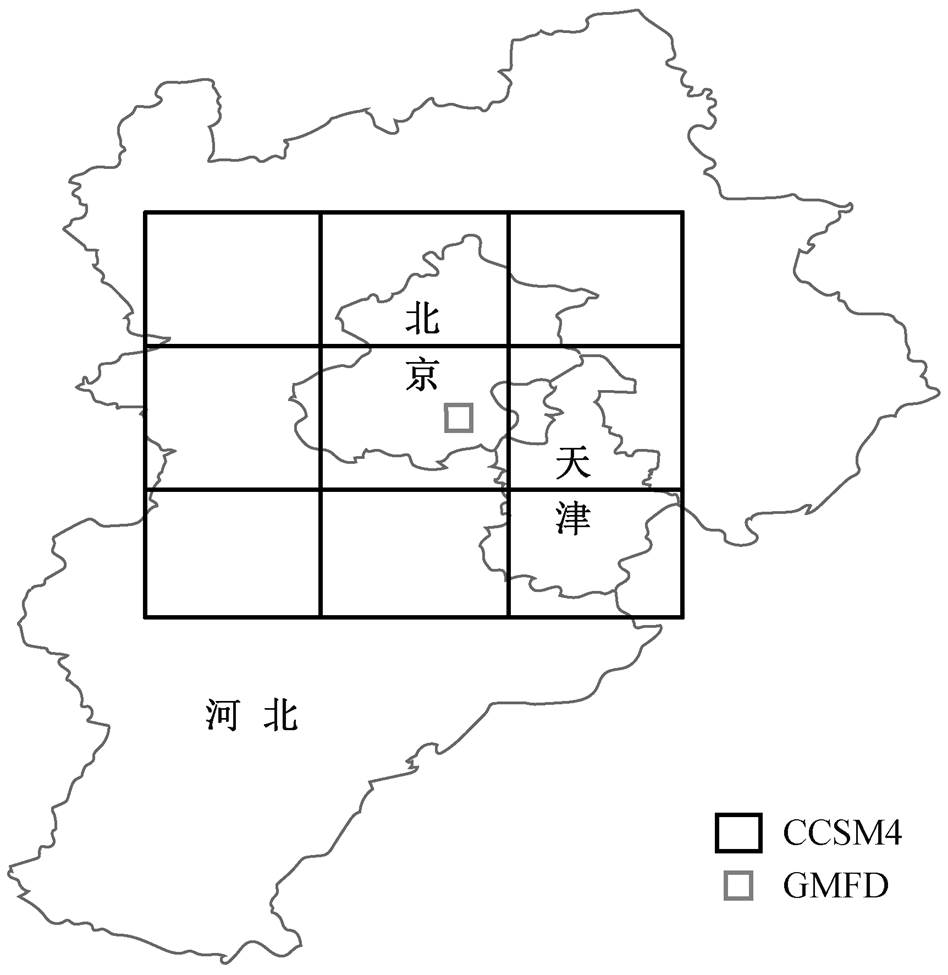
图1 全球气候模式 CCSM4 与格点化观测数据 GMFD 的分辨率对比示例
Fig. 1 Comparision of resolution between general circulation model CCSM4 and gridded observation data GMFD
摘要 针对中国地区的气候预估问题, 开发一套高时空分辨率(空间分辨率: 0.25°;时间分辨率: 逐日)的统计降尺度气候变化数据集。降尺度气候预估结果表明: 1)在传统降尺度方法的基础上引入人工神经网络算法, 开发高时空分辨率的降尺度气候数据, 技术上简便可行; 2)将这种新方法应用到模式的历史模拟数据上, 温度和降水的气候态偏差显著减小, 其中部分地区的温度偏差可从 5°C 减至 1°C 以下, 降水偏差可从 5mm 减至0.5mm 以内; 3)将这种新方法应用到模式的未来情景数据上, 既能保留气候模式原有的对长期趋势的估计, 又可进一步微调幅度和空间分布, 其中在 RCP8.5 情景中, 到本世纪末, 中国各地温度普遍升高 3～4°C, 降水总量变化不大, 但有北方增多、南方减少的微弱趋势。所提出的基于人工神经网络的统计降尺度方法对温度变量具有一定的普适性, 所开发的高分辨率气候变化数据集可以在其他全球变化相关学科的研究中使用。
关键词 统计降尺度; 人工神经网络; 气候变化; 气候预估
气候变化预估是当前国际社会普遍关注的重要科学问题之一。联合国政府间气候变化委员会(In-tergovermental Panel on Climate Change, IPCC)领导开展的基于 CMIP5 模式(coupled model intercompa-rison project)的气候预估, 是现阶段对未来全球变暖趋势和幅度问题的权威解答。CMIP5 包含近 50个 GCM (general circulation model), 其中分辨率最低为 3.9° (经度) ×3.9°(纬度)[1], 最高可达 0.2° (经度)×0.2° (纬度)[2], 绝大部分模式的分辨率为 2°(经度)× 1.9°(纬度)(约等于 200km)[3‒4]。CMIP5 模式的预估结果为研究者提供了可靠的全球大尺度数据, 但对于 200km 尺度以下的科学研究, 特别是水文和陆面过程等相关问题, CMIP5 模式预估结果的精度不够。当前, 水文、农业、环境政策和气候变化等领域的学者对高分辨率数据的需求日益增加[5‒7], 开发具有高时空分辨率特性并总体上保持 CMIP5 现有预估结果趋势和幅度的数据集显得十分必要。
20 世纪 90 年代以来, 科学家将上述问题总结为降尺度问题, 提出动力降尺度和统计降尺度两种解决方案。动力降尺度方法用 GCM 的输出驱动区域气候模式(regional climate model, RCM)来产生高分辨率的气候信息, 通常可以将分辨率从 GCM 水平提升至 RCM 水平, 目前为 20～60km[8]。统计降尺度方法则通过计算大尺度预报因子与高分辨率被预报量之间的统计关系进行降尺度, 通常包括天气模态或分型、天气发生器和回归模型[9] 3 类方法。动力降尺度方法完全基于 RCM, 包含完整的物理过程, 其结果可靠性高, 缺点是受限于 RCM 的区域选择, 只适用于区域性研究, 积分时间因需大量计算资源而受限, 通常只积分几年到十几年[8,10‒12]的短时切片。统计降尺度方法计算资源需求少且易于理解, 尤其适合大空间范围和长时间范围的降尺度问题, 缺点是需要从已有的高质量观测数据中发掘统计关系, 而发掘出的统计关系在未来的稳定性不明确[6]。近年来, 随着统计降尺度方法的不断改进, 准确性不断提高, 已经在气候预估领域得到广泛应用[5,7,9,13]。
Wilby 等[14]提出统计降尺度模型, 并对多伦多地区日降水和温度进行降尺度研究, 发现该方法无法解决降水问题。Tatsumi 等[15]使用 SDSM, 分析日本四国地区历史时段和未来时段最高温和最低温对云量变化的影响。Maurer 等[16]成功地证明使用偏差校正和重构模拟方法(bias correction and con-structed analogs, BCCA)对 NCEP/NCAR 再分析资料进行统计降尺度, 可以再现美国加利福尼亚州 11个观测站的日径流。Guo 等[17]探究统计降尺度模型(statistical downscaling model, SDSM)和自动降尺度模型(automated statistical downscaling model, ASD)对北京地区气候变量的降尺度效果, 发现两种方法对温度变量表现较佳, 而对降水变量表现较差, 且ASD 方法整体上略优于 SDSM 方法。Tang 等[8]对比统计降尺度和动力降尺度方法对中国地区温度和降水变量的降尺度效果, 发现统计降尺度方法更适用于对温度进行降尺度, 而两种方法对降水变量的降尺度效果均不理想。
近 10 年来人工神经网络(artificial neural net-work, ANN)技术的兴起, 为传统的基于回归模型的统计降尺度研究提供了新思路。ANN 通过引入隐藏层和误差梯度下降算法, 具有解析普遍意义上的预报因子与被预报量之间非线性关系的能力[18]。例如, Agrawal 等[19]使用卷积神经网络方法, 基于雷达数据预报美国地区的降水变量, 结果表明该方法可以获得较准确的降水量。Tabari 等[20]对比多层感知器神经网络和多元线性回归方法对干旱地区土壤日均温度的统计降尺度效果, 结果显示多层感知器神经网络方法优于多元回归方法。在尝试使用人工神经网络的统计降尺度方法方面, 目前对中国地区气候变化预估的研究依然稀缺。
基于上述背景, 本文旨在发掘人工神经网络在统计降尺度中的潜在价值, 并生成一套针对中国地区未来百年尺度和两种排放情景的高分辨率气候预估数据。
本文关注中国地区日尺度的 3 个核心气候变量: 日最低温(Tmin)、日最高温(Tmax)和日降水量(Pr)。中国地区是典型的季风型气候, 1 月 Tmin 最低, 7 月Tmax 最高且 Pr 最大。因此, 本文重点关注 1 月 Tmin, 7 月 Tmax 和 7 月 Pr 这 3 个变量, 所用数据来自模式数据和观测数据。
CMIP5 模式数据方面, 本文选用美国国家大气研究中心(National Center for Atmospheric Research, NCAR)的气候系统模式(community climate system model 4.0, CCSM4)中输出数据作为 ANN 的输入。CCSM4 是用于模拟地球气候系统的耦合气候模式, 其 4 个模式分量分别为大气、海洋、陆面和海冰, 由一个耦合器连接, 其中大气分量的分辨率为 1°× 1.25°[21], 在所有 CMIP5 模式中属于较高的分辨率。遵照 CMIP5 试验设计中的一般原则, CCSM4包含历史时段(1850—2005 年)和未来时段(2006—2100 年)的试验数据。对于未来时段, 本研究选择RCP2.6 和 RCP8.5 两种排放情景, 以便涵盖未来最乐观到最悲观的预估范围。
观测数据方面, 选用全球气象强迫数据集(glo-bal meteorological forcing dataset, GMFD)作为观测数据, 用于历史时段对 ANN 的训练。GMFD 由普林斯顿大学研发, 空间范围覆盖全球陆地, 时间范围是 1948—2005 年, 分辨率为日。GMFD 由台站观测数据、卫星观测数据和再分析资料合成, 最初是作为离线陆面模式的大气强迫数据而开发[22‒23], 具有目前国际上日平均资料的最高分辨率(0.25°×0.25°), 因此经过人工神经网络降尺度后的数据具有同样的高分辨率。图 1 中以北京为例, 低分辨率的 GCM数据(CCSM4, 黑色网格)与高分辨率的格点观测数据(GMFD, 灰色网格)形成鲜明的对比: CCSM4 的两个网格几乎覆盖整个北京市, 一个格点的面积是GMFD 的20 倍。
除 GMFD 数据外, 为了进行更加客观的对比, 我们还使用另一套高分辨率格点观测数据, 即英国东安格里亚大学气候研究所的格点时间序列数据(climatic research unit gridded time series , CRU TS version 4)作为参考基准。CRU 为月尺度数据, 空间分辨率为 0.5°×0.5°, 由台站观测数据插值得到, 覆盖全球陆地, 时间范围是 1901—2016年[24]。
如图 2 所示, 本文研究时段为 1950—2100 年。其中, 1950—2005 年(共 56 年)为历史时段, CCSM4 和 GMFD 均有数值; 2006—2100 年(共 95 年)为未来时段, 只有 CCSM4 有两个排放情景的数值。在进行统计降尺度时, ANN 降尺度过程将数据分为训练集、验证集和测试集, 其中训练集和验证集从历史时段数据中抽取, 未来时段数据则作为测试集使用; 偏差校正方法(bias correction, BC)贯穿始终。对1950—2005 年的历史数据, 每 4 年的前 3 年作为训练集(共 42 年), 第 4 年作为验证集(共 14 年)。这就可以保证 ANN 在训练过程中更充分地捕捉气候变暖信息, 提升模型的泛化能力。另外, 为便于讨论未来气候针对过去气候的增量, 本文将 1970—1999年定义为气候态(climatology, CLIM), 将 2020—2049 年和 2070—2099 年分别定义为近期未来时段(near-term future, NT)和远期未来时段(long-term future, LT)。
图1 全球气候模式 CCSM4 与格点化观测数据 GMFD 的分辨率对比示例
Fig. 1 Comparision of resolution between general circulation model CCSM4 and gridded observation data GMFD
本文开发的统计降尺度数据集(statistical down-scaling dataset, SD)包含日最低温(Tmin)、日最高温(Tmax)和日降水量(Pr)。Tmin 和 Tmax 均同时使用 ANN中多层感知器神经网络(multilayer perceptron, MLP)和偏差校正(bias correction, BC)方法, 即 SD 温度= ANN+BC; Pr 仅使用偏差校正方法, 即 SD 降水= BC。
图2 数据划分示意图
Fig. 2 Sketch map of the data
1.2.1 日最低温和日最高温
对 Tmin 和 Tmax 的降尺度综合使用 MLP 和 BC。使用 MLP 是为了得到 GCM 预报观测数据之间的统计关系, 同时获得高时空分辨率数据; 使用 BC 是为了修正降尺度数据的平均值和方差。
MLP 由输入层、隐藏层和输出层构成, 其中每一层由多个节点组成, 节点间由求和函数和激活函数相互连接。如图 3 所示, 本文开发的神经网络由两层隐藏层组成, 第一层隐藏层共 60 个节点, 第二层隐藏层共 30 个节点, 记为(60, 30)。测试结果表明, 将隐藏层节点数量从(10, 5)增加到(60, 30), 相关系数评分从 0.864 提升至 0.867; 节点数提升至(60, 30)以上之后, 相关系数评分不再变化。并且, 两层隐藏层的神经网络足以描述当前数据规模下输入‒输出数据间的数学关系, 这与 Tabari 等[20]及Lippmann[25]的结论相同, 因此我们最终选择(60, 30) 的节点设计。
使用 python 中的 sklearn v0.21.3 软件包来实现神经网络。参数调节方面, 我们尝试了 lbfgs, sgd和 adam 这 3 种权重优化算法, 其中 sgd 表现最佳; 还尝试了 identity, logistic, tanh 和 relu 这 4 种激活函数, 其中 relu 表现最佳。值得注意的是, 隐藏层设计、权重优化算法和激活函数的选择可能因为输入数据的不同而有所改变[26‒27]。另外, 我们通过调节alpha 值来控制正则化过程, 可使网络在训练过程中快速地减小相对不重要节点路径的权重。为了避免出现过拟合现象, 将迭代次数设为 100。在训练过程中, 使用相关系数作为衡量标准(代价函数)。
训练神经网络有两点特殊考量。第一, 为保证MLP 中输入信息有更好的空间代表性, 对 CCSM的每一个格点, 都考虑与之相邻的 9 个格点的数据(图 1 中黑色方格)。第二, 气候变暖导致未来时段温度平均值与历史时段有明显的差异, 为保留该重要信息, 需要在进行输入标准化时对其进行有偏标准化, 计算公式如下:
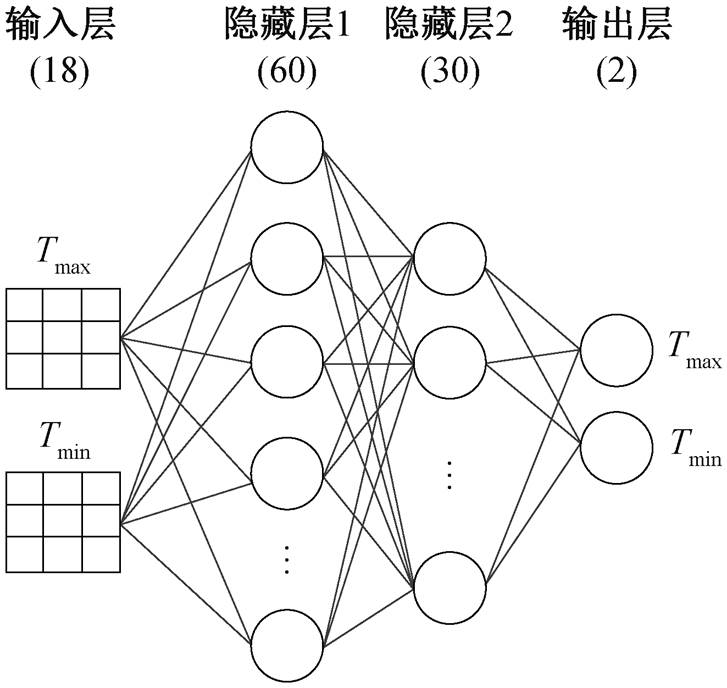
图3 多层感知器神经网络结构
Fig. 3 Architecture of MLP regressor
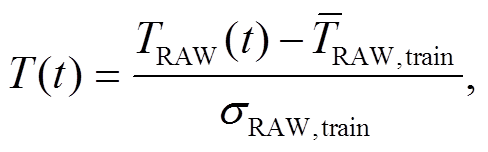(1)
其中, TRAW 是未来时段的 CCSM 数据,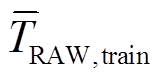 
是历史时段 CCSM 数据的平均值, σRAW,train 是历史时段 CCSM 数据的标准差。
由于 GCM 本身的不确定性, GCM 的输出在空间和时间上往往存在系统性偏差[10]。我们采取与文献[28‒30]类似的做法, 在 MLP 降尺度后, 再使用BC 对数据的平均值和标准差进行校正。无论是统计降尺度还是动力降尺度方法, 都可以进行偏差校正。目前常见的 BC 方法主要有分位数映射(quan-tile mapping)和嵌套偏差校正(nested bias correction)两种。与对全球气候模式每个格点单独进行偏差校正相比, 对降尺度后的输出进行偏差校正的最大优势是消耗的计算资源更少[30]。本文结果中, MLP 降尺度后, 变量的方差小于观测值。因此, 我们逐月对 Tmin 和 Tmax 的平均值和方差进行分位数映射的BC 校正[29]:
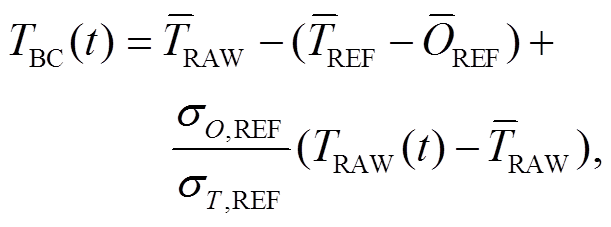(2)
其中, REF 代表整个历史时段, RAW 代表需要进行偏差校正的时段(训练集、验证集和测试集)。特别地, 由于升温趋势明显, 所以 Tmin 和 Tmax 的平均值与历史时段差异显著, 因此将测试集的 95 年分成 9段分别进行偏差校正, 即 2006—2020 年, 2021—2030 年, 2031—2040 年 ······ 2091—2100 年。通过式(1)和(2), 既可保证降尺度后的温度平均值与观测数据保持一致, 又可将方差放大到与观测数据相当的水平。
在求区域平均值时, 考虑到格点面积随纬度增加而减小, 对中国地区的全部格点进行加权(纬度余弦)平均处理。
为了更好地展现 SD 方法的优势, 我们将其与基于多元线性回归(multiple linear regression)方法的统计降尺度结果进行对比。
在温度变量的降尺度计算中, 尽管 ANN 降尺度过程已大幅度地修正了输入量的偏差(特别是均值), 但由于 ANN 降尺度过程不能绝对保证输出量的统计量(均值和方差)与观测数据一致, 若想得到高质量的降尺度数据, BC 方法仍然是必要的。在我们的测试结果中, ANN 对偏差减少的贡献是主要的, BC的贡献是辅助性的。
1.2.2 日降水量
降水量的统计降尺度计算一直是难点[30]。在我们的尝试中, 单纯依赖 ANN 输出的日降水量, 虽然在相关系数和均方根误差上表现最佳(图 4(a)), 但季节变率明显, 天气变率缺失, 得到的降水事件集中在春夏秋三季, 没有表现出日降水量的偏态分布特征(见附录 1～3)(访问 http://xbna.pku.edu.cn 查看附录)。受限于上述情况, 本文不使用 ANN, 只选用 BC 对日降水量做统计降尺度, 计算公式如下:
=
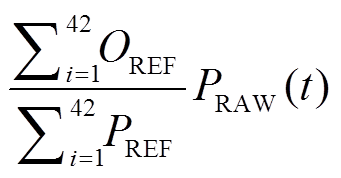, (3)
其中, i 表示训练集的年数(共 42 年), OREF 是训练集中观测数据的日降水量, PREF 是训练集中 CCSM 的日降水量, PRAW 代表需要进行偏差校正的时段(训练集、验证集和测试集)。由于降水是局地事件, 空间代表性小, 因此模式数据不考虑 9 个格点, 只考虑 1 个格点。
为了更好地体现 SD 方法的优势, 我们还比较了一元线性回归(linear regression)方法与泊松回归(Poisson regression)方法(见附录 2 和 3), 其中泊松回归是较多文献中建议对降水使用的降尺度方法[31]。
与 GCM 相比, 本文开发的 SD 数据有两个方面的改进: 1)在 GCM 的基础上, 提供了分辨率更高的空间细节特征; 2)可以修正历史时段 GCM 的系统性偏差, 包括空间分布和时间变率的统计特征。
针对温度重建, 我们对比了多元线性回归、输入为 1 个格点的 MLP 和输入为 9 个格点的 MLP 的方法。以北京为例, 用不同的方法对日最低温(Tmin)和日最高温(Tmax)进行统计降尺度后, CLIM 时段的表现如图 4(b)和(c)所示。统计降尺度后的数据总体上比 GCM 原始输出好, MLP 的表现总体上比多元线性回归方法略好。通过读取程序的输出数据可知, 对于 Tmin, CCSM、多元线性回归和 SD 的RMSD 分别是 2.25°C, 1.87°C 和 1.82°C; 对于 Tmax, CCSM、多元线性回归和 SD 的 RMSD 分别是2.58°C, 2.25°C 和 2.11°C。可见, 无论是 Tmin 还是Tmax, 都是基于 MLP 的 SD 表现略好。需要说明的是, 对于北京格点, 输入选取 9 个格点(图 4 中红色叉号)和 1 个格点(图 4 中红十字)的表现相似, 因为温度具有大尺度空间代表性, 我们最终选用输入为9 个格点的 MLP。成都、广州、哈尔滨、拉萨、兰州、上海和乌鲁木齐 7 个地区不同统计降尺度方法的泰勒图见附录 4～10, 尽管不同地点的 CCSM 原始数据偏差不尽相同, 但最终统计降尺度后的 SD 数据均与北京地区相似, 即温度变量的误差明显小于CCSM 和线性回归。
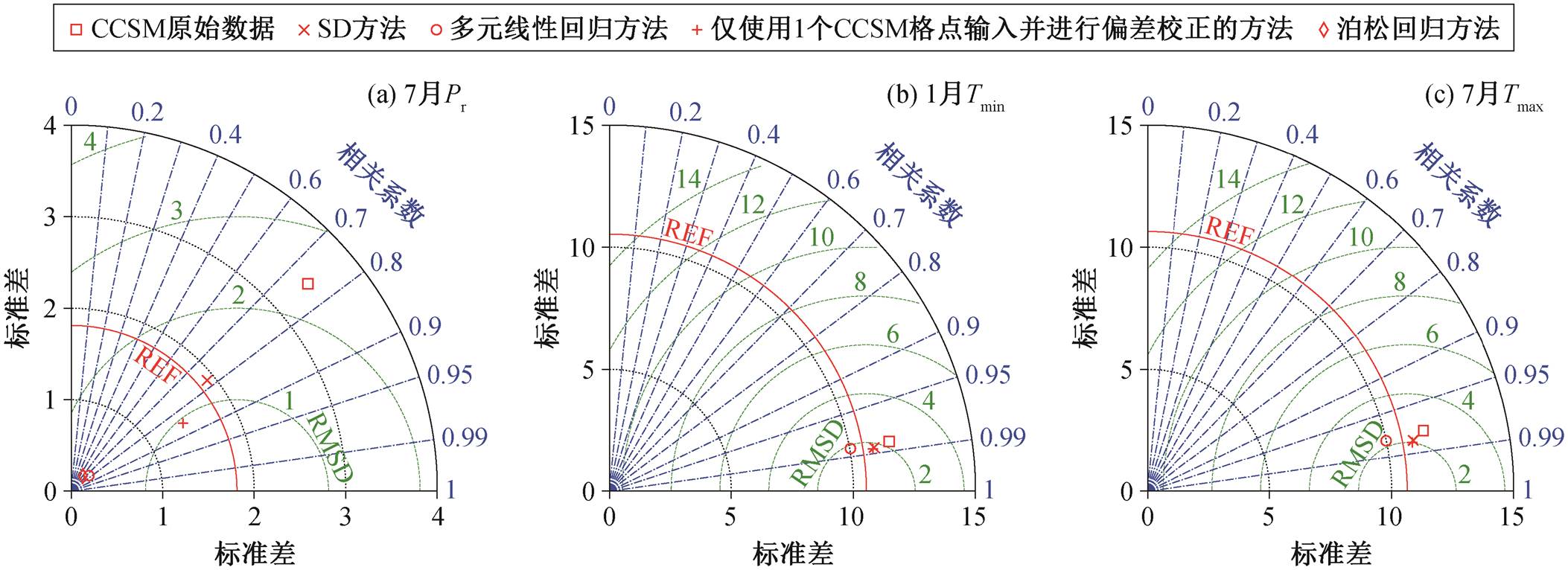
图4 北京格点Tmin, Tmax和Pr不同统计降尺度方法的泰勒图
Fig. 4 Taylor diagram for Tmin, Tmax, and Pr in different statistic downscaling method in Beijing
温度的空间分布如图 5(a1)～(a3)和(b1)～(b3)所示。就 1 月 Tmin 而言, 观测结果中主要体现为南热北冷, 零度线在秦岭‒淮河一带(图 5(a1)); CCSM 的模拟结果在绝大地区有 5°C 的冷偏差, 只在东北和新疆地区存在 1～3°C 的暖偏差; SD 的模拟结果在全国范围内偏差都很小, 在青海和西藏有不超过 1°C的偏差。就 7 月 Tmax 而言, 除高原地区, CRU 的模拟结果全国绝大部分地区在 20°C 以上; CCSM 的模拟结果冷热偏差不规则地分布, 西部偏差最大, 其绝对值可达 5°C 以上; SD 的模拟结果依旧偏差都很小, 在−1～1°C 之间。由此可见, SD 显著地改进了CCSM 中温度空间分布的系统性偏差。值得注意的是, 虽然 SD 的空间表现整体上较佳, 但地形起伏较大的格点(如青藏高原)仍存在较大的偏差, 可能是区域温度空间变率较大和格点内地形差所致。
全国平均温度的时间序列如图6(a)和(b)所示。就 CCSM 而言, 1 月 Tmin 有 2～3°C 的冷偏差, 7 月 Tmax有 1°C 的冷偏差。SD 显著地修正了 CCSM 的系统性冷偏差, 并使年际振幅与观测结果趋同, 与图 5呈现的特点一致。
表 1 和 2 给出温度在训练集和验证集上的量化指标, 可见与 GCM 相比, SD 均具有较高的准确性。就训练集(表 1)而言, 7 月 Tmax 的 SD 模拟结果的平均值和标准差均好于 CCSM, 使得 SD 模拟结果的 RMSE 为 0.73, 小于 CCSM 的 0.91; 1 月 Tmin 的SD 模拟结果平均值优于 CCSM, RMSE 为 1.28, 远小于 CCSM 的 2.98。就验证集(表 2)而言, 7 月 Tmax的 SD 模拟结果平均值和标准差均好于 CCSM, 使得 SD 模拟结果的 RMSE 为 0.55, 远小于 CCSM 的0.89; 1 月 Tmin 的 SD 模拟结果平均值优于 CCSM, RMSE 为 1.01, 远小于 CCSM 的 2.49。
上述结果均表明, CCSM 系统性地低估了 1 月Tmin 和 7 月 Tmax, 特别是在中国南部和西部地区, 这与模式的系统性偏差和格点平均高度的代表性偏差有关; SD 则显著地改善了这些问题, 模拟结果更接近历史观测值。
对降水量的重建, 我们尝试了一元线性回归、泊松回归、输入为 1 个格点的 MLP 和偏差校正 4种方法。以北京为例, 用不同的方法对日降水量进行统计降尺度后, 在 CLIM 时段的表现如图 4(a)所示。统计降尺度后的数据比 GCM 原始输出更接近观测值; BC 和 MLP 比两种回归方法略胜一筹; SD数据的标准差更接近观测值, MLP 的相关系数和均方根误差则表现更佳。一元线性回归、泊松回归、ANN 和 SD 的 RMSD 分别是 1.63, 1.69, 0.95 和 1.25 mm。虽然 ANN 在上述泰勒图(图 4(a))中表现最佳, 但其在时间序列上却呈现过于缓变的季节循环特征, 给出“天天下小雨”的错误信息。以验证集中1997 年的日降水时间序列(附录 1)为例, ANN 的结果主要体现为缓变的季节循环特征, 在春季、夏季和秋季, 几乎每天都会下小雨, 缺少降水本来具有的天气尺度特征。SD 则较好地保留了降水的天气尺度特征, 且每一次的降水强度都与 GMFD 更接近。日降水量具有明显的偏态分布特点, 最大概然集中在 0 mm 处, 越是极端强降水事件, 发生概率越小(见附录2)。SD 与 CRU 最为一致, ANN 体现为小雨为主的分布, 线性回归和泊松回归结果更是只体现天天下小雨的特点(见附录 2)。综合考虑上述对比结果, 我们最终选取偏差校正方法作为日降水的统计降尺度方法, 同时建议在处理降水这种偏态分布变量时, 慎重选择 ANN, 选用类似本文中的BC 方法即可。
降水的空间分布如图 5(c1)～(c3)所示。对 7 月Pr 而言, CRU 的降水集中在广东和广西沿海地区和西南地区南边界, 达到 10mm 以上; CCSM 的 Pr 偏差分布不均匀, 从青藏高原南侧和东侧到四川盆地, 降水显著偏多; SD 的 Pr 偏差都很小, 在−0.5～0.5mm 之间, 成功地订正了模式数据对四川盆地及青藏高原南界区域的高估问题。
全国平均降水量的时间序列如图 6(c)所示。对CCSM 而言, 7 月 Pr 有 1.5mm 的正偏差。SD 显著地修正了 CCSM 的偏差, 并保留了 CCSM 的振幅特征, 与图 5 中的表现一致。
训练集和验证集上降水量的量化指标见表 1 和2。与 GCM 相比, SD 均呈现较好的技巧性。对训练集(表 1)而言, SD 的 7 月 Pr 平均值和标准差均好于CCSM, 使得 SD 的 RMSE 低至 0.59, 小于 CCSM 的1.17。对验证集(表 2)而言, SD 的 7 月 Pr 平均值和标准差同样均好于 CCSM, 使得 SD 的 RMSE 仅为0.44, 远小于 CCSM 的 1.09。
上述分析表明, CCSM 系统性地高估 7 月 Pr, 特别是在我国西南地区, 这与模式模拟降水过程的系统性偏差有关; SD 显著改善了这些问题, 与历史观测值更加接近。
(a1)～(a3) 1 月 Tmin; (b1)～(b3) 7 月 Tmax; (c1)～(c3)7 月 Pr。(a1)～(c1) 1970—1999 年平均 CRU 气候态; (a2)～(c2) CCSM4 与 CRU 的差值; (a3)～(c3) SD 与 CRU 的差值
图5 1970—1999年Tmin, Tmax和Pr平均值的空间分布
Fig. 5 Spatial distribution of meanTmin, Tmax and Pr in 1970‒1999
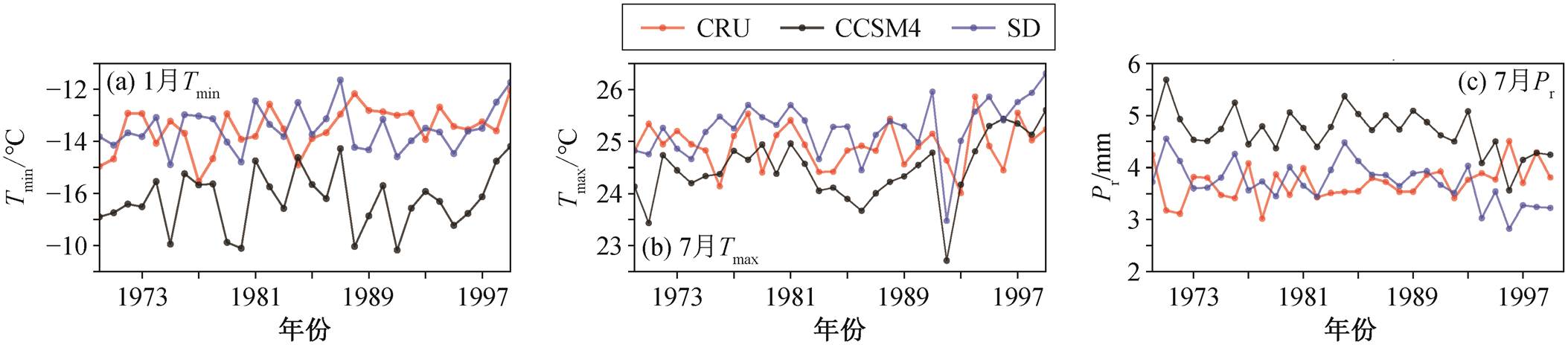
图6 1970—1999年全国所有格点加权平均后Tmin, Tmax和Pr平均值的时间序列
Fig. 6 Time series of China’s weighted average’s meanTmin, Tmax and Pr in 1970‒1999
在历史时段, SD 的预估结果比 GCM 更接近观测值。将这种修正技巧应用到未来时段, 我们期待SD 给出可信度比 GCM 高的预估结果。下面把未来时段分为 RCP8.5 情景(高排放)和 RCP2.6 情景(低排放)分别讨论。
表1 全国Tmin, Tmax和Pr平均值在训练集上的表现
Table 1 Statistics of mean Tmin, Tmax and Pr of China on training samples
指标TmaxTminPr 观测值CCSM4SD观测值CCSMSD观测值CCSMSD 平均值25.0524.5625.25−13.79−16.38−13.623.664.643.67 标准差 0.430.730.66 1.101.120.860.330.470.42 RMSE—0.910.73—2.981.28—1.170.59
说明: 粗体数字表示比另一组数据更接近观测值, 下同。
表2 全国Tmin, Tmax和Pr平均值在验证集上的表现
Table 2 Statistics of meanTmin, Tmax and Pr of China on validation samples
指标TmaxTminPr 观测值CCSMSD观测值CCSMSD观测值CCSMSD 平均值25.1724.5225.21−13.89−16.17−13.703.694.683.74 标准差 0.560.690.59 0.850.880.710.220.400.34 RMSE—0.890.55—2.491.01—1.090.44
中国地区平均 Tmin, Tmax 和 Pr 的时间序列如图 7所示, 中国地区近未来时段的气候变化空间分布如图 8 所示。SD 的预估结果基本上保持 GCM 预估结果的空间分布, 增暖幅度略小, 降水变化幅度相当。CCSM 描述全国普遍增温 2～3°C, 华北地区日降水量增加 1～2mm 的预估结果; SD 预估结果的空间分布与 CCSM 高度相似, 但增温幅度比 CCSM 小0.5°C, 日均降水量与 CCSM 高度一致。从时间序列(图 7)看, SD 对全国 1 月 Tmin 和 7 月 Tmax 升高趋势的估计值比 CCSM 略小, 对 7 月 Pr 的变化趋势估计结果与 CCSM 高度一致。
中国地区在远未来时段的气候变化空间分布如图 9 所示。与近未来时段相比, SD 给出的本世纪末增温幅度更大, 东北‒华北‒西南一线降水增加更显著, 华东‒华南一线降水减少; CCSM 给出的的 1 月Tmin 和 7 月 Tmax 都普遍升高 4～5°C, 降水增加的范围从近未来时段的华北地区扩大到东北‒华北‒西南一线。SD 给出的增温幅度(3～4°C)略小于 CCSM, 降水与 CCSM 高度一致。从时间序列(图 7)看, 到 21世纪末, SD 给出的 1 月 Tmin 升高至−9°C, 7 月 Tmax 升高至 29°C, 全国平均降水也增加 1 mm。
中国地区在近未来时段和远未来时段的气候变化空间分布如图 10 和 11 所示。从总体上看, 温度和降水变化的空间分布与高排放情景 RCP8.5 的预估结果高度相似, 只是幅度明显减小, 物理意义是全球变暖进程弱很多。对于近未来时段, SD 对 1 月Tmin 和 7 月 Tmax 增温幅度的估计比 RCP8.5 情景分别低约 2°C 和 1°C, 对降水变化的估计与 RCP8.5 情景几乎没有差异。对于远未来时段, SD 对 1 月 Tmin 和7 月 Tmax 增温幅度的估计比 RCP8.5 情景分别低约4°C 和 3°C, 对日降水变化的估计比 RCP8.5 情景低约 0.5 mm。
本研究针对中国地区未来 100 年的气候变化预估问题, 开发一套高时空分辨率的统计降尺度数据集, 尝试利用近年来蓬勃发展的 ANN 方法对中国地区的 3 个关键气候变量进行统计降尺度, 并使用训练后的模型对未来气候变化进行预估, 同时证实ANN 方法对温度变量有良好的适用性, 对偏态分布的降水变量则适用性较低, 得到如下主要结论。
1)对整个中国地区 3 个关键气候变量进行统计降尺度(包含人工神经网络和偏差校正), 在不改变气候长期变化趋势的前提下, 成功地开发一套高时空分辨率(空间分辨率: 0.25°, 时间分辨率: 日资料)的气候变化数据集 SD。
2)对于历史气候态, SD 数据集比 CMIP5 GCM的原始输出更接近观测值, 温度和降水的气候态分布都得到显著的改善。
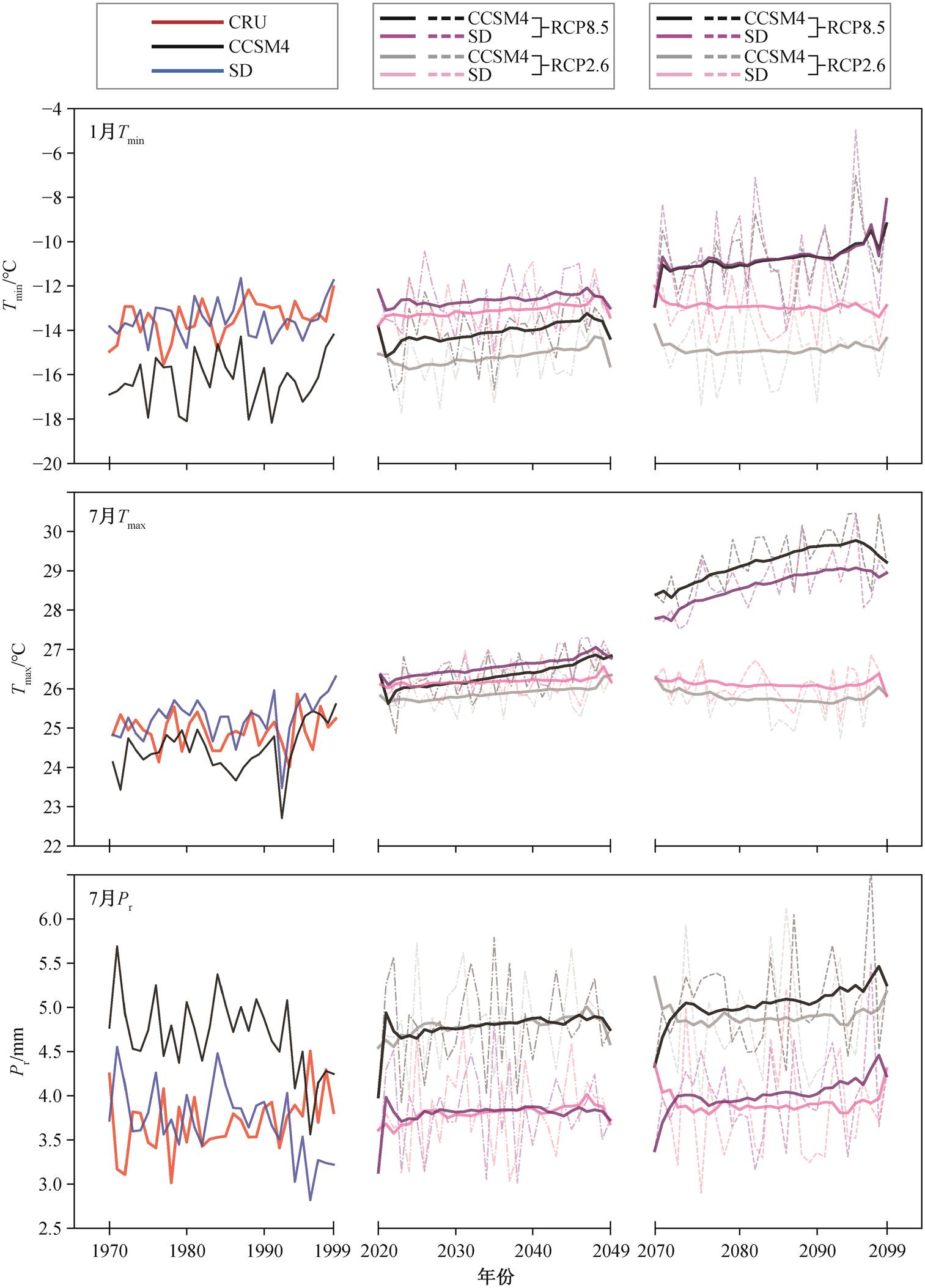
图7 中国地区平均Tmin, Tmax和Pr在历史气候态、近未来时段和远未来时段的时间序列
Fig. 7 Time series of China’s Tmin, Tmax and Pr in historical climotology, near-term future years, and long-term future years
3)SD 数据集总体上保留了 CMIP5 GCM 对未来气候变化趋势的估计, 并对变化幅度有微小的修正, 减少了 CMIP5 预估结果的不确定性。
本研究的工作具有以下意义: 1)探索了在统计降尺度方法中引入最先进的 ANN 算法的可能性, 并给出一种具有普适性的解决方案, 可广泛地用于其他 CMIP5 GCMs 原始输出的降尺度操作中, 显著地提高 GCM 数据的可用性; 2)本文产出的 SD 数据集包含 3 个气候核心变量(Tmin, Tmax 和 Pr), 覆盖未来两种极端排放情景(RCP8.5 和 RCP2.6), 在分辨率和准确性两方面具有显著的优势, 可在其他需要高时空分辨率气候变化数据学科(如水文、农业和环境政策等)的研究中使用。
第一行是 CCSM4 近未来时段与历史气候态的差值, 第二行是 SD近未来时段与历史气候态的差值
图8 RCP8.5 情景中近未来时段相对于历史气候态 Tmin, Tmax 和 Pr 的变化
Fig. 8 Differences of Tmin, Tmax and Pr between near-term future and historical climotology in RCP8.5 scenario
第一行是CCSM4远未来时段与历史气候态的差值, 第二行是SD远未来时段与历史气候态的差值
图9 RCP8.5情景中远未来时段相对于历史气候态Tmin, Tmax和Pr的变化
Fig. 9 Differences of Tmin, Tmax and Pr between long-term future and historical climotology in RCP8.5 scenario
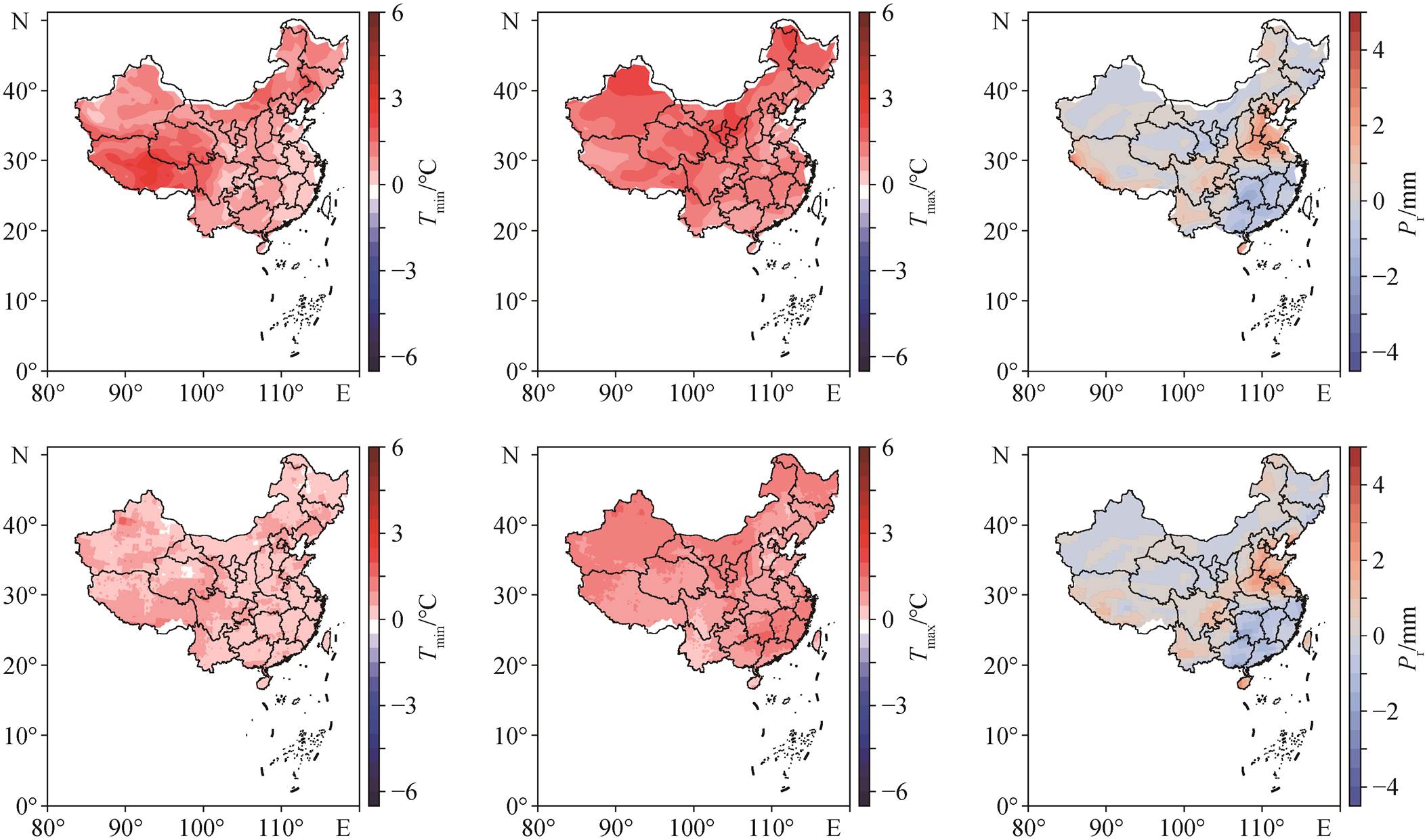
第一行是CCSM4近未来时段与历史气候态的差值, 第二行是SD近未来时段与历史气候态的差值
图10 RCP2.6情景中近未来时段相对于历史气候态Tmin, Tmax和Pr的变化
Fig. 10 Differences of Tmin, Tmax and Pr between near-term future and historical climotology in RCP2.6 scenario
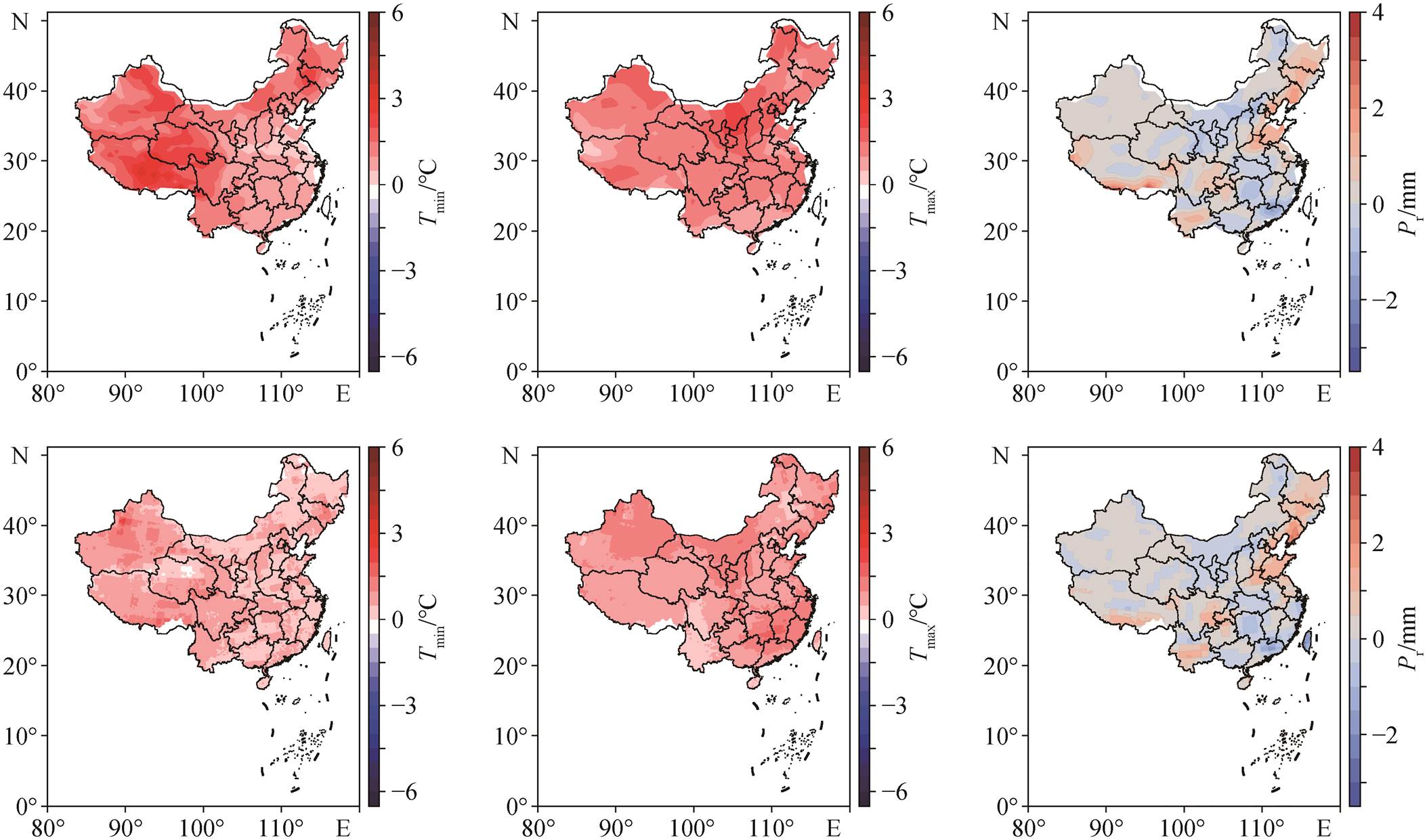
第一行是CCSM4远未来时段与历史气候态的差值, 第二行是SD远未来时段与历史气候态的差值
图11 RCP2.6情景中远未来时段相对于历史气候态Tmin, Tmax和Pr的变化
Fig. 11 Differences of Tmin, Tmax and Pr between long-term future and historical climotology in RCP2.6 scenario
需要说明的是, 本文选取的 CCSM 模式与观测数据之间存在一定程度的偏差, 虽然后期可以进行偏差校正, 但最终 SD 的预估结果仍然可能存在一定程度的模式依赖。后续工作中可考虑使用偏差更小的模式来构建 SD 数据集, 或使用多模式平均的结果。
参考文献
[1] Kay J E, Deser C, Phillips A, et al. The community earth system model (CESM) large ensemble project: a community resource for studying climate change in the presence of internal climate variability. Bulletin of the American Meteorological Society, 2015, 96(8): 1333‒1349
[2] Sakamoto T T, Komuro Y, Nishimura T, et al. MI-ROC4h — a new high-resolution atmosphere-ocean coupled general circulation model. Journal of the Meteorological Society of Japan: SerⅡ, 2012, 90(3): 325‒359
[3] BaoY, Wen X. Projection of China’s near- and long-term climate in a new high-resolution daily down-scaled dataset NEX-GDDP. Journal of Meteorologi-cal Research, 2017, 31(1): 236‒249
[4] 陈晓晨, 徐影, 许崇海, 等. CMIP5全球气候模式对中国地区降水模拟能力的评估. 气候变化研究进展, 2014, 10(3): 217‒225
[5] Fowler H J, Blenkinsop S, Tebaldi C. Linking climate change modelling to impacts studies: recent advances in downscaling techniques for hydrological model-ling. International Journal of Climatology: A Journal of the Royal Meteorological Society, 2007, 27(12): 1547‒1578
[6] Thrasher B, Xiong J, Wang W, et al. Downscaled climate projections suitable for resource management. Eos, Transactions American Geophysical Union, 2013, 94(37): 321‒323
[7] Trzaska S, Schnarr E. A review of downscaling me-thods for climate change projections: African and La-tin American Resilience to Climate Change (ARCC) [EB/OL]. (2014‒09) [2018‒02‒22]. https://www.clima telinks.org/resources/review-downscaling-methods-cli mate-change-projections
[8] Tang J, Niu X, Wang S, et al. Statistical downscaling and dynamical downscaling of regional climate in China: present climate evaluations and future climate projections. Journal of Geophysical Research: Atmo-spheres, 2016, 121(5): 2110‒2129
[9] Wilby R L, Wigley T M L. Downscaling general circu-lation model output: a review of methods and limi-tations. Progress in physical geography, 1997, 21(4): 530‒548
[10] Liu S, Gao W, Liang X Z. A regional climate mo- del downscaling projection of China future climate change. Climate Dynamics, 2013, 41(7/8): 1871‒1884
[11] Zhu X, Wei Z, Dong W, et al. Projected temperature and precipitation changes on the Tibetan Plateau: results from dynamical downscaling and CCSM4. Theoretical and Applied Climatology, 2019, 138(1): 861‒875
[12] Knutson T R, Sirutis J J, Zhao M, et al. Global projections of intense tropical cyclone activity for the late twenty-first century from dynamical downscaling of CMIP5/RCP4.5 scenarios. Journal of Climate, 2015, 28(18): 7203‒7224
[13] Yang X, Wood E F, Sheffield J, et al. Bias correction of historical and future simulations of precipitation and temperature for China from CMIP5 models. Journal of Hydrometeorology, 2018, 19(3): 609‒623
[14] Wilby R L, Dawson C W, Barrow E M. SDSM — a decision support tool for the assessment of regional climate change impacts. Environmental Modelling & Software, 2002, 17(2): 145‒157
[15] Tatsumi K, Oizumi T, Yamashiki Y. Effects of climate change on daily minimum and maximum temperatures and cloudiness in the Shikoku region: a statistical downscaling model approach. Theoretical and Applied Climatology, 2014, 120(1/2): 87‒98
[16] Maurer E P, Hidalgo H G, Das T, et al. The utility of daily large-scale climate data in the assessment of climate change impacts on daily streamflow in Cali-fornia. Hydrology and Earth System Sciences, 2010, 14(6): 1125‒1138
[17] Guo B, Zhang J, Xu T. Comparison of two statistical climate downscaling models: a case study in Beijing region, China. International Journal of Water, 2018, 12(1): 22‒38
[18] Do Hoai N, Udo K, Mano A. Downscaling global weather forecast outputs using ANN for flood pre-diction. Journal of Applied Mathematics, 2011, SI2: 1‒14
[19] Agrawal S, Barrington L, Bromberg C, et al. Machine learning for precipitation nowcasting from radar ima-ges[EB/OL]. (2019‒12‒11) [2020‒04‒13]. https://arx iv.org/abs/1912.12132
[20] Tabari H, Sabziparvar A A, Ahmadi M. Comparison of artificial neural network and multivariate linear reg-ression methods for estimation of daily soil tempe-rature in an arid region. Meteorology and Atmos-pheric Physics, 2011, 110(3): 135‒142
[21] Gent P R, Danabasoglu G, Donner L J, et al. The community climate system model version 4. Journal of climate, 2011, 24(19): 4973‒4991
[22] Xu L, Wang A. Application of the bias correction and spatial downscaling algorithm on the temperature ex-tremes from CMIP5 multimodel ensembles in China. Earth and Space Science, 2019, 6(12): 2508‒2524
[23] Sheffield J, Goteti G, Wood E F. Development of a 50-year high-resolution global dataset of meteorolo-gical forcings for land surface modeling. Journal of Climate, 2006, 19(13): 3088‒3111
[24] Harris I, Osborn T J, Jones P, et al. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Scientific Data, 2020, 7(1): 1‒18
[25] Lippmann R. An introduction to computing with neu-ral nets. IEEE ASSP Magazine, 1987, 4(2): 4‒22
[26] Retalis A, Tymvios F, Katsanos D, et al. Downscaling CHIRPS precipitation data: an artificial neural net-work modelling approach. International Journal of Remote Sensing, 2017, 38(13): 3943‒3959
[27] Sharifi E, Saghafian B, Steinacker R. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline in-terpolation techniques. Journal of Geophysical Re-search: Atmospheres, 2019, 124(2): 789‒805
[28] Hawkins E, Osborne T M, Ho C K, et al. Calibration and bias correction of climate projections for crop modelling: an idealised case study over Europe. Ag-ricultural and Forest Meteorology, 2013, 170: 19‒31
[29] Sachindra D A, Huang F, Barton A, et al. Statistical downscaling of general circulation model outputs to precipitation — part 1: calibration and validation. International Journal of Climatology, 2014, 34(11): 3264‒3281
[30] Sachindra D A, Huang F, Barton A, et al. Statistical downscaling of general circulation model outputs to precipitation — part 2: bias-correction and future projections. International Journal of Climatology, 2014, 34(11): 3282‒3303
[31] Schoof J T, Pryor S C. Downscaling temperature and precipitation: a comparison of regression-based me-thods and artificial neural networks. International Journal of Climatology: A Journal of the Royal Me-teorological Society, 2001, 21(7): 773‒790
Statistical Downscaled Climate Projection Dataset for China Using Artificial Neural Network
Abstract A high-resolution climate change dataset for China is developed. The climatic evaluation results of downscaling suggest as follows. 1) It is feasible to establish one statistical downscaling framework by incorpo-rating the advanced deep learning approach, artificial neural network (ANN), with high robustness. 2) The high-resolution climatology generated by this new method match the observations better than GCMs’ raw outputs. Those large bias induced by GCMs in temperature and precipitation can be reduced from 5°C down to 1°C and from 5 mm down to 0.5 mm, respectively. 3) The future climate projected by this new method have as similar long-term trend as the raw GCM’s results with minor differences in amplitude and spatial pattern. It is estimated that a warmer climate in the whole country with temperature increment at 3‒4°C and a wetter (drier) climate in North China (South China) can be expected around 2100 A. D. under RCP8.5 scenario. More scientists can be encouraged to use this new ANN-based downscaling method and this released high resolution climate change dataset can be used to a wide range of communities related to global change studies.
Key words statistical downscaling; artificial neural network; climate change; climate projection
doi: 10.13209/j.0479-8023.2022.015
国家自然科学基金(41875088, 41630527, 4171101348)资助
收稿日期: 2021‒03‒09;
修回日期: 2021‒05‒18