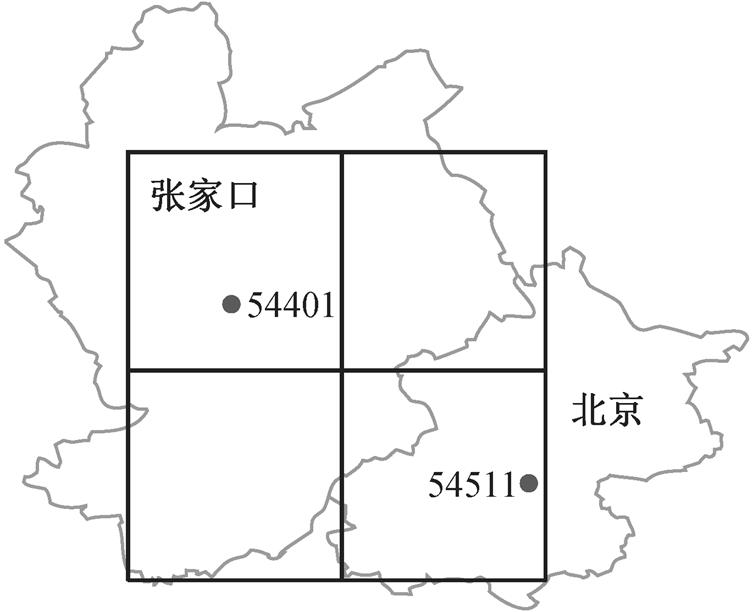
图1 张家口市和北京市气象站所处格点位置
Fig. 1 Location of Zhangjiakou and Beijing weather station
摘要 提出一种基于先进机器学习算法的纯客观、实时天气预报后处理方法。该方法使用历史数值天气预报结果和实况观测值, 训练出一个人工神经网络模型, 再将该模型应用于每日实时发布的数值天气预报结果中, 得到台站级别的天气要素预报结果。于张家口市和北京市分别建立该模型, 并使用 2005—2020 年的观测数据和模式数据进行训练、验证和调优。结果表明, 该模型预报的 5 个常规气象要素的预报误差普遍优于一元线性回归、多元线性回归以及数值天气预报模式的原始输出值, 尤其对 3 天以内的天气预报具有明显优势。基于该模型发展的全自动实时后处理系统已于 2020 年 11 月 1 日开始每日自动化地输出预报结果, 并服务于2022 年北京冬奥会的气象保障工作。
关键词 人工神经网络; 实时天气预报; 数值天气预报; 后处理
第 24 届冬季奥林匹克运动会和第 13 届冬季残疾人奥林匹克运动会的主会场位于张家口市崇礼县、北京市市区奥体中心和北京市延庆区[1], 天气预报是保障此次运动会顺利进行的一项重要工作。
在传统的天气预报方法中, 预报员通过分析天气图进行主观预报[2]。近 30 年来, 随着数值天气预报(numerical weather prediction, NWP)的飞速发展, 预报员制作天气预报的过程逐渐转变为主观与客观相结合的模式, 即“NWP 结果+经验预报”模式[3]。虽然 NWP 依靠计算机进行客观的定量计算, 但其计算是基于网络格点进行的, 代表的意义是一个矩形区域内天气要素的平均值, 而不能针对一个气象台所在的观测站点直接做出要素预报(这恰恰是事后预报效果检验的标准), 这就需要预报员“从格点到站点”进行人工经验订正。当遇到复杂天气形势时, 预报员还要通过多人会商的方式来确定最终的天气要素预报结果, 因此不可避免地在很大程度上带有主观性, 引入不易量化的人为误差[4]。考虑到这些问题, 我们希望提出一种后处理方法来模拟“从 NWP 格点到城市站点”的预报订正过程, 并且这种方法必须是基于客观计算的, 没有任何人为主观性的影响。探索这种后处理系统, 将有助于我国天气预报领域从“主观与客观相结合”的预报模式向单纯客观预报模式转变, 尽快与国际上主流预报模式接轨。
近年来, 人工神经网络方法越来越多地用于气象领域[5‒7]。这是因为, 神经元之间的非线性激活函数可在一定程度上模拟广义的非线性过程, 而天气的变化恰恰是一种典型的非线性过程[8]。在使用机器学习方法改进天气预报方面出现两种截然不同的趋势, 一种是通过卷积神经网络(convolution neural network, CNN)进行图像识别(例如雷达图像、云图图像以及地基光学全天成像等)[9‒11], 实现响应迅速的短临客观预报; 另一种是基于有限站点的多时次和多源观测数据, 采用复杂机器学习模型(如人工神经网络(artificial neural network, ANN), CNN和长短期记忆网络(long short-term memory, LSTM)等)[12‒13],实现单纯用统计算法的 1～3 天客观天气预报。总的来说, 这些方法过于依赖先进的机器学习方法, 忽视基于“全息”的天气动力学过程。本文采用与之不同的思路, 尽可能利用现有的基于“全息”数据进行推算的 NWP 产品, 在此基础上使用先进的机器学习算法, 弥补 NWP 对具体台站预报能力的不足(可视为统计降尺度形态的 NWP 后处理系统)。这样的预报结果, 其动力准确性由以全球观测为基础的NWP 预报来保证, 而误差的系统性减小则由机器学习来保证。我们希望这是一条计算成本小、客观性强、准确性更高的新思路。
此前, 将人工神经网络应用于地面辐射、大气污染物 PM2.5 和站点气象要素预报的工作[13‒16]都停留在科研领域, 将研发模型应用于实际业务工作的少之又少。另外, 前人的工作大多聚焦于北京等发达城市和地区[17‒18], 对冬奥会举办城市张家口地区的天气预报业务关注十分有限[19]。为保障第 24 届冬奥会和第 13 届冬残奥会比赛期间的天气预报工作, 中国气象局牵头开展“智慧冬奥: 2022 年天气预报示范计划项目”, 征集国内气象领域优秀的预报方法。作为参与单位, 我们提出一种基于 ANN 的客观预报方法,可以更好地利用现有的预报产品, 继承过往预报经验, 并彻底排除人为主观干预带来的不确定性。
本文使用的观测数据(observation, OBS)为张家口市气象站(WMO 站号: 54401; 114.92°E, 40.77°N)以及北京市气象站(WMO 站号: 54511; 116.47°E, 39.8°N)的站点观测数据。两个站点所处格点的位置如图 1 所示, 其中黑色框线代表的格点经度范围为 114.5°—115.5°E 和 115.5°—116.5°E (从左至右), 纬度范围为 39.5°—40.5°N 和 40.5°—41.5°N (从下至上)。之所以没有使用冬奥会举办场地之一的北京市延庆区气象站(WMO 站号: 54406; 115.97°E, 40.45°N)资料, 是因为该气象站属于国家一般气象站, 每天只有 00, 06 和 12UTC 这 3 个时次的观测, 且没有可从互联网直接下载的数据来源。
张家口 54401 站和北京 54511 站的 OBS 数据从https://rp5.ru/网站下载, 覆盖的时间为 2005‒02‒15至 2020‒10‒31, 数据的时间间隔为 3 小时。我们提取 2m 温度、2m 相对湿度、站点气压、10m 风向和 10m 风速这 5 个典型变量, 并将风向和风速按照三角函数关系转化为 10m 风速 u 和 v, 以便契合NWP 数据。我们还对 OBS 数据进行必要的质量控制, 对每月数据中超过平均值±3 倍标准差的时次进行标记, 并剔除其中明显错误的数据。
图1 张家口市和北京市气象站所处格点位置
Fig. 1 Location of Zhangjiakou and Beijing weather station
本研究使用的 NWP 数据为美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)发布的全球预报系统(Global Forecast System, GFS)生成的实时预报数据。之所以没有使用欧洲中期天气预报中心(European Centre for Medium Range Weather Forecasts, ECMWF)这一使用更广泛的 NWP 模式结果, 是因为 GFS 的每日实时预报和历史预报数据是完全开源的, 而 ECMWF 的数据大部分不是完全开源的。
GFS 历史预报数据从美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration)的 NCDC 网站(https://www.ncdc.noaa.gov/data-acces s/model-data/model-datasets/global-forcast-system-gfs)下载, 数据覆盖的时间为 2005‒02‒15 至 2020‒10‒ 31, 起报时间为每日 00 UTC, 预报时效为 384 小时, 预报时间间隔为 3 小时, 格点范围为全球, 水平分辨率为 1°×1°, 全要素为 584 个。我们只提取张家口54401 站和北京 54511 站所处格点的数据, 预报时效选取最小 3 小时, 最大 180 小时, 间隔 3 小时; 提取 11 个要素: 2m 温度、2m 湿度、站点气压、10m风速 u、10m 风速 v、总云量、总降水、向下长波辐射、向下短波辐射、向上长波辐射和向上短波辐射, 要素选取的原则基于预报员的经验[4,20]。由于GFS 数据中奇数预报时效(03, 09, 15, …, 177 h)和偶数预报时效(06, 12, 18, …, 180 h)的预报要素略有不同, 故我们在选择总云量、总降水、向下长波辐射、向下短波辐射、向上长波辐射和向上短波辐射这 6 个要素时, 分别选取 3 小时平均值(奇数时次)和6 小时平均值(偶数时次)。
NWP 每日最新预报数据发布于美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration)的 NOMAD 服务器(https://nomads. ncep.noaa.gov/pub/data/nccf/com/gfs/prod/)上, 本文使用的 00 UTC 起报数据一般于 03 UTC 左右即发布完毕。我们用 python 语言撰写一个爬虫脚本, 每日03:30UTC 将当日最新预报数据下载至本地服务器, 之后用 1.2 节的方式提取数据。
本研究将 2005‒02‒15 至 2018‒12‒31 的数据作为训练集, 2019‒01‒01 至 2020‒10‒31 的数据作为验证集。考虑到模型在今后的实际使用中会有不断更新的需求, 本文不使用随机方式选取样本作为验证集, 而是使用数据中最后两年的样本组成验证集。这是因为, 以最新数据作为验证集, 可以得到最接近实况的对未来实际预报效果的估计。从 2020 年11 月 1 日起, 我们将模型放在服务器上自动化运行, 生成当日最新预报结果, 并以此作为预报集(亦称测试集)。
本文基于人工神经网络的 NWP 后处理模型的整体思路如图 2 所示。该模型分为 3 个步骤: 1)训练阶段(2005—2018年), 使用 GFS 和 OBS 数据的训练集进行模型训练; 2)验证阶段(2019—2020 年), 将 GFS 验证集放入模型中, 得到预报数据, 并与OBS 数据的验证集(2019—2020 年)进行对比, 通过调参使模型达到最优估计值, 验证阶段和训练阶段不断循环; 3)预报阶段, 将每日 03 UTC 下载的最新GFS 数据放入模型中, 得到每日最新预报结果, 并上传至中国气象局指定的FTP服务器。
本文使用未经任何后处理的 NWP 模式(GFS 实时预报系统)在站点所处格点上的结果(简称 NWP), 并且将它作为站点天气预报结果的对照组(控制变量组)。
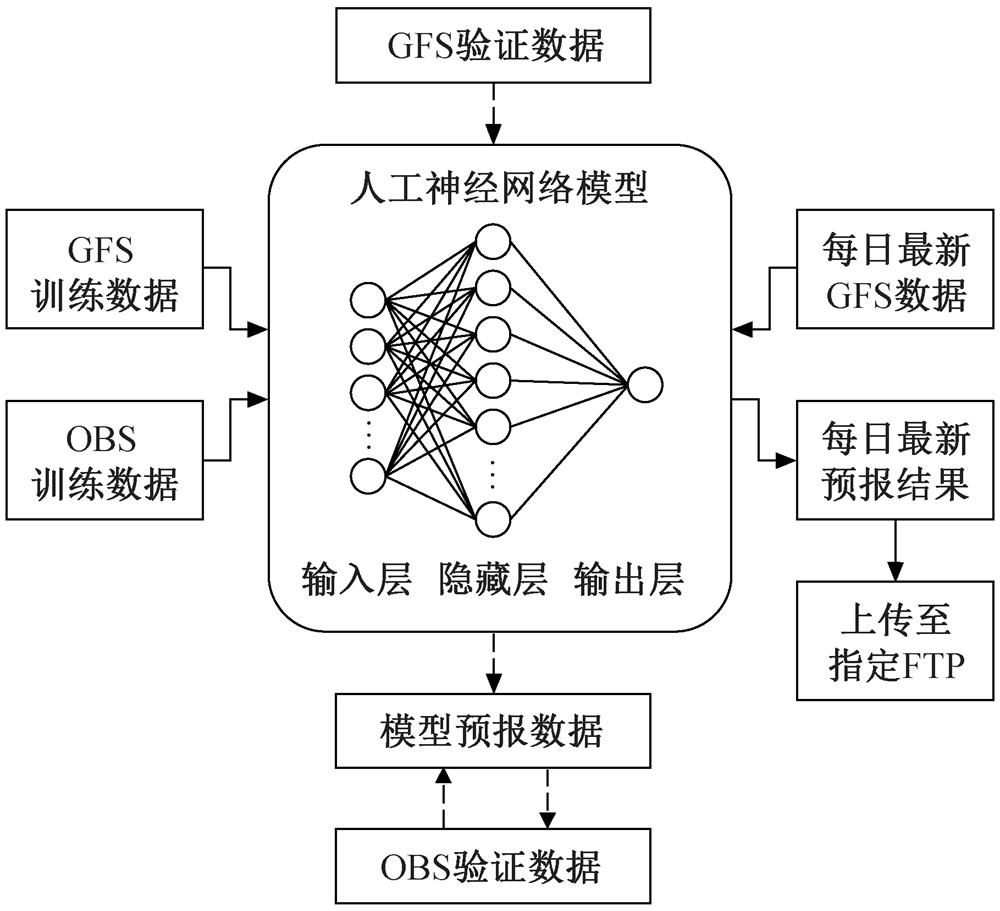
图2 ANN模型整体框架
Fig. 2 Frame of ANN model
一元线性回归(SLR)是统计学中最经典的方法之一, 由于 GFS 格点预报中含有温度、相对湿度、站点气压、u 和 v 这 5 个目标预报变量, 故我们选择SLR 作为模型对比的基线。
多元线性回归(MLR)是另一种常用的回归模型,常用于多因子的归因和重建。本文也使用 MLR模型, 并选取 11 个来自 GFS 格点预报的要素作为自变量。对于 5 个目标预报变量, 需设置 5 个独立的 MLR 模型, 但均使用同样的输入数据集。
人工神经网络模拟生物学中突触与神经元之间电信号的选择传导过程, 是当前受学术界广泛关注的机器学习算法之一[20‒21]。本文使用的 ANN 模型为标准的输入层+隐藏层+输出层模型配置(亦称 BP模型, 图 2)。在隐藏层中, 每一个神经元都选择性地(通过加权实现)接收来自上一层全部神经元的输入信息, 可用下式表示:
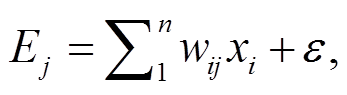(1)
其中, Ej 是节点 j 处的权重加和, wij 是节点 j 与上一层节点 i 之间的权重, xi 是上一层节点 i 处的权重加和(输入层则直接为变量值), n 是上一层的节点总数, ε 是偏差项。
激活函数控制信息从当前层传递到下一层的门限, 合适的非线性激活函数可在一定程度上模拟天气过程[6,22]。本文使用的激活函数是双曲正切函数tanh[23], 计算公式如下:
。 (2)
于是, 在节点j处的最终输出值为
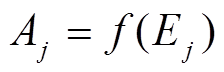。 (3)
将上述过程对每一个神经元分别计算, 并汇总至输出层神经元, 就得到预报结果
, 我们根据与真实值Y之间的差异定义损失函数(loss function)为L。在反向传播(BP)过程中, 为了找到使损失函数L(w)最小的最合适的权重矩阵w, 需要损失函数对权重的梯度逼近0。对权重矩阵w来说, 每执行一轮反向传播, w就更新至w′, 满足公式
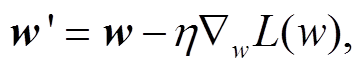(4)
其中, η表示学习率。将上述过程循环执行若干轮, 当执行至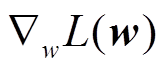
很小, 达到预先设定的阈值时, 人工神经网络模型训练结束。
在准备ANN输入数据时, 本文使用z-score方法, 分别将训练集上的GFS数据和OBS数据进行标准化[24]:
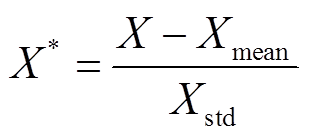, (5)
其中, X是每一个样本, X *是样本标准化后的值, Xmean和Xstd是训练集样本的平均值和标准差。在验证阶段, 先使用训练阶段保存的平均值和标准差, 对GFS验证集进行有偏标准化(而不是对验证集进行无偏标准化), 再对模型输出结果进行反标准化:
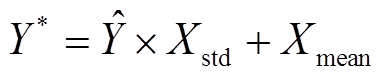, (6)
其中, 是模型输出结果, Y*是反标准化后的结果。最后, 将 Y *与 OBS 的验证集进行比对。
为帮助 ANN 识别输入数据的季节特征, 加入儒略日(Julian Day)特征作为第 12 个输入变量[25‒26]。简单起见, 假定 1 月 15 日(对北半球中纬度地区普遍适用)的儒略日值为−1, 对于全年中任意一天, 可以套用如下余弦公式:
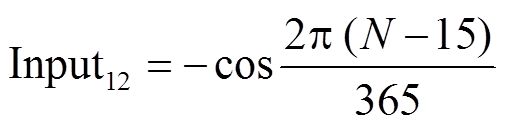, (7)
其中, N代表一年中的第几天(即儒略日)。该特征值在冬天接近−1, 夏天接近 1。
考虑到不同预报时次模型的效果有所不同, 尤其是为了使短期预报不受长期预报误差大的影响, 我们对每个预报时效分别构建独立的ANN模型。与GFS和OBS数据相对应, 本文模型的预报时间间隔为3小时。这样, 在180小时的预报时效中, 对于某个城市, 将会存在60个模型(003h, 006h, …, 177h, 180h)。由于我们的目标预报变量为5个, 故在张家口和北京将分别存在300个(60×5)由独立的ANN网络构成的模型矩阵, 它们就是本研究最终用于业务预报的后处理系统的核心。
本文在模型的实现方面做了两点改进: 1)在隐藏层之间加入“退化层(dropout layer)”, 在训练过程中, 退化层随机断开部分神经元, 这样就能在技术层面防止过拟合(over fitting); 2)为了加快模型收敛速度, 加入“批标准化层(normalization layer)”。
本文使用超参数方式来调优ANN模型中的多个参数[27], 也就是用循环穷举(列举)的方法对重要的参数进行测试。我们分别测试隐藏层数、隐藏层节点数、激活函数、退化层丢掉神经元百分比、优化器和代价函数等参数, 最终选取的参数配置如下: 激活函数为tanh, 隐藏层层数为1, 隐藏层节点为64个, 退化层每次训练随机丢掉30%的神经元, 优化器为AdaDelta, 代价函数为MSE, 样本批处理数为256, 训练轮数为500[28]。图3展示对隐藏层节点数的测试结果, 可见随着隐藏层节点数增加, 模型误差逐渐减小, 但计算代价快速上升, 因此64个节点是一个平衡的选择。其他参数的测试结果均与此类似, 不一一列举。
这里展示验证集上预报结果在日循环、年循环、不同变量和不同预报时效的表现, 使用均方根误差(RMSE)做为评价指标[15,17,23]。
本文提出的 ANN 模型对一天中的不同时刻(简称日循环)有着一致的优秀表现。对比 4 种方法在验证集上逐 3 小时(即每天 8 个预报时刻)的预报偏差, 结果如图 4 所示。对于任意一个时次, 5 个预报要素的统计结果均显示 ANN 模型偏差最小, 表现最佳。需要说明的是, 我们暂时没有考虑预报时效的影响。例如, 无论是提前 1 天、2 天, 还是提前 6天, 只要是 03 UTC 这个时刻的预报, 均计入第一个箱形图中。在气压(P)的箱形图中, NWP 系统误差较大(因格点平均气压主要受格点平均海拔控制, 与单站气压差异显著), 在温度(T)和相对湿度(RH)的箱形图中, NWP 在 06—12 UTC 的预报误差较大, 表现最好的 ANN 模型则没有明显的日循环差异, 所有时刻均表现良好。
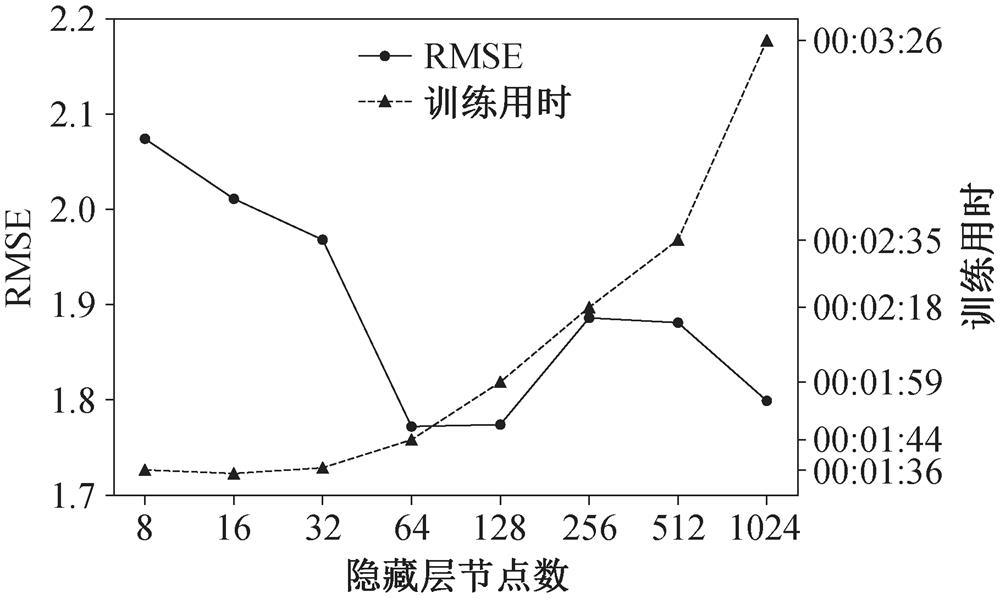
图3 单隐藏层节点数的RMSE和训练所需时间
Fig. 3 RMSE and CPU cost for different number of neurals
如图 5 所示, 本文提出的 ANN 模型在一年中的不同月份(季节)(简称年循环)有着不完全一致, 但总体最优的表现, 不同要素间有一定程度的差异。对于气温和气压, 夏季的预报结果明显优于冬季, 可能是因为夏季气温日变率较小, 模型误差也相应地维持在较小范围内; 冬季则不同, 尤其当寒潮来临时, 气温可以骤降 10℃以上, 模型的误差随之显著增大。气压在变化幅度上有与气温类似的季节特征。相对湿度的年循环则表现为双峰结构, 春、秋季误差大, 冬、夏季误差小, 可能是因为对于华北地区, 虽然冬季干燥, 夏季潮湿, 但冬、夏两季相对湿度的日变率较小, 春、秋两季则因为天气系统的影响, 相对湿度在干、湿间陡然转换(如一场春雨就使地表瞬间由干转湿, 一场沙尘暴又使其由湿变干), 致使模型预报误差较大。风速的误差集中在春季, 可能是因为张家口地区春季大风出现频次在一年中最高。总之, 不论这 5 种气象要素各自有着怎样的年循环特征, 从统计结果来看, ANN 模型无疑都是误差最小, 表现最优的。
以当前时间为原点, 对未来特定时间点(如 24小时、48 小时等)的天气进行预报, 这个特定时间点的远近称为预报时效。简化起见, 这里选择预报时效为 24 小时整倍数的模型输出进行讨论。如图 6所示, 随着预报时效增加, 所有方法的误差都逐渐增大。例如温度, 72 小时(3 天)的预报平均误差仍可控制在 2℃左右, 之后预报误差快速增长, 168 小时(7 天)已接近 3.3℃。纵观 4 种方法的表现, ANN 模型仍然系统性地优于其他方法。
与传统方法相比, ANN 模型在日循环、年循环和预报时效 3 个时间尺度上都有明显的优势。那么, 它对这 5 个预报变量都具有一致的高技巧吗?为了回答这个问题, 我们比较张家口地区 5 个目标要素的 ANN 预报值和真实值, 结果如图 7 所示, 可见ANN 模型对这 5 个变量并没有一致的表现。例如, 气温是预报效果最好的变量(R2=0.97), 气压的预报效果也很好(R2=0.87), 湿度的 R2 值只有 0.59, 风速u 和 v 的预报效果较差(R2 值均小于 0.4)。由图 7 可知, ANN 模型对空间上代表性大且时间上比较平稳的变量(如温度和气压)具有相当好的预报技巧, 而对空间上尺度较小且时间上变率较大的变量(如相对湿度、风速和风向)的预报技巧则相对较差。因此, 建议今后使用这套系统时要更多地关注其对温度和气压的预报结果, 适当地关注其对湿度、风向和风速的预报结果。
为了图示美观, 将PRMSE的NWP预报值减去50 hPa
图4 张家口54401站不同时次的误差对比
Fig. 4 Bias in different hours at station 54401 in Zhangjiakou
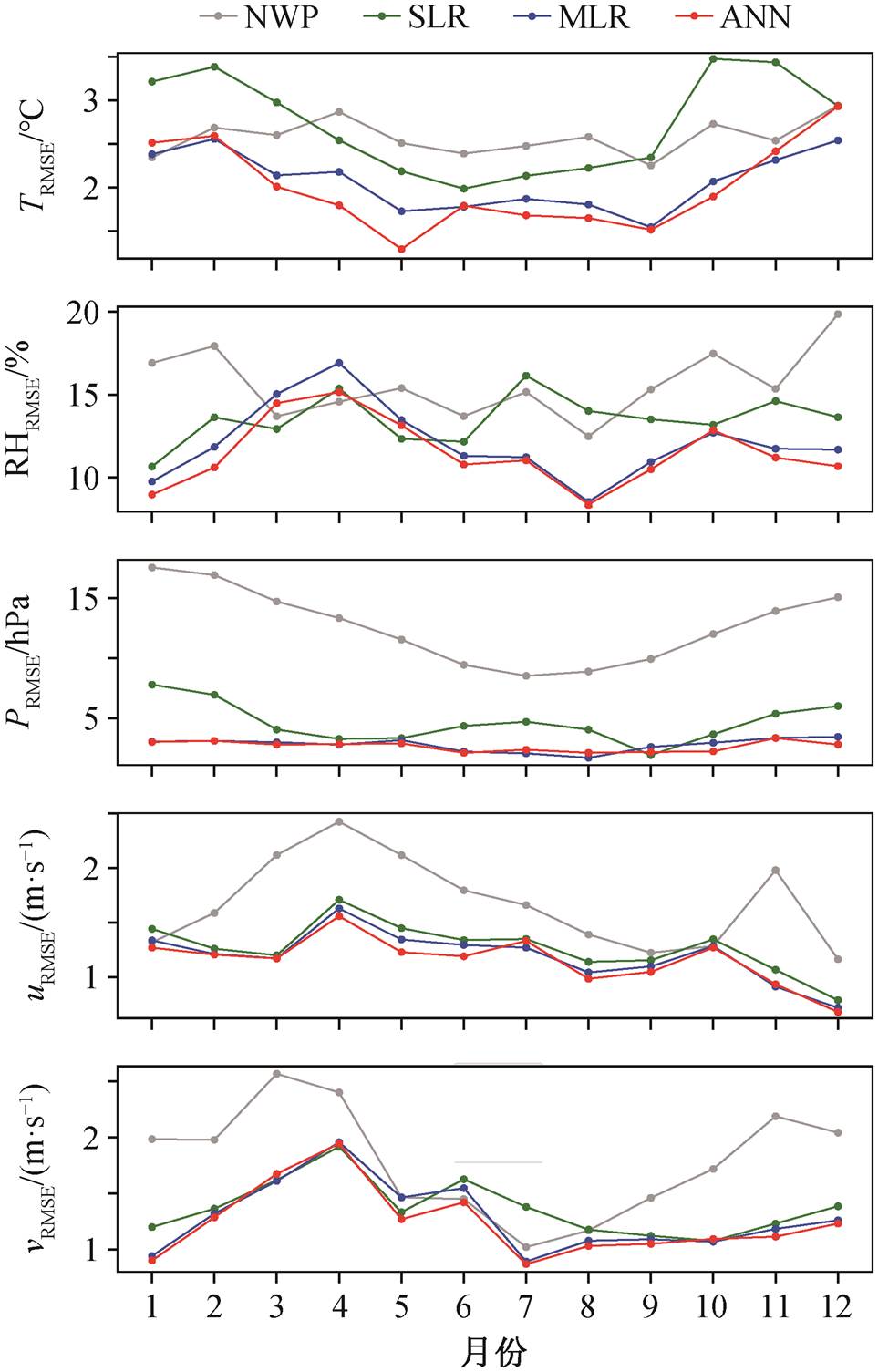
同样将PRMSE的NWP预报值减去50 hPa
图5 张家口54401站不同月份的RMSE对比
Fig. 5 RMSE in different months at station 54401 in Zhangjiakou
现有的 12 个输入变量在 ANN 模型中的相对贡献(敏感度)是一个值得探讨的问题。我们提取张家口站训练好的模型中输入层与隐藏层之间的权重来观察 12 个输入变量对 5 个输出变量的相对贡献, 结果见表 1。对张家口地区而言, 预报变量直接对应的输入变量都是敏感度较高的(如 T 对应 t2m, RH 对应 rh2m, P 对应 p_sfc); 表征天气循环动力过程的经向风 v10m、表征天气循环热力过程的地‒气长波通量 ulwave 和表征季节循环的 JulianDay 是 3 个敏感度普遍较高的因子; 云量 tcc 和降水 prep 在 NWP 输出中的误差较大, 体现在表 1 中, 是两个敏感度普遍较低的因子。从表 1 可以看出, 尽管天气要素之间的联系是复杂的, 但 ANN 模型通过训练时的正则化过程, 可以逐渐提升(降低)重要因子(无关因子)的权重, 这就使得即使在输入端引入更多的噪音, 也可以保证ANN模型最终表现的稳定。
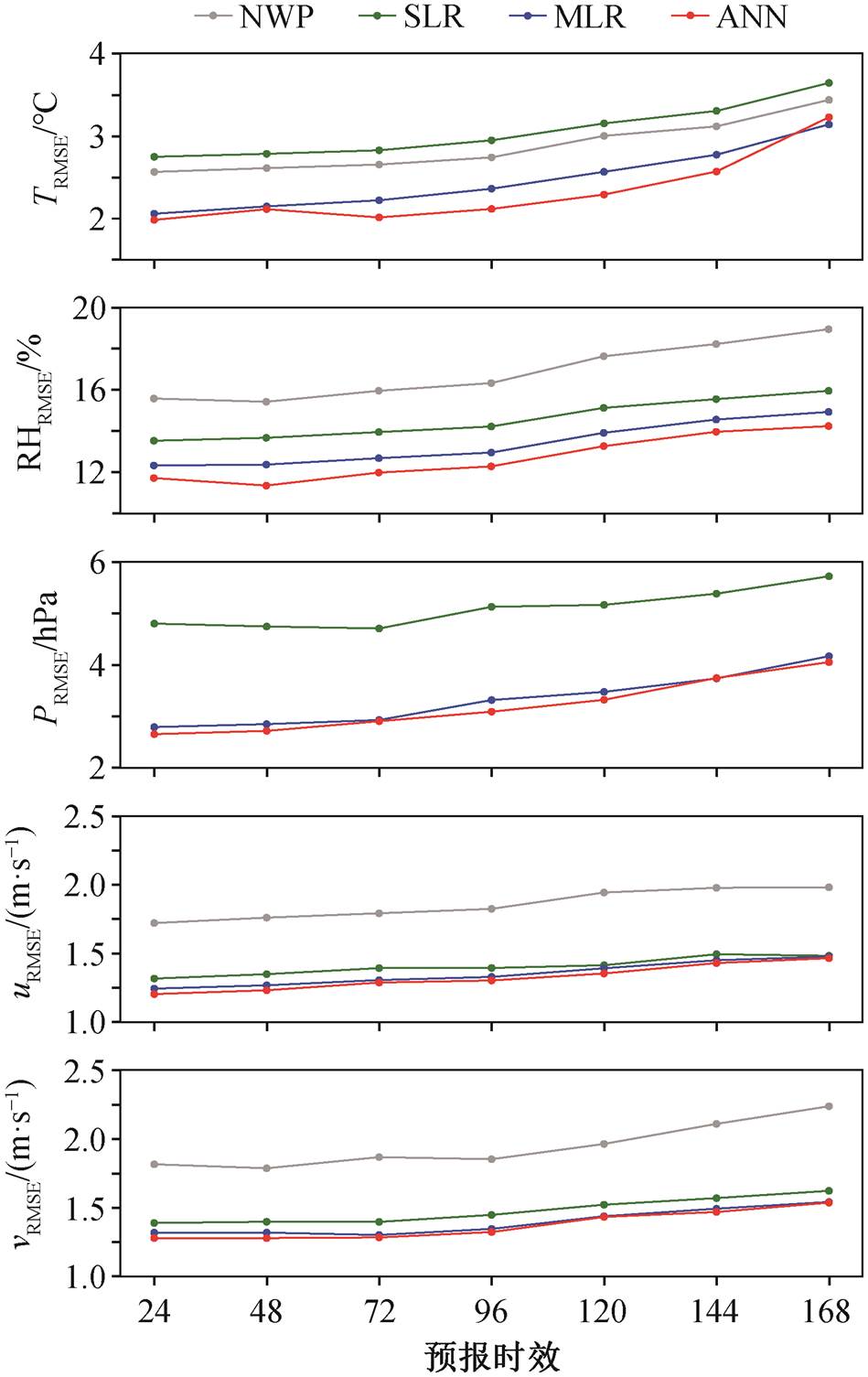
因海拔高度影响, 系统性误差较大, 未显示 PRMSE 的 NWP 预报值
图6 张家口54401站不同时效的RMSE对比
Fig. 6 RMSE in different lead times at station 54401 in Zhangjiakou
构筑 ANN 预报模型之后, 我们开发了与之相适应的自动化预报脚本, 从 2020 年 11 月 1 日开始, 进行为期 80 天的实时运行和监测。图 8 展示从自动化运行所得结果中选取的具代表性的 2021‒01‒03这一天的预报结果。该日的预报结果与 80 多天中的大多数结果相似, 在前 3 天(3～72 小时)的短期预报中, ANN 方法的结果通常都是最好的; 在 3～8 天(75～180 小时)的预报中, 4 种方法的误差波动均较大, ANN 只在统计意义上表现最好, 而对于任意一天的预报结果, 不能保证做到最好。即使这样, 我们仍然推荐用这套客观化和自动化的预报系统逐渐代替预报员的主观预报流程, 因为只有预报全流程实现客观化和自动化, 并把经验量化, 才能大幅度地减少主观随机性, 削减人力成本, 缩短预报的响应时间, 推进预报准确性的持续改进。
由于OBS的风速只精确到整数, 所以u和v的数据点呈带状分布
图7 张家口54401站ANN预报结果
Fig. 7 ANN forecast results at station 54401 in Zhangjiakou
表1 张家口54401站12个输入变量在5个输出变量模型中的敏感度
Table 1 Sensitivity of 12 input variables with respect to 5 output variables in ANN models at station 54401 in Zhangjiakou
输入变量输出变量 T/℃RH/%P/Pau/(m·s−1)v/(m·s−1) t2m0.18120.00930.02810.17020.0640 rh2m0.03670.19770.15580.09910.2353 p_sfc0.07820.10730.50520.02590.0016 u10m0.01240.14790.05830.29140.0743 v10m0.18590.23320.12750.60020.1450 tcc0.12690.09680.00530.11870.0123 prep0.01260.02560.09320.17260.1053 dswave0.08120.14120.31350.13580.0659 dlwave0.05730.11530.02280.08900.3225 uswave0.05480.09260.24660.08250.0692 ulwave0.09830.28240.32760.01000.0393 JulianDay0.14680.11440.06980.29430.1652
说明: 每个输入变量的敏感度值定义为模型中隐藏层 64 个神经元与该输入变量连接的权重之和, 再取 60 个预报时效的平均值; 粗体数字表示敏感度最大的前 3 个输入变量。
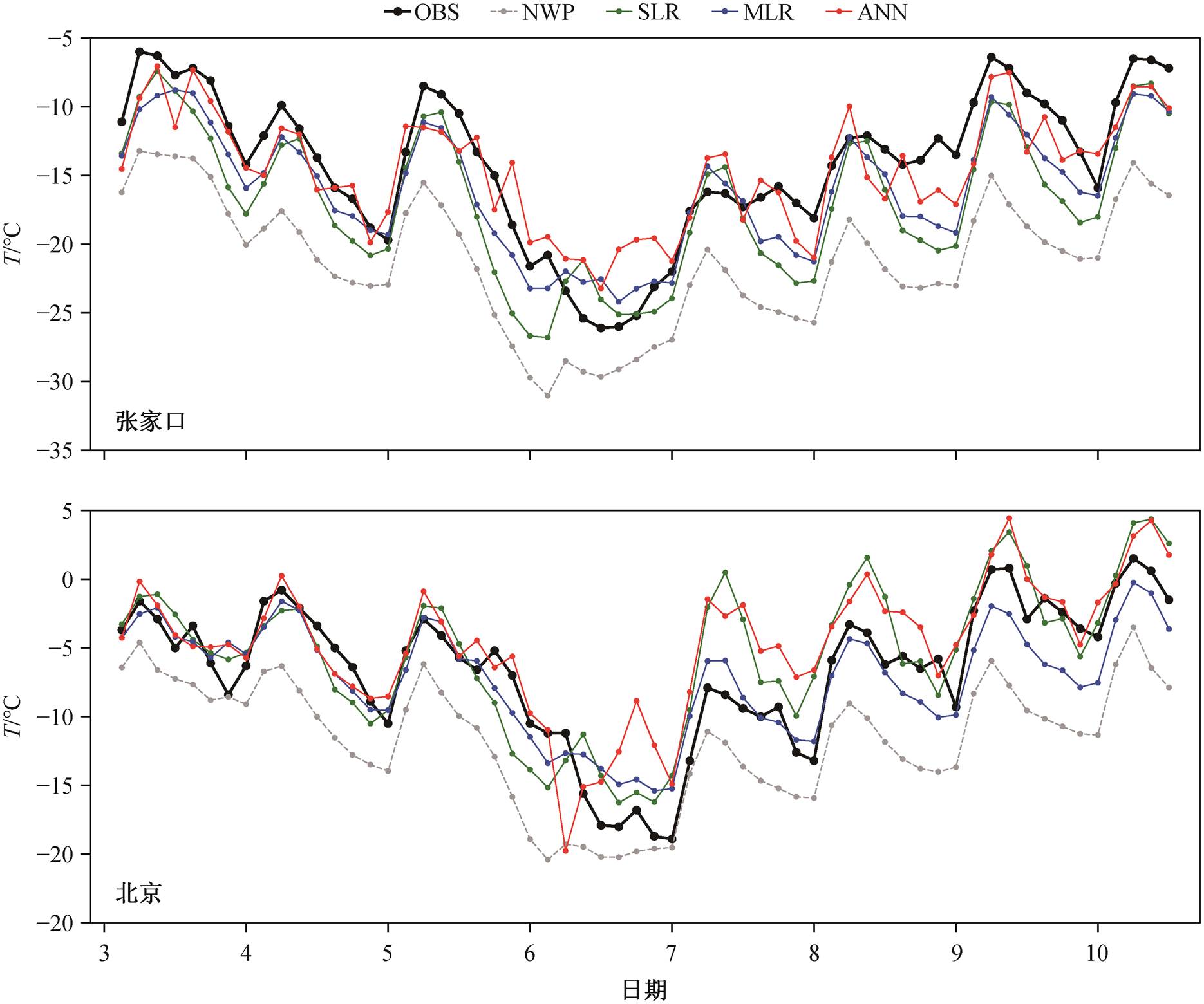
OBS数据2021‒01‒10更新, 其他4条折线是2021‒01‒03起报的180小时预报结果
图8 2021‒01‒03的气温预报结果
Fig. 8 Temperature forecast results at 2021-01-03
本文将人工神经网络算法引入 NWP 预报产品的后处理流程中, 提出一种针对台站天气预报的新模型 ANN, 可以实时制作站点地表气象要素(温度、湿度、气压和风速)未来 8 天的逐 3 小时预报。该 ANN 模型与传统的主观会商预报方式相比, 具有客观、实时、误差小和预报结果稳定的优势; 与传统的回归分析预报方式相比, 在日循环和年循环两种时间尺度上都具有明显优势。在预报时效方面, 短期预报(特别是 3 天以内的预报)的技巧显著高于基准模型, 尤其对于大尺度变量(如温度和气压), 优势更加明显。
本文提出的 ANN 模型已应用于 2022 年举办冬奥会的张家口 54401 和北京 54511 两个站点。全流程的计算机自动化操作, 使得整个预报过程响应时间极短, 预报效果出色。从初步结果看, 与其他后处理方法相比, 3 天以内的预报始终保持一定程度的优势。
该 ANN 模型最终的预报误差主要来源于 NWP本身的预报误差和 ANN 模型引入的误差两个方面, 前者更多地体现为 GFS 预报产品在中国地区的表现(即第二类可预报性问题), 后者即该 ANN 模型在设计时的误差累积, 包括输入变量的选择、输入数据的样本量、模型的层数和神经元节点数、模型的其他参数(激活函数、优化器、批标准化层和退化层等)等。前 3 个因素是本文工作中主要的误差来源, 第 4 个因素主要影响程序训练时的收敛效率, 对最终误差影响较小。
虽然本文从多个角度论证了该 ANN 模型的优异表现, 但该模型仍有如下改进空间。
1)在输入变量的选择方面, 本文经验性地使用11 个地面变量和 1 个年循环变量, 这些变量毫无疑问是预报气象要素的重要因子, 但其他地面要素和高空要素也可能对目标变量有积极贡献。若加入更多的输入变量, 有可能使模型的表现更好。
2)在预报要素的选择方面, 本文选择常见的变量温度、湿度、气压和风速, 这是因为这些变量基本上满足高斯分布, 适合使用广义的回归模型进行预报。对于云量和能见度等分类问题, 可考虑使用softmax激活函数来处理。
3)在预报方法的选择方面, 本文选择基础的ANN 方法。近年来, 复杂 ANN 网络迭代很快, 不仅循环神经网络(RNN 和 LSTM)以及卷积神经网络(CNN)风靡一时, 还有自编码解码器、残差网络和图神经网络[29]等方法面世, 对于天气预报这一非线性的回归问题, 或许有更好的方法使模型的表现进一步提高, 这有待更多的尝试。
4)在起报点和预报时效的选择方面, 本文只讨论 00 UTC 起报的 180 小时预报时效的 GFS 数据。实际上, GFS 每天发布 4 次预报, 最长预报时效可达 384 小时(16 天)。从理论上讲, 可以实现预报结果每天 4 次滚动更新, 每次预报未来两周的天气。本文构建模型的原理与之相同, 如有需求, 只需针对特定起报点和预报时效重复本文流程即可。
本文提出的后处理方法可用于改进当前天气预报流程中的主观预报部分, 且适用于任何有 10 年以上历史观测资料的偏僻站点。本文发展的后处理系统对特殊地点的常规气象保障(如张家口地区冬奥会的气象保障)以及军事领域的定点天气预报具有普适性。本文涉及的自动化 python 代码已经放在Harvard Dataverse (https://doi.org/10.7910/DVN/QB MOTV)托管, 读者可免费下载使用。
参考文献
[1] 缪育聪, 彭艳玉, 李建, 等. 北京冬奥会和冬残奥会历史同期气溶胶污染的高空环流特征研究. 北京大学学报(自然科学版), 2020, 56(5): 815‒823
[2] 杨萍, 张萌, 许小峰. 从《用天气图制作预报的原理》看艾伯克龙比的气象学思想. 气象, 2016, 42 (10): 1271‒1277
[3] 李泽椿, 毕宝贵, 金荣花, 等. 近 10 年中国现代 天气预报的发展与应用. 气象学报, 2014, 72(6): 1069‒1078
[4] Li H C, Yu C, Xia J J, et al. A model output machine learning method for grid temperature forecasts in the Beijing area. Advances in Atmospheric Sciences, 2019, 36(10): 1156‒1170
[5] Raza K, Jothiprakash V. Multi-output ANN model for prediction of seven meteorological parameters in a weather station. Journal of the Institution of Engi-neers (India): Series A, 2014, 95(4): 221‒229
[6] Dupuy F, Duine G, Durand P, et al. Local-scale valley wind retrieval using an artificial neural network applied to routine weather observations. Journal of Applied Meteorology and Climatology, 2019, 58(5): 1007‒1022
[7] Abhishek K, Singh M P, Ghosh S, et al. Weather forecasting model using artificial neural network. Procedia Technology, 2012, 4: 311‒318
[8] Shao J. Improving nowcasts of road surface tempe-rature by a backpropagation neural network. Weather and Forecasting, 1998, 13(1): 164‒171
[9] Klein B, Wolf L, Afek Y, et al. A dynamic convolu-tional layer for short range weather prediction // 2015 IEEE Conference on Computer Vision and Pattern Re-cognition (CVPR). Boston, 2015: 4840‒4848
[10] Zhou K H, Zheng Y G, Dong W S, et al. A deep learning network for cloud-to-ground lightning now-casting with multisource data. Journal of Atmosphe-ric and Oceanic Technology, 2020, 37(5): 927–942
[11] Li Q, Tang S E, Peng X, et al. A method of visibility detection based on the transfer learning. Journal of Atmospheric and Oceanic Technology, 2019, 36(10): 1945–1956
[12] Mehrkanoon S. Deep shared representation learning for weather elements forecasting. Knowledge-Based Systems, 2019, 179(1): 120‒128
[13] Shank D B, Hoogenboom G, McClendon R W. Dew-point temperature prediction using artificial neural networks. Journal of Applied Meteorology and Cli-matology, 2008, 47(6): 1757‒1769
[14] Comrie A C. Comparing neural networks and regres-sion models for ozone forecasting. Journal of the Air & Waste Management Association, 1997, 47(6): 653‒ 663
[15] 邹思琳, 任晓晨, 王成功, 等. 时间精度与空间信息对神经网络模型预报 PM2.5 浓度的影响. 北京大学学报(自然科学版), 2020, 56(3): 417‒426
[16] Chu Y H, Pedro H T C, Li M Y, et al. Real-time forecasting of solar irradiance ramps with smart image processing. Solar Energy, 2015, 114: 91‒104
[17] Li Y P, Lang J W, Ji L, et al. Weather forecasting using ensemble of spatial-temporal attention network and multi-layer perceptron. Asia-Pacific Journal of Atmospheric Sciences, 2020, 7, doi: 10.1007/s13143-020-00212-3
[18] 任晓晨, 邹思琳, 唐娴, 等. 基于集合经验模态分解和 BP 神经网络的北京市PM2.5 预报研究. 北京大学学报(自然科学版), 2019, 55(4): 615‒625
[19] 贾春晖, 窦晶晶, 苗世光, 等. 延庆‒张家口地区复杂地形冬季山谷风特征分析. 气象学报, 2019, 77 (3): 475‒488
[20] Rasp S, Lerch S. Neural networks for postprocessing ensemble weather forecasts. Monthly Weather Revi-ew, 2018, 146(11): 3885‒3900
[21] Ghimire S, Deo R C, Downs N J, et al. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. Journal of Cleaner Production, 2019, 216: 288‒310
[22] Rasel R I, Sultana N, Meesad P. An application of data mining and machine learning for weather forecasting // Meesad P, Sodsee S, Unger H. Recent Advances in Information and Communication Techno-logy 2017: IC2IT 2017. Cham: Springer, 2018: 169‒ 178
[23] Chaloulakou A, Grivas G, Spyrellis N. Neural network and multiple regression models for PM10 prediction in athens: a comparative assessment. Journal of the Air & Waste Management Association, 2003, 53(10): 1183‒1190
[24] Jaafar K, Ismail N, Tajjudin M, et al. Z-score and feedforward neural network (FFNN) for flood modelling at Kuala Krai Station. // 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC). Shah Alam: IEEE, 2016: 92‒97
[25] Koizumi K. An objective method to modify numerical model forecasts with newly given weather data using an Artificial neural network. Weather and Forecasting, 1999, 14(1): 109‒118
[26] McKendry I G. Evaluation of Artificial neural net-works for fine particulate pollution (PM10 and PM2.5) forecasting. Journal of the Air & Waste Manage- ment Association, 2002, 52(9): 1096‒1101
[27] Gagne D J, Haupt S E, Nychka D W, et al. Interpre-table deep learning for spatial analysis of severe hailstorms. Monthly Weather Review, 2019, 147(8): 2827‒2845
[28] Salman A G, Heryadi Y, Abdurahman E, et al. Single layer & multi-layer long short-term memory (LSTM) model with intermediate variables for weather fore-casting. Procedia Computer Science, 2018, 135: 89‒ 98
[29] Wu Z H, Pan S R, Chen F W, et al. A comprehensive survey on graph neural networks. IEEE Transaction on Neural Networks and Learning Systems, 2021, 32(1): 4‒24
Develop an Objective Post-processing System with Artificial Neural Network to Improve Numerical Weather Prediction for the Olympic Winter Games Beijing 2022
Abstract A new objective post-processing system with cutting-edge machine learning algorithm for numerical weather prediction is presented. The core of the system, a matrix of artificial neural network trained by using historical in-situ observations and model results, can be applied on the latest numerical weather prediction results and produce real-time forecast for specific stations. The authors investigate the performance of post-processing system for two stations, Zhangjiakou and Beijing, for the period 2005‒2020. It is shown that the forecasts produced by the new system are significantly more accurate than those produced by raw model forecasts, single-variable linear regression, and multi-variable linear regression, especially in terms of 3-day forecast. The authors developed all the core and auxiliary code by serving as Zhangjiakou and Beijing post-processing systems, which are routinely deployed since Nov. 1, 2020, to facilitate the weather service for the Olympic Winter Games at Beijing in 2022.
Key words artificial neural network; real-time forecast; numerical weather prediction; post-processing
doi: 10.13209/j.0479-8023.2022.011
国家自然科学基金(41875088, 41630527, 4171101348)资助
收稿日期: 2021-02-26;
修回日期: 2021-05-12