图1 实验观测平台及相关设备
Fig.1 Observation platform and related equipment
摘要 利用一对设置在相同气象条件下的黑白标准 A 型蒸发器皿, 观测两者气象要素、水温及蒸发量等动态特征, 并根据现有的 6 个蒸发模型, 探究水温对器皿蒸发量的影响。结果表明: 1)设计的观测方法可以用于研究水温对器皿蒸发的影响。黑皿与白皿之间的水温和蒸发速率呈现明显的差异, 在 50 天的观测期内, 二者平均水温差为 0.4°C, 平均日蒸发量差为 1.1mm/d; 2)在太阳辐射及其他气象要素相同的条件下, 黑白皿水温差每升高 1.0°C, 由水温驱动的日蒸发量差异为 0.808 mm/(d·°C); 3)在水温升高条件下, 没有考虑水温的经典蒸发模型的估值小于观测值, 并且估值的误差也有所增加。
关键词 器皿蒸发; 水温; 蒸发量; 蒸发模型
近年来, 气候变化问题日益严重[1], 根据 2020年世界气象组织(WMO)发布的结果, 全球平均气温比工业化前时期升高 1.1°C, 20 世纪 80 年代以来, 每10 年都比过去 10 年更为温暖, 并且地球水面温度比气温升高得更快[2]。气候变化等因素导致全球水文循环过程发生改变[3-4], 作为水循环中重要的环节, 水面蒸发直接影响区域的水量平衡和能量平衡, 并产生相应的不确定性变化。作为水文和气象站的常规蒸发仪, 蒸发器皿因其简便性、低成本和实用性, 广泛地应用于农业和气象等领域[5-7]。器皿蒸发量是全球水资源评价、江河湖泊水面蒸发以及水库水量计算的重要参考资料和物理指标, 对其进行准确的预测, 可为水资源评价水文气象预报以及农业活动决策等提供科学依据[8]。
关于蒸发量的模拟和预测研究始于 19 世纪初, Dalton[9]率先利用经验流体力学方法, 近似地描述该问题, 即提出蒸发量与水汽压差成正比, 比例系数为与风速有关的函数[10]。该比例系数取决于大气的稳定性[11], 还会因水面和周围下垫面的差异而有所不同[10]。随后, 基于观测实验的回归分析, 并综合考虑风速、气温和湿度等因素对蒸发量的影响, 学者们对 Dalton 公式中的风速函数进行深化和完善[12-15], 形成具有不同适用条件的 Dalton 系列公式。Bowen[16]认为蒸发过程中显热变化和潜热变化的本质都是分子的热运动, 因此从能量平衡的角度引入波文比, 即用显热通量和潜热通量的比值来计算潜热, 较好地解决了显热通量难以获取的问题。Penman[17]首次结合空气动力学和能量平衡原理估算水面蒸发量, 通过引入饱和水汽压-温度曲线的概念, 导出具有深远影响意义的 Penman 公式。基于 Penman 公式, Rotstayn 等[18]在稳态假设下提出计算蒸发皿蒸发量的 PenPan 模型, 其中包含空气动力项[19]和辐射项[20]。PenPan 模型的估计值与观测值吻合良好, 但该模型在夏季通常需要观测参数的周均值作为模型输入量, 在冬季则至少需要月均值作为模型输入[21-22], 即 PenPan 模型对于短时间尺度蒸发量的估测还需进一步优化。一些学者基于边界层扩散[23]或不同对流模式[24]等, 深入探究蒸发皿空气动力学蒸发过程。Thom 等[19]研究蒸发皿蒸发过程中自由对流和强制对流的作用。Lim 等[25]将Fick 的第一扩散定律与边界层理论相结合, 开发一种用于量化水面蒸发过程中水汽分子传输的方法, 可以有效地估算非稳态条件下短时间间隔(半小时)内的蒸发皿蒸发量。
器皿蒸发观测研究中, 一般通过人为加热器皿水体[24,26-27]来模拟器皿水温变化。Raimundo等[28]通过风洞试验和数值模拟, 研究强制对流以及水体加热的条件下不同因素对水面蒸发量的影响, 结果表明蒸发速率主要受风速、水-空气温差以及相对湿度的影响, 其中风速的影响最大。Poós 等[29]在强制对流条件下研究水面蒸发, 通过实验室内参数测定, 根据传统对流理论及 10 种经验关联式确定蒸发速率, 探究空气流速和空气温度的影响, 实测结果表明, 在水体没有被加热的情况下, 蒸发速率随空气流速和空气温度的升高而增加。
基于 Dalton 公式和 Penman 公式发展起来的一系列估算蒸发量的蒸发模型应用较为广泛, 但这些模拟方法中鲜有考虑水温因素对蒸发的影响。器皿蒸发观测研究中多以电加热蒸发器皿水体的方式, 会使得器皿引入额外的人为能量来源, 同时存在加热不均、水体内部有对流运动等问题, 可能造成对实际蒸发量的预测产生较大的低估误差, 进而低估基于器皿蒸发量预测的全球蒸散发量。全球蒸散发量直接关系全球水资源的规划评价和合理调配[8,30], 蒸散发量的低估会对农业需水量管理、旱情监测以及水资源的有效利用等产生重要影响[31-32]。
本研究设计一对黑白蒸发器皿, 定量地观测水温对器皿蒸发量的影响, 通过野外观测黑白器皿的气象要素、水温及蒸发量等动态特征, 将观测的蒸发量与现有的 6 个经典蒸发模型的模拟值进行比较, 探究水温对蒸发皿蒸发量的影响, 揭示水温对器皿蒸发的重要性。
本研究借鉴模拟未来大气中 CO2 浓度升高的FACE 实验思想[33-35], 在相同气象条件的观测现场安装一对标准 A 型蒸发皿, 考虑到黑色的蒸发皿会吸收更多的太阳辐射, 并使水温高于相同尺寸的标准蒸发皿, 将其中一个标准 A 型蒸发皿涂成黑色(黑皿), 另一个保持原有的白色(白皿), 可以实现在其他气象条件相同的条件下蒸发器皿水温的差异, 进而观测水温上升对器皿蒸发的影响。
为了获取器皿蒸发相关数据, 并验证蒸发模型在不同水温条件下的准确性和稳定性, 我们在北京大学深圳研究生院搭建室外观测实验平台(如图 1)。观测点的地理坐标为 22°59′98′′N, 113°98′44′′E, 属于亚热带海洋性气候, 夏季高温多雨, 冬季温和少雨。观测场地设置在楼顶, 周围较为空旷, 下垫面为人造屋顶, 较干燥, 无土壤和植被覆盖。观测项目包括蒸发器皿的气象要素(气温、风速、相对湿度、太阳辐射和大气压等)、蒸发皿水位和蒸发皿水温等, 分别由 Vantage Pro2 自动气象站、精密水位仪(Manual-Precision Water Level Instrument, Model 6541C, Unidata Pty Ltd.)、Cu-Co 热电偶和热红外温度传感器(THI-500, Tasco Co.Ltd.)获取数据, 气象和温度数据均通过数据采集仪(Campbell CR1000)连续获取。所有观测项目每 10 分钟采集一次数据。气象站、水位仪和数据采集仪等设备均通过 PV 模块、太阳能转换器及蓄电池系统供电。观测实验从2016 年 12 月至 2019 年 12 月, 期间由于设备清理、维护和极端天气等因素影响存在中断。为了排除下雨、极端天气和设备清理、维护等的影响, 并且最大程度地呈现不同蒸发皿(黑皿和白皿)之间的水温差异, 本研究采用 50 天无雨天气的气象、温度及水位综合数据。
图1 实验观测平台及相关设备
Fig.1 Observation platform and related equipment
通过 6 种经典蒸发模型, 对黑皿和白皿的蒸发量进行评估, 探究不同水温对蒸发皿蒸发量的影响。6 种经典蒸发模型为 Rohwer-P 模型[12,17]、Pen-man[17,36]模型、Sweers[37]模型、Thom[19]模型、Pen-Pan[18-20]模型和 Lim[25]模型, 除 Lim 外, 其他 5 种蒸发模型均未考虑水温因素。
1) Rohwer-P模型[12,17]:
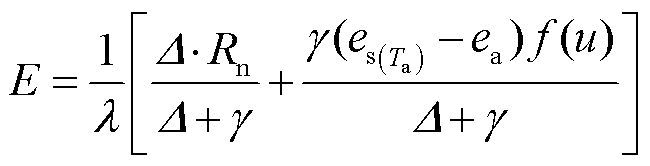, (1)其中, E为水面蒸发量(mm/d), es(Ta)为气温为 Ta时的饱和水汽压(kPa), ea为空气中的水蒸气分压(kPa), λ为汽化潜热(MJ/kg), D为饱和水汽压-温度曲线的斜率(kPa/°C), Rn 为净辐射通量(W/m2), g为温湿常数(kPa/°C), f (u)为风速函数。
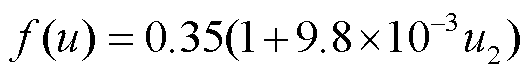, (2)
其中, u2 (m/s)为距蒸发面 2 m 处的风速。
2) Penman 模型[17,36]:
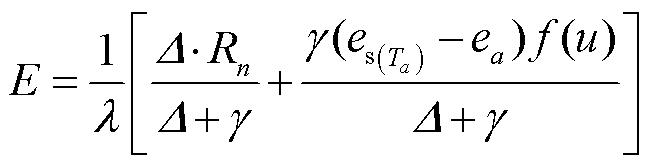, (3)其中, 风速函数 f(u)采用 Penman[36]提出的公式进行计算:
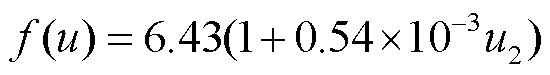。 (4)
3) Sweers 模型[37]:
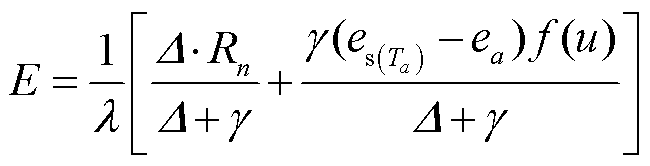, (5)其中, 风速函数f(u)为
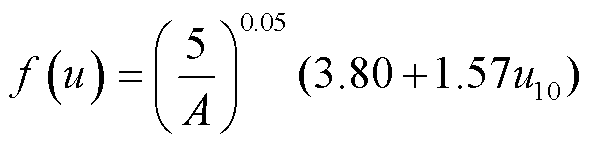, (6)
其中, u10为距蒸发面 10m 处的风速(m/s), A为蒸发面的表面积(m2)。
4) Thom 模型[19]:
, (7)其中, a 和 c 为无量纲常数 (a=1.31, c=2.1), 风速函数 f (u)为
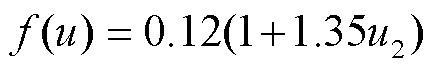。 (8)
5) PenPan 模型[18-20]:
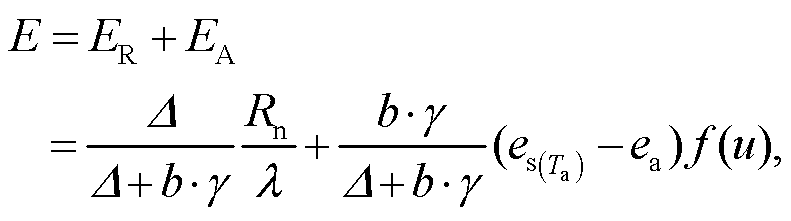(9)其中, ER 为辐射项的蒸发量(mm/d), EA 为空气动力项的蒸发量(mm/d), b 为无量纲常数(b=2.4), 风速函数f (u)为
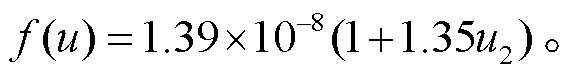(10)
6) Lim 模型[25]:
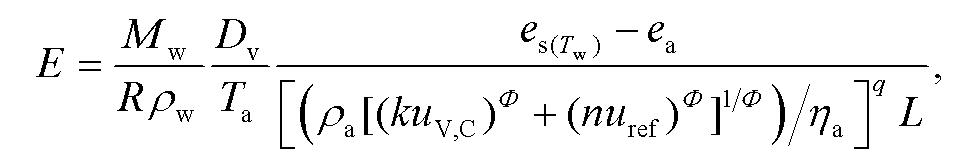(11)其中, E为水面蒸发速率(m/s), Mw为水的摩尔质量(kg/mol), rw为水的密度(kg/m3), es(Tw)为水温为 Tw时蒸发面的饱和蒸汽压(kPa), ra为空气密度(kg/m3), Dv为空气中水蒸气的扩散系数(m2/s), R为理想气体常数(J/(mol·K)), Ta为气温(K), Tw为水面温度(K), uV,C为空气在竖直方向运动的特征速度(m/s), uref为参考高度处水平风速(m/s), ηa为空气的动力黏度(kg/(m·s)), k(k≥0)、n(0<n<1)、Φ(Φ≥0)和 q(−1<q< 0)均为无量纲常数, L为蒸发面的特征长度(m)。
蒸发模型对特定时间尺度内的器皿蒸发速率进行估计, 即可将实验观测的瞬时值通过模型整合为一个较长时间尺度的蒸发量。由于蒸发皿水位会出现较严重的短期(10 分钟间隔)振荡现象, 我们将所有水位数据都进行平滑降噪处理, 并整合为一小时的值。同时, 将所有其他气象和水温数据重新归整为一个小时的平均值。为了更清楚地说明各蒸发模型的性能优劣, 采用偏差百分比(PBIAS)、均方根误差(RMSE)和 Nash-Sutcliffe 效率(NSE)[38]来评估蒸发模型。
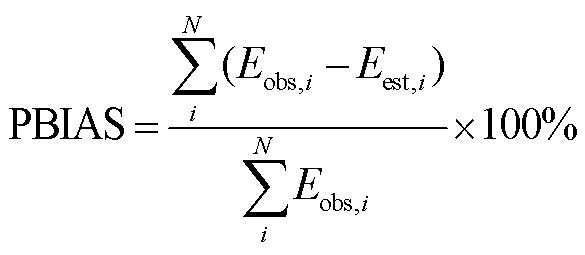, (12)
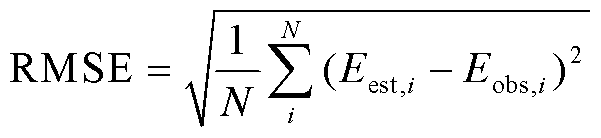, (13)
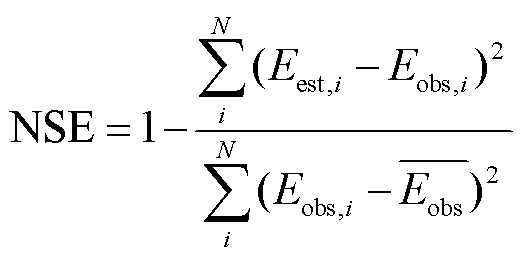, (14)
其中, N 为样本数量, Eest,i 为样本 i 的模型估计值, Eobs,i 为样本 i 的观测值,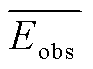 
为平均观测值。PBIAS 为模型比观测值高估或低估的百分比[39]。PBIAS为正值表示模型存在低估偏差, 为负值表示高估偏差[40-41]。NSE 值的范围为(-∞, 1.0], 并且当 NSE 接近 1.0 时, 表示模型模拟质量良好且模型可信度高; 当 NSE 远小于 0 时, 表明模型存在较大的误差。
本文根据蒸发速率较高、中等和较低的原则随机选取 3 个典型代表日(2017 年 6 月 7 日, 2019 年 2月 7 日和 2018 年 12 月 31 日), 分析各观测参数在这3 个代表日的变化特征。3 个代表日的风速、相对湿度、气温、大气压和太阳辐射等微气象参数变化特征如图 2(a)～(f)所示, 水温和蒸发速率的变化特征如图 2(g)～(i)所示。
从图 2 可以看出, 白天气温明显高于夜间, 一般早晨 06:00―07:00 气温开始回升, 06:00 附近处于最小值, 直至下午 14:00 左右达到最高值, 此后温度一直下降, 直到夜间 24:00 后温度下降趋势开始变缓(图 2(d)～(f)); 此外, 3 个代表日的气温变化范围分别为 27～34°C, 8～12°C 和 18～27°C, 可见 3 个代表日恰好落在不同的温度区间, 即对应不同的气候特征。相对湿度和气温基本上呈现相反的趋势(图2(a)～(c)), 且 3 天的相对湿度均为 70%～90%, 有时凌晨 00:00-08:00 相对湿度过低, 可能是前一天的天气影响所致。风速的随机性和波动性较大, 白天07:00―17:00 的风速明显高于夜间(图 2(a)～(c)), 并且通常在 0～4.0m/s 之间变化, 夜间风速较低(接近0), 白天风速较高, 最大风速通常出现在 14:00 左右(图 2(a)～(c))。从图 2(b)可以看出, 3 个代表日的大气压呈现连续波动的特征, 即从午夜 00:00 开始下降, 直至凌晨 4:00 后, 大气压开始回升, 10:00 左右达到一个峰值, 随后下降, 直到 16:00 达到全天最低值, 然后又逐渐升高, 直至夜间 22:00―24:00 达到另一个峰值。这种变化规律与气温有关。此外, 太阳辐射呈现“钟形”曲线的变化特征(图 2(d)～(f)), 从早晨 06:00 开始上升, 最大值一般出现在正午12:00―14:00 之间, 随后逐渐下降, 直至 19:00 前后达到最低, 夜间辐射量为 0。上述结果与陈伯龙等[42]的研究结果基本上一致。
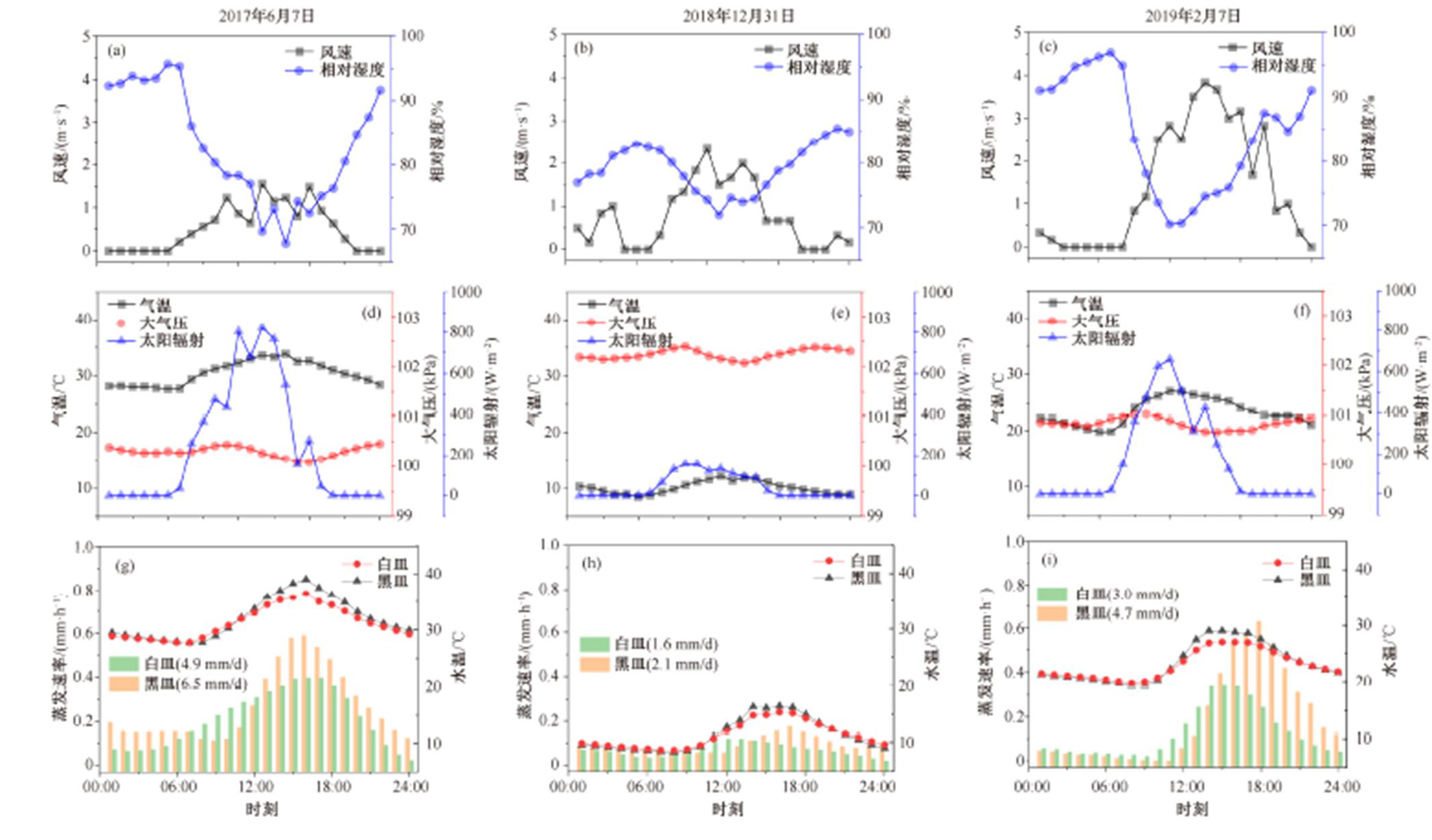
图2 气象参数、水温及蒸发速率变化特征
Fig.2 Variation characteristic of meteorological parameters, water temperature and evaporation rate
黑皿和白皿的水温及蒸发量的变化特征如图 2 (g)～(i)所示。可以看出, 3 个代表日中, 器皿水面温度早晨 08:00 左右最低, 14:00―16:00 达到最大, 3 个代表日水温的变化范围分别为 27～40°C, 8～17°C, 18～30°C, 其中白天时段(尤其是在 14:00―18:00 之间)黑皿水温明显高于白皿。由此可见, 白天有太阳辐射时, 涂黑的器皿具有明显的升温效果, 黑皿水温明显高于白皿, 从而验证了实验设置的合理性。3 个代表日中黑皿与白皿之间的最大温差为2.6°C 和 0.77°C, 0.9°C 和0.12°C, 平均温差为 2.0°C, 和 0.41°C, 由此可见, 在其他气象要素相同的情况下, 黑皿与白皿之间产生明显的水温温差。另外, 结合图 2(d)～(f)和图 2(g)～(i)可以看出, 水温的变化通常滞后于空气温度的变化(这是因为水的比热容大于空气空气, 升温更快, 降温也更快)。这与Hisatake 等[43-44]及 Lim 等[25]的研究结果有所不同。实际上, 水温的变化主要受整个水体能量收支(太阳辐射、蒸发潜热和显热等)的影响。因此, 水温和气温由于地理和气候等因素的不同而出现不同的变化特征是合理的。Rohwer[12]和 Bansal 等[45]测得白天时段水温高于气温, 此结果也被 Kintisch[2]、Adams等[24]和 Martinez 等[46]证明。
3 个代表日蒸发皿的蒸发速率变化趋势如图 2 (g)～(i)所示。通常, 器皿的蒸发速率在夜间较低, 从上午 8:00 开始升高, 并在下午 16:00 前后达到最大值。从图 2(g)～(i)可以看出, 蒸发速率在 3 个代表日的变化范围分别为 0～0.6, 0～0.2 和 0～0.6mm/h。黑皿和白皿在 3 个代表日内的平均蒸发速率分别为0.18 和 0.13mm/h, 平均日蒸发量分别为 4.4 和 3.2mm/d。由此可见, 黑皿的蒸发速率高于白皿, 即黑皿和白皿在其他气象要素相同而水温不同的条件下, 蒸发速率产生明显的差异, 具体来说, 3 个典型日内黑皿和白皿的日蒸发量差异分别为 1.6, 0.5 和1.7mm/d。上述结果表明, 水温对蒸发皿的蒸发速率有明确的控制作用。
在太阳辐射及其他气象要素相同的条件下, 水温对黑白器皿蒸发量的影响如图 3 所示。图 3(a)为观测期内黑皿和白皿的日蒸发量和太阳辐射变化情况, 可以看出, 黑皿的蒸发量总体上大于白皿, 二者的平均日蒸发量分别为 3.4 和 2.3mm/d, 黑皿平均日蒸发量比白皿大 1.1mm/d。此外, 太阳辐射的日最大值基本上在 200～1000W/m2 之间波动, 存在部分较大值(>800W/m2)和较小值(<600W/m2), 分别对应高辐射强度和低辐射强度的天气。通过对观测期间 50 天的水温数据进行分析可知, 在太阳辐射及其他气象要素条件相同的情况下, 黑皿的水温总体上也高于白皿, 二者的平均水温分别为 20.62°C和 20.22°C, 黑皿平均水温比白皿高 0.4°C。
从图 3(b)和(c)可以看出, 在太阳辐射及其他气象要素相同的条件下, 当显著性水平为 0.01时, 黑皿和白皿的日蒸发量均与水温显著正相关, Pearson相关系数分别为 0.41 和 0.50。黑皿日蒸发量与水温的线性拟合方程斜率为 0.113, 大于白皿(0.105), 表明水温对于黑皿蒸发量的影响比对白皿更加明显。由黑白皿之间的水温差和日蒸发量差(图 3(d))可知, 黑白皿水温差与日蒸发量差显著正相关(p<0.001), Pearson 相关系数为 0.57。黑白皿水温差与日蒸发量差的线性拟合方程斜率为 0.808, 表明在太阳辐射及其他气象要素相同的条件下, 黑白皿水温差每升高 1.0°C, 由水温驱动的日蒸发量差异为 0.808 mm/(d·°C)。
为了进一步说明水温对蒸发的影响, 本文基于黑皿和白皿观测数据, 对 6 种常用的经典蒸发模型精度进行评估, 结果如图 4 所示。6 个蒸发模型的估算值基本上分布在 1:1 线的一侧或是离散地分布在 1:1 线两侧。6 个蒸发模型对白皿的蒸发量估算值与实测值之间的 RMSE 分别为 2.00, 0.75, 1.78, 2.83, 1.35 和 1.06mm/d, 对黑皿的 RMSE 分别为3.12, 1.83, 1.21, 2.56, 2.49 和 1.01mm/d; 这 6 个模型对白皿的蒸发量估算值与实测值之间的 R2 分别为0.64, 0.72, 0.56, 0.62, 0.64 和 0.87, 对黑皿的 R2 分别为 0.45, 0.51, 0.40, 0.41, 0.44 和 0.70。可见, 上述经典蒸发模型对黑皿蒸发量的 RMSE 基本上都大于白皿, 而对于黑皿蒸发量, R2 基本上都小于白皿, 这表明对于水温较高的黑皿, 经典蒸发模型的估算误差均大于白皿。此外, 6 个模型对白皿的估算值均分布在黑皿估算值的上方, 并且黑皿蒸发量拟合方程的斜率均低于白皿, 表明在其他气象条件相同的情况下, 对于同一蒸发量, 6 个蒸发模型对水温较高的黑皿蒸发量的估算值偏低, 不同模型均存在不同程度的低估误差。
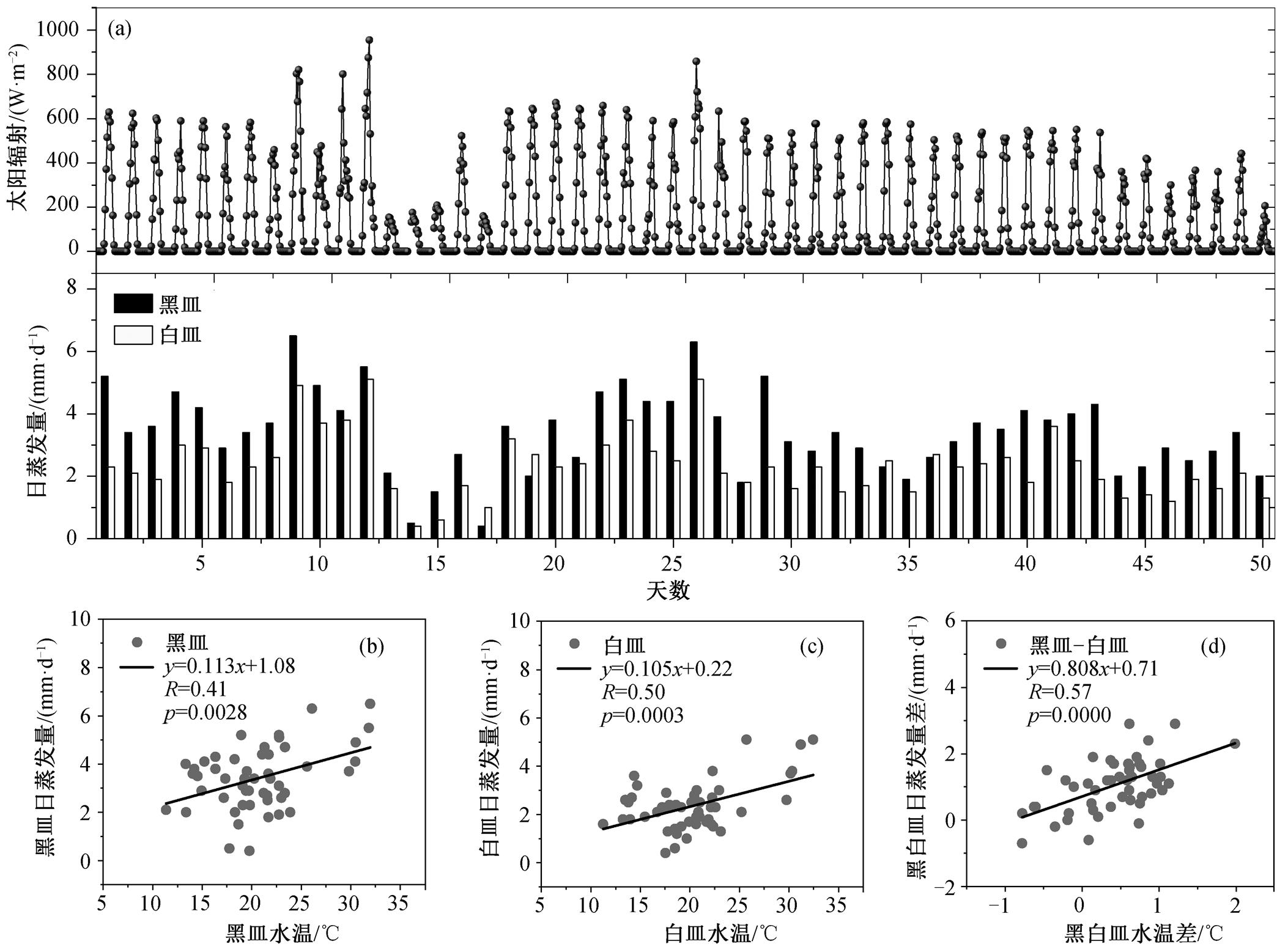
图3 相同气象条件下水温对黑白器皿蒸发量的影响
Fig.3 Influence of water temperature on black and white pan evaporation under the same meteorological conditions
6 个模型的评价指标结果对比如表 1 所示, 可以看出, Lim 模型的估算值与实测值最吻合, RMSE值最低, R2 最大, 表明与其他模型相比, 考虑水温影响的 Lim 模型更接近 1:1 线, 精度更高, Lim 模型在其他气象条件相同、水温不同的情况下, 估算精度不同, 并且对水温较高的黑皿蒸发量的估算仍存在一定的误差(R2 = 0.70)。上述结果表明, 水温因素在估算水面蒸发的模型中不可忽略, 未考虑水温因素的模型可能导致水体蒸发量的预测出现较严重的误差。从表 1 还可以看出, 尽管 Lim 模型比其他不考虑水温的模型性能更佳, 但这 6 个模型的PBIAS绝对值均较大, 而 NSE 值均远离 1.0, 且基本上都小于 0, 说明这些模型对于水温驱动蒸发皿蒸发量的适用性有待深入探究。因此, 对于不同水温条件下器皿蒸发量的估算, 除 Lim 模型精度尚可接受外, 其他 5个现有模型的精度均欠佳, 在未来的研究中, 需要进一步改进 Lim 模型, 或提出新的考虑水温影响的蒸发模型。
表1 不同模型的评价指标对比
Table 1 Comparison of evaluation indicators of different models
模型PBIAS/%RMSE/(mmd)−1NSER2 黑皿白皿黑皿白皿黑皿白皿黑皿白皿 Rohwer-P85.9679.163.122.00−4.86−2.950.450.64 Penman46.4421.771.830.75−1.020.440.510.72 Sweer−14.20−66.301.211.780.13−2.140.400.56 Thom−6.85−58.612.562.83−2.94−6.930.410.62 PenPan67.2851.252.491.35−2.72−0.800.440.64 Lim−10.75−33.821.011.060.39−0.110.700.87
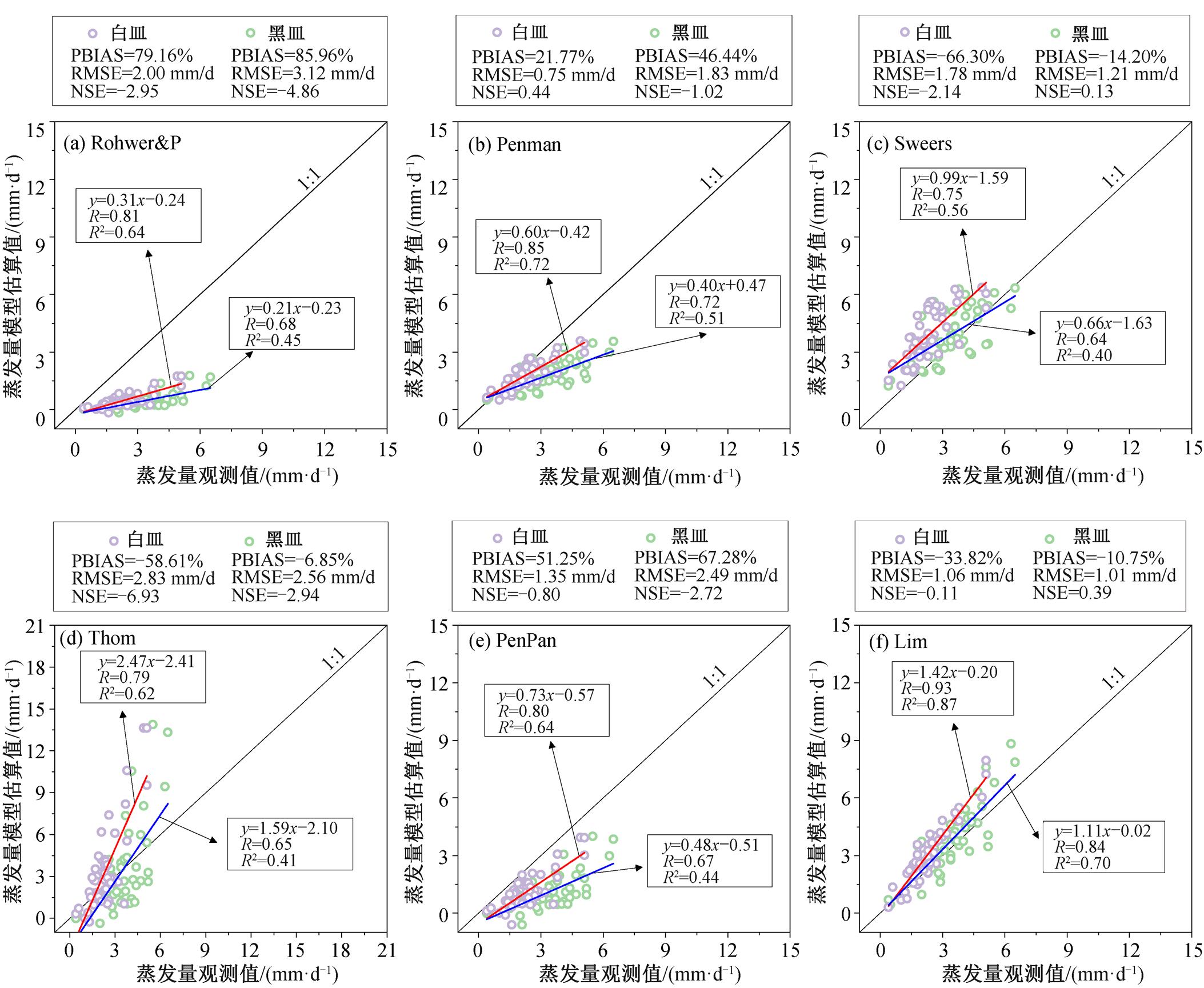
图4 蒸发模型的估算结果与观测结果对比
Fig.4 Comparison of the daily evaporation between the observed and estimated by evaporation models
本研究设计一对黑白蒸发器皿来定量地观测水温对器皿蒸发量的影响, 通过长期观测气象要素、水温和蒸发水位等动态变化特征, 并基于现有的 6 个经典蒸发模型模拟黑皿和白皿的蒸发量, 分析现有蒸发模型的局限性, 并探讨水温对器皿蒸发量的影响, 得到如下结论。
1)本文设计的观测方法可以用于研究水温对蒸发皿蒸发的影响。观测期 50 天内, 黑白蒸发皿的平均水温差为 0.4°C, 平均日蒸发量差为 1.1mm/d。在太阳辐射及其他气象要素相同的条件下, 黑白皿水温差每升高 1.0°C, 由水温驱动的日蒸发量差异为 0.808mm/(d·°C)。
2)由于没有考虑水温的影响, 现有的蒸发模型对水温升高背景下的器皿蒸发量估值普遍偏低。本文中, 6 个经典的器皿蒸发模型的估算值与实测值之间的 RMSE 分别为 3.12, 1.83, 1.21, 2.56, 2.49 和1.01mm/d, R2 分别为 0.45, 0.51, 0.40, 0.41, 0.44和0.70, 且 PBIAS 绝对值均较大, 而 NSE 值均远离1.0 (基本上都小于 0), 说明经典的器皿蒸发模型需要重新考虑水温的影响。
3)考虑水温影响的 Lim 模型可以在一定程度上改善蒸发皿蒸发的估算精度(RMSE≤1.06 mm/d, R2 ≥0.70), 但在估算水温较高的黑皿蒸发量时仍存在一定的误差(PBIAS=−10.75%, NSE=0.39)。因此, 水温对器皿蒸发的影响有待深入探究, 急需建立考虑水温因素的机理性蒸发模型。
致谢 研究工作得到北京大学环境与能源信息工程实验室历届同学对蒸发皿清理与数据采集等方面的协助, 得到王振华工程师、硕士研究生郝祥林等在仪器安装维护与数据分析等方面的协助, 在此表示衷心感谢。
参考文献
[1]Duan K, Caldwell P V, Sun G, et al.Understanding the role of regional water connectivity in mitigating climate change impacts on surface water supply stress in the United States.Journal of Hydrology, 2019, 570: 80-95
[2]Kintisch E.Earth’s lakes are warming faster than its air.Science, 2015, 350: 1449
[3]Brutsaert W, Parlange M.Hydrologic cycle explains the evaporation paradox.Nature, 1998, 396: 30
[4]Yang K, Wu H, Qin J, et al.Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: a review.Global and Planetary Change, 2014, 112: 79-91
[5]Stanhill G, Cohen, S.Global dimming: a review of the evidence for a widespread and significant reduction in global radiation with discussion of its probable causes and possible agricultural consequence.Agricultural and Forest Meteorology, 2001, 107(4): 255-278
[6]Lim W H, Roderick M L, Farquhar G D.A mathematical model of pan evaporation under steady state conditions.Journal of Hydrology, 2016, 540: 641-658
[7]Zuo H C, Chen B L, Wang S X, et al.Observational study on complementary relationship between pan evaporation and actual evapotranspiration and its variation with pan type.Agricultural and Forest Meteorology, 2016, 222: 1-9
[8]Snyder R L.Equation for evaporation pan to evapo-transpiration conversions.Journal of Irrigation and Drainage Engineering, ASCE, 1992, 118(6): 977-980
[9]Dalton J.Experimental essays on the constitution of mixed gases; on the force of steam or vapor from water and other liquids in different temperatures, both in a Torricellian vacuum and in air; on evaporation and on the expansion of gases by heat.Mem Manchester Liter and Phil Soc, 1802(5): 535-602
[10]McJannet D L, Webster I T, Stenson M P, et al.Estimating open water evaporation for the Murray-Darling Basin [R].Canberra: CSIRO, 2008
[11]Liu W T, Katsaros K B, Businger J A.Bulk parame-terization of the air-sea exchange of heat and water vapor including the molecular constraints at the inter-face.Journal of Atmospheric Science, 1979, 36: 1722-1735
[12]Rohwer C.Evaporation from free water surfaces.Washington: USDA Technical Bulletin No.271, 1931: 110
[13]Thornthwaite C W, Holzman B.The determination of evaporation from land and water surfaces.Monthly Weather Review, 1939, 67(1): 4-11
[14]Harbeck G E.A practical field technique for mea-suring reservoir evaporation utilizing mass-transfer theory.Washington: U S Government Printing Office, 1962
[15]Singh V, Xu C Y.Evaluation and generalization of 13 mass-transfer equations for determining free water evaporation.Hydrological Process, 1997, 11(3): 311-323
[16]Bowen I S.The ratio of heat losses by conduction and by evaporation from any water surface.Physical Re-view, 1926, 27: 779-789
[17]Penman H L.Natural evaporation from open water, bare soil and grass.Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1948, 193: 120-145
[18]Rotstayn L D, Roderick M L, Farquhar G D.A simple pan evaporation model for analysis of climate simu-lations: evaluation over Australia.Geophysical Re-search Letter, 2006, 33: L17715
[19]Thom A S, Thony J L, Vauclin M.On the proper employment of evaporation pans and atmometers in estimating potential transpiration.Quarterly Journal of the Royal Meteorological Society, 1981, 107: 711-736
[20]Linacre E T.Estimating US class a pan evaporation from few climate data.Water International, 1994, 19 (1): 5-14
[21]Roderick M L, Hobbins M T, Farquhar G D.Pan evaporation trends and the terrestrial water balance.I.Principles and observations.Geography Compass, 2009, 3: 746-760
[22]Roderick M L, Hobbins M T, Farquhar G D.Pan evaporation trends and the terrestrial water balance.II.Energy balance and interpretation.Geography Com-pass, 2009, 3: 761-780
[23]Schlichting K, Gersten K.Boundary layer theory. 4th.New York: McGraw-Hill, 1960
[24]Adams E E, Cosler D J, Helfrich K R.Evaporation from heated water bodies: predicting combined forced plus free convection.Water Resource Research, 1990, 26(3): 425-435
[25]Lim W H, Roderick M L, Hobbins M T, et al.The aerodynamics of pan evaporation.Agricultural and Forest Meteorology, 2012, 152: 31-43
[26]Jacobs A F G, Heusinkveld B G, Lucassen D G.Temperature variation in a class a evaporation pan.Journal of Hydrology, 1998, 206(12): 75-83
[27]Pauken M T.An experimental investigation of com-bined turbulent free and forced evaporation.Experi-mental Thermal and Fluid Science, 1999, 18(4): 334-340
[28]Raimundo A M, Gaspar A R, Oliveira A V M, et al.Wind tunnel measurements and numerical simulations of water evaporation in forced convection airflow.International Journal of Thermal Sciences, 2014, 86: 28-40
[29]Poós T, Varju E.Mass transfer coefficient for water evaporation by theoretical and empirical correlations, International Journal of Heat and Mass Transfer, 2020, 153: 1-9
[30]Wang K W, Liu X M, Liu C M, et al.The unignorable impacts of pan wall on pan evaporation dynamics.Agricultural and Forest Meteorology, 2019, 274(15): 42-50
[31]聂雄, 屈小娜.水面蒸发计算模型的研究进展.资源·环境, 2018, 29(7): 45-47
[32]Oki T, Kanae S.Global hydrological cycles and world water resources.Science, 2006, 313: 1068-1072
[33]Hendrey G R, Lewin K F, Nagy J.Control of carbon dioxide in unconfined field plots // Hendrey G R.Design and Execution of Experiments on CO2 Enrich-ment Ecosystems Research Report 6.Brussels, 1993: 309-329
[34]Hendrey G R, Ellsworth D S, Lewin K F, et al.A free-air enrichment system for exposing tall forest vegetation to elevated atmospheric CO2.Global Change Biology, 1999, 5: 293-309
[35]冯兆忠, 徐彦森, 尚博.FACE实验技术和方法回顾及其在全球变化研究中的应用.植物生态学报 2020, 44(4): 340-349
[36]Penman H L.Evaporation: an introductory survey.Netherlands Journal of Agricultural Science, 1956, 4(1): 9-29
[37]Sweers H E.A nomograph to estimate the heat-exchange coefficient at the water-air interface as a function of wind speed and temperature, a critical survey of some literature.Journal of Hydrology, 1976, 30(4): 375-401
[38]Nash J E, Sutcliffe J V.River flow forecasting through.Part I.A conceptual models discussion of principles.Journal of Hydrology, 1970, 10: 282-290
[39]Wang K, Liu X, Li Y, et al.A generalized evaporation model for Chinese pans.Journal of Geophysical Research: Atmospheres, 2018, 123(10): 943-966
[40]Gupta H V, Sorooshian S, Yapo P O.Status of auto-matic calibration for hydrologic models: comparison with multilevel expert calibration.J Hydrologic Eng, 1999, 4(2): 135-143
[41]Moriasi D N, Arnold J G, Van Liew M W, et al.Model evaluation guidelines for systematic quantification of accuracy in watershed simulations.Transactions of the ASABE, 2007, 50(3): 885-900
[42]陈伯龙, 左洪超, 高晓清, 等.蒸发皿蒸发及能量变化过程的微气象观测研究.高原气象, 2017, 36 (1): 87-97
[43]Hisatake K, Tanaka S, Aizawa Y.Evaporation rate of water in a vessel.J Appl Phys, 1993, 73: 7395-7401
[44]Hisatake K, Fukuda M, Kimura J, et al.Experimental and theoretical study of evaporation of water in a vessel.J Appl Phys, 1995, 77: 6664-6674
[45]Bansal P K, Xie G.A unified empirical correlation for evaporation of water at low air velocities.Interna-tional Communications in Heat and Mass Transfer, 1998, 25(2): 183-190
[46]Martinez J M M, Alvarez V M, Gonzalez-Real M M, et al.A simulation model for predicting hourly pan evaporation from meteorological data.Journal of Hydrology, 2006, 318: 250-261
Experimental Study of the Influence of Water Temperature on Pan Evaporation
Abstract Based on a pair of black and white standard A-type evaporation pans set under the same meteorological conditions, the dynamic characteristics of meteorological elements, water temperature and evaporation of the two pans were observed.The influence of water temperature on the evaporation of the evaporation pan was explored based on the existing 6 evaporation models.The results showed that 1) the designed observation method can be used to study the effect of water temperature on the pan evaporation.The water temperature and evaporation rate between the two pans were significantly different.During the 50-day observation period, the average water temperature difference between the two pans was 0.4°C, and the average daily evaporation difference was 1.1 mm/d.2) 1°C increase in water temperature difference between black and white pans will produce an evaporation difference of 0.808 mm/d under the same conditions of solar radiation and other meteorological elements.3) Under the condition of rising water temperature, the estimated value of the classical evaporation model without considering the water temperature would be smaller than the actual observed value, and the error of the estimation will also increase correspondingly.
Key words pan evaporation; water temperature; evaporation; evaporation model
doi: 10.13209/j.0479-8023.2021.093
收稿日期: 2021-01-13;
修回日期: 2021-02-23
深圳市知识创新计划基础研究(学科布局)项目(JCYJ20180504165440088)和国家自然科学基金(42001022)资助