(1)摘要 以 2018 年 9 月 28 日印尼 Ms 7.4 地震为背景, 利用张衡一号电磁卫星观测的 ULF 磁场 X, Y 和 Z 三分量数据, 采用滑动四分位(IQR)算法、滑动主成分分析算法(PCA)和短时傅里叶变换算法(STFT), 对震中范围的时空电磁数据进行分析, 结果显示 3 种算法都能有效地提取到震前异常。1)X, Y 和 Z 分量均值震前 7 天开始出现异常, 随着发震时间临近, Y 和 Z 分量的异常程度逐渐增加, 震前 2 天达到峰值, Y 分量最大异常达到0.7nT, 震后异常慢慢消失; 2)震前 5 天主成分出现异常, 第一主成分占比急剧下降, 下降幅度超过 15%, 第二、第三主成分占比急剧上升, 异常持续 3 天; 3)震前 9 天, 13 和 25Hz 功率谱密度占比同时出现大幅异常, 13Hz 占比上升 35%, 25Hz 占比下降超过 40%, 13Hz 占比出现正异常, 最大正异常达到 0.1, 25Hz 占比出现负异常, 最大负异常达到−0.15, 震后异常消失。结合同时段的太阳地磁活动情况, 认为上述电磁异常可以作为印尼地震的前兆。
关键词 印尼地震; 张衡一号; 滑动四分位(IQR); 滑动主成分分析(PCA); 短时傅里叶变换(STFT); 电磁异常
在地震孕育及发生过程中, 震源区及其周围会出现不同程度的电磁辐射现象, 这种辐射电磁场往往提前数天或数小时出现[1–3]。观测资料表明, 电磁异常是对短临地震反应最敏感的地震前兆之一[4–6]。大地震临震前电离层异常扰动及地震电离层耦合机制一直是地震前兆研究的热点[7], 地震科学家通过电磁学途径、化学途径以及声学途径, 论证了电离层扰动与地震孕育过程的关系, 其中电磁学途径主要是监测电磁场、电子温度、电子密度以及电子浓度总含量(TEC)和这些参量在震前以及地震期间存在的异常变化[8]。
在地震电磁分析领域, 通过主成分分析得到的第一分量的能量占比很高, 一般认为其与空间电流体的改变和诸如磁暴之类的全球性磁扰事件有关, 第二、第三主成分可能来自震源或人为干扰信号。Gotoh 等[9]和 Hattori 等[10]利用主成分分析方法, 研究 2000 年日本伊豆地震周边的 ULF 电磁数据, 发现第三主成分的占比出现显著异常。Han 等[11]用该方法研究 1998 年岩首地震, 发现第二主成分异常的映震效果比较明显。
本文采用滑动四分位(IQR)算法、滑动主成分分析算法(PCA)和短时傅里叶变换算法(STFT), 对印尼 Ms7.4 地震震中时空范围的电磁数据进行分析, 发现地震前电磁存在异常扰动现象。
电磁监测试验卫星(张衡一号)是中国地震立体观测体系的第一个天基平台, 也是国家地球物理场探测卫星的首发卫星, 目的是建立一个监测全球空间电磁场、电磁波、电离层等离子和高能粒子沉降等物理量的空间试验平台, 对中国及其周边地区开展准实时监测和跟踪, 开展全球 7 级以上、中国 6 级以上地震电磁信息分析研究, 探索地震电离层响应变化的信息特征及其机理, 为大震预测提供有价值的前兆信息[12]。
张衡一号(ZH-1)共搭载 3 类 8 种科学载荷: 第一类是用于电离层电磁场探测的载荷, 包括高精度磁强计(HPM)、感应式磁力仪(SCM)和电场探测仪(EFD); 第二类是用于原位等离子体参数探测的载荷, 包括朗缪尔探针(LAP)、等离子体分析仪(PAP)和高能粒子探测器(HEPP和意大利HEPD); 第三类是用于电离层结构探测的载荷, 包括 GNSS 掩星接收机(GRO)和三频信标发射机(TBB)[13]。本研究采用的数据是感应式磁力仪(SCM)探测到的 ULF 电磁三分量, 频带范围是 10～200Hz, 灵敏度是 5.0x10−5nT·Hz−1/2@2kHz, 采样率fs=1024Hz。
2018 年 9 月 28 日 UTC 18:02:44, 印尼中苏拉威西省(0.25°S,119.9°Ε)发生 Ms7.4 级地震, 在 UTC 15:00:02 发生过一次 Ms6.0 级地震, 震源深度都是10km。本文以其震中为研究中心, 经纬度±20° (20.25°S—19.75°N, 99.1°—139.9°E)范围为研究区域, 时间范围选择 2018 年 9 月 12 日—10 月 05 日, 即震前 15 天到震后 7 天。根据上述时空范围, 选择对应的ULF 磁场 X, Y 和 Z 三分量时间序列数据。
地磁场的变化和太阳活动都会导致空间电磁场的异常变化, 分析空间电磁异常的同时需关注该时段的空间环境状况, 因此提取 2018 年 9 月 12 日—10 月 05 日的太阳射电通量 F10.7 指数和地磁活动指数(Kp 指数和 Dst 指数), 数据来自美国航空航天局(NASA)的 OMNI-Web 公开数据(http://omniweb.gsfc.nasa.gov/)。根据F10.7 将太阳活动划分为 3 个等级: F10.7>150SFU, 100 SFU
滑动四分位(IQR)算法是稳健统计技术中用于表示数据离散度的一个量, 常用来检查数据的异常情况[18–19], 在地震前兆异常分析领域, 滑动四分位算法是一种常用的算法, 且效果不错[20–21]。本文选取 27 天作为时间窗口, 步长为 1 天, 27 天的均值数据组成时间序列, 并按照从小到大顺序排列为 X= [x1, x2, …, x27]。Q1, Q2 和 Q3 分别为第一、第二和第三四分位数。
(1)四分位距 IQR=Q3–Q1, 基于标准化正太分布计算IQR 与标准差的关系为 IQR=1.34σ, 本文定义Q2± 1.5IQR 作为电磁异常上下边界判断阈值, 采用 2σ作为阈值范围, 置信度为 95%。如果电磁均值在上下边界范围内, 则异常值为 0, 超过上边界为正异常, 低于下边界为负异常。异常值的求解公式如下:
(2)
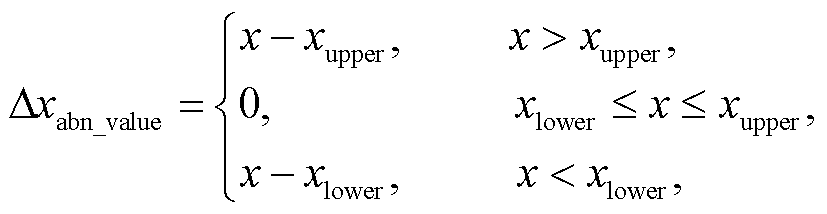(3)xupper是上边界, xlower是下边界, ∆xabn_value是异常值。
主成分分析(principal component analysis, PCA)算法是一种使用最广泛的数据降维算法, 主要通过分离不相关成分来提取主要成分[22–23], 且 PCA 不易受太阳地磁活动影响[24], 具有能分离不同信号、有效地识别相对较弱信号的优势, 可用于地震电磁扰动的研究[25–26]。Chang 等[27]提出滑动 PCA 方法, 采用全球电离层格网数据(GIM), 在 4 次强震(青海地震、本州地震、于田地震和尼泊尔地震)中, 发现震前 10 日内都会出现短时的震前异常。
滑动 PCA 方法的主要思想是将 n 维特征映射到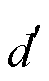
维上, 这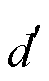维是全新的正交特征(也称为主成分), 是在原有 n 维特征的基础上重新构造出来的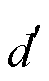维特征。经过多组参数对比, 本文选取滑窗长度为 27天, 太阳辐射周期也为 27 天, 这样可以减少太阳活动的影响[28]。每天 10 个均值组成二维矩阵, 步长为 1 天, 设时序矩阵为
。 (4)样本集为 D={x1, x2, …, xm}, 低维空间维数为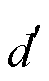, 对所有样本进行中心化:
(5)
计算样本的协方差矩阵 XXT 并做特征值分解, 取最大的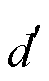个特征值对应的特征向量 W=[w1, w2, …,
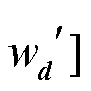。设置重构阈值 t = 95%, 选取使下式成立的最小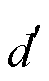值[29], 计算降维重构矩阵 A = DW。
。 (6)短时傅里叶变换(STFT)可以用于量化非平稳信号频率和相位随时间的变化, 基本思想是将时域信号在时间轴上截取成多个固定时长的时间窗, 并假定信号在时间窗内是一个平稳信号, 然后对窗内信号进行傅里叶变换, 沿着时间轴不断地滑动时间窗, 直到信号末端, 便可得到整段信号的时变频谱。短时傅里叶变换(STFT)定义为
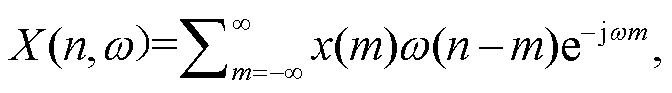(7)其中, x(m)为输入信号; ω(m)是窗函数, 在时间上反转并且有 n 个样本的偏移量; X(n, ω)是时间 n 和频率ω的二维函数, 将信号的时域和频域联系起来进行时频分析。本文窗函数选择 Hanning 窗, 时间窗大小设定为 1024 个数据点, 计算功率谱密度占比, 然后按天聚合, 生成时频图。
采用滑动四分位(IQR)算法, 对 2018 年 9 月 28日印尼 Ms7.4 地震进行分析。数据选取震前 15 天, 震后 7天的 ULF 磁场 X, Y 和 Z 三分量数据。先取绝对值, 再求平均值, 按天聚合, 计算 IQR 值, 结果如图 1 和 2 所示。从图 1 可以发现, 震前 7 天, 三分量均值已经超过 IQR 上限阈值。从图 2 可以发现, X, Y 和 Z分量均值大约在震前 7 天开始出现正异常, 随着发震时间的临近, Y 和 Z 分量的异常程度也逐渐增加, 震前 2 天达到峰值, Y 分量最大异常程度达到0.7 nT, 震后异常渐渐消失。
图 3 为空间活动指数的活动情况。可以看出, 震前 15 天至震后 7 天, 太阳地磁活动较为平静, Kp指数低于 4, Dst 指数大于−30 nT, F10.7 稳定在 69.8 左右。9 月 22 日出现微弱磁暴, 9 月 21 日、24日、25 日、26 日和 27 日, 太阳地磁活动都很平静, 分析结果表明, 图 2 中 9 月 22 日的正异常与磁暴有关, 其他 5 天的异常与地震有关系, 映震效果显著。
采用滑动主成分(PCA)分析方法, 对 2018 年 9月 28 日印尼 Ms7.4 地震进行震前异常分析。选取震前 15天, 震后 7 天的 ULF 磁场 X, Y 和 Z 三分量均值数据。选取滑窗长度为 27 天, 每天 10 个均值组成二维矩阵, 步长为 1 天, 滑窗计算每一天的第一、第二、第三主成分占比, 发现 X 分量映震效果明显。从图 4 可以发现, 震前 5 天第一主成分占比开始大幅下降, 降幅超过 15%, 第二、第三主成分占比开始急剧上升, 异常持续 3 天左右, 震前第三主成分占比先上升, 后下降, 直至恢复正常, 而 9月 23 日、24 日、25 日太阳地磁活动都较为平静, 分析结果显示这 3 天的异常与地震有关系, 映震效果明显。
图1 ULF磁场X分量、Y分量和Z分量均值以及IQR上限
Fig.1 Mean value and IQR upper limit of the X, Y and Z components of ULF magnetic field
对 ULF 磁场 X, Y 和 Z 三分量数据做快速傅里叶变换(FFT), 结果表明在 50Hz 频段以下主要有 13, 25 和 38Hz 等频段。
采用短时傅里叶变换(STFT)算法, 对 2018 年 9月 28 日印尼 Ms7.4 地震进行分析。窗函数选择Hanning 窗, 时间窗大小设定为 1024 个数据点, 数据选取震前 15 天, 震后 7 天的 ULF 磁场 X, Y和Z三分量数据, 计算功率谱密度占比, 结果如图 5 和 6 所示。从图 5 可以发现, 震前 9 天, 13 和 25Hz 功率谱密度占比同时出现大幅异常, 13Hz 占比上升 35%, 25 Hz 占比下降超过 40%, 异常现象持续到发震前一天。从图 6 可以发现, 随着发震时间临近, 13Hz 占比条带颜色逐渐加深, 25Hz 占比条带颜色逐渐变浅, 震后条带颜色才恢复正常。
采用滑动四分位(IQR)算法, 对功率谱密度占比计算 IQR。从图 7 可以发现, 震前 9 天, 13Hz 出现正异常, 25Hz 出现负异常, 其中最大正异常达到0.1, 最大负异常达到−0.15, 震后异常才消失, 9 月17 日、19 日、21 日、24 日和27日太阳地磁活动都较为平静, 没有磁暴发生, 分析结果表明, 这 5 天的异常与地震有关系。地震孕育过程中电磁辐射引入新的频率成分, 扰乱频率成分之间原有的相对占比, 映震效果显著。13 和 25 Hz可能是舒曼谐波。
图2 ULF磁场X分量、Y分量和Z分量IQR异常
Fig.2 IQR anomalies of X, Y and Z components of ULF magnetic field
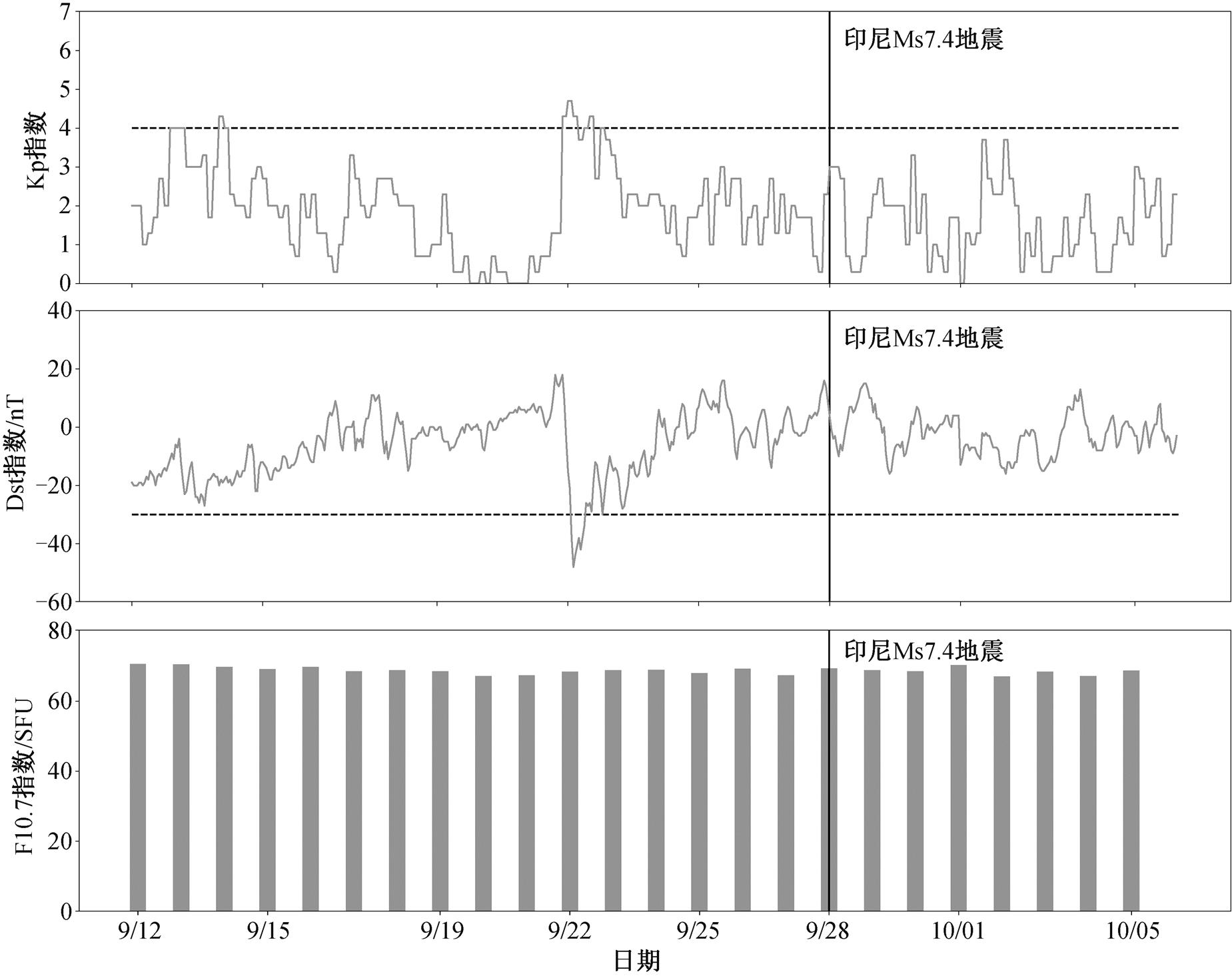
图3 2018 年 9 月 12 日—10 月 5 日空间活动指数分布
Fig.3 Spatial activity indexdistribution from September 12 to October 5, 2018
图4 ULF 磁场 X 分量第一、第二和第三主成分占比
Fig.4 Proportion of the first, second and third principal components of the X component of ULF magnetic field
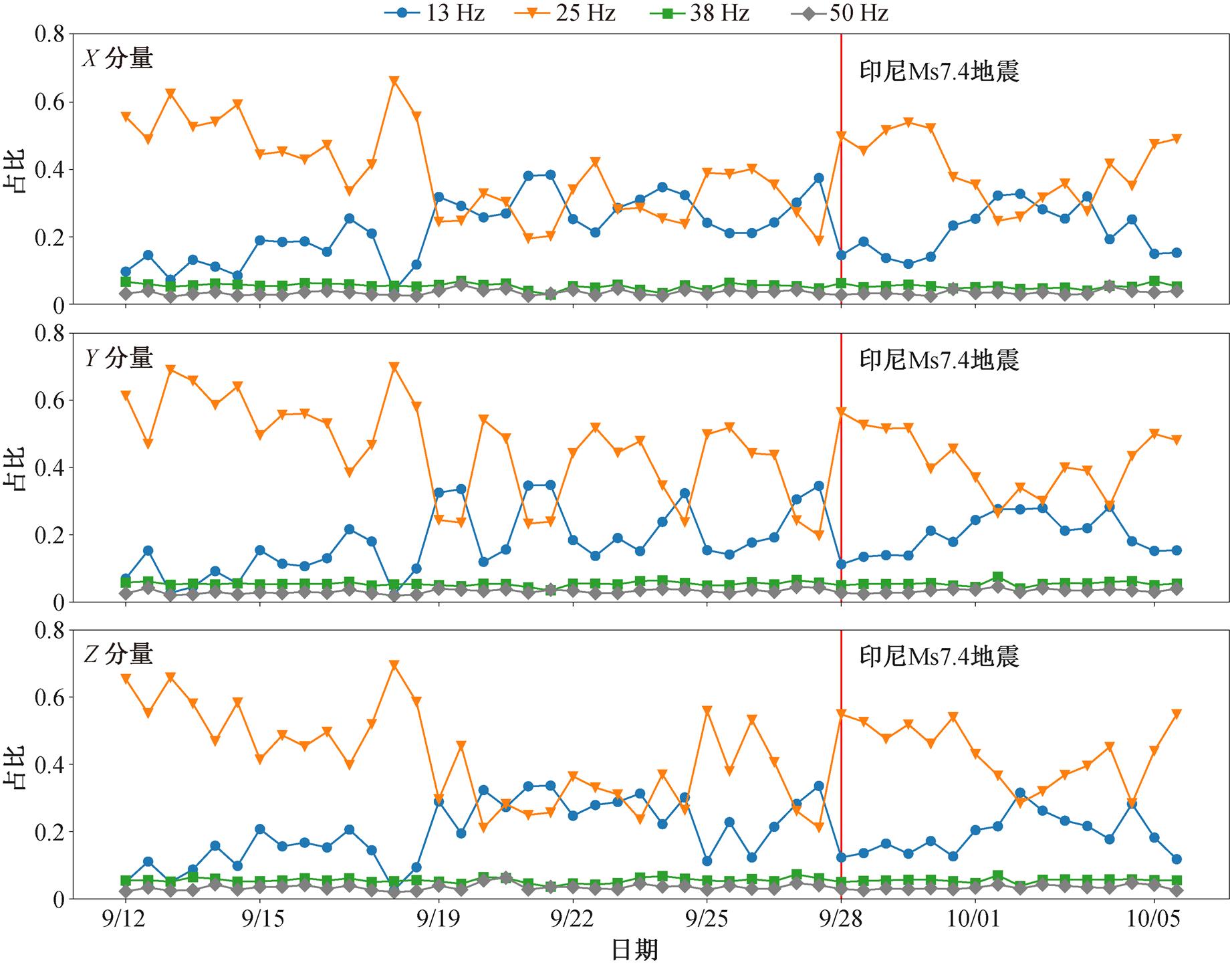
图5 ULF 磁场 X 分量、Y 分量和 Z 分量各频率功率谱密度占比
Fig.5 Ratio of power spectral densities of X, Y and Z components of ULF magnetic field
图6 ULF磁场X分量、Y分量和Z分量功率谱密度占比时频图
Fig.6 Time-frequency diagrams of the ratio of power spectral densities of X, Y and Z components of ULF magnetic field
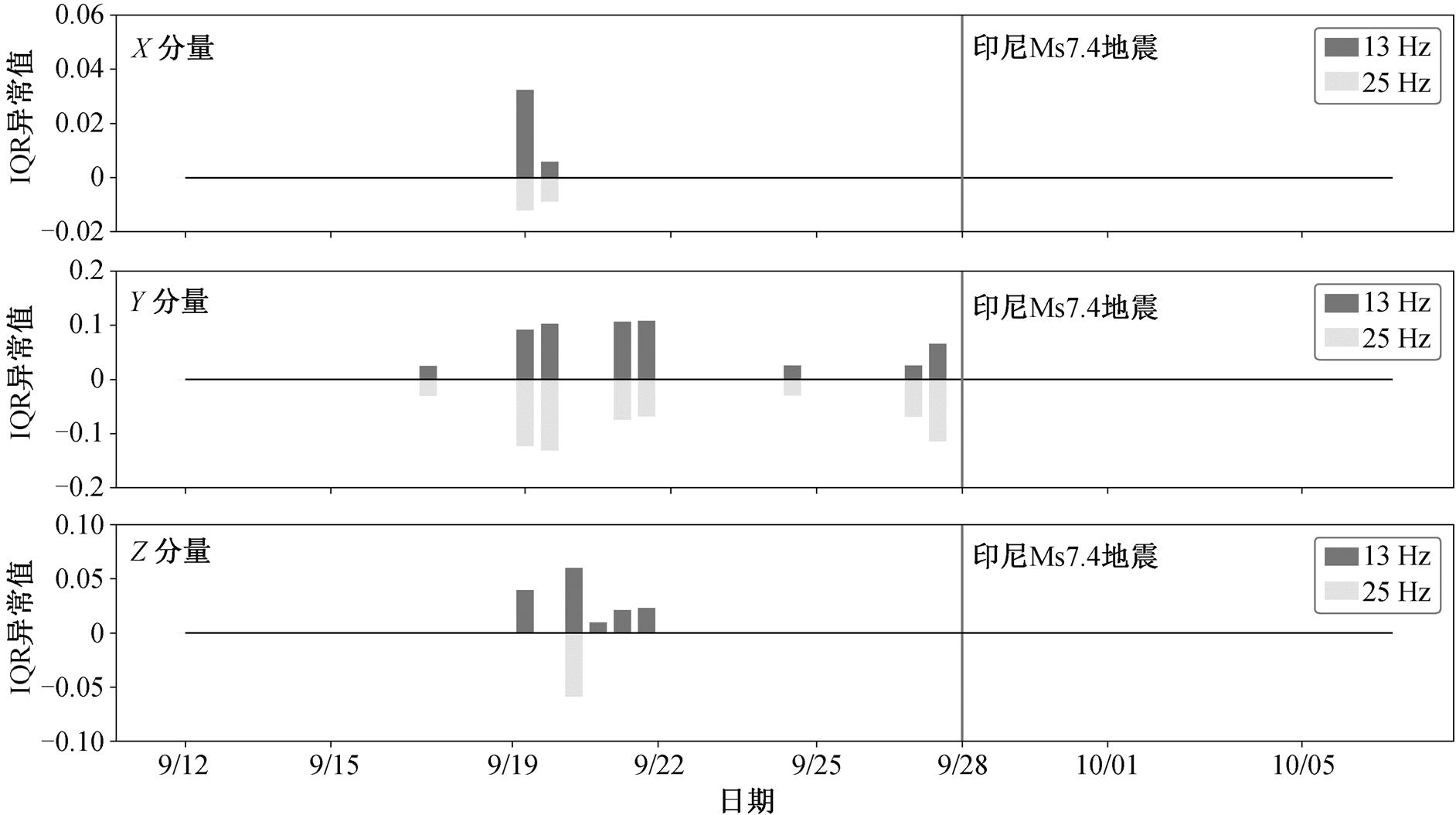
图7 ULF磁场X分量、Y分量和Z分量功率谱密度占比IQR异常
Fig.7 IQR anomalies of the ratio of power spectral densities of X, Y and Z components of ULF magnetic field
本文以 2018 年 9 月 28 日印尼 Ms7.4 地震为背景, 利用张衡一号电磁卫星观测到的 ULF 磁场 X, Y 和 Z 三分量数据, 采用滑动四分位算法、滑动主成分分析算法和短时傅里叶变换算法, 对震中范围时空电磁数据进行分析。结合同时段太阳地磁活动情况, 经过对比分析, 发现 3 种算法都能有效地提取震前显著电磁异常, 且异常出现时间都在地震前几天至一周左右, 与 Han 等[30–31]的研究结果具有较好的一致性。3 种算法对捕捉临震异常以及地震预测有重要的意义, 方便后续在电磁卫星地震领域开展更深入的探索。
综合 3 种算法的分析结果, 关于印尼地震前电磁异常情况总结如下。
1)X, Y 和 Z 分量均值震前 7 天开始出现异常, 随着发震时间临近, Y 和 Z 分量的异常程度逐渐增加, 震前 2 天达到峰值, Y 分量最大异常程度达到 0.7 nT, 震后异常才慢慢消失。
2)震前 5 天主成分开始出现异常, 第一主成分占比急剧下降, 降幅超过 15%, 第二、第三主成分占比急剧上升, 异常现象持续 3 天左右。
3)震前 9 天, 13Hz 和 25Hz 功率谱密度占比同时出现大幅异常, 13Hz 占比上升 35%, 25Hz 占比下降超过 40%, 13Hz 出现正异常, 最大正异常达到0.1, 25Hz 出现负异常,最大负异常达到−0.15, 震后异常才消失。
参考文献
[1]Molchanov O A, Mazhaeva O A, Protopopov M L, et al.Electromagnetic VLF radiation of seismic origin observed on the interkosmos-24 satellite.Geomag-netizm I Aeronomiya, 1992, 32(6): 128–137
[2]Hirano T, Hattori K.ULF geomagnetic changes pos-sibly associated with the 2008 Iwate-Miyagi Nairiku earthquake.Journal of Asian Earth Sciences, 2011, 41(4/5): 442–449
[3]Karakelian D, Klemperer S L, Fraser-Smith A C, et al.Ultra-low frequency electromagnetic measurements associated with the 1998 Mw 5.1 San Juan Bautista, California earthquake and implications for mechani-sms of electromagnetic earthquake precursors.Tecto-nophysics, 2002, 359(1/2): 65–79
[4]Bleier T, Freund F.Earthquake [earthquake warning systems.IEEE Spectrum, 1996, 42(12): 22–27
[5]Huang Q H.Retrospective investigation of geophysi-cal data possibly associated with the Ms8.0 Wen-chuan earthquake in Sichuan, China.Journal of Asian Earth Sciences, 2011, 41(4/5): 421–427
[6]吕亚轩, 王新安, 黄继攀, 等.基于 AETA 电磁扰动对九寨沟 Ms7.0 级地震的研究.北京大学学报(自然科学版), 2019, 55(6): 1007–1013
[7]蔡军涛, 赵国泽, 詹艳, 等.地震期间电离层扰动现象研究.地球物理学进展, 2007, 22(3): 695–701
[8]刘江, 陈聪, 何福秀.基于 GPS 数据的汶川、九寨沟地震震前电离层异常分析.四川地震, 2019(4): 11–15
[9]Gotoh K, Akinaga Y, Hayakawa M, et al.Principal component analysis of ULF geomagnetic data for Izu islands earthquakes in July 2000.J Atmos Elect, 2002, 22: 1–12
[10]Hattori K, Serita A, Gotoh K, et al.ULF geomagnetic anomaly associated with 2000 Izu Islands earthquake swarm, Japan.Physics & Chemistry of the Earth, 2004, 29: 425–435
[11]Han P, Huang Q H, Xiu J G.Principal component analysis of geomagnetic diurnal variation associated with earthquakes: case study of the M6.1 Iwate-ken Nairiku Hokubu earthquake.Chinese Journal of Geophysics, 2009, 52(6): 1556–1563
[12]袁仕耿, 朱兴鸿, 黄建平.电磁监测试验卫星(张衡一号)系统设计与关键技术.遥感学报, 2018, 22 (增刊): 32–38
[13]王兰炜, 胡哲, 申旭辉, 等.电磁监测试验卫星(张衡一号)数据处理方法和流程.遥感学报, 2018, 22 (增刊): 39–55
[14]Fejer B G, De Paula E R, Gonzalez S A, et al.Average vertical and zonal F-region plasma drifts over Jicamarca.Journal of Geophysical Research, 1991, 96(A8): 13901–13906
[15]Fejer B G, Paula E R D, Batista I S, et al.Equatorial F region vertical plasma drifts during solar maxima.Journal of Geophysical Research, 1898, 94(A9): 12049–12054
[16]沈晓飞, 倪彬彬, 顾旭东, 等.第 23 太阳活动周期太阳风参数及地磁指数的统计分析.地球物理学报, 2015, 58(2): 362–370
[17]Lin J W.Potential reasons for ionospheric anomalies immediately prior to China’s Wenchuan earth-quake on 12 May 2008 detected by nonlinear principal component analysis.International Journal of Applied Earth Observation and Geoinformation, 2012, 14(1): 178–191
[18]Guo J, Li W, Liu X, et al.On TEC anomalies as precursor before Mw 8.6 Sumatra earthquake and Mw 6.7 Mexico earthquake on April 11, 2012.Geoscien-ces Journal, 2015, 19(4): 721–730
[19]Guo J, Li W, Yu H, et al.Impending ionospheric anomaly preceding the Iquique Mw 8.2 earthquake in Chile on 2014 April 1.Geophysical Journal Interna-tional, 2015, 203(3): 1461–1470
[20]Fuying Z, Yun W, Jian L, et al.Study on method of detecting ionospheric TEC anomaly before earth-quake.Journal of Geodesy and Geodynamics, 2009, 29(3): 50–54
[21]Marchetti D, Akhoondzadeh M.Analysis of swarm satellites data showing seismo-ionospheric anomalies around the time of the strong Mexico (Mw=8.2) earthquake of 08 September 2017.Advances in Space Research, 2018, 62(3): 614–623
[22]Lin J W.Principal component analysis method in the detection of total electron content anomalies in the 24 hrs prior to large earthquakes.Arabian Journal of Geosciences, 2011, 4(3/4): 575–593
[23]de Souza K T, Luís C L, Ernesto G L.Using the Karhunen-Loove transform to suppress ground roll in seismic data.Earth Sciences Research Journal, 2005, 9(2): 139–147
[24]邹斌, 郭金运, 常晓涛, 等.基于主成分分析与滑动四分位法的震前 TEC 异常探测对比分析.全球定位系统, 2016, 41(4): 63–69
[25]姚休义, 冯志生.地震磁扰动分析方法研究进展.地球物理学进展, 2018, 33(2): 0511–0520
[26]王新安, 雍珊珊, 黄继攀, 等.基于 AETA 监测数据的地震预测研究.北京大学学报(自然科学版), 2019, 55(2): 209–214
[27]Chang X, Zou B, Guo J, et al.One sliding PCA method to detect ionospheric anomalies before strong earthquakes: cases study of Qinghai, Honshu, Hotan and Nepal earthquakes.Advances in Space Research, 2017, 59(8): 2058–2070
[28]安玉柱, 张韧, 王伟民, 等.太阳黑子数与电离层 TEC 的相关性分析.解放军理工大学学报: 自然科学版, 2012, 13(5): 101–106
[29]周志华.机器学习.北京: 清华大学出版社, 2016: 229–232
[30]Han P, Hattori K, Hirokawa M, et al.Statistical analy-sis of ULF seismomagnetic phenomena at Kakioka, Japan, during 2001–2010.Journal of Geophysical Re-search: Space Physics, 2014, 119: 4998–5011
[31]Han P, Hattori K, Zhuang J, et al.Evaluation of ULF seismo-magnetic phenomena in Kakioka, Japan by using Molchan’s error diagram.Geophysical Journal International, 2017, 208(1): 482–490
Research on Indonesia Ms 7.4 Earthquake Based on Data of Zhangheng-1 Electromagnetic Satellite
Abstract Taking the Ms7.4 earthquake in Indonesia on September 28, 2018 as the background, this paper uses the sliding quartile (IQR) algorithm, sliding principal component analysis (PCA) algorithm and short-time Fourier transform (STFT) algorithm to study the space-time electromagnetic data in the epicentral area by using the X, Y and Z components of ULF magnetic field observed by Zhangheng-1 electromagnetic satellite.The results show that the three algorithms can effectively extract the anomaly before the earthquake.1) The mean value of X, Y and Z components began to appear anomaly 7 days before the earthquake.The anomaly degree of Y and Z components increased gradually with the approaching of the earthquake occurrence time, and reached the peak value 2 days before the earthquake.The maximum anomaly degree of Y component reached 0.7 nT, and then slowly disappeared after the earthquake.2) 5 days before the earthquake, the anomaly of the principalcomponent began to appear, the proportion of the first principal component decreased sharply by more than 15%.The proportion of the second and third principal components increased sharply, and the anomaly lasted for 3 days.3) 9 days before the earthquake, the proportion of 13 and 25 Hz power spectral density anomalies appeared at the same time, 13 Hz proportion increased by 35%, 25 Hz proportion decreased by more than 40%.13 Hz proportion appeared positive anomalies and 25 Hz proportion appeared negative anomalies, of which the largest positive anomaly reached 0.1, the largest negative anomaly reached −0.15.The anomalies disappeared after the earthquake.According to the solar geomagnetic activity in the same period of time, the comprehensive analysis shows that the above electromagnetic anomalies can be used as precursors of earthquakes in Indonesia.
Key words Indonesian earthquake; Zhangheng-1; sliding quartile (IQR); principal component analysis (PCA); short-time Fourier transform (STFT); electromagnetic anomalies
doi: 10.13209/j.0479-8023.2021.097
深圳市科技计划项目(JCYJ20190808161401653, JCYJ20180503182125190)资助
收稿日期: 2020–12–05;
修回日期: 2021–01–30