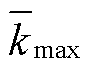)皆处于 4—6 月, 存在明显的春季预报障碍(SPB)现象。在衰减期, 同类型事件的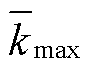分布相似: 弱中部型厄尔尼诺事件的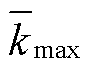皆处于春季, 存在明显的 SPB 现象; 强东部型厄尔尼诺事件的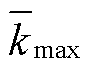分散在其他季度, 不存在 SPB现象。个体事件间存在一定的差异, 可能与事件的特征(如事件类型和强度)有关。摘要 利用长短期记忆网络(LSTM)深度学习算法构建一个热带太平洋 Niño3.4 指数预测模型, 并分析模型的季节预报误差。结果表明, LSTM 模型能够较好地预测厄尔尼诺事件的变化趋势, 但针对不同类型的厄尔尼诺事件有不同的表现。对于 1997/1998 和 2015/2016 强东部型厄尔尼诺事件, 该模型能较准确地预测事件的趋势和峰值, 距平相关系数(ACC)达到 0.93 以上。但是, 对于 1991/1992 和 2002/2003 弱中部型厄尔尼诺事件, 在峰值预测方面表现不好。在厄尔尼诺增长期, 预报误差的季节增长率最大值(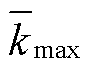)皆处于 4—6 月, 存在明显的春季预报障碍(SPB)现象。在衰减期, 同类型事件的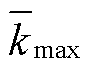分布相似: 弱中部型厄尔尼诺事件的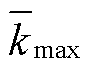皆处于春季, 存在明显的 SPB 现象; 强东部型厄尔尼诺事件的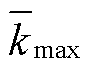分散在其他季度, 不存在 SPB现象。个体事件间存在一定的差异, 可能与事件的特征(如事件类型和强度)有关。
关键词 长短期记忆人工神经网络(LSTM); ENSO; 预报误差; 春季预报障碍(SPB); Niño3.4指数
ENSO (El Niño-Southern Oscillation)预测模型可根据所依据的计算原理分为统计模型和动力学模型两大类[1‒2]。统计模型主要结合大量的历史数据和统计理论(如统计回归和神经网络), 找出大气与海洋变量之间的函数关系。动力学模型主要基于大气‒海洋相互作用的动力学理论, 广泛应用于季节时间尺度的 ENSO 预测。在过去的几十年中, 通过改进初始条件和参数化方案, 开发新的预测方法, ENSO 的预测能力得到很大的提升[3]。然而, 如果将预测模型的起报时间提前 6 个月以上, 两类模型的预测能力都会因春季预极障碍(spring predictabi-lity barrier,SPB)现象而大幅度下降[4‒6]。
SPB 现象最先由 Webster 等[7]发现, 已成为 ENSO预报研究领域非常重要的课题。他们看到, 一旦遇到北半球的春季, 对 ENSO 的预测能力将迅速衰减, 且与预报起始月份和预报提前时间无关。科学家针对 SPB 展开大量研究, 但对其形成原因没有统一的观点[8]。Webster 等[7]率先提出, 海‒气耦合系统在春季处于最敏感时期, 有利于误差增长; 同时, 南亚夏季风也处于发展阶段, 很容易诱发 SPB 现象。Webster[9]进一步指出, 春季是赤道耦合系统最脆弱的季节, 系统的“信噪比”最低, 最易受外界干扰, 从而导致 SPB 形成。此外, Torrence 等[10]认为气候态的转换也是SPB 的诱发因子。然而, Wang 等[11]发现, 当模型中海‒气耦合系数保持不变时, SPB现象仍会出现, 因此弱的海‒气耦合并不能解释模型中的 SPB 现象。通过分析模型的扰动机制, 他们认为春季最大的垂直温度梯度和最弱的东西热力差异有利于耦合系统扰动的增长, 进而使春季海‒气耦合最不稳定, 有利于 SPB 现象的产生。为了验证Wang 等[11]模型中 SPB 的成因, Mu 等[12]将理论模型记为 WF96, 分别计算处于海‒气耦合强不稳定性和弱不稳定性背景下的厄尔尼诺事件的条件非线性最优扰动(conditional nonlinear optimal perturbation, CNOP), 结果表明, 强不稳定性条件下的春季误差增长明显更大, 且初始误差越大, 差异更明显, 因此春季海‒气耦合不稳定性是 SPB 的成因之一。一些研究者从误差增长的角度, 认为平均态的年循环、厄尔尼诺的结构和某些初始误差的联合作用诱发 SPB[13‒14]。最近, Meng 等[15]提出一种基于信息熵理论的全新方法“System Sample Entropy”来预测厄尔尼诺事件, 结果显示, 厄尔尼诺区域前一年的近海平面空气或海表温度复杂度与厄尔尼诺事件强度之间存在非常强的稳定的正相关关系。该方法克服了困扰 ENSO 长期预测的 SPB 问题, 可以提前一年成功地预测事件强度。
随着大数据分析和计算机科学的发展, 人们逐渐意识到机器学习在分析大数据信息和处理非线性问题方面的卓越性。很多科学家试图将机器学习应用于各自领域里未解决的科学问题中, 寻求新的突破。Tangang 等[16]和蒋国荣等[17]发现, 将神经网络算法与经验正交函数分析方法相结合, 对 ENSO 预报可以起到意想不到的效果。刘科峰等[18]也发现, 基于支持向量机与小波分解方法结合的多步递阶预测方法, 可以有效地预报海温距平时间序列。为了得到更好的预报结果, 许柏宁等[19]设置 4 种不同的深度学习网络混合模型, 对区域海表温度异常(sea surface temperature anomaly, SSTA)进行预报, 发现无论在训练集还是测试集上的表现, Sequence-to-Sequence (Seq2Seq2)模型都优于其他模型。Zhang等[20]为了提升沿海海域海表温度的预测能力, 采用长短期记忆人工神经网络(long-short term memory, LSTM)神经网络预测海表温度(sea surface tempera-ture, SST), 并取得较好的预报效果。Ham 等[6]利用卷积神经网络(convolutional neural networks, CNN)预测 ENSO 事件, 结果显示, 在预报提前时间大于6 个月时, 模型的预测能力优于其他预报系统。
SPB 现象是 Webster 等[7]在动力预测模型中发现的, 后续的研究大多基于 ENSO 的动力学机制对SPB产生的原因进行解释。然而, 统计模型的构建并不依赖于动力学框架, 而是基于大数据的统计分析和回归。在过去的研究中, 大多数基于机器学习的 ENSO 预测模型都获得较强的预测能力, 但都没有明确 SPB 现象在机器学习这种新型统计模型中是否存在以及存在或不存在的原因。本文利用 LSTM神经网络建立针对 4 次厄尔尼诺事件的预测模型, 并探究模型中的 SPB 现象及其产生的原因。
LSTM 是 Hochreiter 等[21]1997 年提出的, 是循环神经网络的一种特殊形式。目前, 在翻译语言、图像分析、语音识别、手写识别和时间序列预测方面, LSTM 有着广泛的应用。与传统的循环神经网络相比, LSTM 在隐藏层各神经元中增加记忆单元, 使得时间序列上的记忆信息可控, 每次在隐藏层各单元间传递时, 可以通过几个可控门(输入门、遗忘门和输出门)控制之前信息和当前信息的记忆和遗忘程度。因此, LSTM 具备长期记忆功能, 能有效地应用于处理时间序列的预测问题。
ENSO 是发生在热带太平洋的年际时间尺度的海‒气相互作用异常现象。用 Niño3.4 指数表征ENSO 事件, 其定义为 Niño3.4 区(150°E—170°W, 5°S—5°N)海表温度距平场的空间平均。本文视Niño3.4 指数预报问题为时间序列问题, 选取逐月Niño3.4 指数时间序列作为预报对象, 数据主要来源于 Physical Sciences Laboratory 网站 (https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Niño34), 时间段为 1960 年 1 月到 2018 年 12 月。图 1 展示 1984年 1 月至 2018 年 12 月的 Niño3.4 指数的变化情况, 其中浅灰色圆圈标记本文选取的 4 个典型的厄尔尼诺事件。
为了提升模型的训练效率, 我们先对数据进行归一化处理, 将数据标准化至[0, 1]区间。计算公式如下:
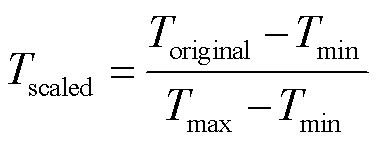, (1)其中, Toriginal为指数初始值, Tmax为指数最大值, Tmin为指数最小值, Tscaled为归一化后的数据。
本文选取 4 个比较典型的厄尔尼诺事件(1991/ 1992, 1997/1998, 2002/2003和2015/2016)为研究对象, 所选模型皆为三层结构, 包括输入层、LSTM层和全连接层, 预报模式为“24-1”, 模型的目标函数为均方误差。我们将数据划分成训练集、验证集和测试集 3 个部分(表 1), 其中训练集用于训练模型的权重参数, 验证集用于调整模型的结构, 测试集用于检验模型的最终效果。
为了评估模型的预报能力, 本文选用均方根误差(root mean square error, RMSE)和距平相关系数(anomaly correlation coefficient, ACC)作为评价标准, 计算公式如下:
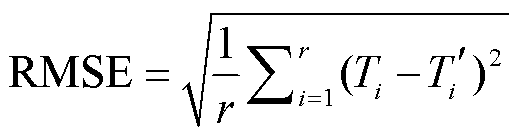, (2)
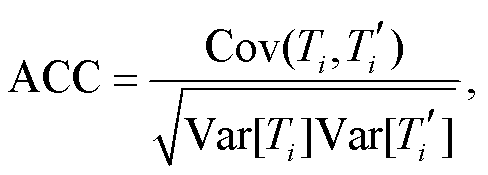(3)
其中, r为样本数, Ti为实测值, Ti′为预测值。我们将预测起点之前的24个Niño3.4指数值作为模型的输入值, 模式输出的预报值即为第25个指数值, 再将预测结果添加进输入序列, 利用第2～25个指数值预报第26个指数值。本文的预报时效定义为预报月份与输入历史数据的最后一个月份间的差值。
本文规定0年代表厄尔尼诺事件发生年, 即Niño3.4指数达到峰值的年份, −1年代表事件发生前一年, 1年代表事件发生后一年。相应地, 我们选取10月、1月和4月作为ENSO事件的预报起点。
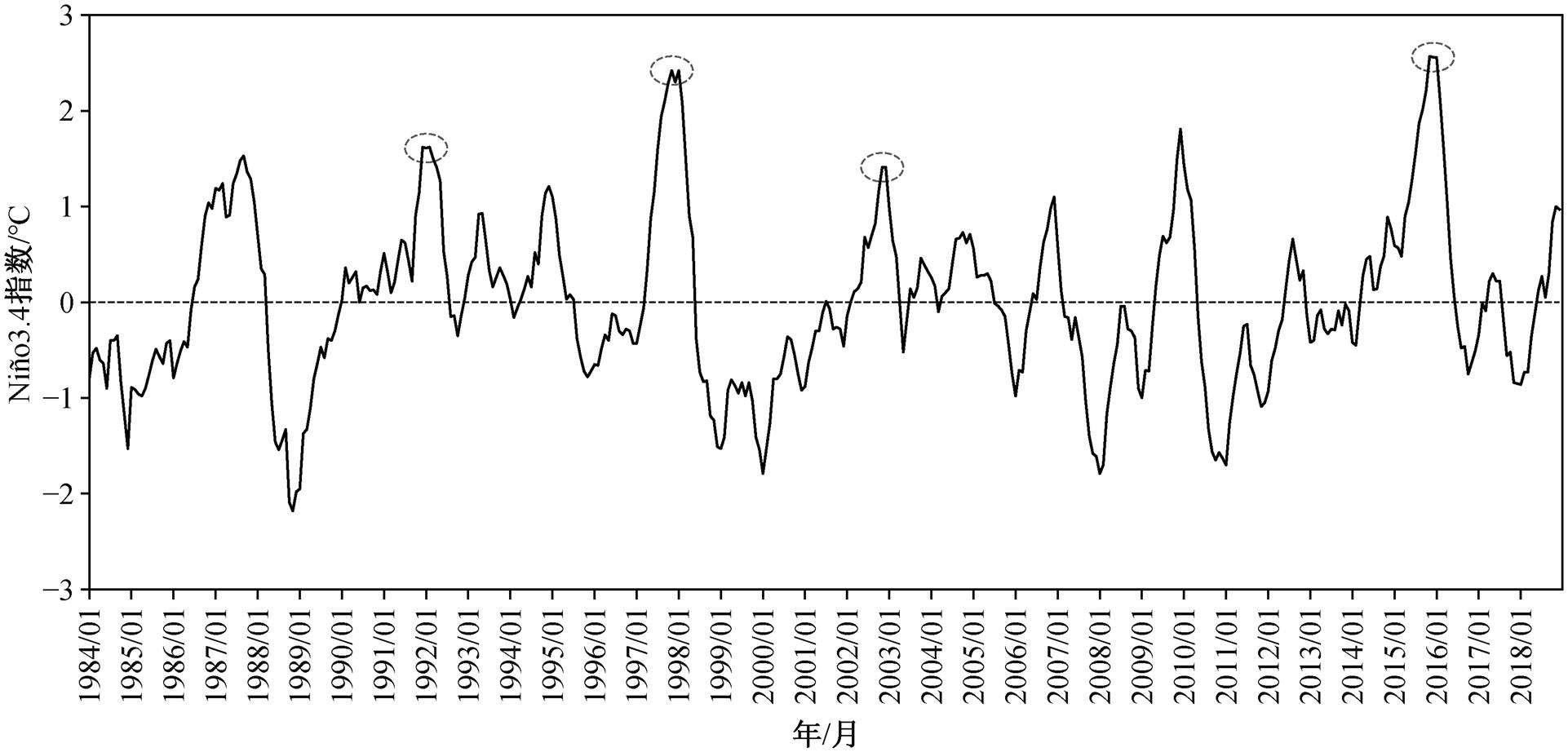
图1 1984年1月至2018年12月的Niño3.4指数变化
Fig.1 Niño3.4 index from January 1984 to December 2018
表1 模型训练集、验证集和测试集数据划分
Table 1 Division of the models’ train set, validation set and test set
事件名称训练集验证集测试集 1991/19921960.01–1988.091988.10–1990.091990.10–1995.10 1997/19981960.01–1994.091994.10–1996.091996.10–2001.10 2002/20031960.01–1999.091999.10–2001.092001.10–2006.10 2015/20161960.01–2012.092012.10–2014.092014.10–2018.12
对于预报月份t, Niño3.4指数预报误差E(t)定义为模型预报值与实测值之差, 表达式如下:
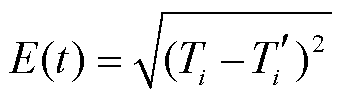。 (4)预报误差在预报月份t的误差增长率k, 则为t+ 1月的预报误差与t月预报误差之差。k值为正(负)代表预报误差增大(减小), k的绝对值越大代表预报误差的变化幅度越大。
根据张雅乐[22]和Wei等[23]的定义, 本研究将Niño3.4指数大于−0.5°的月份至峰值月份划分为厄尔尼诺事件的增长期, 将峰值月份至指数低于−0.5°的月份划分为衰减期。一年可分为4个季度, 分别为1—3月(JFM)、4—6月(AMJ)、7—9月(JAS)和10—12月(OND)。
本文将季度内各预报月误差增长率的平均值设定为预报误差季节增长率
, 则不同季度的预报误差增长率可表示为
, 
, 
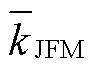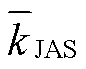和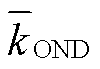
, 各季度的增长率最大值可记为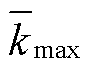。根据张雅乐[22]和Wei等[23]的定义, 当AMJ季度的预报误差增长率相对于其他季度较大时, 则认为此次模型预报过程中存在SPB现象。因此, 从预报起点10月(−1), 1月(0)和4月(0)往后滚动预报12个月, 则可计算出不同预报起点对应的事件增长期的预报误差季节增长率, 将其平均, 则可得出事件增长期的预报误差季节增长率。同理, 从预报起点10月(0), 1月(1)和4月(1)依次往后预报12个月, 则可得到事件衰减期的预报误差季节增长率。
Fang等[24]用不同起始月份的SST自相关系数(滑动窗口为10年)跨越春季时的减小量平均值表征春季持续性障碍(spring persistence barrier)的强度。本文在Fang等[24]的定义基础上, 依据下式计算春季持续性障碍强度指数。
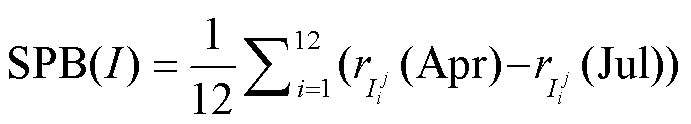, (5)其中, I是滑动窗口的起始年份, i是起始月份, j是滞后时间。
为了测试LSTM模型对ENSO的预报能力, 本文首先选取1997/1998强厄尔尼诺事件作为训练案例。图2给出当预报时效为12个月时, LSTM模型对1996年10月至2001年10月的Niño3.4指数的预报结果与实测值的时间变化。可以看出, 尽管预报时效为12个月, LSTM模型的预测结果依然能够完整地刻画Niño3.4指数的变化趋势。此次预测中, 模型对1997/1998事件的峰值月份和峰值大小的模拟与实测情况基本上吻合, 说明LSTM神经网络在处理时间序列的非线性预测方面具有很好的性能。
图3展示模型预测结果与实测值间距平相关系数ACC和均方根误差RMSE随不同预报时效的变化, 可以更直观地反映模型预测效果。虽然模型对Niño3.4指数的预报能力随着预报时效的加长而有所降低, 但当预报时效为12个月时, 相关系数仍然达到0.93以上。随着预报时效加长, 当预报时效小于6个月时, 均方根误差迅速增大; 当预报时效在6～11个月之间时, 均方根误差变化不大。
图2 1996 年 10 月至 2001 年 10 月期间预报时效为 12 个月的Niño3.4指数模型预测结果与实测值
Fig.2 Prediction results when the lead time is 12 months and observed Niño3.4 index from October 1996 to October 2001
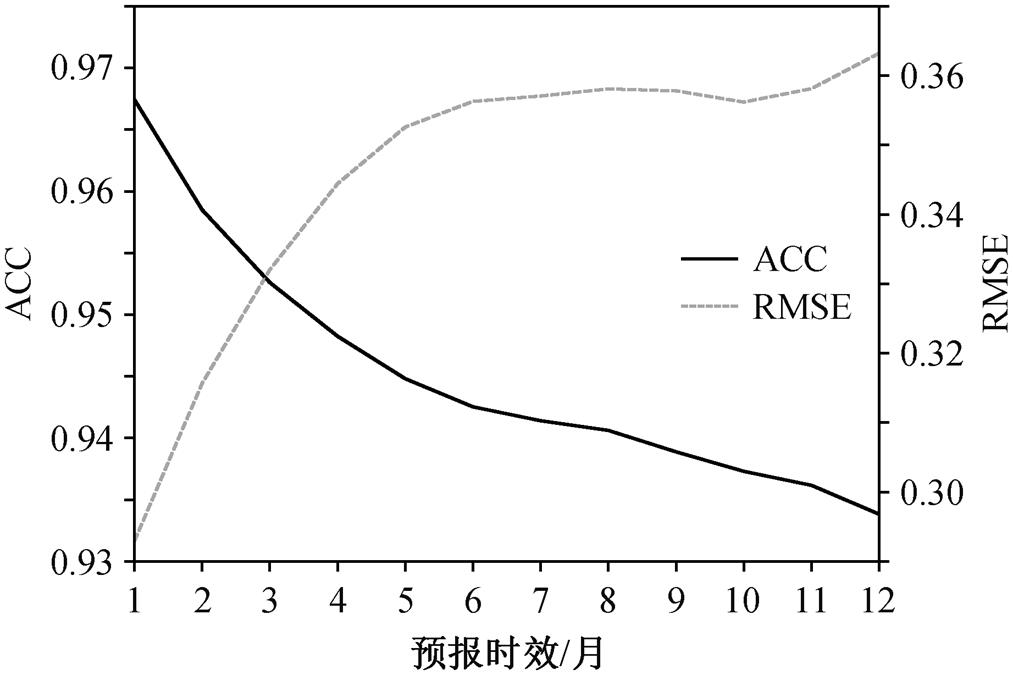
图3 距平相关系数和均方根误差随预报时效的变化
Fig.3 Temporal changes in ACC and RMSE with lead time
严军等[4]基于神经网络‒奇异谱分析, 对ENSO指数进行预测, 在预报时效为12个月时, 相关系数为0.49。刘科峰等[18]利用小波分析和支持向量机预报ENSO指数, 预报时效为12个月时的相关系数为0.89。许柏宁等[19]利用Seq2seq2深度学习模型预报SSTA, 其12个月预报时效的相关系数在0.5左右。Ham等[6]利用卷积神经网络模型预测Niño3.4指数, 12个月预报时效的相关系数在0.65左右。虽然本文预报模型涉及的时间段、学习算法以及参数选择与其他模型之间存在不一致性, 但与大多数模型相比, 本文LSTM时间序列模型对Niño3.4指数的预报能力具有一定的优势。
为了进一步验证LSTM时间序列模型对厄尔尼诺事件的预报效果, 我们继续对1991/1992, 2002/ 2003和2015/2016这3个厄尔尼诺事件进行研究。2015/2016厄尔尼诺事件的Niño3.4指数变化规律与1997/1998事件相似, 都属于强东部型厄尔尼诺事件; 1991/1992与2002/2003厄尔尼诺事件的变化趋势相似, Niño3.4指数峰值相对偏小, 都属于中部型厄尔尼诺事件。
图4对比LSTM模型在不同预报起点往后滚动预报20个月的的预报结果与实测值, 可见不同起报时间的预报结果皆可模拟出各个事件的发展趋势, 随着起报时间向后推移, 模型对事件的预测更为精准。还可以看出, 模型对不同类型厄尔尼诺事件的预报效果不同。对于强东部型厄尔尼诺事件, Niño3.4指数的发展和衰减比较快速和平滑, LSTM模型对Niño3.4指数峰值月份和峰值大小的预报效果较好; 对于中部型厄尔尼诺事件, Niño3.4指数的发展比较平缓, 但起伏较大, LSTM模型的预报效果较差, 尤其是无法模拟出该厄尔尼诺事件发展初期短时间尺度的起伏(图4(a))。
图5呈现4个厄尔尼诺事件增长期和衰减期的预报误差季节增长率(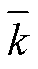
), 可以看出事件增长期的始终为正值, 并且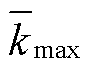在AMJ季度出现3次, OND季度出现一次。与增长期相比, 衰减期各事件的并不是全部为正值, 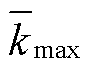也未集中出现在AMJ季度。但是, 在相同类型的厄尔尼诺事件中, 衰减期的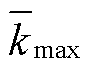有着相似的分布特征, 同为弱中部型的1991/1992事件和2002/2003事件的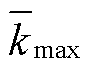均处于AMJ季度, 且数值比其他季度大; 强东部型事件的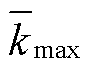则分散在其他季度, 且个体表现不相同, 1997/ 1998事件各季度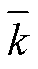值偏小, 2015/2016事件的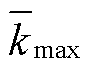位于JFM季度, 误差增长率的最小值却出现在 AMJ季度。
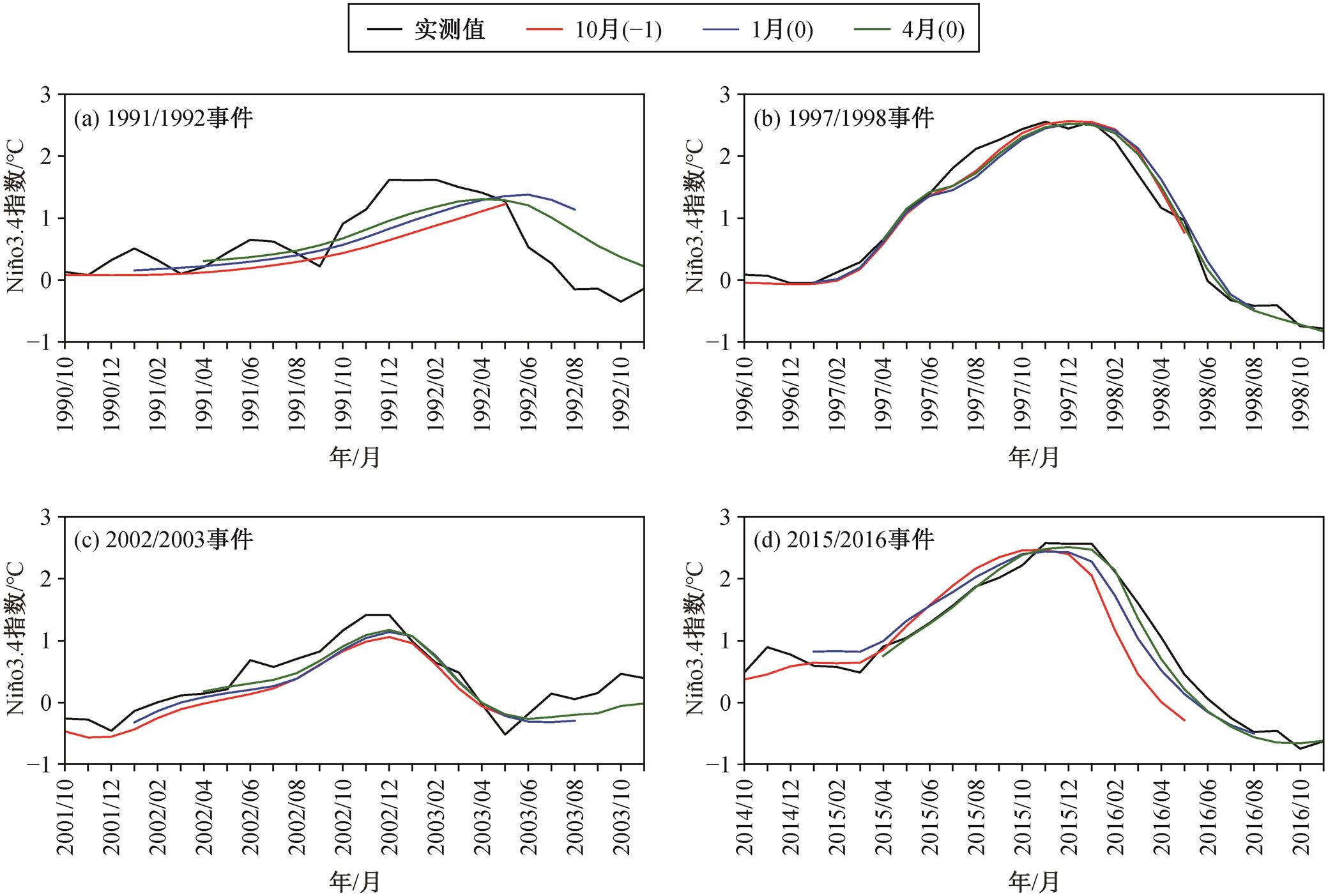
图4 模型对4个厄尔尼诺事件的预测结果与实测值
Fig.4 Model prediction results and observed Niño3.4 index of four El Niño events
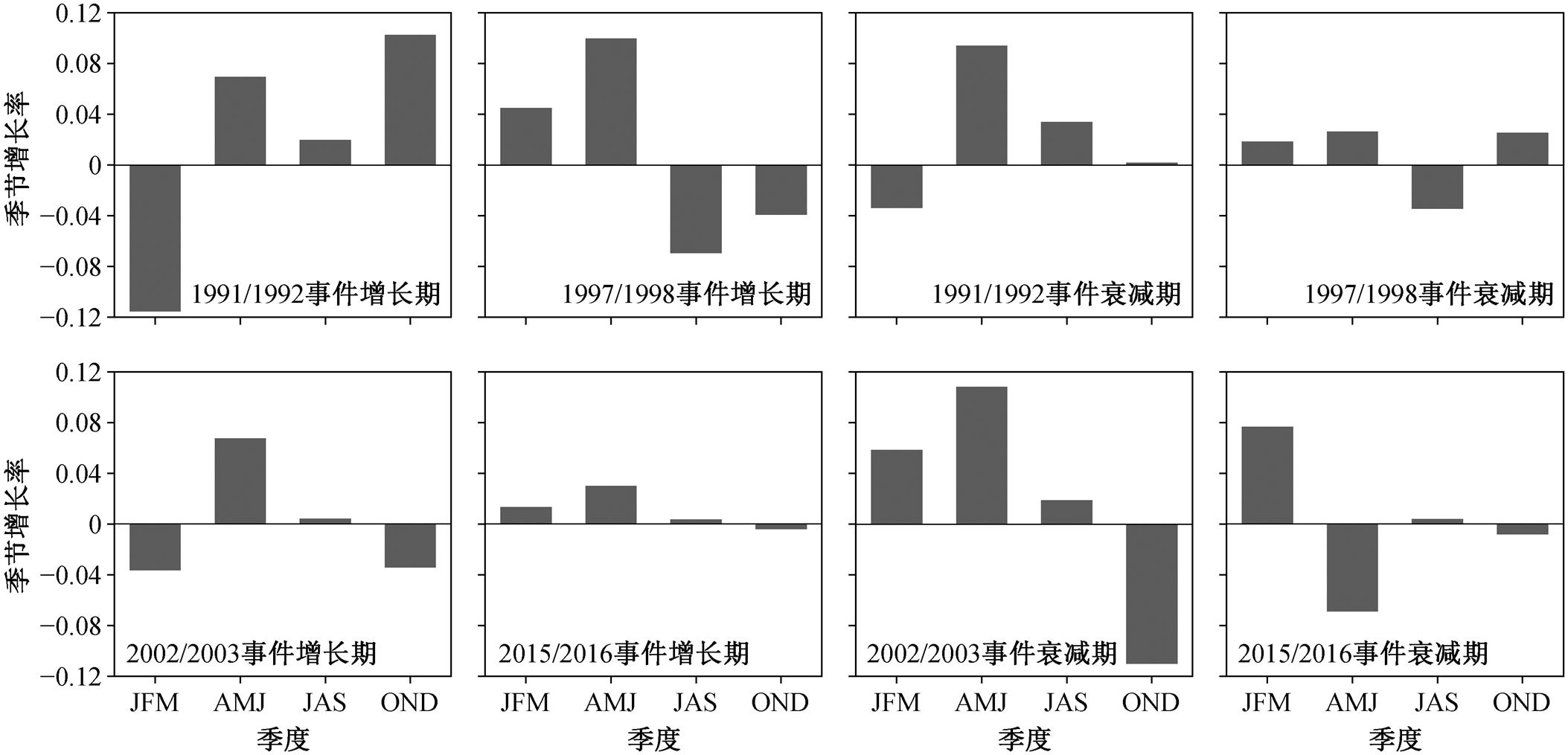
图5 4个事件增长期和衰减期的预报误差季节增长率
Fig.5 Seasonal growth rate of forecast error in growing period and decaying period of four El Niño events
综上所述, 我们发现LSTM模型对不同类型厄尔尼诺事件的预报误差呈现不同的情形, 但对厄尔尼诺事件发展期Niño3.4指数的预报呈现一致性。在增长期, 除1991/1992事件外, 预报误差的季节增长率始终是AMJ季度最大, 且远大于其他季节。实际上, 1991/1992事件的春季误差增长率也不小, 而最大误差增长率出现在OND季度的原因是模型对1991/1992事件峰值的误报(图4(a)), 表明在事件增长期存在明显的SPB现象。在衰减期, 同类型事件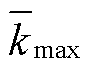的表现相似, 但事件个体间存在一定的差异。因此, 衰减期的Niño3.4指数预测情况可能与事件的特征(如事件类型和强度)有关。
为了探究LSTM模型在预报过程中出现春季预报障碍的原因, 计算Niño3.4指数在不同滞后时间情况下的自相关系数。结果表明, 不论滞后时间为多久, 自相关系数值在第二年的春季都会大幅度降低, 4月之前在0.4以上, 6月之后基本上为负数。这一结果从侧面反映数据信号在夏、秋、冬三季间可以顺利地传递, 但春季数据信号的连续性大幅度下降, 这就是春季持续性障碍现象。本文构建的基于事件发生前30年历史数据训练的LSTM模型, 也无法克服春季持续性障碍产生的春季误差快速增长问题。机器学习算法是基于训练周期内的历史数据, 寻找样本数据与验证数据的误差最小值。本文模型训练使用的是月平均数据, 而春季持续性障碍仅存在于每年的4—6月(3个样本), 相对于总样本数并不大。因此, 追求全局误差最小化的机器学习算法, 并不能建立起有效的克服春季持续性障碍的预测算法。然而, 尽管仍然存在SPB问题, 但LSTM预报模型对强厄尔尼诺事件的整体预报效果是非常优异的(图4(b)和(d))。
ENSO稳定性的季节变化是春季持续性障碍的主要原因, Bjerknes反馈是厄尔尼诺发展的重要物理机制, 涉及多种海‒气反馈, 这些海‒气反馈项可综合量化成BJ(Bjerknes instability)指数。已经证实, BJ指数也是表征Bjerknes反馈的有效指标, 能够有效地诊断ENSO的稳定性[9‒10,24‒25]。Fang等[24]通过计算月BJ指数发现, 在3—5月期间, BJ指数从最小值迅速增长到最大值, 说明春季是ENSO系统从最稳定状态转变成最不稳定状态的过渡期, 也因此造成春季Niño3.4指数持续性的降低。依据式(5)计算1960—2005年间的春季持续性障碍强度指数, 结果如图6所示。可以看出, 1997/1998事件对应的强度指数比1991/1992事件和2002/2003事件低。这一点在模型的预报结果中也有所体现: 模型对1997/1998厄尔尼诺事件的预报效果整体上优于1991/1992事件和2002/2003事件。
1)LSTM模型对强东部型厄尔尼诺事件(1997/ 1998和2015/2016事件)的预报效果优于弱中部型厄尔尼诺事件(1991/1992和2002/2003事件), 主要体现为峰值月份和峰值大小的预报; 在发展趋势方面, 4个事件的预报趋势与实况基本上一致。
2)LSTM模型对厄尔尼诺事件增长期Niño3.4指数的预报都存在明显的SPB现象, 而对衰减期的预报表现不同: 弱中部型事件衰减期的预报出现明显SPB现象, 强东部型事件衰减期的预报不存在SPB现象, 与Wei等[23]的研究结论相似。值得注意的是, 尽管LSTM模型中仍然存在明显的SPB现象, 但对强厄尔尼诺事件的预报效果也非常优异, 因为本文LSTM算法是基于大量历史数据样本集和验证集, 通过迭代训练, 达到误差最小化。对于预报效果优异的案例(如1997/1998事件), 除春季外, 其他季节的误差增长率都比较小。对于预报效果相对较差的案例(如1991/1992事件), 除春季外, 其他季节的误差增长率也较大。
3)LSTM模型在预报过程中出现的SPB现象主要由数据中呈现的持续性障碍和厄尔尼诺事件的性质(分布型、强度和锁相特征等)造成。LSTM模型并不能从物理机制方面规避春季预报障碍。从统计学角度来说, 对于月平均的训练集, 春季持续性障碍的样本仅仅存在于每年的4—6月, LSTM模型追求的是训练集的全局最小化, 无法兼顾短时间尺度的春季误差并建立有效的规避算法。因此, LSTM模型最后呈现的结果更趋向于对厄尔尼诺事件发展趋势的预报, 无法预测短时间尺度的Niño3.4指数变化, 包括4—6月的春季误差快速增长现象。
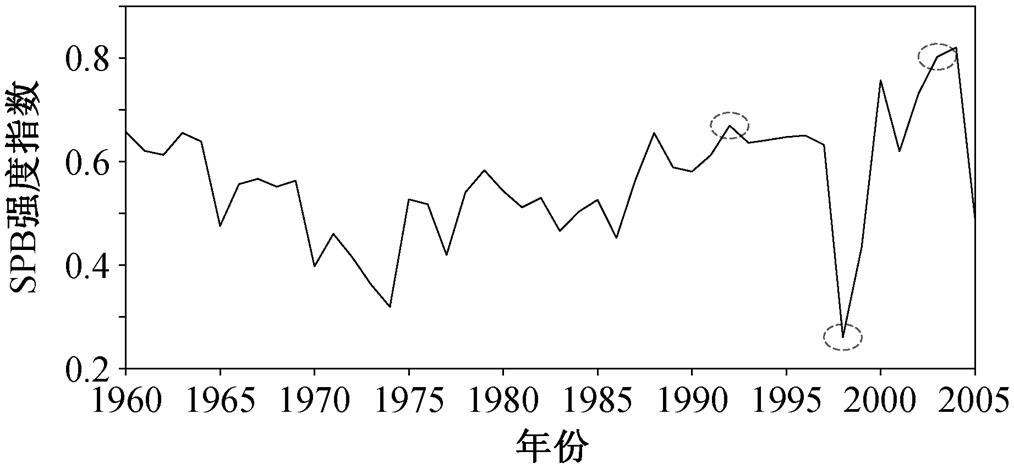
图6 1960—2005年的SPB强度指数
Fig.6 SPB intensity index from 1960 to 2005
参考文献
[1]Oldenborgh G J V, Balmaseda M A, Ferranti L, et al.Did the ECMWF seasonal forecast model outperform statistical ENSO forecast models over the last 15 years?.Journal of Climate, 2005, 18(16): 3240‒3249
[2]Dijkstra H A, Petersik P, Hernandez-Garcia E, et al.The application of machine learning techniques to improve El Niño prediction skill.Frontiers in Physics, 2019, 7: 153
[3]Barnston A G, Tippett M K, L’Heureux M L, et al.Skill of real-time seasonal ENSO model predictions during 2002–11: is our capability increasing?.Bulle-tin of the American Meteorological Society, 2012, 93 (5): 631‒651
[4]严军, 刘健文.基于神经网络–奇异谱分析的 ENSO指数预测.大气科学, 2005, 29(4): 620‒626
[5]Mcphaden M J, Zebiak S E, Glantz M H.ENSO as an integrating concept in earth science.Science, 2006, 314: 1740‒1745
[6]Ham Y G, Kim J H, Luo J J.Deep learning for multi-year ENSO forecasts.Nature, 2019, 573: 568‒572
[7]Webster P J, Yang S.Monsoon and ENSO: selectively interactive system.Quarterly Journal of the Royal Meteorological Society, 1992, 118: 877‒926
[8]杨崧, 邓开强, 段晚锁.季风与 ENSO 的选择性相互作用: 年循环和春季预报障碍的影响.大气科学, 2018, 42(3): 570–589
[9]Webster P J.The annual cycle and the predictability of the tropical coupled ocean-atmosphere system.Meteorology and Atmospheric Physics, 1995, 56(1): 33‒55
[10]Torrence C, Webster P J.The annual cycle of persis-tence in the El Niño/Southern Oscillation.Quarterly Journal of the Royal Meteorological Society, 1998, 124: 1985‒2004
[11]Wang B, Fang Z.Chaotic oscillations of tropical climate: a dynamic system theory for ENSO.Journal of the Atmospheric Sciences, 1996, 53(19): 2786‒802
[12]Mu M, Duan W S.A new approach to studying ENSO predictability: conditional nonlinear optimal perturba-tion.Chinese Science Bulletin, 2003, 48(10): 1045‒ 1047
[13]Mu M, Duan W S, Wang B.Season-dependent dyna-mics of nonlinear optimal error growth and El Niño-Southern Oscillation predictability in a theoretical mo-del.Journal of Geophysical Research: Atmospheres, 2007, 112(D10): 1‒10
[14]Duan W S, Wei C.The ‘spring predictability barrier’ for ENSO predictions and its possible mechanism: results from a fully coupled model.International Journal of Climatology, 2012, 33(5): 1280‒1292
[15]Meng J, Fan J F, Ludescher J, et al.Complexity-based approach for El Niño magnitude forecasting before the spring predictability barrier.Proceedings of the National Academy of Sciences, 2020, 117(1): 177‒83
[16]Tangang F T, Tang B Y, Monahan A H, et al.Fore-casting ENSO Events: a neural network-extended EOF approach.Journal of Climate, 1998, 11(1): 29‒41
[17]蒋国荣, 张韧, 沙文钮.用 EOF 展开和人工神经网络方法预测 ENSO 的研究.海洋预报, 2001, 18(3): 1‒11
[18]刘科峰, 张军, 陈奕德, 等.基于小波分解和支持向量机的 ENSO 预测试验 .解放军理工大学学报(自然科学版), 2011, 12(5): 531‒535
[19]许柏宁, 姜金荣, 郝卉群, 等.一种基于区域海表面温度异常预测的 ENSO 预报深度学习模型.科研信息化技术与应用, 2017, 8(6): 65‒76
[20]Zhang Q, Wang H, Dong J Y, et al.Prediction of sea surface temperature using long short-term memory.IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1745‒1749
[21]Hochreiter S, Schmidhuber J.Long short-term me-mory.Neural Computation, 1997, 9(8): 1735‒1780
[22]张雅乐, 俞永强, 段晚锁, 等.四个耦合模式ENSO后报试验的“春季预报障碍”.气象学报, 2012, 70(3): 506‒519
[23]Wei C, Duan W S.The “Spring Predictability Barrier” phenomenon of ENSO predictions generated with the FGOALS-g model.Atmospheric and Oceanic Science Letters, 2010, 3(2): 87‒92
[24]Fang X H, Zheng F, Liu Z Y, et al.Decadal modula-tion of ENSO spring persistence barrier by thermal damping processes in the observation.Geophysical Research Letters, 2019, 46(12): 6892‒ 6899
[25]Jin Y, Liu Z, Lu Z, et al.Seasonal cycle of back-ground in the tropical pacific as a cause of ENSO sp-ring persistence barrier.Geophysical Research Let-ters, 2019, 46(22): 13371‒13378
Spring Predictability Barrier Phenomenon in ENSO Prediction Model Based on LSTM Deep Learning Algorithm
Abstract A LSTM (long-short term memory) model is applied to the prediction of the Niño3.4 index, and the spring prediction barrier (SPB) issue has been further investigated in the LSTM model.The results show that the model can predict the trend of the Niño3.4 index well, yet revealing different performance in different El Niño events.For the 1997/1998 El Niño and 2015/2016 El Niño, which are strong EP El Niño events, the model performes well on the prediction of Niño3.4 index trend and peaks, and anomaly correlation coefficient (ACC) reaches more than 0.93.But for the weak CP El Niño events, e.g.the 1991/1992 El Niño and 2002/2003 El Niño, it shows relatively poor performance on the prediction of the peak.In the growing period, the maximum season growth rate of prediction error are in AMJ quarter, which indicates obvious SPB phenomenon.However, in the decaying period, the maximum have similar distribution in the same type of events: for the weak CP El Niño events, the maximum are in AMJ quarter, indicating obvious SPB phenomenon; for strong EP El Niño events, the maximum are in other quarter, indicating that there is no SPB phenomenon.The differences in the performance among individuals may be related to the development characteristics of the event itself (such as event type and intensity).
Key words LSTM; ENSO; prediction error; SPB; Niño3.4 index
doi: 10.13209/j.0479-8023.2021.114
收稿日期: 2020–12–25;
修回日期: 2021–04–26
广东省重点领域研发计划(2020B1111020003)、国家重点研发计划(2016YFA0202704)、广西壮族自治区特聘专家经费(2018B08)和国家自然科学基金(41976007, 91958101)资助