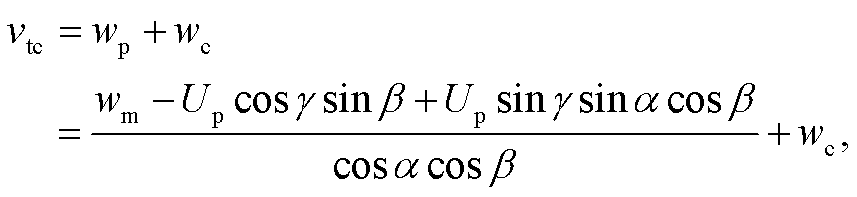 (1)
(1)摘要 基于安装在气象铁塔不同高度的 3 台 Parsivel 激光雨滴谱仪, 研究 2020 年 6—8 月北京地区 31 次降雨过程低边界层的雨滴谱垂直分布特征及其对雷达测量降雨的影响。结果表明, 在雨滴从 280m 下落到 140m的过程中, 雨滴破碎占据主导地位, 大尺度雨滴减少, 小尺度雨滴大量增加; 从 140m 下落到地面的过程中, 雨滴合并占据主导地位, 大尺度和小尺度雨滴均减少, 中等尺度雨滴增加; 对流型降雨中, 随着高度降低, 大尺度雨滴迅速减少, 雨滴破碎对雨滴谱分布的影响较大。北京地区对流型降雨的雨滴谱特征介于海洋型与大陆型之间。由于雨滴谱的分布随高度变化, 不同降雨特征量也随高度发生非线性变化, 因此使用地面的降雨测量结果对气象雷达进行校准以及联合反演降雨会产生 Z-R 错配误差, 这种误差在稳定型降雨和弱降雨中更显著。
关键词 雨滴谱; 垂直分布; Parsivel; 降雨; Z-R错配误差
雨滴数浓度随雨滴直径的变化关系称为雨滴谱, 是基础性的降雨微物理量。通过雨滴谱, 可以计算得到雨强(R)、雷达反射率因子(Z)和液态水含量(LWC)等降雨特征量, 建立用于雷达定量测量降雨的 Z-R 关系(Z=aRb, a 和 b 为系数)[1]。利用电磁波通过降雨时产生的散射和吸收特性, 雨滴谱的三参数 Gamma 分布模型被运用到 TRMM (tropical rain-fall measuring mission)和 GPM (global precipitation measurement)探测卫星的降雨反演算法中, 是实现星载雷达降雨遥感的基础[2]。
在雨滴下落过程中, 会经历碰撞、合并、破碎和蒸发等微物理过程, 导致不同高度的雨滴谱发生变化, 不同季节、不同地形条件以及不同降雨类型的雨滴谱也不同[3]。Bringi 等[4]用 2DVD 和 RD-69雨滴谱仪测量全球多个气候区的降雨, 以标准化截距参数(Nw)和质量加权直径(Dm)的集中分布作为划分依据, 将对流型降雨归纳为海洋型降雨(log10Nw= 4~4.5, Dm=1.5~1.75)和大陆型降雨(log10Nw=3~3.5, Dm=2~2.75)两类。Waldvogel[5]利用地面的雨滴谱仪和波长为 5cm 的垂直指向雷达探测降雨, 发现大范围降雨时存在雨滴谱突变的情况, 这种突变往往伴随零度层亮带的强弱转换和中尺度天气区的转变, 可以通过描述截距的参数 N0 突变(N0 jump)效应来识别。
通常采用数理方程推导、数值模拟和探测等方式, 研究下落过程中雨滴谱的变化规律[6‒8]。探测结果能够验证理论推导和数值模拟的结果, 提高降雨估测精度, 加深对云和降雨微物理过程的理解, 提高数值模拟的准确度, 改进 Z-R 关系。在不同的高度架设雨滴谱仪, 或使用探空飞机进行测量, 将探测结果视为实测值, 用于遥感探测设备的校准和评估[9‒11]。通过基于电磁波在降雨中传播特性进行探测的仪器(如GPM DPR (dual-frequency precipita-tion radar)等机载或星载雷达[4,12‒13]和微降雨雷达(micro rain radar, MRR)等地基雷达[14‒15])实现遥感反演。
大气边界层(atmospheric boundary layer, ABL)是直接受地面动力和热力影响的大气分层, 厚度通常在几百米至几千米之间, 具有很强的湍流特性, 其中的气象要素存在明显的时空变化[16‒17]。因此, 雨滴谱在低大气边界层中是否存在明显的变化以及由此带来的影响值得研究。
有关下落过程中雨滴谱垂直分布的研究已经取得诸多进展。然而, 除采用地面雨滴谱仪与地基遥感设备联合探测的替代方法[2,12,15]外, 缺乏对同一地点低边界层雨滴谱垂直分布进行探测的手段。
Levin 等[9]在阿尔卑斯山两个高度差为 600 m 的观测站架设冲击型雨滴谱仪, 选取稳定型降雨中环境风速小于 2m/s 的观测资料, 发现直径小于 1mm的小雨滴数浓度高海拔大于低海拔, 中雨滴和大雨滴数浓度低海拔大于高海拔。该研究中, 雨滴谱仪安装位置接近地面, 且两个站之间水平距离相隔 5 km, 因此雨滴谱的变化很难完全归因于雨滴在垂直下落过程中的变化。
贾星灿等[10]利用探空飞机对一次降雨过程进行观测, 飞机以 280km/h 的飞行速度从 1200m 盘旋上升至 4200m, 再盘旋下降至 1200m, 上升和下降时间各约 30 分钟。对比宁夏银川站地面观测的雨滴谱数据, 发现地面的雨滴平均谱比空中的雨滴平均谱窄, 空中大雨滴较多, 地面中雨滴和小雨滴较多。他们认为上述现象与雨滴下落时的碰撞、合并、破碎和蒸发有关。由于飞行高度和滞空时间受限等原因, 探空飞机无法探测低大气边界层的雨滴谱, 也无法在一个固定位置进行长时间观测。贾星灿等[10]的最低探测高度与地面相距 1200 m, 其间气象要素变化明显, 雨滴在这段距离上的变化情况可能更复杂。
Peters 等[14]利用波罗的海周边 3 台 MRR 微降雨雷达, 研究雨滴谱的垂直分布, 指出雨强大于 20mm/h 时, 雨滴谱的谱形随高度变化明显, 若采用地面的 Z-R 关系进行降雨估计, 容易产生误差, 并认为这是由雨滴谱的峰值随高度增加而减小造成的, 谱形差异可能与雨滴的碰撞与合并过程有关。
考虑到地物杂波和雷达仰角对探测最低高度的限制, 通常不使用 MRR 和天气雷达等地基遥感探测雨滴谱设备在较低高度获得的数据[13,18]。由于同一地点对不同高度雨滴谱的直接观测资料极其匮乏, 主要通过地面观测仪器实现对 MRR 和天气雷达等降雨测量雷达的校准和评估, 但是, 可能由于雨滴谱的垂直变化产生误差。
上述针对雨滴下落微物理过程进行的研究中, 得出的结论大多模糊, 没有明确对雨滴谱型改变起主要作用的微物理过程是合并还是破碎或蒸发。不同于以往在山体不同高度架设雨滴谱仪的做法, 本研究选取安装在中国科学院大气物理研究所气象铁塔地面、140m 和 280m 高度的 3 台 Parsivel 激光雨滴谱仪, 研究 2020 年 6—8 月低大气边界层雨滴谱及其参数的垂直分布规律, 旨在明确主导的微物理过程, 并探究雨滴谱变化对不同降雨特征量以及雷达测量降雨的影响。
观测地点位于中国科学院大气物理研究所气象铁塔(116.22°E, 39.58°N, 海拔 49m), 分别在 3 个高度(地面、140m 和 280m)架设 3 台 Parsivel 激光雨滴谱仪, 并在 140m 和 280m 两个高度设置超声风温仪和倾角仪。
Parsivel 是德国 OTT Hydromet 公司制造的一款激光雨滴谱仪, 能够同时测量降雨粒子尺度和下落速度, 每分钟输出一组数据[19]。原始数据包含 32个尺度档和 32 个速度档的降水粒子数据, 即每分钟输出一组 32×32=1024 个档位的降水粒子数, 对液态降水粒子尺度的有效探测范围为 0.2~8mm, 速度探测范围为 0.2~20 m/s。
超声风温仪是一款利用超声波测量风速、风向和温度的仪器, 具有精度高、响应快、工作稳定等特点, 采样频率为 10 Hz。
倾角仪是一款采用高质量和高可靠性微机电系统加速度计和陀螺仪测量运动载体姿态参数(横滚和俯仰)的仪器, 将其安装在铁塔的支架上, 能够测量支架在南北和东西两个方向的倾斜程度, 测量范围为±30°, 全量程精度为 0.5°(真实角度与多次测量角度的均方根误差小于 0.5°), 采样频率为 1 Hz。
由于 3 种仪器的采样频率不同, 本文将超声风温仪和倾角仪的数据取分钟平均值。超声风温仪的数据采用郑铮等[20]的方法处理: 若 1 分钟内的 600组数据异常值(仪器输出)占比大于 30%, 则该分钟的数据无效; 反之则对每分钟的 600 组 u (东西向风速)、v (南北向风速)和 w (垂直风速)数据按 3 倍标准差的阈值进行野点剔除, 将剩余数据分为 10 个等距区间; 对出现频率最高区间的全部数据计算平均值, 以此代表该分钟的环境风速。倾角仪的数据保留输出值小数点后一位, 并取分钟平均值, 代表该分钟仪器的横滚和俯仰角度。
雨滴在下落过程中会受到垂直气流的影响, 导致其实际下落速度与静止大气下的速度有所偏离。郑铮等[20]指出, 由于通常情况下环境风随高度增加而增强, 使用架设于高处的雨滴谱仪探测数据时需要修正环境风的影响。另一方面, 大风中雨滴谱仪的观测平面会发生倾斜而产生误差。为此, 刘均慧等[21]提出以下订正方法:
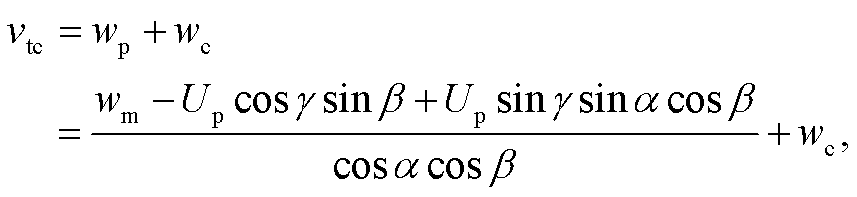 (1)
(1)其中, vtc 为订正后雨滴垂直落度; wp 表示雨滴剔除水平风速影响后的垂直落速; wc 为垂直气流速度; wm 为 Parsivel 雨滴谱仪测量的雨滴速度, 取所在速度区间中值; Up 是雨滴水平移动速度, 并假设雨滴水平移动速度与同一高度水平风速相等; α 和 β 分别为雨滴谱仪受东西向风和南北向风影响产生的倾角, 正方向均为逆时针方向; γ 为水平风风向。
Parsivel 雨滴谱仪测量时, 假定雨滴为球体。当雨滴直径>1mm 时, 在下落过程中会发生形变, 近似成为椭球体, 导致实际测量的是雨滴的长轴。为订正由此产生的误差, 本文采用 Pruppacher 等[22]提出的方法进行轴比订正。
本文所述样本指同一分钟内在 3 个高度采集的降雨信息。采用类似 Tokay 等[23]挑选样本的方法, 对于每个 1 分钟样本, 如果 3 个高度中的任意一个没有采集到降雨、风速和倾角 3 个信息中的一个, 或任意一个高度满足雨滴总数少于 10 和雨强小于0.1mm/h 两个条件之一, 此样本将被舍弃。2020 年6—8 月, 北京地区发生多次降雨, 考虑到降雨的连续性, 将相邻样本间隔时间小于 30 分钟且样本数大于 30 的样本集合, 作为一次降雨过程, 没有被划入降雨过程的样本予以舍弃。最终, 录得 2658 个样本, 31 次降雨过程, 每次降雨过程 3 个高度的累积降雨量如图1所示。
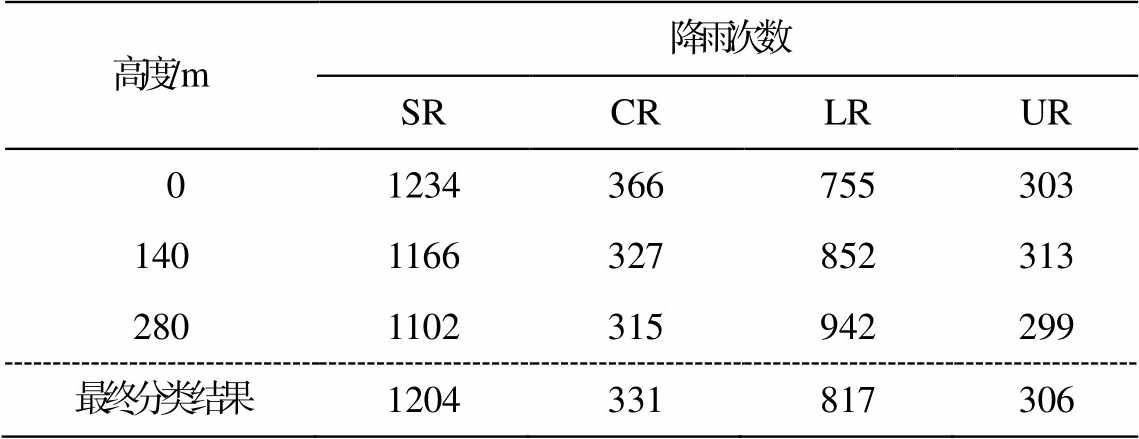
Tzivion 等[3]的研究表明, 降雨类型的改变会影响雨滴谱的分布。本文借鉴 Bringi 等[4]和 Chen 等[12] 的方法, 按照雨强及其标准差, 将降雨分为 4 类(表1)。对于 T 时刻的样本: 1)雨强大于 0.5mm/h, 且(T − 5)~(T + 5)个连续样本(每个样本 1 分钟)的雨强标准差小于 1.5mm/h, 为稳定型降雨(stratiform rain, SR); 2)雨强大于 5mm/h, 且(T − 5)~(T + 5)个连续样本的雨强标准差大于 1.5mm/h, 为对流型降雨(con-vective rain, CR); 3)雨强小于 0.5mm/h, 为弱降雨(light rain, LR); 4)不属于上述 3 类, 为未分类降雨(unclassified rain, UR), 本文不予讨论。
不同高度的降雨分类不完全一致。为便于对比, 需要统一 T 时刻 3 个高度的降雨类型。当有两个以上高度的降雨类型相同时, 以该类型作为 T 时刻的降雨类型; 否则, 以地面的分类结果作为 T 时刻的降雨类型。3 个高度分类结果相同的有 1967 个样本, 占 74.0%; 两个高度分类结果相同的有 670个, 占 25.2%; 三者均不同的有 21 个, 占 0.8%。
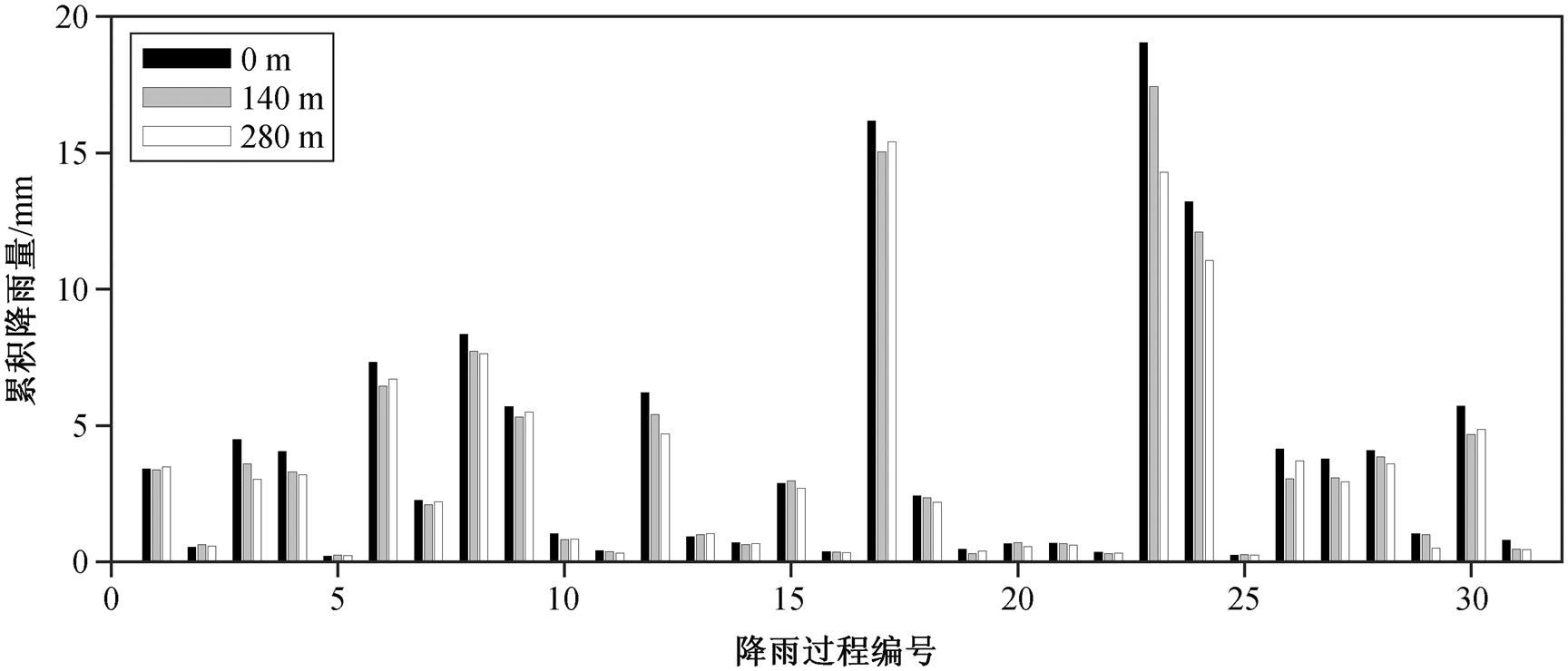
图1 不同高度累积降雨量
Fig.1 Cumulative rainfall at different heights
表1 降雨分类统计结果
Table 1 Statistical result of raintype classification
高度/m降雨次数 SRCRLRUR 01234366755303 1401166327852313 2801102315942299 最终分类结果1204331817306
为了直观地了解雨滴的速度和尺度特点, 图 2给出 3 种降雨类型不同高度的雨滴数随速度和尺度的变化情况。可见, 空中雨滴速度谱的宽度比地面大, 尺度分布范围更广; 对流型降雨(CR)的雨滴尺度分布范围广, 大尺度雨滴显著多于另外两种降雨类型。Atlas 等[24]根据 Gunn 等[25]的实验结果, 提出速度‒尺度关系表达式:
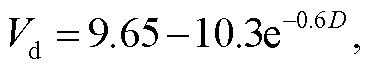 (2)
(2)其中, Vd 是雨滴的下落末速度(m/s), D 是雨滴的直径(mm)。Parsivel 测量的雨滴平均下落速度‒尺度关系与 Atlas 提出的速度‒尺度关系(图 2 中黑色实线)基本上一致。
雨滴谱模型是刻画雨滴谱分布形状的唯一解析方式[26], 对降雨的数值模拟和雷达探测降雨具有重要价值。指数形式的雨滴谱模型包括 M-P (Marsh-all and Palmer)分布和 Gamma 分布, 当形状参数 μ= 0 时, Gamma 分布即为 M-P 分布。与 M-P 分布相比, 三参数 Gamma 分布能够更好地描述雨滴谱分布[26‒28], Bringi 等[4]在 Testud 等[26]的基础上定义标准化 Gam-ma 雨滴谱分布的表达式为
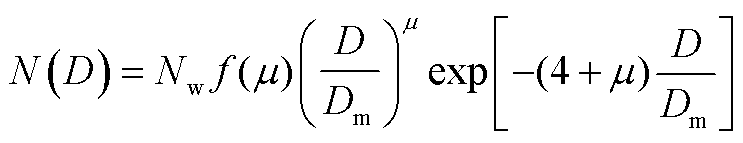 , (3)
, (3)其中, Dm 为雨滴的质量加权直径(mm), N(D)是单位体积和单位尺度区间的雨滴数浓度(m−3·mm−1), Nw, λ 和 μ 分别是标准化截距参数(m−3·mm−1)、斜率参数(mm–1)和形状参数(无量纲),
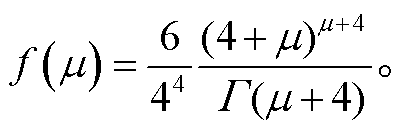 (4)
(4)
雨滴谱参数可由阶矩法计算得到。雨滴谱的 n阶矩定义为
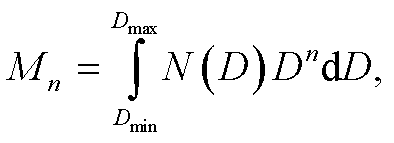 (5)
(5)质量加权直径为
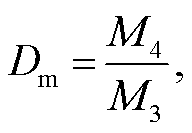 (6)
(6)
标准化截距参数为
 (7)
(7)其中, ρw 是水的密度(假定为 10−3 g/mm3), LWC 为液态水含量(g/m3)。斜率参数为
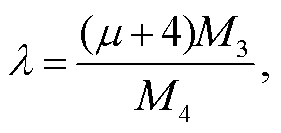 (8)
(8)
形状参数为
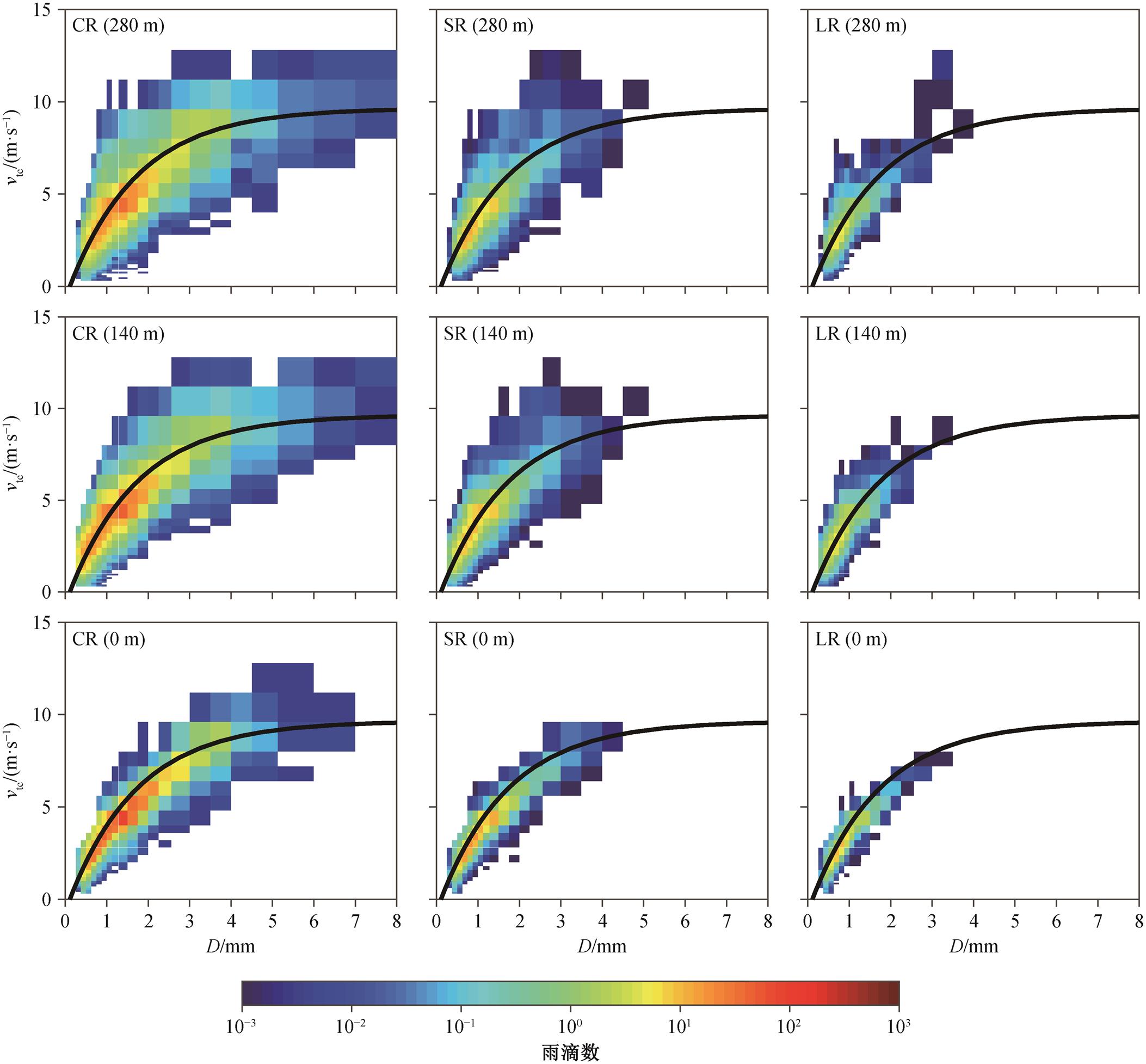
图2 雨滴速度谱
Fig.2 Raindrop velocity sectrum
 (9)
(9)其中,
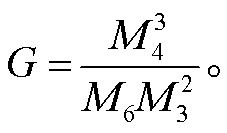 (10)
(10)
标准化截距参数 Nw 代表雨滴直径趋于 0 时的N(D)值; 斜率参数 λ 标示雨滴谱分布的倾斜程度; 形状参数 μ 代表雨滴谱分布的宽度, 当 μ>0 时, 雨滴谱曲线上凸, 反之则下凸。
如图 3 所示, 除弱降雨(LR)外, log10Nw 随高度降低而增大; 形状参数 μ 和斜率参数 λ 在不同的降雨类型中差异明显, CR
对比 3 个高度不同降雨类型的雨滴谱分布(图4)可以发现, 在假定雨滴谱局地水平分布均匀的情况下, 低大气边界层中雨滴谱在垂直方向上发生显著的变化。随着降雨类型和高度的改变, 这种变化呈现不同的特点。图 4 显示, 不同降雨类型的雨滴谱可以明显地区分。从雨滴谱宽度和雨滴数浓度看, CR>SR>LR, 即对流型降雨(CR)的雨滴谱不仅覆盖的尺度范围更大, 数浓度也大于其他两类降雨。
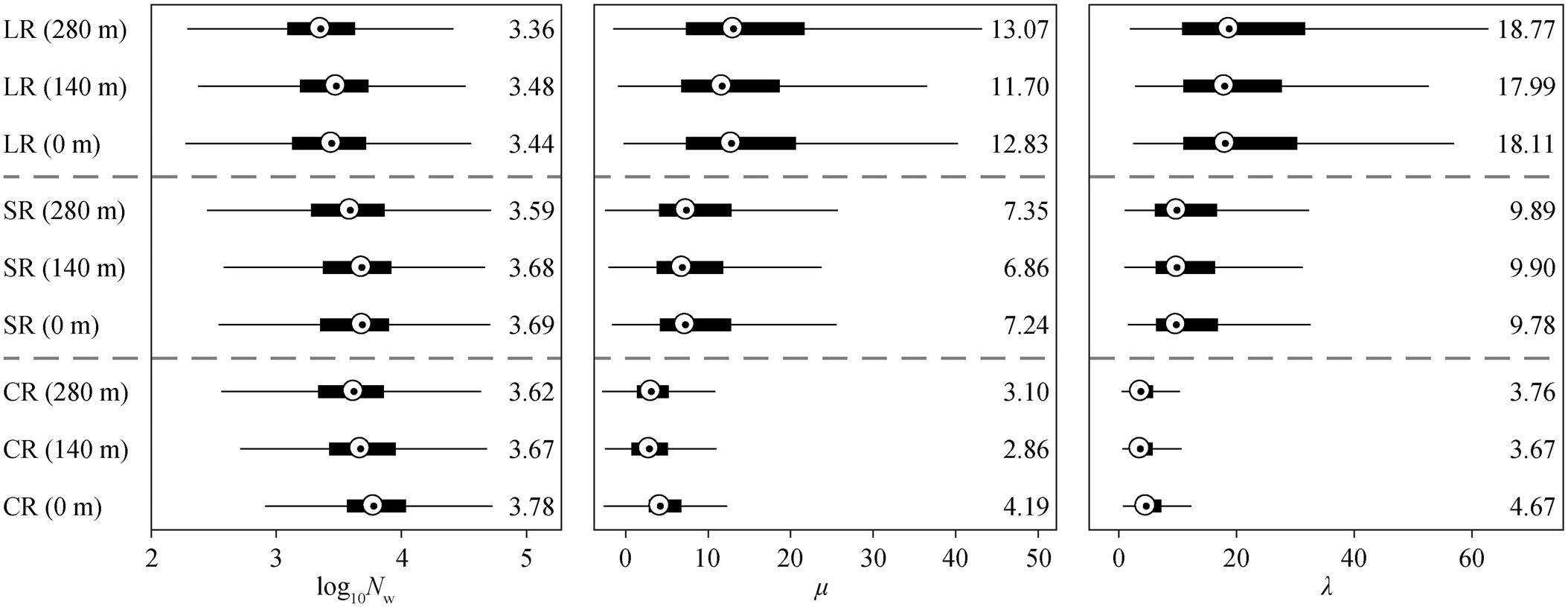
圆点代表中位数, 其数值标示在右侧
图3 雨滴谱参数箱图
Fig.3 Boxplot of DSD parameters
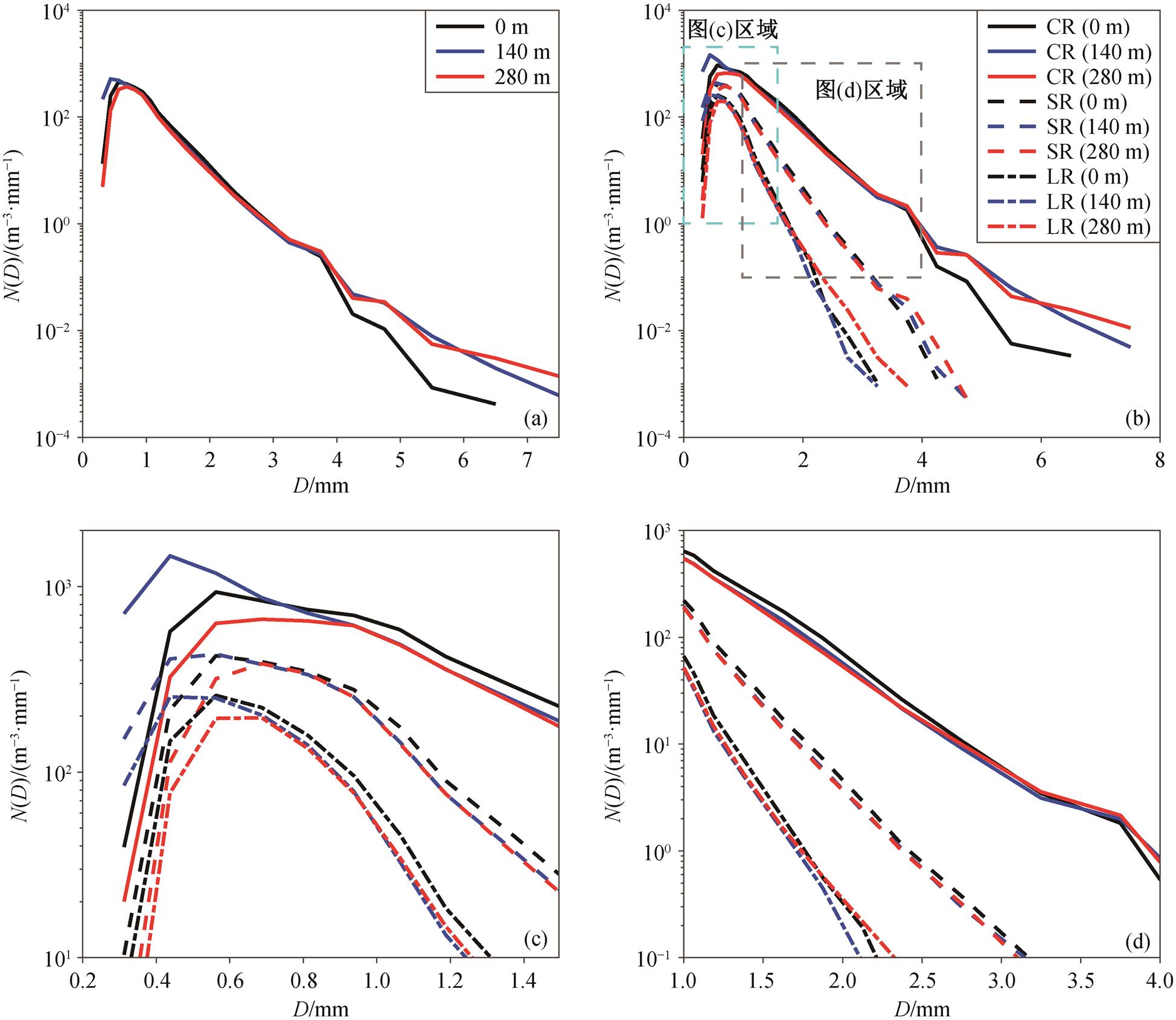
(a)为所有样本的平均值; (b)为稳定型降雨(SR)、对流型降雨(CR)和弱降雨(LR)样本的平均值; (c)和(d)为(b)的局部放大, 图例同(b)
图4 雨滴谱的垂直分布
Fig.4 Vertical variation of DSD
为了探讨不同尺度雨滴的垂直变化规律, 本文按粒径对雨滴做如下分类: 0~1mm 为小尺度雨滴, 1~3mm 为中等尺度雨滴, >3mm 为大尺度雨滴。雨滴下落过程分为两个阶段: 1)从 280m 下落至 140m, 大尺度雨滴略减少, 中等尺度雨滴总体上变化不大, 小尺度雨滴显著增加; 2)从 140m 下落至地面, 大尺度雨滴显著减少(这种情况在对流型降雨中更严重), <0.625mm 的小尺度雨滴显著减少, 中等尺度雨滴明显增加。雨滴数浓度峰值对应的直径随高度发生变化, 280m 的雨滴数浓度峰值对应的雨滴尺度最大, 为 0.687mm (该尺度档的中值, 下同); 地面次之, 为 0.562mm; 140m 最小, 为 0.437mm, 且在最小尺度档(0.312mm)的雨滴数浓度比其他高度有数量级的优势。
上述不同高度雨滴谱的垂直分布特征表明, 在雨滴下落过程中, 雨滴谱发生明显而复杂的变化, 随高度降低, 大雨滴逐渐减少, 小雨滴先增后减, 中等尺度雨滴先不变后增加, 雨滴谱峰值对应的直径先减后增。之前的研究中, 雨滴谱随高度的变化通常是线性的[9‒11,13‒14], 本文结果与之有诸多不同, 可能是观测条件不同所致。
由于气候和地形等因素的影响, 不同地区不同季节的雨滴谱特征往往不同[3‒4]。三参数雨滴谱模型的标准截距参数 Nw 用于刻画雨滴的数量特征, 质量加权直径 Dm 用于刻画雨滴的平均尺度特征。从这两个特征出发, 可以探究不同地区 Nw-Dm 的分布特点。Bringi 等[4]依据 log10Nw 和 Dm 的均值, 对全球多个地区的降雨进行测量, 将对流型降雨归纳成海洋型降雨(log10Nw≈4~4.5, Dm≈1.5~1.75)和大陆型降雨(log10Nw≈3~3.5, Dm≈2~2.75)两种类型。Wen等[15]利用 2DVD 雨滴谱仪和微降雨雷达, 研究梅雨季节中国东部地区降雨特征, 发现与具有相同气候特点的日本冲绳相比, 中国东部地区降雨有更大的Nw值和更小的 Dm 值, 并指出这可能与该地区更多的气溶胶和充足的水汽供应有关。
北京地区降雨的 Nw-Dm 关系具有独特的特征。图 5 展示不同降雨类型 log10Nw 和 Dm 的散点及均值,可以看出不同降雨类型区分明显。北京地区夏季对流型降雨(CR)不同于 Bringi 等[4]提出的海洋型降雨和大陆型降雨, 其 log10Nw≈3.6~3.8, Dm≈1.7~1.9, 介于海洋型与大陆型之间, 说明北京地区夏季降雨的特点既不同于澳大利亚达尔文和巴布亚新几内亚等靠近海边的地区, 也不同于美国科罗拉多州和奥地利格拉茨等内陆地区, 可能是北京地区较多的本地气溶胶以及夏季盛行的西南季风导致同时兼具两种类型的特点。
几类降雨的 Nw 与 Dm 几乎呈指数关系, 但我们同时注意到, 稳定型降雨(SR)中许多样本具有相对低的 Nw 值和高的 Dm 值, 弱降雨中许多样本具有相对高的 Nw 值和低的 Dm 值, 这与 Waldvogel[5]提到的N0 jump 效应对应的情况一致。在大范围降雨中, 雨滴谱存在突变的情况, 往往意味着中尺度天气区的转变, 这种情况可以通过 N0 的突变来识别。从微物理的角度而言, 在零度层附近, 数量较少的大而干的雪花融化会导致小的 Nw 值和大的 Dm 值, 此时零度层亮带较强, 而当小的冰晶粒子融化时, 则会产生大的 Nw 值和小的 Dm 值, 此时零度层亮带较弱, 二者转换时就会出现 N0 jump 效应[4]。
上述分析表明, 由于雨滴谱存在较大的变化, 稳定型降雨和弱降雨在拟合谱参数时易存在误差, 与图 3 的结果一致。Kumar 等[29]也指出, 小雨强的谱参数拟合值变化较大, 参考价值较低。
雨滴下落时受破碎、合并和蒸发等微物理过程影响, 导致雨滴谱发生变化。分析和评估这些微物理过程的作用, 尤其是明确其中起主导作用的微物理过程, 对提升理论研究水平和数值模拟准确性大有裨益。贾星灿等[10]和陈聪等[11]对雨滴下落时经历的微物理过程进行归纳, 张宇等[7]和李其琛等[8]通过数值模拟的方式研究几种微物理过程对雨滴谱的影响, 但这些研究过于笼统, 没有明确哪种过程占主导地位。
Beheng[6]通过数理方程推导, 指出当只有合并作用发生时, 小雨滴数减少, 大雨滴数增加; 雨滴破碎则导致小雨滴数增加。如图 5(d)所示, 在雨滴从 280m 下落到 140m 的过程中, Nw 增大, Dm 的减小, 结合图 4 中大尺度雨滴减少、中尺度雨滴不变、小尺度雨滴大量增加的分布特征, 说明雨滴谱随高度的变化可能是由破碎和蒸发作用导致的。雨滴破碎和蒸发这两种过程, 如果蒸发过程发挥了更重要的作用, 则Nw值应不变或减小, Dm 值减小。这与实际情况不符。另外, 本文研究的降雨过程持续时间均超过 30 分钟, 空气湿度应趋于饱和, 客观上限制了蒸发作用对雨滴谱型的影响。上述分析说明在雨滴从 280m 下落到 140m 的过程中, 破碎发挥了决定性作用。对于雨滴从 140m 下落到地面的过程, 我们需要区分降雨类型来研究, 对流型降雨的特征与从 280m 下落到 140m 的过程相似; 稳定型降雨和弱降雨则相反, Nw 减小, Dm 增大, 地面 Dm的均值略高于 280m。结合图 4 中地面中等尺度雨滴最多的特征, 说明在这一过程中虽然同时发生雨滴的合并、破碎和蒸发等过程, 但雨滴合并占据主导地位。
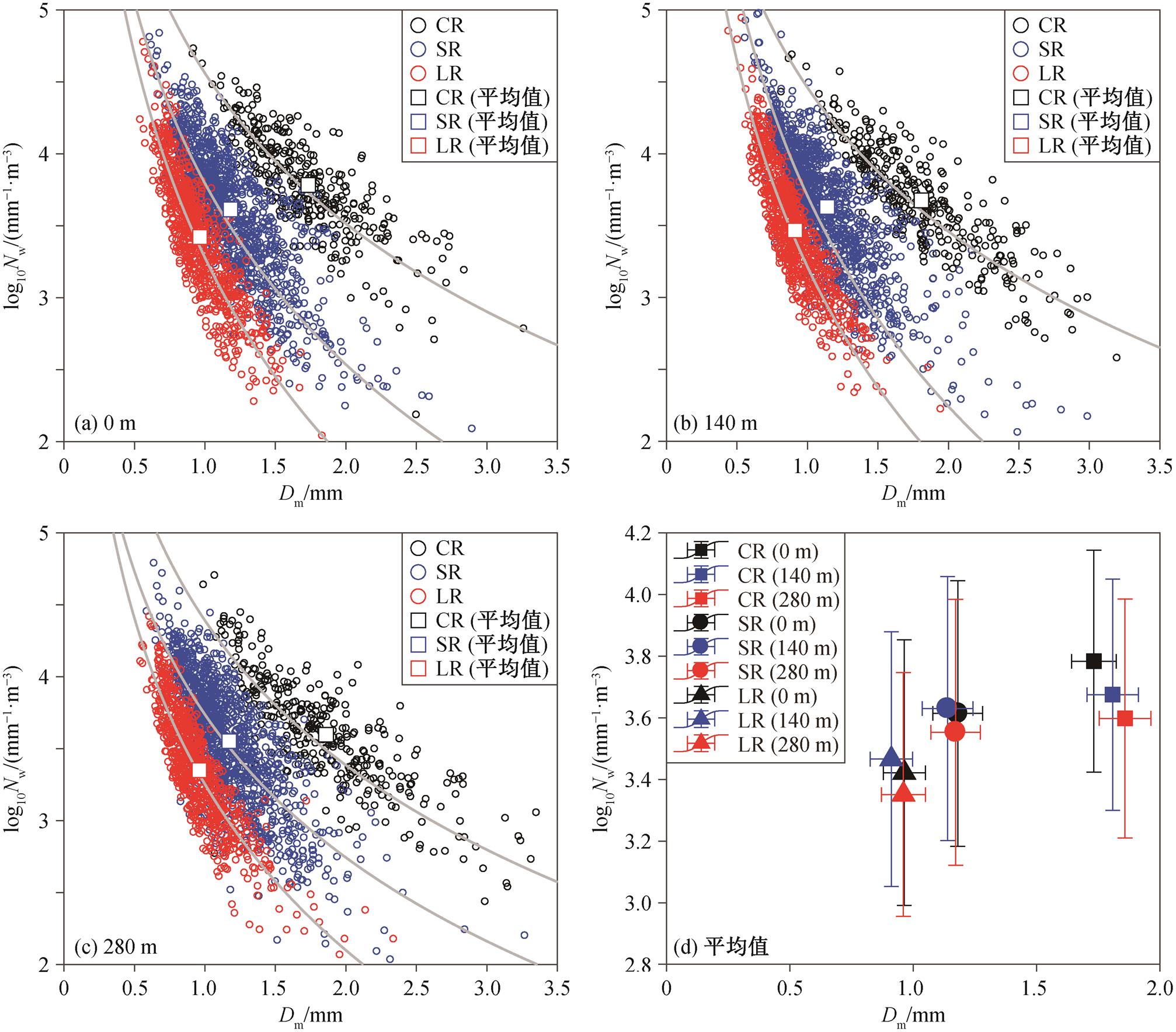
(a)~(c)中灰色实线为不同降雨类型的Nw和Dm指数形式的拟合线; (d)表示3种降雨类型在3个高度的平均情况以及以一倍标准差衡量的变率
图5 Nw-Dm散点图和均值
Fig.5 Scatter and mean of Nw-Dm
从图 6 可以看出, Dm 随着 R 增大而增大, 当 R呈指数级持续增大时, Dm 增速变缓, 说明当雨强增大到一定程度后, 雨滴的破碎与碰撞‒合并达到平衡状态, 此时雨强的增加主要源于 Nw (雨滴数)的增加, 与 Bringi 等[30]的结论一致。不同的降雨类型也有明显的区别, 图 6 中拟合结果显示, 雨强相同时, 与地面和 140m 相比, 280m 的雨滴尺度更大。当R<1mm/h 时, 降雨类型基本上为稳定型降雨(SR)和弱降雨(LR), 140m 的雨滴尺度比地面小; 当 R>1mm/h 时, 降雨类型以对流型降雨(CR)为主, 140m的雨滴尺度比地面大, 结合图 4 中对流型降雨中大尺度雨滴地面比 140m 显著减少的情况, 说明虽然碰撞与合并在雨滴从 140m 下落至地面的过程中占主导地位, 但对流型降雨中大尺度雨滴的破碎过程不可忽略。
综上所述, 雨滴从 280m 下落至 140m 的过程中, 雨滴破碎占据主导地位, 大尺度雨滴减少, 小尺度雨滴大量增加; 雨滴从 140m 下落到地面的过程中, 雨滴合并占据主导地位, 大尺度雨滴和小尺度雨滴均减少, 中等尺度雨滴增加; 对流型降雨中, 大尺度雨滴随高度迅速减少, 雨滴破碎对雨滴谱分布的影响较大。
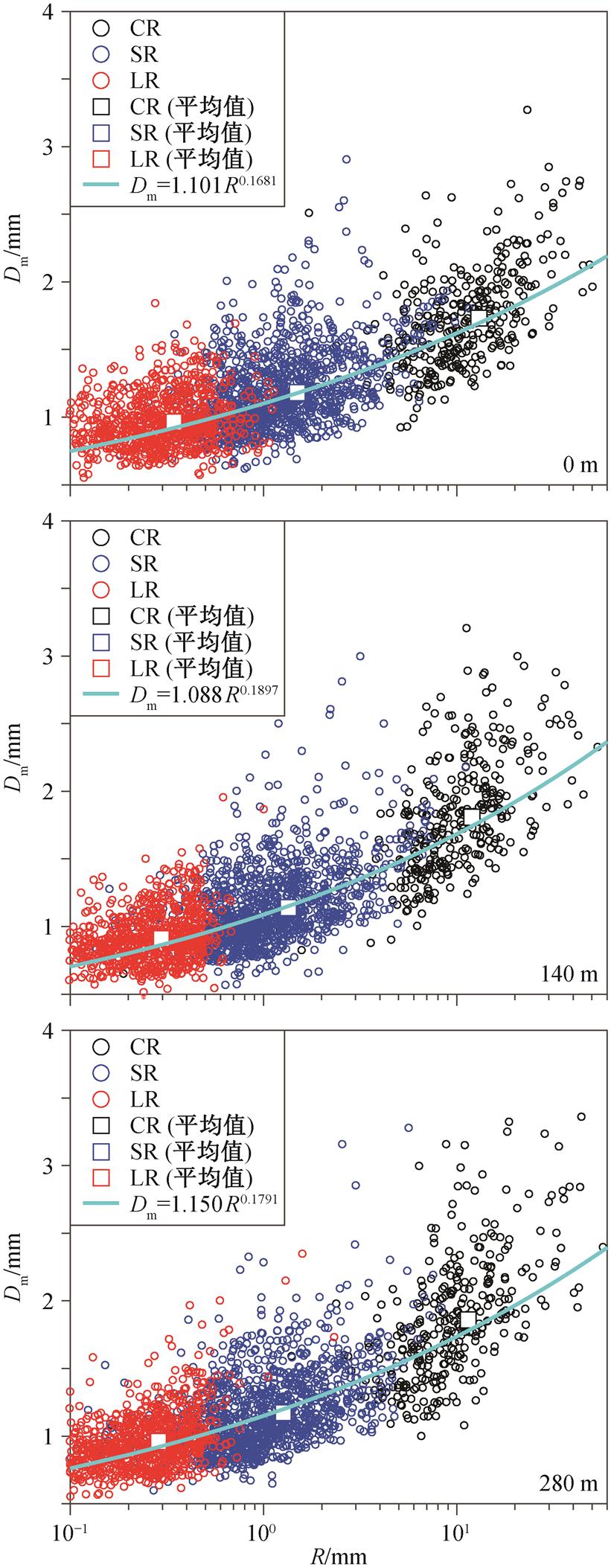
图6 Dm-R散点图及拟合线
Fig.6 Scatter and fit of Dm-R
为了进一步探究雨滴谱分布的垂直变化对降雨特征量的影响, 本文按小(0~1mm)、中(1~3mm)、大(>3mm)三档雨滴直径, 研究不同尺度雨滴对雨滴数浓度 NT (m−3)、液态水含量 LWC (g/m3)、雨强R (mm/h)和雷达反射率因子 Z (mm6/m3) 4 个降雨特征量的平均贡献度。4 个特征量的计算公式如下:
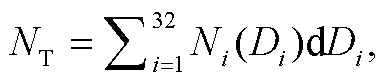 (11)
(11)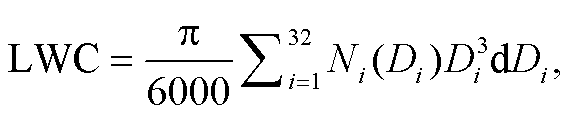 (12)
(12)
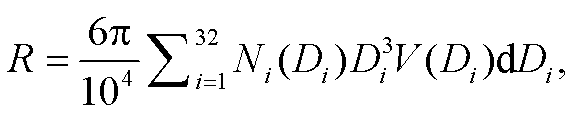 (13)
(13)
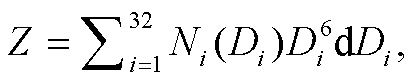 (14)
(14)其中, NT 为 0 阶矩; LWC 为 3 阶矩; R 中包含速度 vtc, 速度与尺度相关, 可以认为 R 与 4 阶矩相关; Z 为6 阶矩。可以预见, 同样的雨滴谱, 不同尺度的雨滴对几个特征量的贡献度会因计算公式不同而出现差异, 6 阶矩会放大大尺度雨滴的影响而弱化小尺度雨滴的影响, 3 阶矩和 4 阶矩会突出中等尺度雨滴对特征量的贡献, 0 阶矩则会弱化中大尺度雨滴的影响。
图7 显示, 不同尺度雨滴对 4 个特征量的贡献差异明显。小尺度雨滴对雨滴数浓度的贡献度最高; 中等尺度雨滴对 LWC 和 R 以及稳定型降雨(SR)和弱降雨(LR)的 Z 贡献度最高; 在对流型降雨(CR)中, 大尺度雨滴对 280m 的 Z 贡献度最高, 140m 次之, 对地面 Z 的贡献度比 140m 少 19.6%, 比 280m少 22.5%。从垂向变化看, 大尺度雨滴对 LWC, R和Z的贡献随高度下降而降低, 在对流型降雨中更显著, 是大尺度雨滴在下落过程中因破碎而减少所致; 中等尺度雨滴对 Z 的贡献度最大, 且地面均大于 140m, 这是因为雨滴从 140m 下落到地面的过程中以合并作用为主导。
不同特征量随高度的变化是非线性的。表 2 给出不同高度 3 种降雨类型的 R, Z 和 NT 平均值, 可以看出, 随着高度降低, R 值均呈增强趋势; Z 值的变化趋势不同于 R 值, 除对流型降雨(CR)的 Z 值随高度降低而减小外, 其余两类降雨 140m 的 Z 值均为 3个高度中最小, 地面 Z 值最大; 雨滴数浓度 280m最小, 140m 最大, 地面与 140m 接近, 但稍小于 140m。结合前述雨滴谱随高度的变化情况, 说明在雨滴下落过程中, 雨滴谱分布的垂直变化对不同的降雨特征量会造成不同的影响: 280m到 140m, 由破碎过程主导, 小尺度雨滴大量增加(提高一个数量级), R 小幅增加, Z减小; 140m到地面, 由碰撞与合并主导, 中等尺度雨滴增加, 总雨滴数减小, 对流型降雨中仍有显著的大雨滴破碎, 雨滴下落过程中R 增大, 稳定型降雨(SR)和弱降雨(LR)的 Z 值增大, 对流型降雨(CR)的Z值减小。对流型降雨之所以有异于其他降雨类型的表现, 应是其大尺度雨滴大量破碎所致。
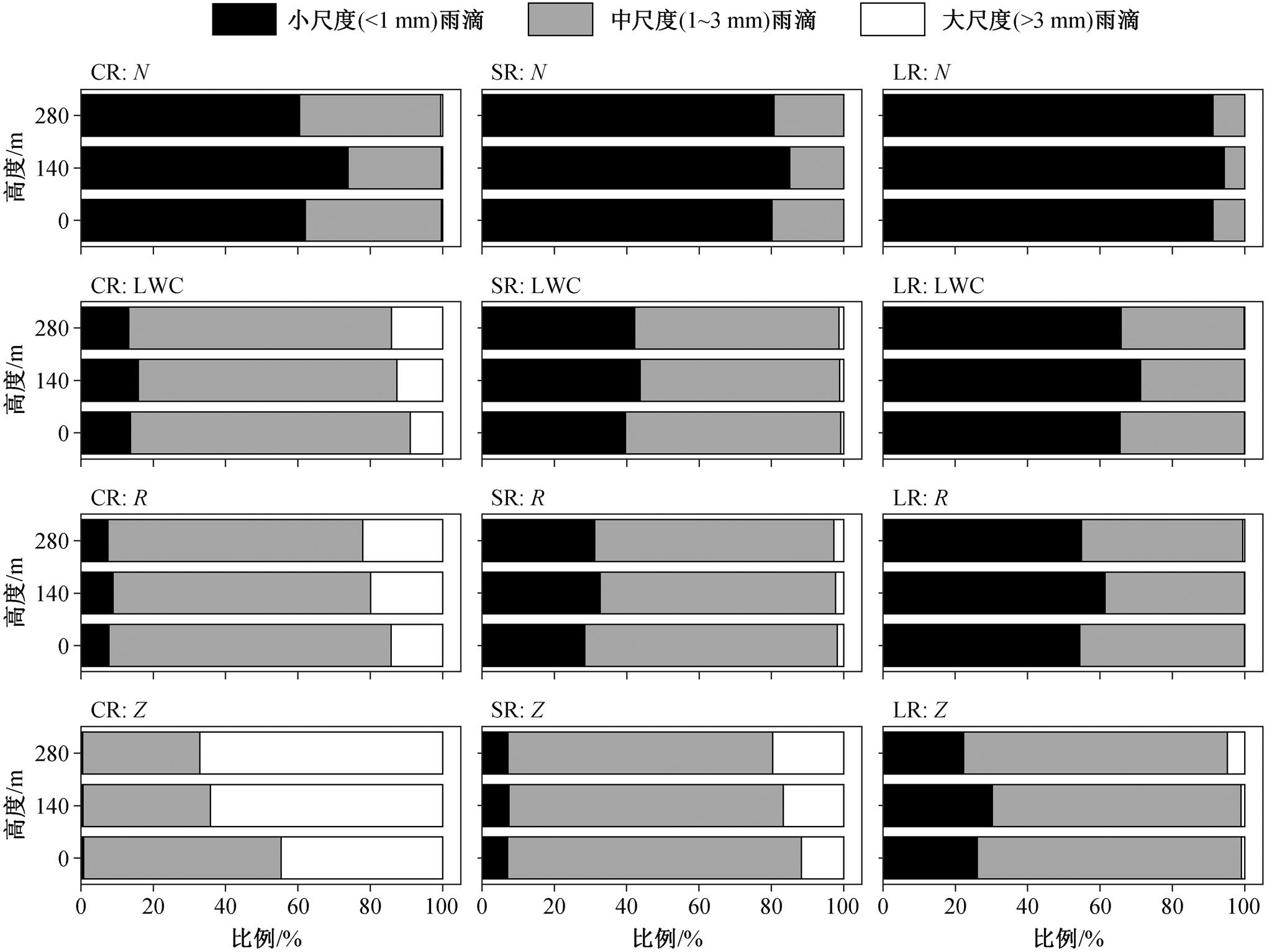
图7 不同尺度雨滴对降雨特征量的贡献度
Fig.7 Contribution of raindrops in different scales for rainfall variables
表2 R, Z和NT的平均值
Table 2 Mean value of R, Z, and NT

降雨类型RZNT 0 m140 m280 m0 m140 m280 m0 m140 m280 m CR13.0011.9711.44132801714318604787.0839.1618.3 SR1.491.351.26610542558227.5241.3195.5 LR0.340.300.2968516693.899.775.5
需要注意的是, 拟合的雨滴谱参数 Nw 随高度的减小而增大, 但观测结果中总雨滴数浓度 NT 随高度的变化没有出现相应的规律, 是否意味着拟合谱参数存在固有的缺陷, 值得继续思考和研究。
本节探讨雨滴谱分布的垂直变化对天气雷达、MRR 和 GPM DPR 等雷达进行校准以及地面降雨测量设备(雨量计和雨滴谱仪)与雷达联合反演降雨产生的影响。
2.5.1 Z-R 错配误差
Z-R 关系是雷达测量降雨的基础。Z 是雷达测量的空中回波, 通过 Z-R 关系 Z=aRb 计算雨强 R。雷达反射率因子 Z 可由雷达直接探测得到, 为提高测量的准确度, 通常以地面雨量计测得的雨强为真值, 对雷达测量结果进行评估和校准。然而, 雷达测量的是空中的 Z 值, 地面雨量计测量的是下落到地面的 R 值, 二者能否直接对应以及由此拟合的 Z-R 关系是否能准确地反演空中和地面的雨强都需要进一步研究。
以往的研究表明, 雨滴谱随着高度的变化而变化, 且这种变化可能对雷达测量降雨的结果产生影响。Yoshikawa 等[13]利用 Ku 波段雷达和二维视频雨滴谱仪 2DVD 探测数据, 分析对流型降雨和稳定型降雨的雨滴谱在近地面 50~300m 的垂直分布, 发现稳定型降雨的雨滴谱没有明显的垂向变化, 但对流型降雨中直径大于 0.5mm 的雨滴在下落过程中增长, 这一差异导致利用 Z-R 关系估计降雨时出现2%左右的误差。陈聪等[11]利用架设于黄山山底(464m)、山腰(1351m)和山顶(1840m)的 3 台 Parsivel激光雨滴谱仪, 对一次混合云降雨过程的探测数据进行分析, 发现直径小于 1mm 的小雨滴数浓度随高度增加而增大, 他们认为这与小雨滴的蒸发与碰撞‒合并有关; 直径大于 1.5mm 的雨滴数浓度和雨强均在山腰处最大, 可能与地形抬升有关; 各物理参量与 R 的拟合结果跟实测结果的一致性随高度增加而减小。
雨强 R 和雷达反射率因子 Z 随高度的变化情况表明, 空中的 Z 值在对流型降雨中比地面大, 在稳定型降雨和弱降雨中比地面小。由于地物杂波和雷达仰角等原因, 雷达无法探测到地面的 Z 值, 通常使用空中的 Z 值反演地面的雨强, 造成 Z-R 的错配。这种错配可能导致 3 种误差: 1)使用地面的雨滴谱资料建立 Z-R 关系, 应用于空中雷达回波Z 反演地面的雨强 R, 导致在对流型降雨中探测到比地面更大的 Z 值, 进而高估地面雨强, 在稳定型降雨和弱降雨中的情况则相反; 2)用地面的 R 值与空中的 Z 值建立 Z-R 关系, 应用于空中雷达回波 Z 反演地面的 R 值[31‒32], 看似不会产生误差, 但考虑到空中 Z 值随高度的变化, 如果建立 Z-R 关系所用 Z 值的高度与实际应用高度不同, 也将带来误差; 3)用地面的 R 值与空中的 Z 值建立 Z-R 关系, 应用于空中的雷达回波 Z 反演空中的 R[2,14], 由于空中的 R 值小于地面, 导致高估空中的 R 值。这 3 种误差中, 前两种更具有普遍性, 第三种通常出现在使用 MRR和 GPM DPR 等雷达测量降雨垂直廓线的场景。
因此, 使用地面的雨量计对雷达反演降雨进行校准以及与雷达联合反演降雨可能会带来误差, 本文将这种由雷达反射率因子 Z 与雨强 R 不匹配导致的误差称为Z-R错配误差。
2.5.2 Z-R错配误差对雷达测量降雨的影响
如果只进行定性分析, 则无法判断雨滴谱分布的垂直变化对雷达测量降雨的影响程度[8,14]。为了定量地探究 Z-R 错配误差对雷达测量降雨的影响, 本文针对前两种更具普遍性的误差情况分别进行讨论。
针对第一种误差情况(使用地面的雨滴谱资料建立 Z-R 关系, 应用于空中雷达回波 Z 反演地面的R 导致的误差), 本文将地面的 R 与地面的 Z 建立的Z-R 关系跟地面的 R 与 280m 的 Z 建立的 Z-R 关系进行对比。当 Z 值相等时, 计算得出的绝对误差和相对误差如表 3 中第 2~3 列所示。显然, 第一种 Z-R错配误差会高估对流型降雨(CR)在地面的雨强, 低估稳定型降雨(SR)和弱降雨(LR)在地面的雨强。对流型降雨的绝对误差较大, 但相对误差(4.69%)远小于稳定型降雨(28.16%)和弱降雨(15.57%)。
针对第二种情况(使用地面的 R 与空中的 Z 建立Z-R 关系, 应用于空中雷达回波 Z 反演地面雨强 R, 因建立 Z-R 关系所用 Z 的高度与实际应用高度不同导致的误差), 本文将地面的 R 与 140m 的 Z 建立的Z-R 关系跟地面的 R 与 280m 的 Z 建立的 Z-R 关系进行对比。当 Z 值相等时, 计算得出的绝对误差和相对误差如表 3 中第 4~5 列所示。可以看出, 将 140m的 Z 与地面的 R 建立的 Z-R 关系应用于 280m 的 Z反演地面雨强 R 时, 对流型降雨(CR)和弱降雨(LR)会高估地面雨强, 稳定型降雨(SR)则会低估地面雨强, 且弱降雨中这种情况会导致更大的相对误差。结果表明, 第二种 Z-R 错配误差是存在的, 虽然影响没有第一种 Z-R 错配误差大, 但仍然不可忽略。
上述结果说明, 由于雨滴谱分布随高度变化, 不同降雨特征量随高度发生非线性变化, 使用地面的降雨测量结果对雷达反演降雨进行校准以及与雷达联合反演降雨会导致 Z-R 错配误差, 且在稳定型降雨和弱降雨中导致的相对误差更大, 即使是相对误差更小的对流型降雨, 也高于 Yoshikawa 等[13]给出的 2%的误差值。
表3 Z-R错配误差
Table 3 Z-R mismatched error
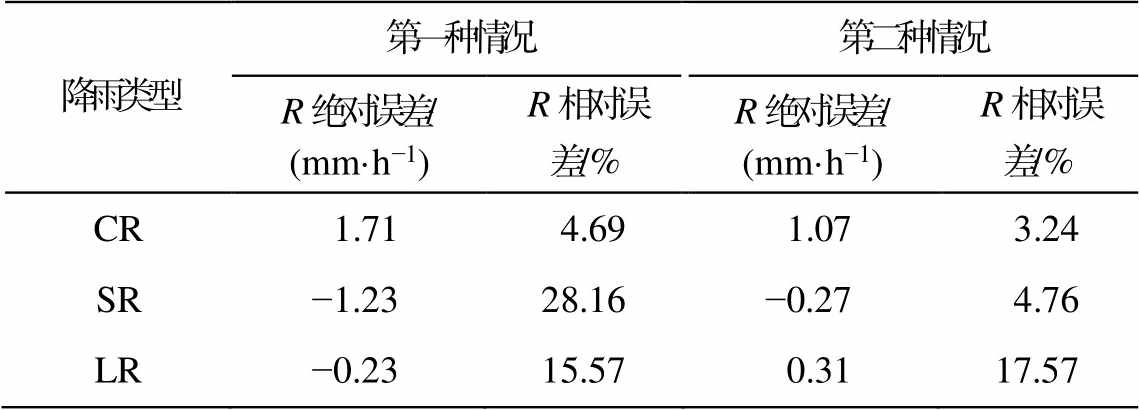
降雨类型第一种情况第二种情况 R绝对误差/(mm·h−1)R相对误差/%R绝对误差/(mm·h−1)R相对误差/% CR1.714.691.073.24 SR−1.2328.16−0.274.76 LR−0.2315.570.3117.57
本文基于安装在中国科学院大气物理研究所气象铁塔地面、140m 和 280m 三个高度的 Parsivel激光雨滴谱仪、超声风温仪和倾角仪, 用直接探测的方式, 研究低大气边界层的降雨。选取 2020 年 6—8 月北京地区 31 次降雨过程 2658 个样本, 将降雨分为对流型降雨、稳定型降雨、弱降雨和未分类降雨4 种类型, 并对前 3 种类型的降雨进行分析, 探讨雨滴谱和雨滴谱参数的垂直分布特征、主导的微物理过程、降雨特征量的变化以及由此导致的 Z-R 错配误差及其影响, 得到以下结论。
1)雨滴下落时, 受破碎、合并和蒸发等不同微物理过程影响, 导致雨滴谱发生变化, 主导这种变化的微物理过程随着降雨类型和高度的不同而改变。在从 280m 下落到 140m 的过程中, 雨滴破碎在其中发挥决定性作用, 大尺度雨滴减少, 小尺度雨滴大量增加; 在从 140m 下落到地面的过程中, 雨滴合并占据主导地位, 大尺度雨滴和小尺度雨滴均减少, 中等尺度雨滴增加; 对流型降雨中, 大尺度雨滴随高度降低迅速减少, 雨滴破碎对雨滴谱分布的影响较大。
2)北京地区降雨的雨滴谱特征介于海洋型降雨与大陆型降雨之间, 可能与该地区较多的气溶胶以及夏季盛行的西南季风有关, 导致存在比大陆型降雨更高的雨滴数浓度和更小的雨滴尺度, 有比海洋型降雨更小的雨滴数浓度和更大的雨滴尺度。
3)因雨滴谱分布随高度变化, 不同降雨特征量随高度发生非线性变化, 使用地面的降雨测量结果对雷达进行校准以及与雷达联合反演降雨会导致Z-R错配误差, 在稳定型降雨和弱降雨中导致的相对误差更大。
由于铁塔高度的限制, 本研究未能对更高的雨滴谱进行探测。因此, 尽管获得很多有趣的发现, 但这些结论是否具有普适性还需要进一步研究。本文认为北京地区的降雨特点介于海洋型与大陆型降雨之间, 并推测可能与本地气溶胶和西南季风有关, 这一论点还需要结合气溶胶和水汽的观测资料以及气候资料进行分析。虽然本文针对多种因素进行订正, 但雨滴下落过程中是否还受到其他因素的影响需要持续论证。此外, 拟合的雨滴谱参数 Nw 随高度的减小而增大, 但观测结果中总雨滴数浓度 NT随高度的变化特征没有相应的规律, 是否意味着拟合谱参数存在固有的缺陷, 值得继续思考和研究。
参考文献
[1]Seliga T A, Bringi V N.Potential use of radar diffe-rential reflectivity measurements at orthogonal pola-rizations for measuring precipitation.Journal of App-lied Meteorology, 1976, 15(1): 69‒76
[2]Tokay A, Petersen W A, Gatlin P, et al.Comparison of raindrop size distribution measurements by collocated disdrometers.Journal of Atmospheric and Oceanic Technology, 2013, 30(8): 1672‒1690
[3]Tzivion S, Feingold G, Levin Z.The evolution of rain-drop spectra.Part II: Collisional collection/breakup and evaporation in a rainshaft.Journal of the Atmos-pheric Sciences, 1989, 46(21): 3312‒3328
[4]Bringi V N, Chandrasekar V, Hubbert J, et al.Rain-drop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis.Journal of the Atmospheric Sciences, 2003, 60(2): 354‒365
[5]Waldvogel A.The N0 jump of raindrop spectra.Jour-nal of the Atmospheric Sciences, 1974, 31(4): 1067‒ 1078
[6]Beheng K D.The evolution of raindrop spectra: a review of microphysical essentials // Testik F Y, Geb-remichael M.Rainfall: state of the science.Washing-ton: American Geophysical Union, 2010: 29‒48
[7]张宇, 牛生杰, 贾星灿.雨滴下落过程谱分布演变的数值模拟.大气科学学报, 2013, 36(6): 699‒707
[8]李其琛, 杜金林.下落过程中雨滴谱和雨的雷达反射率的变化.北京大学学报(自然科学版), 1964(3): 283‒289
[9]Levin Z, Feingold G, Tzivion S, et al.The evolution of raindrop spectra: comparisons between modeled and observed spectra along a mountain slope in Swit-zerland.Journal of Applid Meteorology, 1988, 30(6): 893‒900
[10]贾星灿, 牛生杰.空中、地面雨滴谱特征的观测分析.大气科学学报, 2008, 31(6): 865‒870
[11]陈聪, 银燕, 陈宝君.黄山不同高度雨滴谱的演变特征.大气科学学报, 2015, 38(3): 388‒395
[12]Chen Baojun, Yang Jun, Pu Jiangping.Statistical cha-racteristics of raindrop size distribution in the meiyu season observed in Eastern China.Journal of the Me-teorological Society of Japan, 2013, 91(2): 215‒227
[13]Yoshikawa E, Kida S, Yoshida S, et al.Vertical struc-ture of raindrop size distribution in lower atmospheric boundary layer.Geophysical Research Letters, 2010, 37(20): 1‒6
[14]Peters G, Fisher B, Munster H, et al.Profiles of raindrop size distributions as retrieved by microrain radars.Journal of Applied Meteorology, 2005, 44(12): 1930‒1949
[15]Wen L, Zhao K, Zhang G, et al.Statistical character-istics of raindrop size distributions observed in East China during the Asian summer monsoon season using 2-D video disdrometer and micro rain radar data.Journal of Geophysical Research Atmospheres, 2016, 121(5): 2265‒2282
[16]Stull R B.An introduction to boundary layer meteo-rology.Dordrecht: Springer Netherlands, 1988
[17]盛裴轩.大气物理学.北京: 北京大学出版社, 2013
[18]Zhou L, Dong X, Fu Z, et al.Vertical distributions of raindrops and Z-R relationships using microrain radar and 2-D-video distrometer measurements du-ring the integrative monsoon frontal rainfall experiment (IMFRE).Journal of Geophysical Research: Atmos-pheres, 2020, 125: e2019JD031108
[19]Löffler-Mang M, Joss J.An optical disdrometer for measuring size and velocity of hydrometeors.Journal of Atmospheric & Oceanic Technology, 2000, 17(2): 130‒139
[20]郑铮, 刘晓阳, 周守根, 等.环境风对光学雨滴谱仪探测的影响.北京大学学报(自然科学版), 2020, 56(5): 824‒834
[21]刘均慧, 刘晓阳, 唐继顺, 等.不稳定平台 Parsivel雨滴谱仪测量速度订正.北京大学学报(自然科学版), 2021, 57(6): 1035‒1044
[22]Pruppacher H R, Beard K V.A wind tunnel inves-tigation of the internal circulation and shape of water drops falling at terminal velocity in air.Quarterly Journal of the Royal Meteorological Society, 1970, 96: 247‒256
[23]Tokay A, Bashor P G.An experimental study of small-scale variability of raindrop size distribution.Journal of Applied Meteorology & Climatology, 2010, 49(11): 2348‒2365
[24]Atlas D, Srivastava R C, Sekhon R S.Doppler radar characteristics of precipitation at vertical incidence.Reviews of Geophysics, 1973, 11(1): 1‒35
[25]Gunn R, Kinzer G D.The terminal velocity of fall for water droplets in stagnant air.Journal of Atmospheric Sciences, 1949, 6(4): 243‒248
[26]Testud J, Stéphane O, Black R A, et al.The concept of ‘normalized’ distribution to describe raindrop spectra: a tool for cloud physics and cloud remote sensing.JAM, 2001, 40(6): 1118‒1140
[27]Tokay A, Short D A.Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds.Journal of Applied Meteorology,, 1996, 35(3): 355‒371
[28]Ulbrich C W.Natural variations in the analytical form of the raindrop size distribution.Journal of Applied Meteorology, 1983, 22(10): 1764‒1775
[29]Kumar L S, Lee Y H, Jin T O.Two-parameter gamma drop size distribution models for Singapore.IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(9): 3371‒3380
[30]Bringi V N, Chandrasekar V.Polarimetric doppler weather radar: principles and applications.Cambri-dge: Cambridge University Press, 2001
[31]刘晓阳, 杨洪平, 李建通, 等.新一代天气雷达定量降水估测集成系统.气象, 2010, 36(4): 90‒95
[32]Andrea L, Paola A, Pierluigi C, et al.Radar estima-tion of intense rainfall rates through adaptive calib-ration of the Z-R relation.Atmosphere, 2015, 6(10): 1559‒1577
Vertical Distribution Characteristics of Raindrop Size Distribution at Lower Atmospheric Boundary Layer in Beijing
Abstract Based on three laser optical Parsivel disdrometers installed at different heights on meteorological tower, the vertical distribution characteristics of raindrop size distribution (DSD) and the influences on rainfall measurement by radar in the lower atmospheric boundary layer were investigated, during 31 precipitation episodes in Beijing from June to August 2020.The results show that the break-up process is dominant from 280m to 140m, which leads to the decrease of large scale raindrops and the increase of small scale raindrops.Whereas, from 140m to ground, the collision-coalescence process is dominant on the falling path of raindrops, which leads to the decrease of large and small scale raindrops and the increase of medium scale raindrops.Because of the great influence on DSD by break up, large scale raindrops in convection rain decrease rapidly with height.The DSD of convective rain in Beijing is different from oceanic-like cluster and continental-like cluster.Due to the change of DSD with height, characteristic parameters of rainfall vary nonlinerly.A Z-R mismatch error would be caused when using ground precipitation data for correction of the meteorological radar rainfall estimation, which is heavier in stratiform and light rain.
Key words raindrop size distribution; vertical distribution; Parsivel; precipitation; Z-R mismatch error
doi: 10.13209/j.0479-8023.2021.085
收稿日期: 2020–12–20;
修回日期: 2021–04–16
国家重点研发计划(2017YFC0209602)和国家自然科学基金(41475016)资助