
图1 仪器安装位置示意图
Fig.1 Location of the instruments
摘要 针对高架环境中 OTT-Parsivel 雨滴谱仪测量结果受环境气流影响易出现误差的问题, 开展不稳定平台的 OTT-Parsivel 激光雨滴谱仪探测试验, 提出在不同水平风速环境下的质量控制方法, 给出测量速度订正模型, 并对其进行仿真实验和误差分析。基于 2020 年北京夏季降水过程, 利用 280m 高处 OTT-Parsivel 激光雨滴谱仪、三维超声风温仪和动态倾角传感器的测量数据, 对多次降水个例进行分析。结果表明, 提出的模型对雨滴的垂直下落速度有良好的订正效果, 各尺度通道速度分布更趋于正态分布, 有效粒子数可提高 6%。在缺少倾角测量的情形下, 利用超声风温仪风速数据估计缺失的倾角数据, 估算的倾角值与实测值的一致率可达 96.43%。在水平风速超过 8m/s的大风情况下, OTT-Parsivel 雨滴谱仪测量数据的可用性得到提高。
关键词 雨滴谱; 落速订正; OTT-Parsivel; 水平风速
雨滴谱是反映雨滴数浓度与雨滴尺度关系的重要物理量。通过雨滴谱反演, 可以得到多种降水物理参量, 如雨强、含水量和雷达反射率因子等。精确地测量雨滴谱, 能提高降水物理参量的精确度。
早期测量降水雨滴谱的方法主要有滤纸色斑方法、动力学方法和快速摄影方法[1]等。由于传统方法的准确度和效率低, 逐渐被光电降水粒子测量仪器取代。OTT-Parsivel 雨滴谱仪通常利用粒子对信号的遮挡, 测量粒子尺度和下落速度, 在地面雨滴谱测量中应用越来越广泛, 可为卫星和雷达等遥感测量提供校验。
在近地面处, 垂直气流近似为零, 水平风对其测量的影响可以忽略不计。大气运动速度随高度增加而加大, 在高架测量环境中, 受垂直气流的影响, 雨滴下落速度偏离 Atlas 理论下落速度[2]; 受水平风速的影响, 雨滴会产生水平速度。水平风速引起的塔架摆动和仪器倾斜等状况, 都会造成雨滴下落速度的测量误差。OTT-Parsivel 雨滴谱仪有巨大的优势, 但在风速超过 10m/s 时, 测量结果仍然有相当大的不确定性。Higgins 等[3]评估两种不同观测模式的 OTT-Parsivel 雨滴谱仪在强风下的观测数据, 提出应将受强风影响的观测样本剔除。Bradley 等[4]提出, 为了提高 OTT-Parsivel 雨滴谱仪的测量精度, 应使其采样空间垂直于风向。Lopez 等[5]设计的关节式 OTT-Parsivel 雨滴谱仪, 可以根据水平风速方向、水平风速和雨滴垂直下落速度, 调整其方位角和仰角, 使采样空间垂直于雨滴下落轨迹。Friedrich等[6]利用固定式 OTT-Parsivel 雨滴谱仪和关节式雨滴谱仪分析一次飓风天气, 结果表明关节式 OTT-Parsivel 雨滴谱仪对雨滴下落速度的测量更加准确。
随着高度增加, 风速逐渐增大, 在大风条件下测量数据的占比也逐渐增大。如果将受大风影响的数据完全剔除, 会影响对雨滴谱垂直分布规律的研究。为了提高探测数据的可用性, 本研究利用 2020年夏季北京降水数据, 结合超声风温仪和倾角传感器数据, 尝试对 OTT-Parsivel 雨滴谱仪大风情况下的速度测量结果进行订正, 量化水平风对测速的影响, 拉高探测数据的可用性。
观测点位于北京市中国科学院大气物理研究所大气观测塔(116.22°E, 39.58°N, 海拔 49m, 塔高320m), 在 280m 平台搭载 OTT-Parsivel 二代激光雨滴谱仪、超声风温仪和动态倾角传感器, 安装位置如图 1 所示。本文利用 2020 年 6—8 月 OTT-Parsivel雨滴谱仪的雨滴速度数据、超声风温仪的三维风速数据以及动态倾角传感器的倾角数据进行分析。
OTT-Parsivel 二代激光雨滴谱仪工作时, 激光发射端发射一束长 180mm, 宽 30mm, 高 1mm 的激光, 由接收端接收后转换为电信号。在没有降水粒子经过时, 接收端会形成稳定的电压; 当有降水粒子通过激光束区域时, 由于遮挡作用, 接收端电压变小, 电压减小的幅度与雨滴直径相关, 电压减小持续的时间与雨滴下落速度相关。OTT-Parsivel激光雨滴谱仪有 32 个间隔不等的直径探测通道和32 个速度探测通道, 直径探测范围为 0.2~25mm, 速度探测范围为 0.2~20m/s[7]。32 个速度探测通道所测速度区间的分辨率 R 分别为 0.05m/s (1~10 通道)、0.1m/s (11~15 通道)、0.2m/s (16~20 通道)、0.4m/s (2~25 通道)和 0.8m/s (26~32通道), 数据的时间分辨率为 1 分钟。

图1 仪器安装位置示意图
Fig.1 Location of the instruments
超声风温仪利用超声波测量风速、风向及温度, 可以准确地测量风的三维脉动[8], 测风精度几乎不受环境温度、湿度和降雨影响, 是目前精度较高、响应较快、工作稳定的测风仪, 采样频率为 10Hz。为使超声风温仪数据与 OTT-Parsivel数据频率一致, 本文采用郑铮等[9]的数据处理方式。
倾角传感器采用 MEMS (微机电系统)技术, 测量范围为±30°, 全量程精度为 0.5°, 是一款具有高性价比的电压输出的双轴高精度倾角传感器[10], 采样频率为 1Hz。为了配合 OTT-Parsivel 激光雨滴谱仪数据, 本文对传感器数据做如下处理: 角度传感器输出双轴倾角, 两个方向的倾角均保留输出值小数点后一位, 并取分钟均值作为分钟角度数据。
雨滴下落过程中, 运动速度取决于重力以及空气与雨滴运动速度之差引起的风阻力[6], 大规模上升或下沉的气流以及水平气流会影响雨滴与空气之间的相对速度, 从而影响实际下落速度[11]。OTT-Parsivel 雨滴谱仪的测量速度为雨滴垂直于测量截面的速度, 本文将雨滴下落速度测量误差归因于水平风速和垂直气流的影响: 垂直气流主要影响降水粒子的垂直移动速度, 而不影响仪器测量方向; 水平风速会对测量平面的方向产生影响, 但不影响降水粒子的垂直下落速度。受水平风速影响, 大气观测塔会倾斜, OTT-Parsivel 雨滴谱仪会发生一定倾角的旋转, OTT-Parsivel 雨滴谱仪测量平面与水平面之间出现一定的倾角, 本文讨论中忽略大气观测塔和 OTT-Parsivel 雨滴谱仪的水平移动以及沿垂直方向旋转的影响。
根据右手坐标系原则, 建立如图 2 所示的模型。X 轴指向西, 与三维风速仪的 v 正方向相同; Y轴指向北, 与三维风速仪的 u 正方向相同; Z 轴垂直向下, 与三维风速仪的 w 负方向相同。浅灰色区域为雨滴谱仪的理想测量平面, 深灰色区域为雨滴谱仪的实际测量平面。Up 为雨滴水平移动速度, 假定超声风温仪测量的三维风速代表观测平台的风速, 忽略倾角导致的观测误差, Up 即为超声风温仪观测到的水平风速; wm 为 OTT-Parsivel 雨滴谱仪测量速度, 取所在速度区间的中值; wp 为水平订正后的雨滴垂直落速。α 是 OTT-Parsivel 雨滴谱仪受 u 方向风影响产生的倾角, β 是 OTT-Parsivel 雨滴谱仪受 v方向风影响产生的倾角。雨滴的真实三维速度 Vp与雨滴谱仪测量的三维速度 Vm 之间有如下关系:
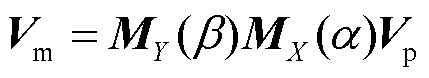 , (1)
, (1)其中, Vp=(Upcosγ, Upsinγ, wp), Vm=(um, vm, wm), γ为水平风向, 单位为(°)。
OTT-Parsivel 雨滴谱仪与动态倾角传感器搭载在同一高度的平台上, 故假定动态倾角传感器测量的倾角为 OTT-Parsivel 雨滴谱仪的旋转倾角, 绕 X轴的旋转变换矩阵 MX (α)和绕 Y 轴的旋转变换矩阵MY (β)[12]分别表示为
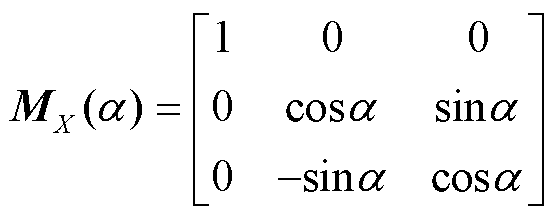 , (2)
, (2)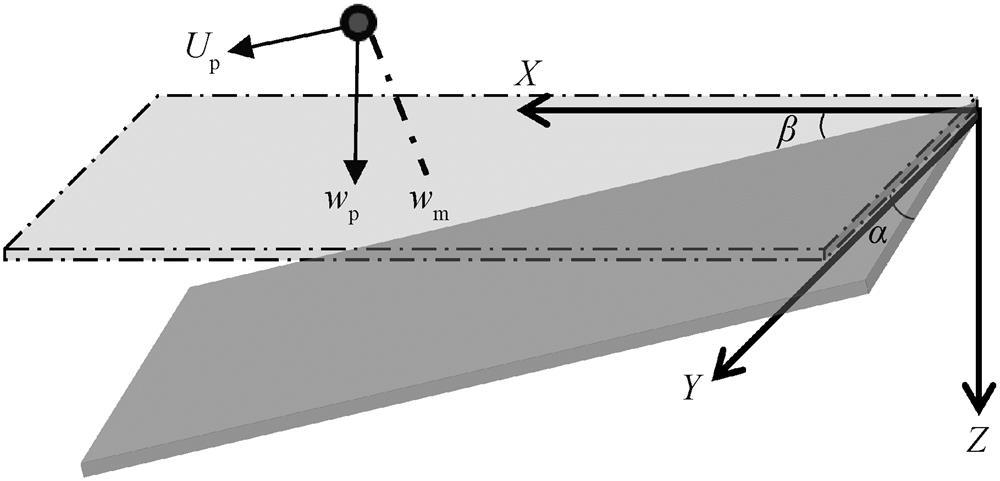
图2 OTT-Parsivel雨滴谱仪测量速度模型
Fig.2 Measurement model of OTT-parsivel
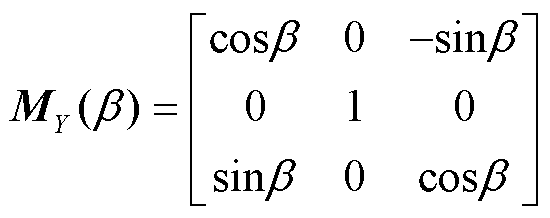 , (3)
, (3)降水粒子在静止大气中的下落末速度表示为
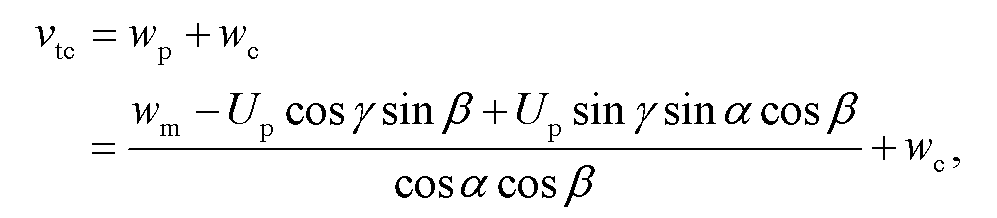 (4)
(4)
其中, vtc为静止大气下的雨滴落速(下面称为订正后雨滴垂直落速), wc为垂直气流速度, 单位均为m/s。水平风速与垂直气流的影响是相互独立的, 故式(4)可以分为水平订正部分wp(本文所述水平订正指水平风速对雨滴谱仪测速结果的订正)和垂直订正部分wc (本文所述垂直订正指垂直气流对雨滴垂直落速的订正)。
依据式(4), 对OTT-Parsivel雨滴谱仪的降水样本数据进行订正, 找到 vtc 所在的速度区间, 将wm区间的粒子移入vtc所在区间。定义订正量为S=vtc − wm,若S > 0, 则订正量为正, 订正后雨滴移入速度更大的区间; 若S<0, 则订正量为负, 订正后雨滴移入速度更小的区间。当S不超过雨滴谱仪的速度分辨率R时, 雨滴所处区间不会发生变化, 即当|Si|≥Ri (i表示第i个速度通道)时, 订正才有意义并且有效。根据Atlas等[2]的研究结果, 静止大气中雨滴下落末速度与直径存在如下关系:
V = 9.65 – 10.3e–0.6D, (5)
其中, D表示雨滴直径(mm), V表示下落末速度(m/s)。若订正后雨滴下落速度vtc与理论下落末速度V落入同一速度区间, 则认为已将OTT-Parsivel雨滴谱仪测量速度订正至理论落速。
表1列出直径探测通道5~20对应尺度雨滴理论下落速度60%误差区间[13]允许速度的上限(1.6V)和下限(0.4V), 前10个直径通道(D<1.25mm)的落速下限落在速度分辨率为0.1m/s的速度区间, 说明0.1m/s的订正量对前10个直径通道有效; 前23个直径通道(D<8mm)的落速下限落在速度分辨率为0.2m/s的速度区间, 说明0.2m/s的订正量对前23个直径通道有效。当订正量为 0.05m/s时, 不存在有效尺度订正范围, 故本文重点分析订正量绝对值超过0.1m/s(本文称之为有效订正量)的情况。
水平风导致OTT-Parsivel雨滴谱仪采样区间倾斜, 影响对雨滴垂直下落速度的测量。我们将订正量分为两部分, 一部分是修正由垂直气流引起的测量误差, 郑铮等[9]已做过详细的讨论, 本文不进一步讨论; 另一部分是修正水平风导致OTT-Parsivel雨滴谱仪测量平面倾斜而引起的测量误差, 本文称为水平订正量。为定量地分析水平风对测量雨滴下落速度的影响, 本文对水平订正部分进行仿真模拟实验。为了与实际情况相符, 仿真实验过程中, 水平风速从0变化至20m/s, 风向变化360°, 倾角α和β分别设置为实测数据的10%, 50%和90%分位点(指倾角分布函数中P=i对应的倾角数据, 其中 i= 10%, 50%, 90%), 仿真实验参数设置如表2所示。
表1 下落速度60%误差区间所在的速度区间
Table 1 Interval of velocity corresponding to ±60% theoretical velocity in different diameters
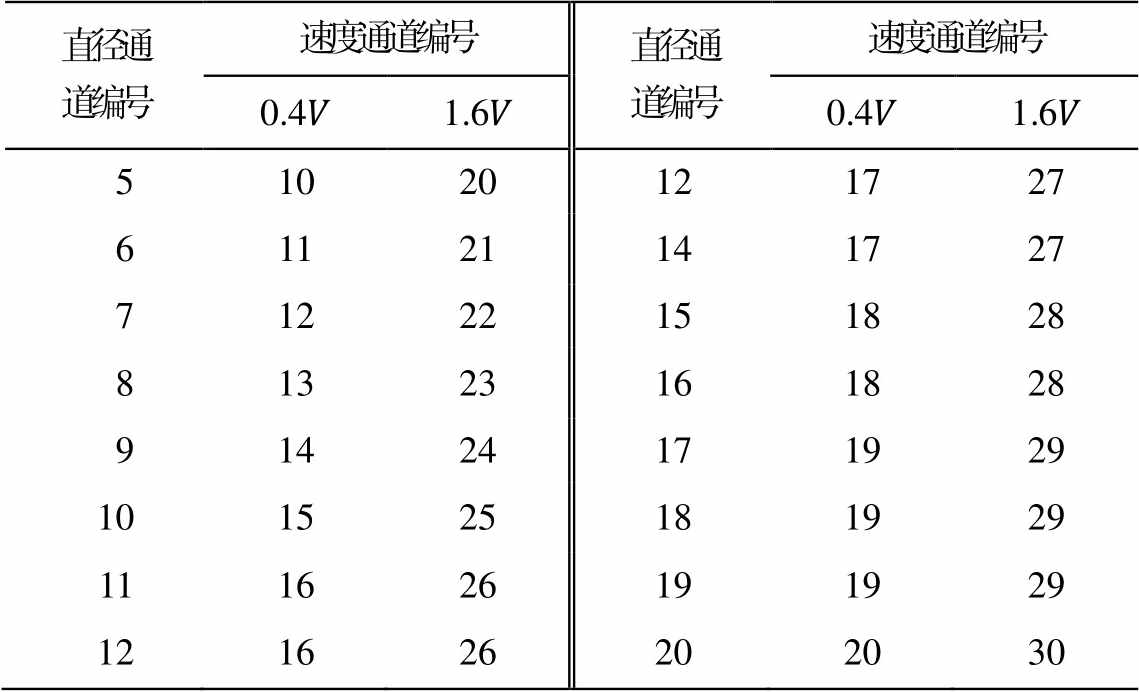
直径通道编号速度通道编号直径通道编号速度通道编号 0.41.60.41.6 51020121727 61121141727 71222151828 81323161828 91424171929 101525181929 111626191929 121626202030
图3展示直径探测通道11(D=1.375mm)在不同倾角下的水平订正量。从圆心向外, 水平风速由0增至20m/s, 圆周数字表示风向, 0°表示v=0, u∈(0, 20 m/s); 90°表示u = 0, v∈(–20, 0 m/s)。其他直径探测通道在不同倾角下的水平订正量呈现相同的规律(图略)。
以图 3(a)中−150°风向为例, 随着水平风速加大(从 0 增至 0.2m/s), 水平订正量表现为增加趋势。随着倾角增大, |S|=0.05m/s 的范围缩小, 说明达到有效订正量所需的水平风速逐渐减小。
当水平风向在−120°~150°和 −30°~60°区间时, 订正量对风速更加敏感, 更易达到最大订正量。以−150°风向为例, 当水平风速为 11 m/s 时, 订正量可达 0.2m/s, 此时 90°风向仍无有效订正量(图 3(a))。随着倾角增大, 同一风向对风速的敏感性逐渐增加, 不敏感的风向范围逐渐减小。
表2 水平订正仿真实验参数设置
Table 2 Parameter setting of horizontal correction simulation conditions
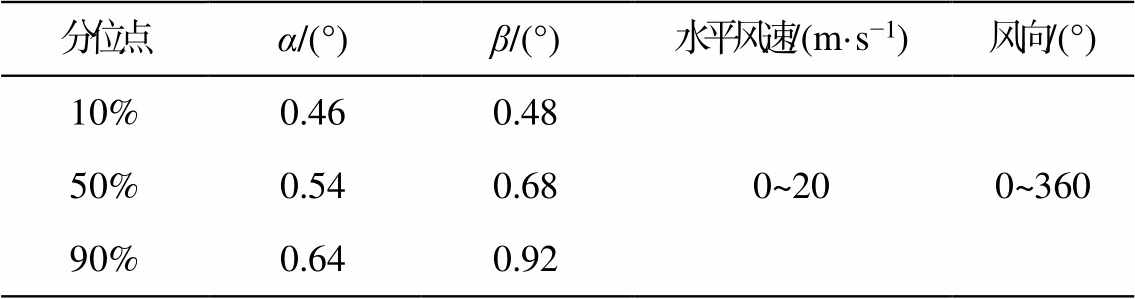
分位点α/(°)β/(°)水平风速/(m·s−1)风向/(°) 10%0.460.480~200~360 50%0.540.68 90%0.640.92
图 4 展示倾角达到 90%分位点(α=0.64°, β= 0.92°)时, 不同风向情况下达到有效水平订正量时要求的最小水平风速。大倾角情况下, 水平订正量达到 0.1m/s 所需的最小水平风速为 6m/s, 达到 0.2 m/s 所需的最小水平风速为 11m/s。实际情况下, 需要更大的水平风速才能达到有效订正量。水平订正量对水平风速的敏感性不强, 在图 4 中橙色曲线上方区域以及橙色与蓝色曲线之间区域, 风速和风向的改变都不会影响订正量的数值。
在一定的风向范围(如西北风或东南风区域)内, 水平订正量对风速的敏感性较弱, 水平风速超过 20 m/s 才能达到有效订正量。随着倾角增加, 对水平风速不敏感的风向范围逐渐减小。
为了分析水平订正量对倾角的敏感性, 对不同倾角下的水平订正进行仿真实验。为了明显地表示倾角对订正量的影响, 水平风速取 20m/s, 风向取−150°, −120°和−100°。
图 5 显示水平风速为 20m/s 时, 水平订正量与倾角的关系。可以看出, 随着倾角变大, 水平订正量逐渐增加。水平订正量对倾角的敏感性取决于风向, 当水平风的 u 量更大时, 水平订正量对 β 更敏感, 等值线基本上沿横轴分布(图 5(a)); 当水平风 v分量更大时, 水平订正量对 α 更敏感, 等值线沿纵轴分布(图 5(c))。总体来说, 订正量对倾角不敏感, 本文实验中动态传感器的精度为 0.5°, 可以满足订正模型所需精度。
OTT-Parsivel 雨滴谱仪的探测阈值为 0.001 mm/h。为了提高信噪比, 需要剔除降水强度小于0.1mm/h 的样本。本文定义降水时长超过 30 分钟, 降水间隔小于 30 分钟的连续样本为一次降水过程。2020 年 6 月 25 日为一次大风降水过程, 降水时段为 19:44—22:05, 共采集到 108 条样本数据, 其中水平风速为大风速的有 44 条, 占此次降水总样本数的 40%。本文中大风速指水平风速大于 8m/s, 小风速指水平风速小于 8m/s。
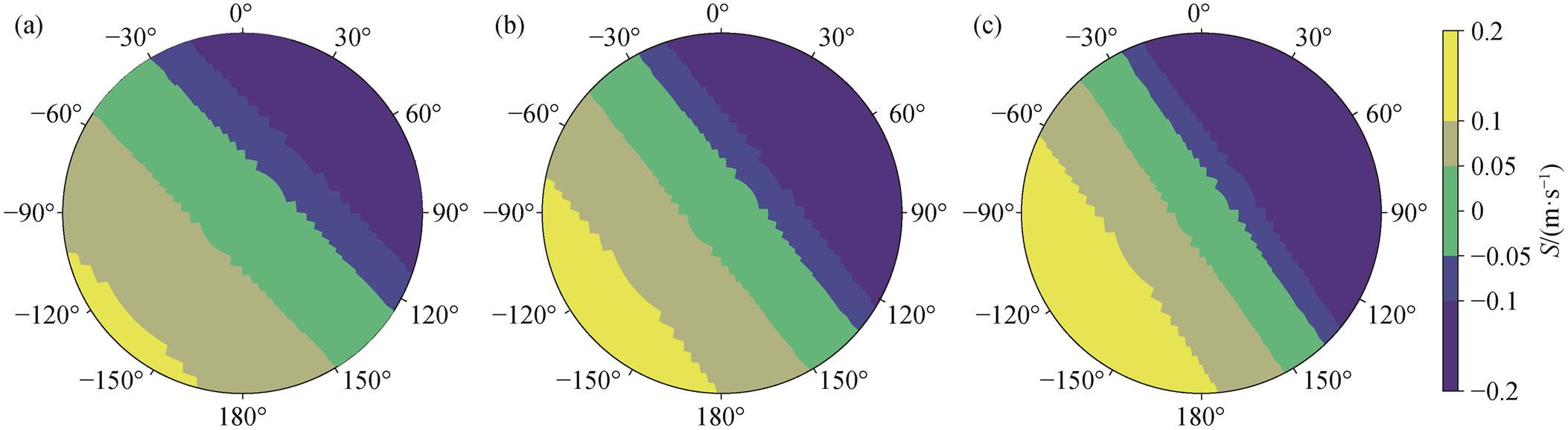
(a) α=0.46°, β=0.48°; (b) α=0.54°, β=0.68°; (c) α=0.64°, β=0.92°
图3 水平订正量仿真实验结果
Fig.3 Simulation results of correction
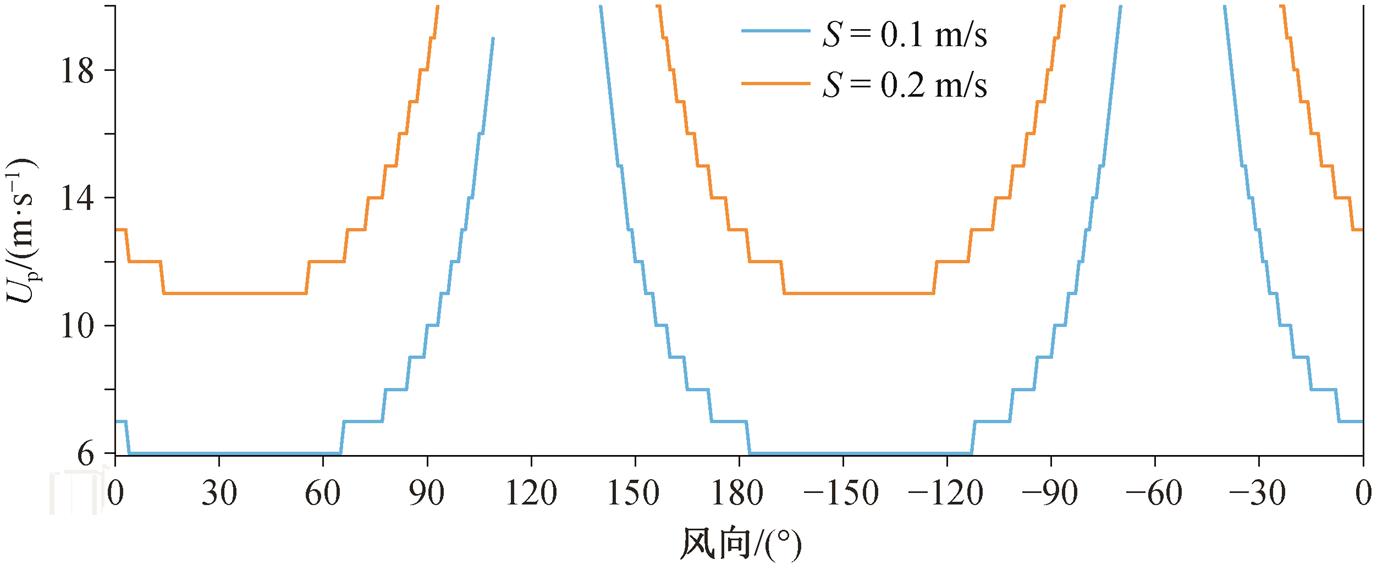
图4 不同风向对应达到有效订正量的最小水平风速
Fig.4 Minimum horizontal wind speed matching effective correction with different wind directions
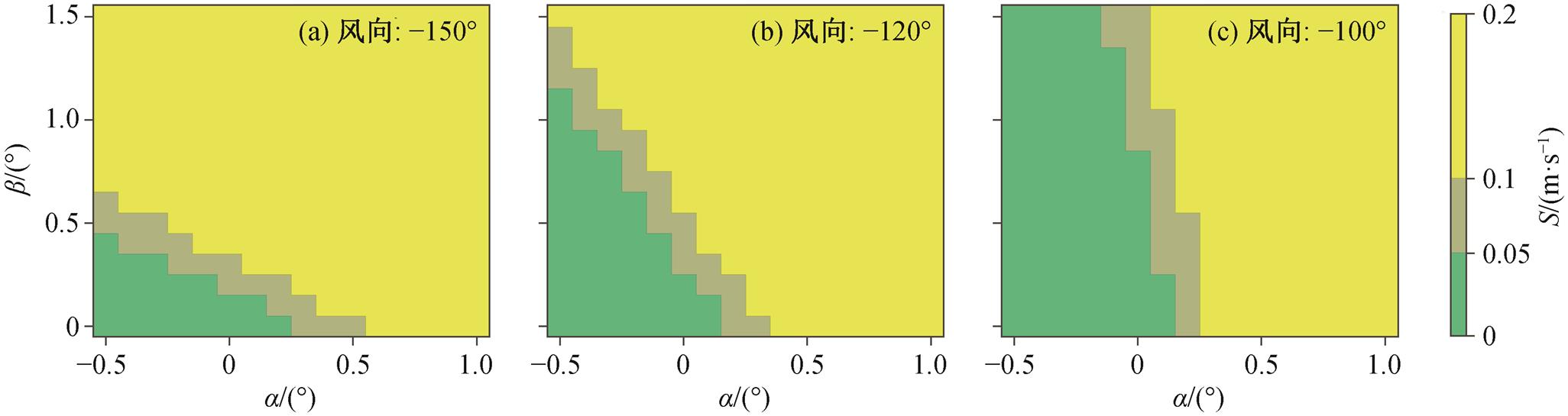
图5 水平订正量与倾角的关系
Fig.5 Relationship of horizontal correction and angle
受仪器探测灵敏度的影响, 直径小于 0.5mm的粒子参考意义较小, 直径大于 5mm 的粒子在自然界中较少, 随机性较大, 因此本文选择直径探测通道 5~20 进行分析。速度订正前, 对雨滴谱数据均进行轴比订正[14]; 速度订正后, 均用 60%速度误差区间[12]的方法进行质量控制, 定义进行质量控制后的雨滴总数为有效粒子数。
Kim 等[15]提出忽略水平风影响, 利用垂直气流订正雨滴垂直下落速度的方法(称为订正方法 B):
vtc = wm + wc 。 (6)
本文提出的订正模型(称为订正方法 A)是在订正方法 B 的基础上加入水平订正。假定风温仪测量的三维风速可以代表测量平面的风速, 忽略倾角导致的观测误差, 则雨滴的水平移动速度就是超声风温仪观测到的水平风速。OTT-Parsivel 雨滴谱仪观测到雨滴速度为 wm, 利用式(3)和(5)订正后, 雨滴垂直下落速度为 vtc, 找到 vtc 所在速度区间, 将 wm区间的雨滴数移动至vtc区间。
图 6 对比 2020 年 6 月 25 日降水过程中风速大于8m/s 的样本订正前后速度谱, 可见水平订正主要影响各通道粒子个数, 进而影响垂直下落速度。在此次降水的大风速(Up≥8m/s)时段内, OTT-Parsivel测得 11553 个雨滴, 有效粒子数为 9879 个, 有效率为 85.51%; 利用订正方法 B 得到的有效粒子数为10505 个, 有效率为 90.93%; 利用订正方法 A 得到的有效粒子数为 10598 个, 有效率为 91.73%。
图 7 中, 若圆点落入误差条范围内, 则认为订正后雨滴下落速度与理论速度一致。与只做垂直气流订正(黄色圆点)相比, 用本文提出的模型订正后, 雨滴下落速度增加 4.5% (红色圆点), 更接近理论下落速度。垂直气流与水平风速同时订正的效果好于单独订正的原因可能是, 单因素的改变不会使雨滴下落速度的改变超过所在速度区间的分辨率。
垂直订正和水平订正后有效粒子数的相对变化如表 3 所示。随着雨滴直径增大, 有效粒子数相对变化率逐渐减小。当雨滴直径大于 1mm 时, 有效粒子数相对变化率小于 1%, 且两种方法的相对变化率相同。主要原因在于, 随着粒子直径增大, 速度区间也变大, 垂直风速成为影响粒子速度区间的主要因素。
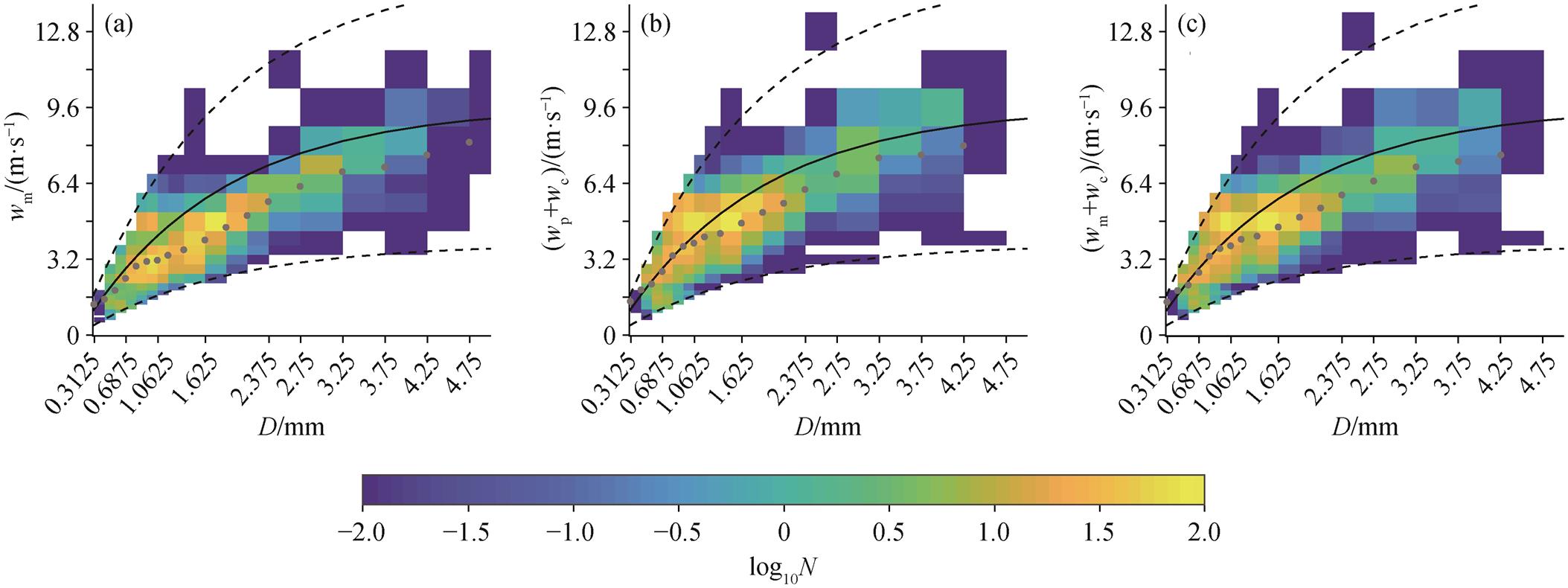
(a)OTT-Parsivel 雨滴谱仪测得的速度谱; (b)用订正方法 A 订正后的速度谱; (c)用订正方法 B 订正后的速度谱。黑色实线表示 Atlas理论下落速度, 黑色虚线表示 60%的误差区间, 颜色填充表示雨滴数目, 灰色圆点表示雨滴平均下落速度; 数据经过质量控制, 直径探测通道为3~20, 风速大于 8 m/s; D为直径区间中值点, 下同
图6 2020 年 6 月 25 日订正前后雨滴速度谱对比
Fig.6 Comparsion between corrected and original raindrop velocity sectrum on June 25, 2020
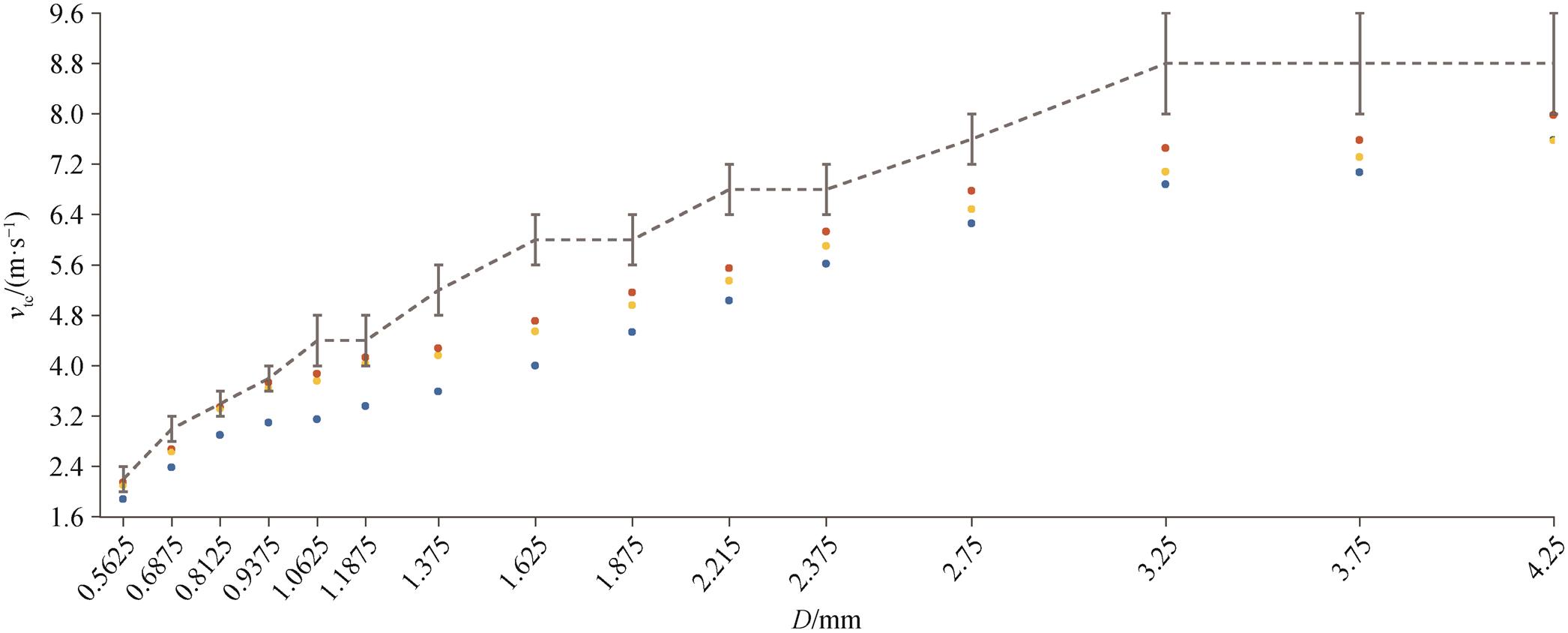
灰色虚线表示每个直径探测通道对应理论下落速度所在速度区间的中值, 误差条表示每个速度区间的分辨率, 红色圆点表示用订正方法 A 订正后的平均下落速度, 黄色圆点表示用订正方法 B 订正后的平均下落速度, 蓝色圆点表示OTT-Parsivel雨滴谱仪测得的平均下落速度原始数据; 计算平均下落速度的数据均经过质量控制
图7 2020 年 6 月 25 日 20:22—21:56 雨滴垂直下落速度订正前后对比
Fig.7 Comparsion between corrected and original falling velocity, 20:22‒21:56, June 25, 2020
表3 订正前后雨滴数在各粒径的相对变化
Table 3 Relative change between corrected and original raindrop size distribution in different diameters
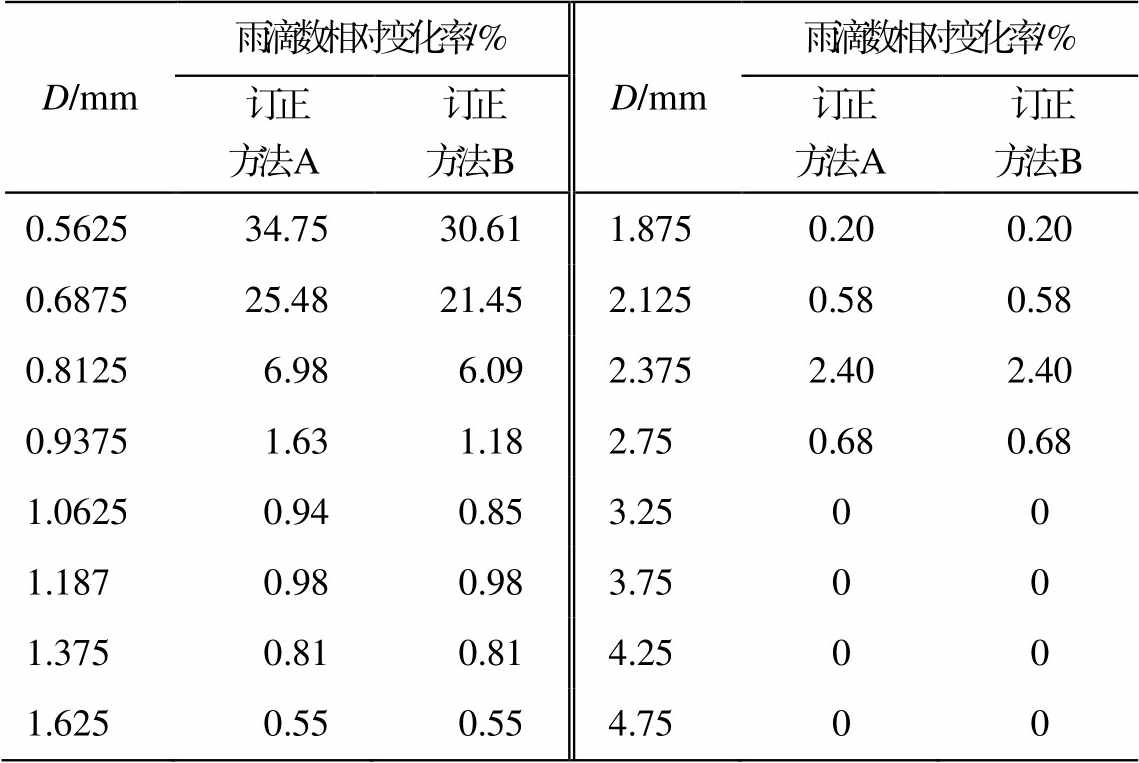
D/mm雨滴数相对变化率/%D/mm雨滴数相对变化率/% 订正方法A订正方法B订正方法A订正方法B 0.562534.7530.611.8750.200.20 0.687525.4821.452.1250.580.58 0.81256.986.092.3752.402.40 0.93751.631.182.750.680.68 1.06250.940.853.2500 1.1870.980.983.7500 1.3750.810.814.2500 1.6250.550.554.7500
说明: 均为质量控制后的结果, 直径探测通道为5~20。
图 8 显示直径探测通道 13~16 (直径依次为1.875, 2.125, 2.375 和 2.75 mm)中粒子数随速度的变化, 与订正方法 B (黑色实线)相比, 订正方法 A (黑色点画线)的高速粒子增加, 低速粒子减少, 在直径相同情况下, 粒子数随速度的变化曲线分布右偏程度减小, 更趋于正态分布, 表明水平订正的主要作用在于修正雨滴谱的分布形态。
综上所示, 水平订正主要从以下两个方面影响雨滴平均下落速度: 一是将 60%速度误差区间外的粒子订正至 60%速度误差区间内, 有效粒子数增加; 二是修正各直径探测通道的速度谱, 使之更趋于正态分布。
在实际应用场景中, 无法保证同时架设 OTT-Parsivel 雨滴谱仪、三维超声风温仪和动态倾角传感器 3 台仪器。本次实验过程中, 2018—2019 年缺少倾角数据, 故本文尝试在不使用实测倾角数据的情况下, 对 OTT-Parsivel 雨滴谱仪的测量数据进行订正, 提高数据的可用时长。Amin 等[16]通过研究不同长宽比的高层建筑在强风作用下的位移, 发现随着风速增加, 位移逐渐增大。这种位移会造成建筑物倾斜, 使其与水平面之间产生夹角, 故同一方向的风速与倾角之间存在一定的因果关系, 在缺少倾角数据的情况, 可以利用同一方向的风速估算此方向的倾角值。
参考雷达反演降水中的概率配对方法[17], 假设风速是倾角的主要影响因素, 在一定区域内的同一方向, 任一时刻出现风速 u 的概率为 P(u)du, 出现倾角 α 的概率为 P(α)dα。若 u 和 α 两个随机变量一一对应, 必有 P(u)du=P(α)dα, 若已知 u 和 α 的概率分布, 那么依据概率相等原理, 即可决定 u 与 α 的关系。为了突出大风速在风速‒倾角关系中的作用, 利用 Atlas 等[18]提出的累积分布函数概率配对方法建立 u 与 α 的关系(同样建立 v 与 β 的关系):
 (7)
(7)其中, CDF为累积概率, umin为u的最小值, αmin为α的最小值。
当给出一个积分上限 ui 值时, 可通过式(5)找到一个对应的积分上限 αi, 这样就配对得到一对(ui, αi) 值(其中 i=1, 2, …, n), 使得 ui 逐渐变大, 最终获得一组(ui, αi)值。由于动态倾角传感器的精度为 0.5°以及 OTT-Parsivel 雨滴谱仪的分档测量模式, 同样将倾角每 0.5°划分为一档, 用得到的数据(ui, αi)对倾角 αi 按 0.5°分档, 求得对应的风速范围, 建立风速‒倾角查算表。
将 2020 年 6—8 月 19 次降水过程按 8:2 的比例随机划分训练集和验证集, 训练集共 15 次降水过程, 2445 条数据; 验证集共 4 次降水过程, 674 条数据。α的波动范围为(−0.5°, 1°), β的波动范围为(0°, 1.5°), 计算得到风速‒倾角查算表, 如表 4 所示。
利用验证集数据, 分别按查算表(表 4)中估计倾角数据(简称估计值)和实际探测的倾角数据(简称实测值), 对雨滴测速 wm 做水平订正。图 9 中, 当雨滴下落速度大于 4m/s 时, 估计值和实测值的水平订正结果均落入同一速度区间, 且速度越大, 落在中间黑色斜线上的数据点越多。原因可能是, 随着速度增大, 速度分辨率逐渐增大, 水平订正效果对风速的敏感性降低, 估计值与实测值的水平订正效果差别不大。雨滴下落速度小于 3m/s 时, 部分数据点位于灰色区域外, 说明在低速区域存在订正效果不一致的情况。可能的原因是, 雨滴落速较小, 降水粒子落入的 OTT-Parsivel 速度区间的速度分辨率较小, 对倾角的敏感性较高。
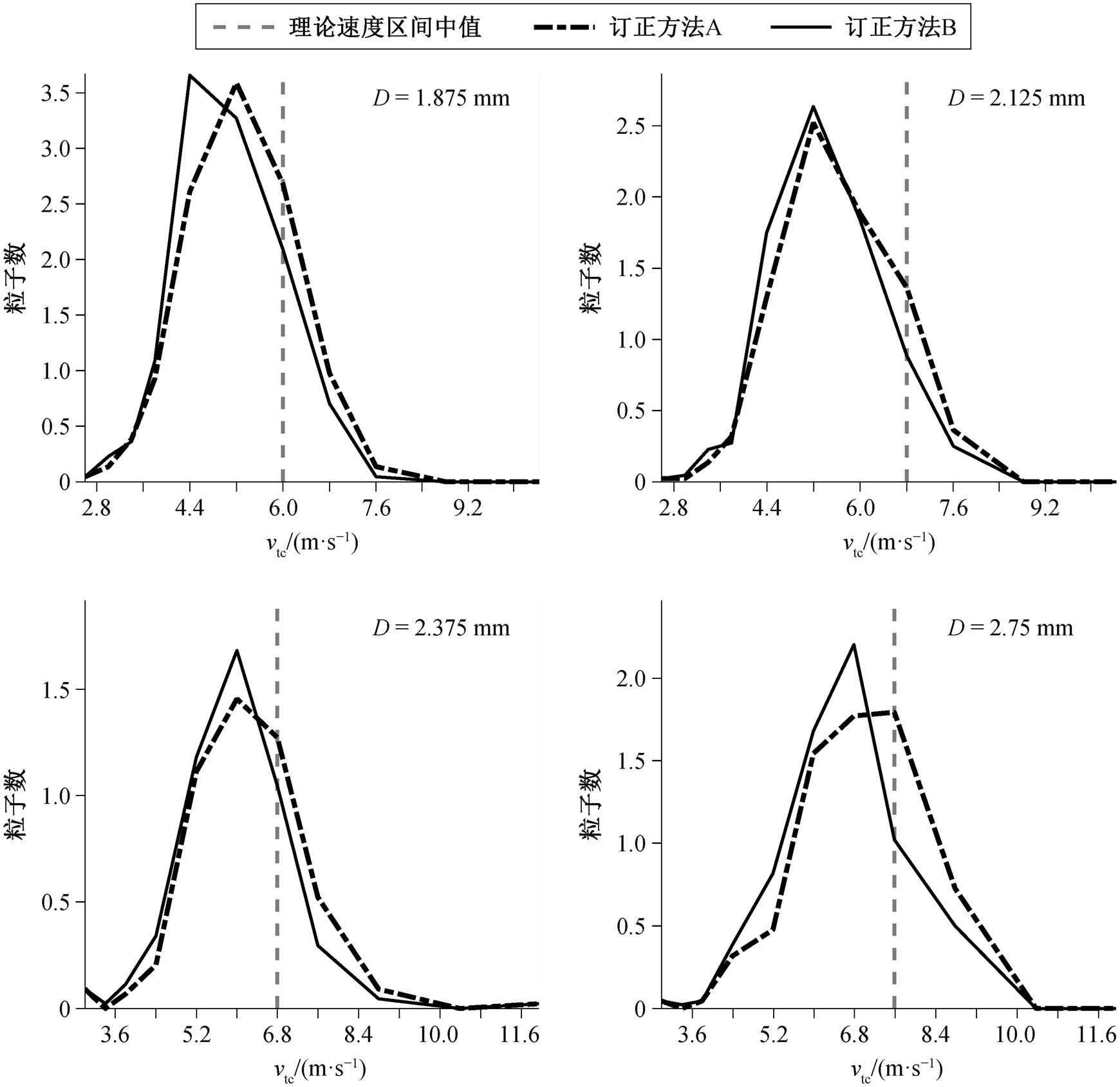
图8 订正后特定直径通道雨滴数与下落速度的关系
Fig.8 Relationship between the number of raindrops and faliing velocity in specific diameter after correction
表4 风速‒倾角查算表
Table 4 Wind speed and angle tables

u/(m·s−1)α/(°)v/(m·s−1)β/(°) (6, 20)(−0.5, 0)(−20, −14)(0, 0.5) (−12, 6)(0, 0.5)(−14, 6)(0.5, 1) (−20, −12)(0.5, 1)(6, 20)(1, 1.5)
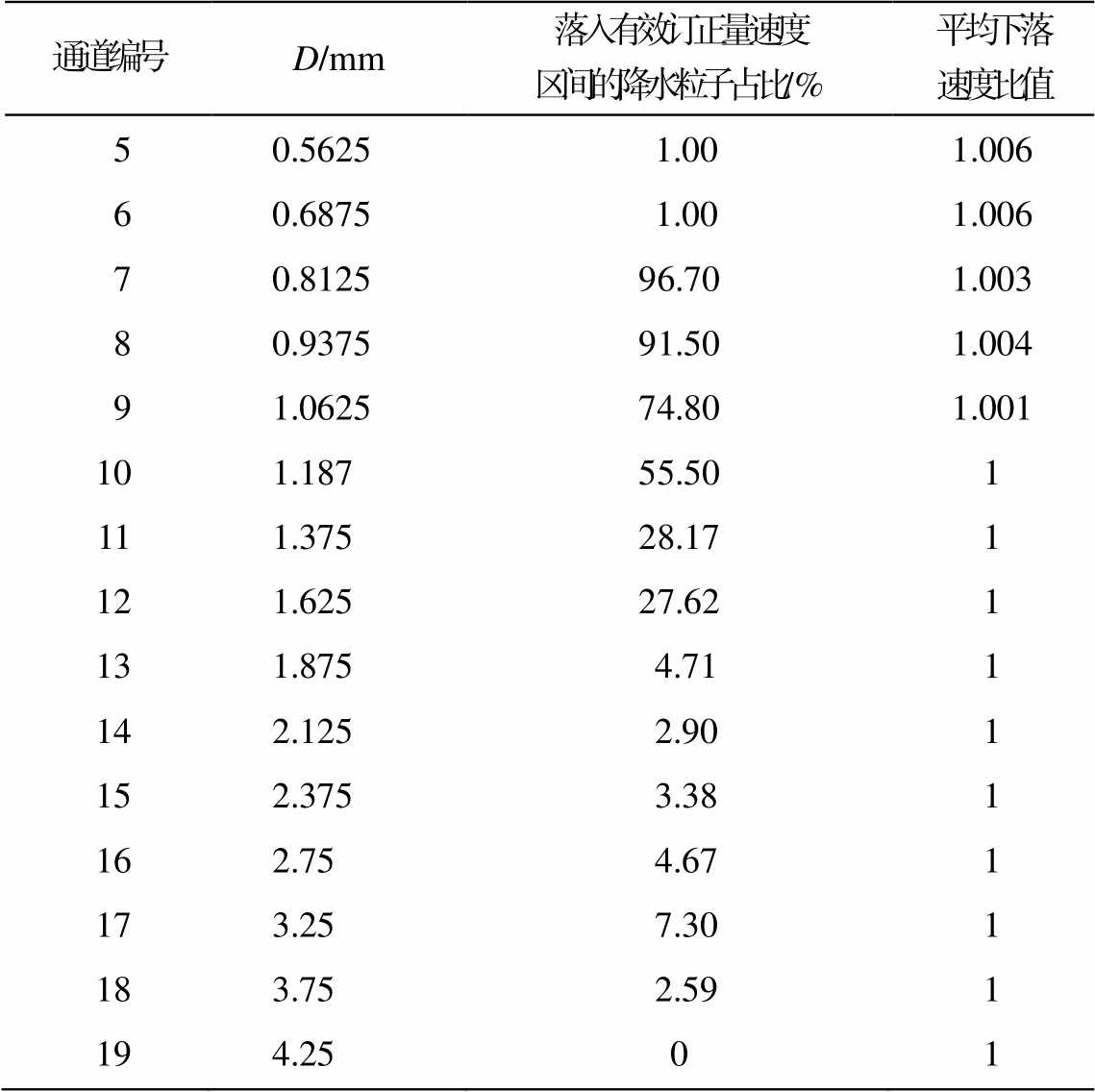
表 5 列出直径探测通道 5~19 倾角估计值与实测值水平订正后雨滴平均下落速度的比值。D<1mm 时, 与实测值相比, 估计值订正后的雨滴平均下落速度偏大, 但误差不超过 1%; D>1mm 时, 估计值与实测值订正效果一致。小尺度粒子理论下落速度小, 落入 OTT-Parsivel 雨滴谱仪速度区间的速度分辨率低。根据 2.2 节的仿真实验结果, 水平订正量最大可达 0.2m/s, 当降水粒子较小时, 大部分粒子落入存在有效订正量的速度范围内。以表 5 中通道 9 (D =1.0625mm)和 12 (D =1.625mm)为例, 通道 9 中落入有效订正量速度区间的降水粒子占所有降水粒子的 74.80%, 通道 12 中落入有效订正量速度区间的降水粒子占所有降水粒子的 27.62%。在风速和倾角相同的情况下, 粒子越小, 有订正效果的粒子占比越大, 订正效果越明显, 所以小粒子的水平订正效果对倾角更加敏感。用两种方法进行水平订正后, 若雨滴速度落入同一区间, 则可认为两者效果“一致”, 本文试验中有 96.34%的数据表现“一致”。从整体上看, 利用实测数据和估计值带来的误差较小, 使用本文提出的查算表估计倾角数据, 再进行水平订正的方法具有可行性。
基于以上分析, 本文提出如下高架测量环境中的质量控制方法: 在水平风速较小(Up<8m/s)的情况下, 首先对雨滴谱实测样本做轴比订正, 再对样本做垂直气流订正, 垂直气流由三维风速仪测量得到, 最后用 60%误差速度标准进行质量控制; 在水平风速较大(Up≥8m/s)的情况下, 首先对雨滴谱实测样本做轴比订正, 再对样本做水平订正和垂直订正, 环境气流由三维风速仪测量得到, 倾角数据利用查算表得到, 最后用 60%误差速度标准进行质量控制。
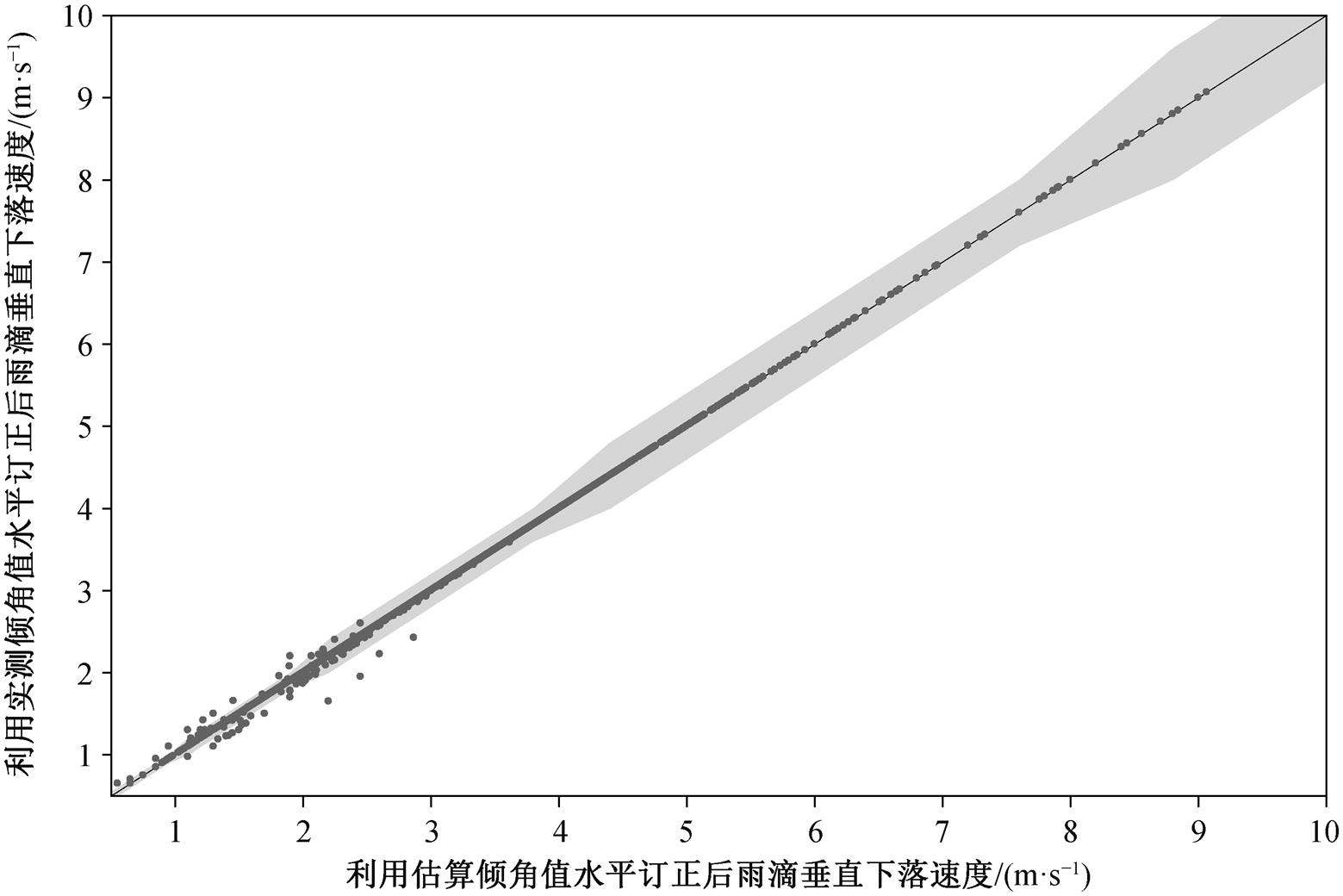
黑色实线表示垂直下落速度相同, 灰色区域表示订正后落入同一速度区间
图9 估算倾角值与实测倾角值水平订正后下落速度
Fig.9 Relationship of velocity between actual angle and estimated angle
表5 利用倾角估计值与实测值水平订正后平均下落速度的比值
Table 5 Ratio of velocity between estimated and actual angle in different diameters
通道编号D/mm落入有效订正量速度区间的降水粒子占比/%平均下落速度比值 50.5625 1.001.006 60.6875 1.001.006 70.812596.701.003 80.937591.501.004 91.062574.801.001 101.18755.501 111.37528.171 121.62527.621 131.875 4.711 142.125 2.901 152.375 3.381 162.75 4.671 173.25 7.301 183.75 2.591 194.2501
本文将雨滴实测落速与理论值的偏差归因于环境垂直气流和水平风速两方面影响, 垂直气流主要影响粒子的运动状态, 水平风速影响采样区间的方向。基于实际测量中无法保证同时架设三台仪器的情况, 本文根据风速数据与实测倾角数据建立查算表来估算倾角。倾角传感器测量的倾角是大气观测塔的摆动和延伸臂形变等一系列因素共同作用的结果, 倾角不是风速单一变量的函数, 与大气观测塔的高度、建筑材料及形状均有关系[16], 故本文提出的查算表应用区域有限。
本文假设超声风温仪测量的风速即为雨滴的水平移动速度, 这是一种理想情况。实际上, 因环境气流的影响, 雨滴水平速度的计算十分复杂。由于仪器采样频率存在差别, 数据预处理的误差会对后续结果造成影响, 在分钟级别, 风速并不稳定, 采用统一的风速信息订正也会造成误差。
对于直径小于 0.5mm 的小粒子, 异常粒子主要分布在 1.6V 以上的速度区间, 且理论落速值小, 误差速度区间小, 在订正量相同的情况下, 容易将粒子订正至 60%速度误差区间之外, 因此可以考虑去除垂直气流订正, 只做水平风速订正。
本文利用架设于 280m 高度处 OTT-Parsivel 激光雨滴谱仪、超声风温仪和动态倾角传感器, 基于2020 年 6—8 月北京多个大风降雨过程的探测数据, 讨论在不稳定平台上 OTT-Parsivel 雨滴谱仪的测速模型, 利用环境风进行测速订正, 并提出质量控制方法, 可对大风天气下 OTT-Parsivel 雨滴谱仪测量速度进行订正。
通过加入水平订正, 完善了测速订正方法, 修正了水平风导致仪器倾斜带来的测速误差。通过建立风速‒倾角查算表, 解决了缺少倾角数据降水样本的问题。利用 2020 年 6—8 月大风降水过程验证本文提出的订正方法, 结果表明加入水平订正后, 有效粒子数增加, 雨滴平均垂直下落速度更接近理论下落末速度理论值。
通过上述处理, 可将大风情况下 OTT-Parsivel雨滴谱仪的测量数据变为可用数据, 进一步分析雨滴谱的垂直分布特征及其对雷达定量估计降水的影响; 在无法探测垂直气流的情况下, 可以更准确地估计环境垂直气流。
参考文献
[1]万和跃, 濮江平, 刘思瑶.雨滴谱探测技术发展及应用概述.科技创新导报, 2015, 12(31): 166‒167
[2]Atlas D, Srivastava R C, Sekhon R S.Doppler radar characteristics of precipitation at vertical incidence.Reviews of Geophysics, 1973, 11(1): 1‒35
[3]Higgins S, Friedrich K, Masters F J, et al.Articulating and stationary Parsivel disdrometer measurements in conditions with strong winds and heavy rainfall.Journal of Atmospheric and Oceanic Technology, 2013, 30(9): 2063‒2080
[4]Bradley S G, Stow C D.Reply.J Appl Meteor, 1975, 14: 426–428
[5]Lopez C R, Masters F J, Friedrich K.Capture and characterization of wind-driven rain during tropical cyclones and supercell thunderstorms [EB/OL] // 13th Int Conf on Wind Engineering.Amsterdam: Inter-national Association for Wind Engineering.(2011) [2020‒08‒12].https://atoc.colorado.edu/~friedrik/PU BLICATIONS/2011_ICWE_Lopez.pdf
[6]Friedrich K, Kalina E A, Masters F J, et al.Drop-size distributions in thunderstorms measured by optical disdrometers during Vortex2.Monthly Weather Rev-iew, 2013, 141(4): 1182‒1203
[7]Löffler-Mang M, Joss J.An optical disdrometer for measuring size and velocity of hydrometeors.Journal of Atmospheric and Oceanic Technology, 2000, 17(2): 130‒139
[8]Coppin P A, Taylor K J.A three-component sonic anemometer/thermometer system for general micro-meteorological research.Boundary-Layer Meteorolo-gy, 1983, 27(1): 27‒42
[9]郑铮, 刘晓阳.环境气流对光学雨滴谱仪探测的影响.北京大学学报(自然科学版), 2020, 56(5): 824‒ 834
[10]苏君, 王占平.基于MEMS加速度传感器的倾角仪设计方法.实验科学与技术, 2006(增刊1): 112‒114
[11]Marion J B, Thornton S T.Classical dynamics of particles and systems.Classical dynamics of particles and systems.Physics Today, 1966, 19(4): 101‒102
[12]Lee W C, Dodge P, Marks F D, et al.Mapping of airborne Doppler radar data.Journal of Atmospheric and Oceanic Technology, 1994, 11(2): 572‒578
[13]Jaffrain J, Berne A.Experimental quantification of the sampling uncertainty associated with measurements from Parsivel disdrometers.Journal of Hydrometeo-rology, 2011, 12(3): 352‒370
[14]Pruppacher H R, Beard K V.A wind tunnel inves-tigation of the internal circulation and shape of water drop falling at terminal velocity in air.Quarterly Journal of the Royal Meteorological Society, 1970, 96: 247‒256
[15]Kim D K, Song C K.Characteristics of vertical velo-cities estimated from drop size and fall velocity spec-tra of a Parsivel disdrometer.Atmospheric Measu-rement Techniques, 2018, 11(6): 1‒29
[16]Amin J A, Ahuja A K.Characteristics of wind forces and responses of rectangular tall buildings.Interna-tional Journal of Advanced Structural Engineering, 2014, 6: 66
[17]王丽荣, 裴宇杰, 王立荣, 等.概率配对法在华北南部雷达定量估测降水中的应用//中国气象学会2008年年会大气物理学分会场论文集.北京, 2008: 1‒7
[18]Atlas D, Rosenfeld D, Short D A.The estimation of convective rainfall by area integrals: 1.the theo-retical and empirical basis.Journal of Geophysical Research Atmospheres, 1990, 95(D3): 2153‒2160
Correction of Measured Speed of OTT-Parsivel on Unstable Platform
Abstract Aiming at the problem that the measurement results of OTT-Parsivel in elevated environment are prone to error due to the influence of ambient air flow, the authors propose the detection test of OTT-Parsivel on unstable platform, proposes the quality control method under different levels of wind speed, gives the measurement speed correction model, and gives simulation and error analysis.Based on the summer precipitation process in Beijing in 2020, several precipitation cases are analyzed by using the measured data of OTT-Parsivel, three-dimensional ultrasonic wind thermometer and dynamic inclination sensor at 280 meters.The results show that the proposed model has a good correction effect on the vertical falling velocity of raindrops, the velocity distribution of each dimension tends to be normal distribution, and the number of effective particles can increased by 6%.When the horizontal wind speed exceeds 8 m/s, the availability of OTT-Parsivel raindrop spectrometer measurement data is improved.
Key words raindrop size distribution; correction of falling velocity; OTT-Parsivel; horizontal wind speed
doi: 10.13209/j.0479-8023.2021.075
收稿日期: 2020–09–22;
修回日期: 2020-12–28
国家重点研发计划(2017YFC0209602)和国家自然科学基金(41475016)资助