卷积神经网络在图像分类、目标检测等领域得到广泛应用。随着网络效果提升, 网络规模愈发庞大, 需要高额存储空间和计算资源, 使网络部署到资源受限的端侧硬件平台变得困难。因此, 在保证模型精度的同时, 需尽可能降低模型参数量和计算消耗。研究者们提出过若干模型压缩方法, 如模型剪枝[1-5]、权重量化[6-9]和神经网络结构搜索[10-12]等。其中, 模型剪枝方法能大幅度地减少模型参数量和运算量, 成为模型压缩的主流方法, 又可分为非结构化剪枝方法和结构化剪枝方法。
非结构化剪枝方法[13]认为卷积神经网络中存在小值权重, 对网络最终输出贡献少, 可将其置 0,以便减少网络运算量。采用此类方法的模型压缩效果较好, 但部署到端侧设备时, 硬件平台要具有相应的稀疏矩阵运算加速库才能实现提速, 故非结构化剪枝方法在部署中通用性差。
结构化剪枝方法将整个卷积核视为被裁剪对象, 对于硬件部署更加友好, 受到研究者青睐。Li等[14]提出基于卷积核 L1 范数的简单有效的剪枝方法, 通过裁剪 L1 范数小的卷积核, 实现模型压缩和加速。在此基础上, Frankle 等[15]利用 L2 范数寻找大规模模型中的最小子网络, 实现模型剪枝。He等[16]将卷积核视为欧式空间中的点, 计算每个卷积层的几何中位数, 将靠近几何中心点的卷积核裁减掉, 实现模型压缩。
以上剪枝方法往往需要大规模的模型训练和剪枝以及小规模的模型微调 3 个步骤。当剪枝率过大时, 通过已有剪枝方法得到的小规模模型会因信息丢失严重及语义表达能力不足从而导致较大的精度损失。本文在模型微调前, 对小规模的模型进行全局信息优化, 使其在微调后可以取得较大的压缩率,并具有极低的精度损失。此优化方法可嵌入任何一种结构化剪枝方法中, 具有工程易用性。
1 研究方法
在适中剪枝率情况下, 剪枝方法对不同卷积层有不同的剪枝率[13], 即剪枝后每个卷积层的卷积核个数不同(见图 1)。对于保留较多卷积核的卷积层,因保留了较多的原模型信息, 故在微调后可恢复语义表达能力。对于保留较少卷积核的卷积层, 因其原模型信息破坏较为严重, 导致模型精度下降。所以, 如果能使剪枝后模型尽可能多地具备原模型信息, 则可保证剪枝后模型的高精度。

图1 VGG16 部分卷积层剪枝前后对比
Fig. 1 Comparison of convolution layers before and after pruning in VGG16
1.1 现有剪枝方法不足

1.2 剪枝后模型信息优化

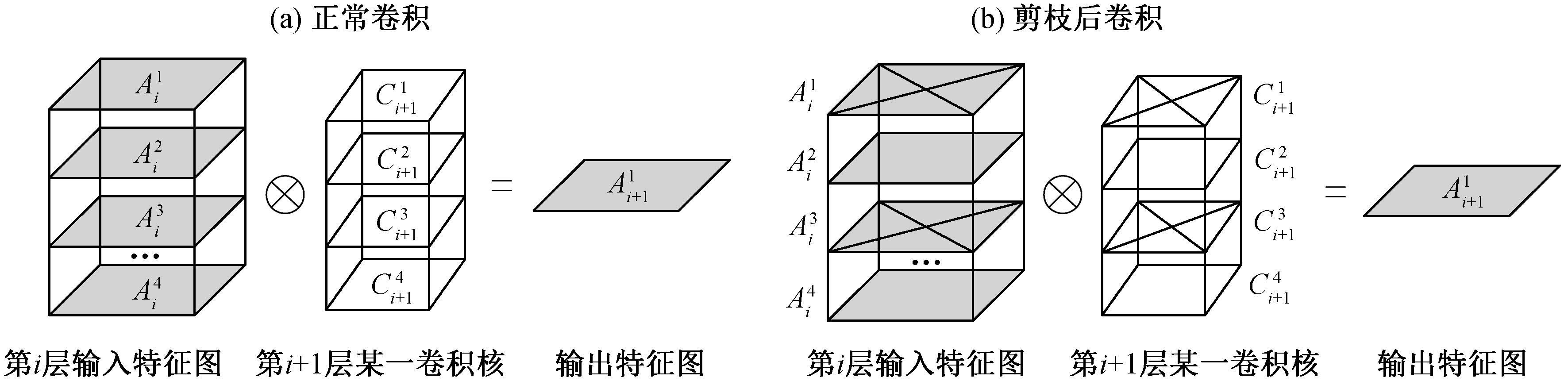
图2 正常卷积与剪枝后卷积的区别
Fig. 2 Difference between normal convolution and convolution after pruning
综上所述, 将剪枝后模型信息保留优化问题转化为求解形如式(1)的优化问题, 通过改进的 Matrix Sketching 算法求解[17]。改进后的剪枝模型微调优化算法流程如算法 1 所示。

由式(1)及算法 1 可知, 改进后的微调优化方法将原模型信息引入剪枝后模型, 并最小化二者间信息误差, 从而实现对剪枝后模型某些卷积层的信息补偿, 进而在微调后获得更高精度。原理解释如图3 所示。
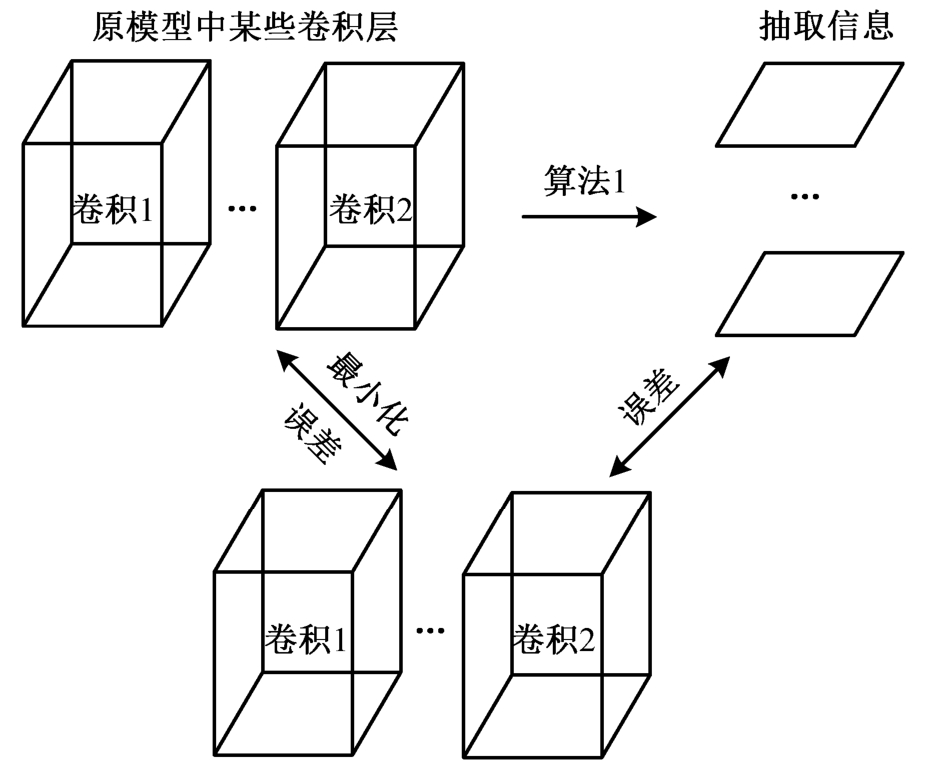
图3 算法原理解释
Fig. 3 Explanation of algorithm
1.3 模型特殊结构处理
残差网络 ResNet[18]中的残差模块可以解决深层网络无法有效训练的问题, 使深层网络的准确度得以提升, 其跳连结构已应用在许多大规模网络中。将现有剪枝方法应用于 YOLOv3[19]等存在跳连结构的模型时, 均需保证剪枝后模型在跳连相加处通道数相同。如图 4 所示, 剪枝后模型在微调前需保证 c1 ′ = c2′, 进而保证跳连相加可以顺利进行, 但会严重地限制剪枝方法的压缩效果, 故此类特殊结构也是限制模型压缩效果的重要因素。
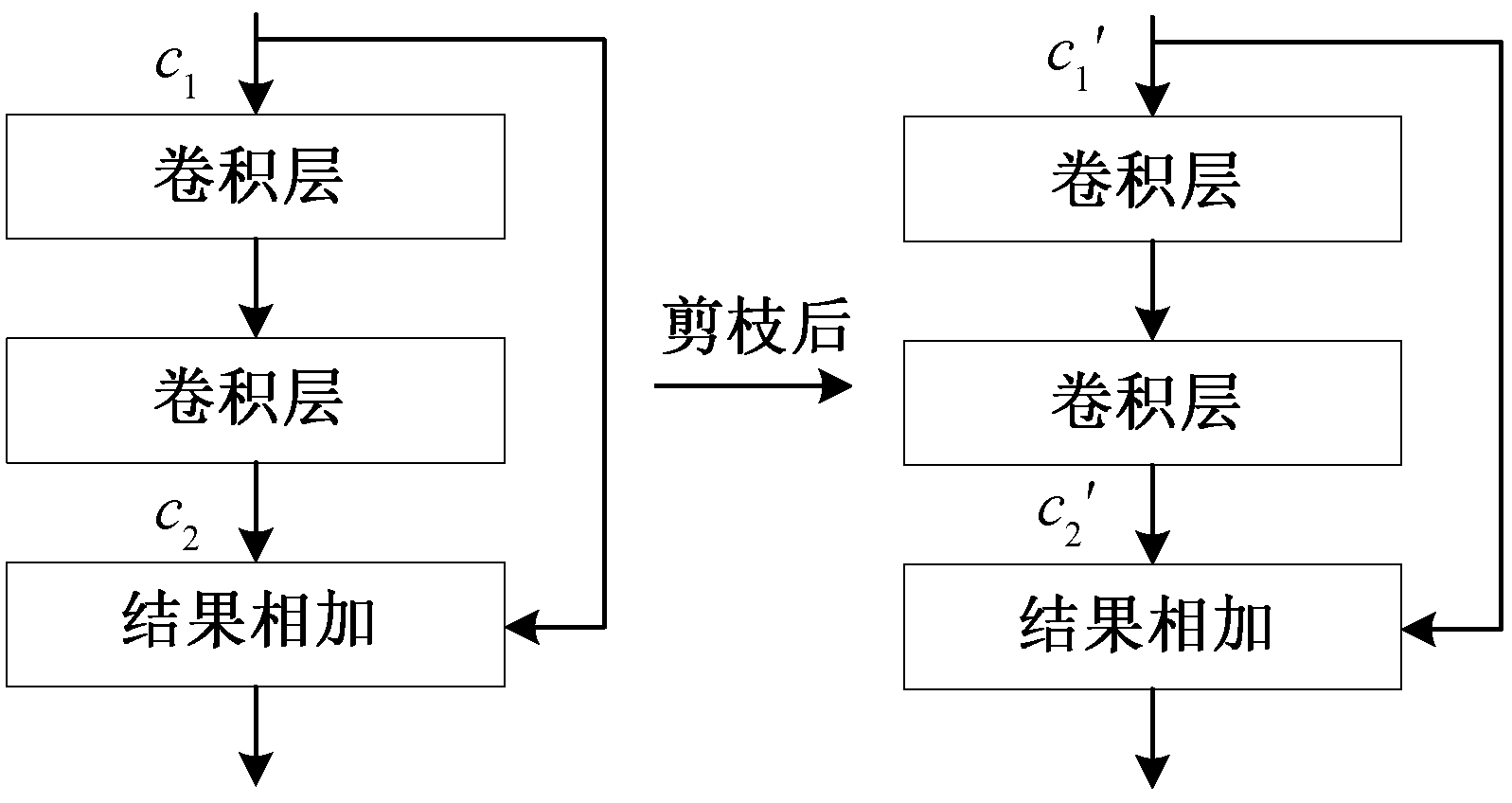
图4 模型跳连部分的剪枝
Fig. 4 Pruning of shortcut in the model
在现有剪枝方法上嵌入本文提出的微调优化方法, 可在初步剪枝时不必要求跳连相加处通道数相同, 而是在微调时, 通过算法 1 将保留较多通道数的卷积层 1c′优化为 2c′, 在保证最大化压缩率的同时,还可以保证模型精度。
2 实验结果与方法对比
本文将算法 1 嵌入不同的剪枝方法, 并在主流图像分类模型和目标检测模型上进行对比实验来证明本文提出微调优化方法的有效性及普遍适用性。
2.1 实验数据与评价指标
本文采用图像分类数据集 CIFAR10 和 CIFAR 100, 在 VGG16 模型上验证微调优化方法在分类任务中的效果。利用大规模遥感数据集 Visdrone[20],在 Anchor-base 目标检测模型 YOLOv3 和 Anchorfree 目标检测模型 CenterNet[21]上, 验证微调优化方法在目标检测任务中的效果。数据集概况见表 1。
表1 本文所用数据集概况
Table 1 Overview of the datasets used in the article
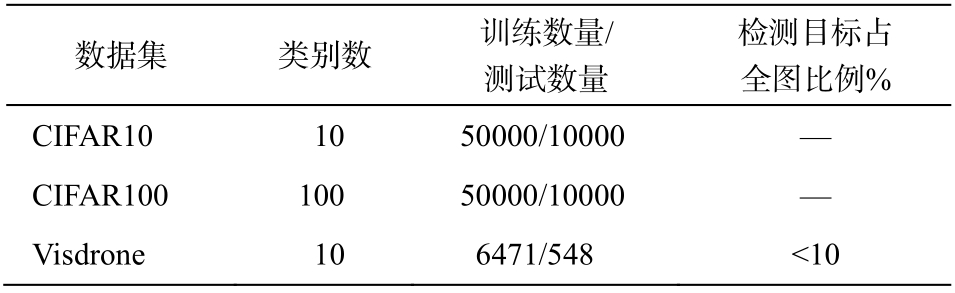
数据集 类别数 训练数量/测试数量检测目标占全图比例%CIFAR10 10 50000/10000 —CIFAR100 100 50000/10000 —Visdrone 10 6471/548 <10
对于图像分类任务, 采用测试集准确率(Acc)作为评价指标。对于目标检测任务, 输入图片分辨率均为 608×608, 采用交并比(IOU)阈值为 0.5、置信度(confidence)阈值为 0.1、非极大值抑制(NMS)阈值为 0.5 情况下的平均精度均值(mAP)作为评价指标。
2.2 方法验证与对比
将微调优化方法分别嵌入 L1 剪枝方法[14]和 Network Slimming (NS)剪枝方法[22], 在 VGG16 模型上, 利用 CIFAR10 和 CIFAR100 数据集进行实验,实验结果如表 2 所示。
表2 各剪枝方法在CIFAR10 和CIFAR100 数据集的效果对比
Table 2 Effects of various pruning methods on CIFAR10 and CIFAR100
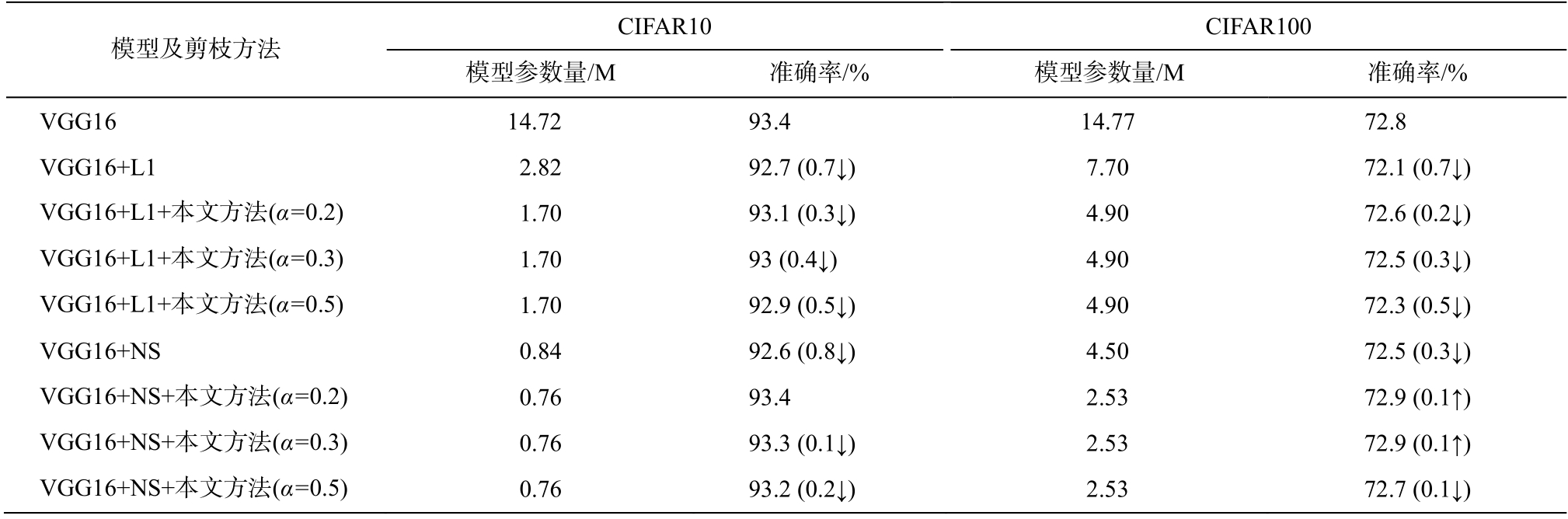
说明: ↓表示相较于原网络精度下降; ↑表示相较于原网络精度上升; α 表示剪枝率阈值, 对剪枝高于此阈值的卷积层进行信息优化。
模型及剪枝方法 CIFAR10 CIFAR100模型参数量/M 准确率/% 模型参数量/M 准确率/%VGG16 14.72 93.4 14.77 72.8 VGG16+L1 2.82 92.7 (0.7↓) 7.70 72.1 (0.7↓)VGG16+L1+本文方法(α=0.2) 1.70 93.1 (0.3↓) 4.90 72.6 (0.2↓)VGG16+L1+本文方法(α=0.3) 1.70 93 (0.4↓) 4.90 72.5 (0.3↓)VGG16+L1+本文方法(α=0.5) 1.70 92.9 (0.5↓) 4.90 72.3 (0.5↓)VGG16+NS 0.84 92.6 (0.8↓) 4.50 72.5 (0.3↓)VGG16+NS+本文方法(α=0.2) 0.76 93.4 2.53 72.9 (0.1↑)VGG16+NS+本文方法(α=0.3) 0.76 93.3 (0.1↓) 2.53 72.9 (0.1↑)VGG16+NS+本文方法(α=0.5) 0.76 93.2 (0.2↓) 2.53 72.7 (0.1↓)
由表 2 可知, 在图像分类任务中, 在已有的若干剪枝方法中嵌入微调优化方法, 可以同时提高压缩率和剪枝后模型的准确率。可以看出, 此微调优化方法对带有模型稀疏化训练的剪枝方法更适用。通过模型稀疏化训练, 模型中更多的卷积核可被裁剪, 此时通过微调优化方法, 可使模型在尽可能高的压缩率下获得更高的精度恢复, 实现模型参数量与精度间的平衡。将此方法嵌入 Network Slimming剪枝后的 VGG16 网络进行微调时, 剪枝后模型精度比原模型略有提高, 说明经过此方法优化后的模型具备较优的初始化参数及学习能力。
为了证明算法在其他任务中的有效性, 采用遥感数据集 Visdrone, 在 Anchor-base 目标检测模型YOLOv3 和 Anchor-free 目标检测模型 CenterNet 上进行实验, 结果如表 3 所示。
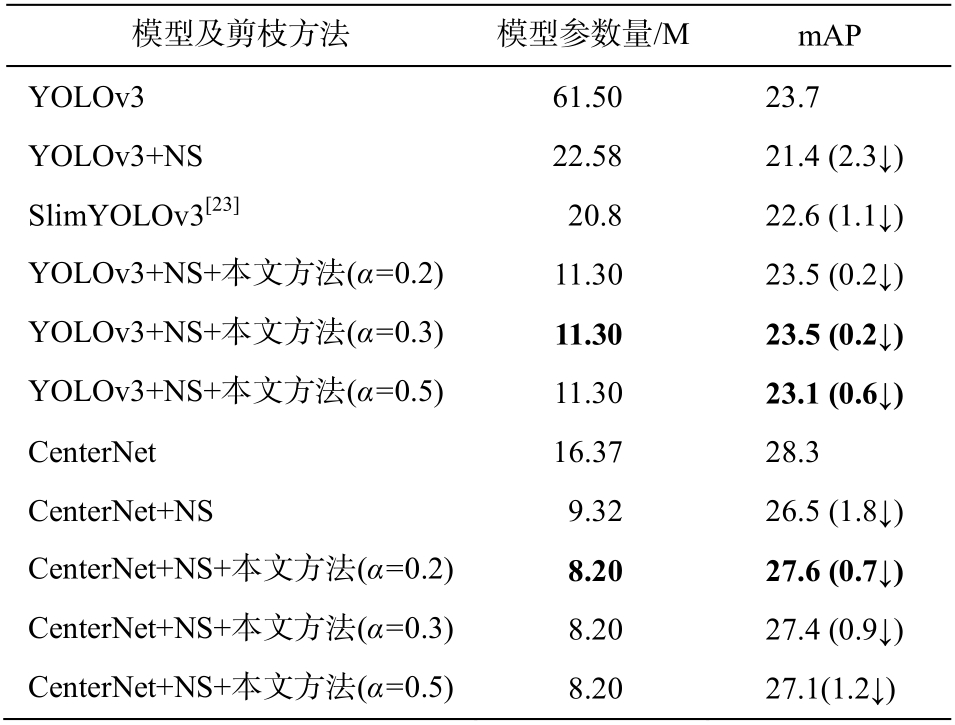
由表 3 可知, 在目标检测任务中, 本文所提微调优化方法对于主流 Anchor-base 模型和 Anchor-Free 模型均具有适用性, 在最大程度上保证模型精度的同时, 可以降低模型参数量和复杂度。
表3 各剪枝方法在Visdrone 数据集效果对比
Table 3 Effects of various pruning methods on Visdrone
模型及剪枝方法 模型参数量/M mAP YOLOv3 61.50 23.7 YOLOv3+NS 22.58 21.4 (2.3↓)SlimYOLOv3[23] 20.8 22.6 (1.1↓)YOLOv3+NS+本文方法(α=0.2) 11.30 23.5 (0.2↓)YOLOv3+NS+本文方法(α=0.3) 11.30 23.5 (0.2↓)YOLOv3+NS+本文方法(α=0.5) 11.30 23.1 (0.6↓)CenterNet 16.37 28.3 CenterNet+NS 9.32 26.5 (1.8↓)CenterNet+NS+本文方法(α=0.2) 8.20 27.6 (0.7↓)CenterNet+NS+本文方法(α=0.3) 8.20 27.4 (0.9↓)CenterNet+NS+本文方法(α=0.5) 8.20 27.1(1.2↓)
3 结论
本文针对现有剪枝方法在高压缩率时精度严重下降的问题, 提出一种基于全局信息的模型剪枝微调优化方法。对于剪枝率过大的卷积层, 此优化方法将未剪枝模型的全局权重信息引入剪枝后模型中, 从而解决了模型跳连结构对剪枝方法的限制问题。在图像分类任务和目标检测任务中的实验结果表明, 将已有剪枝方法中嵌入此优化方法, 在获得高压缩率的同时, 只有极低的精度损失。
在未来的工作中, 我们将进一步探索剪枝后模型在微调前的权重优化, 使本文提出的微调优化方法在不失通用性的前提下获得更高的压缩率, 以便在端侧智能设备的部署与加速。
[1] Changpinyo S, Sandler M, Zhmoginov A. The power of sparsity in convolutional neural networks [EB/OL].(2017-02-21)[2020-05-20]. https://arxiv.org/abs/1702.06257
[2] Liu Z, Sun M, Zhou T, et al. Rethinking the value of network pruning [EB/OL]. (2019-03-05)[2020-05-20]. https://arxiv.org/abs/1810.05270
[3] Wen W, Wu C, Wang Y, et al. Learning structured sparsity in deep neural networks // Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelno, 2016: 2082-2090
[4] Zhou H, Alvarez J M, Porikli F. Less is more: towards compact CNNS // European Conference on Computer Vision. Cham: Springer, 2016: 662-677
[5] Han S, Mao H, Dally W J. Deep compression: compressing deep neural network with pruning, trained quantization and Huffman coding [EB/OL]. (2015-11-20)[2020-05-20]. https://arxiv.org/abs/1510.00149v3
[6] Rastegari M, Ordonez V, Redmon J, et al. XNORNet:imagenet classification using binary convolutional neural networks // European Conference on Computer Vision. Cham: Springer, 2016: 525-542
[7] Zhou Shuchang , Wu Yuxin , Ni Zekun , et al. DoReFa-Net: training low bitwidth convolutional neural networks with low bitwidth gradients [EB/OL]. (2018-02-02)[2020-05-20]. https://arxiv.org/abs/1606.06160
[8] Jacob B, Kligys S, Chen B, et al. Quantization and training of neural networks for efficient integerarithmetic-only inference [EB/OL]. (2017-12-15)[2020-05-20]. https://arxiv.org/abs/1712.05877
[9] Courbariaux M, Bengio Y. Binarynet: training deep neural networks with weights and activations constrained to +1 or -1 [EB/OL]. (2016-04-18)[2020-05-20]. https://arxiv.org/abs/1511.00363
[10] Jin J, Yan Z, Fu K, et al. Neural network architecture optimization through submodularity and supermodularity [EB/OL]. (2018-02-21)[2020-05-20]. https://arxiv.org/abs/1609.00074
[11] Baker B, Gupta O, Naik N, et al. Designing neural network architectures using reinforcement learning[EB/OL]. (2016-11-07)[2020-05-20]. https://arxiv.org/abs/1611.02167v1
[12] Zhang L L, Yang Y, Jiang Y, et al. Fast hardwareaware neural architecture search [EB/OL]. (2020-04-20)[2020-05-20]. https://arxiv.org/abs/1910.11609
[13] Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural network // Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, 2015:1135-1143
[14] Li H, Kadav A, Durdanovic I, et al. Pruning filters for efficient convnets [EB/OL]. (2017-03-10)[2020-05-20]. https://arxiv.org/abs/1608.08710
[15] Frankle J, Carbin M. The lottery ticket hypothesis:finding sparse, trainable neural networks [EB/OL].(2019-03-04)[2020-05-20]. https://arxiv.org/abs/1803.03635
[16] He Y, Liu P, Wang Z, et al. Pruning filter via geometric median for deep convolutional neural networks acceleration // IEEE Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 4340-4349
[17] Liberty E. Simple and deterministic matrix sketching[EB/OL]. (2012-07-11)[2020-05-20]. https://arxiv.org/abs/1206.0594
[18] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition // IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas,2016: 770-778
[19] Redmon J, Farhadi A. YOLOv3: an incremental improvement [EB/OL]. (2018-04-08)[2020-05-20].https://arxiv.org/abs/1804.02767
[20] Zhu Pengfei, Wen Longyin, Du Dawei, et al. Vision meets drones: past, present and future [EB/OL].(2020-01-16) [2020-05-20]. https://arxiv.org/abs/200 1.06303
[21] Zhou X, Wang D, Krähenbühl P. Objects as points[EB/OL]. (2019-04-25)[2020-05-20]. https://arxiv.org/abs/1904.07850
[22] Liu Zhuang, Li Jianguo, Shen Zhiqiang, et al. Learning efficient convolutional networks through network slimming // IEEE International Conference on Computer Vision. Venice, 2017: 2736-2744
[23] Zhang Pengyi, Zhong Yunxin, Li Xiaoqiong. SlimYO LOv3: narrower, faster and better for real-time UAV applications [EB/OL]. (2019-07-25) [2020-05-20].https://arxiv.org/abs/1907.11093