随着工业化的日益发达, 过去被忽略的对人体有害的细小颗粒物(PM2.5)产生的危害逐渐引起社会关注。1997 年, 美国首次提出细颗粒物(PM2.5)的标准: 环境空气中空气动力学当量直径小于等于 2.5微米的颗粒物。虽然 PM2.5 在地球大气中含量很少,但因其具有粒径小、面积大、活性强、易附带病毒和有害物质、悬浮时间长和输送距离远等特点, 会给空气质量和人体健康带来极大的危害。以 PM2.5为主的室外空气污染关联多种疾病, 包括与臭氧有关的慢性阻塞性肺病、与 PM2.5 有关的急性下呼吸道疾病、脑血管病、缺血性心脏病和肺癌等, 每年导致全球超过 300 万人过早死亡, 且该现象主要发生在亚洲地区[1], 中国每年由于 PM2.5 污染导致的过早死亡人数在 165 万至 219 万之间[2]。
对 PM2.5 的预测方法主要有统计模型、模式模拟(化学传输模型)以及深度学习模型等方法。Baker等[3]用非线性回归模型对单来源的 PM2.5 浓度进行预测; 周广强等[4]基于 WRF-chem 模式进行华东区域 PM2.5 浓度预报; 王茜等[5]基于 CMAQ 空气质量数值预报模式, 采用学习型线性回归方法, 显著地提高上海市 PM2.5 预报的准确率。目前, 卷积神经网络、径向基神经网络、支持向量机和粒子群优化等深度学习方法已经用于研究空气质量与多种气象数据之间的非线性关系[6-9]。
华北地区 PM2.5 污染情况较为严重, 因此前人的研究多关注北京及周边地区。珠三角地区也是受空气污染危害较为严重的地区, 2004—2013 年间,珠三角地区每年由 PM2.5 污染导致的过早死亡人数在 3.3 万至 4.5 万之间[10]。鉴于上述背景, 本文聚焦于珠三角地区 PM2.5 浓度的预测, 通过对广州市PM2.5 浓度监测数据进行处理, 利用差分整合移动平均自回归模型、反向传播神经网络和长短期记忆模型, 对广州市 PM2.5 浓度数据进行学习, 并结合EEMD 集合经验模态分解方法预测 PM2.5 浓度值,力求找到最优预报模型。
1 研究方法
1.1 集合经验模态分解方法
经验模态分解(empirical mode decomposition,EMD)是 Huang 等[11]提出的一种对非平稳信号进行时频分析的方法, 该方法依据自身时间尺度特征对信号进行分解, 与傅立叶分解和小波分解相比,EMD 方法理论上可以对任何数据进行分解, 既适用于对线性的稳定信号的分析, 也适用于对非线性的不稳定信号的分析, 并且对于平稳信号, EMD 方法也可以比其他时频分解方法更好地反映信号的物理意义。EMD 方法的实质是通过特征时间尺度来识别信号中的所有震动模态, 从高频到低频, 分解出一系列本征模函数(intrinsic mode function, IMF),原始信号是一系列 IMF 与剩余部分的叠加。
EMD 方法是将原始信号各尺度的分量从高频到低频不断地进行提取, 能量最大的高频分量代表原始信号的主要特征。由于数据的不连续性, 不同时间尺度的成分可能被分解到一个特征模态函数分量中, 或者同一时间尺度的成分会被分解到不同特征模态函数中, 因此原始信号分解出的 IMF 会包含不同频率的分量, 这种现象称为模态混叠。为解决模态混叠问题, Wu 等[12]提出集合经验模态分解方法(ensemble empirical mode decomposition, EEMD)。EEMD 方法通过在整个时频空间添加白噪声, 使不同尺度的信号自适应地映射到与背景白噪音相关的尺度上。由于白噪声的均值为 0, 经过多次平均后,加入原始信号的噪声均值也为 0。
1.2 差分整合移动平均自回归模型
博克思-詹金斯(Box-Jenkins)方法是一种较精准的对时间序列进行分析和预测的算法, 差分整合移动平均自回归模型(autoregressive integrated moving average model, ARIMA (p, d, q))是该算法中一种常用的模型, 其中 AR 表示自回归, p 为自回归项数; MA 为滑动平均, q 为滑动平均数; d 为使原始序列平稳所需的差分次数。建立 ARIMA 模型的步骤如下。
1) 平稳性检验和白噪声检验。只有平稳非白噪声序列才能使用 ARIMA 模型进行分析预测。对于不平稳的数据, 则需要进行差分运算, 直至平稳。从理论上讲, 差分运算次数越多, 从时间序列提取的非平稳信息越多。但是, 每次差分运算过程都会造成信息损失, 因此在实际应用中, 差分运算次数通常不超过两次。
2) 模型定阶, 即确定 p 和 q 的取值。定阶原则可以采用 AIC 准则, 即赤池信息准则: 以模型的误差服从独立正态分布为条件, 通常表示为
其中, k 是参数的数量, L 是似然函数。AIC 鼓励数据拟合的优良性, 但避免出现过拟合, 所以需优先考虑AIC 最小的模型。
3) 模型评估, 即对模型的噪声序列进行独立性检验, 若不通过, 则重新拟合模型, 直到模型通过白噪声检验。由于 PM2.5 浓度值具有较强的自相关性, 本文用 ARIMA 模型对 PM2.5 的浓度值进行预测, 并与神经网络模型的预测结果进行对照。
1.3 神经网络
1) BP 神经网络(back propagation neural network,BP)。这是一种按照误差反向传播训练的多层前馈网络, 包括输入层、隐藏层和输出层, 其中隐藏层可以包括一层或多层神经元。BP 算法包括前向传播和误差的反向传播两个过程。在前向传播过程中, 神经元通过“激活函数”处理产生输出结果。若前向传播的实际输出与期望输出不相符, 则进行误差的反向传播。误差的反向传播采用梯度下降法(其中梯度表示函数增加最快的方向), 因此沿着相反的方向可以更快地找到函数的最小值。反向传播过程中, 输出误差通过隐藏层向输入层逐层反传,将误差分摊给各个单元, 调整输入节点与隐层节点的联接强度以及隐层节点与输出节点的联接强度,并调整阈值, 确定与最小误差对应的网络参数。本文中 BP 神经网络选择含两个隐藏层的全连接神经网络, 第一层含 65 个神经元, 第二层含 16 个神经元, 激活函数为ReLU 函数。
2) 长短期记忆网络(long short-term memory,LSTM)。循环神经网络(recurrent neural network,RNN)可以弥补传统神经网络的缺陷, 通过保留先前时间点的信息来确保信息的连续性, 可以达到更好的预报效果。目前, RNN 在语音识别、机器翻译和时间序列预报方面都取得显著的效果。PM2.5 的浓度序列存在时间上的自相关性, RNN 可以较好地利用这一特征, 对 PM2.5 浓度进行预测。但是, RNN比较适合根据近处的信息来推测所需信息, 如果需要用到较远处的信息, 则可能预测失败。这一问题被称为长依赖问题。为了解决该问题, Hochreiter 等[13]于 1997 年提出 LSTM 神经网络, 用于提取间隔时间较长的信息。LSTM 通过一种“门”结构来决定向输入数据添加或删除信息, 即通过忘记门、输入门和输出门来控制输入数据包含的信息。
1.4 评估指标
本研究选取平均绝对误差(mean absolute error, MAE)、均方根误差(root mean squared error,RMSE)、Index of Agreement (IA)和解释方差得分(explained variance score, Var)作为评价PM2.5 浓度预报模型优劣的指标, 计算公式如下:
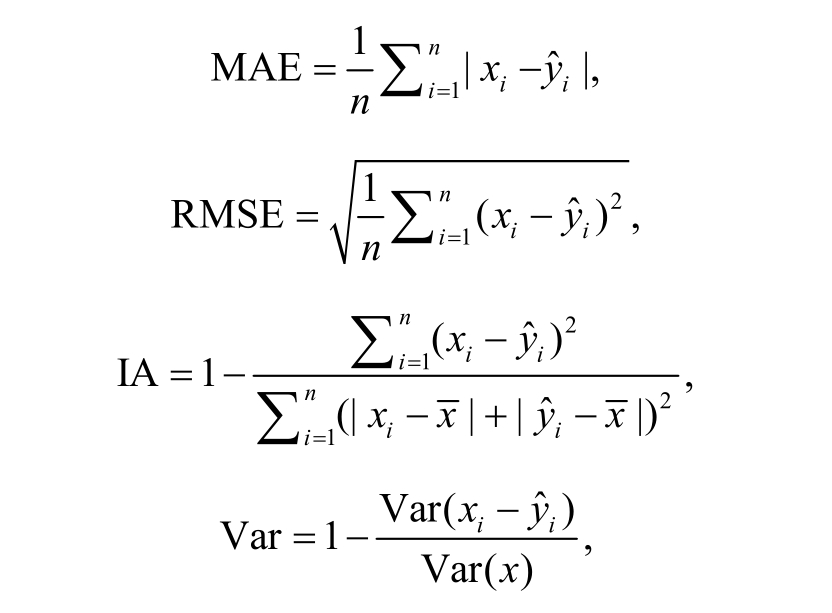
其中, n 为样本数, xi 为观测值,  为预测值。
为预测值。
2 数据来源及预处理
本文所用数据来自中国空气质量历史数据网站(http://beijingair.sinaapp.com)。选取广州市 2015 年1 月 2 日至 2019 年 12 月 31 日逐小时 PM2.5 数据, 包括该网站中广州市 12 个监测站点(广雅中学、市五中、天河职幼、广东商学院、市 86 中、番禺中学、花都师范、市监测站、九龙镇镇龙、麓湖、帽峰山森林公园和体育西)的监测数据, 并对各监测站点数据求取平均值, 以此代表广州市逐小时PM2.5 浓度值。图 1 为 2015 年初到 2019 年底广州市PM2.5 浓度的时间序列, 可以看出夏季 PM2.5 浓度显著低于冬春两季。

图1 广州市PM2.5 浓度值时间序列(逐小时)
Fig. 1 Time series of PM2.5 hourly concentration of Guangzhou city
我们对部分缺测数据进行样条插值, 得到有效数据, 并依次对广州市 PM2.5 浓度求取每 6, 12 和 24 h 的平均值, 选取 2015 年 1 月 2 日至 2018 年 12 月 31日的数据作为训练集, 2019 年 1 月 1 日至 2019 年 12月 31 日的数据作为测试集。李建东等[14]的研究结果表明, 北京、上海和广州等城市的 PM2.5 浓度存在较明显的“周末效应”, 即周末因人类活动减少导致污染物的排放量降低, PM2.5 浓度值存在 7 天左右的显著周期。因此, 本文用前 6 天的数据作为PM2.5浓度历史数据, 对第 7 天的 PM2.5 浓度值进行预测。
3 实验设计
1) EEMD 分解对神经网络预报结果的影响。本文对原始数据进行 EEMD 分解, 得到 10 个从高频到低频的模态函数 IMF1~IMF10, r 为趋势项, 结果如图 2 所示。EEMD 分解得到的各模态周期如表 1所示, IMF1 和 IMF2 的周期分别是 3.18 和 7.61 天,为日信号; IMF3 和 IMF4 的周期分别是 16.84 和33.06 天, 为月信号; IMF5 和 IMF6 的周期分别是69.19 和 140.38 天, 为季节信号; IMF7~IMF10 的周期分别是 268.71, 481.31, 912.5 和 1825 天, 为年信号。本文保留 IMF1 和 IMF2, 将 IMF3 与 IMF4 相加, IMF5 与 IMF6 相加, IMF7~IMF10 与趋势相 r 相加, 形成 5 组新的时间序列, 如图 3 所示。针对 5 组新的时间序列, 选取时间间隔为 24 h 的观测数据,用 BP 神经网络对分解得到的 5 组序列分别进行预测, 对预测结果求和, 得到 PM2.5 日浓度预报值。
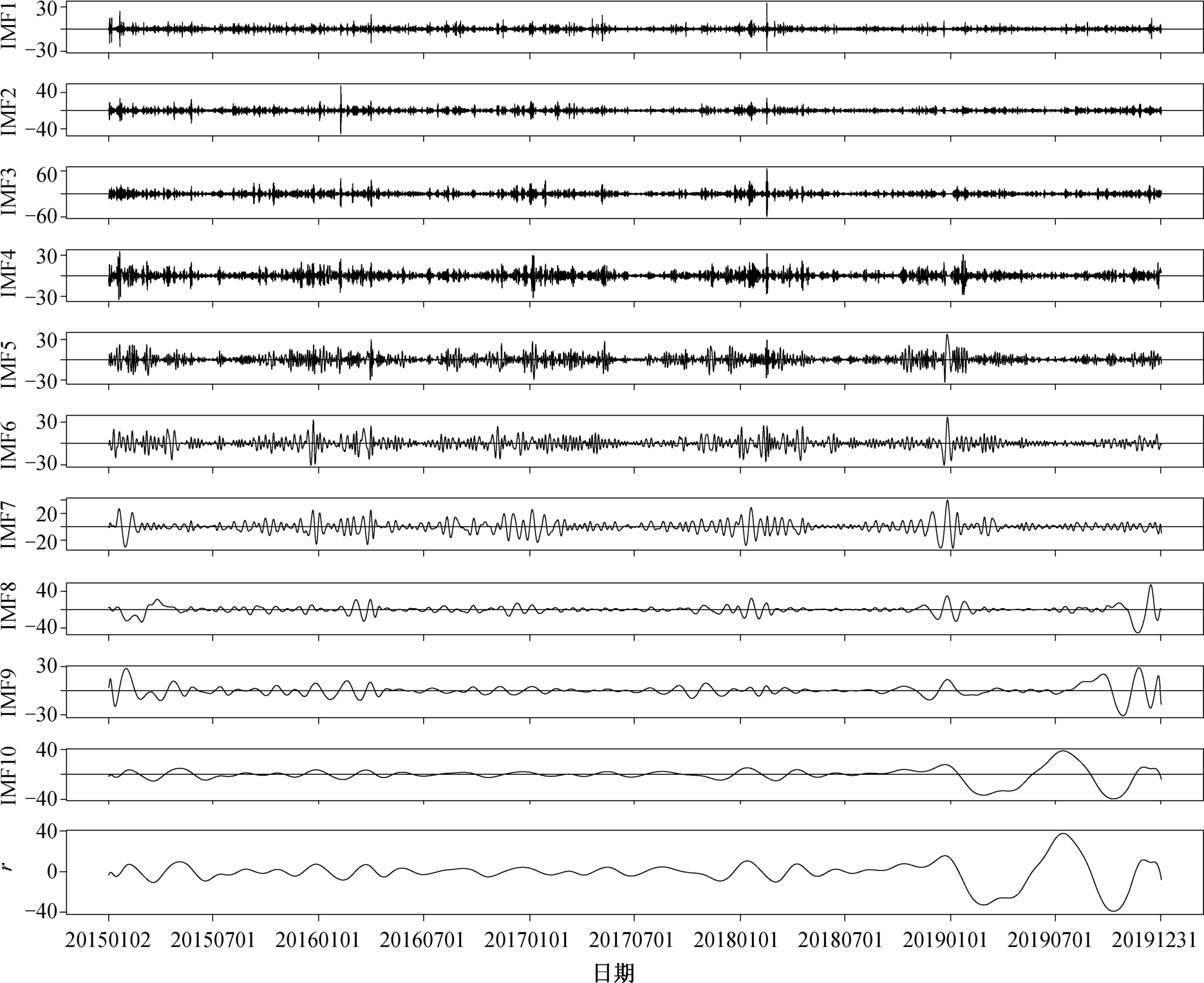
图2 PM2.5 原始序列分解结果
Fig. 2 PM2.5 original sequence decomposition results
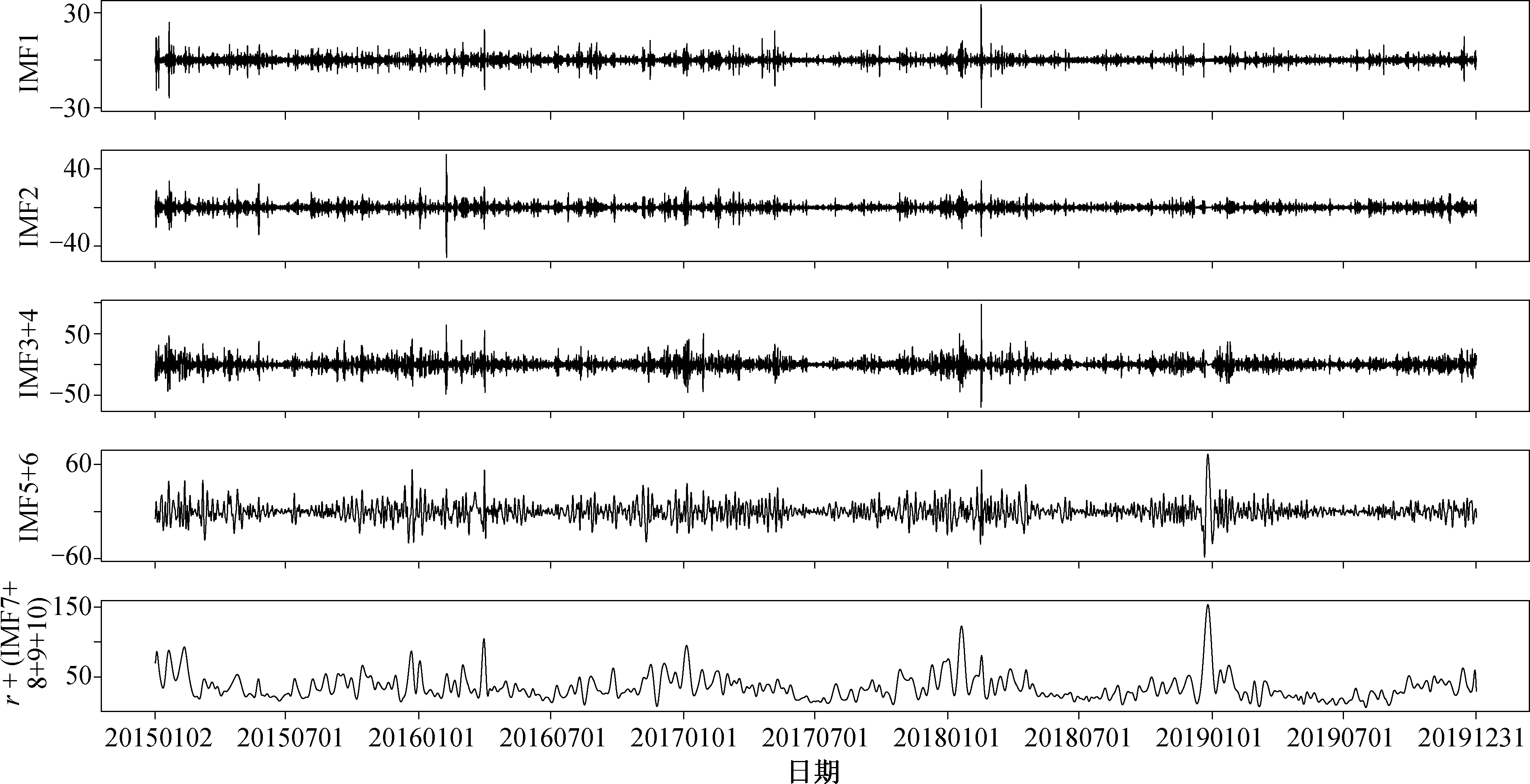
图3 5 组新时间序列
Fig. 3 Five new time series
表1 PM2.5 各IMF 分量的平均周期
Table 1 Mean period of each IMF component of PM2.5
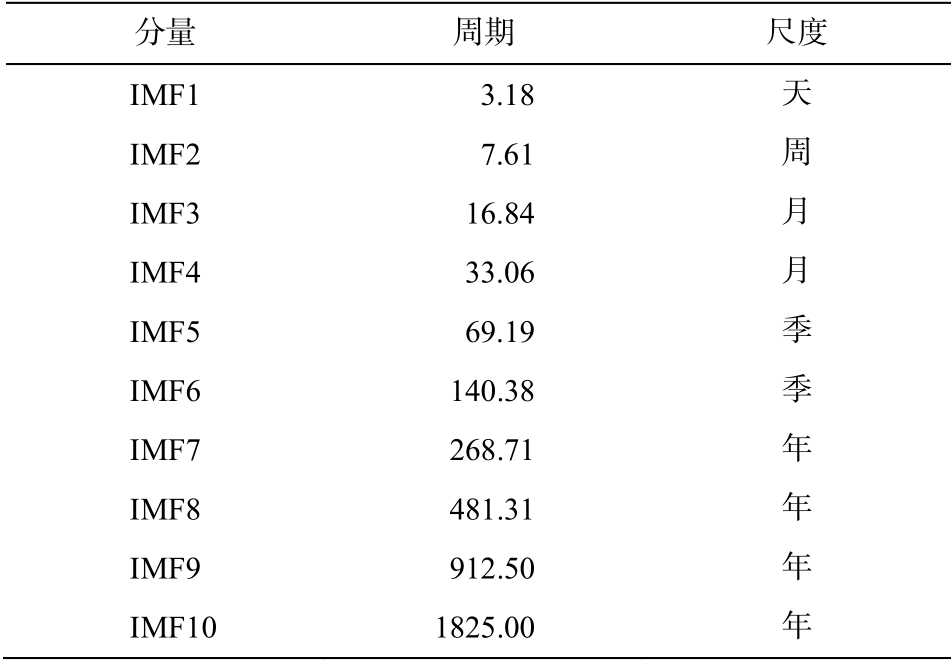
分量 周期 尺度IMF1 3.18 天IMF2 7.61 周IMF3 16.84 月IMF4 33.06 月IMF5 69.19 季IMF6 140.38 季IMF7 268.71 年IMF8 481.31 年IMF9 912.50 年IMF10 1825.00 年
2) 时间分辨率对不同模型预报结果的影响。本文分别对 6, 12 和 24 h 的观测值进行平均, 选取未进行 EEMD 分解的初始数据, 分别用 ARIMA 模型、BP 神经网络和 LSTM 神经网络对 2019 年 PM2.5浓度值进行预报, 探究传统统计学模型与神经网络模型对预报效果的影响及不同神经网络对预报效果的影响。
4 结果分析
4.1 EEMD 分解处理对预报结果的影响
图 4 展示模态分解前后的预测误差, 可以看出,对于 BP 神经网络, 经 EEMD 分解处理后的预测结果具有更小的 MAE 和 RMSE 值以及更大的 IA 和Var 值, 说明 EEMD 模态分解可以提高 PM2.5 浓度值的预报精度。

图4 有无EEMD 分解时BP 神经网络的预报效果
Fig. 4 Effect of EEMD on BP neural network
为了进一步探究 EEMD 分解对不同模态预报精度的提升情况, 本文对按周期分类的 5 组时间序列预报结果求取相对误差, 结果如图 5 所示。可以看出, IMF1~IMF4 (高频部分)预报结果的相对误差远大于低频部分(周期为季和年), 其中 IMF1 的相对误差最大, IMF5 和 IMF6 的相对误差最小, 说明EEMD 分解对预报效果的提升集中于低频部分。

图5 EEMD 分解后 BP 神经网络各模态预报结果的相对误差
Fig. 5 Relative error of each mode of BP neural network after EEMD decomposition
本文仅对 EEMD 是否可以优化预报效果进行简要的探讨。由于进行 EEMD 分解会极大地增加计算量, 加上本研究的主要目的是探究不同神经网络预报效果的优劣以及相关参数(隐藏层层数、各层神经元个数和激活函数等)对预报效果的影响,EEMD 模态分解的影响不是重点考虑因素, 所以后面不再对数据做 EEMD 分解处理。
4.2 时间分辨率及预报模型对预报结果的影响
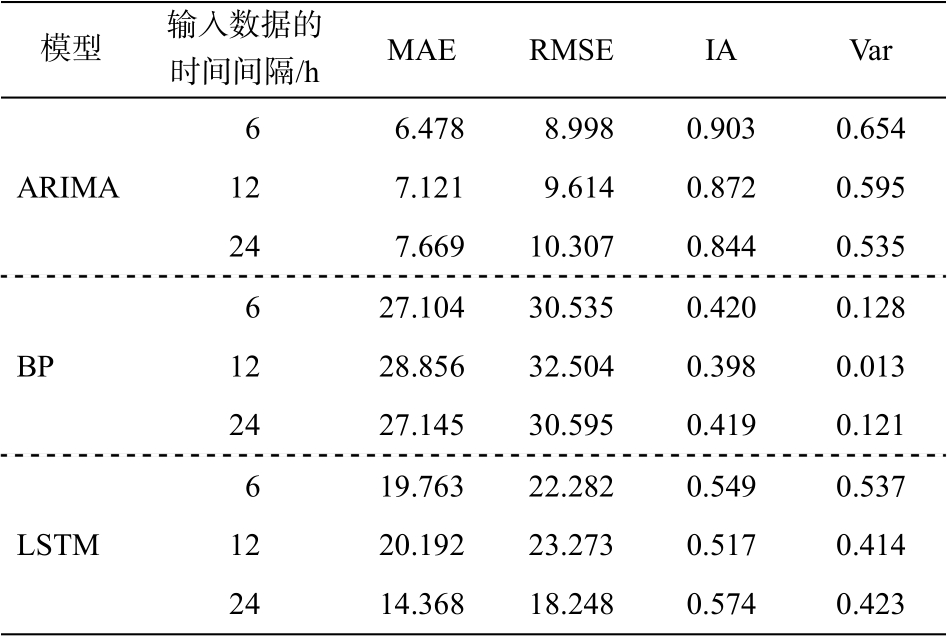
对时间间隔分别为 6, 12 和 24 h, 未进行 EEMD分解的输入数据, ARIMA 模型、BP 神经网络和LSTM 神经网络的预报效果如表 2 所示。可以看出,ARIMA 模型的预报结果符合时间精度越高, 预报效果越好这一规律, 体现为高时间精度的预报结果中 MAE 和 RMSE 值较低, IA 和 Var 值较高, 说明随着输入数据时间精度提高, 模型的拟合能力增强。
表2 ARIMA, BP 和LSTM 对不同时间间隔输入数据的预报效果
Table 2 Effect of ARIMA, BP, LSTM on different time interval
模型 输入数据的时间间隔/h MAE RMSE IA Var 6 6.478 8.998 0.903 0.654 ARIMA 12 7.121 9.614 0.872 0.595 24 7.669 10.307 0.844 0.535 BP 6 27.104 30.535 0.420 0.128 12 28.856 32.504 0.398 0.013 24 27.145 30.595 0.419 0.121 LSTM 6 19.763 22.282 0.549 0.537 12 20.192 23.273 0.517 0.414 24 14.368 18.248 0.574 0.423
对于 BP 神经网络, 输入数据时间间隔为 6 h 的预报效果优于输入数据时间间隔为 12 h 的预报效果, 具有更低的 MAE 和 RMSE 值以及更高的 IA 和Var 值; 输入数据时间间隔为 24 h 的预报效果优于输入数据时间间隔为 12 h 的预报效果, 与输入数据时间间隔为 6 h 的预报效果相近。
对于 LSTM 神经网络, 当输入数据的时间精度从 12 h 提升到 6 h 时, 模型的预报效果有所改善; 当输入数据的时间间隔为 24 h 时, 模型的预报效果显著高于输入数据时间间隔为 6 和 12 h 的预报效果。
对上述现象可能的解释是, 虽然提高输入数据的时间精度会提升模型的预报效果, 但本文选取的预报方式是基于 6 天的 PM2.5 浓度数据预报第 7 天的 PM2.5 浓度值, 因此当输入数据的时间精度分别为 6, 12 和 24 h 时, 输入数据量依次为 24, 12 和 6 个,即对于神经网络预报, 输入层神经元的个数依次为24, 12 和 6 个。当输入数据的时间精度发生变化时,神经网络预报效果的提升或下降是模型复杂度与数据精度共同作用的结果, 即数据精度的提升可以提升预报效果, 但模型复杂度和数据量的增加会增加模型训练的复杂度, 使预报效果变差。
对于 BP 及 LSTM 神经网络, 当输入数据的时间精度从 24 h 提升至 12 h 时, 输入层神经元从 6 个增加至 12 个, 此时模型复杂度提升对预报结果的负面影响高于输入数据时间精度提升对模型的优化程度。当输入数据的时间精度从 12 h 提升至 6 h 时,模型复杂度提升对预报效果的负面影响低于输入数据时间精度提升对模型的优化程度。
从表 2 可知, 当输入数据的时间精度相同时,ARIMA 的预报效果显著地优于 BP 和 LSTM。原因是 PM2.5 浓度数据的自相关性较强, 可以更好地适应自回归模型。就神经网络的预报效果来说, LSTM的表现整体上略优于 BP。
4.3 基于滚动预报的模型优化方案
由于模型用到预报日前一天(t-1)的 PM2.5 浓度值, 因此当前的模型只能进行预报时效为 1 天的试验。为了增加预报时效, 本文采用滚动预报方案对模型进行优化, 并以 BP 神经网络不进行 EEMD 分解为例, 讨论模型的预报效果。
以时间间隔为 24 h 的数据组为输入, 用滚动预报的方式对逐日 PM2.5 浓度值进行预报, 并与同样以 24 h 时间间隔数据为输入的初始预报模型的预报效果进行对比。为增加预报时效, 将 t 时刻的 PM2.5浓度预报值作为下一时刻的输入数据, 对 t+n 时刻的 PM2.5 浓度进行连续滚动预报。
为消除输入数据量增加导致模型复杂化后对预报效果的影响, 在将 t 时刻的数据加入训练集时,剔除原训练集中初始时刻的数据。例如, 若第一次训练的输入为 t 至 t+n 时刻的数据, 则第二次训练时加入 t+n+1 时刻数据, 同时剔除 t 时刻数据, 对 t+1至 t+n+1 时刻的 n+1 个数据进行训练。
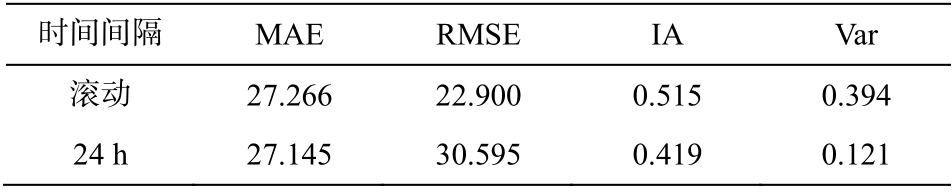
滚动预报模型的预报效果如表 3 所示。当神经网络复杂度相同时, 与输入数据为 PM2.5 逐日浓度值, 逐小时滚动预报 PM2.5 浓度, 再求取 PM2.5 日均值的预报方式相比, 滚动预报模型取得更高的 IA和 Var 值和更小的 RMSE 值, 但 MAE 值差别不大。可见, 滚动预报的效果略有提升, 但需在每次预报后更新训练集数据, 使模型重新学习, 会极大地增加计算量, 但实现了对 t+n 时刻的 PM2.5 浓度值进行连续滚动预报。
表3 BP 神经网络滚动预报效果
Table 3 Effect of rolling forecast by BP
时间间隔 MAE RMSE IA Var滚动 27.266 22.900 0.515 0.394 24 h 27.145 30.595 0.419 0.121
5 与相关研究中 PM2.5 预测效果对比
薛同来等[16]用 BP 神经网络对北京市 PM2.5 浓度进行预测, 设置隐藏层神经元个数为 6, 学习率为 0.1, 并对模型进行 2000 次训练, 对预报效果进行评价, 得到 RMSE 值为 13.41。张立等[17]用混沌粒子群优化算法(chaos particle swarm optimization,CPSO)对 BP 神经网络进行修正, 以 2017 年西安市PM2.5 日均浓度数据为样本建立预测模型, 预报结果的 RMSE 值为 21.3。蒋奇峰等[18]提出一种将量子粒子群(quantum particle swarm optimization, QPSO)算法与径向基神经网络(radial basis function, RBF)算法相结合的预测模型, 并用随机森林(random forest, RF)算法对 PM2.5 浓度的影响因子进行筛选,采用 RF-QPSO-RBF 复合模型, 针对南京市某气象基站的观测数据对 PM2.5 浓度进行预测, 预测结果的 RMSE 值为 7.869。
虽然本文与上述研究的区域和时段不同, 但本文预测结果的最佳 RMSE 值为 8.998,总体上与上述研究的预测水平相当。与上述研究相比, 本文进一步探讨了 EEMD 模态分解对预测效果的影响, 证明通过 EEMD 分解处理可以提升预测效果。
6 结论
1) EEMD 分解可以提升神经网络对 PM2.5 逐日浓度的预报效果, 且主要体现在低频部分。
2) 提升输入数据的时间精度, 可以提高模型的预报效果, 在 ARIMA 自回归模型中体现得较为明显。对于神经网络, 当用固定时长的 PM2.5 浓度数据进行预报时, 时间精度的提升意味着数据量的大幅提升, 会使神经网络的结构变得复杂, 输入层神经元数大量增加, 由此带来的系统误差可能导致整体预报效果下降。因此, 在用神经网络进行 PM2.5浓度预报时, 要充分考虑模型复杂度对预报效果的影响。
3) ARIMA 自回归模型的预报效果整体上优于神经网络模型, 并且, 当输入数据量发生改变时,ARIMA 模型的稳定性较好。与 BP 神经网络相比,LSTM 神经网络对 PM2.5 浓度的预报表现更好。
4) 由于模型使用前一天的 PM2.5 作为输入数据,只能预报 t+1 天的 PM2.5 值。采用滚动预报的方式对模型进行优化后, 能够显著地提升预报时效, 实现对 t+n 天的连续预报, 且预报误差与后报结果相当。
BP 和 LSTM 神经网络的参数设置(如各层神经元个数的选择)会对预报效果产生影响, 本文未对此进行探讨; 此外, 回归分析的激活函数通常使用ReLU 和 tanh, 本文未对 tanh 作为激活函数的预报效果进行探讨。这些问题有待后续工作中进一步完善。
[1] Lelieveld J, Evans J S, Fnais M, et al. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature, 2015, 525: 367-371
[2] Li Jin, Liu Huan, Lv Zhaofeng, et al. Estimation of PM2.5 mortality burden in China with new exposure estimation and local concentration-response function.Environmental Pollution, 2018, 243: 1710-1718
[3] Baker K R, Foley K M. A nonlinear regression model estimating single source concentrations of primary and secondarily formed PM2.5. Atmospheric Environment,2011,45(22): 3758-3767
[4] 周广强, 谢英, 吴剑斌, 等. 基于 WRF-Chem 模式的华东区域 PM2.5 预报及偏差原因. 中国环境科学,2016, 36(8): 2251-2259
[5] 王茜, 吴剑斌, 林燕芬. CMAQ 模式及其修正技术在上海市 PM2.5 预报中的应用检验. 环境科学学报,2015, 35(6): 1651-1656
[6] 任晓晨, 邹思琳, 唐娴, 等. 基于集合经验模态分解和 BP 神经网络的北京市 PM2.5 预报研究. 北京大学学报(自然科学版), 2019, 55(4): 615-625
[7] 郑毅, 朱成璋. 基于深度信念网络的 PM2.5 预测. 山东大学学报(工学版), 2014, 44(6): 19-25
[8] 戴李杰, 张长江, 马雷鸣. 基于机器学习的 PM2.5短期浓度动态预报模型. 计算机应用, 2017, 37(11):3057-3063
[9] 曲悦, 钱旭, 宋洪庆, 等. 基于机器学习的北京市PM2.5 浓度预测模型及模拟分析. 工程科学学报,2019, 41(3): 401-407
[10] Lu Xingcheng, Lin Changqing, Li Ying, et al. Assessment of health burden caused by particulate matter in southern China using high-resolution satellite observation. Environment International, 2017, 98:160-170
[11] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454: 903-995
[12] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method.Advances in Adaptive Data Analysis, 2009, 1(1): 1-41
[13] Hochreiter S, Schmidhuber J. Long short-term memory. Neural computation, 1997, 9(8): 1735-1780
[14] 李建东, 铁学熙, 曹军骥. 城市地区PM2.5 周末效应的初步研究. 地球环境学报, 2015, 6(4): 224-230
[15] 张雪梅. 广州某区 PM2.5 和气态污染物质量浓度的日变化特征及其相关性分析. 广州环境科学, 2017,32(1): 8-11
[16] 薛同来, 赵冬晖, 韩菲. 基于BP 神经网络的北京市PM2.5 浓度预测. 新型工业化, 2019, 9(8): 88-91
[17] 张立, 王腾军, 刘帅令, 等. 基于CPSO-BP 神经网络的 PM2.5 浓度预测模型. 甘肃科学学报, 2020,32(2): 47-50
[18] 蒋奇峰, 杜景林, 周芸, 等. 一种基于 QPSO-RBF模型预测 PM2.5 浓度值的方法研究及应用. 计算机应用与软件, 2020, 37(9): 202-208