随着卷积神经网络(convolutional neural networks,CNN)在计算机视觉、自然语言处理以及语音识别等领域的成功应用, 研究者们对图神经网络(graph neural networks, GNN)在图学习方面的潜力产生极大的兴趣。图像、自然语言和语音信号都属于欧几里德数据结构(Euclidean data structure), 这类数据结构排列整齐, 很容易定义其中的邻居。例如, 可以用矩阵表示一张图片中的每个像素点, 将文本和语音信号视为一维序列。这种数据结构的特性使得我们很容易定义作用于其上的卷积操作, 用来提取局部特征。然而, 图(graph)却是一种非欧几里德数据结构(non-Euclidean data structure), 其中的节点并不是规则的排列。并且, 对于不同节点, 其邻居数目不同, 因此传统 CNN 的卷积操作无法直接运用到图中。
图卷积神经网络(graph convolutional networks,GCN)将 CNN 中的卷积概念扩展到图中, 通过定义作用于图上的卷积操作来提取节点的邻域信息。由于图卷积操作可以对图结构以及图上的邻域信息进行有效的提取, 所以 GCN 在图表示学习领域表现出强大的优势。研究表明, GCN 在很多图挖掘任务(如节点分类、边分类、链接预测和聚类等)中有最优的表现[1-2]。
已有的图卷积神经网络大多基于静态图设计,即模型对图的建模和表示进行学习, 假设图结构不改变。然而, 现实中提取的图是动态变化的, 图中的节点和边都会随着时间而有插入和删除, 节点属性和边属性也会随时间而改变。例如, 在一个以用户为节点, 用户间交易为边的金融网络中, 一个具有现实意义的任务就是识别其中的可疑用户(例如洗钱组织成员)或可疑交易(例如信用卡诈骗交易)。在这个图中, 随着用户间不断进行交易, 图结构也随之不断地变化, 因此我们不仅需要关注图中当前时刻的信息, 也需要分析图上历史时刻的信息。如图 1 所示, 银行账户 F 在时刻 t 可能是一个正常用户, 之后加入某洗钱组织, 从而在 t+1 时刻开始一些可疑交易(虚线箭头所示 F→D, D→B, B→C,C→F), 因此在 t+2 时刻, 根据账户 H 与账户 F 之间的联系以及历史交易记录等, 需要考虑 H 是否有可能也变成了可疑用户。在图不断变化的场景下, 需要用动态模型去提取动态图上的结构信息以及历史时刻信息, 从而得到具有丰富信息的节点表示。
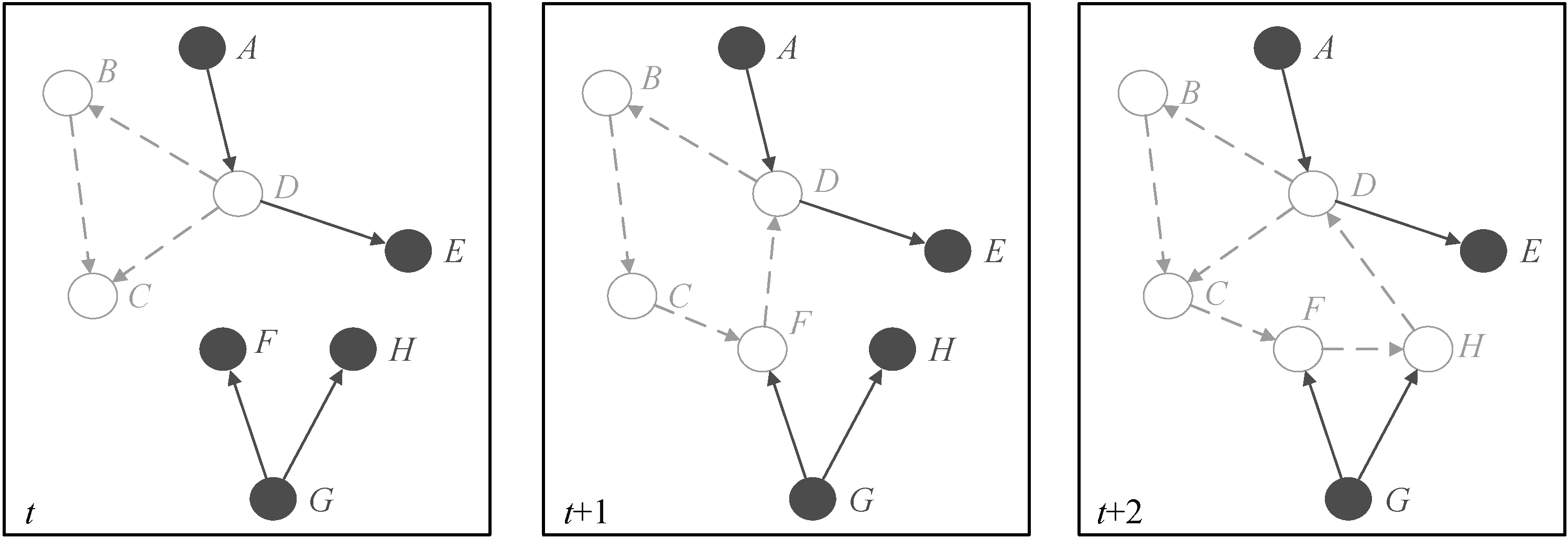
图1 动态图示例
Fig. 1 An example of a dynamic graph
本文提出一个基于时空建模的动态图卷积神经网络(dynamic graph convolutional network, DynGCN)来建模动态图上的节点表示问题。模型将动态图的节点表示学习视为时间维度和空间维度信息的聚合, 并引入自适应的模型更新机制, 感知图结构的动态性。为了进一步验证模型的建模能力, 在多组比特币交易数据集上进行链接预测任务, 实验结果表明了 DynGCN 模型对动态图节点信息提取的有效性。
1 相关工作
1.1 静态图表示学习方法
传统的图表示学习方法是在图的邻接矩阵计算出的相似矩阵上进行奇异向量分解(singular vector decomposition, SVD), 得到节点的低维向量表示[3-4]。这种方法非常直观, 但基于 SVD 的操作却缺乏可扩展性。另一类方法是受 Word2Vec[5]对单词向量表示学习的启发, 将处理句子的方法迁移到处理图中(如 DeepWalk[6]和 Node2Vec[7]), 在图中设计随机游走策略, 得到节点序列, 然后将这些节点序列视为句子, 输入 SkipGram[5]模型, 学习到节点的低维向量表示。随着深度学习在很多领域表现出的巨大优势, 如 GNN[8-12]广泛应用于节点表示学习领域, 第三类方法主要通过设计图卷积算子来学习图中节点的邻域信息。以上方法都聚焦在静态图上的节点表示学习, 而缺乏对图动态性的建模。
1.2 动态图表示学习方法
1.2.1 基于矩阵分解的方法
解决动态图上节点表示学习问题的一个思路是, 将静态图上的方法进行扩展, 比如加入某些更新机制。DANE[13]就是采用这种方法, 将动态图视为时序上的一系列快照(snapshot), 每个快照是一个静态图, t 时刻的向量表示是由 t-1 时刻的特征向量更新而来, 不是在每个时间切片上都重新计算。相似地, DHPE[14]也动态地更新学习到的表示向量, 同时通过广义的奇异值分解(generalized singular value decomposition, GSVD)和矩阵摄动理论(matrix perturbation theory), 保留高阶相似性。在不断更新求近似的过程中, 这类增量 SVD 的方法会产生越来越严重的误差累积, 因此 Zhang 等[15]提出一种 SVD重启的最大误差界限理论, 通过设置最优的重启时间来减少学习过程中的误差累积。
1.2.2 基于随机游走的方法
受静态图上基于随机游走方法的启发, 一些研究者提出在动态图上随机游走的方法。DNE 模型[16]采用一种与 LINE[17]等价的可分解的目标函数来学习新节点的表示向量, 同时也提出一种对受到最大影响原始节点的嵌入向量调整机制。另一方面, CTDNE[18]将动态图建模为连续时间上的过程,为条边设置多个相关的时间戳, 同时将随机游走的路径限制在符合边的时间序列路径上。CTDNE 将动态性和时序性考虑进随机游走的过程中, 同时也保证了模型的可扩展性。
1.2.3 基于自编码器的方法
此类动态图表示学习方法是基于一些非监督学习框架, 例如自编码器。DynGEM[19]利用前一时刻的自编码器来初始化当前时刻的训练参数, 从而能够保留节点表示的历史信息。同时, DynGEM 通过一个启发式的算法, 根据不同时刻的图结构, 将SDNE[20]的架构进行调整, 从而适应新的图结构。考虑到 DynGEM 只利用过去一个时刻的历史信息,Goyal 等[21]随之提出 dyngraph2vec 模型, 可以编码更多的历史时刻信息, 但架构更复杂, 不具有更好的可扩展性。
1.2.4 基于点过程的方法
为了将图的动态性建模为连续的而不是分段的时间切片, 基于点过程的方法, 尝试将图中的边视为一个事件, 则一个事件的发生会反过来影响整个网络结构。KnowEvolve[22]和 DyRep[23]是其中的重要研究成果。DyRep 将图的动态性考虑为关联过程(association process)和通信过程(communi-cation process) 两个过程, 将图中的节点表示视为关联过程和通信过程中间的调解者, 这两个过程反过来又带来节点表示的更新。DynamicTriad 模型[24]也受点过程的启发, 尝试建模图中的闭合三点(两两之间有边相连的 3 个节点)是如何从开放的三点(3 个节点中有两个节点之间没有边相连)的状态发展而来。DynamicTriad 模型认为闭合三点的形成是图的动态性的反映。这类方法考虑了连续时间的因素,在事件建模和预测方面有很强的优势。
1.2.5 基于图卷积的方法
随着图卷积神经网络在获取图结构信息方面表现出的巨大优势, 一种新的动态图嵌入学习的方法是将 GCN 与 RNN (如 LSTM 等)相结合, 其中 GCN用来提取图结构上的信息, RNN 则用来建模时间维度上的动态变化。Seo 等[25]提出两种 GCRN 架构,其共同特征是利用 GCN 来学习节点的向量表示,然后将一段时间学习到的向量序列输入 LSTM 模型, 建模序列上的动态性。两种架构的唯一区别在于, 其中一个模型将传统的 LSTM 中的欧几里德 2D卷积运算修改为图卷积运算。相似地, Manessi 等[26]提出 WD-GCN/CD-GCN 结合 LSTM 的变种和扩展的图卷积运算来建模图结构及其长短期依赖。不同的是, WD-GCN 的输入是图序列, 而 CD-GCN 的输入是对应的节点特征的有序序列。
进一步地, GCN-GAN 模型[27]将带权动态图上的时序性链接预测任务建模为 GCN 与 RNN 的架构,再与生成性对抗网络(generative adversarial networks,GAN)相结合。GCN-GAN 模型同样运用GCN 去学习每个时间片上的拓扑结构特征, 然后运用 LSTM去学习序列性的变化, 采用 GAN 的学习框架去生成下一个时间步, 从而学习到更有效的节点表示。STAR[28]模型加入对偶注意力(attention)机制来增强GCN 和 RNN 架构的学习能力。Evolve-GCN[29]模型改变了之前方法中学习节点表示在时序上的动态性的思路, 转而去学习 GCN 参数在时序上的动态性。虽然 EvolveGCN 也采用 GCN 与RNN 相结合的方式, 但此结构中的 RNN 用于建模GCN 的权重参数在时间维度上的动态性, 从而学习到动态图上的节点表示。
2 基于时空建模的动态图卷积神经网络
2.1 问题定义
我们定义动态图和动态图上的表示学习如下:一个动态图被表示为多个静态图的序列, 即 G={G1, G2, …, GT}, 其中 Gt=(Vt, Et)表示在时刻 t, t∈{1,2, …, T}的快照。对于图 Gt 的邻接矩阵 At∈RN×N, 如果(vt)i 和(vt)j 之间有边相连, 那么(At)i,j=1, 否则(At)i,j=0。动态图上的节点表示学习为学习到一组映射的序列 F={f1, f2, …, fT}, ∀t∈{1, 2, …, T}, 其中每个映射都将时刻 t 的节点映射为低维向量(yt)v=ft(v), 使得映射后的向量能保留节点的原始信息。也就是说若两个点在原始图中越相似, 则它们映射后的向量就越接近。
2.2 模型架构
本文提出的模型将动态图上的表示学习建模为时间和空间信息的聚合, 同时加入模型自适应机制,可以随着图结构的变化而更新模型参数。如图 2 所示, 模型基本架构由空间卷积层和时间卷积层组成,模型第一层是由一个空间卷积层来聚合节点的邻居信息, 同时利用 GRU 单元自适应更新参数。输出的向量输入第二层的时间卷积层, 聚合当前时刻和历史时刻的信息。由此, 每个节点的表示都融合当前以及历史时刻的邻居信息。最后, 加上一个自适应的空间卷积层, 用来聚合邻居的当前时刻和历史时刻信息。
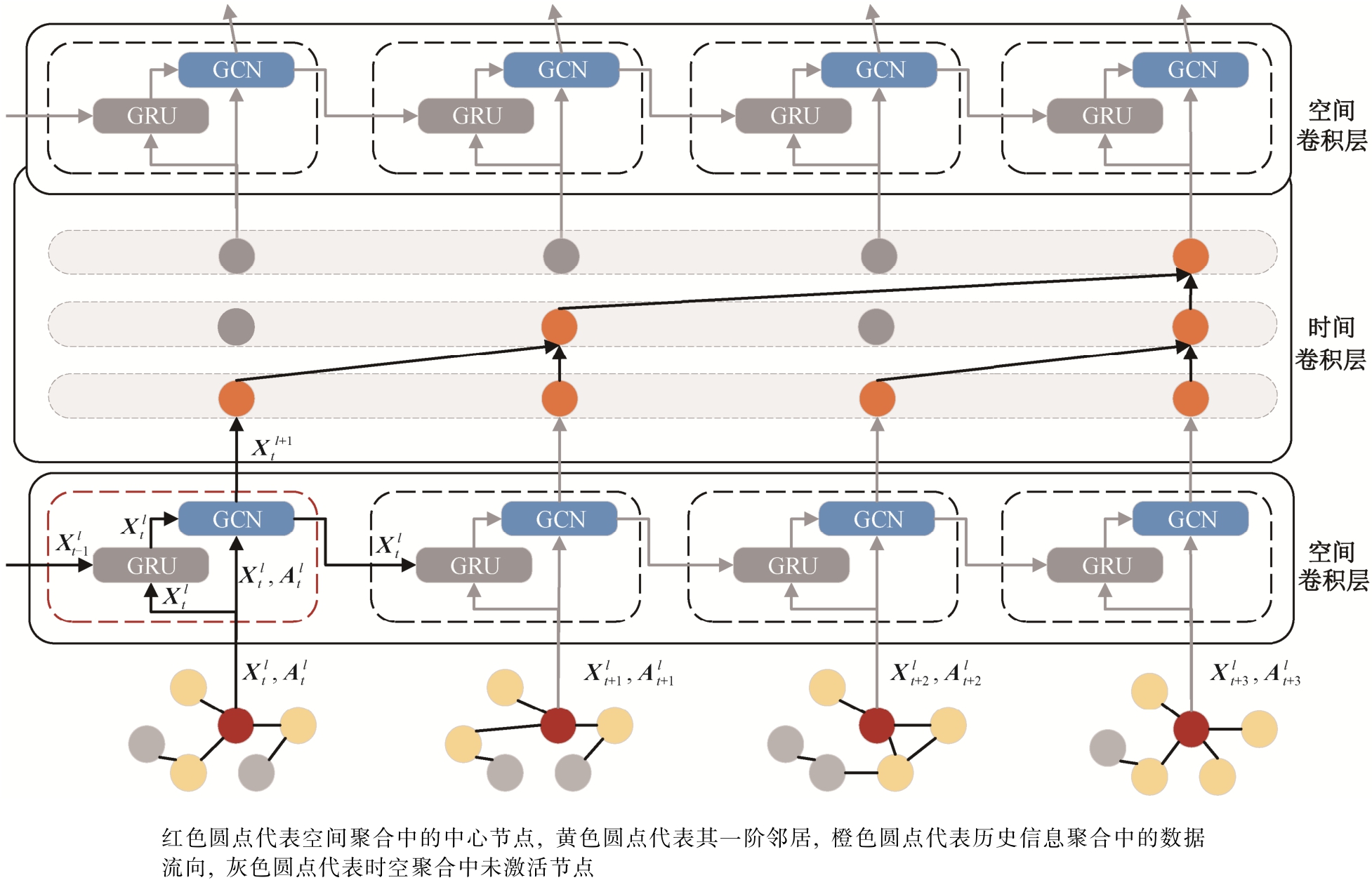
图2 DynGCN 模型架构
Fig. 2 DynGCN model architecture
2.3 空间卷积层
我们利用GCN的图结构提取优势来学习每个时间片下的结构信息。GCN 通过定义的谱图卷积聚合邻居信息, 从而将卷积的思想扩展到图上。形式化地, 对于 t 时刻的图 Gt=(Vt, Et), GCN 的第 l 层输入为第 l -1 层输出的向量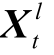 
和邻接矩阵 At, 输出是更新后的节点向量
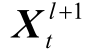。第l 层的运算表示为
考虑到图的动态性, 动态图卷积层在静态 GCN的架构上加入更新机制。因为当图结构改变时, 卷积操作的权重参数也应进行更新, 以便适应新的图结构。动态图卷积层采用 RNN 组件对 GCN 模型的权重参数进行更新, 对于每一个 t∈{1, 2, …, T}和 l∈{1, 2, …, L}, RNN 组件都以参数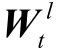 
的初始值为输入, 输出更新后的 
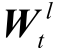。虽然 RNN 的多种实现(如LSTM 和 GRU)都能达到这个目的, 但由于 GRU 结构的输入包含每个时刻的节点表示, 可以为权重参数的更新引入更丰富的图结构信息, 因此我们的架构采用 GRU 的实现方式。
时刻 t 第 l 层的权重更新方式如下:GCN 模块自下而上聚合节点的邻居信息, 而GRU 模块随时间维度自左向右更新权重参数。由此, 空间卷积层动态地获得节点的邻域信息。空间卷积层的操作可以形式化地表示为
其中, 函数 F和 G 分别表示图卷积操作和权重更新操作。
2.4 时间卷积层
在动态图节点表示学习中提取时序信息是非常关键的环节。已有的模型大多采用 RNN 的架构来建模时序变化, 由于基于 RNN 的架构具有复杂的门机制, 因此在运算上更加耗时, 也更消耗内存。同时, 标准的 RNN 在训练中容易出现梯度消失的问题, 并且只能获取较短时间的记忆, 对长时间的序列无法很好地处理。虽然 LSTM 和 GRU 在一定程度上解决了梯度消失和短期记忆的局限, 但相对于基于 CNN 的架构, 在运算速度、内存消耗以及性能表现方面依然处于劣势, 因此我们的模型采用基于 CNN 的架构(即 TCN[30]结构)来获取历史信息。
与 RNN 的架构相比, 由于卷积操作的可并行性, TCN 使得运算速度获得极大提升, 同时其运算对内存的消耗也更小。重要的是, TCN 结构对历史信息的感受域更灵活, 可以通过简单地增大卷积核或增加扩张卷积的 dilation size 来增大感受域, 从而获取更长时间序列的信息。另一方面, RNN 的架构对动态性的建模是将历史信息单纯地归纳入每个时刻的 Hidden state 中, 通过Hidden state 来记忆历史信息。TCN 的卷积结构则通过灵活性的信息聚合方式, 将历史信息与当前时刻的信息相结合, 从而提取动态图中的时序信息和结构信息, 也从另一个角度将时间卷积与空间卷积进行统一。
时间卷积层由一个 1D 的全连接卷积模块(1D fully-convolutional unit)和一个因果卷积模块(causal convolutional unit)构成, 1D 的全连接卷积操作保证输出层与输入层有相同的序列长度, 因果卷积操作则保证在 t 时刻的输出都只由它之前的时刻(包括当前时刻)卷积得到, 由此保证由当前时刻的信息和历史信息去建模未来时刻的预测。在因果卷积阶段, 为使网络结构对更长的时间序列也有更长更灵活的感受域, 在因果卷积中加入扩张卷积(dilated convolutions)的设置, 随着网络层数增加, 卷积的扩张(dilation)值设置为 2 的层数次幂。图 3 展示TCN 中的扩张卷积过程, 其中每层的 dilation size依次为 1, 2 和 4, 卷积核大小为 2。
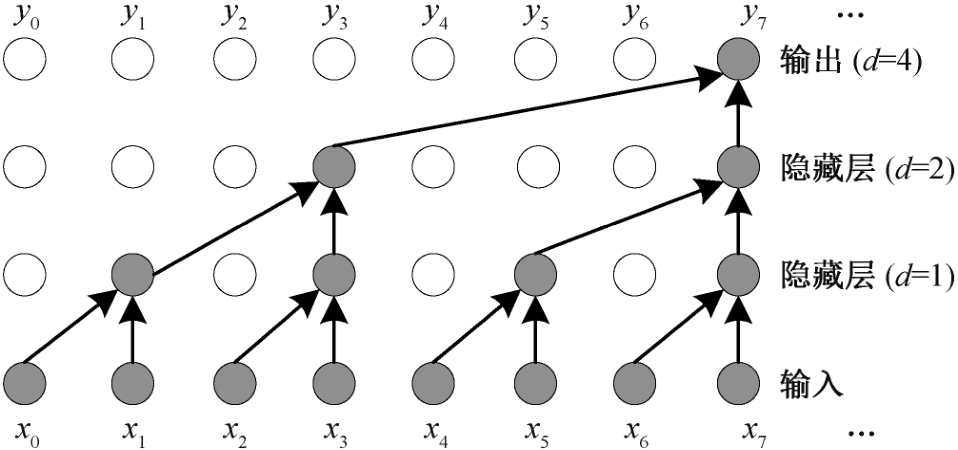
图3 TCN 中扩张卷积示例
Fig. 3 An example of dilation convolution in TCN
形式化地, 给定一个第 l 层的长为 T, 有 M 维特征的输入序列 X l∈RT×M, 以及一个滤波器 f :{0,1, …, k-2}, 对于 X l 的元素 x, 卷积运算H 定义如下:其中, d 是扩张因子, k 是滤波器大小, x - d ·i 代表历史的方向。我们可以通过增加滤波器大小k 或增加扩张因子 d 来增大卷积的感受域。同时, 卷积操作支持对序列的并行运算, 因此在效率上有极大的提升。
时空卷积模型第 l 层空间卷积后的节点嵌入向量是对邻居信息的聚合, 经过时间卷积层后, 可以得到每个节点以及节点邻居的历史信息。在此之上叠加一个空间卷积层, 则每个节点的向量表示都包含它及其邻居的当前和历史时刻信息的聚合。因此, 这种时间卷积与空间卷积相互交叠的模型结构使得输出的节点嵌入向量拥有更丰富的结构信息和历史信息。
2.5 模型训练
为了测试模型的表示能力, 我们在特定的边分类任务中对模型进行训练。边分类任务在很多现实场景下有很强的现实意义, 例如对金融网络中的犯罪识别, 就需要对两个账户之间的连边进行边分类研究。动态图下的边分类任务旨在预测某条边(u,v)在 t 时刻的边标签类别。为了对边进行分类, 我们需要边的两个端点的节点向量表示。给定有边相连的两个节点 u 和 v 在 t 时刻的向量表示分别为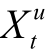 
和 
, 用参数矩阵 P 来预测边(u, v)的标签:
模型的交叉熵损失函数为
其中,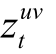 
表示边的真实标签类别; 权重参数 αuv 是平衡类别分布的权重的超参数, 实验的数据集均存在严重的类别不均衡问题, 通过调节 αuv 来平衡分类类别的比重。
3 实验
3.1 数据集
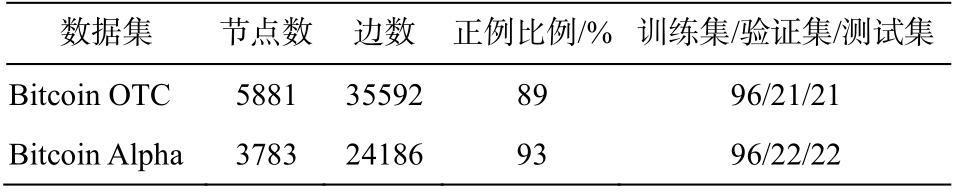
在两个金融领域数据集上进行模型验证。数据集来自两个不同的比特币交易网站的用户之间的信任度评分网络。数据集的详细信息如表 1 所示。
Bitcoin OTC①http://snap.standford.edu/data/soc-sign-bitcoin-otc.html;数据集是从比特币交易网站中提取的用户之间的信任度评分网络。用户用-10 (完全不信任)到+10(完全信任)对其他用户进行打分, 每个打分用相应的时间戳代表打分时间。数据集的时间跨度约为 5 年, 我们设置 13.8 天的时间间隔, 数据集共产生 138 个时间步。将 138 个时间步切分为训练集、验证集和测试集, 切分比例见表 1。另外,Bitcoin OTC 数据集的类别分布极不均衡, 89%的数据都是正例, 负例只占很少的部分。
表1 数据集信息
Table 1 Dataset statistics
数据集 节点数 边数 正例比例/% 训练集/验证集/测试集Bitcoin OTC 5881 35592 89 96/21/21 Bitcoin Alpha 3783 24186 93 96/22/22
Bitcoin Alpha②http://snap.standford.edu/data/soc-sign-bitcoin-alpha.html数据集同样是一个比特币用户之间的信任网络, 但用户和评分数据提取自另一个比特币平台 BTC-Alpha。评分数据为 2010 年 11 月8 日—2016 年 1 月 22 日, 设置 13.6 天的时间间隔,将数据集分为 140 个时间步。训练集、验证集和测试集的划分比例见表 1。评分依然从-10 (完全不信任)到+10 (完全信任), 但是与 Bitcoin OTC 的 89%的正例比例相比, Bitcoin Alpha 有更高的正例比例( 93%)。
由于两个数据集都存在类别严重不均衡问题,在反欺诈场景下, 负例的评分类别更值得关注。所以, 我们把负分的类别作为分类的主类别, 更加注重负分类的分类情况。
3.2 对比模型
我们使用静态方法和动态方法, 将 DynGCN 模型与一些现有模型进行对比。在对比模型中, 动态方法是从不同的方向进行: 节点导向的(基于节点表示向量的动态性)、模型导向的(基于模型参数)以及各自不同的动态建模方式。
GCN 这是一个静态的图卷积模型, 也是进行图表示学习的经典方法。模型通过谱卷积聚合节点的邻居信息来学习节点的嵌入向量。由于动态图中的每一个时间步都会产生一个图的快照, 我们对每个时间步都采用同一个 GCN 模型, 即不考虑图的动态性, GCN 模型基于每个时间步上的图进行训练。
GCN-GRU[25] 将 GCN 与序列建模相结合, 首先通过 GCN 架构学习每个时间快照下节点的表示向量, 再将这些向量输入 GRU 单元, 学习节点表示的动态性。此方法对动态性的表示建立在节点表示向量上, 属于节点导向的方法。为了更好地进行对比, 本实验将原方法中的 ChebNet 更换为 GCN, 将LSTM 替换为 GRU。
EvolveGCN 这是一种模型导向的方法。此方法也将 GCN 与 RNN 相结合, 但与 GCN-GRU 不同,EvolveGCN 中采用 RNN 建模 GCN 参数的更新。整个模型训练沿着卷积层从下到上和时间维从前到后进行。将动态性建模到 RNN 的隐向量中, 针对每个时间步, 学习到更新后的 GCN 权重参数, 节点的表示向量经过更新后的权重参数, 进行图卷积运算,得到更新后的节点表示。EvolveGCN 有 EvolveGCNH 和 EvolveGCN-O 两种实现方法。-H 类采用 GRU进行动态建模, -O 类采用 LSTM 进行动态性建模。我们的对比基于这两种方法。
3.3 实验设置
两个数据集在每个时间步上的边都比较少, 导致每个时间步的图快照很稀疏。为了让图表示学习算法有更好的学习能力, 我们设置每条边的生存时长为自边产生起 10 个时间步的时间窗口。实验中,对历史信息的步长设置为 10。所有模型的 GCN 卷积层数都为 2, Bitcoin OTC 数据集的 em-bedding size 设置为 110, Bitcoin Alpha 的 embedding size 设置为 90, 同时设置两层 GCN 卷积的 embed-ding size为相同值。输入的节点特征设置为节点的出度/入度值。模型中的权重初始化均为正态分布初始化,并且都采用 Adam 优化器, dropout 的比例均设置为0.3, 学习率(learning rate)设置为 0.001。我们在损失函数中加入 L2 正则化项, L2 正则的权重设置为0.0005。所有测试集上的结果均在验证集最优的迭代轮下记录。
3.4 实验结果
表 2 展示 DynGCN 模型与对比模型的分类表现对比。两个数据集的类别不均衡使得模型的分类能力面临很大挑战, 但本文的 DynGCN 模型取得最好的分类能力, 比其他模型有明显的优势。对于整体的分类能力, 我们对比准确率和加权 F1 值; 由于小类对反金融欺诈有更强的现实意义, 我们也对比小类的 F1 值以及对应的精确率和召回率。表 2 中所有的实验结果均为在验证集上取得最优时的测试结果。
从表 2 可以发现, DynGCN 有最高的分类准确率和加权 F1 值, 表明 DynGCN 有很好的总体分类性能表现。对于小类的分类结果, DynGCN 也达到最好的 F1 值和精确率。虽然从召回率来看, DynGCN略低于 GCN 和 GCN-GRU, 但 DynGCN 仍然优于其他方法, 因为其他方法虽然有更高的召回率, 却以更低的精确率为代价。作为精确率和召回率的调和平均值, F1 值在分类性能上是更有效的评估标准。
表2 边分类任务实验结果
Table 2 Experimental results for edge classification tasks
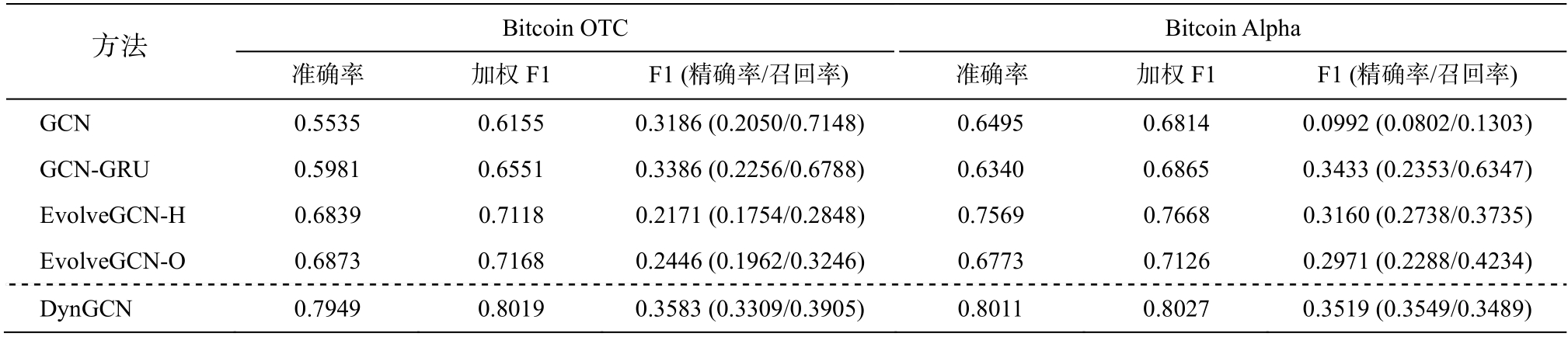
方法 Bitcoin OTC Bitcoin Alpha准确率 加权F1 F1 (精确率/召回率) 准确率 加权F1 F1 (精确率/召回率)GCN 0.5535 0.6155 0.3186 (0.2050/0.7148) 0.6495 0.6814 0.0992 (0.0802/0.1303)GCN-GRU 0.5981 0.6551 0.3386 (0.2256/0.6788) 0.6340 0.6865 0.3433 (0.2353/0.6347)EvolveGCN-H 0.6839 0.7118 0.2171 (0.1754/0.2848) 0.7569 0.7668 0.3160 (0.2738/0.3735)EvolveGCN-O 0.6873 0.7168 0.2446 (0.1962/0.3246) 0.6773 0.7126 0.2971 (0.2288/0.4234)DynGCN 0.7949 0.8019 0.3583 (0.3309/0.3905) 0.8011 0.8027 0.3519 (0.3549/0.3489)
进一步地, 我们绘制在 Bitcoin Alpha 测试集上小类的 F1 值和分类准确率随时间变化曲线(图 4)。可以看出, 静态的 GCN 方法与其他动态方法有明显的差距, 并且 DynGCN 的优势在各个时间步都更明显。另外, GCN 方法的准确率也更低。因为 GCN是为静态图设计的, 未考虑图上的动态性, GCN 在动态图上的性能劣势反映动态性建模的必要性和优势。
从图 4 可以看出, DynGCN 模型的优势在整个时间轴上都可以保持。特别地, 对于时间步 15, 其他方法的分类能力都非常差, 而 DynGCN 模型依然保持 F1 值的绝对优势。这得益于 DynGCN 模型对时空信息的双重建模, 能对于时间序列上的突变情况有较为稳定的表现。另外, 相比两个类型的EvolveGCN, DynGCN 都有更好的分类表现, 因为EvolveGCN 只关注模型权重参数的动态性而忽略图结构的变化。GCN-GRU 的相对更低分类能力是因为,虽然每个节点的历史信息都被考虑, 但由于 DynGCN独特的时空卷积操作以及模型更新机制, 对于更高层次的表示学习, 仍然是 DynGCN 更有优势。
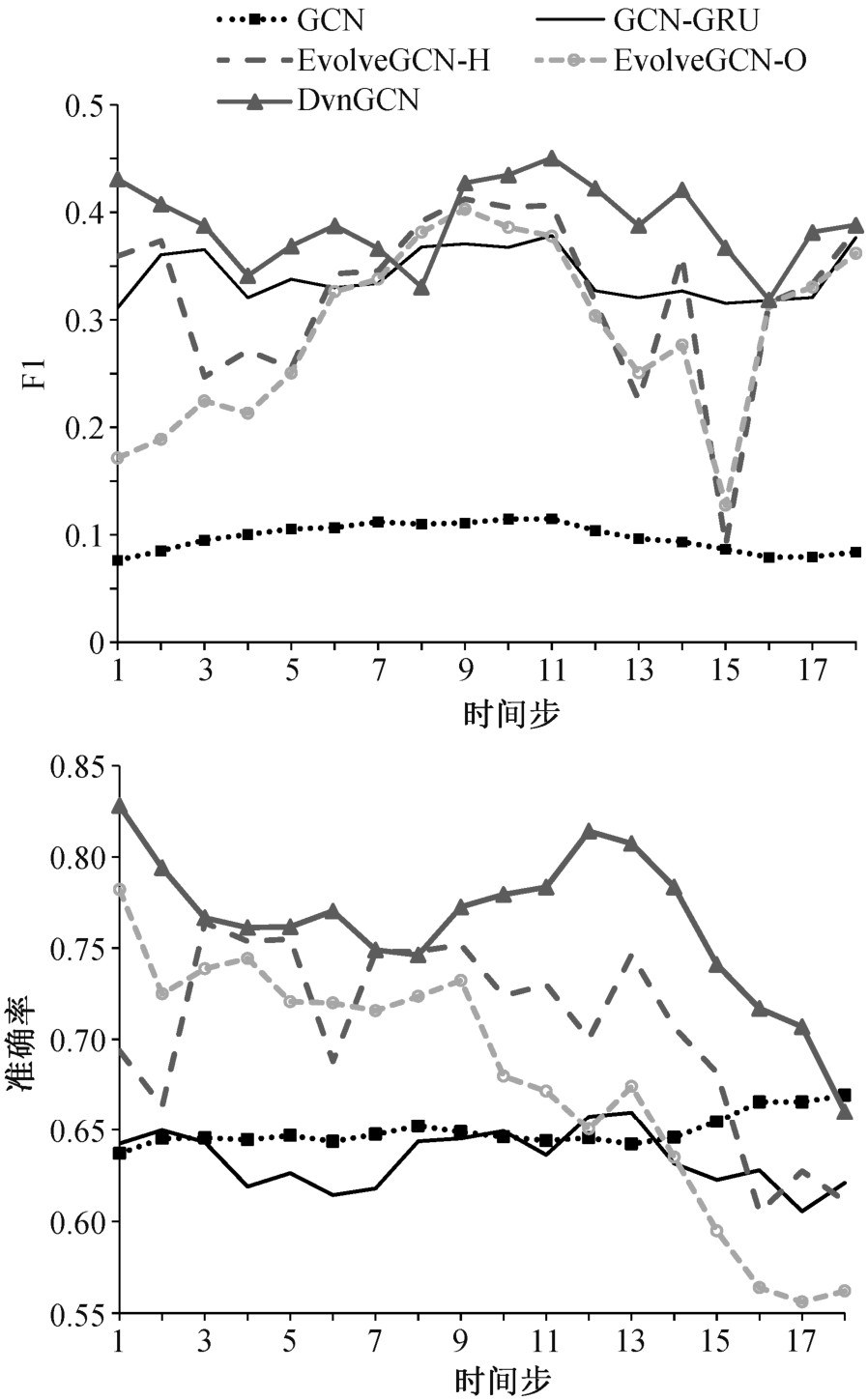
图4 F1 值和准确率随时间变化曲线
Fig. 4 F1 and accuracy score over time
4 总结
本文提出一种动态图的表示学习模型 DynGCN,通过时间卷积和空间卷积的交替进行以及自适应的模型更新机制, 聚合时间维度和空间维度的信息,可以学习到更有效的节点表示。进一步地, 在两个类别分类极其不均衡的动态金融网络中进行边分类任务, 结果表明DynGCN 模型优于所有对比模型。
本文对动态图表示学习的研究具有很强的现实意义, 也可为未来的研究方向提供多种可能性。后续工作中, 可以进一步提升模型的可扩展性, 将模型的图表示学习任务扩展到更广泛的领域, 如节点分类、链接预测和聚类等, 同时增加对其他领域数据集的学习和分析。
[1] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks [EB/OL]. (2017-02-22)[2020-05-20]. https://arxiv.org/abs/1609.02907
[2] Hamilton W, Ying Zhitao, Leskovec J. Inductive representation learning on large graphs // Guyon I,Luxburg U V, Bengio S, et al. Advances in Neural Information Processing Systems. Long Beach: Current Accociate, 2017: 1024-1034
[3] Cao Shaosheng, Lu Wei, Xu Qiongkai. GraRep: learning graph representations with global structural information // Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. New York, 2015: 891-900
[4] Ou Mingdong, Cui Peng, Pei Jian, et al. Asymmetric transitivity preserving graph embedding // Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, 2016: 1105-1114
[5] Mikolov T, Chen Kai, Corrado G, et al. Efficient estimation of word representations in vector space[EB/OL]. (2013-09-07)[2020-05-20]. https://arxiv.org/abs/1301.3781v3
[6] Perozzi B, Al-Rfou R, Skiena S. Deepwalk: online learning of social representations // Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York,2014: 701-710
[7] Grover A, Leskovec J. Node2vec: scalable feature learning for networks // Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, 2016: 855-864
[8] Bruna J, Zaremba W, Szlam W, et al. Spectral networks and locally connected networks on graphs[EB/OL]. (2013-12-21)[2020-05-20]. https://arxiv.org/abs/1312.6203
[9] Chen Jie, Ma Tengfei, Xiao Cao. FastGCN: fast learning with graph convolutional networks via importance sampling [EB/OL]. (2018-01-30)[2020-05-20].https://arxiv.org/abs/1801.10247
[10] Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering // Lee D D, Sugiyama M, Luxburg U V, et al. Advances in Neural Information Processing Systems. Barcelona, 2016: 3844-3852
[11] Hamilton W, Ying Zhitao, Leskovec J. Inductive representation learning on large graphs // Guyon I.Luxburg U V, Bengio S, et al. Advances in Neural Information Processing Systems. Long Beach, 2017:1024-1034
[12] Veličković P, Cucurull G, Casanova A, et al. Graph attention networks // International Conference on Learning Representations [EB/OL]. (2018-02-04) [2020-05-20]. https://arxiv.org/abs/1710.10903v1
[13] Li Jundong, Dani H, Hu Xia, et al. Attributed network embedding for learning in a dynamic environment //Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. New York,2017: 387-396
[14] Zhu Dingyuan, Cui Peng, Zhang Ziwei, et al. Highorder proximity preserved embedding for dynamic networks. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(11): 2134-2144
[15] Zhang Ziwei, Cui Peng, Pei Jian, et al. Timers: errorbounded SVD restart on dynamic networks [EB/OL].(2017-11-27)[2020-05-20]. https://arxiv.org/abs/1711.09541
[16] Du Lun, Wang Yun, Song Guojie, et al. Dynamic network embedding: an extended approach for skipgram based network embedding // Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm, 2018: 2086-2092
[17] Tang Jian, Qu Meng, Wang Mingzhe, et al. Line:large-scale information network embedding // Proceedings of the 24th International Conference on World Wide Web. Florence, 2015: 1067-1077
[18] Nguyen G H, Lee J B, Rossi R A, et al. Continuoustime dynamic network embeddings // Companion Proceedings of the Web Conference. Lyon, 2018: 969-976
[19] Goyal P, Kamra N, He Xinran, et al. Dyngem: deep embedding method for dynamic graphs [EB/OL].(2018-05-29)[2020-05-20]. https://arxiv.org/abs/1805.11273
[20] Wang Daixin, Cui Peng, Zhu Wenwu. Structural deep network embedding // Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, 2016: 1225-1234
[21] Goyal P, Chhetri S R, Canedo A. dyngraph2vec: capturing network dynamics using dynamic graph representation learning [EB/OL]. (2018-09-07)[2020-05-20]. https://arxiv.org/abs/1809.02657v2
[22] Trivedi R, Dai Hanjun, Wang Yichen, et al. Knowevolve: deep temporal reasoning for dynamic knowledge graphs // Proceedings of the 34th International Conference on Machine Learning. Sydney, 2017:3462-3471
[23] Trivedi R, Farajtabar M, Biswal P, et al. Representation learning over dynamic graphs [EB/OL]. (2018-03-11)[2020-05-20]. https://arxiv.org/abs/1803.04051v2
[24] Zhou Lekui, Yang Yang, Ren Xiang, et al. Dynamic network embedding by modeling triadic closure process // Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence. New Orleans, 2018:571-578
[25] Seo Y, Defferrard M, Vandergheynst P, et al. Structured sequence modeling with graph convolutional recurrent networks [EB/OL]. (2016-12-22)[2020-05-20]. https://arxiv.org/abs/1612.07659
[26] Manessi F, Rozza A, Manzo M. Dynamic graph convolutional networks. Pattern Recognition, 2020,97: 107000
[27] Lei Kai, Qin Meng, Bai Bo, et al. GCN-GAN: a nonlinear temporal link prediction model for weighted dynamic networks // IEEE Conference on Computer Communications. Paris, 2019: 18758423
[28] Xu Dongkuan, Cheng Wei, Luo Dongsheng, et al.Spatio-temporal attentive rnn for node classification in temporal attributed graphs // Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao, 2019: 3947-3953
[29] Pareja A, Domeniconi G, Chen Jie, et al. EvolveGCN:evolving graph convolutional networks for dynamic graphs [EB/OL]. (2019-11-18)[2020-05-20]. https://arxiv.org/abs/1902.10191v3
[30] Bai Shaojie, Kolter J Z, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling [EB/OL]. (2018-04-19)[2020-05-20]. https://arxiv.org/abs/1803.01271