量子计算技术给现有 RSA 和椭圆曲线公钥密码算法的安全性带来巨大的挑战。Shor[1]提出一种可快速破解大整数分解和离散对数问题的量子算法, Gidney 等[2]发现只需要 2000 万个量子比特即可在 8 小时内破解的 RSA2048 算法。为征集合适的替代性公钥密码算法标准, 美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)自 2016 年起开始征集具有后量子特性的公钥加密、密钥交换和数字签名方案。其中, 基于格上困难问题的方案具有计算速度较快[3]、密钥和密文较小[4]等优势, 受到广泛关注, 成为热门的后量子密码候选方案[5]。
Lyubashevsky 等[6]提出的环上错误学习(ring learning with errors, RLWE)问题是许多格密码算法的理论基础。RLWE 密码算法中的关键运算是多项式乘法运算, 可以采用基于蝶形运算的数论变换(number theoretic transform, NTT)快速实现[7-8]。NTT要求密码算法使用特定的模数, 以 NewHope 算法[9]为代表的密钥交换算法和以 BLISS 算法[10]为代表的数字签名算法均选择适用于 NTT 的参数, 以便提高运算速度。NTT 多项式乘法硬件的实现受到学术界的广泛关注, 其设计难点在于, 一方面 NTT 控制逻辑包含多层循环嵌套的原位运算结构, 存储器中的多项式系数存取调度复杂且带宽要求较高; 另一方面, 蝶形运算在 NTT 计算过程中执行次数多, 例如 512 维多项式每次 NTT 需要执行 2304 次蝶形运算, 而 1024 维多项式每次 NTT 需要执行 5120 次蝶形运算, NTT 中循环调用的蝶形运算模块包含模约减运算, 这是多项式乘法硬件实现的性能瓶颈, 进而影响密码算法的整体效率和运算时延。
在现有的硬件平台中, FPGA 具有开发周期较短且通用性较强的优势。它由诸多可编程的逻辑资源组成, 广泛地应用于密码算法的优化、实现和评估中[11]。本文提出一种 NTT 多项式乘法优化方法和硬件架构, 并对优化的硬件实现以及现有硬件实现进行评估, 为格密码硬件设计提供参考。
1 相关工作
Pöppelmann 等[12]在 FPGA 上的 BLISS 数字签名实现达到比 RSA 签名和 ECDSA 签名更大的吞吐量且占用面积更小。Bos 等[4]的研究表明, 使用 Newhope 密钥交换算法, 通过 TLS 提供 web 页面, 能够实现比 ECDHE 算法或 NTRU 算法更大的网络吞吐量。Newhope 密钥交换算法和 BLISS 数字签名能够高效实现的重要原因是均设定模数为 12289, 该模数支持基于 NTT 的多项式乘法, 可将多项式乘法的时间复杂度从 O(n2)降低到O(nlogn)。
尽管 NTT 大幅减少了多项式乘法的复杂度, 但NTT 多项式乘法需要预缩放和后缩放等运算步骤,造成一定的运算时延。此外, NTT 的原位运算实现需要较大的数据存取带宽, 一般的双端口 RAM 不能直接满足其数据存取需求。学者们提出针对多项式乘法中预缩放运算和数据存取的优化技术。Roy等[13]通过整合 NTT 正变换和预缩放运算来减少模乘运算次数, 还提出一种高位宽的数据存储结构,该方案虽然提高了存储器的吞吐量, 但需要消耗额外的时钟周期进行数据重排。Oder 等[14]首次在FPGA 上完整地实现 NewHope 密钥交换算法, 但其模约减模块中包含延时较大的关键路径, 并且数据存取带宽不足, 需占用额外的时钟周期等待数据流。然而, 等待期间运算单元处于空闲状态, 因此电路效率并不高。
由于多项式系数在商环中运算, NTT 中蝶形运算采用的模约减算法是多项式乘法优化的一个重点。模约减算法与除法运算密切相关。Poppelmann[15]提出一种基于长除法的基本模约减(Generic)算法, 并采用高层次综合的方法, 在 FPGA 上实现该算法的流水线模块。基本模约减算法采用“比较器-减法器”逻辑链的结构, 且逻辑链的长度与模数正相关, 因此基本模约减算法往往需要较长的逻辑链。由于 Poppelmann[15]提出的电路面积消耗较大,且该电路的性能优化过程中需要插入的流水线级数较多, 因此整个硬件模块效率不高。Barrett 约减[16]是一种基于商估计的算法, 在蝶形运算中有较多的应用实例。2015 年, Liu 等[17]提出 SAMS2 模约减,该方法是一种以移位、加法、乘法和两次减法组成的模约减算法优化实现, 适合在资源受限的微控制器上实现。Poppelmann[15]实现了完全采用移位和加减法代替乘法的 FPGA 硬件实现, 该实现的电路面积比基本模约减算法显著减小, 但电路最大工作频率相对较低。Xing 等[18]在 FPGA 上实现一种对加法树器优化的 Barrett 约减方案, 能够同时输出商和剩余, 但由于乘数的汉明重量较大, 需构建较复杂的加法器树。Banerjee 等[19]提出一种模数可控制的模算术电路, 并给出其 ASIC 实现。由于 Barrett 约减原理的限制, 其硬件实现需要比较器-减法器电路, 用以解决商估计值存在的误差。Montgomery约减、模乘和模幂算法[20]一直广泛应用于密码优化实现和实现领域, 但经典的 Montgomery 约减实现中也需要比较器-减法器电路, 以便得到最终结果。Alkim 等[9]提出一种适用于蝶形运算的不完全模约减(incomplete reduction)算法(ADPS 算法)。不完全模约减是将输入约减到某个宽松的数值范围,而不要求约减结果为非负最小剩余。ADPS 算法对加法结果采用不完全 Barrett 约减, 对乘法结果采用不完全 Montgomery 约减。当模数取 12289 时, ADPS算法通过选取合适的寄存器宽度和运算参数, 可恰好使乘法结果约减到 14 比特以内的无符号整数, 免去 Barrett 约减和 Montgomery 约减的判断及减法操作。与传统 Barrett 或 Montgomery 相比, 不完全约减能够节省比较器和减法器资源, 因此非常适合软、硬件实现。Jati 等[21]在 FPGA 平台上实现 ADPS算法, 由于纯组合电路的实现路径延时较大, 该实现通过插入 3 级流水线来提高电路的最大工作频率。
Longa 等[22]提出一种适用于模数 q=k·2p+1 的模约减算法(LN 模约减), 并应用于 NTT 多项式乘法中。LN 模约减也是一种不完全约减算法, 包括用于加法结果约减的 K-RED 算法以及用于乘法结果约减的 K-RED2x 算法, 且运算过程中采用有符号整数表示参数, 实验结果表明基于 LN 模约减的NTT 比基于 ADPS 算法的 NTT 软件实现速度提高86%以上。Kuo 等[23]提出的 LN 模约减算法同样适用于硬件实现, 为适配 FPGA 片上的数字信号处理器单元(DSP)并避免寄存器中数值溢出, 他们将原方案中参数的有符号数表示调整为无符号数表, 由此实现一种适用于 FPGA 的流水线电路结构, 并达到较高的电路性能。但是, 该实现中使用的加法器数量较多。
综上所述, 设计 NTT 中高带宽的多项式系数存取方案以及蝶形运算中模约减的高效实现方法, 仍是多项式乘法硬件实现中困难的问题。本文提出一种基于 LN 模约减的 NTT 多项式乘法硬件实现优化方法, 并提供不同层级的流水线优化实现。
2 多项式乘法的高效算法
整数环用 Z 表示, Zq 为模整数 q 的商环, R=Z[ X ]/ ( X n+ 1)是模多项式 Xn+1 的整系数多项式环,其中 n 为多项式维度即多项式系数的个数, Rq=Zq[X]/(Xn+1)表示系数模 q 的整系数多项式环。对于 n 维 多项式 a= (a 0 , …, an -1), b= ( b0 , … , bn -1)∈Rq,其中 a0 , …, an -1 ,b0 , …, bn -1∈Zq 表示多项式系数, 多项式乘法运算 ab 是一种卷积形式的运算, 如果直接计算, 则 Rq 上的多项式乘法需要 n2 次模乘运算[7]。本节主要介绍整系数模 q 运算采用的高效模约减算法, 以及采用 NTT 计算 Rq 上的多项式乘法。
2.1 高效模约减算法
LN 模约减适用于形如 q = k· 2 p+ 1的模数, 其中 k 为奇数, 且2p ＞ k。对于 a, b∈ Zq, 以求乘积 x=a · b对模数 q 的模运算为例, 其思路是利用 k· 2p≡-1 modq的特性, 把 xmodq 的计算转化为 x· kmodq,再消去乘 k 的影响。特别地, q 取 12289 时, k 取 3, p取 12。LN 模约减包含 K-RED 和 K-RED2x 两种算法形式, K-RED 算法将 x 表示为 x = x0 + 2 p x1, 从而得到算法 1。
算法 1 和算法 2 的输出 r 均为有符号数, Kuo 等[23]采用 LN 模约减, 并对 r 加一个模数 q 的整数倍, 确保约减最终结果非负。其加法结果的约减采用KRED 算法, 乘法结果的约减采用 K-RED-2x 算法,约减过程引入的 k 和 k2 均可以通过预计算等方式消除。
2.2 NTT 多项式乘法
NTT 的原理是将标准域的多项式乘法运算转换为 NTT 域上多项式系数对位点乘运算。对于一个满足维度 n 为 2 的正整数次幂且模数 q ≡ 1mod2n的多项式 a, NTT 正变换如算法 3 所示, 其中 ωn 是Zq中的本原n 阶单位根, φ 是 ω n模 q 的平方根。
由于多项式 a 的系数均由随机采样获得, 可认为采样结果是倒位序的, 从而将算法 3 的第 1 行省去[23]。算法 3 的第 10～14 行即蝶形运算, 处于 NTT变换的最内层循环, 在串行实现的 NTT 变换中, 蝶形运算作为一个算术逻辑单元被循环调用。由于每次 K-RED 算法将结果缩放 k 倍, K-RED2x 算法将结果缩放 k2 倍, 若将算法 3 中每个 ωn 在预计算时均乘以 k-1, 则最终得到的～a 相当于每个多项式系数都乘以缩放系数 klogn。NTT 逆变换与算法 3 类似, 区别在于其中预计算的φ 幂替换为 φ-1幂, 且最后需要给各系数乘以缩放因子 n-1。
在采用 NTT 计算多项式乘法时, 首先采用基于蝶形运算的 NTT 正变换, 将标准域下的多项式转化为 NTT 域下的多项式, 两个 NTT 域多项式将系数对位点乘, 点乘结果再通过 NTT 逆变换转换到标准域, 如算法 4 所示。
算法 4 中, 除正反 NTT 变换和系数对位点乘运算外, 还包括正 NTT 变换前乘 φ i的预缩放(第 2～3行)和逆 NTT 变换后乘 φ- i的后缩放(第 12 行), 其中算法 4 的后缩放已经与乘 n-1运算合并。此外, 为消除 LN 模约减引入的系数 k 幂, 需要在运算中引入相应的逆系数。
3 面向硬件实现的优化
尽管现有模约减和多项式乘法已有较高效的算法, 但其硬件实现技术还不成熟。本节以 NewHope密钥交换算法和 BLISS 数字签名算法中通用的 Rq(q=12289) 为例, 介绍多项式乘法算法的硬件优化方法。
3.1 基于LN 模约减的蝶形运算硬件优化
LN 模约减包含由层级的加法器级联形成的加法树结构, Kuo 等[23]的硬件实现广泛采用二输入加法器构建加法树结构。在主流 FPGA 架构中, 六输入查找表(LUT)结构可以高效地例化为三输入加法器, 其占用的逻辑资源量与二输入加法器相同[24],因此三输入加法器的路径延时与普通加法器的差异很小而集约程度更高。
基于优化 LN 模约减的蝶形运算结构如图 1 所示。优化的思路是尽可能采用三输入加法器构建硬件模块, 有助于节省 LUT 逻辑资源。图 1 中的 KRED 算法使用一个三输入加法器, K-RED2x 算法模块使用两个三输入加法器, 整个蝶形运算模块共使用 5 个三输入加法器。Kuo 等[23]中提出的硬件结构使用 10 个加法器, 而本文采用三输入加法器合并加减法逻辑, 可节省 50%的加法器数量。
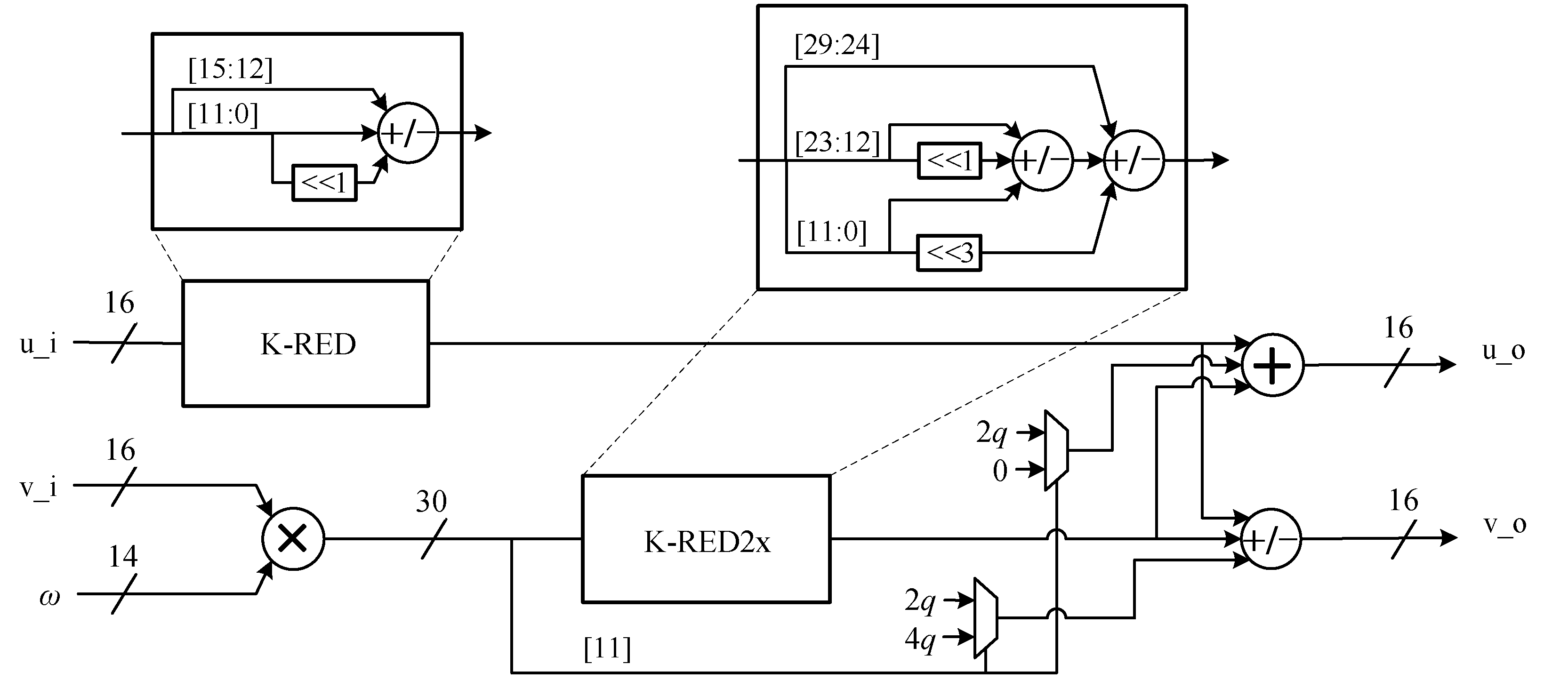
图1 基于优化LN 模约减的蝶形运算结构
Fig. 1 Butterfly operation structure based on optimized LN modular reduction
3.2 多项式乘法的硬件优化
根据 Poppelmann [15]提出的方法, 算法 4 中第2～3 行的预缩放运算可以整合在正 NTT 变换中。该优化只需要调整每次蝶形运算中 ω 的取值, 即将NTT 算法 3 中第 8 行改为 ω= ROM[ m+ i]。采用该优化得到的 NTT 正变换结果与带有预缩放的普通NTT 运算结果一致, 可减少算法 4 中 10.5%的模乘运算, 得到算法 5。
与算法 4 相比, 算法 5 的另一个优势是节省预计算参数对存储的占用, 算法 4 需要 3n 个预计算参数, 而算法 5 需要 2.5n 个预计算参数, 可以减少16.7%的只读存储器空间占用。算法 5 将 LN 模约减引入的系数 k 幂在后缩放阶段(第 8 行)消除。
算法 3 中, 由于每次蝶形运算需要获取两个多项式系数并写入两个多项式系数, 但每个双端口存储器每个时钟周期仅能读或写两个地址的数据, 因此蝶形运算的直接原位运算实现需要额外的时钟周期执行数据读写, 造成数据驻留[14]。为提高存储器的吞吐, 本文采用乒乓结构的存储器存取方式, 即例化两个相同大小的存储器 RAM0 和 RAM1, 多项式系数的初始值存储在 RAM0 中, 当算法 3 中 log t为奇数时, 蝶形运算模块从 RAM0 读取多项式系数,RAM1 写入蝶形运算得到的新系数结果; 当 log t 为偶数时, 蝶形运算模块从 RAM1 读取多项式系数,RAM0 写入蝶形运算得到的新系数结果。对于 log n为偶数的情况, NTT 的最终结果将存储在 RAM0 中。
4 基于 FPGA 的多项式乘法运算实现
4.1 基于 LN 模约减的蝶形运流水线设计
在 FPGA 平台上, 由于多项式数据量较大, 其系数存储一般采用块 RAM (block RAM, BRAM)实现, 而较高位宽的乘法运算一般采用 DSP 实现。BRAM 和 DSP 都有丰富的逻辑资源, 可采用流水线技术达到高工作频率。
基于优化 LN 模约减的蝶形运算流水线实现如图 2 所示。灰色的流水线层级作为基本流水线, 能确保一般时钟频率要求, 白色的流水线层级间仅有一层算术逻辑, 可供更高性能要求的实现选择插入。硬件实现方面采用以下 3 个方面的设计优化。
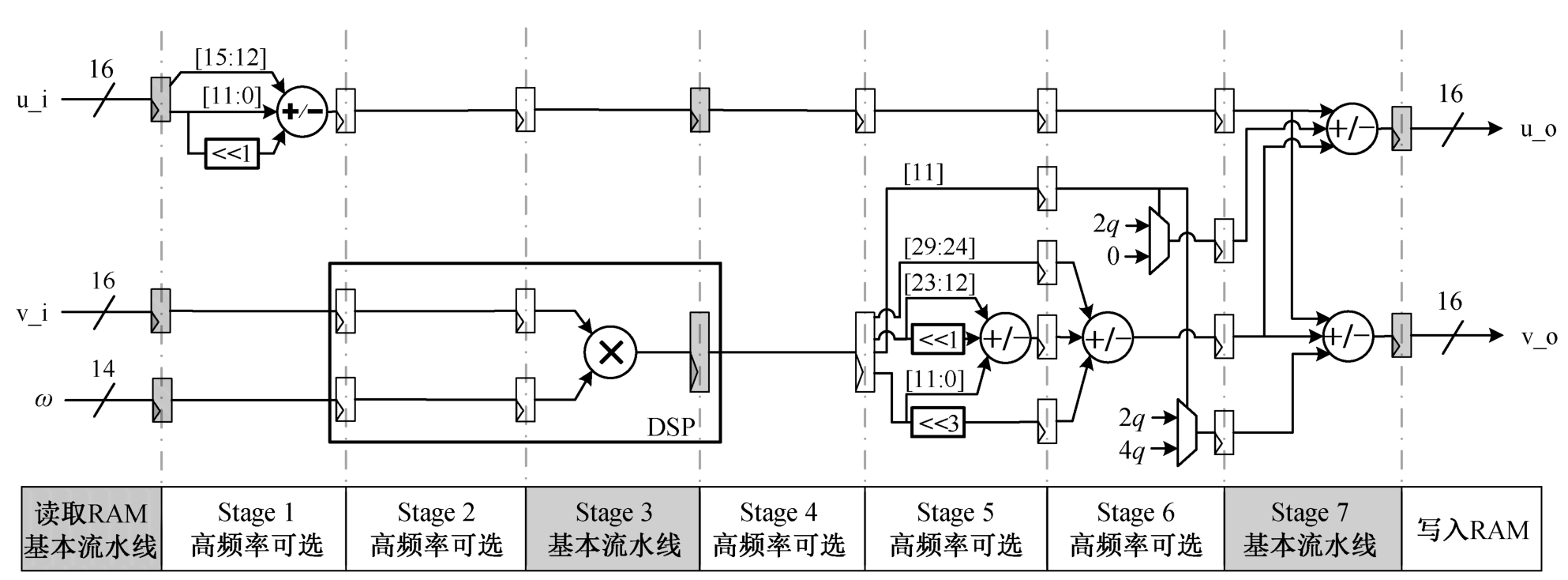
图2 基于优化LN 模约减的蝶形运算流水线实现
Fig. 2 Pipeline implementation of butterfly operation based on optimized LN modular reduction
1) 可选的流水线层级。由于图 1 所示的组合逻辑层级较多, 其组合逻辑产生的路径延时较大。为改善路径延时, 我们在 u_o 和 v_o 对应的路径插入相同级数的流水线, 确保结果在同一时钟周期输出。流水线层级可通过条件编译选择, 从而调整电路所需的面积和最大工作频率。
2) 充分利用移位寄存器资源。在 FPGA 中, 部分 LUT 资源可以作为移位寄存器使用, 从而节省FPGA 的触发器(FF)资源。调用移位寄存器时, 要求流水线层级间不存在组合逻辑, 例如图 2 中减法器输出至 u_o 路径不是关键路径, 其作为时延插入的流水线结构可采用移位寄存器实现。
3) 充分利用 DSP 单元资源。蝶形运算中的乘法运算需要占用一个 DSP 单元, 除乘法器资源外,我们的流水线实现还使用 DSP 单元的 3 层流水线寄存器资源, 有利于减少 DSP 外部 FF 的占用。
4.2 系统总体结构设计
如图 3 所示, 多项式乘法处理器的硬件结构主要包含控制模块、蝶形运算模块和存储模块。控制模块负责控制蝶形运算模块的运算逻辑以及存储模块的读写地址、写使能以及乒乓转换; 蝶形运算模块可以实现蝶形运算以及模乘运算; 存储模块包括RAM 和 ROM, RAM 存储多项式系数及其运算中间值, ROM 存储多项式乘法运算过程中的预计算参数, 执行正 NTT 变换时, 从 ROM 读取 k -1φ i 区域对应参数, 执行逆 NTT 变换时, 从 ROM 读取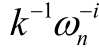
区域对应参数, 执行后缩放运算时, 从 ROM 读取φ- i k -(4+2log n) n-1 区域对应参数。
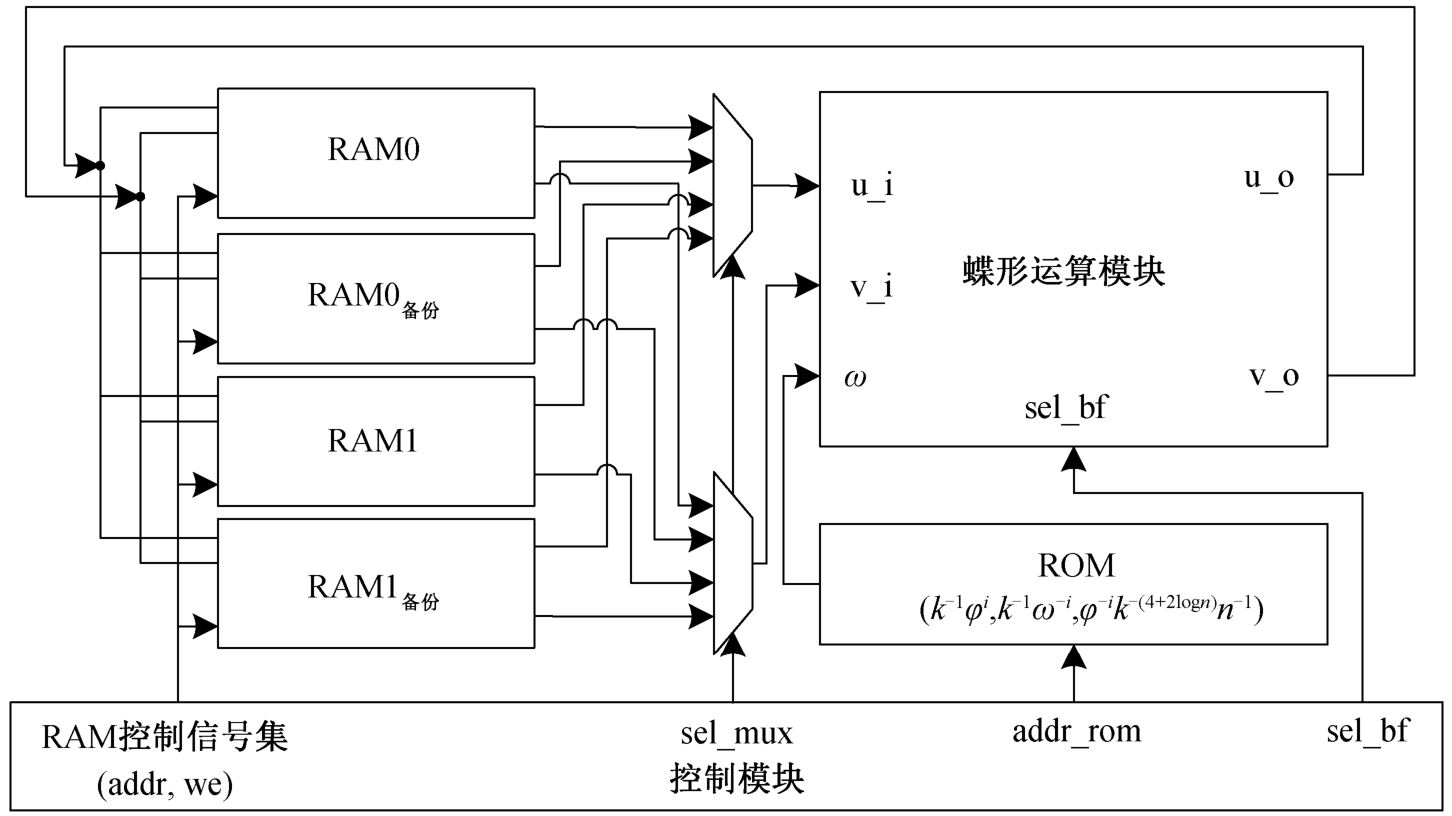
图3 多项式乘法处理器总体架构
Fig. 3 Overall architecture of polynomial multiplication processor
对于流水线层级为 ε 的蝶形运算模块, 数据输出和读入之间有 ε 个时钟周期的延时。因此, 当一个存储器由读向写方向改变时, 另一个存储器还未完成写操作, 即在读写方向改变时会造成 ε 个时钟周期的流水线数据驻留。本文采用备份 RAM 作为缓冲区, 确保数据存取时数据通路始终保持全流水。备份 RAM 的原理是, 当原 RAM 写入没有完成时, 控制模块选通备份 RAM 读出多项式系数, 确保这部分数据与原 RAM 对应地址的数据相同。例如, 起始时 ROM0 为读出方向, ROM1 和 RAM1 备份同时写入; ROM0 读出完成时, 控制模块选通RAM1 备份读出多项式系数, RAM1 继续完成 ε 个时钟周期的写入操作; RAM1 写入完成后, 控制模块选通 RAM1 读出多项式系数, ROM0 和 RAM0 备份同时写入。由于 ε 数值较小, 当兵乓方向转换时, 从RAM0 备份读出的数据与 ROM0 相同, 且整个运算过程不会产生读写地址冲突, 可以确保运算结果的正确性。
5 实验结果与评估
为比较采用不同模约减算法的蝶形运算模块的面积和性能, 我们将本文提出的硬件实现优化方法与现有实现方法进行对比评估。实验参数采用通用的模数 q=12289, 多项式维度 n=1024。测试平台采用 Xilinx 公司的 XC7A200T 型号 FPGA。
5.1 蝶形运算硬件评估
分别给出基于优化 LN 模约减的蝶形运算模块及其他现有蝶形运算模块在低面积、均衡型以及高速率 3 种频率设计要求下的实现数据, 以便充分地比较各方案在不同时序要求下的性能。低面积表示占用逻辑资源较少, 以 3 级流水线实现; 均衡型表示兼顾资源占用量与运算速度, 以 5 级流水线实现;高速率表示工作频率高, 以 8 级以上流水线实现。评估结果如表 1 所示, Montgomery, Barrett 和 Generic算法所在的行表示该硬件实现的蝶形运算模块中采用对应的模约减算法。FPGA 中的资源类型较多,本文只列举占用基本逻辑资源(Slice)及其中 LUT 和FF 资源的数量。表中所有硬件实现均占用 1 个 DSP单元。
Kuo 等[23]仅提供一种流水线设计, 我们将基于优化LN 模约减的均衡型实现与他们的方案进行对比。结果表明, 由于三输入加法器的引入, 本文的优化共减少 12.7%的 Slice, 并减少 32.2%的 LUT 资源占用。
基于优化 LN 模约减的低面积实现需要的硬件资源最少, 与基于优化 LN 模约减的均衡型实现相比, 进一步节省 27.1%。基于优化 LN 模约减的高性能实现能达到最高的工作频率, 且比基于 ADPS 模约减的高性能实现节省 21.3%的硬件资源。
在完全约减的实现方案中, 基于 Montgomery算法的蝶形运算模块资源占用较少, 且工作效率较高, 也能够满足 250 MHz 以上的工作频率要求, 与Barrett 算法和 Generic 算法相比, 优势较为明显。Poppelmann 等[15]给出的基于高层次综合的实现方法虽然能够实现相对较高的工作频率, 但占用的逻辑资源较多。相较而言, 基于不完全约减的蝶形运算实现在面积和性能上均优于完全约减的蝶形运算, 基于优化 LN 模约减的蝶形运算实现综合效果最优。
5.2 多项式乘法运算硬件评估
采用表 1 中基于优化 LN 模约减的蝶形运算模块高性能实现完成算法 5 的硬件实现, 共占用151 个 Slice。本文多项式乘法硬件实现与现有硬件实现的比较结果如表 2 所示, 其中 AT 积(area time product)表示电路面积与运算时延的乘积, AT 积越小表示电路效率越高。为便于比较, 表 2 中所有硬件实现的 AT 积均做归一化处理。
表1 蝶形运算硬件实现评估
Table 1 Evaluation of butterfly operations on hardware
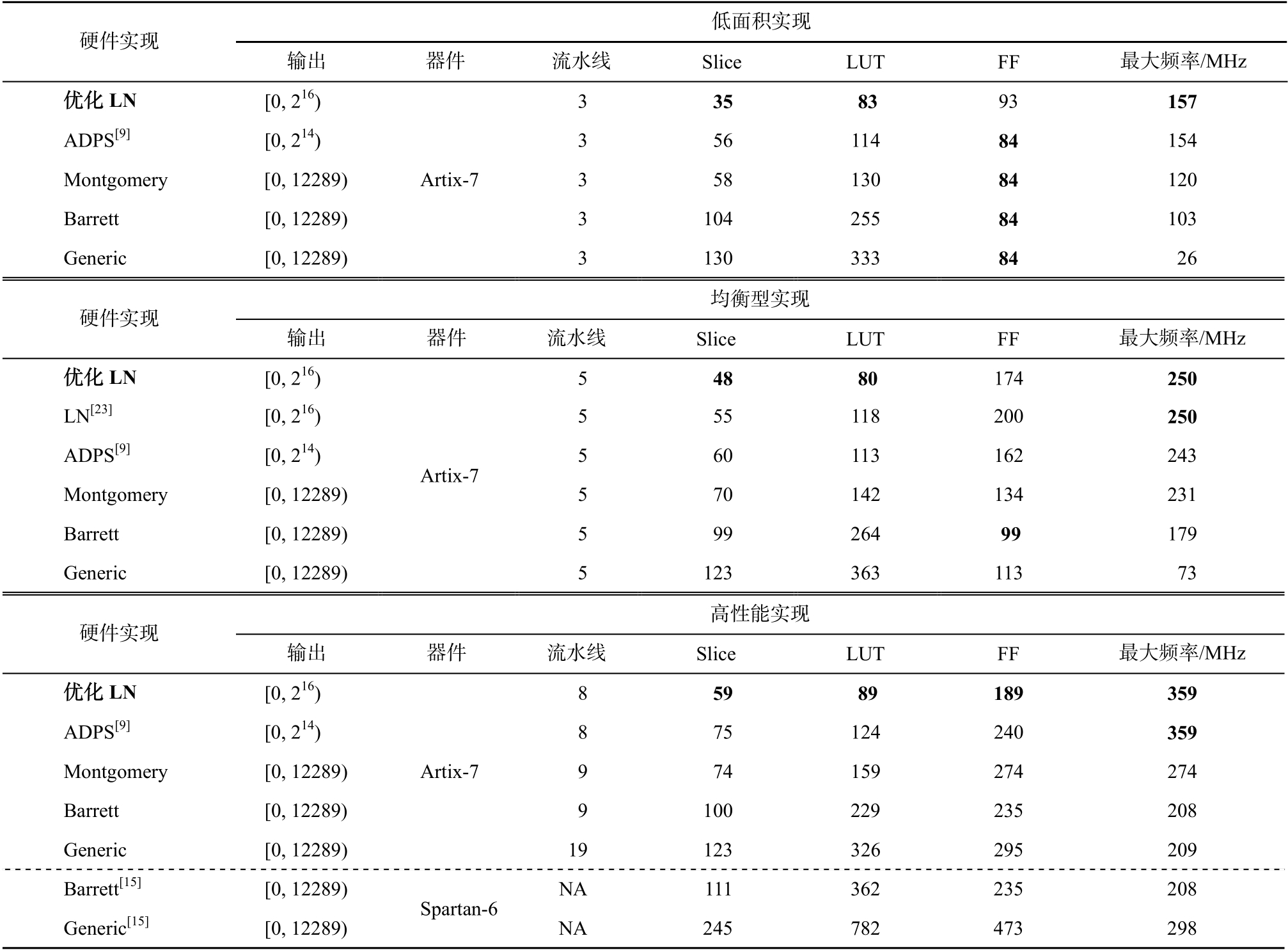
说明: 粗体标记表示最优结果, 下同。
硬件实现低面积实现images/BZ_11_1189_512_1190_514.png输出 器件 流水线 Slice LUT FF 最大频率/MHz优化LN [0, 216)3 35 83 93 157 ADPS[9] [0, 214) 3 56 114 84 154 Montgomery [0, 12289) 3 58 130 84 120 Barrett [0, 12289) 3 104 255 84 103 Generic [0, 12289) 3 130 333 84 26硬件实现 均衡型实现件 流水线 Slice LUT FF 最大频率/MHz 5 48 80 174 250 5 55 118 200 250 5 60 113 162 243 tix-75 70 142 134 231 5 99 264 99 179 5 123 363 113 73高性能实现件 流水线 Slice LUT FF 最大频率/MHz 8 59 89 189 359 8 75 124 240 359 tix-79 74 159 274 274 Artix-7输出 器优化LN [0, 216)LN[23] [0, 216)ADPS[9] [0, 214)Montgomery [0, 12289)Barrett [0, 12289)Generic [0, 12289)Ar硬件实现输出 器优化LN [0, 216)ADPS[9] [0, 214)Montgomery [0, 12289)Barrett [0, 12289) 9 100 229 235 208 Generic [0, 12289) 19 123 326 295 209 Barrett[15] [0, 12289)Spartan-6 Ar NA 111 362 235 208 Generic[15] [0, 12289) NA 245 782 473 298
可以看出, 相比其他多项式乘法硬件实现, 本文硬件实现的工作频率最高, 可达 300 MHz 以上,主要得益于合理的流水线设计。多项式乘法模块的硬件实现要根据设计的目标工作频率确定蝶形运算模块的流水线级数。对于工作频率要求较低的硬件实现, 蝶形运算模块的模约减运算一般为关键路径,可选择适当的流水线级数, 达到目标工作频率; 对于工作频率要求较高的硬件实现, 蝶形运算可以采用流水线技术进一步优化, 但 NTT 控制逻辑的循环嵌套会产生较复杂的选通电路, 且其插入流水线的成本很高, 因此控制逻辑更容易成为关键路径。
本文硬件实现的电路面积同样具有优势, 其特点是具有均衡的 LUT 和 FF 数量, 并且充分利用DSP 和 BRAM 中的逻辑资源, 因此即使插入更多级数的流水线, 电路面积并没有大幅增加。Xing等[23]、Kuo 等[18]和 Neng 等[25]通过例化 2～4 个并行的蝶形运算模块, 实现更低的运算时延, 相应的代价是电路面积明显大于本文硬件实现。Kuo 等[23]采用了基于 LN 模约减的蝶形运算, 且 4 个并行的蝶形运算模块有效地提高了运算速度, 但该实现没有消除预缩放运算, 也需要更多 BRAM 存储预计算的参数值, 且工作频率不高, 因此各硬件资源的效率不高。Xing 等[18]提出的 4 路蝶形运算模块并行实现的运算时延最小, 且该硬件实现不占用 BRAM, 但其蝶形运算模块采用优化的 Barrett 约减导致整体工作频率不高, 且该硬件实现同样未消除预缩放运算, 因此 LUT, FF 与 DSP 的效率均明显低于本文的硬件实现。文献[25]中 FF 的效率更高, 但考虑到现有 FPGA 器件每个 Slice 结构中 FF 与 LUT 的数量比值一般为 2, 而文献[25]中 LUT 和 FF 的利用很不均衡, 最终 Slice 的占用会受数量较多的 LUT 影响, 因此其基本逻辑资源的 AT 积约为本文硬件实现的1.3 倍, DSP 和BRAM 的 AT 积效率与本文硬件实现接近。Oder 等[14]实现了较少的逻辑资源占用, 但其单次多项式系数读取和模约减运算均需要大于 1 个时钟周期, 造成流水线数据驻留, 因此其各类硬件资源的效率不高。文献[21]的多项式乘法运算采用Alkim 等[9]的模约减方法, 比本文硬件实现效率较低。表 2 中 Fritzmann 等[26]的时延未计入系数对位乘法步骤, 其工作频率按照等同于本文硬件实现的工作频率计算, 该硬件实现可作为 RISC-V 处理器的密码协处理器, 尽管比软件实现具有更高的性能,但需要额外的软硬件通信开销, 因此与纯硬件实现相比, 在效率上不占优势。
表2 多项式乘法运算硬件实现评估
Table 2 Evaluation of polynomial multiplication module on hardware
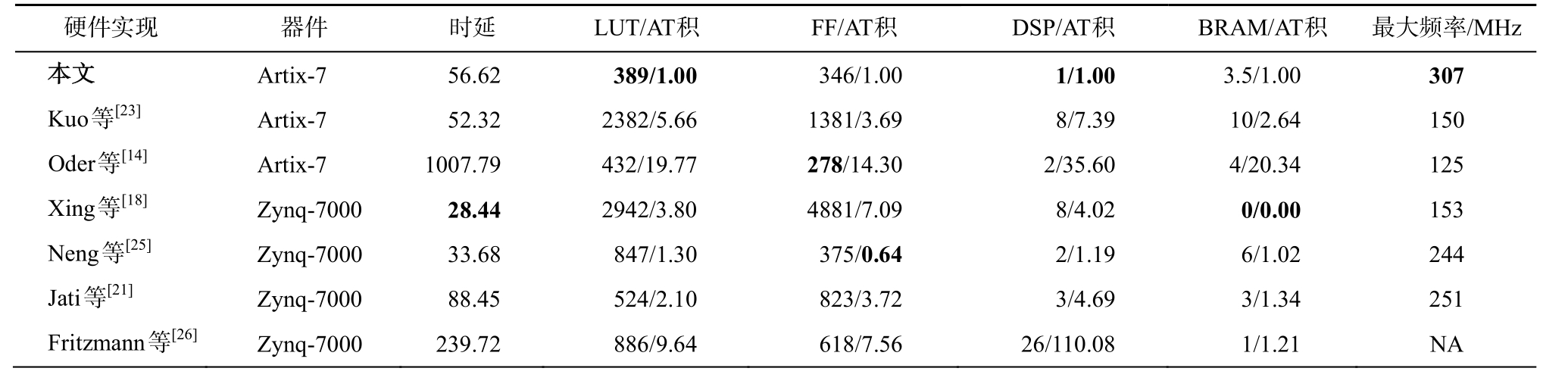
硬件实现 器件 时延 LUT/AT 积 FF/AT 积本文 Artix-7 56.62 389/1.00 346/1.00 Kuo 等[23] Artix-7 52.32 2382/5.66 1381/3.69 Oder 等[14] Artix-7 1007.79 432/19.77 278/14.30 Xing 等[18] Zynq-7000 28.44 2942/3.80 4881/7.09 Neng 等[25] Zynq-7000 33.68 847/1.30 375/0.64 Jati 等[21] Zynq-7000 88.45 524/2.10 823/3.72 Fritzmann 等[26] Zynq-7000 239.72 886/9.64 618/7.56 DSP/AT 积 BRAM/AT 积 最大频率/MHz 1/1.00 3.5/1.00 307 8/7.39 10/2.64 150 2/35.60 4/20.34 125 8/4.02 0/0.00 153 2/1.19 6/1.02 244 3/4.69 3/1.34 251 26/110.08 1/1.21 NA
总体而言, 本文提出的多项式乘法硬件实现技术至少能够提高 22.3%的工作频率, 并提高 FPGA逻辑资源 22.8%的效率。根据 Xing 等[18]的实现结果, 在免去顺序倒置操作的情况下, 多项式乘法运算约占 NewHope 算法全部密码运算时延的 80%, 本研究对多项式乘法运算的频率提升大约能够减少New-Hope 算法 15%的密码运算时延。
6 总结
本文提出一种格密码中多项式乘法的硬件实现优化方法, 能够使用更小的电路面积实现更高的工作频率, 对基于格的后量子密码实现具有一定的参考价值。本文给出的蝶形运算模块流水线实现能够满足不同的时序要求, 包括低面积、均衡型和高性能实现。其中, 低面积实现可以达到 150 MHz 以上的频率要求, 且占用电路资源少; 均衡型实现提供较好的性能与电路面积权衡, 能够满足 250 MHz 以上的中高频率要求; 高性能实现能够提供 350 MHz 以上的高频率要求。实验结果表明, 与现有的硬件实现方法相比, 多项式乘法硬件优化技术能够得到 22.8%的效率提升。
[1] Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Journal on Computing, 1997, 26(5):1484-1509
[2] Gidney C, Ekera M. How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits[EB/OL]. (2019-05-23) [2020-02-21]. https://arxiv.org/abs/1905.09749
[3] Nejatollahi H, Dutt N, Ray S, et al. Post-quantum lattice-based cryptography implementations: a survey.ACM Computing Surveys, 2019, 51(6): 1-41
[4] Bos J, Costello C, Ducas L, et al. Frodo: take off the ring! practical, quantum-secure key exchange from LWE // Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security.New York: ACM, 2016: 1006-1018
[5] 张平原, 蒋瀚, 蔡杰, 等. 格密码技术近期研究进展. 计算机研究与发展, 2017, 54(10): 2121-2129
[6] Lyubashevsky V, Peikert C, Regev O. On ideal lattices and learning with errors over ring // Annual International Conference on the Theory and Applications of Cryptographic Techniques. French Riviera,2010: 1-23
[7] Pöppelmann T, Güneysu T. Towards efficient arithmetic for lattice-based cryptography on reconfigurable hardware // Proceedings of LATINCRYPT’12.Berlin Heidelberg: Springer, 2012: 139-158
[8] 芮康康, 王成华, 范赛龙, 等. 一种高性能 R-LWE格加密算法的电路结构及其 FPGA 实现. 数据采集与处理, 2019, 34(4): 689-696
[9] Alkim E, Ducas L, Pöppelmann T, et al. Post-quantum key exchange — a new hope // Proceedings of the 25th USENIX Security’16. Austin: USENIX Association,2016: 327-343
[10] Ducas L, Durmus A, Lepoint T, et al. Lattice signatures and bimodal Gaussians // Proceedings of CRYPTO’13. Berlin: Springer, 2013: 40-56
[11] Basu K, Soni D, Nabeel M, et al. NIST post-quantum cryptography — a hardware evaluation study [EB/OL].(2019-01-17) [2020-03-15]. https://eprint.iacr.org/20 19/047.pdf
[12] Pöppelmann T, Ducas L, Güneysu T. Enhanced lattice-based signatures on reconfigurable hardware //Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin Heidelberg: Springer, 2014: 353-370
[13] Roy S S, Vercauteren F, Mentens N, et al. Compact ring-LWE cryptoprocessor // Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin Heidelberg: Springer,2014: 371-391
[14] Oder T, Guneysu T. Implementing the NewHope —simple key exchange on low-cost FPGAs // Lecture Notes in Computer Science. Cham: Springer, 2017:128-142
[15] Poppelmann T. Efficient implementation of ideal lattice-based cryptography [D]. Bochum: Ruhr-University Bochum, 2017
[16] Barrett P. Implementing the Rivest Shamir and Adleman public key encryption algorithm on a standard digital signal processor // Proceedings of CRYPTO’86.Berlin: Springer, 1987: 311-323
[17] Liu Z, Seo H, Roy S S, et al. Efficient ring-LWE encryption on 8-bit avr processors // Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin Heidelberg: Springer,2015: 663-682
[18] Xing Y, Li S. An efficient implementation of the NewHope key exchange on FPGAs. IEEE Transactions on Circuits and Systems I: Regular Papers,2020, 67(3): 866-878
[19] Banerjee U, Ukyab T S, Chandrakasan A P. Sapphire:a configurable crypto-processor for post-quantum lattice-based protocols. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019,2019(4): 17-61
[20] Montgomery P L. Modular multiplication without trial division. Mathematics of Computation, 1985, 44:519-521
[21] Jati A, Gupta N, Chattopadhyay A, et al. SPQCop:side-channel protected post-quantum cryptoprocessor[EB/OL]. (2019-06-30) [2020-02-21]. https://eprint.iacr.org/2019/765.pdf.
[22] Longa P, Naehrig M. Speeding up the number theoretic transform for faster ideal lattice-based cryptography // Proceedings of International Conference on Cryptology and Network Security. Berlin: Springer, 2016: 124-139
[23] Kuo P C, Li W D, Chen Y W, et al. High performance post-quantum key exchange on FPGAs [EB/OL].(2017-06-12) [2020-02-21]. https://eprint.iacr.org/2017/690.pdf
[24] Xilinx. UG949 — UltraFast design methodology guide for the vivado design suite (v2019.1) [EB/OL].(2019-06-26) [2020-02-21]. https://www.xilinx.com/support/documentation/sw_manuals/xilinx2019_1/ug9 49-vivado-design-methodology.pdf
[25] Neng Z, Bohan Y, Chen C, et al. Highly efficient architecture of NewHope-NIST on FPGA using lowcomplexity NTT/INTT. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020(2): 49-72
[26] Fritzmann T, Sharif U, Mullergritschneder D, et al.Towards reliable and secure post-quantum coprocessors based on RISC-V // Design, Automation,and Test in Europe. Piscataway, 2019: 1148-1153